Insight-HXMT Study of the Inner Accretion Disk in the Black Hole Candidate EXO 1846–031
Abstract
We study the spectral evolution of the black hole candidate EXO 1846031 during its 2019 outburst, in the 1–150 keV band, with the Hard X-ray Modulation Telescope. The continuum spectrum is well modelled with an absorbed disk-blackbody plus cutoff power-law, in the hard, intermediate and soft states. In addition, we detect an 6.6 keV Fe emission line in the hard intermediate state. Throughout the soft intermediate and soft states, the fitted inner disk radius remains almost constant; we suggest that it has settled at the innermost stable circular orbit (ISCO). However, in the hard and hard intermediate states, the apparent inner radius was unphysically small (smaller than ISCO), even after accounting for the Compton scattering of some of the disk photons by the corona in the fit. We argue that this is the result of a high hardening factor, , in the early phases of outburst evolution, well above the canonical value of 1.7 suitable to a steady disk. We suggest that the inner disk radius was close to ISCO already in the low/hard state. Furthermore, we propose that this high value of hardening factor in the relatively hard state is probably caused by the additional illuminating of the coronal irradiation onto the disk. Additionally, we estimate the spin parameter with the continuum-fitting method, over a range of plausible black hole masses and distances. We compare our results with the spin measured with the reflection-fitting method and find that the inconsistency of the two results is partly caused by the different choices of .
1 Introduction
A black hole (BH) low-mass X-ray binary is composed of a stellar-mass BH and a companion star with a mass similar to or lower than the solar mass. Such a system normally experiences a long period of quiescence followed by a short-lived outburst lasting for months to years (Tanaka & Shibazaki, 1996; Chen et al., 1997; Tomsick & Kaaret, 2000). During an outburst, its luminosity varies by several orders of magnitude (Remillard & McClintock, 2006; Reynolds & Miller, 2013; Plotkin et al., 2015; Aneesha et al., 2019). The variability is usually detected on timescales as short as milliseconds (van der Klis, 2006; Belloni & Stella, 2014; Motta, 2016). In addition, complex spectral features (Remillard & McClintock, 2006; Tao et al., 2018) are also seen during outbursts.
A typical outburst is usually divided into several different spectral states (Fender et al., 2004; Homan & Belloni, 2005; Done et al., 2007) based on their spectral and timing behavior. In the initial phase of the outburst (low-hard state, LHS), the luminosity is low and the spectrum is dominated by a non-thermal hard component with a power-law form. In the standard scenario, the accretion disk is truncated far from the innermost stable circular orbit (ISCO) (Esin et al., 1997) and the inner region is filled with a hot, geometrically thick, radiatively inefficient flow (Narayan & Yi, 1995). In an alternative scenario, a relatively cool inner disk (in addition to a hot corona and an outer, truncated disk) may also exist near ISCO (Liu et al., 2007; Miller et al., 2006). Radio observations in the LHS show the presence of a compact jet launched from the innermost region (Fender et al., 2004). At this stage, strong noise components dominate the power-density spectra (PDS) and a low-frequency quasi-periodic oscillation (LFQPO) starts to show up (Remillard & McClintock, 2006). As the accretion rate increases, the source enters the hard intermediate state (HIMS) and soft intermediate state (SIMS) and the spectrum gradually softens. The compact jet disappears between HIMS and SIMS. As the accretion rate increases further, the source enters the high soft state (HSS) and the accretion disk reaches ISCO (or, in the alternative scenario, the outer disk joins the inner disk, removing the coronal gap). In the HSS, the X-ray spectrum is dominated by the disk component (Mitsuda et al., 1984; Makishima et al., 1986). LFQPOs nearly disappear at this stage although occasionally there are some faint signs of oscillations (Motta et al., 2012; Belloni & Motta, 2016). Later on, the source decays in flux, and passes through the lower intensity intermediate and hard states before returning back to quiescence. For a canonical BH transient, the evolution of a full outburst presents a counterclockwise q-shaped loop on the hardness-intensity diagram (Homan et al., 2001; Belloni et al., 2005; Zhang et al., 2020a).
The study of the intrinsic properties of an accretion disk (e.g., disk temperature and inner disk radius) helps us to better understand the physical phenomena occurring during an outburst; however, this inference relies on an accurate measurement of the disk emission. The observed disk spectrum must be corrected for the fraction of emitted disk photons that have been upscattered into the power-law component (Shimura & Takahara, 1995; Peris et al., 2016). To do so, Steiner et al. (2009) developed a self-consistent disk-corona model, named simpl, which accounts for the fraction of Compton-scattered disk photons in the computation of the total disk emission (Yao et al., 2005). This model provides a more accurate normalization of the disk emission, and therefore of the apparent inner disk radius and color temperature (Steiner et al., 2017; Sridhar et al., 2020; Zdziarski et al., 2021). The true physical radius and effective temperature are then related to the apparent (fitted) radius and temperature via a hardening factor (Kubota et al., 1998). Numerical simulations (Shimura & Takahara, 1995; Davis et al., 2005; Shafee et al., 2006) suggest a canonical value of . However, some studies suggest that the value of varies during the outburst evolution (e.g., Merloni et al. 2000; Davis & El-Abd 2019; Guan et al. 2021), especially in the LHS and HIMS (e.g., Dunn et al. 2011; Salvesen et al. 2013).
The accurate estimation of the disk emission is also important for the measurement of the spin parameter, especially for the continuum-fitting method (Zhang et al., 1997b; McClintock et al., 2014). The other main technique to measure the spin parameter is the reflection-fitting method (Fabian et al., 1989; Reynolds, 2014). However, the results obtained from the two techniques do not always agree with each other when the spin is non-extremal, i.e., (Miller et al., 2009; Steiner et al., 2011). Salvesen & Miller (2021) found that the discrepancies on spin measurements can be brought into agreement when we account for the uncertainties on .
To constrain the outburst evolution of disk parameters, coronal parameters and hardening factor, a broadband X-ray spectral coverage is required, so that thermal component and comptonized component can be fitted simultaneously and self-consistently. This is why our team has been monitoring BH outbursts with the Hard X-ray Modulation Telescope (Insight-HXMT), over the 1–150 keV band. One of the X-ray transients we have studied (the subject of this work) is EXO 1846–031, located at R.A. 18h49m16s.99, Dec. 03∘03′55′′.4, with a 90% error radius of 2′′ (Mereminskiy et al., 2019).
The first outburst of EXO 1846–031 was detected by EXOSAT on 1985 April 3 (Parmar et al., 1993), and lasted for several months. After that, the source stayed in hibernation for over 30 years. Based on its spectrum associated with an ultra-soft component and a hard power-law tail, Parmar et al. (1993) suggested EXO 1846–031 to be a BH candidate. The recent outburst was first reported by MAXI/GSC (Negoro et al., 2019) on 2019 July 23. The outburst was followed in the radio bands with the VLA (Miller-Jones et al., 2019) and MeerKAT (Williams et al., 2019), and in the X-ray bands with NuSTAR (Miller et al., 2019), NICER (Bult et al., 2019) and Swift. The Hard X-ray Modulation Telescope (Insight-HXMT) was also triggered by Target of Opportunity (ToO) observations (Yang et al., 2019a, b) of the source from 2019 August 2 to October 25. Draghis et al. (2020) found an obvious reflection feature in the NuSTAR spectrum. They reported an inclination angle of of the accretion disk and a high spin value of . Wang et al. (2021) investigated the spectral properties in the HIMS and the HSS with NuSTAR and Insight-HXMT, respectively. They suggested that the reflection component observed in the two spectral states originate from different sources of illumination; they also found that disk wind and jet probably co-existed in the HIMS in this source. Liu et al. (2021) performed a detailed timing analysis with the observations of Insight-HXMT, NICER and MAXI and found LFQPOs in the HIMS.
In this paper, we report on the broad-band spectral evolution of EXO 1846–031 using the Insight-HXMT observations. In particular, we will show the effect of Compton scattering and of a variable hardening factor on our measurement of the disk parameters. Additionally, we measure the spin parameter with the continuum-fitting method and compare it with the one derived from the reflection-fitting method. The paper is organized as follows: in Section 2, we introduce the observations and data processing methods. The results are presented in Section 3. The discussion and conclusion follow in Sections 4 and 5, respectively.
2 Observations and Data Reduction
2.1 Observations
Following the MAXI/GSC discovery of a new outburst of EXO 1846–031, we triggered Insight-HXMT tartget-of-opportunity observations, which covered 85 days, from 2019 August 2 to October 25 (Table LABEL:tab:obsinf).
Insight-HXMT (Zhang et al., 2014, 2020b) is the first Chinese X-ray astronomy satellite, launched on 2017 June 15. It has a 550-km low-Earth-orbit with an inclination of . It contains three slat-collimated instruments, sensitive to different energy ranges: the High Energy (HE) (Liu et al., 2020), Medium Energy (ME) (Cao et al., 2020), and Low Energy (LE) (Chen et al., 2020) X-ray Telescopes. HE, ME and LE are sensitive to the 20.0–250.0 keV, 5.0–30.0 keV and 1.0–15.0 keV bands, with detection areas of 5100 , 952 and 384 , respectively. The corresponding time resolutions are 4 s, 240 s and 1 ms.
2.2 Data Reduction
We used the Insight-HXMT Data Analysis software (hxmtdas) v2.02111http://hxmt.org/software.jhtml to analyze all the data. The filtering criteria for the good time intervals were: (1) an offset angle from the pointing direction ; (2) a pointing direction above earth ; (3) a value of the geomagnetic cutoff rigidity 8 GeV; (4) a rejection of data within 300 s of the South Atlantic Anomaly passage. A detailed explanation of the Insight-HXMT data reduction is published on its website222http://hxmt.org/SoftDoc.jhtml. Backgrounds rates were estimated with the tools: lebkgmap, mebkgmap, hebkgmap (version 2.0.9), based on the standard Insight-HXMT background models (Liao et al., 2020a; Guo et al., 2020; Liao et al., 2020b). We obtained the response files with the tasks lerspgen, merspgen and herspgen.
We rebinned the spectra to a minimum of 30 counts per bin using the ftools (Blackburn, 1995) task grppha. We modelled them with xspec Version 12.10.1333https://heasarc.gsfc.nasa.gov/docs/xanadu/Xspec/ (Arnaud, 1996). We used the statistics, and added a systematic uncertainty of 1.5%. The energy bands adopted for our spectral analysis are: 1.0–10.0 keV (LE), 10.0–30.0 keV (ME) and 30.0–150.0 keV (HE). We jointly fitted the spectra of the three instruments and included a multiplicative constant to account for the relative flux calibration uncertainties (Li et al., 2020). All spectral models include a photoelectric absorption, modelled with TBabs and ‘wilm’ abundances (Wilms et al., 2000). The results of our spectral analysis are presented in the Section 3.2. We only report results from observations with an exposure time longer than 200 s. All uncertainties are quoted at the 90% confidence level.
3 Results
3.1 Light Curves and Hardness Ratio
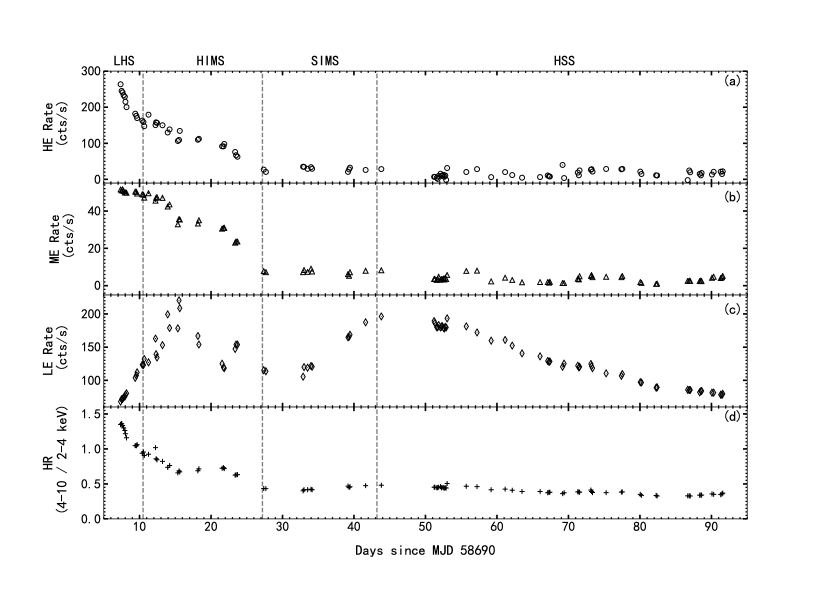
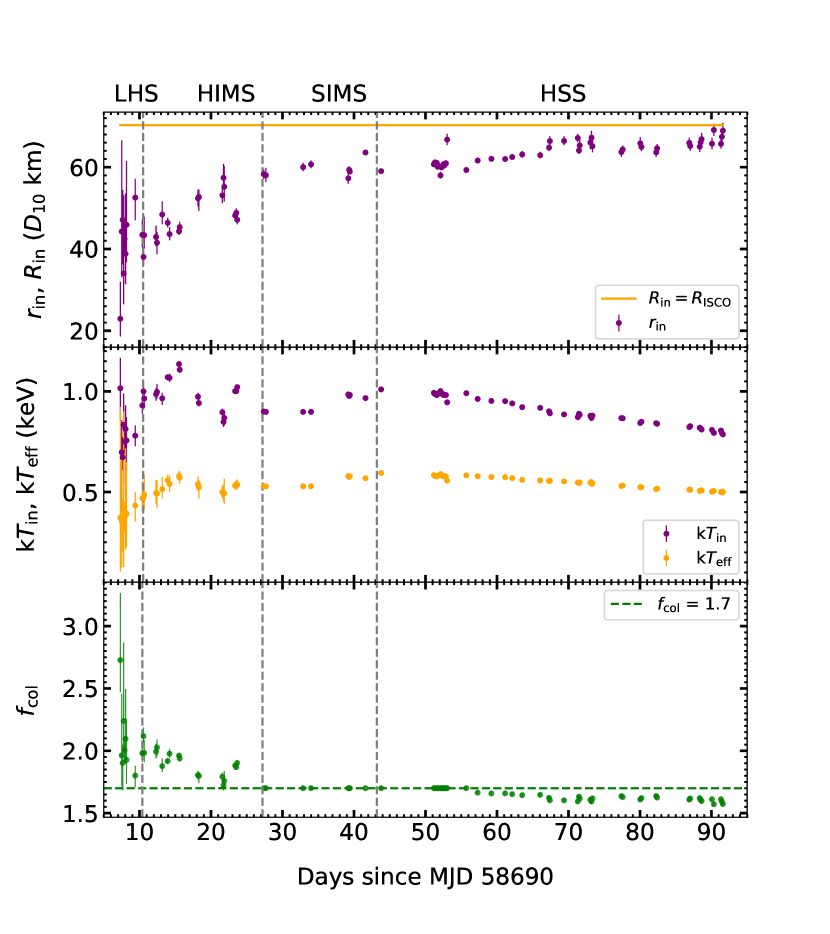
Figure 1 shows the long-term light curves in different energy bands and the evolution of the LE hardness ratio (defined as the 4–10 keV count rate divided by the 2–4 keV rate). The HE and ME count rates show a similar evolution: first a decrease with time and then a relatively low, stable level (Figure 1). Instead, the LE light curve shows a more complex evolution, with two peaks. The LE count rate rapidly increased after MJD 58697.35, reached a peak value of cts s-1 on MJD 58705.53, and then decreased gradually. Then, it increased again during the SIMS and finally decreased to a relatively low value ( cts s-1) during the HSS. We do not know the exact reason for the formation of these two peaks. From the LE hardness ratio we see that the spectrum gradually softened with time (bottom panel of Figure 1).
Liu et al. (2021) subdivided the outburst into four spectral states based on the relative changes in the hardness-intensity diagram and the fractional rms integrated over the –32 Hz band. In the following spectral analysis, we will adopt their spectral state classification, except for their definition of the LHS. Their preliminary classification was based on hardness ratios and included only the first three Insight-HXMT observations in the LHS. Here, we used spectral analysis to obtain a more accurate classification of this state. We adopted the canonical definition of LHS as the epochs when the photon index 1.5–1.7 and the disk flux fraction 20% (Remillard & McClintock, 2006; Belloni, 2010). With this definition, the LHS interval includes the first eight Insight-HXMT observations (Section 3.2.1).
3.2 Broad-band Spectral Models
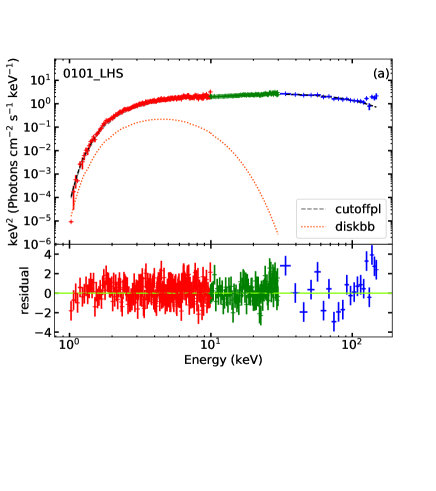
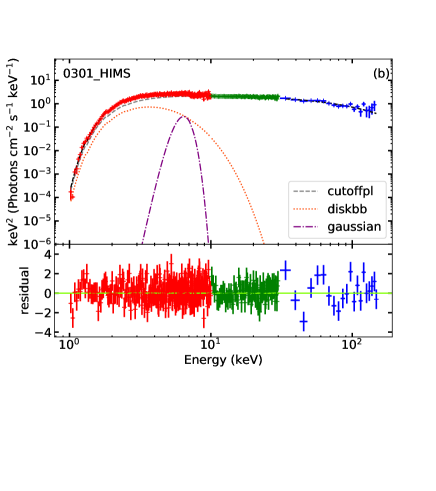
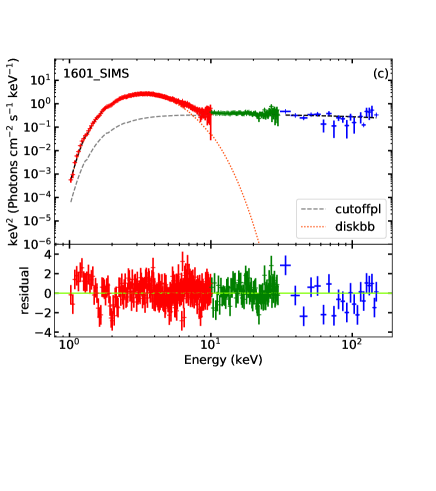
3.2.1 cutoffpl + diskbb model
The continuum X-ray emission of BH X-ray binaries generally consists of a thermal/soft and a non-thermal/hard component. The former represents the disk emission and is usually fitted with a multi-color disk-blackbody component (diskbb in xspec) (Mitsuda et al., 1984; Makishima et al., 1986). The latter represents the coronal emission, i.e., it comes from the Comptonization of disk photons in a hot electron cloud (Eardley et al., 1975; Sunyaev & Titarchuk, 1980). It is usually fitted with a power-law component, with or without a high-energy cutoff (cutoffpl or powerlaw). We tried different combinations of the cutoffpl and diskbb components in each spectral state (alone or in combination). Based on the F-test probability (ftest command in xspec), we found that both components are always present throughout the outburst, with a probability 99.9%.
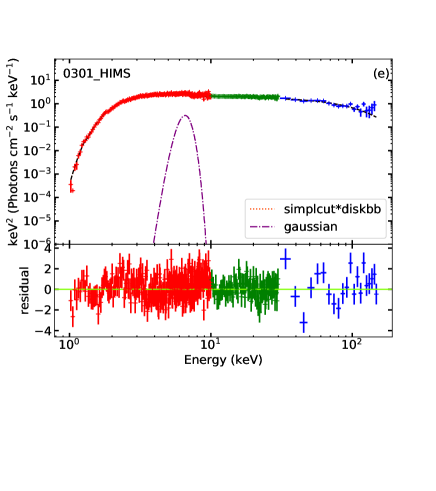
In some epochs, the fit is improved with the addition of a Gaussian emission line (the energy of the line is limited to between 6.4 and 7 keV) around 6.4–6.6 keV, corresponding to Fe K emission. In order to test the significance of this emission line, we followed the approach described by several previous works (Barrière et al., 2015; Bhalerao et al., 2015; Sidoli et al., 2017; Ge et al., 2020; Wang et al., 2021) and used the simftest444https://heasarc.gsfc.nasa.gov/xanadu/xspec/manual/node126.html routine in XSPEC with 10,000 simulations for the observation with the longest exposure time in each spectral state. The probabilities of the line to be required in each state, from LHS to HIMS, SIMS and HSS, are P = 98.1%, 99.9%, 99.3%, and 57.7%, corresponding to a significance of 2.35, 5, 2.7, and 0.8, respectively. Additionally, we also calculated the ratio between the normalization of the gaussian component and its error, and we only included the gaussian when the ratio is larger than 3, which is true only at HIMS. The line significance and the ratio increases if we combine multiple spectra in each state, as shown in Wang et al. (2021). However, here we are monitoring the time evolution of the spectra, therefore we prefer not to combine them. Hence, we only included the Fe line in our fits to the HIMS spectra. The mean value of the best-fitting central energy of the line in the 18 HIMS epochs (Tables LABEL:tab:fitting and LABEL:tab:fitting_1sc1d) is keV, with a 1 scatter of 0.15 keV. Thus, the line is consistent with both neutral (6.4 keV) and He-like (6.7 keV) iron.
To check the robustness of our results, we refitted the observation with the longest exposure time of each spectral state with the reflection model relxill (Dauser et al., 2013; García et al., 2014) plus diskbb. We obtained best-fitting values of and similar to those derived from the simpler model; the latter is therefore preferred. We also fitted some LHS and HIMS data with the high density reflection model relxillD to check whether the disk component was really required. For the LHS and HIMS spectra, the relxillD component alone gives /dof = 1451.90/1300 and 1262.59/1326, respectively. Adding a diskbb component improves the two fits by = 78.82 and 29.97, respectively, for the loss of 2 dof. The F-test probabilities of and indicate that the diskbb component is significantly required by the LHS and HIMS data. In addition, we compared the best-fitting parameters of diskbb component obtained from model relxillD+diskbb and the simpler model. The best-fitting values of and all vary slightly, and , respectively. Besides, the evolution trends of and from the LHS to the HIMS are all consistent with those derived from the simpler model, thus our main results will not be affected.
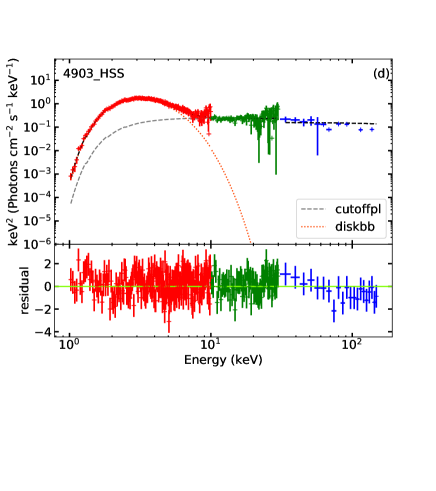
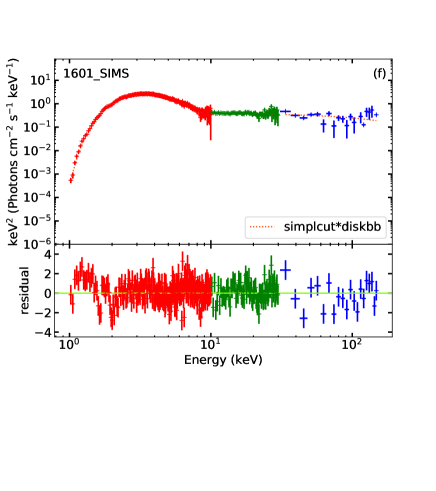
We show a representative sample of unfolded spectra (one for each state), together with the corresponding models, in Figure 2.
We set out to determine the evolution of the main physical parameters over the course of the outburst. As a first step of our analysis, we fitted each spectrum with a free absorbing column density parameter (red datapoints in Figure 3a). The best-fitting value of is stable in the SIMS and HSS, but there is some scatter in the LHS and HIMS. There is some degeneracy between the best-fitting values of and , which makes it difficult to determine the intrinsic evolution of the disk parameters. To reduce this hindrance, we froze at the mean value ( cm-2, red line in Figure 3a) derived from the SIMS and HSS fits, and refitted all the spectra with fixed .
The cutoff energy of the (dominant) power-law component is well constrained for most of the spectra in the LHS and HIMS (Figure 3). Instead, in the SIMS and HSS, the power-law component weakens: the low-energy spectrum becomes dominated by the diskbb component, and the high-energy tail above 60–70 keV becomes dominated by background counts. For this reason, if we let the cutoff energy vary freely in the fit, most of the times will peg at its upper limit, meaning that a free cutoff energy does not provide a significant improvement to the fit. To better constrain in the HSS, we also tried a simultaneous fit of several spectra near the peak of the outburst, to increase the signal to noise. The cutoff energy obtained with this method is formally constrained between 46 and 100 keV. However, the corresponding photon index is only , even lower than in the LHS and HIMS, which we regard as unphysical. This contradicts the expectations from the observed evolution (strong softening) of the hardness ratio from LHS to HSS. We suspect that the main reason for this unphysical fitting result is the strong degeneracy between the photon index and the cutoff energy. The two quantities cannot be well constrained simultaneously after the evolution of the source into the SIMS, and the presence or absence of a cutoff makes no substantial difference to the rest of the spectrum. To keep the model self-consistent throughout the outburst evolution, we fixed at 500 keV in the SIMS and HSS. The photon index then increases to , which is more consistent with the typical value of photon index in the soft state. In addition, other parameters such as ( keV), the fraction of diskbb component () and the fraction of cutoffpl component () at this time all in the canonical range of soft state.
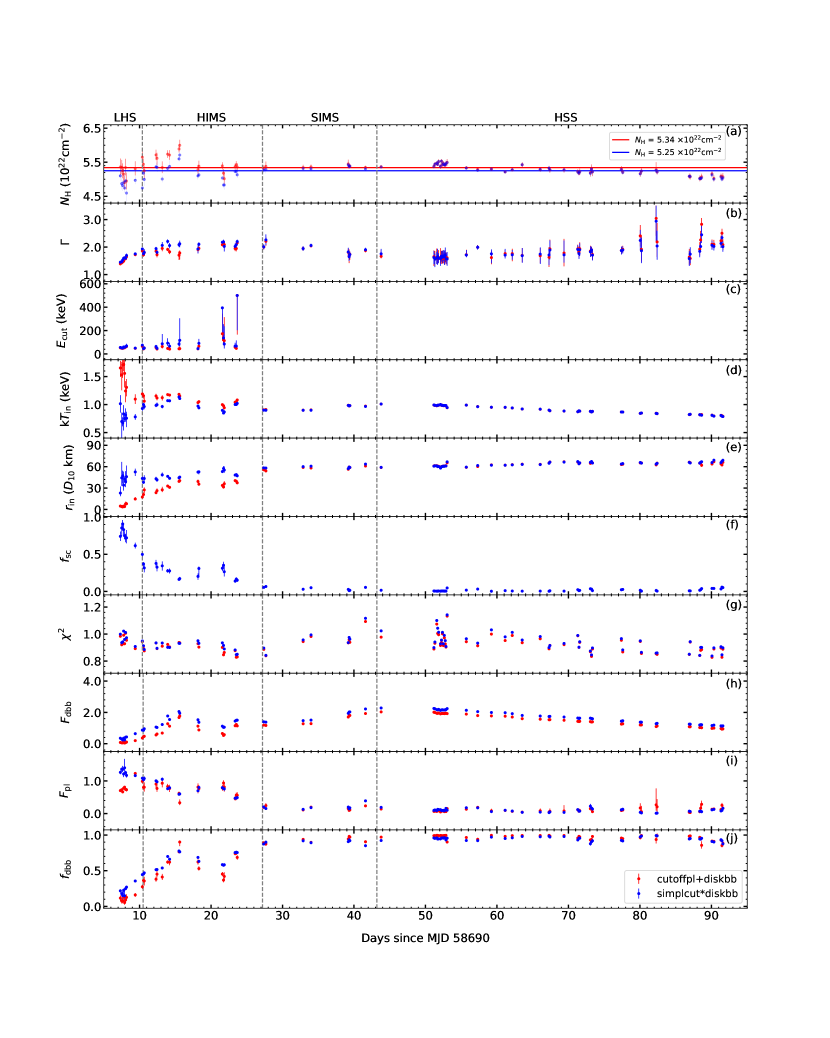
We show the best-fitting parameters (Table LABEL:tab:fitting) of the cutoffpl + diskbb model (with the assumed constant ), as well as the unabsorbed bolometric disk flux, power-law flux, and the ratio between disk flux and the total flux, as red dots in Fig 3. The four parameters of interest are the power-law photon index, the cutoff energy (only in the LHS and HIMS), the inner disk radius and the peak disk temperature.
The photon index gradually increased from 1.4 to 2.2 as the source evolved from the LHS to the HIMS, and then remained almost constant within uncertainties in the SIMS and HSS.
fluctuated between 40 and 90 keV when the source was in the LHS and the HIMS, except for the last few observations of the HIMS. As mentioned above, it was unconstrained in the SIMS and HSS, and was fixed at 500 keV for fitting purposes in xspec; we did not plot such data points as shown in Figure 3c.
The inner-disk color temperature unexpectedly decreased during the LHS. It remained approximately constant around 1 keV throughout the HIMS. Finally, it gradually decreased (as expected) during the outburst decline in the HSS.
The apparent inner radius of the accretion disk, ( where is the diskbb normalization), unexpectedly increased during the LHS and HIMS. This is seemingly inconsistent with the canonical scenario that the inner disk moves towards ISCO during those states (Remillard & McClintock, 2006; Muñoz-Darias et al., 2011; Tao et al., 2015). We will suggest a possible explanation in Section 3.3. After reaching its peak in the SIMS, remained mostly constant throughout the HSS, apart from a slight increasing trend (only by 10%) near the end of that state. We interpret the evolution of as evidence that the disk had reached a steady state (Shakura-Sunyaev solution) and the inner disk radius had settled at ISCO at the beginning of the HSS.
The unabsorbed disk flux increased rapidly and then decreased slowly in the LHS and HIMS, then starts to increase again in the SIMS and decrease slightly in the HSS. The power-law flux increased slowly in the LHS and then started to decrease after reached HIMS. The ratio between the disk flux and the total flux, , increased significantly in the LHS and HIMS, reached its peak in the SIMS and remained almost constant () after that.
3.2.2 simplcut * diskbb model
Before we try to attribute any physical meaning to the unusually small value of in the LHS and HIMS, we need to be aware that a phenomenological cutoffpl + diskbb model does not self-consistently account for the photons that are removed from the disk component and upscattered into the power-law component. As a result, the normalization of the disk emission (hence, ) is usually underestimated by such model when a corona is present (Yao et al., 2005). To get around this problem, we re-fitted the spectra with the self-consistent Comptonization model simplcut (Steiner et al., 2017) applied to a disk-blackbody seed spectrum.
When fitting the simplcutx*diskbb model, we adopted the same method described in Section 3.2.1 to determine the value of . We fixed it at the mean value during the SIMS and HSS ( cm-2, blue line in Figure 3a) for all the subsequent spectral modelling.
Panels (e) and (f) of Figure 2 show two representative unfolded spectra and residuals based on the simplcut*diskbb model (one for the HIMS, and one for the SIMS).
The fitting statistics of the two models is equally good: the reduced only varies by up to 2%. The best-fitting parameter values (Table LABEL:tab:fitting_1sc1d) of the simplcut*diskbb model are shown as blue dots in Figure 3. Compared to the cutoffpl model, the simplcut model has one more parameter: , defined as the fraction of seed photons scattered into the power-law distribution. Its value decreases rapidly from 0.91 in the LHS to 0.13 in the HIMS, and then remains constant in the SIMS and HSS, at 0.05. As before, the high-energy cutoff is unconstrained for the observations in the SIMS and HSS. Most of the other parameters are consistent between the two models. In particular, we obtain the same best-fitting values of and for the SIMS and HSS observations. Instead, in the LHS and HIMS, the apparent radius derived from simplcut*diskbb is higher than the value initially obtained from cutoffpl + diskbb, and the color temperature is lower. We argue that the self-consistent Comptonization model provides more plausible values of those two quantities. Although the anomalous behavior of and is now reduced, it is not entirely removed. Even in the Comptonization model, is still smaller in the LHS and HIMS than in the HSS, and the disk temperature is surprisingly higher (1 keV) at those same epochs. This suggests that there is a physical reason for this strange behaviour. We propose that it is caused by changes in the hardening factor.
3.3 Evolution of the hardening factor
The hardening factor (also called color correction factor) accounts for the deviation of the disk emission from a pure blackbody spectrum (Shimura & Takahara, 1995). The peak effective temperature is related to the fitted color temperature by the relation . Conversely, the relation between physical inner radius, , and apparent inner radius, , is:
| (1) |
(Kubota et al., 1998), where is the general relativity correction factor, is diskbb normalization, is the inclination angle of the accretion disk and is the distance in units of 10 kpc. We can plausible assume that and (”canonical” value from Shimura & Takahara 1995) in the SIMS and at least near the peak of the HSS, before the start of the decline (i.e., MJD 58717–58745). We adopt an inclination angle of (Draghis et al., 2020). Instead, the distance is completely unconstrained, in the absence of a detected optical counterpart555The value of 7 kpc introduced by Parmar et al. (1993) is only a guess based on a now out-of-date analogy with the luminosity of other BH transients.. The fitted value of in the first epoch of the HSS is km, and this value is indeed substantially unchanged throughout MJD 58717–58745. Then, from Eq.(1), km. In the LHS and HIMS, the physical inner radius must be at least as large as (it may be equal if there is already a condensed thin disk in the innermost region). Thus, in our proposed scenario, we can determine the minimum value of required to make in the early epochs. We obtain in the first few days of LHS observations. In the last part of the LHS and HIMS, decreases to 1.7–2.4. Conversely, in the declining phase of the HSS, a canonical value implies . This can be interpreted in two alternative ways: either the inner disk was starting to recede from ISCO after MJD 58745, or it was still at ISCO but the hardening factor declined to . Finally, we derived the effective temperature . We find that with our estimated hardening factors, increased monotonically during the LHS (as expected) instead of showing an unphysical decline in the first part of the outburst. We show the evolution of radii, temperatures and in Figure 4.
4 Discussion
4.1 The inner disk radius in the initial hard state
The early stages of transient BH outbursts are characterized by the coupled evolution of a corona and of the underlying disk. For EXO 1846031, the evolution of the coronal parameters follows the canonical expectations. For example, the scattering fraction follows the same trend seen in recent outbursts of well-known BH transients such as GX 339–4 (Sridhar et al., 2020), XTE J1550–564 (Connors et al., 2020) and 4U 1630–47 (Connors et al., 2021). Instead, the evolution of the disk parameters may have subtle differences.
Our spectral modelling shows (Section 3.2) that if the hardening factor is kept constant from LHS to HSS, the inner radius of the disk is smaller in the LHS than in the HSS. We reject this possibility as unphysical: the inner disk radius in the LHS must be at least as large as in the HSS. If we assume that the inner disk radius is constant throughout the entire outburst, must be decreasing from 2.7 at the beginning of the outburst, towards the canonical value of 1.6 in the HSS. With this assumption, we preserve the scaling law throughout the outburst, characteristic of a radiatively efficient disk with constant inner radius. Finally, if we also allow for the possibility that in the LHS, the hardening factor must be even higher at the beginning of the outburst ().
In previous studies of BH transients, a “canonical” value of (from Shimura & Takahara 1995) was usually adopted for the soft state, to account for a “diluted” disk spectrum. However, there are several observations of BH outbursts that show convincing evidence of a variable hardening factor, especially in the initial hard state. For example in GX 339-4, Salvesen et al. (2013) proposed that a variable hardening factor is an alternative to disk truncation, to explain changes in the disk spectrum. Other sources with possible evidence of variable hardening factor are 4U 195711 (Maitra et al., 2014), MAXI J1820070 (Guan et al., 2021), and MAXI J1348630 (Zhang et al., 2022). From simulations of disk spectra, Merloni et al. (2000) also suggested a variable hardening factor –3, arguing that increases when the disk emission is relatively less dominant. This result is supported by a global study of disk properties by Dunn et al. (2011). They found that for almost all BH transients, is relatively stable in the disk-dominated state, but increase from 1.6 to 2.6 as the disk fraction decreases. The variation of may be caused by changes in the accretion energy dissipation (Merloni et al., 2000), in the vertical disk structure (Davis et al., 2005), in the magnetic energy density (Blaes et al., 2006) and in the disk density and optical depth (Soria et al., 2008).
The presence or absence of a full disk has important implications also for the interpretation of QPOs. LFQPOs with a centroid frequency between 0.7 and 8 Hz have been detected in the HIMS of EXO 1846–031 by Liu et al. (2021) from a timing analysis of the same Insight-HXMT data used in this work. If there was already a thin disk at or very close to ISCO, as we have suggested here, this geometry disfavours QPO models (e.g., Stella & Vietri 1998; Ingram et al. 2009; Varniere & Vincent 2016) that require significant changes in the inner disk edge. Instead, jet precession would be a viable model. The presence of a jet in EXO 1846031 was confirmed by VLA (Miller-Jones et al., 2019) and MeerKAT (Williams et al., 2019) detections in the HIMS. By comparison, the BH transient MAXI J1820070 is another source in which LFQPOs have been detected in the LHS (e.g., Wang et al. 2020; Ma et al. 2021) and the disk is thought to be non-truncated based on the reflection-fitting method (Buisson et al., 2019). A likely interpretation for the origin of the QPOs is jet precession (Ma et al., 2021).
4.2 Additional contributions to the hardening factor in the LHS and HIMS
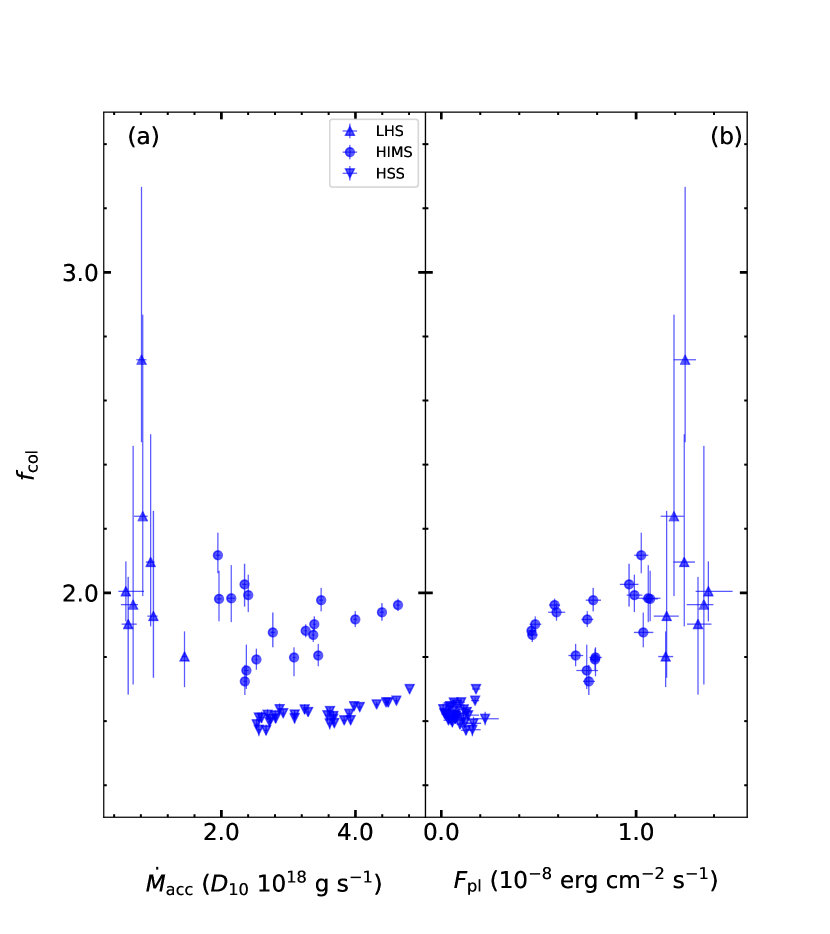
Done & Davis (2008) reported a detailed investigation of in a disk-dominated state. Their work shows that increases as the mass accretion rate increases, which links the variation of to the mass accretion rate. To examine if this relationship is still valid in a hard state, we plot as a function of in the LHS, HIMS and most of the HSS in Figure 5a. Data points between MJD 58717 and 58745 are excluded here since we have assumed a constant in this period (we explained this in Section 3.3). It is clear that and indeed show a positive correlation in the HSS, which is in good agreement with the results of Done & Davis (2008). However, the values of in the LHS and HIMS where are relatively low, is significantly higher than that in the HSS. We thus suspect that there should be additional contributions to the in the LHS and HIMS.
We show the relationship between and power-law flux in Figure 5b, in which increases as increases throughout the outburst. Apparently, gradually decreases as the source evolves from the LHS to the HIMS and becomes negligible in the HSS. This implies that the high value of in the LHS and the HIMS is probably associated with the hard emission. Compared to HSS, the additional power-law emission in the hard state will heat up the disk surface, leading to an increase in the disk temperature, which results in a significant increase in . Similar results that increases as the disk fraction decreases have been reported by Merloni et al. (2000) and Dunn et al. (2011). We plot versus in Figure 5b, which is to emphasize the contribution of the power-law flux when the source was in the LHS and HIMS.
4.3 Constraints on system parameters
Using the reflection-fitting method, Draghis et al. (2020) obtained a spin parameter as high as . They applied 12 reflection models to the NuSTAR spectra to test this value, with different assumptions on coronal geometry, disk density and emission spectrum, and obtained consistent spin values. However, Wang et al. (2021) studied the same NuSTAR data with two reflection models and argued that the spin cannot be constrained. Here, we try to constrain the spin parameter with the continuum-fitting method, and test whether the result is consistent with the extreme value claimed by Draghis et al. (2020).
As discussed in Section 3.3, the inner disk radius reached the ISCO in the HSS, with km (for and ). We apply the relationship between the ISCO radius and the spin parameter (Zhang et al. 1997a; see also Bardeen et al. 1972):
| (2) |
where , and . Thus, from Equation 2, we can derive as a function of and distance. Since neither the BH mass nor the distance is known, we determined over a grid of values spanning a mass range of 5–15 (based on the distribution of kinematic masses in Galactic BH transients; Özel et al. 2010; Corral-Santana et al. 2016) and a distance of 2–12 kpc (based on the distribution of Galactic BH distances in Tetarenko et al. 2016).
The values of the spin parameter versus BH mass for different distances are shown in Figure 6a. The extreme value of suggested by Draghis et al. (2020) is consistent only with a small distance (–4 kpc) and relatively high mass (). However, this combination of mass and distance would imply a peak Eddington ratio –0.04 in the HSS. This is much lower than the typical X-ray luminosities observed in the disk-dominated states of other Galactic BHs (Tetarenko et al., 2016). We also calculate the spin parameter when the inclination is assumed to be (Wang et al., 2021), as shown in Figure 6b. In this case, the extreme value of is consistent with the combination of distance (–6 kpc) and mass (–14 ). The corresponding peak Eddington ratio would then be 0.1 but is still lower than expected and observed in most other systems (Tang et al., 2011; Yan & Yu, 2015). For a higher Eddington ratio, the spin parameter has to be non-extremal.
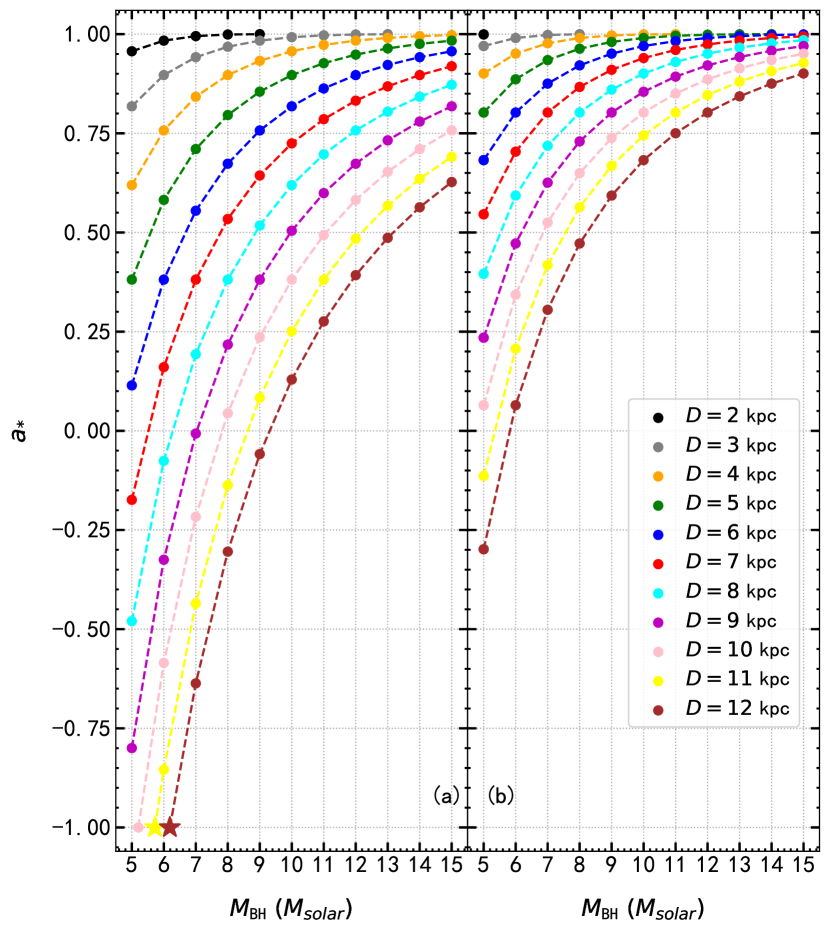
Previous work has already reported the inconsistency of the spin measurements obtained for the same systems with the reflection-fitting and continuum-fitting methods. For example, for GRO J165540, the reflection-fitting method provides a higher spin than the continuum-fitting method (Shafee et al., 2006; Reis et al., 2009; Reynolds, 2014), similar to what we found here for EXO 1846031. Allowing for uncertainties in at a level of 0.2–0.3 can alleviate the discrepancy (Salvesen & Miller, 2021); this effect is more pronounced for non-extremal spins. For example, if we assume a smaller value of the hardening factor, , we can reach for –6 kpc and at , or –9 kpc and –14 at . The corresponding peak Eddington ratio would then be 0.09 and 0.22, respectively.
In general, for the same continuum parameters, lower values of imply higher Eddington ratios. We conclude that, in principle, the inconsistency of the spin parameter measured with the continuum-fitting and reflection-fitting methods can be somewhat mitigated by the choice of . However, without knowing its mass and distance, we cannot draw a further conclusion about the spin parameter of the BH in EXO 1846–031.
5 Conclusions
We have presented a broad-band (1–150 keV band) spectral analysis of the 2019 outburst of the BH candidate EXO 1846031, based on Insight-HXMT observations. The source exhibited state transitions from the LHS to the HIMS, SIMS and HSS. The broad-band spectra can be well modelled with diskbb plus cutoffpl components. Most of the best-fitting parameter values are consistent with those inferred in other “canonical” BH transients. In particular, the almost constant diskbb normalization in the SIMS and HSS indicates that the accretion disk reached ISCO in the two states, and suggests a value of km. However, the apparent inner radius in the LHS and HIMS is unphysically small (in some epochs, smaller than that in the HSS), even after we take into account the fraction of disk photons upscattered into the Comptonization component. In order to ensure that the true radius is at least never smaller than ISCO in the hard state, we need to allow for a variable hardening factor, decreasing as the outburst progresses and the disk becomes brighter and more dominant. If we normalize the hardening factor to its canonical value at the SIMS and the beginning of the HSS, we find that at the beginning of the LHS. Conversely, the last phase of the HSS is consistent with a small decrease of below the canonical value.
Furthermore, we find the value of the hardening factor in the relatively hard states is significantly higher than that in the HSS. We suggest that the coronal irradiation onto the disk provides additional contributions to the hardening factor in the LHS and HIMS.
Using our continuum-fitting parameters, we also tested previous claims of an extreme spin for this BH, inferred from reflection-fitting. We derived the range of acceptable spin values as a function of a plausible range of BH masses and distances based on two inclination angles. The inconsistency of the spin measured with the continuum-fitting and reflection-fitting methods is partly due to the different choices of .
In conclusion, our study has shown that plays an important role for the intrinsic emission and physical parameters of the accretion disk, and for our understanding of the outburst evolution. It also influences the measurement of the spin parameter in the continuum-fitting method. Therefore, we argue that should never simply be assumed as a constant value, especially when the disk emission evolves over a broad range of luminosities (Salvesen et al., 2013). More specifically in the case of EXO 1846031, there is empirical evidence that the accretion disk was close to ISCO already in the initial hard state (unless ). A similar non-canonical interpretation was proposed for several other transient BH candidates (Reis et al., 2008, 2010; Parker et al., 2015; García et al., 2018, 2019; Buisson et al., 2019; Kara et al., 2019). Simultaneous broad-band investigations of the early outburst evolution in BH X-ray binaries, such as those made possible by Insight-HXMT, hold the key for the physical understanding of state transitions.
References
- Aneesha et al. (2019) Aneesha, U., Mandal, S., & Sreehari, H. 2019, MNRAS, 486, 2705, doi: 10.1093/mnras/stz1000
- Arnaud (1996) Arnaud, K. A. 1996, in Astronomical Society of the Pacific Conference Series, Vol. 101, Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby & J. Barnes, 17
- Bardeen et al. (1972) Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347, doi: 10.1086/151796
- Barrière et al. (2015) Barrière, N. M., Krivonos, R., Tomsick, J. A., et al. 2015, ApJ, 799, 123, doi: 10.1088/0004-637X/799/2/123
- Belloni et al. (2005) Belloni, T., Homan, J., Casella, P., et al. 2005, A&A, 440, 207, doi: 10.1051/0004-6361:20042457
- Belloni (2010) Belloni, T. M. 2010, States and Transitions in Black Hole Binaries, ed. T. Belloni, Vol. 794, 53, doi: 10.1007/978-3-540-76937-8_3
- Belloni & Motta (2016) Belloni, T. M., & Motta, S. E. 2016, Transient Black Hole Binaries, ed. C. Bambi, Vol. 440, 61, doi: 10.1007/978-3-662-52859-4_2
- Belloni & Stella (2014) Belloni, T. M., & Stella, L. 2014, Space Sci. Rev., 183, 43, doi: 10.1007/s11214-014-0076-0
- Bhalerao et al. (2015) Bhalerao, V., Romano, P., Tomsick, J., et al. 2015, MNRAS, 447, 2274, doi: 10.1093/mnras/stu2495
- Blackburn (1995) Blackburn, J. K. 1995, in Astronomical Society of the Pacific Conference Series, Vol. 77, Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, 367
- Blaes et al. (2006) Blaes, O. M., Davis, S. W., Hirose, S., Krolik, J. H., & Stone, J. M. 2006, ApJ, 645, 1402, doi: 10.1086/503741
- Buisson et al. (2019) Buisson, D. J. K., Fabian, A. C., Barret, D., et al. 2019, MNRAS, 490, 1350, doi: 10.1093/mnras/stz2681
- Bult et al. (2019) Bult, P. M., Gendreau, K. C., Arzoumanian, Z., et al. 2019, The Astronomer’s Telegram, 12976, 1
- Cao et al. (2020) Cao, X., Jiang, W., Meng, B., et al. 2020, Science China Physics, Mechanics, and Astronomy, 63, 249504, doi: 10.1007/s11433-019-1506-1
- Chen et al. (1997) Chen, W., Shrader, C. R., & Livio, M. 1997, ApJ, 491, 312, doi: 10.1086/304921
- Chen et al. (2020) Chen, Y., Cui, W., Li, W., et al. 2020, Science China Physics, Mechanics, and Astronomy, 63, 249505, doi: 10.1007/s11433-019-1469-5
- Connors et al. (2020) Connors, R. M. T., García, J. A., Dauser, T., et al. 2020, ApJ, 892, 47, doi: 10.3847/1538-4357/ab7afc
- Connors et al. (2021) Connors, R. M. T., García, J. A., Tomsick, J., et al. 2021, ApJ, 909, 146, doi: 10.3847/1538-4357/abdd2c
- Corral-Santana et al. (2016) Corral-Santana, J. M., Casares, J., Muñoz-Darias, T., et al. 2016, A&A, 587, A61, doi: 10.1051/0004-6361/201527130
- Dauser et al. (2013) Dauser, T., Garcia, J., Wilms, J., et al. 2013, MNRAS, 430, 1694, doi: 10.1093/mnras/sts710
- Davis et al. (2005) Davis, S. W., Blaes, O. M., Hubeny, I., & Turner, N. J. 2005, ApJ, 621, 372, doi: 10.1086/427278
- Davis & El-Abd (2019) Davis, S. W., & El-Abd, S. 2019, ApJ, 874, 23, doi: 10.3847/1538-4357/ab05c5
- Done & Davis (2008) Done, C., & Davis, S. W. 2008, ApJ, 683, 389, doi: 10.1086/589647
- Done et al. (2007) Done, C., Gierliński, M., & Kubota, A. 2007, A&A Rev., 15, 1, doi: 10.1007/s00159-007-0006-1
- Draghis et al. (2020) Draghis, P. A., Miller, J. M., Cackett, E. M., et al. 2020, ApJ, 900, 78, doi: 10.3847/1538-4357/aba2ec
- Dunn et al. (2011) Dunn, R. J. H., Fender, R. P., Körding, E. G., Belloni, T., & Merloni, A. 2011, MNRAS, 411, 337, doi: 10.1111/j.1365-2966.2010.17687.x
- Eardley et al. (1975) Eardley, D. M., Lightman, A. P., & Shapiro, S. L. 1975, ApJ, 199, L153, doi: 10.1086/181871
- Esin et al. (1997) Esin, A. A., McClintock, J. E., & Narayan, R. 1997, ApJ, 489, 865, doi: 10.1086/304829
- Fabian et al. (1989) Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729, doi: 10.1093/mnras/238.3.729
- Fender et al. (2004) Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105, doi: 10.1111/j.1365-2966.2004.08384.x
- García et al. (2014) García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76, doi: 10.1088/0004-637X/782/2/76
- García et al. (2018) García, J. A., Steiner, J. F., Grinberg, V., et al. 2018, ApJ, 864, 25, doi: 10.3847/1538-4357/aad231
- García et al. (2019) García, J. A., Tomsick, J. A., Sridhar, N., et al. 2019, ApJ, 885, 48, doi: 10.3847/1538-4357/ab384f
- Ge et al. (2020) Ge, M. Y., Ji, L., Zhang, S. N., et al. 2020, ApJ, 899, L19, doi: 10.3847/2041-8213/abac05
- Guan et al. (2021) Guan, J., Tao, L., Qu, J. L., et al. 2021, MNRAS, doi: 10.1093/mnras/stab945
- Guo et al. (2020) Guo, C.-C., Liao, J.-Y., Zhang, S., et al. 2020, Journal of High Energy Astrophysics, 27, 44, doi: 10.1016/j.jheap.2020.02.008
- Homan & Belloni (2005) Homan, J., & Belloni, T. 2005, Ap&SS, 300, 107, doi: 10.1007/s10509-005-1197-4
- Homan et al. (2001) Homan, J., Wijnands, R., van der Klis, M., et al. 2001, ApJS, 132, 377, doi: 10.1086/318954
- Ingram et al. (2009) Ingram, A., Done, C., & Fragile, P. C. 2009, MNRAS, 397, L101, doi: 10.1111/j.1745-3933.2009.00693.x
- Kara et al. (2019) Kara, E., Steiner, J. F., Fabian, A. C., et al. 2019, Nature, 565, 198, doi: 10.1038/s41586-018-0803-x
- Kubota et al. (1998) Kubota, A., Tanaka, Y., Makishima, K., et al. 1998, PASJ, 50, 667, doi: 10.1093/pasj/50.6.667
- Li et al. (2020) Li, X., Li, X., Tan, Y., et al. 2020, Journal of High Energy Astrophysics, 27, 64, doi: 10.1016/j.jheap.2020.02.009
- Liao et al. (2020a) Liao, J.-Y., Zhang, S., Chen, Y., et al. 2020a, Journal of High Energy Astrophysics, 27, 24, doi: 10.1016/j.jheap.2020.02.010
- Liao et al. (2020b) Liao, J.-Y., Zhang, S., Lu, X.-F., et al. 2020b, Journal of High Energy Astrophysics, 27, 14, doi: 10.1016/j.jheap.2020.04.002
- Liu et al. (2007) Liu, B. F., Taam, R. E., Meyer-Hofmeister, E., & Meyer, F. 2007, ApJ, 671, 695, doi: 10.1086/522619
- Liu et al. (2020) Liu, C., Zhang, Y., Li, X., et al. 2020, Science China Physics, Mechanics, and Astronomy, 63, 249503, doi: 10.1007/s11433-019-1486-x
- Liu et al. (2021) Liu, H.-X., Huang, Y., Xiao, G.-C., et al. 2021, Research in Astronomy and Astrophysics, 21, 070, doi: 10.1088/1674-4527/21/3/70
- Ma et al. (2021) Ma, X., Tao, L., Zhang, S.-N., et al. 2021, Nature Astronomy, 5, 94, doi: 10.1038/s41550-020-1192-2
- Maitra et al. (2014) Maitra, D., Miller, J. M., Reynolds, M. T., Reis, R., & Nowak, M. 2014, ApJ, 794, 85, doi: 10.1088/0004-637X/794/1/85
- Makishima et al. (1986) Makishima, K., Maejima, Y., Mitsuda, K., et al. 1986, ApJ, 308, 635, doi: 10.1086/164534
- McClintock et al. (2014) McClintock, J. E., Narayan, R., & Steiner, J. F. 2014, Space Sci. Rev., 183, 295, doi: 10.1007/s11214-013-0003-9
- Mereminskiy et al. (2019) Mereminskiy, I. A., Krivonos, R. A., Medvedev, P. S., & Grebenev, S. A. 2019, The Astronomer’s Telegram, 12969, 1
- Merloni et al. (2000) Merloni, A., Fabian, A. C., & Ross, R. R. 2000, MNRAS, 313, 193, doi: 10.1046/j.1365-8711.2000.03226.x
- Miller et al. (2006) Miller, J. M., Homan, J., & Miniutti, G. 2006, ApJ, 652, L113, doi: 10.1086/510015
- Miller et al. (2009) Miller, J. M., Reynolds, C. S., Fabian, A. C., Miniutti, G., & Gallo, L. C. 2009, ApJ, 697, 900, doi: 10.1088/0004-637X/697/1/900
- Miller et al. (2019) Miller, J. M., Zoghbi, A., Gandhi, P., & Paice, J. 2019, The Astronomer’s Telegram, 13012, 1
- Miller-Jones et al. (2019) Miller-Jones, J., Russell, T., Sivakoff, G., & Tetarenko, A. 2019, The Astronomer’s Telegram, 12977, 1
- Mitsuda et al. (1984) Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741
- Motta et al. (2012) Motta, S., Homan, J., Muñoz Darias, T., et al. 2012, MNRAS, 427, 595, doi: 10.1111/j.1365-2966.2012.22037.x
- Motta (2016) Motta, S. E. 2016, Astronomische Nachrichten, 337, 398, doi: 10.1002/asna.201612320
- Muñoz-Darias et al. (2011) Muñoz-Darias, T., Motta, S., Stiele, H., & Belloni, T. M. 2011, MNRAS, 415, 292, doi: 10.1111/j.1365-2966.2011.18702.x
- Narayan & Yi (1995) Narayan, R., & Yi, I. 1995, ApJ, 452, 710, doi: 10.1086/176343
- Negoro et al. (2019) Negoro, H., Nakajima, M., Sugita, S., et al. 2019, The Astronomer’s Telegram, 12968, 1
- Özel et al. (2010) Özel, F., Psaltis, D., Narayan, R., & McClintock, J. E. 2010, ApJ, 725, 1918, doi: 10.1088/0004-637X/725/2/1918
- Parker et al. (2015) Parker, M. L., Tomsick, J. A., Miller, J. M., et al. 2015, ApJ, 808, 9, doi: 10.1088/0004-637X/808/1/9
- Parmar et al. (1993) Parmar, A. N., Angelini, L., Roche, P., & White, N. E. 1993, A&A, 279, 179
- Peris et al. (2016) Peris, C. S., Remillard, R. A., Steiner, J. F., et al. 2016, ApJ, 822, 60, doi: 10.3847/0004-637X/822/2/60
- Plotkin et al. (2015) Plotkin, R. M., Gallo, E., Markoff, S., et al. 2015, MNRAS, 446, 4098, doi: 10.1093/mnras/stu2385
- Reis et al. (2010) Reis, R. C., Fabian, A. C., & Miller, J. M. 2010, MNRAS, 402, 836, doi: 10.1111/j.1365-2966.2009.15976.x
- Reis et al. (2009) Reis, R. C., Fabian, A. C., Ross, R. R., & Miller, J. M. 2009, MNRAS, 395, 1257, doi: 10.1111/j.1365-2966.2009.14622.x
- Reis et al. (2008) Reis, R. C., Fabian, A. C., Ross, R. R., et al. 2008, MNRAS, 387, 1489, doi: 10.1111/j.1365-2966.2008.13358.x
- Remillard & McClintock (2006) Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49, doi: 10.1146/annurev.astro.44.051905.092532
- Reynolds (2014) Reynolds, C. S. 2014, Space Sci. Rev., 183, 277, doi: 10.1007/s11214-013-0006-6
- Reynolds & Miller (2013) Reynolds, M. T., & Miller, J. M. 2013, ApJ, 769, 16, doi: 10.1088/0004-637X/769/1/16
- Salvesen & Miller (2021) Salvesen, G., & Miller, J. M. 2021, MNRAS, 500, 3640, doi: 10.1093/mnras/staa3325
- Salvesen et al. (2013) Salvesen, G., Miller, J. M., Reis, R. C., & Begelman, M. C. 2013, MNRAS, 431, 3510, doi: 10.1093/mnras/stt436
- Shafee et al. (2006) Shafee, R., McClintock, J. E., Narayan, R., et al. 2006, ApJ, 636, L113, doi: 10.1086/498938
- Shimura & Takahara (1995) Shimura, T., & Takahara, F. 1995, ApJ, 445, 780, doi: 10.1086/175740
- Sidoli et al. (2017) Sidoli, L., Tiengo, A., Paizis, A., et al. 2017, ApJ, 838, 133, doi: 10.3847/1538-4357/aa671a
- Soria et al. (2008) Soria, R., Wu, K., & Kunic, Z. 2008, in X-rays From Nearby Galaxies, ed. S. Carpano, M. Ehle, & W. Pietsch, 48–51. https://arxiv.org/abs/0711.2448
- Sridhar et al. (2020) Sridhar, N., García, J. A., Steiner, J. F., et al. 2020, ApJ, 890, 53, doi: 10.3847/1538-4357/ab64f5
- Steiner et al. (2017) Steiner, J. F., García, J. A., Eikmann, W., et al. 2017, ApJ, 836, 119, doi: 10.3847/1538-4357/836/1/119
- Steiner et al. (2009) Steiner, J. F., Narayan, R., McClintock, J. E., & Ebisawa, K. 2009, PASP, 121, 1279, doi: 10.1086/648535
- Steiner et al. (2011) Steiner, J. F., Reis, R. C., McClintock, J. E., et al. 2011, MNRAS, 416, 941, doi: 10.1111/j.1365-2966.2011.19089.x
- Stella & Vietri (1998) Stella, L., & Vietri, M. 1998, ApJ, 492, L59, doi: 10.1086/311075
- Sunyaev & Titarchuk (1980) Sunyaev, R. A., & Titarchuk, L. G. 1980, A&A, 500, 167
- Tanaka & Shibazaki (1996) Tanaka, Y., & Shibazaki, N. 1996, ARA&A, 34, 607, doi: 10.1146/annurev.astro.34.1.607
- Tang et al. (2011) Tang, J., Yu, W.-F., & Yan, Z. 2011, Research in Astronomy and Astrophysics, 11, 434, doi: 10.1088/1674-4527/11/4/006
- Tao et al. (2015) Tao, L., Tomsick, J. A., Walton, D. J., et al. 2015, ApJ, 811, 51, doi: 10.1088/0004-637X/811/1/51
- Tao et al. (2018) Tao, L., Chen, Y., Güngör, C., et al. 2018, MNRAS, 480, 4443, doi: 10.1093/mnras/sty2157
- Tetarenko et al. (2016) Tetarenko, B. E., Sivakoff, G. R., Heinke, C. O., & Gladstone, J. C. 2016, ApJS, 222, 15, doi: 10.3847/0067-0049/222/2/15
- Tomsick & Kaaret (2000) Tomsick, J. A., & Kaaret, P. 2000, ApJ, 537, 448, doi: 10.1086/308999
- van der Klis (2006) van der Klis, M. 2006, Rapid X-ray Variability, Vol. 39, 39–112
- Varniere & Vincent (2016) Varniere, P., & Vincent, F. H. 2016, A&A, 591, A36, doi: 10.1051/0004-6361/201527711
- Wang et al. (2020) Wang, Y., Ji, L., Zhang, S. N., et al. 2020, ApJ, 896, 33, doi: 10.3847/1538-4357/ab8db4
- Wang et al. (2021) Wang, Y., Ji, L., García, J. A., et al. 2021, ApJ, 906, 11, doi: 10.3847/1538-4357/abc55e
- Williams et al. (2019) Williams, D., Fender, R., Woudt, P., & Miller-Jones, J. 2019, The Astronomer’s Telegram, 12992, 1
- Wilms et al. (2000) Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914, doi: 10.1086/317016
- Yan & Yu (2015) Yan, Z., & Yu, W. 2015, ApJ, 805, 87, doi: 10.1088/0004-637X/805/2/87
- Yang et al. (2019a) Yang, Y.-J., Soria, R., Russell, D., et al. 2019a, The Astronomer’s Telegram, 13036, 1
- Yang et al. (2019b) Yang, Y.-J., Xiao, G., Soria, R., et al. 2019b, The Astronomer’s Telegram, 13037, 1
- Yao et al. (2005) Yao, Y., Zhang, S. N., Zhang, X., Feng, Y., & Robinson, C. R. 2005, ApJ, 619, 446, doi: 10.1086/426374
- Zdziarski et al. (2021) Zdziarski, A. A., De Marco, B., Szanecki, M., Niedźwiecki, A., & Markowitz, A. 2021, ApJ, 906, 69, doi: 10.3847/1538-4357/abca9c
- Zhang et al. (2020a) Zhang, L., Altamirano, D., Cúneo, V. A., et al. 2020a, MNRAS, 499, 851, doi: 10.1093/mnras/staa2842
- Zhang et al. (2014) Zhang, S., Lu, F. J., Zhang, S. N., & Li, T. P. 2014, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 9144, Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray, ed. T. Takahashi, J.-W. A. den Herder, & M. Bautz, 914421, doi: 10.1117/12.2054144
- Zhang et al. (1997a) Zhang, S. N., Cui, W., & Chen, W. 1997a, ApJ, 482, L155, doi: 10.1086/310705
- Zhang et al. (1997b) Zhang, S. N., Ebisawa, K., Sunyaev, R., et al. 1997b, ApJ, 479, 381, doi: 10.1086/303870
- Zhang et al. (2020b) Zhang, S.-N., Li, T., Lu, F., et al. 2020b, Science China Physics, Mechanics, and Astronomy, 63, 249502, doi: 10.1007/s11433-019-1432-6
- Zhang et al. (2022) Zhang, W., Tao, L., Soria, R., et al. 2022, arXiv e-prints, arXiv:2201.11919. https://arxiv.org/abs/2201.11919
| ExpIDa | Start Time | Start Time | HE Rateb | ME Ratec | LE Rated | HE Expe | ME Exp | LE Exp | state |
| (day) | (MJD) | (cts ) | (cts ) | (cts ) | (s) | (s) | (s) | ||
| 0101 | 2019-08-02T06:14:48 | 58697.35 | 3001 | 2359 | 718 | LHS | |||
| 0102 | 2019-08-02T10:09:02 | 58697.50 | 3062 | 1964 | 1436 | LHS | |||
| 0103 | 2019-08-02T13:19:55 | 58697.63 | 2816 | 1823 | 762 | LHS | |||
| 0104 | 2019-08-02T16:30:48 | 58697.78 | 1987 | 1703 | 718 | LHS | |||
| 0105 | 2019-08-02T19:41:41 | 58697.95 | 616 | 1637 | 1715 | LHS | |||
| 0106 | 2019-08-02T22:52:33 | 58698.03 | 2896 | 1890 | 563 | LHS | |||
| 0107 | 2019-08-03T02:03:26 | 58698.18 | 447 | 1350 | 656 | LHS | |||
| 0201 | 2019-08-04T07:33:08 | 58699.40 | 3892 | 2751 | 690 | LHS | |||
| 0301 | 2019-08-05T07:24:32 | 58700.39 | 3643 | 2540 | 700 | HIMS | |||
| 0302 | 2019-08-05T11:18:58 | 58700.55 | 2548 | 1500 | 1102 | HIMS | |||
| 0303 | 2019-08-05T14:29:49 | 58700.66 | 1421 | 848 | 299 | HIMS | |||
| 0401 | 2019-08-06T02:29:39 | 58701.26 | 500 | 287 | 299 | HIMS | |||
| 0502 | 2019-08-07T05:47:50 | 58702.32 | 2768 | 1880 | 691 | HIMS | |||
| 0503 | 2019-08-07T09:26:08 | 58702.45 | 1255 | 794 | 539 | HIMS | |||
| 0601 | 2019-08-08T02:12:29 | 58703.21 | 768 | 1311 | 1130 | HIMS | |||
| 0701 | 2019-08-08T21:17:40 | 58703.94 | 2549 | 1564 | 1163 | HIMS | |||
| 0703 | 2019-08-09T03:48:43 | 58704.20 | 1659 | 1314 | 838 | HIMS | |||
| 0801 | 2019-08-10T06:41:48 | 58705.36 | 1883 | 2147 | 1592 | HIMS | |||
| 0802 | 2019-08-10T10:35:08 | 58705.53 | 2742 | 1864 | 1371 | HIMS | |||
| 0803 | 2019-08-10T13:45:57 | 58705.63 | 814 | 959 | 658 | HIMS | |||
| 0901 | 2019-08-13T01:30:34 | 58708.17 | 1836 | 1266 | 835 | HIMS | |||
| 0902 | 2019-08-13T05:22:20 | 58708.30 | 2421 | 1631 | 1197 | HIMS | |||
| 1001 | 2019-08-16T12:15:31 | 58711.55 | 1164 | 2994 | 2765 | HIMS | |||
| 1002 | 2019-08-16T16:03:46 | 58711.75 | 2247 | 1777 | 1736 | HIMS | |||
| 1003 | 2019-08-16T19:14:36 | 58711.85 | 696 | 671 | 599 | HIMS | |||
| 1101 | 2019-08-18T07:14:35 | 58713.38 | 3342 | 2324 | 2072 | HIMS | |||
| 1102 | 2019-08-18T11:00:05 | 58713.50 | 1538 | 2202 | 1975 | HIMS | |||
| 1103 | 2019-08-18T14:10:56 | 58713.70 | 264 | 1255 | 1229 | HIMS | |||
| 1301 | 2019-08-22T06:47:11 | 58717.38 | 2714 | 1867 | 1399 | SIMS | |||
| 1303 | 2019-08-22T13:36:56 | 58717.68 | 917 | 589 | 599 | SIMS | |||
| 1501 | 2019-08-27T18:51:16 | 58722.88 | 3534 | 3039 | 2119 | SIMS | |||
| 1601 | 2019-08-28T21:53:27 | 58723.99 | 4836 | 3419 | 1541 | SIMS | |||
| 1701 | 2019-09-03T01:55:34 | 58729.16 | 2048 | 1370 | 397 | SIMS | |||
| 1702 | 2019-09-03T05:25:45 | 58729.31 | 556 | 2391 | 1257 | SIMS | |||
| 1703 | 2019-09-03T08:44:47 | 58729.44 | 3297 | 2398 | 1217 | SIMS | |||
| 1801 | 2019-09-05T12:45:46 | 58731.63 | 1901 | 3967 | 1533 | SIMS | |||
| 1901 | 2019-09-07T17:14:33 | 58733.82 | 3952 | 2610 | 2040 | HSS | |||
| 2201 | 2019-09-15T01:49:09 | 58741.21 | 1666 | 1839 | 718 | HSS | |||
| 2202 | 2019-09-15T05:20:18 | 58741.31 | 3896 | 2486 | 1436 | HSS | |||
| 2204 | 2019-09-15T11:52:26 | 58741.57 | 2889 | 1967 | 2179 | HSS | |||
| 2205 | 2019-09-15T15:03:15 | 58741.70 | 2876 | 1920 | 2155 | HSS | |||
| 2206 | 2019-09-15T18:14:04 | 58741.84 | 2037 | 1348 | 1162 | HSS | |||
| 2208 | 2019-09-16T00:35:41 | 58742.10 | 480 | 1047 | 838 | HSS | |||
| 2209 | 2019-09-16T03:46:30 | 58742.24 | 3889 | 2584 | 838 | HSS | |||
| 2210 | 2019-09-16T06:52:15 | 58742.33 | 1752 | 2313 | 958 | HSS | |||
| 2211 | 2019-09-16T10:08:08 | 58742.53 | 1437 | 2046 | 1482 | HSS | |||
| 2212 | 2019-09-16T13:18:57 | 58742.63 | 2928 | 1977 | 2274 | HSS | |||
| 2213 | 2019-09-16T16:29:46 | 58742.76 | 2645 | 1785 | 1556 | HSS | |||
| 2214 | 2019-09-16T19:40:35 | 58742.89 | 824 | 555 | 359 | HSS | |||
| 2215 | 2019-09-16T22:51:24 | 58743.03 | 286 | 387 | 619 | HSS | |||
| 2301 | 2019-09-19T14:02:31 | 58745.71 | 3672 | 2490 | 2693 | HSS | |||
| 2401 | 2019-09-21T04:14:14 | 58747.21 | 1873 | 3466 | 2858 | HSS | |||
| 2601 | 2019-09-23T02:23:00 | 58749.19 | 3664 | 3677 | 2274 | HSS | |||
| 2701 | 2019-09-25T00:31:11 | 58751.14 | 4617 | 3725 | 1855 | HSS | |||
| 2801 | 2019-09-26T00:22:50 | 58752.13 | 3701 | 3639 | 1556 | HSS | |||
| 2901 | 2019-09-27T09:46:58 | 58753.51 | 4988 | 3443 | 1377 | HSS | |||
| 3001 | 2019-09-29T22:13:09 | 58756.03 | 4537 | 3129 | 1317 | HSS | |||
| 3102 | 2019-10-01T04:34:57 | 58757.28 | 2925 | 1884 | 761 | HSS | |||
| 3103 | 2019-10-01T08:01:33 | 58757.40 | 2768 | 1874 | 479 | HSS | |||
| 3203 | 2019-10-03T07:45:33 | 58759.39 | 2531 | 1726 | 898 | HSS | |||
| 3301 | 2019-10-05T05:26:59 | 58761.30 | 4398 | 2966 | 1736 | HSS | |||
| 3302 | 2019-10-05T09:04:46 | 58761.46 | 3211 | 2074 | 388 | HSS | |||
| 3303 | 2019-10-05T12:15:40 | 58761.56 | 1143 | 712 | 239 | HSS | |||
| 3401 | 2019-10-07T00:23:37 | 58763.14 | 532 | 1240 | 562 | HSS | |||
| 3402 | 2019-10-07T03:41:08 | 58763.23 | 3444 | 2344 | 599 | HSS | |||
| 3403 | 2019-10-07T07:12:40 | 58763.36 | 1914 | 1217 | 239 | HSS | |||
| 3701 | 2019-10-11T07:47:38 | 58767.40 | 3206 | 2047 | 1240 | HSS | |||
| 3702 | 2019-10-11T11:24:31 | 58767.53 | 1534 | 2150 | 1017 | HSS | |||
| 3802 | 2019-10-13T23:15:55 | 58770.05 | 2602 | 2095 | 2028 | HSS | |||
| 3803 | 2019-10-14T03:00:59 | 58770.21 | 1841 | 1230 | 1017 | HSS | |||
| 3901 | 2019-10-16T03:56:56 | 58772.26 | 2611 | 1735 | 1197 | HSS | |||
| 3902 | 2019-10-16T07:29:26 | 58772.40 | 2920 | 1950 | 1676 | HSS | |||
| 4602 | 2019-10-20T19:37:11 | 58776.89 | 1764 | 1382 | 1317 | HSS | |||
| 4603 | 2019-10-20T22:48:00 | 58777.03 | 2316 | 1562 | 1436 | HSS | |||
| 4701 | 2019-10-22T06:19:14 | 58778.35 | 1516 | 2122 | 2095 | HSS | |||
| 4702 | 2019-10-22T09:47:07 | 58778.52 | 1097 | 2050 | 2214 | HSS | |||
| 4703 | 2019-10-22T12:57:58 | 58778.62 | 1659 | 1459 | 1356 | HSS | |||
| 4801 | 2019-10-23T23:40:30 | 58780.07 | 2534 | 1702 | 1616 | HSS | |||
| 4803 | 2019-10-24T06:18:54 | 58780.31 | 1503 | 1839 | 1637 | HSS | |||
| 4901 | 2019-10-25T05:53:35 | 58781.30 | 1310 | 2188 | 2274 | HSS | |||
| 4902 | 2019-10-25T09:21:10 | 58781.48 | 1655 | 1866 | 2211 | HSS | |||
| 4903 | 2019-10-25T12:32:02 | 58781.57 | 1204 | 1263 | 898 | HSS |
| ExpID | Model | k | /dof | ||||||||
| (keV) | (keV) | (keV) | (keV) | ||||||||
| 0101 | CDa | … | … | 1280.8/1302 | |||||||
| 0102 | CD | … | … | 1328.6/1443 | |||||||
| 0103 | CD | … | … | 1336.9/1442 | |||||||
| 0104 | CD | … | … | 1388.9/1401 | |||||||
| 0105 | CD | … | … | 1364.9/1470 | |||||||
| 0106 | CD | … | … | 1231.5/1224 | |||||||
| 0107 | CD | … | … | 1222.4/1281 | |||||||
| 0201 | CD | … | … | 1197.2/1342 | |||||||
| 0301 | CDGb | 1250.3/1325 | |||||||||
| 0302 | CDG | 1232.1/1378 | |||||||||
| 0303 | CDG | 995.1/1137 | |||||||||
| 0502 | CDG | 1235.5/1323 | |||||||||
| 0503 | CDG | 1128.0/1264 | |||||||||
| 0601 | CDG | 1268.5/1394 | |||||||||
| 0701 | CDG | 1324.9/1435 | |||||||||
| 0703 | CDG | 1222.0/1351 | |||||||||
| 0802 | CDG | 1328.3/1417 | |||||||||
| 0803 | CDG | 1214.4/1299 | |||||||||
| 0901 | CDG | 1234.3/1329 | |||||||||
| 0902 | CDG | 1285.6/1423 | |||||||||
| 1001 | CDG | 1323.7/1469 | |||||||||
| 1002 | CDG | 1205.3/1424 | |||||||||
| 1003 | CDG | 1084.8/1256 | |||||||||
| 1101 | CDG | 1281.5/1461 | |||||||||
| 1102 | CDG | 1195.0/1443 | |||||||||
| 1103 | CDG | 1123.4/1352 | |||||||||
| 1301 | CD | … | … | 1134.7/1280 | |||||||
| 1303 | CD | … | … | 944.3/1125 | |||||||
| 1501 | CD | … | … | 1213.4/1285 | |||||||
| 1601 | CD | … | … | 1322.7/1347 | |||||||
| 1701 | CD | … | … | 1047.1/1120 | |||||||
| 1702 | CD | … | … | 1188.9/1242 | |||||||
| 1703 | CD | … | … | 1252.6/1334 | |||||||
| 1801 | CD | … | … | 1615.0/1478 | |||||||
| 1901 | CD | … | … | 1400.2/1433 | |||||||
| 2201 | CD | … | … | 1121.2/1261 | |||||||
| 2202 | CD | … | … | 1129.2/1212 | |||||||
| 2204 | CD | … | … | 1332.5/1241 | |||||||
| 2205 | CD | … | … | 1361.1/1355 | |||||||
| 2206 | CD | … | … | 1219.1/1225 | |||||||
| 2208 | CD | … | … | 1091.1/1192 | |||||||
| 2209 | CD | … | … | 1180.3/1259 | |||||||
| 2210 | CD | … | … | 1151.6/1149 | |||||||
| 2211 | CD | … | … | 1093.9/1196 | |||||||
| 2212 | CD | … | … | 1278.0/1315 | |||||||
| 2213 | CD | … | … | 1189.9/1284 | |||||||
| 2214 | CD | … | … | 989.4/1095 | |||||||
| 2215 | CD | … | … | 1312.9/1159 | |||||||
| 2301 | CD | … | … | 1327.1/1407 | |||||||
| 2401 | CD | … | … | 1257.3/1377 | |||||||
| 2601 | CD | … | … | 1422.5/1423 | |||||||
| 2701 | CD | … | … | 1393.7/1464 | |||||||
| 2801 | CD | … | … | 1361.1/1376 | |||||||
| 2901 | CD | … | … | 1120.2/1197 | |||||||
| 3001 | CD | … | … | 1194.6/1238 | |||||||
| 3102 | CD | … | … | 1098.9/1234 | |||||||
| 3103 | CD | … | … | 1094.3/1195 | |||||||
| 3203 | CD | … | … | 1084.7/1177 | |||||||
| 3301 | CD | … | … | 1287.7/1304 | |||||||
| 3302 | CD | … | … | 1150.9/1277 | |||||||
| 3303 | CD | … | … | 1079.1/1150 | |||||||
| 3401 | CD | … | … | 999.4/1150 | |||||||
| 3402 | CD | … | … | 940.5/1127 | |||||||
| 3403 | CD | … | … | 973.1/1094 | |||||||
| 3701 | CD | … | … | 1155.2/1211 | |||||||
| 3702 | CD | … | … | 1135.6/1309 | |||||||
| 3802 | CD | … | … | 1091.6/1155 | |||||||
| 3803 | CD | … | … | 985.5/1151 | |||||||
| 3901 | CD | … | … | 1008.9/1181 | |||||||
| 3902 | CD | … | … | 1033.9/1217 | |||||||
| 4602 | CD | … | … | 1026.0/1209 | |||||||
| 4603 | CD | … | … | 1124.0/1195 | |||||||
| 4701 | CD | … | … | 1009.0/1200 | |||||||
| 4702 | CD | … | … | 1160.7/1320 | |||||||
| 4703 | CD | … | … | 1110.5/1255 | |||||||
| 4801 | CD | … | … | 1027.2/1241 | |||||||
| 4803 | CD | … | … | 1121.5/1261 | |||||||
| 4901 | CD | … | … | 1180.2/1316 | |||||||
| 4902 | CD | … | … | 1099.1/1327 | |||||||
| 4903 | CD | … | … | 1062.9/1197 |
| ExpID | Model | k | /dof | |||||||||
| (keV) | (keV) | (keV) | (keV) | |||||||||
| 0101 | SDa | … | … | 1300.6/1302 | ||||||||
| 0102 | SD | … | … | 1350.8/1443 | ||||||||
| 0103 | SD | … | … | 1358.3/1442 | ||||||||
| 0104 | SD | … | … | 1431.5/1401 | ||||||||
| 0105 | SD | … | … | 1411.3/1470 | ||||||||
| 0106 | SD | … | … | 1238.3/1224 | ||||||||
| 0107 | SD | … | … | 1245.7/1281 | ||||||||
| 0201 | SD | … | … | 1218.3/1342 | ||||||||
| 0301 | SDGb | 1256.9/1325 | ||||||||||
| 0302 | SDG | 1257.8/1378 | ||||||||||
| 0303 | SDG | 1006.9/1137 | ||||||||||
| 0502 | SDG | 1236.3/1323 | ||||||||||
| 0503 | SDG | 1130.7/1264 | ||||||||||
| 0601 | SDG | 1301.4/1394 | ||||||||||
| 0701 | SDG | 1294.0/1435 | ||||||||||
| 0703 | SDG | 1216.5/1351 | ||||||||||
| 0802 | SDG | 1320.0/1417 | ||||||||||
| 0803 | SDG | 1209.3/1299 | ||||||||||
| 0901 | SDG | 1262.7/1329 | ||||||||||
| 0902 | SDG | 1325.2/1423 | ||||||||||
| 1001 | SDG | 1373.2/1469 | ||||||||||
| 1002 | SDG | 1303.8/1424 | ||||||||||
| 1003 | SDG | 1117.2/1256 | ||||||||||
| 1101 | SDG | 1289.1/1461 | ||||||||||
| 1102 | SDG | 1222.9/1443 | ||||||||||
| 1103 | SDG | 1149.3/1352 | ||||||||||
| 1301 | SD | … | … | 1147.3/1280 | ||||||||
| 1303 | SD | … | … | 947.5/1125 | ||||||||
| 1501 | SD | … | … | 1229.0/1285 | ||||||||
| 1601 | SD | … | … | 1338.5/1347 | ||||||||
| 1701 | SD | … | … | 1048.9/1120 | ||||||||
| 1702 | SD | … | … | 1210.6/1242 | ||||||||
| 1703 | SD | … | … | 1283.4/1334 | ||||||||
| 1801 | SD | … | … | 1650.3/1478 | ||||||||
| 1901 | SD | … | … | 1466.7/1433 | ||||||||
| 2201 | SD | … | … | 1134.4/1261 | ||||||||
| 2202 | SD | … | … | 1140.3/1212 | ||||||||
| 2204 | SD | … | … | 1365.4/1241 | ||||||||
| 2205 | SD | … | … | 1413.3/1355 | ||||||||
| 2206 | SD | … | … | 1241.5/1225 | ||||||||
| 2208 | SD | … | … | 1106.1/1192 | ||||||||
| 2209 | SD | … | … | 1202.7/1259 | ||||||||
| 2210 | SD | … | … | 1163.5/1149 | ||||||||
| 2211 | SD | … | … | 1109.4/1196 | ||||||||
| 2212 | SD | … | … | 1301.9/1315 | ||||||||
| 2213 | SD | … | … | 1221.2/1284 | ||||||||
| 2214 | SD | … | … | 994.4/1095 | ||||||||
| 2215 | SD | … | … | 1323.5/1159 | ||||||||
| 2301 | SD | … | … | 1357.7/1407 | ||||||||
| 2401 | SD | … | … | 1284.8/1377 | ||||||||
| 2601 | SD | … | … | 1467.1/1423 | ||||||||
| 2701 | SD | … | … | 1433.3/1464 | ||||||||
| 2801 | SD | … | … | 1393.1/1376 | ||||||||
| 2901 | SD | … | … | 1144.1/1197 | ||||||||
| 3001 | SD | … | … | 1214.8/1238 | ||||||||
| 3102 | SD | … | … | 1110.8/1234 | ||||||||
| 3103 | SD | … | … | 1093.6/1195 | ||||||||
| 3203 | SD | … | … | 1095.1/1177 | ||||||||
| 3301 | SD | … | … | 1290.4/1304 | ||||||||
| 3302 | SD | … | … | 1152.6/1277 | ||||||||
| 3303 | SD | … | … | 1084.2/1150 | ||||||||
| 3401 | SD | … | … | 1005.8/1150 | ||||||||
| 3402 | SD | … | … | 952.9/1127 | ||||||||
| 3403 | SD | … | … | 981.4/1094 | ||||||||
| 3701 | SD | … | … | 1169.9/1211 | ||||||||
| 3702 | SD | … | … | 1155.1/1309 | ||||||||
| 3802 | SD | … | … | 1096.9/1155 | ||||||||
| 3803 | SD | … | … | 995.1/1151 | ||||||||
| 3901 | SD | … | … | 1014.5/1181 | ||||||||
| 3902 | SD | … | … | 1047.0/1217 | ||||||||
| 4602 | SD | … | … | 1028.6/1209 | ||||||||
| 4603 | SD | … | … | 1127.4/1195 | ||||||||
| 4701 | SD | … | … | 1010.6/1200 | ||||||||
| 4702 | SD | … | … | 1189.3/1320 | ||||||||
| 4703 | SD | … | … | 1130.8/1255 | ||||||||
| 4801 | SD | … | … | 1039.6/1241 | ||||||||
| 4803 | SD | … | … | 1132.0/1261 | ||||||||
| 4901 | SD | … | … | 1192.4/1316 | ||||||||
| 4902 | SD | … | … | 1123.0/1327 | ||||||||
| 4903 | SD | … | … | 1074.9/1197 |