INK: Injecting $k$ NN Knowledge in Nearest Neighbor Machine Translation

Wenhao Zhu¹ , Jingjing Xu² , Shujian Huang¹ , Lingpeng Kong³, Jiajun Chen¹
¹ National Key Laboratory for Novel Software Technology, Nanjing University
² Shanghai AI Laboratory ³ The University of Hong Kong
[email protected], [email protected]
[email protected], [email protected], [email protected]

Abstract

Neural machine translation has achieved promising results on many translation tasks. However, previous studies have shown that neural models induce a non-smooth representation space, which harms its generalization results. Recently, $k$ NN-MT has provided an effective paradigm to smooth the prediction based on neighbor representations during inference. Despite promising results, $k$ NN-MT usually requires large inference overhead. We propose an effective training framework INK to directly smooth the representation space via adjusting representations of $k$ NN neighbors with a small number of new parameters. The new parameters are then used to refresh the whole representation datastore to get new $k$ NN knowledge asynchronously. This loop keeps running until convergence. Experiments on four benchmark datasets show that INK achieves average gains of 1.99 COMET and 1.0 BLEU, outperforming the state-of-the-art $k$ NN-MT system with $\textrm{0.02}\times$ memory space and 1.9 $\times$ inference speedup¹¹1Code will be released at https://github.com/OwenNJU/INK.

1 Introduction

Neural machine translation (NMT) have achieved promising results in recent years Vaswani et al. (2017); Ng et al. (2019); Qian et al. (2021b). The target of NMT is to learn a generalized representation space to adapt to diverse scenarios. However, recent studies have shown that neural networks, such as BERT and GPT, induce non-smooth representation space, limiting the generalization abilities Gao et al. (2018); Ethayarajh (2019); Li et al. (2020). In NMT, we also observe a similar phenomenon in the learned representation space where low-frequency tokens disperse sparsely, even for a strong NMT model (More details are described in Section Experiments). Due to the sparsity, many “holes” could be formed. When it is used to translate examples from an unseen domain, the performance drops sharply Wang et al. (2022a, b)

Recently, $k$ -Nearest-Neighbor Machine Translation ( $k$ NN-MT) (Khandelwal et al., 2021) provides an effective solution to smooth predictions by equipping an NMT model with a key-value datastore. For each entry, the value is the target token and key is the contextualized representation at the target position. It requires a training set to record tokens and representations. By aggregating nearest neighbors during inference, the NMT model can achieve decent translation results Khandelwal et al. (2021); Zheng et al. (2021); Jiang et al. (2022). Despite the success, $k$ NN-MT also brings new issues with the increasing scale of training data. Retrieving neighbors from a large datastore Wang et al. (2022a) at each decoding step is time-consuming Martins et al. (2022a); Meng et al. (2022). Furthermore, once the datastore is constructed, representations can not be easily updated, limiting the performance ceiling of $k$ NN-MT.

Refer to caption — Figure 1: The overview of our training loop. We refine the representation space of an NMT model according to the extracted $k$ NN knowledge. The new parameters are then used to refresh the datastore to update $k$ NN knowledge asynchronously.

Given above strengths and weaknesses of $k$ NN-MT, we propose to directly smooth the representation space with a small number of parameters. In this paper, we propose a training framework INK, to iteratively refine the representation space with the help of extracted $k$ NN knowledge (Fig. 1). Specifically, we adjust the representation distribution by aligning three kinds of representations with Kullback-Leibler (KL) divergence to train a small number of adaptation parameters. First, we align the contextualized representation and its target embedding to keep semantic meanings. Second, we align the contextualized representations of a target token and align the extracted $k$ NN contextualized representations to address the sparsely dispersing problem. After a training epoch, we refresh the datastore asynchronously with refined models to update $k$ NN representations. During inference, we only load the off-the-shelf NMT model and tune adaptation parameters.

We conduct experiments on four benchmark datasets. Experiment results show that our framework brings average gains of 1.99 COMET and 1.0 BLEU. Compared with the state-of-the-art $k$ NN-MT method (i.e. Robust $k$ NN-MT; Jiang et al. 2022), INK achieves better translation performance with 0.02 $\times$ memory space and 1.9 $\times$ inference speed. Our contributions can be summarized below:

•

We propose a training framework to smooth the representation space according to $k$ NN knowledge.
•

We devise an inject-and-refine training loop in our framework. Experiments show that refreshing the datastore asynchronously matters.
•

Our INK system achieves promising improvements and beats the state-of-the-art $k$ NN-MT system.

2 Background

This section briefly introduces the working process of $k$ NN-MT and the architecture of adapter Bapna and Firat (2019). For the latter, we will use it to improve the representation space in our framework.

2.1 $k$ NN-MT

Given an off-the-shelf NMT model $\mathcal{M}$ and training set $\mathcal{C}$ , $k$ NN-MT memorizes training examples explicitly with a key-value datastore $\mathcal{D}$ and use $\mathcal{D}$ to assist the NMT model during inference.

Memorize representations into datastore

Specifically, we feed training example $(X,Y)$ in $\mathcal{C}$ into $\mathcal{M}$ in a teacher-forcing manner Williams and Zipser (1989). At time step $t$ , we record the contextualized representation²²2By default, the last decoder layer’s output is used as the contextualized representation of the translation context ( $X,Y_{<t}$ ). ${h_{t}}$ as key and the corresponding target token $y_{t}$ as value. We then put the key-value pair into the datastore. In this way, the full datastore $\mathcal{D}$ can be created through a single forward pass over the training dataset $\mathcal{C}$ :

\mathcal{D}=\{(h_{t},y_{t})~{}|~{}\forall y_{t}\in Y,(X,Y)\in\mathcal{C}\}

(1)

where each datastore entry explicitly memorizes the mapping relationship between the representation $h_{t}$ and its target token $y_{t}$ .

Translate with memorized representations

During inference, the contextualized representation of the test translation context $(X,Y_{<t})$ will be used to query the datastore for nearest neighbor representations and their corresponding target tokens $\mathcal{N}_{k}=\{(\hat{h},\hat{y})\}_{1}^{k}$ . Then, the retrieved entries are converted to a distribution over the vocabulary:

p_{\text{knn}}(y|X,Y_{<t})\propto\sum_{(\hat{h},\hat{y})\in\mathcal{N}_{k}}\mathbbm{1}(y=\hat{y})e^{\frac{-d(h_{t},\hat{h})}{T}}

(2)

where $h_{t}$ denotes $h(X,Y_{<t})$ for short, $d$ measures Euclidean distance and $T$ is the temperature.

2.2 Adapter

Previous research shows that adapter can be an efficient plug-and-play module for adapting an NMT model Bapna and Firat (2019). In common, the adapter layer is inserted after each encoder and decoder layer of $\mathcal{M}$ . The architecture of the adapter layer is simple, which includes a feed-forward layer and a normalization layer. Given the output vector $z\in\mathcal{R}^{d}$ of a specific encoder/decoder layer, the computation result of the adapter layer can be written as:

\widetilde{z}=W_{2}^{T}[W_{1}^{T}\cdot f(z)]+z

(3)

where $f$ denotes layer-normalization, $W_{1}\in\mathcal{R}^{d\times d^{\prime}}$ , $W_{2}\in\mathcal{R}^{d^{\prime}\times d}$ are two projection matrices. $d^{\prime}$ is the inner dimension of these two projections. Bias term and activation function is omitted in the equation for clarity. $\widetilde{z}$ is the output of the adapter layer.

3 Approach: INK

This section introduces our training framework INK. The key idea of the proposed approach is to use $k$ NN knowledge to smooth the representation space. The training process is built on a cycled loop: extracting $k$ NN knowledge to adjust representations via a small adapter. The updated parameters are then used to refresh and refine the datastore to get new $k$ NN knowledge. We define three kinds of alignment loss to adjust representations, which are described in Section 3.1, Section 3.2, and Section 3.3. An illustration of the proposed framework is shown in Figure 2.

3.1 Align Contextualized Representations and Token Embeddings

The basic way to optimize the adapter to minimize the KL divergence between the NMT system’s prediction probability $p_{\text{nmt}}$ and the one-hot golden distribution $p_{\text{gold}}$ :

\begin{split}\mathcal{L}^{a}_{t}&=D_{\text{KL}}[\ p_{\text{gold}}(y|X,Y_{<t})\parallel p_{\text{nmt}}(y|X,Y_{<t})\ ]\\ &=-\log\frac{\sum_{(w,v)\in\mathcal{E}}\mathbbm{1}(v=y_{t})\kappa(h_{t},w)}{\sum_{(w,v)\in\mathcal{E}}\kappa(h_{t},w)}\end{split}

where $\mathcal{E}$ is the embedding matrix. $w$ and $v$ denote the token embedding and its corresponding token respectively. $h_{t}$ denotes the contextualized representation $h(X,Y_{<t})$ . $y_{t}$ denotes the target token. $\kappa(h_{t},w)=e^{h_{t}^{T}w}$ . Following the widely-accepted alignment-and-uniformity theory (Wang and Isola, 2020), this learning objective aligns the contextualized representation $h_{t}$ with the tokens embedding of its corresponding target token.

3.2 Align Contextualized Representations and $k$ NN Token Embeddings

Previous research in $k$ NN-MT has shown that the nearest neighbors in the representation space can produce better estimation via aggregating $k$ NN neighbors Khandelwal et al. (2021); Zheng et al. (2021); Yang et al. (2022). Apart from the reference target token, the retrieval results provide some other reasonable translation candidates. Taking the translation case in Figure 2 as an example, retrieval results provide three candidate words, where both “happens” and “occurs” are possible translations. Compared with the basic one-hot supervision signal, the diverse $k$ NN knowledge in the datastore can be beneficial for building a representation space with more expressive abilities.

Therefore, we extract $k$ NN knowledge by using the contextualized representation $h_{t}$ to query the datastore for nearest neighbors $\mathcal{N}_{k}=\{(\hat{h},\hat{y})\}_{1}^{k}$ (illustrated in Fig. 2). For more stable training, we reformulate the computation process of $k$ NN distribution as kernel density estimation (KDE) Parzen (1962).

Formulation

The general idea of KDE is to estimate the probability density of a point by referring to its neighborhood, which shares the same spirit with $k$ NN-MT. The computation of $k$ NN distribution can be written as:

p_{\text{knn}}(y|X,Y_{<t})=\frac{\sum_{(\hat{h},\hat{y})\in\mathcal{N}_{k}}\mathbbm{1}(y=\hat{y})\kappa(h_{t},\hat{h})}{\sum_{(\hat{h},\hat{y})\in\mathcal{N}_{k}}\kappa(h_{t},\hat{h})}

(4)

where $\kappa$ can be set as any kernel function. Thus, Equation 2 can be seen as a special case of Equation 4 by setting $\kappa(\cdot,\cdot)=e^{-d(\cdot,\cdot)/T}$ .

After extracting $k$ NN knowledge, we use it to smooth the representation space by by minimizing the KL divergence between the $k$ NN distribution $p_{\text{knn}}$ and NMT distribution $p_{\text{nmt}}$ :

\begin{split}\mathcal{L}^{i}_{t}&=D_{\text{KL}}[\ p_{\text{knn}}(y|X,Y_{<t})\parallel p_{\text{nmt}}(y|X,Y_{<t})\ ]\\ &=-\sum_{\bar{y}\in\mathcal{Y}}p_{\text{knn}}(\bar{y})\cdot\log\frac{\sum_{(w,v)\in\mathcal{E}}\mathbbm{1}(v=\bar{y})\kappa(h_{t},w)}{\sum_{(w,v)\in\mathcal{E}}\kappa(h_{t},w)\cdot p_{\text{knn}}(\bar{y})}\end{split}

where $\mathcal{Y}$ denotes identical tokens in nearest neighbors $\mathcal{N}_{k}$ and $p_{\text{knn}}(\bar{y})$ denotes $p_{\text{knn}}(y=\bar{y}|X,Y_{<t})$ for short. $\mathcal{E}$ is the embedding matrix. $w$ and $v$ denote the token embedding and its corresponding token respectively. $h_{t}$ denotes $h(X,Y_{<t})$ for short. $\kappa$ is the kernel function. Following the widely-accepted alignment-and-uniformity theory (Wang and Isola, 2020), this learning objective encourages $h_{t}$ to align with the embeddings of retrieved reasonable tokens, e.g., “occurs”, “happens”.

3.3 Align Contextualized Representations of the Same Target Token

Although $k$ NN knowledge could provide fruitful translation knowledge, it is also sometimes noisy Zheng et al. (2021); Jiang et al. (2022). For example, in Figure 2, the retrieved word “works” is a wrong translation here.

To address this problem, we propose to adjust local representation distribution. Specifically, our solution is to optimize the $k$ NN distribution towards the reference distribution by minimizing the KL divergence between the gold distribution $p_{\text{gold}}$ and $k$ NN distribution $p_{\text{knn}}$ . Thanks to the new formulation (Eq. 4), we can choose kernel function here to achieve better stability for gradient optimization. In the end, we find that exponential-cosine kernel works stably in our framework:

\kappa(h,h_{t})=e^{\cos(h,h_{t})}

(5)

Therefore, the loss function can be written as:

\begin{split}\mathcal{L}^{r}_{t}&=D_{\text{KL}}[\ p_{\text{gold}}(y|X,Y_{<t})\parallel p_{\text{knn}}(y|X,Y_{<t})\ ]\\ &=-\log\frac{\sum_{(\hat{h},\hat{y})\in\mathcal{N}_{k}}\mathbbm{1}(\hat{y}=y_{t})\kappa(h_{t},\hat{h})}{\sum_{(\hat{h},\hat{y})\in\mathcal{N}_{k}}\kappa(h_{t},\hat{h})}\\ \end{split}

where $\mathcal{N}_{k}$ is the retrieved k nearest neighbors. $\hat{h}$ and $\hat{y}$ denotes the neighbor representations and the corresponding target token. $h_{t}$ denotes $h(X,Y_{<t})$ for short. Following the widely-accepted alignment-and-uniformity theory (Wang and Isola, 2020), this learning objective aligns the contextualized representation of the same target token. With this goal, we can make the $k$ NN knowledge less noisy in the next training loop by refreshing the datastore with the updated representations.

3.4 Overall Training Procedure

The combined learning objective

To summarize, we adjust representation space via a small adapter with the combination of three alignment loss $\mathcal{L}_{t}^{a}$ , $\mathcal{L}_{t}^{i}$ , $\mathcal{L}_{t}^{r}$ . Given one batch of training examples $\mathcal{B}=\{(X,Y)\}$ , the learning objective is minimizing the following loss:

\mathcal{L}=\frac{1}{|\mathcal{B}|}\sum_{(X,Y)\in\mathcal{B}}\sum_{t}(\mathcal{L}_{t}^{a}+\alpha\mathcal{L}^{i}_{t}+\beta\mathcal{L}^{r}_{t})

(6)

where $\alpha$ , $\beta$ is the interpolation weight. We notice that, in general, all three learning objective pull together closely related vectors and push apart less related vectors in the representation space, which has an interesting connection to contrastive learning Lee et al. (2021); An et al. (2022) by sharing the similar goal.

Refresh datastore asynchronously

In our training loop, once the parameters are updated, we refresh the datastore with the refined representation. In practice, due to the computation cost, we refresh the datastore asynchronously at the end of each training epoch to strike a balance between efficiency and effectiveness As the training reaches convergence, we drop the datastore and only use the optimized adapter to help the off-the-shelf NMT model for the target domain translation.

4 Experiments

4.1 Setting

We introduce the general experiment setting in this section. For fair comparison, we adopt the same setting as previous research of $k$ NN-MT Khandelwal et al. (2021); Zheng et al. (2021); Jiang et al. (2022), e.g., using the same benchmark datasets and NMT model. For training INK, we tune the weight $\alpha$ and $\beta$ among {0.1, 0.2, 0.3}. More implementation details are reported in the appendix.

Target Domain Data

We use four benchmark German-English dataset (Medical, Law, IT, Koran) Tiedemann (2012) and directly use the pre-processed data³³3https://github.com/zhengxxn/adaptive-knn-mt released by Zheng et al. (2021). Statistics of four datasets are listed in Table 1.

Dataset	# Train	# Dev	# Test
Medical	248,099	2,000	2,000
Law	467,309	2,000	2,000
IT	222,927	2,000	2,000
Koran	17,982	2,000	2,000

Table 1: Statistics of four datasets. #Train, #Dev, #Test represent the number of sentence pairs in training, development, and test sets, respectively.

NMT Model

We choose the winner model⁴⁴4https://github.com/facebookresearch/fairseq/tree/main/examples/wmt19 Ng et al. (2019) of WMT’19 German-English news translation task as the off-the-shelf NMT model for translation and datastore construction, which is based on the big Transformer architecture Vaswani et al. (2017).

Systems	Mem.	Medical		Law		IT		Koran		Avg.
Systems		COMET	BLEU	COMET	BLEU	COMET	BLEU	COMET	BLEU	COMET	BLEU
Off-the-shelf NMT	-	46.87	40.00	57.52	45.47	39.22	38.39	-1.32	16.26	35.57	35.03
$k$ NN-KD	-	56.20	56.37	68.60	60.65	-1.57	1.48	-13.05	19.60	27.55	34.53
NMT + Datastore Augmentation
V- $k$ NN	$\times\textrm{1.7}$	53.46	54.27	66.03	61.34	51.72	45.56	0.73	20.61	42.98	45.45
A- $k$ NN	$\times\textrm{1.7}$	57.45	56.21	69.59	63.13	56.89	47.37	4.68	20.44	47.15	46.79
R- $k$ NN^†	$\times\textrm{1.7}$	58.05	54.16	69.10	60.90	54.60	45.61	3.99	20.04	46.44	45.18
R- $k$ NN	$\times\textrm{43.8}$	57.70	57.12	70.10	63.74	57.65	48.50	5.28	20.81	47.68	47.54
NMT + Representation Refinement
Adapter	$\times\textrm{1.0}$	60.14	56.88	70.87	60.64	66.86	48.21	4.23	21.68	50.53	46.85
INK (ours)	$\times\textrm{1.0}$	61.64^∗	57.75^∗	71.13	61.90^∗	68.45^∗	49.12^∗	8.84^∗	23.06^∗	52.52	47.85

Table 2: Results on four datasets. “Mem.” stands for the added memory. “COMET” and “BLEU” are two metrics for evaluating translation performance. Scores shown in bold denote the highest performance among different systems. INK achieves better performance than the state-of-the-art

k

NN-MT system, i.e., R-

k

NN, with the least memory space. INK also outperforms the fine-tuned adapter baseline by a large margin. The annotation “*” indicates that the improvement is siginificant (

p<0.1

). R-

k

NN^† denotes the situation where the key file of R-

k

NN is removed, and the approximate distance is used for inference. We can see that the state-of-the-art

k

NN-MT system still relies on the key file to maintain a high level of translation performance.

Baselines

For comparison, we consider three $k$ NN-MT systems, which use datastore in different fashions. We report the translation performance of the adapter baseline to show the effectiveness of our training framework. Besides, we report the translation performance of $k$ NN-KD, which is another work using $k$ NN knowledge to help NMT.

•

V- $k$ NN Khandelwal et al. (2021), the vanilla version of $k$ -nearest-neighbor machine translation.
•

A- $k$ NN Zheng et al. (2021), an advanced variants of $k$ NN-MT, which dynamically decides the usage of retrieval results and achieve more stable performance.
•

R- $k$ NN Jiang et al. (2022), the state-of-the-art $k$ NN-MT variant, which dynamically calibrates $k$ NN distribution and control more hyperparameters, e.g. temperature, interpolation weight.
•

Adapter Bapna and Firat (2019), adjusting representation by simply align contextualized representation and token embeddings.
•

$k$ NN-KD Yang et al. (2022), aiming at from-scratch train a NMT model by distilling $k$ NN knowledge into it.

Metric

To evaluate translation performance, we use the following two metrics:

•

BLEU Papineni et al. (2002), the standard evaluation metric for machine translation. We report case-sensitive detokenized sacrebleu⁵⁵5https://github.com/mjpost/sacrebleu.
•

COMET Rei et al. (2020), a recently proposed metric, which has stronger correlation with human judgement. We report COMET score computed by publicly available wmt20-comet-da⁶⁶6https://github.com/Unbabel/COMET model.

Approximate Nearest Neighbor Search

We follow previous $k$ NN-MT studies and use Faiss⁷⁷7https://github.com/facebookresearch/faiss index Johnson et al. (2019) to represent the datastore and accelerate nearest neighbors search. Basically, the key file can be removed to save memory space once the index is built. But, it is an exception that R- $k$ NN relies on the key file to re-compute accurate distance between query representation and retrieved representations.

4.2 Main Results

We conduct experiments to explore the following questions to better understand the effectiveness of our proposed framework and relationship between two ways of smoothing predictions:

•

RQ1: Can we smooth the representation space via small adapter and drop datastore aside during inference?
•

RQ2: How much improvement can be brought by using $k$ NN knowledge to adjust the representation distribution?
•

RQ3: Will together using adapter and datastore bring further improvement?

INK system achieves the best performance by smoothing the representation space

Table 2 presents the comparison results of different systems. Due to the poor quality of representation space, the off-the-shelf NMT model does not perform well. The performance of $k$ NN-KD is unstable, e.g., it performs poorly on IT dataset. $k$ NN-MT systems generate more accurate translation. Among them, R- $k$ NN achieves the best performance, which is consistent with previous observation Jiang et al. (2022). Our INK system achieves the best translation performance with the least memory space. Compared with the strongest $k$ NN-MT system, i.e. R- $k$ NN, INK achieves better performance on three out of four domains (Medical, IT, Koran). In average, INK outperforms R- $k$ NN with an improvement of 4.84 COMET and 0.31 BLEU while occupying 0.02 $\times$ memory space.

Representation refinement according to $k$ NN knowledge brings large performance improvement

In Table 2, compared with the adapter baseline that simply align the contextualized representations and word embeddings, INK outperforms it by 1.99 COMET and 1.00 BLEU in average, which demonstrates the effectiveness of adjusting representation distribution with $k$ NN knowledge. To better show the effect of INK framework, we use adapters of different sizes to refine the representation space. Figure 3 shows the BLEU scores and added memory of different systems on four datasets. We can see that representation-refined system occupies much less memory than the datastore-enhanced system. In general, INK systems locates on the top-right of each figure, which means that INK achieves higher BLEU scores with less memory space. In most cases, INK outperforms adapter with a large margin, which demonstrates the superiority of our training framework.

Mean $k$ NN Acc (%)	Systems	[0, 1k)	[1k, 5k)	[5k, 10k)	[10k, 20k)	[20k, 30k)	[30k, 42k)
$k$ =8	NMT	77.75	73.25	71.88	66.00	64.38	51.13
$k$ =8	INK	84.25	79.00	77.63	72.25	70.50	84.13
$k$ =16	NMT	76.25	70.88	69.13	63.19	61.31	34.06
$k$ =16	INK	83.81	77.31	75.75	70.00	67.88	79.50
$k$ =32	NMT	74.59	68.06	66.25	60.19	57.31	30.13
$k$ =32	INK	83.41	75.41	73.50	67.44	54.84	57.09
$k$ =64	NMT	72.97	64.89	62.97	56.67	52.22	28.13
$k$ =64	INK	83.20	73.16	70.80	64.31	60.38	43.05

Table 3: The quality of different systems’ representation space. We use mean

k

NN accuracy as the evaluate metric and evaluate representations correspond to different tokens (the higher the token id, the lower the token frequency.). Bold text denotes the higher score in the two system. INK consistently improves the representation distribution, especially for low-frequency tokens.

Jointly applying adapter and datastore can further smooth predictions

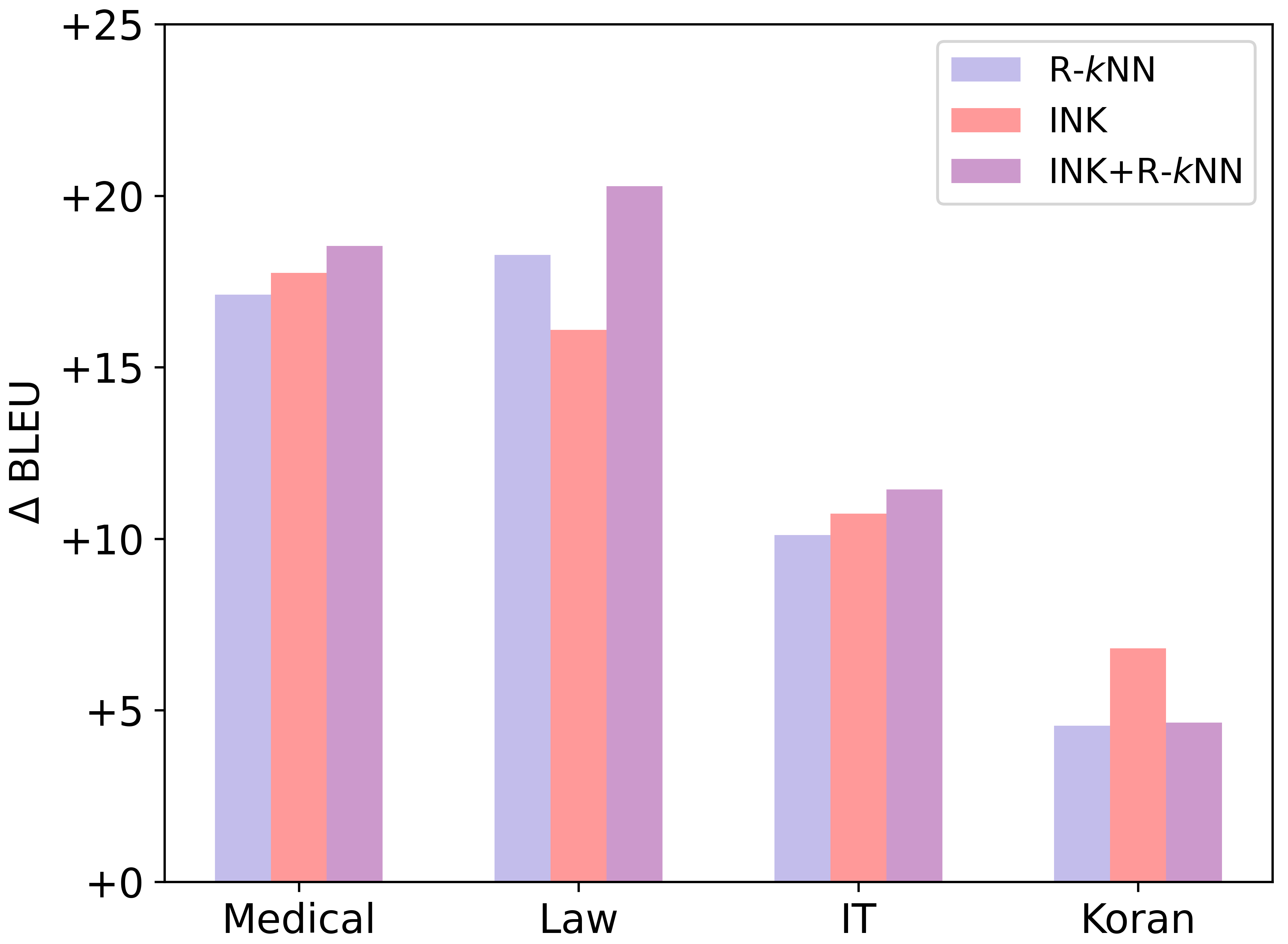
Given the fact that both INK and datastore can smooth predictions, we take a step further and explore to use them together as a hybrid approach. Specifically, on top of our INK system, we follow the fashion of R- $k$ NN to use an additional datastore to assist it during inference. Experiment results are shown in Figure 4. On three out of four datasets, we can observe further improvements over INK. On the Law dataset, the performance improvement even reaches 4.19 BLEU. On the Medical and IT dataset, the performance improvement is 0.71 BLEU and 0.79 BLEU respectively. Such phenomenon indicates that the representation space of the NMT model is not fully refined by the adapter. If a more effective framework can be designed, the benefit of smoothing representation space will be further revealed. The results on the Koran dataset is an exception here. We suggest that it is because of the sparse training data, which makes it difficult to accurately estimate $k$ NN distribution during inference.

5 Analysis and Discussion

We conduce more analysis in this section to better understand our INK system.

INK greatly refines the representation space of the NMT model

Inspired by Li et al. (2022), we evaluate the quality of the representation space by computing mean $k$ NN accuracy, which measures the ratio of k-nearest representations sharing the same target token with the query representation. Ideally, all of the representations in a neighborhood should share the same target token. Here, we use the contextualized representations from the unseen development set as the query. For each query, the nearest representations from the training set will be checked. Table 3 shows the evaluation results on medical dataset. INK achieves higher accuracy than the NMT model consistently. For low frequency tokens, the representation quality gap is especially large.

Systems	BLEU	$\Delta$
INK w/o datastore refresh	56.95	-0.80
INK w/o $\mathcal{L}^{r}_{t}$	57.25	-0.50
INK w/o $\mathcal{L}^{i}_{t}$	57.26	-0.49
INK	57.75	-

Table 4: Ablation study for our INK framework on Medical dataset. All techniques introduced in INK are necessary. Asynchronously refreshing the datastore is important for smoothing representations.

Ablation study

To show the necessity of different proposed techniques in our INK framework, we conduct ablation study in this section. In Table 4, we can see that keeping the datastore frozen degenerates the translation performance most, which demonstrates the necessity of refreshing datastore asynchronously during training. Removing either of the two alignment loss ( $\mathcal{L}^{i}_{t}$ and $\mathcal{L}^{r}_{t}$ ) would cause the translation performance to decline, which validates their importance for adjusting the representation distribution.

INK enjoys faster inference speed

After refining the representation space, our adapted system no longer need to querying datastore during inference. We compare the inference speed ⁸⁸8We evaluate the inference speed on a single NVIDIA Titan-RTX. of INK and R- $k$ NN. Considering that decoding with large batch size is a more practical setting Helcl et al. (2022), we evaluate their inference speed with increasing batch sizes. To make our evaluation results more reliable, we repeat each experiment three times and report averaged inference speed. Table 5 shows the results. As the decoding batch size grows, the speed gap between the two adapted system becomes larger. Our INK can achieve up to 1.9 $\times$ speedup. Besides, due to the fact that neural parameters allows highly parallelizable computation, the inference speed of INK may be further accelerated in the future with the support of non-autoregressive decoding Qian et al. (2021a); Bao et al. (2022).

Systems	Batch=8	Batch=32	Batch=128
R- $k$ NN	14.0	26.1	29.4
INK	19.9	46.4	55.1
Speedup	1.4 $\times$	1.8 $\times$	1.9 $\times$

Table 5: Inference speed (sents/s) of MT systems on Law dataset. Compared with R-

k

NN, INK enjoys up to 1.9

\times

speedup on inference speed.

6 Related Work

Nearest Neighbor Machine Translation

$k$ NN-MT presents a novel paradigm for enhancing the NMT system with a symbolic datastore. However, $k$ NN-MT has two major flaws: (1) querying the datastore at each decoding step is time consuming and the datastore occupies large space. (2) the noise representation in the datastore can not be easily updated, which causes the retrieval results to include noise.

Recently, a line of work focuses on optimizing system efficiency. Martins et al. (2022a) and Wang et al. (2022a) propose to prune datastore entries and conduct dimension reduction to compress the datastore. Meng et al. (2022) propose to in-advance narrow down the search space with word-alignment to accelerate retrieval speed. Martins et al. (2022b) propose to retrieve a chunk of tokens at a time and conduct retrieval only at a few decoding steps with a heuristic rule. However, according to their empirical results, the translation performance always declines after efficiency optimization.

To exclude noise in the retrieval results, Zheng et al. (2021) propose to dynamically decide the usage of retrieved nearest neighbors with a meta- $k$ network. Jiang et al. (2022) propose to dynamically calibrate the $k$ NN distribution and control more hyperparameters in $k$ NN-MT. Li et al. (2022) propose to build datastore with more powerful pre-trained models, e.g. XLM-R Conneau et al. (2020). However, all of this methods rely on a full datastore during inference. When the training data becomes larger, the inference efficiency of these approaches will becomes worse. Overall, it remains an open challenge to deploy a high-quality and efficient $k$ NN-MT system.

Using $k$ NN knowledge to build better NMT models

As datastore stores a pile of helpful translation knowledge, recent research starts exploring to use $k$ NN knowledge in the datastore to build a better NMT model. As an initial attempt, Yang et al. (2022) try to from scratch train a better NMT model by distilling $k$ NN knowledge into it. Different from their work, we focus on smoothing the representation space of an off-the-shelf NMT model and enhancing its generalization ability via a small adapter. Besides, in our devised inject-and-refine training loop we keep datastore being asynchronously updated, while they use a fixed datastore.

7 Conclusion

In this paper, we propose a novel training framework INK, to iteratively refine the representation space of the NMT model according to $k$ NN knowledge. In our framework, we devise a inject-and-refine training loop, where we adjust the representation distribution by aligning three kinds of representation and refresh the datastore asynchronously with the refined representations to update $k$ NN knowledge. Experiment results on four benchmark dataset shows that INK system achieves an average gain of 1.99 COMET and 1.0 BLEU. Compared with the state-of-the-art $k$ NN system (Robust $k$ NN-MT), our INK also achieves better translation performance with 0.02 $\times$ memory space and 1.9 $\times$ inference speed up.

8 Limitation

Despite promising results, we also observe that refreshing and querying the datastore during training is time-consuming. Our proposed training framework usually takes 3 $\times$ $\sim$ 4 $\times$ training time. In future work, we will explore methods to improve training efficiency. We include a training loop to dynamically use the latest datastore to inject knowledge into neural networks. However, we still find that the $k$ NN knowledge still helps the inference even after our training loops, demonstrating that there still remains space to improve the effectiveness of knowledge injection.

Acknowledgement

We would like to thank the anonymous reviewers for their insightful comments. Shujian Huang is the corresponding author. This work is supported by National Science Foundation of China (No. 62176120), the Liaoning Provincial Research Foundation for Basic Research (No. 2022-KF-26-02).

References

An et al. (2022) Chenxin An, Jiangtao Feng, Kai Lv, Lingpeng Kong, Xipeng Qiu, and Xuanjing Huang. 2022. Cont: Contrastive neural text generation. arXiv preprint arXiv:2205.14690.
Bao et al. (2022) Yu Bao, Hao Zhou, Shujian Huang, Dongqi Wang, Lihua Qian, Xinyu Dai, Jiajun Chen, and Lei Li. 2022. latent-GLAT: Glancing at latent variables for parallel text generation. In Proceedings of the Annual Meeting of the Association for Computational Linguistics (ACL).
Bapna and Firat (2019) Ankur Bapna and Orhan Firat. 2019. Simple, scalable adaptation for neural machine translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing and the International Joint Conference on Natural Language Processing (EMNLP-IJCNLP).
Conneau et al. (2020) Alexis Conneau, Kartikay Khandelwal, Naman Goyal, Vishrav Chaudhary, Guillaume Wenzek, Francisco Guzmán, Edouard Grave, Myle Ott, Luke Zettlemoyer, and Veselin Stoyanov. 2020. Unsupervised cross-lingual representation learning at scale. In Proceedings of the Annual Meeting of the Association for Computational Linguistics (ACL).
Ethayarajh (2019) Kawin Ethayarajh. 2019. How contextual are contextualized word representations? Comparing the geometry of BERT, ELMo, and GPT-2 embeddings. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP).
Gao et al. (2018) Jun Gao, Di He, Xu Tan, Tao Qin, Liwei Wang, and Tieyan Liu. 2018. Representation degeneration problem in training natural language generation models. In International Conference on Learning Representations (ICLR).
Helcl et al. (2022) Jindřich Helcl, Barry Haddow, and Alexandra Birch. 2022. Non-autoregressive machine translation: It’s not as fast as it seems. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT).
Jiang et al. (2022) Hui Jiang, Ziyao Lu, Fandong Meng, Chulun Zhou, Jie Zhou, Degen Huang, and Jinsong Su. 2022. Towards robust k-nearest-neighbor machine translation. arXiv preprint arXiv:2210.08808.
Johnson et al. (2019) Jeff Johnson, Matthijs Douze, and Hervé Jégou. 2019. Billion-scale similarity search with gpus. IEEE Transactions on Big Data.
Khandelwal et al. (2021) Urvashi Khandelwal, Angela Fan, Dan Jurafsky, Luke Zettlemoyer, and Mike Lewis. 2021. Nearest neighbor machine translation. In International Conference on Learning Representations (ICLR).
Lee et al. (2021) Seanie Lee, Dong Bok Lee, and Sung Ju Hwang. 2021. Contrastive learning with adversarial perturbations for conditional text generation. In ICLR.
Li et al. (2020) Bohan Li, Hao Zhou, Junxian He, Mingxuan Wang, Yiming Yang, and Lei Li. 2020. On the sentence embeddings from pre-trained language models. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP).
Li et al. (2022) Jiahuan Li, Shanbo Cheng, Zewei Sun, Mingxuan Wang, and Shujian Huang. 2022. Better datastore, better translation: Generating datastores from pre-trained models for nearest neural machine translation. arXiv preprint arXiv:2212.08822.
Martins et al. (2022a) Pedro Martins, Zita Marinho, and Andre Martins. 2022a. Efficient machine translation domain adaptation. In Proceedings of the Workshop on Semiparametric Methods in NLP: Decoupling Logic from Knowledge.
Martins et al. (2022b) Pedro Henrique Martins, Zita Marinho, and André FT Martins. 2022b. Chunk-based nearest neighbor machine translation. arXiv preprint arXiv:2205.12230.
Meng et al. (2022) Yuxian Meng, Xiaoya Li, Xiayu Zheng, Fei Wu, Xiaofei Sun, Tianwei Zhang, and Jiwei Li. 2022. Fast nearest neighbor machine translation. In Findings of the Association for Computational Linguistics.
Ng et al. (2019) Nathan Ng, Kyra Yee, Alexei Baevski, Myle Ott, Michael Auli, and Sergey Edunov. 2019. Facebook FAIR’s WMT19 news translation task submission. In Proceedings of the Conference on Machine Translation (WMT).
Ott et al. (2019) Myle Ott, Sergey Edunov, Alexei Baevski, Angela Fan, Sam Gross, Nathan Ng, David Grangier, and Michael Auli. 2019. fairseq: A fast, extensible toolkit for sequence modeling. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT).
Papineni et al. (2002) Kishore Papineni, Salim Roukos, Todd Ward, and Wei-Jing Zhu. 2002. Bleu: a method for automatic evaluation of machine translation. In Proceedings of the Annual Meeting of the Association for Computational Linguistics (ACL).
Parzen (1962) Emanuel Parzen. 1962. On estimation of a probability density function and mode. The Annals of Mathematical Statistics.
Qian et al. (2021a) Lihua Qian, Hao Zhou, Yu Bao, Mingxuan Wang, Lin Qiu, Weinan Zhang, Yong Yu, and Lei Li. 2021a. Glancing transformer for non-autoregressive neural machine translation. In Proceedings of the Annual Meeting of the Association for Computational Linguistics (ACL).
Qian et al. (2021b) Lihua Qian, Yi Zhou, Zaixiang Zheng, Yaoming Zhu, Zehui Lin, Jiangtao Feng, Shanbo Cheng, Lei Li, Mingxuan Wang, and Hao Zhou. 2021b. The volctrans GLAT system: Non-autoregressive translation meets WMT21. In Proceedings of the Conference on Machine Translation (WMT).
Rei et al. (2020) Ricardo Rei, Craig Stewart, Ana C Farinha, and Alon Lavie. 2020. COMET: A neural framework for MT evaluation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP).
Tiedemann (2012) Jörg Tiedemann. 2012. Parallel data, tools and interfaces in OPUS. In Proceedings of the Eighth International Conference on Language Resources and Evaluation (LREC).
Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Advances in Neural Information Processing Systems (NeurIPS).
Wang et al. (2022a) Dexin Wang, Kai Fan, Boxing Chen, and Deyi Xiong. 2022a. Efficient cluster-based $k$ -nearest-neighbor machine translation. In Proceedings of the Annual Meeting of the Association for Computational Linguistics (ACL).
Wang et al. (2022b) Qiang Wang, Rongxiang Weng, and Ming Chen. 2022b. Learning decoupled retrieval representation for nearest neighbour neural machine translation. In Proceedings of the International Conference on Computational Linguistics (COLING).
Wang and Isola (2020) Tongzhou Wang and Phillip Isola. 2020. Understanding contrastive representation learning through alignment and uniformity on the hypersphere. In Proceedings of the International Conference on Machine Learning (ICML), Proceedings of Machine Learning Research.
Williams and Zipser (1989) Ronald J Williams and David Zipser. 1989. A learning algorithm for continually running fully recurrent neural networks. Neural Computation.
Yang et al. (2022) Zhixian Yang, Renliang Sun, and Xiaojun Wan. 2022. Nearest neighbor knowledge distillation for neural machine translation. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT).
Zheng et al. (2021) Xin Zheng, Zhirui Zhang, Junliang Guo, Shujian Huang, Boxing Chen, Weihua Luo, and Jiajun Chen. 2021. Adaptive nearest neighbor machine translation. In Proceedings of the Annual Meeting of the Association for Computational Linguistics (ACL).

Appendix A Used Scientific Artifacts

Below lists scientific artifacts that are used in our work. For the sake of ethic, our use of these artifacts is consistent with their intended use.

•

Fairseq (MIT-license), a sequence modeling toolkit that allows researchers and developers to train custom models for translation, summarization and other text generation tasks.
•

Faiss (MIT-license), a library for approximate nearest neighbor search.

Appendix B Implementation Details

We reproduce baseline systems with their released code. We implement our system with fairseq Ott et al. (2019). Adam is used as the optimizer and inverse sqrt is used as the learning rate scheduler. We set 4k warm-up steps and a maximum learning rate as 5e-4. We set batch size as 4096 tokens. All INK systems are trained on a single Tesla A100. During inference, we set beam size as 4 and length penalty as 0.6.

INK: Injecting kkNN Knowledge in Nearest Neighbor Machine Translation