Infrared acceleration radiation
Abstract
We present an exactly soluble electron trajectory that permits an analysis of the soft (deep infrared) radiation emitted, the existence of which has been experimentally observed during beta decay via lowest order inner bremsstrahlung. Our treatment also predicts the time evolution and temperature of the emission, and possibly the spectrum, by analogy with the closely related phenomenon of the dynamic Casimir effect.
pacs:
41.60.-m (Radiation by moving charges), 04.70.Dy (Quantum aspects of black holes)Introduction. -The transmutation of a nucleus via beta decay involves the abrupt creation of an electron or positron, followed by its expulsion from the nucleus. Although this process can be fully understood only in the context of quantum field theory, there is a long history of classical treatments Bloch and Nordsieck (1937). Viewed classically, beta decay involves the sudden appearance of a charged particle, which has been modeled by assigning a step function trajectory to a classical charge Chang and Falkoff (1949). The resulting acceleration might be expected to produce electromagnetic radiation, see Figure 1, and indeed, such radiation has been observed Ballagh et al. (1983). The process of photon production accompanying beta decay is sometimes referred to as ‘inner bremmstrahlung (IB).’
The use of a step function is unrealistic, but convenient mathematically Jackson (1999). Fortunately, there is a smoother acceleration function that nevertheless permits an exact treatment of the radiation emission, and we give that treatment here. By extending the period of acceleration being modeled, we can make a connection with the well-known Davies-Fulling-Unruh effect Davies (1975); Fulling (1973); Unruh (1976): in the frame of the charged particle, there is a thermal bath of photons with a temperature proportional to acceleration. Closely related is the emission of quanta by an accelerating mirror (moving mirror radiation) Moore (1970); DeWitt (1975); Fulling and Davies (1976); Davies and Fulling (1977) and the correspondence to black hole radiation Hawking (1975). The interconnection of charged particle acceleration and the above mentioned quantum field theory effects has been the subject of much investigation. In this paper we will not attempt to review these linkages at a fundamental level, but instead we use the known results phenomenologically to extend the discussion of inner bremmstrahlung.

Step function example. -If the electron is initially at rest and imagined to be instantaneously accelerated to a final constant speed, where , then (see e.g. Zangwill (2013)),
| (1) |
Working with unit charge, the angular differential distribution of radiated energy is found to be Jackson (1999):
| (2) |
where is the angle between the final velocity and the observation point of the radiation. Integration of Eq. (2) over solid angle and over frequencies IR/UV-limited by cutoffs gives the energy radiated by the electron. The total energy is rendered finite in this interval,
| (3) |
The detector sets the energy scale sensitivity. Eq. (3) is lowest order IB energy Chang and Falkoff (1949), and has been observed to great accuracy Ballagh et al. (1983). The foregoing treatment is sometimes referred to as the instantaneous collision formalism Cardoso et al. (2003a, b).
Not only is it physically desirable to avoid the infinite acceleration of Eq. (1), but the mathematical use of the discrete step velocity limits the final results to quantities independent of time. The radiated energy Eq. (3), is characterized by universality and a classical limit from a corresponding time-dependent trajectory Bloch and Nordsieck (1937). Knowing the continuous acceleration responsible for deep IR could help provide a simple underlying physical connection to gravitation via the Equivalence Principle.
Smooth acceleration. -Under the above motivations, we consider the trajectory,
| (4) |
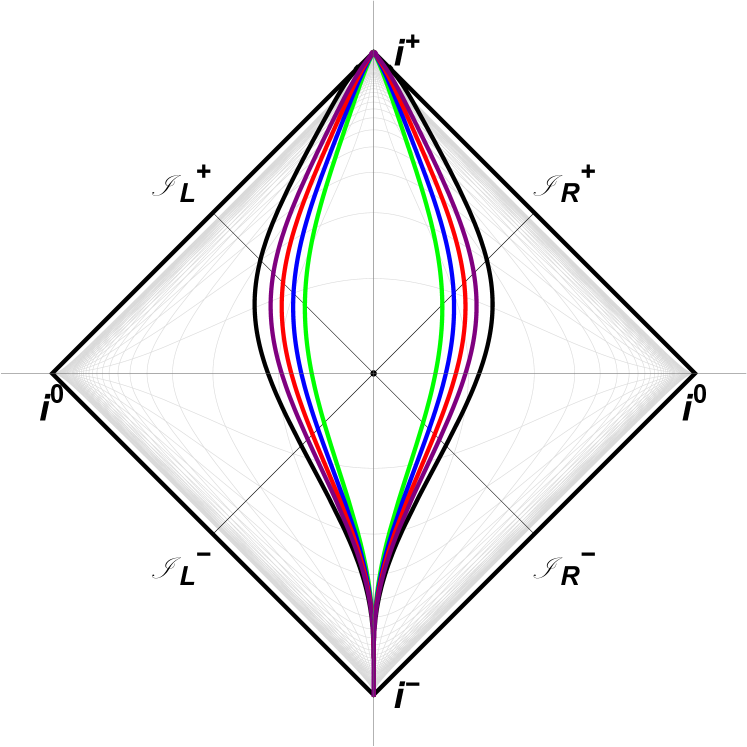
The asymptotic speeds are as (the electron moves to the right by convention111In the closely related moving mirror model, (see Good (2017)), the usual convention is to move to the left (see Figure 3). The difference is a sign change in the angular distribution. The energy remains invariant. Jackson (1999)), matching Eq. (1). The proper acceleration, , has time-dependence, , and possesses asymptotic inertia. See Figure 2 & 3 for illustration. Here is the dimensionful acceleration parameter of the model which corresponds to the sensitivity in frequency range of the detector and sets the scale: . With large , the speed of Eq. (4) approaches the step function example, Eq. (1). However, no such approximation is needed to obtain Eqs. (2) or (3).
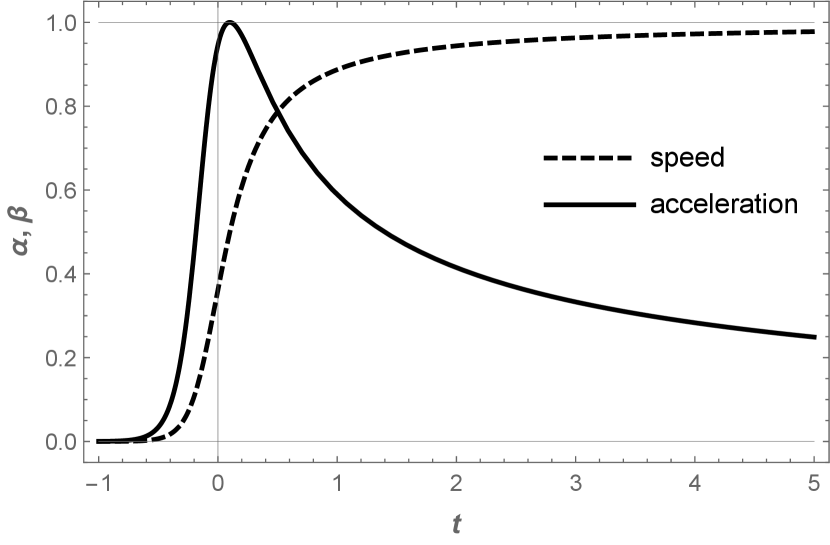
Time-distribution & power. -The time-dependent power distribution is computed using Eq. (4) with straightforward vector algebra (see the procedure in Good et al. (2019)),
| (5) |
where again, is the final constant speed, and is the time-dependent velocity. Integration over time, gives the time-independent angular differential distribution of energy, which turns out to be identical to result for the step-function trajectory, Eq. (2).
Moreover, using the Lorentz-invariant proper acceleration in , we obtain the total power radiated,
| (6) |
The total radiated energy for the entire trajectory is readily obtained by integrating Eq. (6) over time, which again yields an identical result to the step-function case, given by Eq. (3). The fact that the more realistic smooth trajectory recapitulates the earlier results justifies the use of our choice of Eq. (4). However, our model has the advantage that we can examine the behavior of the accelerated charge over time.
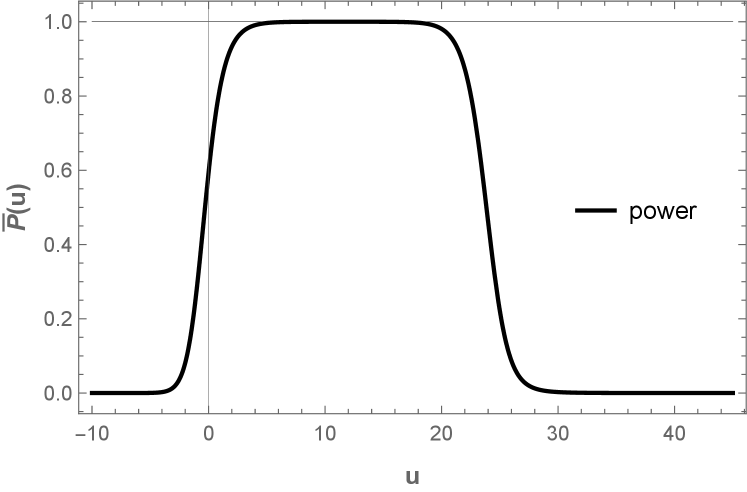
Equilibrium emission. -Interestingly, a period of constant emission is present in the power measured by a far away observer. Best represented as the change of energy with respect to retarded time , and written as such that
| (7) |
we write . Formulating in terms of retarded time, gives a lengthy result, but we plot the measure at high final asymptotic speeds and reveal a constant power plateau indicative of thermal emission. Additionally, beta Bogolubov coefficients corroborates this radiative equilibrium via an explicit Planck distribution in Eq. (10). See a plot of the power plateau in Figure 4.
Radiation reaction. -Having computed the power, , we now turn to the self-force, . It is analytically tractable, and a concise expression is given in terms of speed ,
| (8) |
The self-force is zero at maximum power. Integrating over distance gives the work done,
| (9) |
That is, taking Eq. (8) over using, , where ranges from , one obtains the energy associated with the self-force. The resulting work is , the equal and opposite of Eq. (3). This demonstrates consistency between the radiation reaction and conservation of energy.
Universality, spectra & temperature. -The preceding results derived in the context of IB are the same for the scattering of Faddeev-Kulish electrons in QED where a cloud of soft photons exist in the dressed state Tomaras and Toumbas (2020). Moreover, the same results hold true for the perfectly reflecting moving mirror Good (2017) of the dynamical Casimir effect. In turn, the accelerated boundary correspondence between mirrors and black holes Good et al. (2020), demonstrates trajectory Eq. (4) induces an exact analog of black hole evaporation leading to a remnant Wilczek (1993). The unexpected synthesis of IB, clouds, mirrors, and remnants corroborate the universality of the deep infrared.
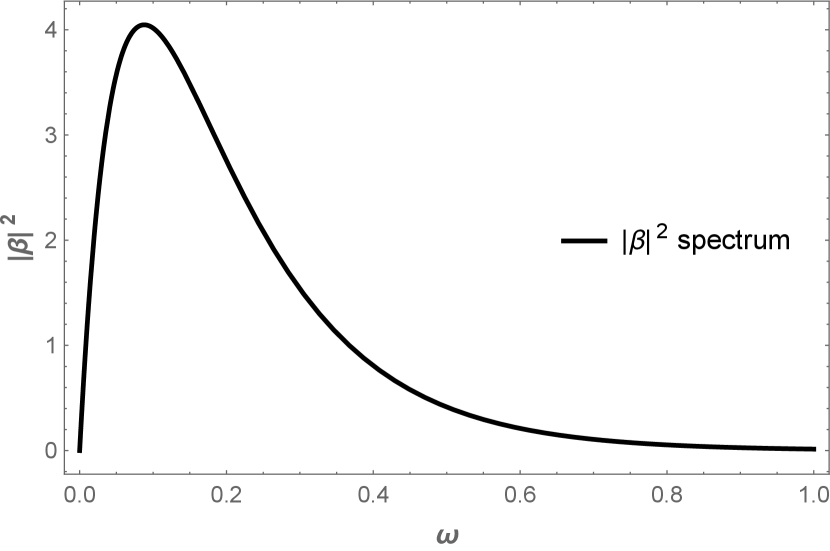
Since accelerating boundaries radiate soft particles whose long wavelengths lack the capability to probe the internal structure of the source Strominger (2017), we compute, in the spirit of analogy, the moving mirror spectrum (scaled by ) as an illustration of what the soft-spectrum for IB might look like. Combining the results for each side of the mirror Good (2017) by adding the squares of the beta Bogolubov coefficients, the overall spectrum is
| (10) |
Here , and . The total frequency is . A numerical integration of
| (11) |
confirms the total energy radiated, Eq. (3). Given the close association between accelerating mirrors and charges, we postulate that the IB spectrum in beta decay is likely to be of the same form as Eq. (10). We have plotted the spectrum of the moving mirror radiation in Figure 5. If experiment confirms our prediction, then one could regard soft IB from beta decay as an analogue of the dynamical Casimir effect.
The explicit Planck factor demonstrates the particles, , are distributed with a temperature,
| (12) |
in the high frequency approximation Hawking (1975). Recall , is the scale set by the sensitivity of detection. Thermal emission is not surprising considering the power plateau (Figure 4) and the close analogy for quantum and classical quantities of powers Good and Linder (2022); Zhakenuly et al. (2021) and self-forces Myrzakul et al. (2021); Ford and Vilenkin (1982) between mirrors and electrons.
Conclusion. - We have calculated the deep infrared radiation emitted by a rapidly accelerating classical point charge using a smooth trajectory that permits exact solution of all relevant quantities. We have derived novel time-dependent power and angular distribution formula. The soft self-force was computed, universality was highlighted across several distinct systems, and Bogolubov coefficient spectra were obtained, demonstrating consistency with the observed energy. The temperature of the light is found via a Planck distribution. The key result, from which the others flow, is an analytic continuous equation of motion for infrared acceleration radiation.
Acknowledgements. -We thank Stephen Fulling for useful discussion. Funding comes in part from the FY2021-SGP-1-STMM Faculty Development Competitive Research Grant No. 021220FD3951 at Nazarbayev University. Appreciation is given to the organizers, speakers, and participants of the QFTCS Workshop: May 23-27, 2022, at which preliminary results were first presented and helpful feedback are included therein.
References
- Bloch and Nordsieck (1937) F. Bloch and A. Nordsieck, Phys. Rev. 52, 54 (1937).
- Chang and Falkoff (1949) C. S. W. Chang and D. L. Falkoff, Phys. Rev. 76, 365 (1949).
- Ballagh et al. (1983) H. C. Ballagh et al., Phys. Rev. Lett. 50, 1963 (1983).
- Jackson (1999) J. D. Jackson, Classical electrodynamics; 3rd ed. (Wiley, New York, NY, 1999).
- Davies (1975) P. C. W. Davies, J. Phys. A 8, 609 (1975).
- Fulling (1973) S. A. Fulling, Phys. Rev. D 7, 2850 (1973).
- Unruh (1976) W. G. Unruh, Phys. Rev. D 14, 870 (1976).
- Moore (1970) G. T. Moore, J. of Math. Phys. 11, 2679 (1970).
- DeWitt (1975) B. S. DeWitt, Phys. Rept. 19, 295 (1975).
- Fulling and Davies (1976) S. A. Fulling and P. C. W. Davies, Proc. R. Soc. Lond. A 348, 393 (1976).
- Davies and Fulling (1977) P. Davies and S. Fulling, Proc. R. Soc. Lond. A A356, 237 (1977).
- Hawking (1975) S. Hawking, Commun. Math. Phys. 43, 199 (1975).
- Zangwill (2013) A. Zangwill, Modern electrodynamics (Cambridge Univ. Press, Cambridge, 2013).
- Cardoso et al. (2003a) V. Cardoso, O. J. C. Dias, and J. P. S. Lemos, Phys. Rev. D 67, 064026 (2003a), arXiv:hep-th/0212168 .
- Cardoso et al. (2003b) V. Cardoso, J. P. S. Lemos, and S. Yoshida, Phys. Rev. D 68, 084011 (2003b), arXiv:gr-qc/0307104 .
- Good (2017) M. R. R. Good, Reflecting at the Speed of Light (World Scientific, Singapore, 2017).
- Good et al. (2019) M. R. Good, M. Temirkhan, and T. Oikonomou, Int. J. Theor. Phys. 58, 2942 (2019), arXiv:1907.01751 [gr-qc] .
- Tomaras and Toumbas (2020) T. N. Tomaras and N. Toumbas, Phys. Rev. D 101, 065006 (2020).
- Good et al. (2020) M. R. Good, E. V. Linder, and F. Wilczek, Phys. Rev. D 101, 025012 (2020), arXiv:1909.01129 [gr-qc] .
- Wilczek (1993) F. Wilczek, in International Symposium on Black holes, Membranes, Wormholes and Superstrings (1993) pp. 1–21, arXiv:hep-th/9302096 .
- Strominger (2017) A. Strominger, (2017), arXiv:1703.05448 [hep-th] .
- Good and Linder (2022) M. R. R. Good and E. V. Linder, Eur. Phys. J. C 82, 204 (2022), arXiv:2111.15148 [gr-qc] .
- Zhakenuly et al. (2021) A. Zhakenuly, M. Temirkhan, M. R. R. Good, and P. Chen, Symmetry 13, 653 (2021), arXiv:2101.02511 [gr-qc] .
- Myrzakul et al. (2021) A. Myrzakul, C. Xiong, and M. R. R. Good, Entropy 23, 1664 (2021), arXiv:2101.08139 [gr-qc] .
- Ford and Vilenkin (1982) L. Ford and A. Vilenkin, Phys. Rev. D 25, 2569 (1982).