Influence of grain bidispersity on dense granular flow
in a two dimensional hopper
Abstract
Discrete element method is conducted to investigate the bidisperse dense granular flow having big and small grains in a two dimensional hopper. A half-circular dynamical force arch is observed above the outlet and Beverloo’s law is verified to describe the relationship between flow rate and outlet size. The bidisperse flow can reach the maximum flow rate when a small fraction of big grains is added into the monodisperse flow with only small grains. The distributions of contact force, packing fraction and grain velocity indicate that the flow properties in the hopper are closely related to the local flow characteristics of the key area which almost overlaps with the force arch. The interior packing structures, i.e., ordered arrangement for monodisperse flow and disordered arrangement for bidisperse flow, play a dominant role in the flow pattern transition from mass flow to funnel flow. The earlier occurrence of the transition can effectively increase the grain velocity and therefore improve the flow rate.
pacs:
45.70.Mg, 64.60.-i, 75.40.GbI Introduction
Dense granular flow is often encountered in natural environments and industrial productions and has attracted extensive interest in the scientific and engineering fieldsJaeger1996 (1, 2, 3). Complex phenomena, such as mass-to-funnel flow pattern transitionPT22P243 (4, 5, 6, 7, 8, 9), mixing and segregationHuangEPJE2013 (10, 11, 12), and avalanchesBursik2005 (13, 14) have been widely investigated. The dense flow with bidisperse grains in a hopper is an important research topic because of its ubiquity. Understanding of the whole flow rate and interior flow behavior is of primary importance in ensuring reproducible and efficient handling in industrial operations.
The quantitative model for the dense flow rate of monodisperse grains in a hopper was first proposed by HagenHagen1852 (15) and rediscovered by Beverloo et al.Beverloo1961 (16). In this model, the outlet is located at the center of the hopper. The relationship between flow rate and outlet size takes the following form:
| (1) |
where is the spatial dimension, i.e, = 2 and 3 for 2D and 3D respectively. is the outlet size. is the grain diameter. is the effective gravity acceleration. is a fitting dimensional coefficient that is possibly related to factors such as friction coefficient and bulk density. is regarded being resulted from the empty annulus effect related to the geometric shape of the grain. The free-fall arch hypothesis assumes that the grains are closely compacted above the outlet and the contact force has a half-circular structure. The grains fall freely with zero initial velocity from the force arch region. Beverloo’s formula has been verified for the past few decadesNeddermanCES1982 (17, 18, 19, 20, 24, 21, 22, 23).
When the flow comprises bidisperse mixtures with big and small grains, Arteaga and Tüzün modified Beverloo’s equation as followsArteagaCES1990 (22, 23):
| (2) |
where the subscript represents the bidisperse mixtures. is the mean diameter. and are the diameters of big and small grains. The mixing index is defined by the mass ratio . and are the masses of single big and small grains. and represent the monodisperse flow containing only small and big grains. The others represent the bidisperse flow that mixes big and small grains. The experimental results show that the difference between grain diameters greatly affects the flow rate and local flow behavior. Coarse and fine continuous flows are defined when the flow is dominated by big and small grains respectively. Dilatancy occurs as a result of the grain’s flowing, which in turn results in a lower dynamical packing fraction compared with that observed in the initial static packing case. The flow rate decreases along with an increasing mixing index, and the maximum dynamical packing fraction appears at a moderate mixing index. The dispersity of grains results in empty annuluses and for the coarse and fine continuous flows, respectively.
Benyamine and Zhou et alBenyaminePRE2014 (24, 25) replicated the bidisperse flow in a hopper via experiments and simulations, in which the outlet was formed by two plat baffles. Their findings reveal that the bidisperse flow has a higher dynamical packing fraction compared with the monodisperse case. However, they reported the maximum flow rate at a moderate mixing index. Such discrepancy might be ascribed to the grain shape, which takes the form of smooth glass spheres in their experiments. Although they found no fall arch, the flow behavior was still gradually affected by the local flow properties in the region, especially around the outlet. These results indicate that both grain velocity and packing fraction have self-similarity characteristics. Meanwhile, the expressions proposed by BeverlooBeverloo1961 (16) and JandaZuriguel2012PRL108P248001 (18) equally fit the relationships between flow rate and outlet size. To obtain further insights into the influence of grain dispersity on the flow kinetic properties, the bidisperse flow with big and small grains warrants intensive investigation.
In this paper, numerical simulations are performed to explore the bidisperse flow in a two dimensional(2D) hopper. The simulation method is first described in Sec. II. The key area and corresponding calculation of the flow rate are also introduced. In Sec. III, the dependence of the flow rate on outlet size is tested by using Beverloo’s formula. The influence of size and mass ratios on flow rate is repeatedly examined. Afterwards, the effect of grain dispersity on the distribution of packing fraction, grain velocity, and contact force is examined. The transition from mass flow to funnel flow patterns are then discussed for both monodisperse and bidisperse flows. The major results are summarized in the conclusion.
II Simulation method
Discrete element method(DEM) is applied to investigate the granular flow in a quasi-2D hopper as shown in Fig.1(a). The rectangular hopper comprises two walls with height , width , and thickness . A central outlet formed by two plat baffles is located at height . The size of the outlet can be changed in the simulations. The grains are composed of circular disks and have the same thickness as that of the hopper.
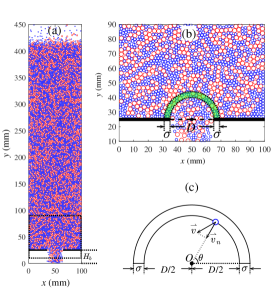
In the simulations, the particle motion is described using Newton’s equations similar to our previous worksHuang2006PRE (26, 27, 28, 21). The effective gravity acceleration is set as . The Verlet algorithm is used to update the positions and velocities of the grains in each simulation time step. The translational motion in the hopper plane and the rotational motion along to the axis perpendicular to the hopper plane are both considered. The interaction between two contacted grains is treated as soft spheres, in which the forces along the normal and tangential directions are considered. The normal interaction is a function of the overlap at the contacting point modeled by using the Cundall-Strack formula Cundall1979 (29, 30).
| (3) |
The tangential component is taken as the minor tangential force with a memory effect and the dynamic frictional force.
| (4) |
In Eqs.(3)(4), and represent the normal and tangential directions at the contact point, respectively. and denote the displacements that take place since the time when the contact is first established. The detailed values can be calculated as follows:
,
, ,
,
where is the restitution coefficient. and are the masses of the contacting grain and grain . , characterize the normal and tangential stiffness of the grains. and are the Young’s modulus and Poisson’s ratio, respectively. The friction coefficient is fixed in our simulations. The collision between the grain and wall is treated as the grain-grain collision, except that the wall has infinite mass and diameter. The detailed values are presented in Table 1.
Table 1 The parameters of the grains
| Quantity | Symbol | Value |
|---|---|---|
| Diameter of small grain (mm) | 2.0 | |
| Density () | 7.8 | |
| Young modulus (GPa) | E | 1.0 |
| Poison ratio | 0.3 | |
| Friction coefficient | 0.5 | |
| Simulation time-step (s) |
At the beginning of each simulation, the outlet is closed and the hopper is completely empty. The grains are randomly poured into the hopper and fall down under the self-gravity. The initial piling height is about . Afterward, the outlet is opened and the flow is triggered. The periodical condition is adopted to maitain a constant packing height, which means that the gains re-enter the hopper from the top after passing through its bottom. In the simulations, the small grain diameter is fixed at . The big to small grain diameter ratio is defined as .
Our previous works show that the flow properties in a key area are crucial to both the flow state and granular outflow rateHuang2006PRE (26, 27, 21, 31). The same key area is selected as shown in Fig.1 (b) denoted by the dotted lines. The width of the key area is set to . The local packing fraction can be directly calculated from the ratio of volume occupied by grains in the key area to the whole volume of the key area. Therefore, the local packing fraction and flow rate are both directly calculated.
| (5) | ||||
where represents the summation of all grains in the key area. As shown in Fig.1(c), is the flow rate of grain contributing to the key area. is the grain area, and is the intersection between the grain and the key area. is the normal velocity relative to the inner circle with the size of the left or right outlet as shown in Fig.1(c). is the area of the key area. According to the conservation law of mass, the local flow rate of the key area is equal to that of the outlet in a steady flow state.
III RESULTS AND DISCUSSIONS
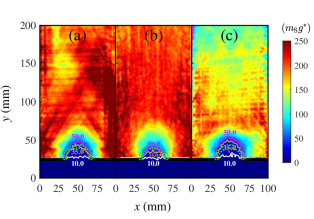
In Beverloo’s arguments, the dense flow rate is determined based on the hypothesized free-fall arch above the outlet. For the analysis, spatial maps of the time-averaged contact force between grains are plotted for three mixing indexes, namely and . The diameters of the small and big grains are set as and . A half-circular dynamical force arch is clearly observed above the outlet labeled by the contour solid lines and . The key area is marked by green dotted lines. The shape of the force arch almost overlaps with that of the key area. A strong contact force is observed for those grains above the force arch, which indicates that these grains are closely crowded. When these grains continue flowing toward the outlet, the contact force becomes weaker, and the half-circular arch gradually turns into a flat line labeled by . In other words, the squeezed grains become loose and fall out of the hopper under the effects of self-gravity.
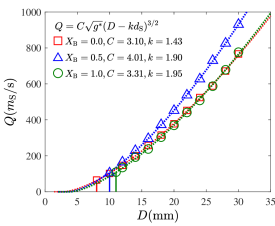
An interesting point from Fig.2 is that the force arch labeled by and for is obviously smaller than that for and . Following the free-fall arch hypothesis, a larger flow rate corresponds to a larger force arch. To test this prediction, Fig.3 plots the flow rate of the key area as a function of outlet size for the same flow conditions used in Fig.2. Simulation results coincide well with Beverloo’s equation in the power law of 3/2. The fitting parameter is equivalent to and for the monodisperse flow with small and big grains, respectively. The flow with bidisperse grains has moderate fitting parameters , which is consistent with the free-fall arch hypothesis. A bigger grain has a larger empty annulus, which results in a smaller effective outlet size and flow rate. However, Fig.3 shows that the flow rate at the bidisperse case of is larger than that at the monodisperse cases of and , which contradicts to free-fall arch hypothesis. In addition, colgging is frequently observed at the outlet size of for the monodisperse flow in our simulations, and the clogging for the bidisperse flow tends to happen at a moderate outlet size. This finding agrees with the observations of BenyamineBenyaminePRE2014 (24).
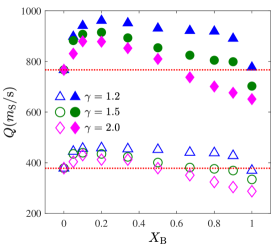
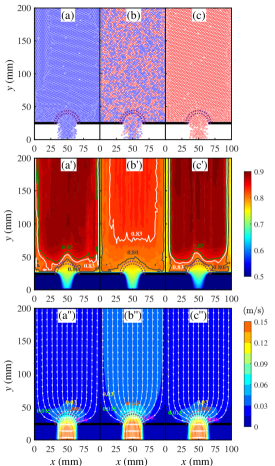
Fig.4 plots the time-averaged flow rate as a function of the mixing index for two outlet sizes and . A non-monotonic behavior is observed for diameter ratios and . Compared with the monodisperse flow with small grains, adding a small amount of big grains will obviously increase the flow rate. However, the flow rate decreases after the addition of big grains cross a specific threshold. In general, granular flowability is improved when a low amount of small grains is added into the monodisperse flow with big grains, and the maximum flow rate is observed at a certain low mixing index.
Given that flow rate is determined by the physical quantities of grain velocity and packing fraction, the detailed variances in flow rate resulting from the mixing degree of bidisperse grains warrant further investigation. The initial static packing fraction is examined before the start of granular flow. Even though the grains are randomly poured into the hopper, the size monotonicity results in near crystallization everywhere for the monodisperse grains. A higher static packing fraction is obtained for and . When the grains are bidisperse, the ordered structure is destroyed and the grains randomly pile up in the hopper. The static packing fraction is for .
Fig.5(a)(b)(c) present the snapshots of steady dense flows for the same conditions shown in Fig.2. Compared with initial static packing, due to their monodisperse size, the interior crystallization structure of the grains is kept at the region located far from the outlet for the monodisperse flow ( and ) shown in Fig.5(a)(c). The close-packed structure becomes loose when the grains approach the outlet. By contrast, an ordered arrangement is never observed for the bidisperse flow () from the beginning of the granular flow to the stable flow state as shown in Fig.5(b). Fig.5(a’)(b’)(c’) plots the corresponding distribution of dynamical packing fraction in the steady dense flow state. The dynamical packing fraction at the region located far from the outlet is always higher than that around the outlet. A half circular-like shape appears around the outlet and almost overlaps with the key area. The dynamical packing fraction in the key area as denoted by the dotted lines is for , and for . After the grains pass through the key area, the packing fraction decreases continuously until the grains flow out of the hopper for both monodisperse and bidisperse flows.
Fig.5(a”)(b”)(c”) plots the grain velocity distribution using the same parameters in Fig.2. The streamlines of granular flow are represented by the white solid lines. The contour color denotes the magnitude of grain velocity. Two stagnant zones are located at the left and right walls as denoted by for each case. The streamlines are a series of parallel lines that emerge when the grains are located far from the outlet and then converge as these grains approach the outlet. The streamlines for the bidisperse case are slightly more deeper than those for the monodisperse cases and . The region located far from the outlet is occupied by different colors, where blue corresponds to and and cyan corresponds to as labelled by and respectively. The ordered and disordered arrangements of grains produce two flow patterns, namely, mass flow and funnel flow, which will be further explored in the following section. A similar half circular-like shape reappears around the outlet, and overlaps with the key area as indicated by the dotted lines. The corresponding grain velocity is labelled as .
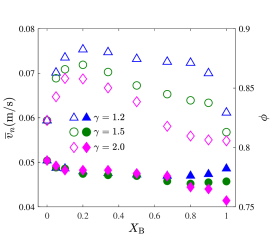
Simulation results indicate that the flow properties are closely related to the local flow characteristics around the outlet, i.e., key area. We now examine how the mixing degree affects the two decisive physical quantities of flow rate in the key area. In Fig.6, the mean normal grain velocity and packing fraction of the key area are plotted as functions of the mixing index for and . The outlet size is fixed at . The maximum normal grain velocity is achieved for the bidisperse flow with smaller . Meanwhile, the monodisperse flow with small grains always has the largest packing fraction. The variance in grain velocity is consistent with that in flow rate. Simulations are also performed for outlet size . The same results are obtained, that is, adding a low amount of big grains into the monodisperse flow with small grains will increase of the grain velocity and reduce the packing fraction, thereby suggesting that increasing grain velocity can effectively improve flow rate Huang2011PLA (27).
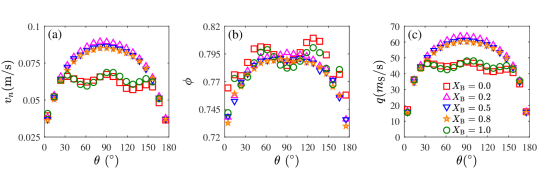
Fig.7 shows the time-averaged normal velocity , packing fraction and flow rate in the subregions of the key area for a fixed diameter ratio . Both the monodisperse flows () and the bidisperse flows () share the same symmetrical profile. In Fig.7(a), all grain velocities sumultaneously fall together at the two side regions. The grain velocity in the center subregions for the monodisperse flow is always smaller than that for the bidisperse flow. Furthermore, the former has a fluctuating shape, whereas the latter has a parabolic shape. In Fig.7(b), the monodisperse flow always has a higher packing fractions than that of the bidisperse flow except at the center regions. However, the fluctuating and parabolic distributions are preserved for monodisperse and bidisperse flows, respectively, thereby suggesting that the ordered crystallization structure leads to fluctuations in grain velocity and packing fraction in the monodisperse flow. A symmetrical distribution is also observed for the flow rate shown in Fig.7(c). Fig.7 proves that the normal velocity mainly determines the flow rate in the subregion and that the fluctuation in packing density play a dominant role in flow rate fluctuation Huang2018CPB (28).
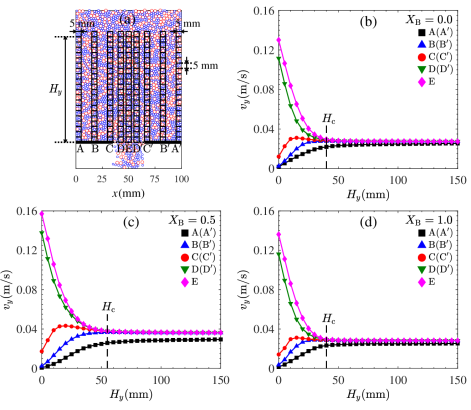
According to the above observations, the monodisperse or bidisperse grains affect on the flow behaviors because grain dispersity leads to an ordered and disordered interior packing structure. To illustrate the detailed influence of mixing degree on the interior flow patterns, i.e., mass flow and funnel flow, the vertical mean velocities () of the grains located at positions and are measured as shown in Fig.8(a). The selected regions have a width of and height of . Each square has a height of . The intersection between the grain and cell is calculated at every time step. The vertical mean velocity as a function of the granular packing height () is presented in Fig.8(b), (c) and (d) for and , respectively. Given the symmetry, the results at the positions of and are averaged. The critical transition height is introduced to decide the flow pattern transition between the mass and funnel flows where the vertical grain velocity coincides at the positions of and . When , except those near the side walls, the grains demonstrate a uniform vertical velocity, which suggests that they flow down in the mass flow pattern. When , the flow takes a funnel flow pattern until the grains flow across the outlet. The grain velocity continues to increase at positions and when approaching the outlet, and slows down to zero at the positions , , and given the presence of baffles.
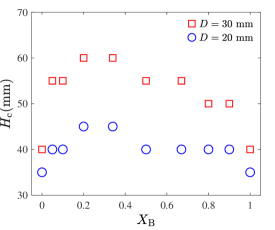
Fig.9 plots the critical transition height as a function of mixing index for outlet sizes and . The variance trend of is similar to those of flow rate and mean normal velocity as shown in Fig.4 and Fig.6. The critical transition height for the monodisperse flow is obviously smaller than that for the bidisperse flow. The maximum height is reported at a low mixing index. The interior arrangement of the grains has an inherent and robust influence on the flow properties. Moreover, adding a low amount of big grains into the monodisperse flow having small grains can effectively increase the grain velocity, especially around the outlet, compared with the monodisperse flows having only small or big grains. This results may be ascribe to the breakdown of the ordered packing structure, which increase the tendency for a mass-to-funnel flow transition to occur in the hopper.
IV Conclusions
This work numerically examines the bidisperse dense granular flow in a two-dimensional hopper by using the discrete element method. The analysis of the contact force between grains reveals the existence of a half-circular dynamical force arch above the outlet. Although the size of the force arch contradicts the free-fall arch hypothesis, the simulation results validate Beverloo’s law that describes the relationship between flow rate and outlet size. Flow rate has a non-monotonic dependence on the mixing index and reaches its maximum value at a small mixing index.
The monodisperse flow reveals a crystallized structure before the start of the granular flow. While, grains pile up in a disorderly manner in the bidisperse case which corresponds to a smaller packing fraction. When the flow is triggered, the initial close packing becomes loose especially around the outlet. The analysis of both packing fraction and grain velocity reveals a significant change in flow behavior at the key area. The ordered and disordered packing structures lead to the fluctuation and parabolic profiles of the normal grain velocity and packing fraction, respectively. Furthermore, the fluctuation in packing density plays a dominant role in the local fluctuation of flow rate, and the parabolic shape of the grain velocity mainly determines the entire profile of flow rate.
The ordered and disordered packing structures for monodisperse and bidisperse flows lead to different critical transition heights , where the flow transforms from a mass flow pattern to a funnel flow pattern. These results indicate that the earlier occurrence of the mass-to-funnel flow pattern transition corresponds to higher grain velocity and larger flow rate. These findings provide further insights into the influence of grain bidispersity on the dense flow behaviors. Further studies may test the rheology of bidisperse granular flow by using the continuous model Macaulay2020 (32, 33).
Acknowledgements.
This work is financially supported by the National Natural Science Foundation of China (Grant No. 11574153).References
- (1) H. M. Jaeger, S. R. Nagel, and R. P. Behringer, Granular solids, liquids, and gases, Rev. Mod. Phys. 68, 1259 (1996).
- (2) I. S. Aranson, and L. S. Tsimring, Patterns and collective behavior in granular media: Theoretical concepts, Rev. Mod. Phys. 78, 641 (2006).
- (3) R. M. Iverson, The physics of debris flows, Rev. Geophys. 35, 245 (1997).
- (4) R. M. Nedderman and U. Tüzün, A kinematic model for the flow of granular materials, Powder Tech. 22, 243 (1979).
- (5) A. W. Roberts and C. M. Wensrich, Flow dynamics or ’quaking’ in gravity discharge from silos, Chem. Eng. Sci. 57, 295 (2002).
- (6) M. Wjcik , J. Tejchman and G. G. Enstad, Confined granular flow in silos with inserts - Full-scale experiments, Powder Tech. 222, 15 (2012).
- (7) Y. Zhang, F. Jia, Y. Zeng, Y. Han, and Y. Xiao, DEM study in the critical height of flow mechanism transition in a conical silo, Powder Tech. 331, 98 (2018).
- (8) S. Ji, S. Wang, and Z. Peng, Influence of external pressure on granular flow in a cylindrical silo based on discrete element method, Powder Tech. 356, 702 (2019).
- (9) S. Wang, M. Zhuravkov, and S. Ji, Granular flow of cylinder-like particles in a cylindrical hopper under external pressure based on DEM simulations, Soft Matter 16, 7760 (2020).
- (10) D. C. Huang, M. Lu, S. Sen, M. Sun, Y. D. Feng and A. N. Yang, Spin Brazil-nut effect and its reverse in a rotating double-walled drum, Eur. Phys. J. E 36, 9855 (2013).
- (11) Q. Shi, G. Sun, M. Y. Hou and K. Q. Lu, Density-driven segregation in vertically vibrated binary granular mixtures, Phys. Rev. E 75, 061302 (2007).
- (12) W. G. Wang, Z. Z. Zhou, J. Zong and M. Y. Hou, DEM simulation of granular segregation in two-compartment system under zero gravity, Chin. Phys. B 26, 044501 (2017).
- (13) M. Bursik, A. Patra, E. B. Pitman, C. Nichita, J. L. Macias, R. Saucedo and O. Girina, Advances in studies of dense volcanic granular flows, Rep. Prog. Phys. 68, 271 (2005).
- (14) D. V. Denisov, K. A. Lörinca, J. T. Uhi, K. A. Dahmen and P. Schall, Universality of slip avalanches in flowing granular matter, Nat. Commum. 7, 10641 (2016).
- (15) B. P. Tighe and M. Sperl, Pressure and motion of dry sand: translation of Hagen’s paper from 1852, Granular Matter 9, 141 (2007).
- (16) W. A. Beverloo, H. A. Leniger, J. van de Velde, The flow of granular solids through orifices, Chem. Eng. Sci. 15, 260 (1961).
- (17) R. M. Nedderman, U. Tüzün, S. B. Savage, and G. T. Houlsby, The flow of granular materials-I: Discharge rates from hoppers, Chem. Eng. Sci. 37, 1597 (1982).
- (18) A. Janda, I. Zuriguel, and D. Maza, Flow rate of particles through apertures obtained from self-Similar density and velocity profiles, Phys. Rev. Lett. 108, 248001 (2012).
- (19) M. A. Aguirre, J. G. Grande, A. Calvo, L. A. Pugnaloni, and J.-C. Gminard, Pressure independence of granular flow through an aperture, Phys. Rev. Lett. 104, 238002 (2010).
- (20) H. W. Zhu, L. P. Wang, Q. F. Shi, L. S. Li, and N. Zheng, Improvement in flow rate through an aperture on a conveyor belt: Effects of bottom wall and packing configurations, Powder Tech. 345, 676 (2019).
- (21) X. Y. Zhou, S. K. Liu, Z. H. Zhao, X. Li, C. H. Li, M. Sun, and D. C. Huang, Dilute-to-dense flow transition and flow-rate behavior of lateral bifurcated granular flow, Powder Tech. 383, 536 (2021).
- (22) P. Arteaga and U. Tüzün, Flow of binary mixtures of equal-density granules in hoppers - size segregation, flowing density and discharge rates, Chem. Eng. Sci. 45, 205 (1990).
- (23) S. Humby, U. Tüzün, and A. B. Yu, Prediction of hopper discharge rates of binary granular mixtures, Chem. Eng. Sci. 53, 483 (1998).
- (24) M. Benyamine, M. Djermane, B. Dalloz-Dubrujeaud, and P. Aussillous, Discharge flow of a bidisperse granular media from a silo, Phys. Rev. E 90, 032201 (2014).
- (25) Y. Zhou, P. Ruyer, and P. Aussillous, Discharge flow of a bidisperse granular media from a silo: Discrete particle simulations, Phys. Rev. E 92, 062204 (2015).
- (26) D. C. Huang, G. Sun, and K. Q. Lu, Relationship between the flow rate and the packing fraction in the choke area of the two-dimensional granular flow, Phys. Rev. E 74, 061306 (2006).
- (27) D. C. Huang, G. Sun, and K. Q. Lu, Influence of granule velocity on gravity-driven granular flow, Phys. Lett. A 375, 3375 (2011).
- (28) T. W. Wang, X. Li, Q. Q. Wu, T. F. Jiao, X. Y. Liu, M. Sun, F. L Hu, and D. C. Huang, Numerical simulations of dense granular flow in a two-dimensional channel: The role of exit position, Chin. Phys. B 27, 124704 (2018).
- (29) P. A. Cundall, and O. D. L. Strack, A discrete numerical model for granular assemblies, Gotechnipue 29, 47 (1979).
- (30) J. Schäfer, S. Dippel, and D. E Wolf, Force Schemes in Simulations of Granular Materials, J. Phys. I France 6, 5 (1996).
- (31) D. C. Huang, G. Sun, and K. Q. Lu, A stochastic description of transition between granular flow states, Commun. Theor. Phys. 48, 729 (2007).
- (32) M. Macaulay, and P. Rognon, Two mechanisms of momentum transfer in granular flows, Phys. Rev. E 101, 050901(R) (2020).
- (33) O. Pouliquen, C. Cassar, P. Jop, Y. Forterre, and M. Nicolas, Flow of dense granular material: towards simple constitutive laws, J. Stat. Mech. 7, P07020 (2006).