Inflation with shallow dip and primordial black holes
Abstract
Primordial black holes may arise through ultra slow-roll inflation. In this work we study a toy model of ultra slow-roll inflation with a shallow dip. The ultra slow-roll stage enhances the curvature perturbations and thus the primordial scalar power spectrum. We analyze the features of the power spectrum numerically and analytically, and then give a rough estimate of the lower and upper bound of the enhancement. These large perturbations also produce second order gravitational waves, which are in the scope of future observations.
keywords:
Primordial black holes , Gravitational waves , Ultra slow-roll inflation1 Introduction
Inflationary cosmology has great success in solving the puzzles of standard big bang theory. In addition, it provides elegant explanations for the temperature fluctuations of the cosmic microwave background (CMB) and the seeds for large scale structure (LSS) formation. Present observations of CMB [1] and LSS [2, 3, 4, 5] have significantly constrained inflation on scales larger than several Gpc. However, the constraints on small scales are much more weaker, leaving the details of inflationary dynamics on these scales unknown.
A bold but intriguing postulation is that primordial black holes (PBHs) may arise in very early universe [6, 7, 8]. These black holes are a type of hypothetical objects formed from the collapse of overdense region caused by large perturbations on small scales. Due to the primordial origin, they have a wide range of mass down to the Planck mass ( g) and up to as heavy as supermassive black holes. The PBHs lighter than g have evaporated through Hawking radiation [9, 10], while those heavier still survive at present epoch. These relic PBHs are natural dark matter candidate because they are collision-less and friction-less. They are also considered as the sources of the gravitational wave signals observed by LIGO/Virgo/KAGRA [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26]. Current data from various channels of observations have imposed severe constraints on the mass (energy) fraction of PBHs [27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45]. For example, the mass range is strongly limited by the spectral distortion of the CMB [46, 47, 48, 49], the range by Pulsar Timing Arrays [50], where is the solar mass. These are indirect constraints that rely on some model details. Some direct constraints like gravitational lensing [33, 51, 52], constrains the mass range stringently. In most mass windows, the fraction of PBHs as dark matter is less than . However, there is still an asteroid mass window, , in which the PBHs could contribute a large fraction or the total of dark matter.
The most commonly considered mechanism of generating the large perturbations required for PBH formation is inflation, which provides the origin of the primordial quantum fluctuations naturally. To have the PBHs formed, the curvature perturbations need to be enhanced sufficiently. For gaussian distributed curvature perturbations, the primordial scalar power spectrum at scales related to the PBH formation is required to be roughly seven orders larger than that at CMB scales [53]. This may change if the details like non-Gaussianities and non-linear effects are considered [54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72]. The enhancement can be realised in various inflation models, of which one of the simplest is the single field inflation with an ultra slow-roll (USR) stage. Usually, the USR phase appears if the potential has, for instance, a quasi-inflection point [27, 73, 74, 75, 76, 77, 77, 78, 79, 80], a local minimum/maximum [81, 82, 83, 57, 84, 85, 86, 87], etc. When the inflaton rolls over these features, the slow roll phase transitions to be USR and the inflaton is largely decelerated. In such a stage the curvature perturbations and the primordial power spectrum would be amplified. The PBHs may form after these amplified perturbations re-enter the horizon, provided that the enhancement is sufficient and the USR phase is long enough. The enhancement mechanism is also widely studied in inflation models constructed with piecewise potentials [88, 89, 90, 91]. This type of theories are useful to show the details of the amplification mechanism. However, the non-smooth features may lead to sharp and instantaneous transitions. As is discussed recently [92, 93, 94, 95, 96, 97, 98, 99, 100], such transitions may have significant loop corrections from the small scales to the power spectrum at large scales and spoil the CMB observations.
| Sets | ||||||
|---|---|---|---|---|---|---|
| 0.1912 | ||||||
| 0.1930 | 0.096 | 0.0254076 | 0.01 | |||
| 0.1920 | 0.095 | 0.024643 | 0.01 | |||
| 0.1935 | 0.098 | 0.02569 | 0.01 |
Hence it is of great importance to consider smooth and more realistic models. One may also consider non-standard theories like non-canonical scalar field [101, 102, 103, 104, 105, 106, 107, 108], modified gravity [109, 110, 111, 112, 113], multi-field inflation [114, 115, 116, 117, 118, 119], etc.
In this work we consider the non-monotonic model proposed in [87]. The potential has a shallow dip, with a local minimum and a local maximum. We study the primordial power spectrum both numerically and analytically. In particular, we try to improve the analytical expression of the power spectrum. The analytical description of the power spectrum [120, 121, 122, 123, 124, 86] is meaningful since it relates the model parameters or the slow-roll parameters to the PBH abundance directly. If the analytical expression is highly precise, it would be instructive for building models. We also study the second order gravitational waves (GWs) produced by the large perturbations [125, 126, 127, 128, 129, 130, 131, 132]. These GWs are in the scope of future observatories. The detection of stochastic GWs background would imply new physics of the universe. However, the non-detection would also impose strong constraints on the early universe. Compared to [87], We used the same model and the mechanism of USR, but with different parameter sets, which are related to the asteroid mass PBHs. The improvements in this paper are primarily the analysis of the scalar power spectrum and the gravitational waves induced by scalar perturbations. Although our results do not provide an explicit relationship between the power spectrum and the model parameters, we believe our study enhances the understanding of how ultra slow-roll inflation amplifies curvature perturbations, leading to PBH formation.
This paper is organized as follows. We first introduce the model briefly in section 2, then we solve the perturbations and give the numerical and analytical power spectrum in section 3. The PBH formation and the induced gravitational waves are considered in section 4 and 5, respectively. The summary is given in the final section.
2 The model
The model proposed in [87] contains two parts,
| (1) |
where is the inflaton field, , and . There are six parameters in our model, , , , , , and . The first part of the potential in Equation (1) provides the feature, which is controlled by the parameter . The second part is a standard slow-roll potential proportional to the parameter , which is constrained by the CMB observations by using (with ). The parameter controls the size of the feature, and cannot be severely constrained. To have a successful ultra slow-roll inflation model, must be sufficiently small. In our model we set . Since , the parameter can also be constrained by using the constraints on . The remaining parameters , , and are relatively free. These free parameters describe the characteristics of the dip feature. For example, the parameter determines the shape of the potential dip. To some extent, is manually tuned to ensure that the fraction is appropriate for achieving ultra slow-roll inflation. In our work we set . For excessively large values of the inflaton becomes confined within the dip, and inflation turns to be standard slow-roll for too small values. The parameter gives the position of the dip, thus controls when the ultra slow-roll stage happens and the peak scale of the power spectrum. We choose the values of in Tab. 1 so that the peak of the power spectrum lies in the range . Therefore, the formed primordial black holes have asteroid mass. The parameter tells the depth of the dip. It is related to the slow roll parameter and the duration of the ultra slow-roll stage. In this work the parameter is fine tuned and it sensitively affects the amplitude of the power spectrum.
The field equation of the inflaton is
| (2) |
where dot represents time derivative and is the Hubble parameter, with the scale factor. One may also write this equation with the e-folding number,
| (3) |
where the subscripts and represent the derivative with respect to the inflaton field and the e-folding number , respectively. Note that the e-folding number and the time coordinate are related by . Defining the slow-roll parameters,
| (4) |
the evolution equation (3) then becomes
| (5) |



where
| (6) |
is the potential slow-roll parameter. The “” sign appears because of the nonmonotonicity of the potential in our theory. For the usual slow-roll inflation, the potential is monotonic (for inflation period) and is always positive (or negative) in inflation phase. For USR inflation with a quasi-inflection point (but still monotonic), the potential is extremely flat and the slope . Equation (5) has a “” sign and straightforwardly gives around the plateau. In our theory, equation (5) has “” sign before the inflaton rolls down to the local minimum. After the inflaton passes through the local minimum, equation (5) has a “” sign before the local maximum. In this period we have . As is analyzed in [87], this stage is crucial since the curvature perturbations grow as in the USR stage. In this way, the curvature perturbations and thus the power spectrum are enhanced sufficiently so that the condition of PBH formation is satisfied. The evolution of is shown in Fig. 1.
3 The curvature perturbations and the power spectrum
3.1 The analytical approach
The USR stage amplifies the curvature perturbations. To be more specific, let us consider the evolution of the curvature perturbations analytically. The evolution equation of the curvature perturbation modes is
| (7) |
Note that represents the curvature perturbation and is its Fourier mode with wave number . It is also convenient to work in the conformal time coordinate and use the Mukhanov-Sasaki variable. In this work however, we deal with the equation (7) directly. For constant and , the general solution is
| (8) |
where and , with the Bessel function of the first kind and the Gamma function. and are coefficients with dependence, and .
Based on the above observation and the evolution of the slow-roll parameters, we divide the inflation process into four stages, the slow-roll stage (), the USR stage (), the constant-roll stage (), and the final slow-roll stage (). We neglect the slow-roll parameter for the moment due to its smallness. We will discuss the impact of in next subsection. The parameter is approximated as
| (9) |
Note that corresponds to the start of inflation.


From the numerical evolution of the background quantities in Fig. 1, we see that the slow-roll parameter starts growing and exceeds unity after the constant-roll stage. This certainly violates the slow-roll condition. However, in (9) we assume that for the inflation process turns back to be slow-roll and for simplicity. This approximation is reasonable provided that the constant-roll phase lasts long enough, in which case the scales responsible for PBH production have exited the horizon and being frozen for a long time at , so that they would not be affected by the final stage ().
Under this setup we can solve the curvature perturbation modes in each stage analytically. The coefficients are obtained by the continuity conditions at transitions. Finally, the power spectrum in the late time limit () is given by
| (10) |
The coefficients are computed in the Apendix. We show the comparison of the numerically calculated power spectrum 111We use the Bunch-Davis vacuum as the initial conditions. and the analytical one in Fig. 2. We see that they have some differences. First, there is a discrepancy for the modes that exit the horizon in slow-roll regime (). This is because the analytical approach neglected the evolution of the slow-roll parameter in deriving the analytical power spectrum (10). To understand this, let us consider the expansion of the power spectrum (10) in ,
| (11) |
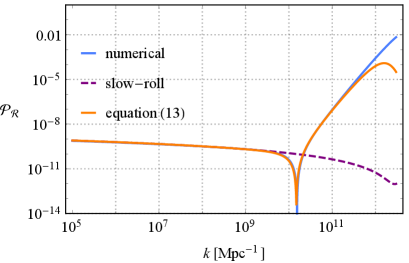
where is evaluated at the time when the CMB pivot scale exits the horizon. In this equation and the rest of this paper, . Hence represents the scale that exits the horizon at transition . The coefficients are functions of slow-roll parameters and the duration of the each stage of inflation, hence the effects of super-horizon evolution are included in them. This expansion gives a scale invariant power spectrum for scales , as is shown in Fig. 2. As a rough modification which includes the evolution of , we replace the constant parameter by ,
| (12) |
The slow-roll parameter is computed at horizon crossing time . On the other hand, the series of in the above square brackets are derived at the end of inflation so that the super-horizon evolution of the curvature perturbations are included. This implies that the approximation (12) is only valid for . In this regime the power spectrum can be written as
| (13) |
This expression is not applicable for the scales . We show the comparison of (13) and the numerical one in Fig. 3. We see that this modification gives a more accurate result for the modes . Now the remaining problem is, to what scales the approximation (13) is applicable. Unfortunately, the exact bound is not known since this expression is not derived rigorously. We will investigate this problem in our future work.
The second difference is the oscillations around the peak, which is absent in the numerical power spectrum. The oscillations are fundamentally linked to the specifics of the transition between the slow roll phase and the ultra-slow-roll (USR) phase. Reference [133] parametrized this transition using an analytical model, comparing smooth and instantaneous transitions. It was found that oscillations vanish if the transition lasts more than approximately one e-fold. In essence, the oscillations are a result of instantaneous (sharp) transitions, such as those described by the analytical approximation (9) in our work, as well as the step model discussed in references [89] and [91].
The third difference is that, the analytical power spectrum has a slightly steeper growth rate before the peak. This is also related to the ignorance of the evolution of . The expansion (11) predicts a growth rate of due to the constant [122]. This conclusion would be changed if the evolution of is considered. As is shown in Fig. 1, the parameter grows with before the transition at , hence grows with (). Therefore the -dependence of the parameter slightly reduces the growth of the power spectrum. This is consistent with the numerical results.
At last, the analytical power spectrum predicts a larger amplitude of peak, indicating a deviation from the realistic model. We will discuss this issue in next subsection.
3.2 The enhancement
We are interested in how many orders of magnitude the power spectrum could be enhanced, since this is responsible for the PBH production. For the toy model (9), the magnitude of enhancement of the power spectrum is [89, 90, 91]
| (14) |
where the factor . However, this estimation would be problematic for realistic models since there are uncertainties in determining the bounds of the integral (14). This is because the transitions between slow-roll and ultra slow-roll are non-instantaneous. One may intuitively replace the integral bounds and by and ,

| (15) |
where are the e-folding numbers when . This estimation predicts an enhancement close to the exact value for short transitions (). Nevertheless, it underestimates the enhancement since the curvature perturbations grow even if . Mathematically, the equation (7) has exponentially growing solution as long as , irrespective of whether the mode is sub-horizon or super-horizon. Neglecting the parameter , this corresponds to . Hence, a conservative estimate for the upper bound of is
| (16) |
where corresponds to . We compare the enhancement predicted by equation (15), (16), and the numerical results in Tab. 2 and Fig. 4. We see that the magnitude of enhancement is between the estimate (15) and (16). As expected, the equation (15) gives a close but lower estimate of enhancement. The equation (16) overestimates the enhancement because of the ignorance of the details of each stage. As was pointed out in [122, 133], the stages before and after USR and the details of the transitions between different stages have significant effects on the amplitude of the power spectrum. Therefore, an exact estimate for the amplitude of the peak should contain the information of the whole inflation process.
| Sets | ||||
|---|---|---|---|---|
| 7.0 | 6.7 | 8.6 | ||
| 5.8 | 5.4 | 7.7 | ||
| 5.3 | 5.1 | 7.2 | ||
| 2.3 | — | 4.7 |
4 PBH formation

PBHs can be formed when the large fluctuations re-enter the horizon. The mass fraction of PBHs at formation is [53, 36]
| (17) |
where the density fraction is related to the curvature perturbation by
| (18) |
In this paper the equation of state since we assume the PBHs and the GWs are formed in radiation domination. The threshold is the critical value of density contrast over which the PBHs could be formed. Its value depends on the details of the collapse and still has uncertainties. In this work we set [62]. The parameter is the fraction of mass collapsed to be PBHs that has . is the standard deviation of , defined by
| (19) |
where is the window function. Due to the increasing of the power spectrum, has its maximum at , hence one has . Furthermore, the mass of the produced PBHs are related to the wave number by
| (20) |
where is the solar mass and the relativistic degrees of freedom. The fraction of PBHs as dark matter at present time can be expressed as
| (21) |
Now, the fraction can be computed by using the power spectrum .
To produce the PBHs with mass in the range , in which the PBHs could constitute all the dark matter, the power spectrum should peak at . In our model, the parameter set gives , leading to the PBHs with for , as is shown in Fig. 5.
In Fig. 6 we show how the parameters , , and are related to the enhancement of the power spectrum and the fraction of PBH as dark matter. We choose these parameters because they are directly related to the dip feature of the potential. We study the effects of a specific parameter by fixing the other parameters. Now let us discuss the results. First, we see that there is a fine tuning problem for the parameters. That is, each parameter has a very narrow space that allows for USR. Inappropriate parameters could result in either the inflation field being permanently confined within the potential dip (blue region) or in a total e-folding number of less than 50 (gray region), failing to meet the minimum requirement for inflation. Second, considering the requirements for PBH formation, the range of permissible parameter values will be even narrower. Due to the sensitivity of the exponential dependency, primordial black holes will be overproduced when the enhancement exceeds slightly than 7 (the exact value depends on the details of PBH production, for example the threshold ), whereas when it is slightly less than 7, the abundance of PBHs will be too low to be considerable. These results arise from the exponential dependence of the abundance on the power spectrum. At last, we argue that the parameter space where the peak of the power spectrum exceeds () could exhibit notable nonlinear behavior. Within such regimes, the linear perturbation theory may break down as the perturbations reach significant magnitudes.
5 The induced gravitational waves
The scalar perturbations decouple with the GWs at linear order. However, they couple at nonlinear orders. Hence, the large scalar perturbations are possible to induce GWs at nonlinear orders. This topic has been widely studied in previous literatures [125, 126, 29, 129, 130, 131, 132]. We follow these works and study the induced GWs in our model. Let us consider the metric
| (22) |
where and are the first order scalar perturbations and is the second order transverse-traceless tensor perturbation, representing the induced GWs. In the absence of anisotropic stress part, one has . In Fourier space, the equation of is given by
| (23) |
with .



Here prime denotes the derivative with respect to the conformal time , and is the Fourier mode of defined by
| (24) |
where and are two unit vector bases perpendicular to that are orthogonal to each other. is the source term of the induced GWs defined by
| (25) |



Note that the equation of state parameter is introduced.
The energy density of the GWs in sub-horizon is
| (26) |
where overline denotes the average over oscillations. The dimensionless power spectrum could be defined by the two-point correlation function,
| (27) |
where the index , represent the polarization modes , . The energy density of GWs per logarithmic wavelength is
| (28) |
The power spectrum of GWs has a lengthy expression. The final result of the energy density at production is [129]
| (29) |
where is the step function. The energy density of GWs at present time is then
| (30) |
where is the energy density of radiation at present time. We stress that the formula (29) is obtained by taking the oscillation average of the trigonometric functions, and the assumption that the GWs are produced in radiation dominated era. If the GWs were produced in matter dominated era, this formula would be modified [129].

Using the numerical power spectrum, the energy density of the induced GWs can be obtained. The Fig. 7 shows how the dip feature parameters , , and are related to the peak amplitude of the induced GWs. The results of model parameters in Tab. 1 are shown in Fig. 8. An interesting feature is that, the parameter sets and , whose corresponding PBH abundance is exponentially suppressed since the peak of the power spectrum is not large enough, lead to detectable stochastic GWs by future observatories. This is because the induced GWs are not the product of PBHs, but are of the large perturbations. This confirms the idea that the non-detection of stochastic GWs would strongly constrain the early universe. Recently, the pulsar timing array (PTA) collaborations reported strong evidence for the presence of stochastic GW background [145, 146, 147, 148, 149], possibly from supermassive black-hole binaries, but the possibility of other sources like scalar induced GWs are not excluded. If they are induced GWs, they would give a lot of new implications for the primordial curvature perturbations and PBHs [150, 151, 152, 153, 154, 155, 156, 157].
6 Discussion and conclusions
In this work we studied the inflation model proposed in our previous work [87]. The model features a shallow local minimum. Inflation transitions to USR stage when the inflaton rolls over the local minimum. In this stage the perturbations and thus the power spectrum are amplified. For appropriate parameter choices, it is possible to produce PBHs that contribute a large fraction to the dark matter and be consistent with the observations on CMB scales simultaneously. The induced second order GWs are one of the indirect probes of PBHs. The GWs induced by the large perturbations that produce the asteroid mass PBHs are detectable by future experiments like LISA, DECIGO, etc. If these GWs are not observed in future experiments, one would have strong constraints on the primordial scalar power spectrum.
An important issue discussed in this work is the analytical power spectrum. The numerical solution gives the exact power spectrum while the analytical expression would reveal how the power spectrum is controlled by the model parameters. Due to the exponential dependence between the PBH fraction and the power spectrum, a tiny difference of power spectrum would lead to a large deviation of prediction for PBHs. Therefore, an accurate analytical power spectrum would be important and helpful for model building. We expect to give a complete and more accurate power spectrum in future work.
Acknowledgements
This work is supported in part by the National Natural Science Foundation of China (Grants No. 12165013, 11975116, 12005174, 12375049, and 12475062). B.-M. Gu is supported by Jiangxi Provincial Natural Science Foundation under Grant No. 20224BAB211026. F.-W. Shu is supported by the Key Program of the Natural Science Foundation of Jiangxi Province under Grant No. 20232ACB201008. K. Yang acknowledges the support of Natural Science Foundation of Chongqing (Grant No. CSTB2024NSCQ-MSX0358).
Appendix A The coefficients and
For , the slow-roll conditions are satisfied and we have
| (31) |
By imposing the Bunch-Davis initial condition, the coefficients and can be determined,
| (32) |
Hence
| (33) |
In the USR stage (), the solution is
| (34) |
with . The coefficients and are determined by the continuity conditions of and at , namely,
| (35) |
The result is
| (36) | ||||
| (37) | ||||
where , is the Wronskian, is the Gamma function, and is the regularized hypergeometric function. After the USR stage, the inflaton undergoes a constant-roll phase (), in which the curvature perturbation is
| (38) |
with . The coefficients and can be obtained by repeating the above matching conditions at ,
| (39) | ||||
| (40) | ||||
In the final slow-roll stage we have
| (41) |
Note that we assumed that and in this stage. The coefficients and are given by the matching at ,
| (42) | ||||
| (43) | ||||
Using the asymptotic property of the Bessel functions, we have
| (44) |
Thus, the power spectrum in the late time limit is given by
| (45) |
References
- [1] Planck collaboration, Planck 2018 results. X. Constraints on inflation, Astron. Astrophys. 641 (2020) A10 [1807.06211].
- [2] SDSS collaboration, Cosmological parameters from SDSS and WMAP, Phys. Rev. D 69 (2004) 103501 [astro-ph/0310723].
- [3] SDSS-III collaboration, The Eleventh and Twelfth Data Releases of the Sloan Digital Sky Survey: Final Data from SDSS-III, Astrophys. J. Suppl. 219 (2015) 12 [1501.00963].
- [4] DES collaboration, Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing, Phys. Rev. D 98 (2018) 043526 [1708.01530].
- [5] Planck collaboration, Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641 (2020) A6 [1807.06209].
- [6] Y.B. Zel’dovich and I.D. Novikov, The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model, Sov. Astron. 10 (1966) 602.
- [7] S. Hawking, Gravitationally collapsed objects of very low mass, Mon. Not. Roy. Astron. Soc. 152 (1971) 75.
- [8] B.J. Carr and S.W. Hawking, Black holes in the early universe, Mon. Not. Roy. Astron. Soc. 168 (1974) 399.
- [9] S.W. Hawking, Black hole explosions, Nature 248 (1974) 30.
- [10] S.W. Hawking, Particle Creation by Black Holes, Commun. Math. Phys. 43 (1975) 199.
- [11] M. Sasaki, T. Suyama, T. Tanaka and S. Yokoyama, Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914, Phys. Rev. Lett. 117 (2016) 061101 [1603.08338].
- [12] M. Raidal, V. Vaskonen and H. Veermäe, Gravitational Waves from Primordial Black Hole Mergers, JCAP 09 (2017) 037 [1707.01480].
- [13] Y. Ali-Haïmoud, E.D. Kovetz and M. Kamionkowski, Merger rate of primordial black-hole binaries, Phys. Rev. D 96 (2017) 123523 [1709.06576].
- [14] M. Raidal, C. Spethmann, V. Vaskonen and H. Veermäe, Formation and Evolution of Primordial Black Hole Binaries in the Early Universe, JCAP 02 (2019) 018 [1812.01930].
- [15] V. Vaskonen and H. Veermäe, Lower bound on the primordial black hole merger rate, Phys. Rev. D 101 (2020) 043015 [1908.09752].
- [16] V. De Luca, G. Franciolini, P. Pani and A. Riotto, The evolution of primordial black holes and their final observable spins, JCAP 04 (2020) 052 [2003.02778].
- [17] V. De Luca, G. Franciolini, P. Pani and A. Riotto, Primordial Black Holes Confront LIGO/Virgo data: Current situation, JCAP 06 (2020) 044 [2005.05641].
- [18] S. Clesse and J. Garcia-Bellido, GW190425, GW190521 and GW190814: Three candidate mergers of primordial black holes from the QCD epoch, Phys. Dark Univ. 38 (2022) 101111 [2007.06481].
- [19] A. Hall, A.D. Gow and C.T. Byrnes, Bayesian analysis of LIGO-Virgo mergers: Primordial vs. astrophysical black hole populations, Phys. Rev. D 102 (2020) 123524 [2008.13704].
- [20] V. De Luca, V. Desjacques, G. Franciolini, P. Pani and A. Riotto, GW190521 Mass Gap Event and the Primordial Black Hole Scenario, Phys. Rev. Lett. 126 (2021) 051101 [2009.01728].
- [21] K.W.K. Wong, G. Franciolini, V. De Luca, V. Baibhav, E. Berti, P. Pani et al., Constraining the primordial black hole scenario with Bayesian inference and machine learning: the GWTC-2 gravitational wave catalog, Phys. Rev. D 103 (2021) 023026 [2011.01865].
- [22] G. Hütsi, M. Raidal, V. Vaskonen and H. Veermäe, Two populations of LIGO-Virgo black holes, JCAP 03 (2021) 068 [2012.02786].
- [23] V. De Luca, G. Franciolini, P. Pani and A. Riotto, Bayesian Evidence for Both Astrophysical and Primordial Black Holes: Mapping the GWTC-2 Catalog to Third-Generation Detectors, JCAP 05 (2021) 003 [2102.03809].
- [24] G. Franciolini, V. Baibhav, V. De Luca, K.K.Y. Ng, K.W.K. Wong, E. Berti et al., Searching for a subpopulation of primordial black holes in LIGO-Virgo gravitational-wave data, Phys. Rev. D 105 (2022) 083526 [2105.03349].
- [25] G. Franciolini, R. Cotesta, N. Loutrel, E. Berti, P. Pani and A. Riotto, How to assess the primordial origin of single gravitational-wave events with mass, spin, eccentricity, and deformability measurements, Phys. Rev. D 105 (2022) 063510 [2112.10660].
- [26] G. Franciolini and P. Pani, Searching for mass-spin correlations in the population of gravitational-wave events: The GWTC-3 case study, Phys. Rev. D 105 (2022) 123024 [2201.13098].
- [27] P. Ivanov, P. Naselsky and I. Novikov, Inflation and primordial black holes as dark matter, Phys. Rev. D 50 (1994) 7173.
- [28] B.J. Carr, K. Kohri, Y. Sendouda and J. Yokoyama, New cosmological constraints on primordial black holes, Phys. Rev. D 81 (2010) 104019 [0912.5297].
- [29] R. Saito and J. Yokoyama, Gravitational-Wave Constraints on the Abundance of Primordial Black Holes, Prog. Theor. Phys. 123 (2010) 867 [0912.5317].
- [30] A. Barnacka, J.F. Glicenstein and R. Moderski, New constraints on primordial black holes abundance from femtolensing of gamma-ray bursts, Phys. Rev. D 86 (2012) 043001 [1204.2056].
- [31] F. Capela, M. Pshirkov and P. Tinyakov, Constraints on primordial black holes as dark matter candidates from capture by neutron stars, Phys. Rev. D 87 (2013) 123524 [1301.4984].
- [32] B. Carr, F. Kuhnel and M. Sandstad, Primordial Black Holes as Dark Matter, Phys. Rev. D 94 (2016) 083504 [1607.06077].
- [33] H. Niikura et al., Microlensing constraints on primordial black holes with Subaru/HSC Andromeda observations, Nature Astron. 3 (2019) 524 [1701.02151].
- [34] B. Carr, M. Raidal, T. Tenkanen, V. Vaskonen and H. Veermäe, Primordial black hole constraints for extended mass functions, Phys. Rev. D 96 (2017) 023514 [1705.05567].
- [35] M. Zumalacarregui and U. Seljak, Limits on stellar-mass compact objects as dark matter from gravitational lensing of type Ia supernovae, Phys. Rev. Lett. 121 (2018) 141101 [1712.02240].
- [36] M. Sasaki, T. Suyama, T. Tanaka and S. Yokoyama, Primordial black holes—perspectives in gravitational wave astronomy, Class. Quant. Grav. 35 (2018) 063001 [1801.05235].
- [37] H. Niikura, M. Takada, S. Yokoyama, T. Sumi and S. Masaki, Constraints on Earth-mass primordial black holes from OGLE 5-year microlensing events, Phys. Rev. D 99 (2019) 083503 [1901.07120].
- [38] P. Montero-Camacho, X. Fang, G. Vasquez, M. Silva and C.M. Hirata, Revisiting constraints on asteroid-mass primordial black holes as dark matter candidates, JCAP 08 (2019) 031 [1906.05950].
- [39] R. Laha, Primordial Black Holes as a Dark Matter Candidate Are Severely Constrained by the Galactic Center 511 keV -Ray Line, Phys. Rev. Lett. 123 (2019) 251101 [1906.09994].
- [40] B. Dasgupta, R. Laha and A. Ray, Neutrino and positron constraints on spinning primordial black hole dark matter, Phys. Rev. Lett. 125 (2020) 101101 [1912.01014].
- [41] B. Carr, K. Kohri, Y. Sendouda and J. Yokoyama, Constraints on primordial black holes, Rept. Prog. Phys. 84 (2021) 116902 [2002.12778].
- [42] B. Carr and F. Kuhnel, Primordial Black Holes as Dark Matter: Recent Developments, Ann. Rev. Nucl. Part. Sci. 70 (2020) 355 [2006.02838].
- [43] A.M. Green and B.J. Kavanagh, Primordial Black Holes as a dark matter candidate, J. Phys. G 48 (2021) 043001 [2007.10722].
- [44] S. Mittal, A. Ray, G. Kulkarni and B. Dasgupta, Constraining primordial black holes as dark matter using the global 21-cm signal with X-ray heating and excess radio background, JCAP 03 (2022) 030 [2107.02190].
- [45] O. Özsoy and G. Tasinato, Inflation and Primordial Black Holes, 2301.03600.
- [46] D.J. Fixsen, E.S. Cheng, J.M. Gales, J.C. Mather, R.A. Shafer and E.L. Wright, The Cosmic Microwave Background spectrum from the full COBE FIRAS data set, Astrophys. J. 473 (1996) 576 [astro-ph/9605054].
- [47] J. Chluba, A.L. Erickcek and I. Ben-Dayan, Probing the inflaton: Small-scale power spectrum constraints from measurements of the CMB energy spectrum, Astrophys. J. 758 (2012) 76 [1203.2681].
- [48] K. Kohri, T. Nakama and T. Suyama, Testing scenarios of primordial black holes being the seeds of supermassive black holes by ultracompact minihalos and CMB -distortions, Phys. Rev. D 90 (2014) 083514 [1405.5999].
- [49] T. Nakama, B. Carr and J. Silk, Limits on primordial black holes from distortions in cosmic microwave background, Phys. Rev. D 97 (2018) 043525 [1710.06945].
- [50] Z.-C. Chen, C. Yuan and Q.-G. Huang, Pulsar Timing Array Constraints on Primordial Black Holes with NANOGrav 11-Year Dataset, Phys. Rev. Lett. 124 (2020) 251101 [1910.12239].
- [51] J.M. Diego et al., Dark Matter under the Microscope: Constraining Compact Dark Matter with Caustic Crossing Events, Astrophys. J. 857 (2018) 25 [1706.10281].
- [52] M. Oguri, J.M. Diego, N. Kaiser, P.L. Kelly and T. Broadhurst, Understanding caustic crossings in giant arcs: characteristic scales, event rates, and constraints on compact dark matter, Phys. Rev. D 97 (2018) 023518 [1710.00148].
- [53] S. Young, C.T. Byrnes and M. Sasaki, Calculating the mass fraction of primordial black holes, JCAP 07 (2014) 045 [1405.7023].
- [54] S. Young and C.T. Byrnes, Primordial black holes in non-Gaussian regimes, JCAP 08 (2013) 052 [1307.4995].
- [55] C. Pattison, V. Vennin, H. Assadullahi and D. Wands, Quantum diffusion during inflation and primordial black holes, JCAP 10 (2017) 046 [1707.00537].
- [56] G. Franciolini, A. Kehagias, S. Matarrese and A. Riotto, Primordial Black Holes from Inflation and non-Gaussianity, JCAP 03 (2018) 016 [1801.09415].
- [57] M. Biagetti, G. Franciolini, A. Kehagias and A. Riotto, Primordial Black Holes from Inflation and Quantum Diffusion, JCAP 07 (2018) 032 [1804.07124].
- [58] J.M. Ezquiaga and J. García-Bellido, Quantum diffusion beyond slow-roll: implications for primordial black-hole production, JCAP 08 (2018) 018 [1805.06731].
- [59] V. Atal and C. Germani, The role of non-gaussianities in Primordial Black Hole formation, Phys. Dark Univ. 24 (2019) 100275 [1811.07857].
- [60] S. Passaglia, W. Hu and H. Motohashi, Primordial black holes and local non-Gaussianity in canonical inflation, Phys. Rev. D 99 (2019) 043536 [1812.08243].
- [61] S. Young, I. Musco and C.T. Byrnes, Primordial black hole formation and abundance: contribution from the non-linear relation between the density and curvature perturbation, JCAP 11 (2019) 012 [1904.00984].
- [62] S. Young, The primordial black hole formation criterion re-examined: Parametrisation, timing and the choice of window function, Int. J. Mod. Phys. D 29 (2019) 2030002 [1905.01230].
- [63] A. Kehagias, I. Musco and A. Riotto, Non-Gaussian Formation of Primordial Black Holes: Effects on the Threshold, JCAP 12 (2019) 029 [1906.07135].
- [64] J.M. Ezquiaga, J. García-Bellido and V. Vennin, The exponential tail of inflationary fluctuations: consequences for primordial black holes, JCAP 03 (2020) 029 [1912.05399].
- [65] N. Kitajima, Y. Tada, S. Yokoyama and C.-M. Yoo, Primordial black holes in peak theory with a non-Gaussian tail, JCAP 10 (2021) 053 [2109.00791].
- [66] D.G. Figueroa, S. Raatikainen, S. Rasanen and E. Tomberg, Implications of stochastic effects for primordial black hole production in ultra-slow-roll inflation, JCAP 05 (2022) 027 [2111.07437].
- [67] Y.-F. Cai, X.-H. Ma, M. Sasaki, D.-G. Wang and Z. Zhou, One Small Step for an Inflaton, One Giant Leap for Inflation: a novel non-Gaussian tail and primordial black holes, 2112.13836.
- [68] Y.-F. Cai, X.-H. Ma, M. Sasaki, D.-G. Wang and Z. Zhou, Highly non-Gaussian tails and primordial black holes from single-field inflation, JCAP 12 (2022) 034 [2207.11910].
- [69] S. Young, Peaks and primordial black holes: the effect of non-Gaussianity, JCAP 05 (2022) 037 [2201.13345].
- [70] G. Ferrante, G. Franciolini, A. Iovino, Junior. and A. Urbano, Primordial non-Gaussianity up to all orders: Theoretical aspects and implications for primordial black hole models, Phys. Rev. D 107 (2023) 043520 [2211.01728].
- [71] S. Pi and M. Sasaki, Logarithmic Duality of the Curvature Perturbation, Phys. Rev. Lett. 131 (2023) 011002 [2211.13932].
- [72] R. van Laak and S. Young, Primordial black hole isocurvature modes from non-Gaussianity, JCAP 05 (2023) 058 [2303.05248].
- [73] J. Yokoyama, Chaotic new inflation and formation of primordial black holes, Phys. Rev. D 58 (1998) 083510 [astro-ph/9802357].
- [74] S.-L. Cheng, W. Lee and K.-W. Ng, Production of high stellar-mass primordial black holes in trapped inflation, JHEP 02 (2017) 008 [1606.00206].
- [75] J. Garcia-Bellido and E. Ruiz Morales, Primordial black holes from single field models of inflation, Phys. Dark Univ. 18 (2017) 47 [1702.03901].
- [76] J.M. Ezquiaga, J. Garcia-Bellido and E. Ruiz Morales, Primordial Black Hole production in Critical Higgs Inflation, Phys. Lett. B 776 (2018) 345 [1705.04861].
- [77] C. Germani and T. Prokopec, On primordial black holes from an inflection point, Phys. Dark Univ. 18 (2017) 6 [1706.04226].
- [78] M. Cicoli, V.A. Diaz and F.G. Pedro, Primordial Black Holes from String Inflation, JCAP 06 (2018) 034 [1803.02837].
- [79] O. Özsoy, S. Parameswaran, G. Tasinato and I. Zavala, Mechanisms for Primordial Black Hole Production in String Theory, JCAP 07 (2018) 005 [1803.07626].
- [80] M. Cicoli, F.G. Pedro and N. Pedron, Secondary GWs and PBHs in string inflation: formation and detectability, JCAP 08 (2022) 030 [2203.00021].
- [81] K. Kannike, L. Marzola, M. Raidal and H. Veermäe, Single Field Double Inflation and Primordial Black Holes, JCAP 09 (2017) 020 [1705.06225].
- [82] G. Ballesteros and M. Taoso, Primordial black hole dark matter from single field inflation, Phys. Rev. D 97 (2018) 023501 [1709.05565].
- [83] M.P. Hertzberg and M. Yamada, Primordial Black Holes from Polynomial Potentials in Single Field Inflation, Phys. Rev. D 97 (2018) 083509 [1712.09750].
- [84] S.S. Mishra and V. Sahni, Primordial Black Holes from a tiny bump/dip in the Inflaton potential, JCAP 04 (2020) 007 [1911.00057].
- [85] D.G. Figueroa, S. Raatikainen, S. Rasanen and E. Tomberg, Non-Gaussian Tail of the Curvature Perturbation in Stochastic Ultraslow-Roll Inflation: Implications for Primordial Black Hole Production, Phys. Rev. Lett. 127 (2021) 101302 [2012.06551].
- [86] A. Karam, N. Koivunen, E. Tomberg, V. Vaskonen and H. Veermäe, Anatomy of single-field inflationary models for primordial black holes, 2205.13540.
- [87] B.-M. Gu, F.-W. Shu, K. Yang and Y.-P. Zhang, Primordial black holes from an inflationary potential valley, Phys. Rev. D 107 (2023) 023519 [2207.09968].
- [88] K. Kefala, G.P. Kodaxis, I.D. Stamou and N. Tetradis, Features of the inflaton potential and the power spectrum of cosmological perturbations, Phys. Rev. D 104 (2021) 023506 [2010.12483].
- [89] K. Inomata, E. McDonough and W. Hu, Primordial black holes arise when the inflaton falls, Phys. Rev. D 104 (2021) 123553 [2104.03972].
- [90] I. Dalianis, G.P. Kodaxis, I.D. Stamou, N. Tetradis and A. Tsigkas-Kouvelis, Spectrum oscillations from features in the potential of single-field inflation, Phys. Rev. D 104 (2021) 103510 [2106.02467].
- [91] K. Inomata, E. McDonough and W. Hu, Amplification of primordial perturbations from the rise or fall of the inflaton, JCAP 02 (2022) 031 [2110.14641].
- [92] J. Kristiano and J. Yokoyama, Ruling Out Primordial Black Hole Formation From Single-Field Inflation, 2211.03395.
- [93] A. Riotto, The Primordial Black Hole Formation from Single-Field Inflation is Not Ruled Out, 2301.00599.
- [94] S. Choudhury, M.R. Gangopadhyay and M. Sami, No-go for the formation of heavy mass Primordial Black Holes in Single Field Inflation, 2301.10000.
- [95] S. Choudhury, S. Panda and M. Sami, No-go for PBH formation in EFT of single field inflation, 2302.05655.
- [96] J. Kristiano and J. Yokoyama, Response to criticism on ”Ruling Out Primordial Black Hole Formation From Single-Field Inflation”: A note on bispectrum and one-loop correction in single-field inflation with primordial black hole formation, 2303.00341.
- [97] S. Choudhury, S. Panda and M. Sami, Quantum loop effects on the power spectrum and constraints on primordial black holes, 2303.06066.
- [98] H. Firouzjahi and A. Riotto, Primordial Black Holes and Loops in Single-Field Inflation, 2304.07801.
- [99] G. Franciolini, A. Iovino, Junior., M. Taoso and A. Urbano, One loop to rule them all: Perturbativity in the presence of ultra slow-roll dynamics, 2305.03491.
- [100] J. Fumagalli, Absence of one-loop effects on large scales from small scales in non-slow-roll dynamics, 2305.19263.
- [101] Y.-F. Cai, X. Tong, D.-G. Wang and S.-F. Yan, Primordial Black Holes from Sound Speed Resonance during Inflation, Phys. Rev. Lett. 121 (2018) 081306 [1805.03639].
- [102] G. Ballesteros, J. Beltran Jimenez and M. Pieroni, Black hole formation from a general quadratic action for inflationary primordial fluctuations, JCAP 06 (2019) 016 [1811.03065].
- [103] A.Y. Kamenshchik, A. Tronconi, T. Vardanyan and G. Venturi, Non-Canonical Inflation and Primordial Black Holes Production, Phys. Lett. B 791 (2019) 201 [1812.02547].
- [104] J. Lin, Q. Gao, Y. Gong, Y. Lu, C. Zhang and F. Zhang, Primordial black holes and secondary gravitational waves from and inflation, Phys. Rev. D 101 (2020) 103515 [2001.05909].
- [105] C. Chen, X.-H. Ma and Y.-F. Cai, Dirac-Born-Infeld realization of sound speed resonance mechanism for primordial black holes, Phys. Rev. D 102 (2020) 063526 [2003.03821].
- [106] Z. Yi, Q. Gao, Y. Gong and Z.-h. Zhu, Primordial black holes and scalar-induced secondary gravitational waves from inflationary models with a noncanonical kinetic term, Phys. Rev. D 103 (2021) 063534 [2011.10606].
- [107] M. Solbi and K. Karami, Primordial black holes and induced gravitational waves in -inflation, JCAP 08 (2021) 056 [2102.05651].
- [108] Z. Teimoori, K. Rezazadeh, M.A. Rasheed and K. Karami, Mechanism of primordial black holes production and secondary gravitational waves in -attractor Galileon inflationary scenario, 2107.07620.
- [109] S. Pi, Y.-l. Zhang, Q.-G. Huang and M. Sasaki, Scalaron from -gravity as a heavy field, JCAP 05 (2018) 042 [1712.09896].
- [110] C. Fu, P. Wu and H. Yu, Primordial Black Holes from Inflation with Nonminimal Derivative Coupling, Phys. Rev. D 100 (2019) 063532 [1907.05042].
- [111] S. Heydari and K. Karami, Primordial black holes in nonminimal derivative coupling inflation with quartic potential and reheating consideration, Eur. Phys. J. C 82 (2022) 83 [2107.10550].
- [112] S. Kawai and J. Kim, Primordial black holes from Gauss-Bonnet-corrected single field inflation, Phys. Rev. D 104 (2021) 083545 [2108.01340].
- [113] D. Frolovsky, S.V. Ketov and S. Saburov, Formation of primordial black holes after Starobinsky inflation, Mod. Phys. Lett. A 37 (2022) 2250135 [2205.00603].
- [114] J. Garcia-Bellido, A.D. Linde and D. Wands, Density perturbations and black hole formation in hybrid inflation, Phys. Rev. D 54 (1996) 6040 [astro-ph/9605094].
- [115] G.A. Palma, S. Sypsas and C. Zenteno, Seeding primordial black holes in multifield inflation, Phys. Rev. Lett. 125 (2020) 121301 [2004.06106].
- [116] M. Braglia, D.K. Hazra, F. Finelli, G.F. Smoot, L. Sriramkumar and A.A. Starobinsky, Generating PBHs and small-scale GWs in two-field models of inflation, JCAP 08 (2020) 001 [2005.02895].
- [117] R.-G. Cai, C. Chen and C. Fu, Primordial black holes and stochastic gravitational wave background from inflation with a noncanonical spectator field, Phys. Rev. D 104 (2021) 083537 [2108.03422].
- [118] S. Hooshangi, A. Talebian, M.H. Namjoo and H. Firouzjahi, Multiple field ultraslow-roll inflation: Primordial black holes from straight bulk and distorted boundary, Phys. Rev. D 105 (2022) 083525 [2201.07258].
- [119] S.R. Geller, W. Qin, E. McDonough and D.I. Kaiser, Primordial black holes from multifield inflation with nonminimal couplings, Phys. Rev. D 106 (2022) 063535 [2205.04471].
- [120] S. Chongchitnan and G. Efstathiou, Accuracy of slow-roll formulae for inflationary perturbations: implications for primordial black hole formation, JCAP 01 (2007) 011 [astro-ph/0611818].
- [121] H. Motohashi and W. Hu, Primordial Black Holes and Slow-Roll Violation, Phys. Rev. D 96 (2017) 063503 [1706.06784].
- [122] C.T. Byrnes, P.S. Cole and S.P. Patil, Steepest growth of the power spectrum and primordial black holes, JCAP 06 (2019) 028 [1811.11158].
- [123] J. Liu, Z.-K. Guo and R.-G. Cai, Analytical approximation of the scalar spectrum in the ultraslow-roll inflationary models, Phys. Rev. D 101 (2020) 083535 [2003.02075].
- [124] G. Tasinato, An analytic approach to non-slow-roll inflation, Phys. Rev. D 103 (2021) 023535 [2012.02518].
- [125] K.N. Ananda, C. Clarkson and D. Wands, The Cosmological gravitational wave background from primordial density perturbations, Phys. Rev. D 75 (2007) 123518 [gr-qc/0612130].
- [126] D. Baumann, K. Ichiki, P.J. Steinhardt and K. Takahashi, Gravitational wave spectrum induced by primordial scalar perturbations, hep-th/0703290v1.
- [127] R. Saito and J. Yokoyama, Gravitational wave background as a probe of the primordial black hole abundance, Phys. Rev. Lett. 102 (2009) 161101 [0812.4339].
- [128] E. Bugaev and P. Klimai, Induced gravitational wave background and primordial black holes, Phys. Rev. D 81 (2010) 023517 [0908.0664].
- [129] K. Kohri and T. Terada, Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations, Phys. Rev. D 97 (2018) 123532 [1804.08577].
- [130] R.-g. Cai, S. Pi and M. Sasaki, Gravitational Waves Induced by non-Gaussian Scalar Perturbations, Phys. Rev. Lett. 122 (2019) 201101 [1810.11000].
- [131] K. Inomata and T. Nakama, Gravitational waves induced by scalar perturbations as probes of the small-scale primordial spectrum, Phys. Rev. D 99 (2019) 043511 [1812.00674].
- [132] G. Domènech, Scalar Induced Gravitational Waves Review, Universe 7 (2021) 398 [2109.01398].
- [133] P.S. Cole, A.D. Gow, C.T. Byrnes and S.P. Patil, Smooth vs instant inflationary transitions: steepest growth re-examined and primordial blackholes, JCAP 05 (2024) 022[2204.07573].
- [134] S. Clark, B. Dutta, Y. Gao, L.E. Strigari and S. Watson, Planck Constraint on Relic Primordial Black Holes, Phys. Rev. D 95 (2017) 083006 [1612.07738].
- [135] S. Clark, B. Dutta, Y. Gao, Y.-Z. Ma and L.E. Strigari, 21 cm limits on decaying dark matter and primordial black holes, Phys. Rev. D 98 (2018) 043006 [1803.09390].
- [136] M. Boudaud and M. Cirelli, Voyager 1 Further Constrain Primordial Black Holes as Dark Matter, Phys. Rev. Lett. 122 (2019) 041104 [1807.03075].
- [137] W. DeRocco and P.W. Graham, Constraining Primordial Black Hole Abundance with the Galactic 511 keV Line, Phys. Rev. Lett. 123 (2019) 251102 [1906.07740].
- [138] R. Laha, J.B. Muñoz and T.R. Slatyer, INTEGRAL constraints on primordial black holes and particle dark matter, Phys. Rev. D 101 (2020) 123514 [2004.00627].
- [139] D. Croon, D. McKeen, N. Raj and Z. Wang, Subaru-HSC through a different lens: Microlensing by extended dark matter structures, Phys. Rev. D 102 (2020) 083021 [2007.12697].
- [140] B.J. Kavanagh, D. Gaggero and G. Bertone, Merger rate of a subdominant population of primordial black holes, Phys. Rev. D 98 (2018) 023536 [1805.09034].
- [141] LIGO Scientific, Virgo collaboration, Search for Subsolar Mass Ultracompact Binaries in Advanced LIGO’s Second Observing Run, Phys. Rev. Lett. 123 (2019) 161102 [1904.08976].
- [142] P.D. Serpico, V. Poulin, D. Inman and K. Kohri, Cosmic microwave background bounds on primordial black holes including dark matter halo accretion, Phys. Rev. Res. 2 (2020) 023204 [2002.10771].
- [143] R. H. Cyburt, B. D. Fields, K. A. Olive and E. Skillman, New BBN limits on physics beyond the standard model from , Astropart. Phys. 23, 313-323 (2005) [arXiv:astro-ph/0408033 [astro-ph]].
- [144] K. Schmitz, New Sensitivity Curves for GravitationalWave Experiments, (2020).
- [145] H. Xu et al., Searching for the Nano-Hertz Stochastic Gravitational Wave Background with the Chinese Pulsar Timing Array Data Release I, Res. Astron. Astrophys. 23 (2023) 075024 [2306.16216].
- [146] NANOGrav collaboration, The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background, Astrophys. J. Lett. 951 (2023) L8 [2306.16213].
- [147] NANOGrav collaboration, The NANOGrav 15 yr Data Set: Observations and Timing of 68 Millisecond Pulsars, Astrophys. J. Lett. 951 (2023) L9 [2306.16217].
- [148] D.J. Reardon et al., Search for an Isotropic Gravitational-wave Background with the Parkes Pulsar Timing Array, Astrophys. J. Lett. 951 (2023) L6 [2306.16215].
- [149] J. Antoniadis et al., The second data release from the European Pulsar Timing Array III. Search for gravitational wave signals, 2306.16214.
- [150] NANOGRAV collaboration, The NANOGrav 11-year Data Set: Pulsar-timing Constraints On The Stochastic Gravitational-wave Background, Astrophys. J. 859 (2018) 47 [1801.02617].
- [151] A. Ashoorioon, K. Rezazadeh and A. Rostami, NANOGrav signal from the end of inflation and the LIGO mass and heavier primordial black holes, Phys. Lett. B 835 (2022) 137542 [2202.01131].
- [152] Y.-F. Cai, X.-C. He, X. Ma, S.-F. Yan and G.-W. Yuan, Limits on scalar-induced gravitational waves from the stochastic background by pulsar timing array observations, 2306.17822.
- [153] K. Inomata, K. Kohri and T. Terada, The Detected Stochastic Gravitational Waves and Sub-Solar Primordial Black Holes, 2306.17834.
- [154] P.F. Depta, K. Schmidt-Hoberg and C. Tasillo, Do pulsar timing arrays observe merging primordial black holes?, 2306.17836.
- [155] G. Franciolini, A. Iovino, Junior., V. Vaskonen and H. Veermae, The recent gravitational wave observation by pulsar timing arrays and primordial black holes: the importance of non-gaussianities, 2306.17149.
- [156] L. Liu, Z.-C. Chen and Q.-G. Huang, Implications for the non-Gaussianity of curvature perturbation from pulsar timing arrays, 2307.01102.
- [157] H. Firouzjahi and A. Talebian, Induced Gravitational Waves from Ultra Slow-Roll Inflation and Pulsar Timing Arrays Observations, 2307.03164.