Infinite-layer nickelates as Ni- Hund’s metals
Abstract
The recent and exciting discovery of superconductivity in the hole-doped infinite-layer nickelate Nd1-δSrδNiO2 draws strong attention to correlated quantum materials. From a theoretical view point, this new class of unconventional superconducting materials provides an opportunity to unveil new physics in correlated quantum materials. Here we study the temperature and doping dependence of the local spectrum as well as the charge, spin and orbital susceptibilities from first principles. By using ab initio LQSGW+DMFT methodology, we show that onsite Hund’s coupling in Ni- orbitals gives rise to multiple signatures of Hund’s metallic phase in Ni- orbitals. The proposed picture of the nickelates as an (two orbital) Hund’s metal differs from the picture of the Fe-based superconductors as a five orbital Hund’s metal as well as the picture of the cuprates as doped charge transfer insulators. Our finding unveils a new class of the Hund’s metals and has potential implications for the broad range of correlated two orbital systems away from half-filling.
Introduction. Although the mechanisms of unconventional superconductivity remain elusive, the discoveries of new classes of unconventional superconductors have proliferated experimentally. These experimental efforts revived the interest in correlated quantum materials and provided opportunities to unveil new physics hidden within them. To illustrate, in the cuprate superconductors Bednorz and Müller (1986), superconductivity emerges from the bad metallic states realized by doping a charge transfer insulator Zaanen et al. (1985). Strong electron correlation in the bad metallic normal states arises due to the proximity to Mott insulator transition Mott and Peierls (1937); Mott (1949), i.e., “Mottness”. According to the theory of conventional superconductors, it is improbable that this bad-metallic phase would support superconductivity. This motivated the theoretical proposals of superconducting pairing mechanisms beyond the Bardeen-Cooper-Schrieffer (BCS) paradigm Lee et al. (2006); Garg et al. (2008); Keimer et al. (2015). This in turn lead to the discovery of other unconventional superconductors wherein a superconducting phase emerged from the bad-metal ”parent” state in a different way. For example, in the multi-orbital Fe-based superconductors Kamihara et al. (2006, 2008), the on-site Hund’s coupling () promotes bad metallic behavior in their normal phase de’ Medici et al. (2011); de’ Medici (2011); Georges et al. (2013); Isidori et al. (2019). This gives rise to the new concept of “Hundness”. Hundness-induced correlated metals, Hund’s metals Haule and Kotliar (2009); Yin et al. (2011), play the role of a reliable reference system for Fe-based superconducting materials Georges et al. (2013); Haule and Kotliar (2009); Yin et al. (2011); de’ Medici (2017); Lanatà et al. (2013); Villar Arribi and de’ Medici (2018); Bascones et al. (2012); Ryee et al. (2020a) and ruthenates Georges et al. (2013); Werner et al. (2008); Mravlje et al. (2011); Hoshino and Werner (2015); Mravlje and Georges (2016).
Recently, the thrilling discovery of Ni-based superconductors Li et al. (2019, 2020); Gu et al. (2020a); Zeng et al. (2020) turns the spotlight on correlated quantum materials and their unconventional superconductivity Sawatzky (2019); Xiang et al. (2020). NdNiO2 and infinite-layer cuprates, e.g. CaCuO2, are isostructural Hayward et al. (1999); Hayward and Rosseinsky (2003), where the two dimensional Ni-O plane is geometrically analogous to the Cu-O plane in the cuprate. The Ni- orbital of each Ni1+ ion can be expected to be half-filled with an effective spin-1/2 on each site according to the oxidation state rules. In combination, this makes NdNiO2 a promising cuprate analog Botana and Norman (2020); Kitatani et al. (2020); Hirsch and Marsiglio (2019); Wu et al. (2020); Karp et al. (2020); Lang et al. (2020).
However, the differences from cuprates are striking. Its parent compound is seldom regarded as a charge transfer insulator Ikeda et al. (2013, 2016); Fu et al. (2019); Kitatani et al. (2020) and there is no sign of long-range magnetic orders Hayward and Rosseinsky (2003) down to 1.7 K. In addition, its parent compound shows a resistivity upturn upon cooling Li et al. (2019), which is common in heavy-fermion superconductors and is often due to Kondo effects Hepting et al. (2020); Lechermann (2020a). The sign change of the Hall coefficient implies that electrons as well as holes may play an important role in the materials properties Li et al. (2019), implying its multi-orbital nature Adhikary et al. (2020); Lechermann (2020a); Goodge et al. (2020). Moreover, it is debatable whether the doped hole forms a spin singlet or triplet doublon with the original hole on a Ni ion Jiang et al. (2020); Zhang and Vishwanath (2020); Hu and Wu (2019); Werner and Hoshino (2020); Zhang et al. (2020); Chang et al. (2019); Sakakibara et al. (2019), suggesting possible Hund metal physics Wang et al. (2020); Lechermann (2020a); Petocchi et al. (2020); Lechermann (2020a). These similarities and differences to various unconventional superconductors are puzzling, but they do provide a chance to explore hidden aspects of electron correlation.
In this paper, we will investigate a new aspect of the multi-orbital physics in infinite-layer nickelates from first principles. By using ab initio linearized quasiparticle self-consistent GW (LQSGW) and dynamical mean-field theory (DMFT) method Tomczak (2015); Choi et al. (2016, 2019), we investigated the origin of the electron correlation in the infinite-layer nickelate normal phases. Ab initio LQSGW+DMFT is a diagrammatically motivated ab initio approaches for correlated electron systems. As a simplification of diagrammatically controlled full GW+EDMFT approach Sun and Kotliar (2002); Biermann et al. (2003); Nilsson et al. (2017), it calculates electronic structure by using ab initio linearized quasiparticle self-consistent GW approaches Kutepov et al. (2012, 2017). Then it adds one-shot correction to local electron self-energy by summing over all possible local Feynmann diagrams within DMFT Georges et al. (1996); Metzner and Vollhardt (1989); Müller-Hartmann (1989); Brandt and Mielsch (1989); Janiš (1991); Georges and Kotliar (1992); Jarrell (1992); Rozenberg et al. (1992); Georges and Krauth (1992). For the impurity orbital in the DMFT step, we choose a very localized orbital spanning a large energy window, which contains most strongly hybridized bands along with upper and lower Hubbard bands. Having chosen the shape of the correlated orbitals, all the other parameters to define DMFT problem are determined accordingly: double-counting energy within local GW approximation and Coulomb interaction tensor within constrained random phase approximation (cRPA) Aryasetiawan et al. (2004). This method has been validated against various classes of correlated electron systems including paramagnetic Mott insulators La2CuO4Choi et al. (2016), Hund metal FeSe Choi et al. (2019), and correlated narrow-gap semiconductors FeSb2 Chikina et al. (2020).
Within ab initio LQSGW+DMFT, we found multiple signatures of Hundness associated with the Ni- subshell in the compounds. This finding differentiates the infinite-layer nickelates from the cuprates. In particular, we found that Hundness becomes apparent among the Ni- orbitals but not the Ni- orbitals. This is a distinctive feature of the infinite-layer nickelates from Fe-based superconductors as five-orbital Hund’s metals.
Methods. Following the literature Leonov et al. (2020); Ryee et al. (2020b); Botana and Norman (2020); Wang et al. (2020); Olevano et al. (2020); Bernardini et al. (2019); Sakakibara et al. (2019); Hepting et al. (2020), we studied La1-δBaδNiO2 instead of Nd1-δSrδNiO2 to avoid the difficulty in the treatment of the Nd- band. This is acceptable, as it has been reported that LaNiO2 at the lattice parameters of NdNiO2 has a similar electronic structure of NdNiO2 within open Nd- core approximation Botana and Norman (2020). It has been experimentally demonstrated that the Nd- states of Nd-based infinite layer nickelates are well localized and do not influence the relevant physics close to the Fermi level Hepting et al. (2020); Rossi et al. (2020). The effect of Ba doping has been treated within the virtual crystal approximation. For its justification, please see the supplementary materials. For the LQSGW+DMFT scheme, the code ComDMFT Choi et al. (2019) was used. For the LQSGW part of the LQSGW+DMFT scheme, the code FlapwMBPT Kutepov et al. (2017) was used. For the details of electronic structure calculation, please see the supplementary materials.
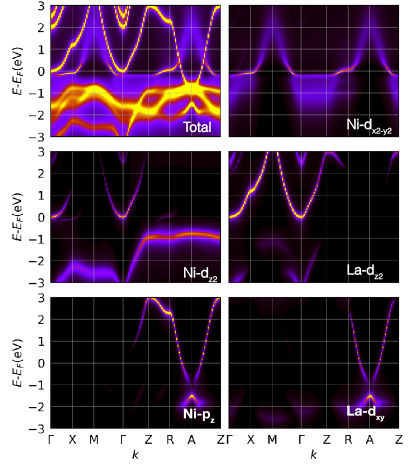
Results and Discussions. The low-energy electronic structure of La1-δBaδNiO2 shows multi-orbital characters. In particular, the two bands crossing the Fermi-energy have substantial Ni- orbital character. Fig. 1 shows the electronic structure of La0.8Ba0.2NiO2 within ab initio LQSGW+DMFT. Consistent with the results obtained with other electronic structure methodologies such as DFT Adhikary et al. (2020); Bernardini et al. (2019); Botana and Norman (2020); Jiang et al. (2019); Lechermann (2020b, a); Lee and Pickett (2004); Sakakibara et al. (2019); Zhang et al. (2019); Hepting et al. (2020); Wu et al. (2020); Karp et al. (2020); Been et al. (2020); Gu et al. (2020b), DFT+DMFT Wang et al. (2020); Kitatani et al. (2020), and one-shot G0W0 Olevano et al. (2020), the total spectral function shows that there are two bands crossing the Fermi level. Of these two bands, the lower energy band shows strong two dimensional character, and it is dominated by the Ni- orbital. The remaining band, the so called self-doping band, is the higher energy band which shows strong hybridization between other Ni orbitals and La orbitals. The band dispersion of the self-doping band varies strongly along the direction normal to the Ni-O plane (), demonstrating its strong 3-dimensional character Hepting et al. (2020). Moreover, the orbital character of the self-doping band is strongly dependent on . In the =0 plane, the orbital character of the self-doping band is mostly La- and Ni- Lee and Pickett (2004); Lechermann (2020b), In contrast, in the plane, where is the lattice constant along the direction, its orbital character is mostly La- and Ni-. This analysis is consistent with a recent two band model study from first-principles, showing that the two Fermi-level-crossing bands can be spanned by a Ni- orbital and an axial orbital Adhikary et al. (2020). The axial orbital is not centered on a single atom. Instead, its density is centered on both the Ni and La atoms.
| Materials | ||||||
|---|---|---|---|---|---|---|
| La0.8Ba0.2NiO2 | 1.94 | 1.89 | 1.89 | 1.59 | 1.04 | |
| FeSe | 1.22 | 1.19 | 1.19 | 1.44 | 1.26 |
Orbital occupation in the Ni- orbitals differentiates the and orbitals. As summarized in Table 1, the Ni- orbitals are partially filled but the Ni- orbitals are fully-filled in La0.8Ba0.2NiO2. This orbital occupation profile is far from a prediction based on oxidation state rules, i.e., 2, 2, 2, 2, and 1 for Ni-, Ni-, Ni-, Ni-, and Ni-, respectively. Intriguingly, the difference stands out especially for the Ni- orbital, which is far from the expected double occupation Leonov et al. (2020); Petocchi et al. (2020). This discrepancy can be explained by the hybridization between Ni-d and La- orbitals. The strong hybridization between these two orbitals in the --- plane makes the Ni-d orbital exhibit a dispersion which is distinct from its dispersion in isolation (the flat band at EF-1eV in the --- plane in Fig. 1(c)) Choi et al. (2020). Indeed, upon Ba doping up to 0.3, only 25% of the added holes go into the Ni- orbitals, while the remaining holes go into other orbitals, especially the La-, La- and Ni- orbitals (as shown in the supplementary materials). This is consistent with other theoretical studies at low-doping Leonov et al. (2020); Wang et al. (2020), and it makes the - differentiation in orbital occupation robust against low extrinsic hole-doping. Here we note that the orbital occupation as well as the orbital resolved spectral functions are dependent on the choice of the Wannier orbitals. To construct atomic-orbital-like Wannier orbitals tightly bounded and centered on the atoms, we constructed 31 atom-centered Wannier orbitals for each spin (see the supplementary materials).
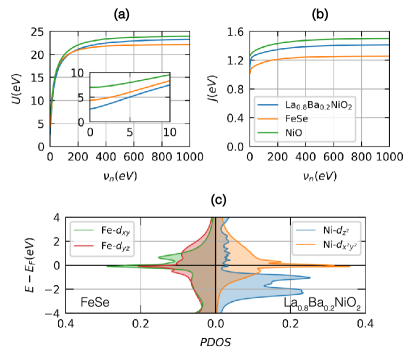
Based on the Coulomb interaction calculation within the constrained random phase approximation (cRPA), it is legitimate to assume the dominance of Hundness over “Mottness” in La1-δBaδNiO2. Fig. 2 shows the on-site Hubbard and Hund interactions among five Ni- orbitals within the constrained random phase approximation. For comparison, we plotted the and of Ni- orbitals in NiO and Fe- orbitals in FeSe. As is typical, is strongly frequency-dependent, while is not. Interestingly, the static of the Ni- orbitals in La0.8Ba0.2NiO2 is much smaller than it is in the charge-transfer insulator NiO. It is even smaller than the of Fe- orbitals in the Hund’s metal FeSe. In contrast, the of the Ni- orbitals in La0.8Ba0.2NiO2 is even larger than the of Fe- in the Hund’s metal FeSe. Judging from the fact that the Ni- orbitals in La1-δBaδNiO2 and the Fe- orbitals in FeSe show similar bandwidths, we can safely assume the dominant role of Hundness over Mottness in La1-δBaδNiO2.
To understand the origin of strong correlations in the infinite-layer nickelates further, we calculated the temperature and doping dependence of Ni- local spectra as well as static spin- and orbital-susceptibility. These one- and two-particle quantities are “litmus-papers” to quantify the relative strength of Hundness versus Mottness. Hund’s metals show various characteristic behaviors. One is spin-orbital separation: a two-step screening process in which local spin moment is screened at much lower temperature than local orbital polarization. Another is the absence of the pseudo gap in the local spectra. At high temperature when quasiparticle spectral weight near the Fermi level is transferred into high-energy Hubbard bands, spectral weight at the Fermi level is still not negligible and the local spectra is dominated by a single incoherent peak. In contrast, in the correlated metallic system where Mottness dominates, spin-orbit separation is negligible. In addition, the high-temperature spectral weight at the Fermi level is depleted due to the quasiparticle spectral weight transfer and pseudogap forms at the Fermi level at the high temperature. By calculating these quantities, we found multiple Hundness signatures. More importantly, these signatures are primarily evident in the active Ni- orbitals and not the inactive Ni- orbitals.
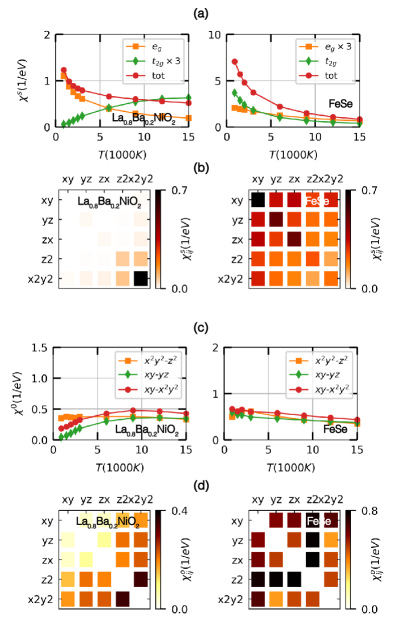
Five Ni- orbitals in La1-δBaδNiO2 show clear spin-orbital separation. Fig. 3(a) and Fig. 3(c) show the temperature dependence of the static local susceptibility in spin () and orbital () channels. These are defined as , and . Here is the orbital-resolved spin operator and is the orbital resolved occupation operator. According to Deng et al. Deng et al. (2019), the temperatures at which the screening of the spin and orbital degrees of freedom becomes noticeable are one of the key measures with which to distinguish between Mott and Hund physics. These onset screening temperatures in spin and orbital channels can be obtained by estimating the temperature at which these susceptibilities deviates from Curie-like behaviors. In the Mott regime, these two energy scales coincide. In contrast, in the Hund regime, the orbital onset temperature is much higher than the spin onset temperature. At a temperature between these two onset temperatures, the spin susceptibility is Curie-like but the orbital-susceptibility is Pauli-like. This is exactly the behavior seen in FeSe. In FeSe, the local spin susceptibility is Curie-like (red dots in Fig. 3(a)), but the local orbital susceptibility approaches its maximum upon cooling (red dots in Fig. 3(c)). La0.8Ba0.2NiO2 behaves like FeSe. The spin degree of freedom (red dots in Fig. 3(a)) shows Curie-like behavior. In contrast, the orbital susceptibility between any Ni- orbital pair shows a downturn of the susceptibility upon cooling (red dots in Fig. 3(c)).
However, there is an important distinction between the Ni- orbitals in La1-δBaδNiO2 and Fe- orbitals in FeSe: The orbitals in La1-δBaδNiO2 are inactive. In spite that Ni- is almost fully filled in La1-δBaδNiO2, the inactivity of Ni- orbitals for the Hundness-related two-particle quantities ( and ) is a non-trivial question. Inactivity in the one-particle level (single particle Green’s function) is not sufficient to assure inactivity in the two-particle level (the local susceptibilities). This can be illustrated by the charge susceptibility data obtained within multitier GW+EDMFT by F. Petocchi et al. Petocchi et al. (2020). As shown in Fig. 3 of the paper, the intraorbital charge fluctuation associated with Ni- orbitals is not negligible but comparable to the fluctuation associated with Ni- although Ni-dxz/yz orbital is almost fully-filled within their approach. To convince the inactivity of Ni- orbitals in the two particle level, their Hundness-related two-particle quantities ( and ) should be examined explicitly.
First, spin fluctuations are not active among the Ni- orbitals. Fig. 3 (b) shows . In FeSe, all possible pairs of Fe- orbitals show a strong spin response. In contrast, only the Ni- subspace exhibits a strong spin response in La0.8Ba0.2NiO2, while the response due to the remaining pairs is strongly suppressed. The temperature dependence of the spin susceptibility in the t2g subspace () further supports the distinction between the Ni- orbital and Fe- orbitals. Here, . As shown in Fig. 3 (a), (green diamonds) in La0.8Ba0.2NiO2 strongly deviates from the Curie-like behaviors of . This does not occur in FeSe. Most strikingly, approaches zero upon cooling.
Second, the static orbital susceptibility shows the suppression of orbital fluctuations in the Ni-t2g subspace. Fig. 3(d) shows . In FeSe, all possible pairs of Fe- orbitals show a strong orbital response. In contrast, the in the Ni- subspace are strongly suppressed in La0.8Ba0.2NiO2. The temperature dependence of the orbital susceptibility in the t2g subspace (), shown in Fig. 3 (c), is another distinction between Ni- orbitals and F- orbitals. Here, in contrast to FeSe, where (green diamonds) follows (orange squares), (green diamonds) in La0.8Ba0.2NiO2 strongly deviates from (orange squares). Most strikingly, approaches zero upon cooling.
Once we narrow down our view from all Ni- orbitals into only the Ni- orbitals, we can successfully find all signatures of a Hund’s metal. Two Ni- orbitals in La1-δBaδNiO2 show clear spin-orbital separation. Fig. 3(a) and Fig. 3(c) depict the temperature dependence of static local spin () and orbital () susceptibility. Here . (orange squares in Fig. 3(a)) shows Curie-like temperature dependence but (orange squares in Fig. 3(c)) shows Pauli-like temperature dependence.
Here we note that there are two more characteristic phenomena of Hund’s metal. One is the spin freezing phase Werner et al. (2008). At a temperature where orbital fluctuation is screened but spin flucuation is not, spin fluctuation doesn’t decay to zero at long imaginary time (), where is inverse temperature. The other is orbital-decoupling: the suppression of the instantaneous interorbital charge fluctuationde’ Medici (2011). In these two quantities, we also found evidances of Ni- Hundness. Please see the supplementary materials.
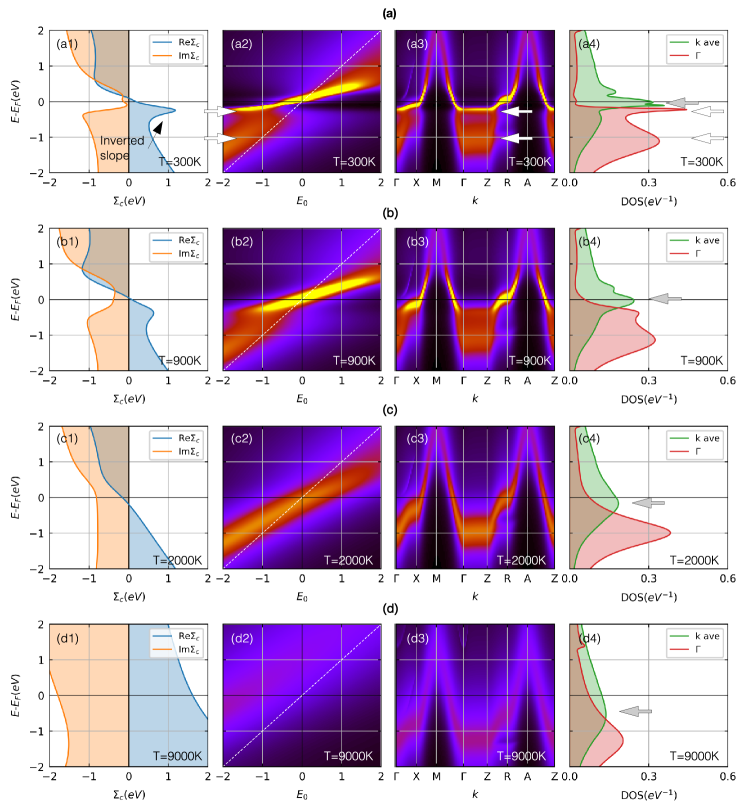
Hund’s physics in the infinite-layer nickelates can be tested further by measuring the temperature evolution of the Ni--orbital-resolved spectral function, which dominates the spectra at the Fermi level. According to Deng et al.Deng et al. (2019), the high-temperature spectra of the orbital-resolved density of states can be used to confirm Hund’s metal physics. At low temperature, spectral weight at the Fermi level is dominated by quasiparticle resonance peak in both Hund’s and Mott’s metallic phase. However, at a high temperature when quasiparticle spectral weight at the Fermi level are transferred to high-energy Hubbard bands, local spectra distinguish Hund-like and Mott-like metallic systems. In the metallic phase where Mott features dominate, the upper and lower Hubbard bands are well separated from each other due to its proximity to Hubbard-Mott transition and pseudo-gap forms. In contrast, in Hund’s metallic phase, the upper Hubbard band is overlapping with the lower Hubbard band and the whole spectra is dominated by a single incoherent peak that has a large value at the Fermi level. This Hund’s metallic features are accompanied by shoulder-like structure in the electron self-energy imaginary part as well as the inverted slope of the self-energy real part near the Fermi level Stadler et al. (2015, 2019).
Fig. 4 shows the temperature evolution of the Ni--orbital-resolved spectral function of La0.8Ba0.2NiO2. Here we note that the estimated onset screening temperature in the spin and orbital channels are 3000K and 35000K, respectively. Importantly, up to T=15000K, we were not able to observe pseudo gap formation in the Ni- projected density of states. Instead, the local spectrum is composed of a single incoherent peak that has a large value at the Fermi level. In addition, the center of the incoherent peak moves away from the Fermi-level upon heating. Furthermore, the correlation part of the electronic self-energy shows expected Hund’s metallic behaviors. As shown in Fig. 4 (a1) there is a shoulder-like structure in its imaginary part self-energy at T=300K. The slope of the real part self-energy is inverted accordingly. To check its role in the spectral properties, we constructed an auxiliary Green’s function of , which is often used to study Hund’s metal physics in the various Hund-Hubbard models Stadler et al. (2019); Kugler et al. (2019). Due to the shoulder-like structure in the electron self-energy, the band structure of the auxiliary system is strongly renormalized with a renormalization factor of 0.2 near the Fermi level. Furthermore, at the negative bare energy (), there is strong redistribution of the spectral weight, resulting in an additional incoherent peak. This creates the waterfall features in the Ni- orbital resolved spectral function in real materials. As shown in Fig. 4 (a3), the spectral weight along the - line is split into strongly renormalized coherent peak and incoherent peak. As the temperature increases, the shoulder-like structure in the imaginary part of the self-energy becomes weaker. Subsequently, the coherenet and the coherent peaks merge.
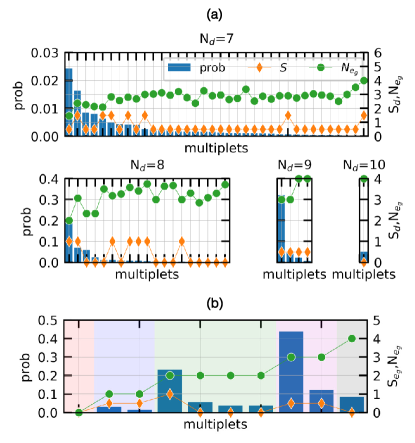
To clarify the microscopic origin of Ni- Hund’s metallic behaviors, we investigate the reduced local many-body density or local probabilities of Ni-3 multiplet states in the atomic limit. Fig. 5 (a) shows the valence histogram for the Ni-3 multiplets in La0.8Ba0.2NiO2. That is, it shows a partial trace of the density matrix of the full Hilbert space, where this partial trace excludes the Ni-3 subsystem in order to reveal the probability that a given multiplet state in the correlated Ni-3 subsystem is occupied. It is traced further over the secondary spin quantum number. We decompose the Ni-3 subspace according to the total charge () of the mutliplet states, and find that for 7, 8, 9 and 10, the most probable states involve the total spin , , , and as well as the occupation of the orbitals () is 1.47. 2, 3, and 4, respectively. Interestingly, these can be interpreted as the multiplets which maximize the total spin of the Ni- electron in each subspace; these are not the multiplets which maximize the total spin of all N-3 electrons in each subspace. The reduced local many-body density on the Ni- multiplets shown in Fig. 5 (b) supports this observation. The most probable Ni- multiplet in each subspace is the one with maximum Ni- total spin (). Again, this supports our conclusion that Hund metallic behaviors are limited to the Ni- orbitals.
In addition to onsite Hund’s coupling, the crystal-field splitting between Ni- and Ni- orbitals is another important factor to control the physical quantities to judge Hundness versus Mottness. The crystal field splitting plays a two-faced role in those quantities. On one hand, it amplifies Hundness signatures. To illustrate, the non-zero crystal field splitting suppresses spin Kondo temperature but enhances orbital Kondo temperatures, thus boosting spin-orbital separation Kugler et al. (2019). Thus, the spin-orbital separation in the system with a non-zero crystal-field can not be the signature of Hundness. On the other hand, it enhances Mottness signatures. The crystal field splitting makes possible Ni- spin-singlet lower in energy than the spin-triplet states Werner and Millis (2007). It also increases the separation between lower and upper Hubbard bands, thus promoting pseudo-gap formation. The enhancement of the Mottness signatures can be understood by using the Kanamori Hamiltonian in its atomic limit. By assuming inactivity Ni- orbitals, the local physics at the Ni site may be understood by the -Kanamori Hamiltonian. In its atomic limit with vanishing intersite hopping, the Hamiltonian is given by
| (1) |
Here, , , and are the crystal-field splitting which is positive, intraorbital Coulomb interaction, interorbital Coulomb interaction, and Hund’s coupling, respectively. When , triplet states are always the lowest-energy states in N= 2 subspace. However, non-zero crystal-field splitting enables the singlet ground states formation in subspace when . Here we note that in the realistic materials. Furthermore, the promotes pseudo-gap formation by enhancing the separation between upper and lower Hubbard bands in the weakly hole-doped regime from filling. The separation () is given by when triplet states are the ground states in subspace and when a singlet is the ground state in subspace. Here is the energy gap when =0. in the electron occupation of regardless of subspace ground state. For the derivation, please see the supplementary materials.
Despite the crystal-field-induced enhancement of the pseudo-gap as well as singlet population, both measures advocate Hund’s metallicity of La1-δBaδNiO2 as shown in Fig. 5(b) and Fig. 4. Together with the spin-orbital separation shown in Fig. 3, these signatures indicate that La1-δBaδNiO2 is a strong candidate of two-orbital Hund’s metal.
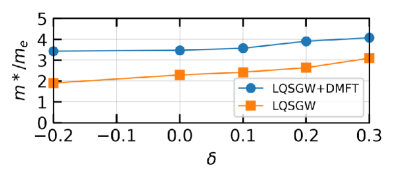
Lastly, we propose another experiment to support Ni- Hundness in the infinite-layer nickelates: the doping dependence of Ni- band effective mass. In a paramagnetic system where the proximity to Mott transition dominates electron correlation and single-band is a good minimum model to describe the low-energy physics, the effective mass is expected to be maximum in the undoped system and decreases if the system is either hole-doped or electron-doped. In contrast, as demonstrated by the Fe-based superconductors de’ Medici et al. (2014), the effective mass of Hund’s metals changes monotonically from hole-doped side to electron-doped side in Hund’s metals. Fig. 6 shows the doping dependence of the cyclotron effective mass of the Ni- bands in the plane. Both LQSGW+DMFT and LQSGW methods show that the effective mass increases monotonically from electron doped side to hole-doped side. This monotonic doping dependence of the effective mass could be confimed by other experiments such as specific heat measurement as well as angle-resolved photoemission spectroscopy. In contrast to other signatures proposed in this paper, the doping dependence of the Ni- band effective mass does not require high temperature measurements.
Conclusion. By using ab initio LQSGW+DMFT methodology, we demonstrated that on-site Hund’s coupling in Ni- orbitals results in multiple signatures of Hund’s metallic phase in Ni- orbitals. Our finding sheds a new light on Hundness in the correlated quantum materials and has potential implications for the broad range of correlated two orbital systems away from half-filling and the role of on-site Hund’s coupling Stadler (2019); de’ Medici (2011); Werner and Hoshino (2020).
Acknowledgments. S.C. thanks G. L. Pascut, and C-.J-. Kang and for useful conversation. This work was supported by the U.S Department of Energy, Office of Science, Basic Energy Sciences as a part of the Computational Materials Science Program. S. R and M. J. H were supported by NRF Korea (2018R1A2B2005204 and 2018M3D1A1058754). This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.
References
- Bednorz and Müller (1986) J. G. Bednorz and K. A. Müller, Z. Physik B - Condensed Matter 64, 189 (1986).
- Zaanen et al. (1985) J. Zaanen, G. A. Sawatzky, and J. W. Allen, Phys. Rev. Lett. 55, 418 (1985).
- Mott and Peierls (1937) N. F. Mott and R. Peierls, Proc. Phys. Soc. 49, 72 (1937).
- Mott (1949) N. F. Mott, Proc. Phys. Soc. A 62, 416 (1949).
- Lee et al. (2006) P. A. Lee, N. Nagaosa, and X.-G. Wen, Rev. Mod. Phys. 78, 17 (2006), publisher: American Physical Society.
- Garg et al. (2008) A. Garg, M. Randeria, and N. Trivedi, Nature Physics 4, 762 (2008), number: 10 Publisher: Nature Publishing Group.
- Keimer et al. (2015) B. Keimer, S. A. Kivelson, M. R. Norman, S. Uchida, and J. Zaanen, Nature 518, 179 (2015), number: 7538 Publisher: Nature Publishing Group.
- Kamihara et al. (2006) Y. Kamihara, H. Hiramatsu, M. Hirano, R. Kawamura, H. Yanagi, T. Kamiya, and H. Hosono, J. Am. Chem. Soc. 128, 10012 (2006), publisher: American Chemical Society.
- Kamihara et al. (2008) Y. Kamihara, T. Watanabe, M. Hirano, and H. Hosono, J. Am. Chem. Soc. 130, 3296 (2008), publisher: American Chemical Society.
- de’ Medici et al. (2011) L. de’ Medici, J. Mravlje, and A. Georges, Phys. Rev. Lett. 107, 256401 (2011).
- de’ Medici (2011) L. de’ Medici, Phys. Rev. B 83, 205112 (2011).
- Georges et al. (2013) A. Georges, L. d. Medici, and J. Mravlje, Annual Review of Condensed Matter Physics 4, 137 (2013).
- Isidori et al. (2019) A. Isidori, M. Berović, L. Fanfarillo, L. de’ Medici, M. Fabrizio, and M. Capone, Phys. Rev. Lett. 122, 186401 (2019).
- Haule and Kotliar (2009) K. Haule and G. Kotliar, New J. Phys. 11, 025021 (2009), publisher: IOP Publishing.
- Yin et al. (2011) Z. P. Yin, K. Haule, and G. Kotliar, Nature Materials 10, 932 (2011).
- de’ Medici (2017) L. de’ Medici, Phys. Rev. Lett. 118, 167003 (2017), tex.ids: demedici_HundInducedFermiLiquid_2017a, demedici_SupplementaryHundInduced_2017.
- Lanatà et al. (2013) N. Lanatà, H. U. R. Strand, G. Giovannetti, B. Hellsing, L. de’ Medici, and M. Capone, Phys. Rev. B 87, 045122 (2013), publisher: American Physical Society.
- Villar Arribi and de’ Medici (2018) P. Villar Arribi and L. de’ Medici, Phys. Rev. Lett. 121, 197001 (2018), publisher: American Physical Society.
- Bascones et al. (2012) E. Bascones, B. Valenzuela, and M. J. Calderón, Phys. Rev. B 86, 174508 (2012), publisher: American Physical Society.
- Ryee et al. (2020a) S. Ryee, P. Sémon, M. J. Han, and S. Choi, npj Quantum Mater. 5, 1 (2020a), number: 1 Publisher: Nature Publishing Group.
- Werner et al. (2008) P. Werner, E. Gull, M. Troyer, and A. J. Millis, Phys. Rev. Lett. 101, 166405 (2008).
- Mravlje et al. (2011) J. Mravlje, M. Aichhorn, T. Miyake, K. Haule, G. Kotliar, and A. Georges, Phys. Rev. Lett. 106, 096401 (2011), publisher: American Physical Society.
- Hoshino and Werner (2015) S. Hoshino and P. Werner, Phys. Rev. Lett. 115, 247001 (2015).
- Mravlje and Georges (2016) J. Mravlje and A. Georges, Phys. Rev. Lett. 117, 036401 (2016), publisher: American Physical Society.
- Li et al. (2019) D. Li, K. Lee, B. Y. Wang, M. Osada, S. Crossley, H. R. Lee, Y. Cui, Y. Hikita, and H. Y. Hwang, Nature 572, 624 (2019).
- Li et al. (2020) D. Li, B. Y. Wang, K. Lee, S. P. Harvey, M. Osada, B. H. Goodge, L. Kourkoutis, and H. Hwang, Phys. Rev. Lett. 125, 027001 (2020), publisher: American Physical Society.
- Gu et al. (2020a) Q. Gu, Y. Li, S. Wan, H. Li, W. Guo, H. Yang, Q. Li, X. Zhu, X. Pan, Y. Nie, and H.-H. Wen, arXiv:2006.13123 [cond-mat] (2020a), arXiv: 2006.13123.
- Zeng et al. (2020) S. Zeng, C. S. Tang, X. Yin, C. Li, Z. Huang, J. Hu, W. Liu, G. J. Omar, H. Jani, Z. S. Lim, K. Han, D. Wan, P. Yang, A. T. S. Wee, and A. Ariando, arXiv:2004.11281 [cond-mat] (2020), arXiv: 2004.11281.
- Sawatzky (2019) G. A. Sawatzky, Nature 572, 592 (2019).
- Xiang et al. (2020) Y. Xiang, Q. Li, Y. Li, H. Yang, Y. Nie, and H.-H. Wen, arXiv:2007.04884 [cond-mat] (2020), arXiv: 2007.04884.
- Hayward et al. (1999) M. A. Hayward, M. A. Green, M. J. Rosseinsky, and J. Sloan, J. Am. Chem. Soc. 121, 8843 (1999), publisher: American Chemical Society.
- Hayward and Rosseinsky (2003) M. A. Hayward and M. J. Rosseinsky, Solid State Sciences International Conference on Inorganic Materials 2002, 5, 839 (2003).
- Botana and Norman (2020) A. Botana and M. Norman, Phys. Rev. X 10, 011024 (2020), publisher: American Physical Society.
- Kitatani et al. (2020) M. Kitatani, L. Si, O. Janson, R. Arita, Z. Zhong, and K. Held, npj Quantum Materials 5, 1 (2020), number: 1 Publisher: Nature Publishing Group.
- Hirsch and Marsiglio (2019) J. E. Hirsch and F. Marsiglio, Physica C: Superconductivity and its Applications 566, 1353534 (2019).
- Wu et al. (2020) X. Wu, D. Di Sante, T. Schwemmer, W. Hanke, H. Y. Hwang, S. Raghu, and R. Thomale, Phys. Rev. B 101, 060504 (2020), publisher: American Physical Society.
- Karp et al. (2020) J. Karp, A. S. Botana, M. R. Norman, H. Park, M. Zingl, and A. Millis, Phys. Rev. X 10, 021061 (2020), publisher: American Physical Society.
- Lang et al. (2020) Z.-J. Lang, R. Jiang, and W. Ku, arXiv:2005.00022 [cond-mat] (2020), arXiv: 2005.00022.
- Ikeda et al. (2013) A. Ikeda, T. Manabe, and M. Naito, Physica C: Superconductivity 495, 134 (2013).
- Ikeda et al. (2016) A. Ikeda, Y. Krockenberger, H. Irie, M. Naito, and H. Yamamoto, Appl. Phys. Express 9, 061101 (2016).
- Fu et al. (2019) Y. Fu, L. Wang, H. Cheng, S. Pei, X. Zhou, J. Chen, S. Wang, R. Zhao, W. Jiang, C. Liu, M. Huang, X. Wang, Y. Zhao, D. Yu, S. Wang, and J.-W. Mei, arXiv:1911.03177 [cond-mat] (2019), arXiv: 1911.03177.
- Hepting et al. (2020) M. Hepting, D. Li, C. J. Jia, H. Lu, E. Paris, Y. Tseng, X. Feng, M. Osada, E. Been, Y. Hikita, Y.-D. Chuang, Z. Hussain, K. J. Zhou, A. Nag, M. Garcia-Fernandez, M. Rossi, H. Y. Huang, D. J. Huang, Z. X. Shen, T. Schmitt, H. Y. Hwang, B. Moritz, J. Zaanen, T. P. Devereaux, and W. S. Lee, Nature Materials 19, 381 (2020), number: 4 Publisher: Nature Publishing Group.
- Lechermann (2020a) F. Lechermann, Phys. Rev. X 10, 041002 (2020a), publisher: American Physical Society.
- Adhikary et al. (2020) P. Adhikary, S. Bandyopadhyay, T. Das, I. Dasgupta, and T. Saha-Dasgupta, arXiv:2005.01243 [cond-mat, physics:quant-ph] (2020), arXiv: 2005.01243.
- Goodge et al. (2020) B. H. Goodge, D. Li, M. Osada, B. Y. Wang, K. Lee, G. A. Sawatzky, H. Y. Hwang, and L. F. Kourkoutis, arXiv:2005.02847 [cond-mat] (2020), arXiv: 2005.02847.
- Jiang et al. (2020) M. Jiang, M. Berciu, and G. A. Sawatzky, Phys. Rev. Lett. 124, 207004 (2020), publisher: American Physical Society.
- Zhang and Vishwanath (2020) Y.-H. Zhang and A. Vishwanath, Phys. Rev. Research 2, 023112 (2020), publisher: American Physical Society.
- Hu and Wu (2019) L.-H. Hu and C. Wu, Phys. Rev. Research 1, 032046 (2019).
- Werner and Hoshino (2020) P. Werner and S. Hoshino, Phys. Rev. B 101, 041104 (2020), publisher: American Physical Society.
- Zhang et al. (2020) G.-M. Zhang, Y.-f. Yang, and F.-C. Zhang, Phys. Rev. B 101, 020501 (2020), publisher: American Physical Society.
- Chang et al. (2019) J. Chang, J. Zhao, and Y. Ding, arXiv:1911.12731 [cond-mat] (2019), arXiv: 1911.12731.
- Sakakibara et al. (2019) H. Sakakibara, H. Usui, K. Suzuki, T. Kotani, H. Aoki, and K. Kuroki, arXiv:1909.00060 [cond-mat] (2019), arXiv: 1909.00060.
- Wang et al. (2020) Y. Wang, C.-J. Kang, H. Miao, and G. Kotliar, Phys. Rev. B 102, 161118 (2020), publisher: American Physical Society.
- Petocchi et al. (2020) F. Petocchi, V. Christiansson, F. Nilsson, F. Aryasetiawan, and P. Werner, Phys. Rev. X 10, 041047 (2020), publisher: American Physical Society.
- Tomczak (2015) J. M. Tomczak, J. Phys.: Conf. Ser. 592, 012055 (2015).
- Choi et al. (2016) S. Choi, A. Kutepov, K. Haule, M. van Schilfgaarde, and G. Kotliar, npj Quantum Materials 1, 16001 (2016).
- Choi et al. (2019) S. Choi, P. Semon, B. Kang, A. Kutepov, and G. Kotliar, Computer Physics Communications 244, 277 (2019).
- Sun and Kotliar (2002) P. Sun and G. Kotliar, Phys. Rev. B 66, 085120 (2002).
- Biermann et al. (2003) S. Biermann, F. Aryasetiawan, and A. Georges, Phys. Rev. Lett. 90, 086402 (2003).
- Nilsson et al. (2017) F. Nilsson, L. Boehnke, P. Werner, and F. Aryasetiawan, Phys. Rev. Materials 1, 043803 (2017).
- Kutepov et al. (2012) A. Kutepov, K. Haule, S. Y. Savrasov, and G. Kotliar, Phys. Rev. B 85, 155129 (2012).
- Kutepov et al. (2017) A. Kutepov, V. Oudovenko, and G. Kotliar, Computer Physics Communications 219, 407 (2017).
- Georges et al. (1996) A. Georges, G. Kotliar, W. Krauth, and M. J. Rozenberg, Rev. Mod. Phys. 68, 13 (1996).
- Metzner and Vollhardt (1989) W. Metzner and D. Vollhardt, Phys. Rev. Lett. 62, 324 (1989).
- Müller-Hartmann (1989) E. Müller-Hartmann, Z. Physik B - Condensed Matter 74, 507 (1989), tex.ids: muller-hartmann_CorrelatedFermionsLattice_1989a.
- Brandt and Mielsch (1989) U. Brandt and C. Mielsch, Z. Physik B - Condensed Matter 75, 365 (1989).
- Janiš (1991) V. Janiš, Z. Physik B - Condensed Matter 83, 227 (1991).
- Georges and Kotliar (1992) A. Georges and G. Kotliar, Phys. Rev. B 45, 6479 (1992).
- Jarrell (1992) M. Jarrell, Phys. Rev. Lett. 69, 168 (1992).
- Rozenberg et al. (1992) M. J. Rozenberg, X. Y. Zhang, and G. Kotliar, Phys. Rev. Lett. 69, 1236 (1992).
- Georges and Krauth (1992) A. Georges and W. Krauth, Phys. Rev. Lett. 69, 1240 (1992).
- Aryasetiawan et al. (2004) F. Aryasetiawan, M. Imada, A. Georges, G. Kotliar, S. Biermann, and A. I. Lichtenstein, Phys. Rev. B 70, 195104 (2004).
- Chikina et al. (2020) A. Chikina, J.-Z. Ma, W. H. Brito, S. Choi, P. Sémon, A. Kutepov, Q. Du, J. Jandke, H. Liu, N. C. Plumb, M. Shi, C. Petrovic, M. Radovic, and G. Kotliar, Phys. Rev. Research 2, 023190 (2020), publisher: American Physical Society.
- Leonov et al. (2020) I. Leonov, S. L. Skornyakov, and S. Y. Savrasov, Phys. Rev. B 101, 241108 (2020), publisher: American Physical Society.
- Ryee et al. (2020b) S. Ryee, H. Yoon, T. J. Kim, M. Y. Jeong, and M. J. Han, Phys. Rev. B 101, 064513 (2020b), publisher: American Physical Society.
- Olevano et al. (2020) V. Olevano, F. Bernardini, X. Blase, and A. Cano, Phys. Rev. B 101, 161102 (2020), arXiv: 2001.09194.
- Bernardini et al. (2019) F. Bernardini, V. Olevano, and A. Cano, arXiv:1910.13269 [cond-mat] (2019), arXiv: 1910.13269.
- Rossi et al. (2020) M. Rossi, H. Lu, A. Nag, D. Li, M. Osada, K. Lee, B. Y. Wang, S. Agrestini, M. Garcia-Fernandez, Y.-D. Chuang, Z. X. Shen, H. Y. Hwang, B. Moritz, K.-J. Zhou, T. P. Devereaux, and W. S. Lee, arXiv:2011.00595 [cond-mat] (2020), arXiv: 2011.00595.
- Jiang et al. (2019) P. Jiang, L. Si, Z. Liao, and Z. Zhong, Phys. Rev. B 100, 201106 (2019).
- Lechermann (2020b) F. Lechermann, Phys. Rev. B 101, 081110 (2020b), publisher: American Physical Society.
- Lee and Pickett (2004) K.-W. Lee and W. E. Pickett, Phys. Rev. B 70, 165109 (2004).
- Zhang et al. (2019) H. Zhang, L. Jin, S. Wang, B. Xi, X. Shi, F. Ye, and J.-W. Mei, (2019).
- Been et al. (2020) E. Been, W.-S. Lee, H. Y. Hwang, Y. Cui, J. Zaanen, T. Devereaux, B. Moritz, and C. Jia, arXiv:2002.12300 [cond-mat] (2020), arXiv: 2002.12300.
- Gu et al. (2020b) Y. Gu, S. Zhu, X. Wang, J. Hu, and H. Chen, Communications Physics 3, 1 (2020b), number: 1 Publisher: Nature Publishing Group.
- Choi et al. (2020) M.-Y. Choi, W. E. Pickett, and K.-W. Lee, arXiv:2005.03234 [cond-mat] (2020), arXiv: 2005.03234.
- Deng et al. (2019) X. Deng, K. M. Stadler, K. Haule, A. Weichselbaum, J. von Delft, and G. Kotliar, Nat Commun 10, 2721 (2019).
- Stadler et al. (2015) K. Stadler, Z. Yin, J. von Delft, G. Kotliar, and A. Weichselbaum, Phys. Rev. Lett. 115, 136401 (2015).
- Stadler et al. (2019) K. M. Stadler, G. Kotliar, A. Weichselbaum, and J. von Delft, Annals of Physics 405, 365 (2019).
- Kugler et al. (2019) F. B. Kugler, S.-S. B. Lee, A. Weichselbaum, G. Kotliar, and J. von Delft, Phys. Rev. B 100, 115159 (2019), publisher: American Physical Society.
- Werner and Millis (2007) P. Werner and A. J. Millis, Phys. Rev. Lett. 99, 126405 (2007), publisher: American Physical Society.
- de’ Medici et al. (2014) L. de’ Medici, G. Giovannetti, and M. Capone, Phys. Rev. Lett. 112, 177001 (2014), publisher: American Physical Society.
- Stadler (2019) K. M. Stadler, A model study of strong correlations in Hund metals, Text.PhDThesis, Ludwig-Maximilians-Universität München (2019).