Inference in parametric models with many L-moments
Abstract
L-moments are expected values of linear combinations of order statistics that provide robust alternatives to traditional moments. The estimation of parametric models by matching sample L-moments has been shown to outperform maximum likelihood estimation (MLE) in small samples from popular distributions. The choice of the number of L-moments to be used in estimation remains ad-hoc, though: researchers typically set the number of L-moments equal to the number of parameters, as to achieve an order condition for identification. This approach is generally inefficient in larger samples. In this paper, we show that, by properly choosing the number of L-moments and weighting these accordingly, we are able to construct an estimator that outperforms MLE in finite samples, and yet does not suffer from efficiency losses asymptotically. We do so by considering a “generalised” method of L-moments estimator and deriving its asymptotic properties in a framework where the number of L-moments varies with sample size. We then propose methods to automatically select the number of L-moments in a given sample. Monte Carlo evidence shows our proposed approach is able to outperform (in a mean-squared error sense) MLE in smaller samples, whilst working as well as it in larger samples. We then consider extensions of our approach to conditional and semiparametric models, and apply the latter to study expenditure patterns in a ridesharing platform in Brazil.
Keywords: L-statistics; generalised method of moments; tuning parameter selection methods; higher-order expansions.
1 Introduction
L-moments, expected values of linear combinations of order statistics, were introduced by Hosking (1990) and have been successfully applied in areas as diverse as computer science (Hosking, 2007; Yang et al., 2021), hydrology (Wang, 1997; Sankarasubramanian and Srinivasan, 1999; Das, 2021; Boulange et al., 2021), meteorology (Wang and Hutson, 2013; Šimková, 2017; Li et al., 2021) and finance (Gourieroux and Jasiak, 2008; Kerstens et al., 2011). By appropriately combining order statistics, L-moments offer robust alternatives to traditional measures of dispersion, skewness and kurtosis. Models fit by matching sample L-moments (a procedure labeled “method of L-moments” by Hosking (1990)) have been shown to outperfom maximum likelihood estimators in small samples from flexible distributions such as generalised extreme value (Hosking et al., 1985; Hosking, 1990), generalised Pareto (Hosking and Wallis, 1987; Broniatowski and Decurninge, 2016), generalised exponential (Gupta and Kundu, 2001) and Kumaraswamy (Dey et al., 2018).
Statistical analyses of L-moment-based parameter estimators rely on a framework where the number of moments is fixed (Hosking, 1990; Broniatowski and Decurninge, 2016). Practitioners often choose the number of L-moments equal to the number of parameters in the model, so as to achieve the order condition for identification. This approach is generally inefficient.111In the generalised extreme value distribution, there can be asymptotic root mean-squared error losses of 30% with respect to the MLE when the target estimand are the distribution parameters (Hosking et al., 1985; Hosking, 1990). In our Monte Carlo exercise, we verify root mean squared errror losses of over 10% when the goal is tail quantile estimation. It also raises the question of whether overidentifying restrictions, together with the optimal weighting of L-moment conditions, could improve the efficiency of “method of L-moments” estimators, as in the framework of generalised-method-of-moment (GMM) estimation (Hansen, 1982). Another natural question would be how to choose the number of L-moments in finite samples, as it is well-known from GMM theory that increasing the number of moments with a fixed sample size can lead to substantial biases (Koenker and Machado, 1999; Newey and Smith, 2004). In the end, one can only ask if, by correctly choosing the number of L-moments and under an appropriate weighting scheme, it may not be possible to construct an estimator that outperforms maximum likelihood estimation in small samples and yet achieves the Cramér-Rao bound assymptotically. Intuitively, the answer appears to be positive, especially if one takes into account that Hosking (1990) shows L-moments characterise distributions with finite first moments.
The goal of this paper lies in answering the questions outlined in the previous paragraph. Specifically, we propose to study L-moment-based estimation in a context where: (i) the number of L-moments varies with sample size; and (ii) weighting is used in order to optimally account for overidentifying conditions. In this framework, we introduce a “generalised” method of L-moments estimator and analyse its properties. We provide sufficient conditions under which our estimator is consistent and asymptotically normal; we also derive the optimal choice of weights and introduce a test of overidentifying restrictions. We then show that, under independent and identically distributed (iid) data and the optimal weighting scheme, the proposed generalised L-moment estimator achieves the Cramér-Rao lower bound. We provide simulation evidence that our L-moment approach outperforms (in a mean-squared error sense) MLE in smaller samples; and works as well as it in larger samples. We then construct methods to automatically select the number of L-moments used in estimation. For that, we rely on higher order expansions of the method-of-L-moment estimator, similarly to the procedure of Donald and Newey (2001) and Donald et al. (2009) in the context of GMM. We use these expansions to find a rule for choosing the number of L-moments so as to minimise the estimated (higher-order) mean-squared error. We also consider an approach based on -regularisation (Luo et al., 2015). We provide computational code to implement both methods,222The repository https://github.com/luisfantozzialvarez/lmoments_redux contains R script that implements our main methods, as well as replication code for our Monte Carlo exercise and empirical application. and evaluate their performance through Monte Carlo simulations. With these tools, we aim to introduce a fully automated procedure for estimating parametric density models that improves upon maximum likelihood in small samples, and yet does not underperform in larger datasets.
We also consider two extensions of our main approach. First, we show how the generalised method-of-L-moment approach introduced in this paper can be extended to the estimation of conditional models. Second, we show how our approach may be used in the analysis of the “error term” in semiparametric models, and apply this extension to study the tail behaviour of expenditure patterns in a ridesharing platform in São Paulo, Brazil. We provide evidence that the heavy-tailedness in consumption patterns persists even after partialing out the effect of unobserved time-invariant heterogeneity and observable heterogeneity in consumption trends. With these extensions, we hope more generally to illustrate how the generalised-mehtod-of-L-moment approach to estimation may be a convenient tool in a variety of settings, e.g. when a model’s quantile function is easier to evaluate than its likelihood. The latter feature has been explored in followup work by one of the authors (Alvarez and Orestes, 2023; Alvarez and Biderman, 2024).
Related literature
This paper contributes to two main literatures. First, we relate to a couple of papers that, building on Hosking’s original approach, propose new L-moment-based estimators. Gourieroux and Jasiak (2008) introduce a notion of L-moment for conditional moments, which is then used to construct a GMM estimator for a class of dynamic quantile models. As we argue in more detail in Section 6, while conceptually attractive, their estimator is not asymptotically efficient (vis-à-vis the conditional MLE), as it focuses on a finite number of moment conditions and does not optimally explore the set of overidentifying restrictions available in the parametric model. In contrast, our proposed extension of the generalised method-of-L-moment estimator to conditional models is able to restore asymptotic efficiency. In an unconditional setting, Broniatowski and Decurninge (2016) propose estimating distribution functions by relying on a fixed number of L-moments and a minimum divergence estimator that nests the empirical likelihood and generalized empirical likelihood estimators as particular cases. Even though these estimators are expected to perform better than (generalized) method-of-L-moment estimators in terms of higher-order properties (Newey and Smith, 2004), both would be first-order inefficient (vis-à-vis the MLE) when the number of L-moments is held fixed. In this paper, we thus focus on improving L-moment-based estimation in terms of first-order asymptotic efficiency, by suitably increasing the number of L-moments with sample size and optimally weighting the overidentifying restrictions, while retaining its known good finite-sample behaviour. We do note, however, that one of our suggested approaches to select the number of L-moments aims at minimising an estimate of the higher-order mean-squared error, which may be useful in improving the higher-order behaviour of estimators even when a bounded (as a function of sample sizes) number of L-moments is used in estimation.
Secondly, we contribute to a literature that seeks to construct estimators that, while retaining asymptotic (first-order) unbiasedness and efficiency, improve upon maximum likelihood estimation in finite samples. The classical method to achieve finite-sample improvements over the MLE is through (higher-order) bias correction (Pfanzagl and Wefelmeyer, 1978). However, analytical bias corrections may be difficult to implement in practice, which has led the literature to consider jaccknife and bootstrap corrections (Hahn et al., 2002). More recently, Ferrari and Yang (2010) introduced a maximum -likelihood estimator for parametric models that replaces the log-density in the objective function of the MLE with , where is a tuning parameter. They show that, by suitably choosing in finite samples, one is able to trade-off bias and variance, thus enabling MSE improvements over the MLE. Moreover, if asymptotically at a rate, the estimator is asymptotically unbiased and achieves the Crámer-Rao lower bound. There are some important differences between our approach and maximum -likelihood estimation. First, we note that the theoretical justification for our construction is distinct from their method. Indeed, for a fixed number of L-moments, our proposed estimator is first-order asymptotically unbiased, whereas the maximum -likelihood estimator is inconsistent in an asymptotic regime with fixed and consistent but first-order biased if slowly enough. Therefore, whereas the choice of the tuning parameter is justified as capturing a tradeoff between first-order bias and variance; the MSE-optimal choice of L-moments in our setting concerns a tradeoff between the first-order variance of the estimator and its higher-order terms. This is precisely what we capture in our proposal to select the number of L-moments by minimising an estimator of the higher-oder MSE; whereas presently no general rule for choosing the tuning parameter in maximum -likelihood estimation exists (Yang et al., 2021).
Structure of paper
The remainder of this paper is organised as follows. In the next section, we briefly review L-moments and parameter estimation based on these quantities. Section 3 works out the asymptotic properties of our proposed estimator. In Section 4 we conduct a small Monte Carlo exercise which showcases the gains associated with our approach. Section 5 proposes methods to select the number of L-moments and assesses their properties in the context of the Monte Carlo exercise of Section 4. Section 6 presents the extensions of our main approach, as well as the empirical application. Section 7 concludes.
2 L-moments: definition and estimation
Consider a scalar random variable with distribution function and finite first moment. For , Hosking (1990) defines the -th L-moment as:
| (1) |
where is the quantile function of , and the , , are shifted Legendre polynomials.333Legendre polynomials are defined by applying the Gramm-Schmidt orthogornalisation process to the polynomials defined on (Kreyszig, 1989, p. 176-180). If denotes the -th Legendre polynomial, shifted Legendre polynomials are related to the standard ones through the affine transformation (Hosking, 1990). Expanding the polynomials and using the quantile representation of a random variable (Billingsley, 2012, Theorem 14.1), we arrive at the equivalent expression:
| (2) |
where, is the -th order statistic of a random sample from with observations. Equation (2) motivates our description of L-moments as the expected value of linear combinations of order statistics. Notice that the first L-moment corresponds to the expected value of .
To see how L-moments may offer “robust” alternatives to conventional moments, it is instructive to consider, as in Hosking (1990), the second L-moment. In this case, we have:
where and are independent copies of . This is a measure of dispersion. Indeed, comparing it with the variance, we have:
from which we note that the variance puts more weight to larger differences.
Next, we discuss sample estimators of L-moments. Let be an identically distributed sample of observations, where each , , is distributed according to . A natural estimator of the -th L-moment is the sample analog of (1), i.e.
| (3) |
where is the empirical quantile process:
| (4) |
with being the -th sample order statistic. The estimator given by (3) is generally biased (Hosking, 1990; Broniatowski and Decurninge, 2016). When observations may be assumed to be independent, researchers thus often resort to an unbiased estimator of , which is given by an empirical analog of (2):
| (5) |
In practice, it is not necessary to iterate over all size subsamples of to compute the sample -th L-moment through (5). Hosking (1990) provides a direct formula that avoids such computation.
We are now ready to discuss the estimation of parametric models based on matching L-moments. Suppose that belongs to a parametric family of distribution functions , where and for some . Let denote the theoretical -th L-moment, where is the quantile function associated with . Let , and be the vector stacking estimators for the first L-moments (e.g. (3) or (5)). Researchers then usually estimate by solving:
As discussed in Section 1, this procedure has been shown to lead to efficiency gains over maximum likelihood estimation in small samples from several distributions. Nonetheless, the choice of L-moments appears rather ad-hoc, as it is based on an order condition for identification. One may then wonder whether increasing the number of L-moments used in estimation – and weighting these properly –, might lead to a more efficient estimator in finite samples. Moreover, if one correctly varies the number of L-moments with sample size, it may be possible to construct an estimator that does not undeperform MLE even asymptotically. The latter appears especially plausible if one considers the result in Hosking (1990), who shows that L-moments characterise a distribution with finite first moment.
In light of the preceding discussion, we propose to analyse the behaviour of the “generalised” method of L-moments estimator:
| (6) |
where may vary with sample size; and is a (possibly estimated) weighting matrix. In Section 3, we work out the asymptotic properties of this estimator in a framework where both and diverge, i.e. we index by the sample size and consider the asymptotic behaviour of the estimator in the large-sample limit, for sequences where .444We maintain the indexing of by implicit to keep the notation concise. In this setting, the phrase “as ” should be read as meaning that a property holds in the limit , for any sequence with . The phrase “as with , where and , should be read as meaning that a property holds in the limit , for any sequence with and . ,555As it will become clear in Section 3, our framework nests the setting with fixed as a special case by properly filling the weighting matrix with zeros. We derive sufficient conditions for an asymptotic linear representation of the estimator to hold. We also show that the estimator is asymptotically efficient, in the sense that, under iid data and when optimal weights are used, its asymptotic variance coincides with the inverse of the Fisher information matrix. In Section 4, we conduct a small Monte Carlo exercise which showcases the gains associated with our approach. Specifically, we show that our L-moment approach entails mean-squared error gains over MLE in smaller samples, and performs as well as it in larger samples. In light of these results, in Section 5 we propose to construct a semiautomatic method of selection of the number of L-moments by working with higher-order expansions of the mean-squared error of the estimator – in a similar fashion to what has already been done in the GMM literature (Donald and Newey, 2001; Donald et al., 2009; Okui, 2009; Abadie et al., 2023). We also consider an approach based on -regularisation borrowed from the GMM literature (Luo et al., 2015). We then return to the Monte Carlo setting of Section 4 in order to assess the properties of the proposed selection methods. In Section 6, we consider extensions of our main approach to the estimation of conditional models and a class of semiparametric models.
In this paper, we will focus on the case where estimated L-moments are given by (3). As shown in Hosking (1990), under random sampling and finite second moments, for each , , which implies that the estimator (6) using either (3) or (5) as are first-order asymptotically equivalent when is fixed. However, in an asymptotic framework where increases with the sample size, this need not be the case. Indeed, note that, for , is not even defined, whereas is. Relatedly, the simulations in Section 4 show that, for values of close to , the generalised-method-of L-moment estimator (6) based on breaks down, whereas the estimator based on does not.666The latter phenomenon is corroborated by our theoretical results in Section 3 for the estimator based on , which allow for to be much larger that . We thus focus on the properties of the estimator that relies on , as it is especially well-suited for settings where one may wish to make large.
3 Asymptotic properties of the generalised method of L-moments estimator with many moments
3.1 Setup
As in the previous section, we consider a setting where we have a sample with identically distributed observations, , for , where belongs to a parametric family , ; and for some . We will analyse the behaviour of the estimator:
| (7) |
where is the empirical quantile process given by (4); is the quantile function associated with ; are a set of (possibly estimated) weights; are a set of quantile “weighting” functions with ; and . This setting encompasses the generalised-method-of-L-moment estimatior discussed in the previous section. Indeed, by choosing , where are the shifted Legendre polynomials on , and , we have the generalised L-moment-based estimator in (6) using (3) as an estimator for the L-moments.777The rescaling by is adopted so the polynomials have unit -norm. We leave fixed throughout.888In Remark 4 later on, we briefly discuss an extension to sample-size-dependent trimming. All limits are taken jointly with respect to and .
To facilitate analysis, we let ; and write for the matrix with entry . We may then rewrite our estimator in matrix form as:
3.2 Consistency
In this section, we present conditions under which our estimator is consistent.
We impose the following assumptions on our environment. In what follows, we write .
Assumption 1 (Consistency of empirical quantile process).
The empirical quantile process is uniformly consistent on , i.e.
| (8) |
1 is satisfied in a variety of settings. For example, if , … are iid and the family is continuous with a (common) compact support; then (8) follows with and (Ahidar-Coutrix and Berthet, 2016, Proposition 2.1.). Yoshihara (1995) and Portnoy (1991) provide sufficient conditions for uniform consistency (8) to hold when observations are dependent. We also note that, for the result in this section, it would have been sufficient to assume weak convergence in the norm (see Mason (1984), Barrio et al. (2005) and references therein). We only state results in the -norm because convergence statements regarding the empirical quantile process available in the literature are usually proved in .
Assumption 2 (Quantile weighting functions).
The functions constitute an orthonormal sequence on .
2 is satisfied by (rescaled) shifted Legendre polynomials, shifted Jacobi polynomials and other weighting functions.
Next, we impose restrictions on the estimated weights. In what follows, we write, for a matrix , .
Assumption 3 (Estimated weights).
There exists a sequence of nonstochastic symmetric positive semidefinite matrices such that, as , ;999The notation expresses convergence in outer probability to zero. We state our main assumptions and results in outer probability in order to abstract from measurability concerns. We note these results are equivalent to convergence in probability when the appropriate measurability assumptions hold. .
3 restricts the range of admissible weight matrices. Notice that trivially satisfies these assumptions. By the triangle inequality, 3 implies that .
Finally, we introduce our identifiability assumption. For some , let :
Assumption 4 (Strong identifiability and suprema of norm of parametric quantiles).
For each :
Moreover, we require that .
The first part of this assumption is closely related to the usual notion of identifiability in parametric distribution models. Indeed, if is compact, is continuous, , , the constitute an orthonormal basis in (this is the case for shifted Legendre polynomials), and , then part 1 is equivalent to identifiability of the parametric family .
As for the second part of the assumption, we note that boundedness of the norm of parametric quantiles uniformly in is satisfied in several settings. If the parametric family has common compact support, then the assumption is trivially satisfied. More generally, if we assume is compact and is jointly continuous and bounded on , then the condition follows immediately from Weierstrass’ theorem, as in this case: .
Under the previous assumptions, the estimator is consistent.
3.3 Asymptotic linear representation
In this section, we provide conditions under which the estimator admits an asymptotic linear representation. In what, follows, define ; and write for the Jacobian of with respect to , evaluated at . We assume that:
Assumption 5.
There exists an open ball in containing such that and is differentiable on , uniformly in . Moreover, is continuously differentiable on for each ; and, for each , is square integrable on .
Assumption 6.
converges weakly in to a zero-mean Gaussian process with continuous sample paths and covariance kernel .
Assumption 7.
is twice continuously differentiable on , for each . Moreover, .
Assumption 8.
The smallest eigenvalue of is bounded away from , uniformly in .
Assumption 5 requires to be an interior point of . It also implies the objective function is countinuously differentiable on a neighborhood of , which enables us to linearise the first order condition satisfied with high probability by .
Weak convergence of the empirical quantile process (6) has been derived in a variety of settings, ranging from iid data (Vaart, 1998, Corollary 21.5) to nonstationary and weakly dependent observations (Portnoy, 1991). In the iid setting, if the family is continuously differentiable with strictly positive density over a (common) compact support; then weak-convergence holds with and . In this case, the covariance kernel is . Similarly to the discussion of Assumption 1, Assumption 6 is stronger than necessary: it would have been sufficient to assume , which is implied by weak convergence in .
7 is a technical condition which enables us to provide an upper bound to the linearisation error of the first order condition satisfied by .
8 is similar to the rank condition used in the proof of asymptotic normality of M-estimators (Newey and McFadden, 1994), which is known to be equivalent to a local identification condition under rank-regularity assumptions (Rothenberg, 1971). In our setting, where varies with sample size, we show in Supplemental LABEL:app_relation that a stronger version of 4 implies 8.
Proposition 2.
| (9) |
Proof.
See Supplemental Appendix LABEL:proof_asymptotic_linear. ∎
In the next subsection, we work out an asymptotic approximation to the distribution of the leading term in (9).
Remark 1.
Note that Proposition (2) does not impose any restrictions on the rate of growth of L-moments. This stands in contrast with results in the literature exploring the behaviour of GMM estimator in asymptotic sequences with an increasing number of moments (Koenker and Machado, 1999; Donald et al., 2003; Han and Phillips, 2006), where rate restrictions are typically required to establish an asymptotic linear representation. This difference may be essentially attributed to the special structure implied by L-moments in our setting – being written as the projection coefficients of the same quantile function on an orthonormal sequence in –, that enable us to finely control the linearisation error in terms of the -norm.
3.4 Asymptotic distribution
Finally, to work out the asymptotic distribution of the proposed estimator, we rely on a strong approximation concept. The idea is to construct, in the same underlying probability space, a sequence of Brownian bridges that approximates, in the supremum norm, the empirical quantile process. This can then be used to conduct inference based on a Gaussian distribution. In Supplemental Appendix LABEL:app_inferece_bahadur, we alternatively show how a Bahadur-Kiefer representation of the quantile process can be used to conduct inference in the iid case. In this alternative, one approximates the distribution of the leading term of (9) by a transformation of independent Bernoulli random variables.
We first consider a strong approximation to a Gaussian process in the iid setting. We state below a classical result, due to Csorgo and Revesz (1978):
Theorem 1 (Csorgo and Revesz (1978)).
Let be an iid sequence of random variables with a continuous distribution function which is also twice differentiable on , where and . Suppose that for . Assume that, for :
where denotes the density of . Moreover, assume that is nondecreasing (nonincreasing) on an interval to the right of (to the left of ). Then, if the underlying probability space is rich enough, one can define, for each , a Brownian bridge such that, if :
| (10) |
and, if
| (11) |
for arbitrary .
The above theorem is much stronger than the weak convergence of 6. Indeed, Theorem 1 requires variables to be defined in the same probability space and yields explicit bounds in the sup norm; whereas weak convergence is solely a statement on the convergence of integrals (Vaart and Wellner, 1996). Suppose the approximation (10)/(11) holds in our context. Let be as in the statement of the theorem, and assume in addition that . A simple application of Bessel’s inequality then shows that:
| (12) |
Note that the distribution of the leading term in the right-hand side is known (by Riemann integration, it is Gaussian) up to . This representation could thus be used as a basis for inference. The validity of such approach can be justified by verifying that the Kolmogorov distance between the distribution of and that of the leading term of the representation goes to zero as and increase. We show that this indeed is true later on, where convergence in the Kolmogorov distance is obtained as a byproduct of weak convergence.
Next, we reproduce a strong approximation result in the context of dependent observations. The result is due to Fotopoulos and Ahn (1994) and Yu (1996).
Theorem 2 (Fotopoulos and Ahn (1994); Yu (1996)).
Let be a strictly stationary, -mixing sequence of random variables, with mixing coefficient satisfying . Let denote the distribution function of . Suppose the following Csorgo and Revesz conditions hold:
-
a.
is twice differentiable on , where and ;
-
b.
;
as well as the condition:
-
c.
.
Let , where and . Then, if the probability space is rich enough, there exists a sequence of Brownian bridges with covariance kernel and a positive constant such that:
| (13) |
A similar argument as the previous one then shows that, under the conditions of the theorem above:
| (14) |
Differently from the iid case, the distribution of the leading term on the right-hand side is now known up to and the covariance kernel . The latter could be estimated with a Newey and West (1987) style estimator.
To conclude the discussion, we note that the strong representation (12) (resp. (14)) allows us to establish asymptotic normality of our estimator. Indeed, let be the leading term of the representation on the right-hand side of (12) (resp. (14)), and be its variance. Observe that is distributed according to a multivariate standard normal. It then follows by Slutsky’s theorem that . Since pointwise convergence of cdfs to a continuous cdf implies uniform convergence (Parzen, 1960, page 438), and given that is positive definite, we obtain that:
| (15) |
which justifies our approach to inference based on the distribution of the leading term on the right-hand side of (12) (resp. (14)).
We collect the main results in this subsection under the corollary below.
Corollary 1.
Remark 2 (Optimal choice of weighting matrix under Gaussian approximation).
Under (12), the optimal choice of weights that minimises the variance of the leading term is:
| (16) |
where denotes the generalised inverse of a matrix . This weight can be estimated using a preliminary estimator for . A similar result holds under (14), though in this case one also needs an estimator for the covariance kernel . In Supplemental LABEL:app_computations, we provide an estimator for in the iid case when the are shifted Legendre Polynomials.
Remark 3 (A test statistic for overidentifying restrictions).
The strong approximation discussed in this subsection motivates a test statistic for overidentifying restrictions. Suppose . Denoting by the objective function of (7), we consider the test-statistic:
An analogous statistic exists in the overidentified GMM setting (Newey and McFadden, 1994; Wooldridge, 2010). Under the null that the model is correctly specified (i.e. that there exists such that ), we can use the results in this section to compute the distribution of this test statistic. Specifically, if the optimal weighting scheme is adopted, the distribution of the test statistic under the null may be approximated by a chi-squared distribution with degrees of freedom. To establish this fact, we rely on an anticoncentration result due to Götze et al. (2019). See Supplemental Appendix LABEL:app_test for details.
Remark 4 (Sample-size-dependent trimming).
It is possible to adapt our assumptions and results to the case where the trimming constants , are functions of the sample size and, as , and . In particular, Theorem 6 of Csorgo and Revesz (1978) provides uniform strong approximation results for sample quantiles ranging from , where . This could be used as the basis for an inferential theory on a variable-trimming L-moment estimator under weaker assumptions than those in this section. For a given , a data-driven method for selecting and could then be obtained by choosing these constants so as to minimise an estimate of the variance of the leading term in (9). See Athey et al. (2023) for a discussion of this approach in estimating the mean of a symmetric distribution; and Crump et al. (2009) for a related approach when choosing trimming constants for the estimated propensity score in observational studies.
Remark 5 (Inference based on the weighted bootstrap).
In Supplemental LABEL:app_bootstrap, we show how one can leverage the strong approximations discussed in this section to conduct inference on the model parameters using the weighted bootstrap.
3.5 Asymptotic efficiency
Supplemental Appendix LABEL:app_efficiency discusses efficiency of our proposed L-moment estimator. Specifically, we show that, when no trimming is adopted (), the optimal weighting scheme (16) is used, the constitue an orthonormal basis in (recall this is satisfied by shifted Legendre polynomials), and the data is iid, the generalised method of L-moments estimator is assymptotically efficient, in the sense that its asymptotic variance coincides with the inverse of the Fisher information matrix of the parametric model.101010In the dependent case, “efficiency” should be defined as achieving the efficiency bound of the semiparametric model that parametrises the marginal distribution of the , but leaves the time series dependence unrestricted up to regularity conditions (Newey, 1990; Komunjer and Vuong, 2010). Indeed, in general, our L-moment estimator will be inefficient with respect to the MLE estimator that models the dependency structure between observations. See Carrasco and Florens (2014) for further discussion. We leave details to the Supplemental Appendix, though we briefly outline the argument here. The idea is to consider the alternative estimator:
| (17) |
for a grid of points and weights , . This is a weighted version of a “percentile-based estimator”, which is used in contexts where it is difficult to maximise the likelihood (Gupta and Kundu, 2001). It amounts to choosing so as to match a weighted combination of the order statistics in the sample. In the Supplemental Appendix, we show that, under a suitable sequence of gridpoints and optimal weights, this estimator is asympotically efficient. We then show, by using the fact that the form an orthonormal basis, that estimator (17) can be seen as a generalised L-moment estimator that uses infinitely many L-moments. The final step of the argument then consists in showing that a generalised L-moment estimator that uses a finite but increasing number of L-moments is asymptotically equivalent to estimator (17), which implies that a generalised L-moment estimator under optimal weights is no less efficient than the (efficient) percentile estimator.
4 Monte Carlo exercise
In our experiments, we draw random samples from a distribution function belonging to a parametric family . Following Hosking (1990), we consider the goal of the researcher to be estimating quantiles of the distribution by using a plug-in approach: first, the researcher estimates ; then she estimates by setting . As in Hosking (1990), we consider . In order to compare the behaviour of alternative procedures in estimating more central quantiles, we also consider the median . We analyse sample sizes . The number of Monte Carlo draws is set to .
We compare the root mean squared error of four types of generalised method of L-moment estimators under varying choices of with the root mean squared error obtained were to be estimated via MLE. We consider the following estimators: (i) the generalised method of L-moments estimator that uses the càglàd L-moment estimates (3) and identity weights (Càglàd FS);111111To be precise, our choice of weights does not coincide with actual identity weights. Given that the coefficients of Legendre polynomials rapidly scale with – and that this increase generates convergence problems in the numerical optimisation – we work directly with the underlying estimators of the probability-weighted moments (Landwehr et al., 1979), of which L-moments are linear combinations. When (estimated) optimal weights are used, such approach is without loss, since the optimal weights for L-moments constitute a mere rotation of the optimal weights for probability-weighted moments, in such a way that the optimally-weighted objective function for L-moments and probability-weighted moments coincide. In other cases, however, this is not the case: a choice of identity weights when probability-weighted moments are directly targeted coincides with using as a weighting matrix for L-moments, where is a matrix which translates the first probability-weighted moments onto the first L-moments. For small , we have experimented with using the “true” L-moment estimator with identity weights, and have obtained the same patterns presented in the text. (ii) a two step-estimator which first estimates (i) and then uses this preliminary estimator121212This preliminary estimator is computed with . to estimate the optimal weighting matrix (16), which is then used to reestimate (Càglàd TS); (iii) the generalised method of L-moments estimator that uses the unbiased L-moment estimates (5) and identity weights (Unbiased FS); and (iv) the two-step estimator that uses the unbiased L-moment estimator in the first and second steps (Unbiased TS). The estimator of the optimal-weighting matrix we use is given in Supplemental LABEL:app_computations.
4.1 Generalised Extreme value distribution (GEV)
and .
Table 1 reports the RMSE of each procedure, divided by the RMSE of the MLE, under the choice of that achieves the smallest RMSE. Values above 1 indicate the MLE outperforms the estimator in consideration; and values below 1 indicate the estimator outperforms MLE. The value of that minimises the RMSE is presented under parentheses. Some patterns are worth highlighting. Firstly, the L-moment estimator, under a proper choice of and (estimated) optimal weights (two-step estimators) is able to outperform MLE in most settings, especially at the tail of the distribution function. Reductions in these settings can be as large as . At the median, two-step L-moment estimators behave similarly to the MLE. The performance of two-step càglàd and unbiased estimators is also quite similar. Secondly, the power of overidentifying restrictions is evident: except in four out of twenty-four cases, two-step L-moment estimators never achieve a minimum RMSE at , the number of parameters. These exceptions are found at the smallest sample size (), where the benefit of overidentifying restrictions may be outweighed by noisy estimation of the weighting matrix.131313Indeed, as we discuss in Supplemental Appendix LABEL:app_selection, a higher-order expansion of our proposed estimator shows that correlation of the estimator of the optimal weighting matrix with sample L-moments plays a key role in the higher-order bias and variance of the two-step estimator. Thirdly, the relation between and in the two-step Càglàd estimator is monotonic, as expected from our theoretical discussion. Finally, the role of optimal weights is clear: first-step estimators tend to underperform the MLE as the sample size increases. In larger samples, and when optimal weights are not used, the best choice tends to be setting close to or equal to , which reinforces the importance of weighting when overidentifying restrictions are included.
To better understand the patterns in the table, we report in Figure 1, the relative RMSE curve for different sample sizes and choices of . The role of optimal weights is especially striking: first-step estimators usually exhibit an increasing RMSE, as a function of . In contrast, two-step estimators are able to better control the RMSE across . It is also interesting to note that the two-step unbiased L-moment estimator behaves poorly when is close to . This suggests that, in settings where one may wish to make large, the càglád estimator is preferrable.141414This is also in accordance with our theoretical results for the càglád-based estimator, which essentially place no restriction on the growth rate of .
4.2 Generalised Pareto distribution (GPD)
Following Hosking and Wallis (1987), we consider the family of distributions:
and .
Table 2 and Figure 2 summarise the results of our simulation. Overall patterns are similar to the ones obtained in the GEV simulations. Importantly, though, estimation of the optimal weighting matrix impacts two-step estimators quite negatively in this setup. As a consequence, we verify that the choice of (i.e. a just-identified estimator that effectively does not rely on the weights) is optimal for TS estimators at eight out of the sixteen cases in sample sizes smaller than . This behaviour also leads to FS estimators, which do not use estimated weights, outperforming TS estimators at the and quantiles when , and only slightly underperforming TS estimators at some quantiles in larger sample sizes. The latter phenomenon is also partly explained by the just-identified choice improving upon the MLE even in the largest sample size. In all settings, L-moment estimators compare favourably to the MLE.
Càglàd FS 1.020 0.957 0.787 0.649 1.033 0.981 0.949 0.963 1.031 1.000 1.076 1.114 (3) (3) (3) (50) (3) (4) (3) (3) (3) (8) (3) (3) Càglàd TS 1.001 0.955 0.789 0.665 1.006 0.979 0.912 0.855 1.004 0.998 0.996 0.988 (12) (3) (3) (3) (12) (4) (5) (5) (88) (5) (91) (91) Unbiased FS 1.012 0.947 0.819 0.728 1.027 0.974 0.969 1.012 1.031 0.998 1.079 1.125 (3) (3) (3) (3) (3) (6) (3) (3) (3) (9) (3) (3) Unbiased TS 0.994 0.946 0.809 0.661 1.001 0.971 0.903 0.847 1.003 0.995 0.989 0.980 (21) (3) (5) (6) (17) (4) (5) (27) (52) (7) (20) (20)
Càglàd FS 0.978 0.974 0.771 0.543 0.987 0.989 0.912 0.883 0.996 0.998 0.983 0.977 (5) (2) (50) (50) (4) (4) (7) (5) (4) (21) (2) (2) Càglàd TS 0.957 0.974 0.800 0.610 0.980 0.990 0.912 0.859 0.995 0.998 0.979 0.969 (3) (2) (2) (2) (3) (2) (3) (3) (10) (5) (3) (100) Unbiased FS 0.949 0.960 0.806 0.668 0.968 0.981 0.929 0.937 0.995 0.996 0.986 0.989 (5) (2) (15) (6) (4) (10) (5) (4) (4) (24) (2) (2) Unbiased TS 0.932 0.960 0.821 0.679 0.958 0.982 0.923 0.903 0.990 0.995 0.976 0.975 (5) (2) (2) (2) (13) (2) (4) (4) (99) (10) (27) (27)






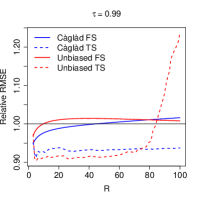
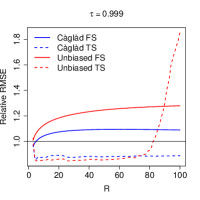





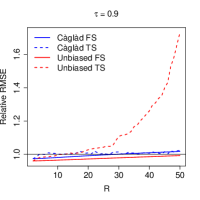




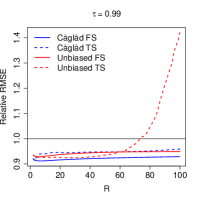





5 Choosing the number of L-moments in estimation
The simulation exercise in the previous section evidences that the number of L-moments plays a crucial role in determining the relative behaviour of the generalised L-moment estimator. In light of this, in this section we introduce (semi)automatic methods to select . We briefly outline two approaches, with the details being left to Supplemental Appendix LABEL:app_selection. We then contrast these approaches in the context of the Monte Carlo exercise of Section 4.
In Supplemental LABEL:higher_order_selector, we derive a higher-order expansion of the “generalised” L-moment estimator (7). We then propose to choose by minimising the resulting higher-order mean-squared error of a suitable linear combination of the parameters. Similar approaches were considered in the GMM literature by Donald and Newey (2001) – where the goal is to choose the number of instruments in linear instrumental variable models –, and Donald et al. (2009) – where one wishes to choose moment conditions in models defined by conditional moment restrictions (in which case infinitely many restrictions are available). Relatedly, Okui (2009) considers the choice of moments in dynamic panel data models; and, more recently, Abadie et al. (2023) use higher order expansions to develop a method of choosing subsamples in linear instrumental variables models with first-stage heterogeneity. Importantly, our higher-order expansions can be used to provide higher-order mean-squared error estimates of target estimands , where is a function indexed by sample size. This can be useful when the parameter is not of direct interest. So, for example, if our goal is quantile estimation, we can choose so as to minimise the higher-order mean-squared error of estimating the target quantile.
In Supplemental LABEL:lasso_selector, we consider an alternative approach to selecting L-moments by employing -regularisation. Following Luo et al. (2015), we note that the first order condition of the estimator (7) may be written as:
for a matrix which combines the L-moments linearly into restrictions. The idea is to estimate using a Lasso penalty. This approach implicitly performs moment selection, as the method yields exact zeros for several entries of . In a GMM context, Luo et al. (2015) introduces an easy-to-implement quadratic program for estimating with the Lasso regularization. In the Appendix, we show how this algorithm may be extended to our L-moment setting and provide conditions for its validity.
To conclude, we return to the Monte Carlo exercise of Section 4. We contrast the RMSE (relatively to the MLE) of the original L-moment estimator due to Hosking (1990) that sets (FS) with a two-step L-moment estimator where is chosen so as to minimise a higher-order MSE of the target quantile (TS RMSE), and a “post-lasso” estimator that estimates using only those L-moments selected by regularised estimation of (TS Post-Lasso). We consider estimators based on the “càglàd” L-moment estimator (3). Additional details on the implementation of each method can be found in Supplemental Appendix LABEL:monte_carlo_select.
Tables 3 and 4 present the results of the different methods in the GEV and GPD exercises. We report in parentheses the average number of L-moments used by each estimator. Overall, the TS RMSE estimator compares favourably to both Hosking’s original estimator and the MLE. In the GEV exercise, the TS RMSE estimator improves upon both the FS estimator and the MLE when ; and works as well as the MLE and better than FS in the largest sample size. As for the GPD exercise, recall that this is a setting where estimation of the optimal weighting matrix impacts two-step estimators more negatively and where the choice improves upon MLE even in the largest sample size. Consequently, TS RMSE underperforms the FS estimator at most quantiles in sample sizes and , and only slightly outperforms it at . Note, however, that differences in the GPD setting are mostly small: the average gain of FS over TS RMSE in the GPD exercise is 0.7 (relative) percentage points (pp) and the largest outperformance is 3.9 pp; whereas, in the GEV exercise, the average gain of TS RMSE over FS is 3.3 pp and the largest is 10.8 pp. More importantly, in both settings, our TS RMSE approach is able to simultaneously generate gains over MLE in smaller samples and mitigate inefficiencies of Hosking’s original method in larger sample sizes. This phenomenon is especially pronounced at the tails of the distributions.
With regards to the Post-Lasso method, we note that it behaves similarly to TS RMSE in larger sample sizes, though it can perform unfavourably vis-à-vis the other L-moment alternatives in the smallest sample size (the method still improves upon MLE at tail quantiles in this scenario). As we discuss in Supplemental Appendix LABEL:monte_carlo_select, this issue can be partly attributed to a “harsh” regularisation penalty being used in the selection step. There is room for improving this step by relying on an iterative procedure to select a less harsh penalty (see Belloni et al. (2012) and Luo et al. (2015) for examples). We also discuss in the Appendix that it could be possible to improve the TS RMSE procedure by including additional higher-order terms in the estimated approximate RMSE. We leave exploration of these improvements as future topics of research.
FS 1.020 0.957 0.787 0.657 1.033 0.982 0.949 0.963 1.031 1.004 1.076 1.114 (3) (3) (3) (3) (3) (3) (3) (3) (3) (3) (3) (3) TS RMSE 1.003 0.964 0.775 0.635 1.008 0.985 0.921 0.875 1.004 1.000 1.007 1.006 (16.64) (3.67) (3.34) (3.48) (32.79) (3.93) (3.99) (4.35) (20.16) (35.38) (41.63) (44.58) TS Post-Lasso 1.012 0.975 0.837 0.708 1.016 0.989 0.928 0.877 1.008 1.000 1.009 1.007 (7.95) (7.95) (7.95) (7.95) (9.25) (9.25) (9.25) (9.25) (9.94) (9.94) (9.94) (9.94)
FS 0.990 0.974 0.800 0.609 0.994 0.990 0.920 0.889 1.004 1.003 0.983 0.977 (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) TS RMSE 0.964 0.997 0.807 0.631 1.001 0.994 0.959 0.919 0.997 0.998 0.980 0.969 (2.85) (4.34) (2.62) (2.94) (73.38) (5.96) (99.2) (99.32) (99.03) (98.63) (99.54) (99.54) TS Post-Lasso 0.996 0.995 0.864 0.689 1.000 1.002 0.966 0.956 0.997 1.000 0.987 0.982 (3.61) (3.61) (3.61) (3.61) (3.86) (3.86) (3.86) (3.86) (4.22) (4.22) (4.22) (4.22)
6 Extensions
6.1 “Residual” analysis in semi- and nonparametric models
In this subsection, we consider a setting where a researcher has postulated a model for a scalar real-valued outcome :
| (18) |
where is a known mapping, is a vector of observable attributes taking values in , is an unobservable scalar real-valued disturbance, and is a nuisance parameter that is known to belong to a subset of a Banach space . We assume that, for each possible value , the map is invertible, and we denote its pointwise inverse by .
We further assume that the researcher has access to an estimator of , and that her goal is to estimate a parametric model for the distribution of , i.e. she considers the model:
| (19) |
Interest in (19) nests different types of “residual” analyses, where one may wish to estimate (19) with an aim to (indirectly) assess the apropriateness of (18) – whenever theory imposes restrictions on the distribution of –, or as a means to construct unconditional prediction intervals for .
In Supplemental Appendix LABEL:app_extension_res, we show how our generalided L-moment approach may be adapted to estimate (19), while remaining agnostic about the first-step estimator of . We do so by borrowing insights from the double-machine learning literature (Chernozhukov et al., 2018, 2022; Kennedy, 2023). Specifically, we employ sample-splitting and debiasing to construct the generalised method-of-L-moment estimator:
| (20) |
where is the empirical quantile function of , with a first-step estimator of computed from a sample independently from . The adjustment term is an estimator of the first-step influence function (Ichimura and Newey, 2022), which reflects the impact of estimating on . The Supplemental Appendix provides the form of this correction in three examples. We also show that the asymptotic distribution of may be computed as in the previous sections, i.e. we can disregard the effect of the first-step estimator once we account for in the estimation.
To further illustrate this approach, we rely on expenditure data in a ridesharing platform collected by Biderman (2018). We observe weekly expenditures (in Brazilian reais) in the platform during eight weeks between August and Semptember 2018, for a subset of 3,961 users of the service in the municipality of São Paulo, Brazil. For these users, we also have access to survey data on sociodemographic traits and commuting motives. We denote by the amount spent by user in week , whereas collects their sociodemographic and commuting information.
Panel 3(a) plots the histogram for the distribution of expenditures in the last week of our sample (late September). The data clearly exhibits heavy tails: the maximum observed expenditure is 417.2 Brazilian reais, whereas average expenditure amounts to 21.20 reais.151515For completeness, in late September 2018, 1USD=4 Brazilian reais. Moreover, 54% of individuals do not spend any money in rides during this period. The solid blue line presentes the density of a GPD distribution fit to this data. The parameters of the distribution are estimated via the two-step generalized method-of L-moment estimator discussed in Section 4, with , which corresponds to the optimal choice for estimating several quantiles across the distribution, according to the RMSE criterion discussed in Section 5. Even though the overidentifying restrictions test clearly rejects the null (p-value 0), we take the plotted density as further confirmation of heavy-tailedness of expenditure patterns, since the estimated GPD density understates mass at larger support points.
We seek to understand whether individual time-invariant heterogeneity, along with persistence in expenditure patterns, is able to explain the observed heavy-tailedness. To accomplish this, we posit the following model for the evolution of expenditures:
where is unobserved time-invariant heterogeneity (here treated as a fixed effect), and is time-varying idiosyncratic heterogeneity that is assumed to be independent across time. The coefficients and measure respectively deterministic trends and persistence in individual consumption patterns. We allow these coefficients to be nonparametric functions of survey information. Finally, we also assume that , meaning that correctly capture mean heterogeneity in consumption trends attributable to .
To estimate the above model, we take first-differences to remove the fixed effect, i.e. we consider:
| (21) |
Under the assumption that the are independent across time, we may then use as a valid instrument for the endogenous variable (Anderson and Hsiao, 1982; Arellano and Bond, 1991). We estimate (21) using the instrumental forest estimator of Athey et al. (2019), which assumes and to be in the closure of the linear span of regression trees.
Panel 3(b) reports the histogram of the residuals in late September, where we adopt sample-splitting and estimate the functions and using data from the weeks prior to the last week in the sample. The distribution is two-sided, with a large mass just below zero, suggesting that model (21) somewhat overpredicts expenditure variation in late September. To assess whether the data exhibits heavy-tails, we estimate a GEV mixture model for the distribution of , assuming that , with , , and and belonging to the GEV family described in Section 4. Our formulation allows for the left- and right-tails to exhibit different decay, e.g. if and and the shape parameter of is negative while is positive, then the left-tail behaves as a Fréchet, while the right-tail behaves as a Weibull distribution. Moreover, if the distributions being mixed by the weights exhibit disjoint supports, then the quantile function of the mixture admits a simple closed-form solution (Castellacci, 2012), which enables us to rely on closed-form expressions for the L-moments of the GEV family to compute theoretical L-moments (Hosking, 1986). We estimate the parameters by relying on the adjusted estimator (20), with two-step optimal weights and the form of correction derived in Example LABEL:example_linear_iv in Supplemental Appendix LABEL:app_extension_res.
The solid blue line in Panel 3(b) reports the fitted density of the GEV mixture, while the shaded blue area plots a 95% uniform confidence band for the density function over the support of . The band is computed using the delta-method and sup-t critical values (Freyberger and Rai, 2018). Overall, the fit appears adequate, as evidenced by the overidentifying restrictions test not rejecting the null at the usual significance levels (). We then use our parameter estimates to test the null hypothesis that the left (right) tail exhibits exponentially light decay, against the alternative that it is heavy-tailed. This corresponds to testing whether the left-tail (right-tail) shape parameter is in the set , against the alternative that it is not.161616When the shape parameter equals zero, the GEV distribution collapses to a Gumbel distribution, which has exponentially light tails (Chernozhukov and Fernández-Val, 2011). When the shape parameter is strictly greater than zero but smaller than one, the distribution collapses to a Weibull distribution with shape parameter greater than one, a region for which the Weibull is known to have exponentially light tails (Foss et al., 2011). The region corresponds to a Fréchet distribution, whereas the region corresponds to a Weibull with shape parameter strictly greater than zero and strictly less than unity – both cases corresponding to heavy-tailed distributions. Upon computation of a 99% confidence interval for the left- (right-) tail shape parameters, we verify that the confidence region for the left-tail shape parameter is entirely contained in the region, whereas the region for the right-tail shape parameter is entirely contained in . We thus reject the null of exponentially light decay for both tails of the distribution. This is evidence that, even after accounting for heterogeneous persistence and trends, as well as time-invarying unobserved heterogeneity, consumption trends still exhibit very extreme expenses.


6.2 Conditional quantile models
Let be the quantile function of a conditional distribution function , where is a scalar outcome and is a set of controls. Following Gourieroux and Jasiak (2008), we define the -th conditional L-moment as:
| (22) |
When , Gourieroux and Jasiak (2008) note that . They suggest estimating nonparametrically, and, for a fixed number of L-moments, to exploit the following unconditional moments in the estimation of conditional parametric models :
| (23) |
where is a vector of transformations of .
In spite of its conceptual attractiveness – L-moment estimation is cast as method-of-moment estimation –, formulation (23) does not directly extend to settings with trimming.171717To implement trimming in this formulation would require nonparametric estimation of both the conditional distribution and conditional quantile functions, whereas our suggested approach solely relies on the latter. Moreover, by working with fixed and , it does not fully exploit the identifying information in the parametric model. In light of these points, Supplemental Appendix LABEL:app_extension_cond proposes an alternative method-of-L-moment estimator for conditional models. We propose to estimate (22) by directly plugging into the representation a nonparametric conditional quantile estimator. Following Ai and Chen (2003), we then optimally optimally exploit the conditional L-moment restrictions by weighting these using weighting functionals . In the Supplemental Appendix, we consider the case where we rely on the quantile series regression estimator of Belloni et al. (2019) for preliminary nonparametric estimation, though in principle any nonparametric estimator of conditional quantile functions for which an approximation theory is available could be used in this first step. Examples of such estimators include local polynomial quantile regression (Yu and Jones, 1998; Guerre and Sabbah, 2012) and quantile regression forests (Meinshausen, 2006; Athey et al., 2019). Under regularity conditions, our estimator admits an asymptotic linear representation that can be used as a basis for inference, and for finding the optimal choice of functional . Moreover, by suitably taking , we expect our optimally-weighted estimator to achieve good finite-sample performance, whilst retaining asymptotic efficiency.
7 Concluding remarks
This paper considered the estimation of parametric models using a “generalised” method of L-moments procedure, which extends the approach introduced in Hosking (1990) whereby a -dimensional parametric model for a distribution function is fit by matching the first L-moments. We have shown that, by appropriately choosing the number of L-moments and under an appropriate weighting scheme, we are able to construct an estimator that is able to outperform maximum likelihood estimation in small samples from popular distributions, and yet does not suffer from efficiency losses in larger samples. We have developed tools to automatically select the number of L-moments used in estimation, and have shown the usefulness of such approach in Monte Carlo simulations. We have also extended our L-moment approach to the estimation of conditional models, and to the “residual analysis” of semiparametric models. We then applied the latter to study expenditure patterns in a ridesharing platform in São Paulo, Brazil.
The extension of the generalised L-moment approach to other semi- and nonparametric settings appears to be an interesting venue of future research. The L-moment approach appears especially well-suited to problems where semi- and nonparametric maximum likelihood estimation is computationally complicated. In followup work, Alvarez and Orestes (2023) propose using the generalised method-of-L-moment approach to estimate nonparametric quantile mixture models, while Alvarez and Biderman (2024) introduce an efficient generalised L-moment estimator for the semiparametric models of treatment effects of Athey et al. (2023). The study of such extensions in more generality is a topic for future research.
Acknowledgements
This paper is based on the first three chapters of Alvarez’s doctoral thesis at the University of São Paulo. We thank Cristine Pinto, Marcelo Fernandes, Ricardo Masini, Silvia Ferrari and Victor Orestes for their useful comments and suggestions. We are also thankful to Ciro Biderman for sharing his dataset with us. All the remaining errors are ours. Luis Alvarez gratefully acknowledges financial support from Capes grant 88887.353415/2019-00 and Cnpq grant 141881/2020-8. Chang Chiann and Pedro Morettin gratefully acknowledge financial support from Fapesp grant 2018/04654-9.
References
- Abadie et al. (2023) Abadie, A., J. Gu, and S. Shen (2023). Instrumental variable estimation with first-stage heterogeneity. Journal of Econometrics.
- Ahidar-Coutrix and Berthet (2016) Ahidar-Coutrix, A. and P. Berthet (2016). Convergence of multivariate quantile surfaces. arXiv:1607.02604.
- Ai and Chen (2003) Ai, C. and X. Chen (2003). Efficient estimation of models with conditional moment restrictions containing unknown functions. Econometrica 71(6), 1795–1843.
- Alvarez and Biderman (2024) Alvarez, L. and C. Biderman (2024). The learning effects of subsidies to bundled goods: a semiparametric approach.
- Alvarez and Orestes (2023) Alvarez, L. and V. Orestes (2023). Quantile mixture models: Estimation and inference. Technical report.
- Anderson and Hsiao (1982) Anderson, T. and C. Hsiao (1982). Formulation and estimation of dynamic models using panel data. Journal of Econometrics 18(1), 47–82.
- Arellano and Bond (1991) Arellano, M. and S. Bond (1991, 04). Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations. The Review of Economic Studies 58(2), 277–297.
- Athey et al. (2023) Athey, S., P. J. Bickel, A. Chen, G. W. Imbens, and M. Pollmann (2023, 07). Semi-parametric estimation of treatment effects in randomised experiments. Journal of the Royal Statistical Society Series B: Statistical Methodology 85(5), 1615–1638.
- Athey et al. (2019) Athey, S., J. Tibshirani, and S. Wager (2019). Generalized random forests. The Annals of Statistics 47(2), 1148 – 1178.
- Barrio et al. (2005) Barrio, E. D., E. Giné, and F. Utzet (2005). Asymptotics for L2 functionals of the empirical quantile process, with applications to tests of fit based on weighted Wasserstein distances. Bernoulli 11(1), 131 – 189.
- Belloni et al. (2012) Belloni, A., D. Chen, V. Chernozhukov, and C. Hansen (2012). Sparse models and methods for optimal instruments with an application to eminent domain. Econometrica 80(6), 2369–2429.
- Belloni et al. (2019) Belloni, A., V. Chernozhukov, D. Chetverikov, and I. Fernández-Val (2019). Conditional quantile processes based on series or many regressors. Journal of Econometrics 213(1), 4 – 29. Annals: In Honor of Roger Koenker.
- Biderman (2018) Biderman, C. (2018, October). E-hailing and last mile connectivity in sao paulo. American Economic Association Registry for Randomized Controlled Trials. AEARCTR-0003518.
- Billingsley (2012) Billingsley, P. (2012). Probability and Measure. Wiley.
- Boulange et al. (2021) Boulange, J., N. Hanasaki, D. Yamazaki, and Y. Pokhrel (2021). Role of dams in reducing global flood exposure under climate change. Nature communications 12(1), 1–7.
- Broniatowski and Decurninge (2016) Broniatowski, M. and A. Decurninge (2016). Estimation for models defined by conditions on their L-moments. IEEE Transactions on Information Theory 62(9), 5181–5198.
- Carrasco and Florens (2014) Carrasco, M. and J.-P. Florens (2014). On the asymptotic efficiency of gmm. Econometric Theory 30(2), 372–406.
- Castellacci (2012) Castellacci, G. (2012). A formula for the quantiles of mixtures of distributions with disjoint supports. Available at SSRN 2055022.
- Chernozhukov et al. (2018) Chernozhukov, V., D. Chetverikov, M. Demirer, E. Duflo, C. Hansen, W. Newey, and J. Robins (2018, 01). Double/debiased machine learning for treatment and structural parameters. The Econometrics Journal 21(1), C1–C68.
- Chernozhukov et al. (2022) Chernozhukov, V., J. C. Escanciano, H. Ichimura, W. K. Newey, and J. M. Robins (2022). Locally robust semiparametric estimation. Econometrica 90(4), 1501–1535.
- Chernozhukov and Fernández-Val (2011) Chernozhukov, V. and I. Fernández-Val (2011). Inference for extremal conditional quantile models, with an application to market and birthweight risks. The Review of Economic Studies 78(2), 559–589.
- Crump et al. (2009) Crump, R. K., V. J. Hotz, G. W. Imbens, and O. A. Mitnik (2009, 01). Dealing with limited overlap in estimation of average treatment effects. Biometrika 96(1), 187–199.
- Csorgo and Revesz (1978) Csorgo, M. and P. Revesz (1978, 07). Strong approximations of the quantile process. Annals of Statistics 6(4), 882–894.
- Das (2021) Das, S. (2021). Extreme rainfall estimation at ungauged locations: information that needs to be included in low-lying monsoon climate regions like bangladesh. Journal of Hydrology 601, 126616.
- Dey et al. (2018) Dey, S., J. Mazucheli, and S. Nadarajah (2018, may). Kumaraswamy distribution: different methods of estimation. Computational and Applied Mathematics 37(2), 2094–2111.
- Donald et al. (2003) Donald, S. G., G. W. Imbens, and W. K. Newey (2003). Empirical likelihood estimation and consistent tests with conditional moment restrictions. Journal of Econometrics 117(1), 55–93.
- Donald et al. (2009) Donald, S. G., G. W. Imbens, and W. K. Newey (2009). Choosing instrumental variables in conditional moment restriction models. Journal of Econometrics 152(1), 28–36.
- Donald and Newey (2001) Donald, S. G. and W. K. Newey (2001). Choosing the number of instruments. Econometrica 69(5), 1161–1191.
- Ferrari and Yang (2010) Ferrari, D. and Y. Yang (2010, 04). Maximum l q -likelihood estimation. Annals of Statistics 38(2), 753–783.
- Foss et al. (2011) Foss, S., D. Korshunov, S. Zachary, et al. (2011). An introduction to heavy-tailed and subexponential distributions, Volume 6. Springer.
- Fotopoulos and Ahn (1994) Fotopoulos, S. and S. Ahn (1994). Strong approximation of the quantile processes and its applications under strong mixing properties. Journal of Multivariate Analysis 51(1), 17–45.
- Freyberger and Rai (2018) Freyberger, J. and Y. Rai (2018). Uniform confidence bands: Characterization and optimality. Journal of Econometrics 204(1), 119–130.
- Götze et al. (2019) Götze, F., A. Naumov, V. Spokoiny, and V. Ulyanov (2019). Large ball probabilities, Gaussian comparison and anti-concentration. Bernoulli 25(4A), 2538 – 2563.
- Gourieroux and Jasiak (2008) Gourieroux, C. and J. Jasiak (2008). Dynamic quantile models. Journal of Econometrics 147(1), 198–205.
- Guerre and Sabbah (2012) Guerre, E. and C. Sabbah (2012). Uniform bias study and bahadur representation for local polynomial estimators of the conditional quantile function. Econometric Theory 28(1), 87–129.
- Gupta and Kundu (2001) Gupta, R. D. and D. Kundu (2001). Generalized exponential distribution: Different method of estimations. Journal of Statistical Computation and Simulation 69(4), 315–337.
- Hahn et al. (2002) Hahn, J., G. Kuersteiner, and W. Newey (2002). Higher order properties of bootstrap and jackknife bias corrected maximum likelihood estimators. Unpublished manuscript.
- Han and Phillips (2006) Han, C. and P. C. B. Phillips (2006). Gmm with many moment conditions. Econometrica 74(1), 147–192.
- Hansen (1982) Hansen, L. P. (1982). Large sample properties of generalized method of moments estimators. Econometrica 50(4), 1029–1054.
- Hosking (1986) Hosking, J. R. (1986). The theory of probability weighted moments. IBM Research Division, TJ Watson Research Center New York, USA.
- Hosking (2007) Hosking, J. R. (2007). Some theory and practical uses of trimmed L-moments. Journal of Statistical Planning and Inference 137(9), 3024–3039.
- Hosking (1990) Hosking, J. R. M. (1990, sep). L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. Journal of the Royal Statistical Society: Series B (Methodological) 52(1), 105–124.
- Hosking and Wallis (1987) Hosking, J. R. M. and J. R. Wallis (1987). Parameter and quantile estimation for the generalized pareto distribution. Technometrics 29(3), 339–349.
- Hosking et al. (1985) Hosking, J. R. M., J. R. Wallis, and E. F. Wood (1985). Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 27(3), 251–261.
- Ichimura and Newey (2022) Ichimura, H. and W. K. Newey (2022). The influence function of semiparametric estimators. Quantitative Economics 13(1), 29–61.
- Kennedy (2023) Kennedy, E. H. (2023). Semiparametric doubly robust targeted double machine learning: a review.
- Kerstens et al. (2011) Kerstens, K., A. Mounir, and I. V. De Woestyne (2011). Non-parametric frontier estimates of mutual fund performance using C- and L-moments: Some specification tests. Journal of Banking and Finance 35(5), 1190–1201.
- Koenker and Machado (1999) Koenker, R. and J. A. Machado (1999). Gmm inference when the number of moment conditions is large. Journal of Econometrics 93(2), 327–344.
- Komunjer and Vuong (2010) Komunjer, I. and Q. Vuong (2010). Semiparametric efficiency bound in time-series models for conditional quantiles. Econometric Theory 26(2), 383–405.
- Kreyszig (1989) Kreyszig, E. (1989). Introductory Functional Analysis with Applications. Wiley.
- Landwehr et al. (1979) Landwehr, J. M., N. C. Matalas, and J. R. Wallis (1979). Probability weighted moments compared with some traditional techniques in estimating gumbel parameters and quantiles. Water Resources Research 15(5), 1055–1064.
- Li et al. (2021) Li, C., F. Zwiers, X. Zhang, G. Li, Y. Sun, and M. Wehner (2021). Changes in annual extremes of daily temperature and precipitation in cmip6 models. Journal of Climate 34(9), 3441–3460.
- Luo et al. (2015) Luo, Y. et al. (2015). High-dimensional econometrics and model selection. Ph. D. thesis, Massachusetts Institute of Technology.
- Mason (1984) Mason, D. M. (1984, 02). Weak convergence of the weighted empirical quantile process in . Annals of Probability 12(1), 243–255.
- Meinshausen (2006) Meinshausen, N. (2006). Quantile regression forests. Journal of Machine Learning Research 7(35), 983–999.
- Newey (1990) Newey, W. K. (1990). Semiparametric efficiency bounds. Journal of Applied Econometrics 5(2), 99–135.
- Newey and McFadden (1994) Newey, W. K. and D. McFadden (1994). Chapter 36 large sample estimation and hypothesis testing. In Handbook of Econometrics, Volume 4, pp. 2111 – 2245. Elsevier.
- Newey and Smith (2004) Newey, W. K. and R. J. Smith (2004). Higher order properties of gmm and generalized empirical likelihood estimators. Econometrica 72(1), 219–255.
- Newey and West (1987) Newey, W. K. and K. D. West (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55(3), 703–708.
- Okui (2009) Okui, R. (2009). The optimal choice of moments in dynamic panel data models. Journal of Econometrics 151(1), 1–16.
- Parzen (1960) Parzen, E. (1960). Modern probability theory and its applications. Wiley.
- Pfanzagl and Wefelmeyer (1978) Pfanzagl, J. and W. Wefelmeyer (1978). A third-order optimum property of the maximum likelihood estimator. Journal of Multivariate Analysis 8(1), 1–29.
- Portnoy (1991) Portnoy, S. (1991). Asymptotic behavior of regression quantiles in non-stationary, dependent cases. Journal of Multivariate Analysis 38(1), 100 – 113.
- Rothenberg (1971) Rothenberg, T. J. (1971). Identification in parametric models. Econometrica 39(3), 577–91.
- Sankarasubramanian and Srinivasan (1999) Sankarasubramanian, A. and K. Srinivasan (1999). Investigation and comparison of sampling properties of L-moments and conventional moments. Journal of Hydrology 218(1-2), 13–34.
- Šimková (2017) Šimková, T. (2017). Statistical inference based on L-moments. Statistika 97(1), 44–58.
- Vaart (1998) Vaart, A. W. v. d. (1998). Asymptotic Statistics. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press.
- Vaart and Wellner (1996) Vaart, A. W. V. d. and J. A. Wellner (1996). Weak convergence and empirical processes. Springer.
- Wang and Hutson (2013) Wang, D. and A. D. Hutson (2013). Joint confidence region estimation of L-moment ratios with an extension to right censored data. Journal of Applied Statistics 40(2), 368–379.
- Wang (1997) Wang, Q. J. (1997). LH moments for statistical analysis of extreme events. Water Resources Research 33(12), 2841–2848.
- Wooldridge (2010) Wooldridge, J. (2010). Econometric analysis of cross section and panel data. Cambridge, Mass: MIT Press.
- Yang et al. (2021) Yang, J., Z. Bian, J. Liu, B. Jiang, W. Lu, X. Gao, and H. Song (2021). No-reference quality assessment for screen content images using visual edge model and adaboosting neural network. IEEE Transactions on Image Processing 30, 6801–6814.
- Yoshihara (1995) Yoshihara, K. (1995). The bahadur representation of sample quantiles for sequences of strongly mixing random variables. Statistics & Probability Letters 24(4), 299 – 304.
- Yu (1996) Yu, H. (1996). A note on strong approximation for quantile processes of strong mixing sequences. Statistics & Probability Letters 30(1), 1 – 7.
- Yu and Jones (1998) Yu, K. and M. C. Jones (1998). Local linear quantile regression. Journal of the American Statistical Association 93(441), 228–237.
See pages - of supplemental.pdf