Incentive Design for Eco-driving in Urban Transportation Networks

We consider an urban transportation network denoted by a graph $\mathcal{N}=(\mathcal{I},\mathcal{L})$, where $\mathcal{I}$ denotes the set of intersections and $\mathcal{L}\subseteq\mathcal{I}\times\mathcal{I}$ denotes the set of links/roads. We aim to design an eco-planner digital platform $\mathsf{P}$ that plans and recommends eco-driving strategies to its users in the network $\mathcal{N}$ before they embark on their trips. The eco-planner $\mathsf{P}$ also commits to providing certain incentives if the users comply with the eco-driving recommendations to reduce their emissions at the expense of increased travel time. The users who subscribe to $\mathsf{P}$ are denoted by a set $U=\{1,\dots,n\}$, where $n$ denotes the number of users.

Before starting her commute, each user $i$, $i\in U$, asks $\mathsf{P}$ to plan the journey by providing her private information, which includes the following:

• •

  Origin-Destination pair $(o_{i},d_{i})\in\mathcal{L}\times\mathcal{L}$, which corresponds to the start and end points of $i$’s journey

• •

  Vehicle type $v_{i}\in V$, where $V=\{v_{1},\dots,v_{l}\}$ is the set of finite number of vehicle types

• •

  Emissions vs. travel time trade-off parameter $\vartheta_{i}\in[0,1]$.

For instance, vehicle type may correspond to not only its classification (sedan, SUV, etc.) but also its engine and fuel types. This information is needed so that $\mathsf{P}$ can predict the emissions of user $i$ on her commute between $(o_{i},d_{i})$ on different routes with different traffic conditions. Emissions vs. travel time trade-off parameter $\vartheta_{i}$ is needed to assess the urgency of user $i$ for her trip, and whether she will accept a certain amount of incentive to reduce her emissions by eco-driving by compromising slightly on her travel time. In this paper, we assume that each user $i$ provides her information $(o_{i},d_{i},v_{i},\vartheta_{i})$ truthfully.

After obtaining the private information $(o_{i},d_{i},v_{i},\vartheta_{i})_{i\in U}$, the eco-planner $\mathsf{P}$ predicts the best eco-driving strategies in terms of a route choice and driving style for each user depending on the predicted traffic conditions for their trips. Then, $\mathsf{P}$ recommends those strategies and persuades the users to follow those strategies by offering incentives $\gamma_{1},\dots,\gamma_{n}$ subject to $\mathsf{P}$’s budget constraint $\sum_{i=1}^{n}\gamma_{i}\leq B$, where $B\in\mathbb{R}_{>0}$ is the total budget of $\mathsf{P}$. The users complete their trips by either complying or not complying with the eco-driving recommendations, and their commutes result in a certain outcome in terms of their individual emissions. Finally, $\mathsf{P}$ transfers the incentives to the users based on their compliance with the recommendations and to compensate for their increased travel times due to their eco-driving and reducing emissions. The incentive mechanism is summarized in Fig. 1.

As stated earlier, we assume that users are truthful and do not strategically manipulate their information. This avoids the issue of adverse selection. Incorporating incentive compatibility constraints will be a topic of our future work. Secondly, to address the issue of moral hazard, whereby the behavior and outcomes of users are not observable, we assume $\mathsf{P}$ employs vehicle telematics [8, 9] to measure the driving style and emissions of each user during her commute. Finally, we assume traffic conditions and network structures where eco-driving results in lower emissions and longer travel times. For example, choosing a longer route with fewer intersections would yield lower emissions as compared to choosing a shorter route through an urban area with plenty of intersections and stop signs. The former route may result in longer travel times, but because of smooth driving, it would result in lower emissions than the latter route. It is important to remark that there could be other scenarios, e.g., eco-driving near signalized intersections [10], where eco-driving improves both travel times and emissions. However, in these scenarios, user’s and eco-planner’s objectives are aligned, and the issue becomes one of information design rather than incentive design.

Since eco-driving strategies can increase travel time by requiring drivers to take longer routes or drive at slower speeds, we assume that drivers, being cost minimizers, optimize their driving behaviors based on the utilities they place on reducing their emissions/fuel consumption versus reducing their travel times. Let $x_{i}=[\begin{array}[]{cc}x_{i}^{t}&x_{i}^{e}\end{array}]^{\top}\in X_{i}\subset\mathbb{R}_{>0}^{2}$ denote the outcome of user $i$’s commute between the origin $o_{i}$ and the destination $d_{i}$, where $x_{i}^{e}$ denotes her emissions and $x_{i}^{t}$ denotes her travel time. Here, $X_{i}$ is assumed to be a convex set denoting all feasible emission-travel time pairs achievable via different driving styles and route choices for $(o_{i},d_{i})$ given $i$’s vehicle type $v_{i}$ and traffic conditions in the network $\mathcal{N}$. In other words, each point $x_{i}\in X_{i}$ denotes an emissions-travel time outcome corresponding to a certain route and driving style.

Each user $i$ chooses her route and driving style that minimizes her cost function

where $\vartheta_{i}\in[0,1]$ is user $i$’s emissions vs. travel time trade-off parameter. In other words, $i$ solves the following convex optimization problem:

where $\theta_{i}=[\begin{array}[]{cc}1-\vartheta_{i}&\vartheta_{i}\end{array}]^{\top}$ is $i$’s preference parameter. Let

be the nominal outcome of user $i$.

Let $R_{i}$ denote the set of routes for the origin-destination pair $(o_{i},d_{i})$, where $r_{i,j}\in R_{i}$ is the $j$-th route containing a path in $\mathcal{N}$ starting from $o_{i}$ and ending at $d_{i}$. The eco-planner invokes a traffic simulator $\mathsf{S}$ to compute the feasible sets of each user. In other words, the simulator $\mathsf{S}$ takes the network $\mathcal{N}$, origin-destination pair $(o_{i},d_{i})$, and vehicle type $v_{i}$ as inputs, and outputs the feasible set $X_{i}\subset\mathbb{R}_{>0}^{2}$.

The first step of the simulator involves computation of $p$ shortest routes $R_{i}=(r_{i,1},\dots,r_{i,p})$ in $\mathcal{N}$ between $(o_{i},d_{i})$. After that, for every $j\in[p]$, $\mathsf{S}$ computes a set of $m\in\mathbb{N}$ points $\hat{X}_{ij}=\{x_{i,j}^{1},\dots,x_{i,j}^{m}\}$, which results from simulating different eco-driving as well as normal driving styles on route $r_{i,j}$ under different traffic conditions. Finally, $\mathsf{S}$ outputs

where $\mathrm{conv}(\cdot)$ denotes the convex hull. Notice that computing feasible sets as in (3) renders (1) to be a linear program.

Before starting their trips, users interact with the eco-planner by providing their information (see Fig. 1). The eco-planner then proposes incentives $\gamma_{1},\dots,\gamma_{n}$ to the users conditioned on their following corresponding eco-driving strategies to reduce emissions. Here, $\gamma_{i}\in\mathbb{R}_{\geq 0}$ denotes the incentive user $i$ receives from the eco-planner $\mathsf{P}$ at the end of her trip between $(o_{i},d_{i})$ if she followed the recommended route and eco-driving strategies to achieve the recommended outcome $x_{i}^{\text{rec}}\in X_{i}$.

We remark that the feasible sets obtained from the simulator are only approximations of the true feasible sets of the users, which can be refined by simulating more number $m$ of traffic scenarios and driving styles. However, using approximated feasible sets does not significantly impact the incentive mechanism. Depending on the quality of the approximation, the eco-planner $\mathsf{P}$ can relax the terms of the contract by transferring the incentive to user $i$ if her actual outcome $x_{i}$ at the end of the trip turned out to be inside a ball of certain radius around the recommended outcome $x_{i}^{\text{rec}}$.

To elucidate, the eco-planner $\mathsf{P}$ computes an approximated feasible set $\hat{X}_{i}\subseteq X_{i}$ from the simulator $\mathsf{S}$, $\hat{X}_{i}$ is a convex polytope. The inclusion of $\hat{X}_{i}$ inside $X_{i}$ is because $X_{i}$ is convex and no simulated point can be outside of $X_{i}$. In the case where $\mathsf{S}$ is able to simulate the boundary points of $X_{i}$, $\hat{X}_{i}$ will be a convex polytope inscribed inside $X_{i}$. Nevertheless, the eco-planner $\mathsf{P}$ will compute the nominal solution $\hat{x}_{i}^{\text{nom}}\in\hat{X}_{i}$ to (2), which will be a projection of the true $x_{i}^{\text{nom}}\in X_{i}$ onto $\hat{X}_{i}$. Putting computational issues aside, if the simulator $\mathsf{S}$ simulates a very large number of cases $m$, the approximation $\hat{X}_{i}$ can be arbitrarily improved. Keeping this in mind, $\mathsf{P}$ transfers the incentive if the actual outcome $x_{i}\in X_{i}$ is with an $\varepsilon$-Euclidean distance from the recommended outcome $x_{i}^{\text{rec}}\in\hat{X}_{i}$.

It is important to note that the nominal solution $x_{i}^{\text{nom}}$ of user $i$ lies at a certain part of the boundary of her feasible set $X_{i}$. To explain this fact, we define the following notions. We say $x_{i}=[\begin{array}[]{cc}x_{i}^{t}&x_{i}^{e}\end{array}]^{\top}\in X_{i}$ pareto dominates $\tilde{x}_{i}=[\begin{array}[]{cc}\tilde{x}_{i}^{t}&\tilde{x}_{i}^{e}\end{array}]^{\top}\in X_{i}$ if either (i) $x_{i}^{t}\leq\tilde{x}_{i}^{t}$ and $x_{i}^{e}<\tilde{x}_{i}^{e}$ OR (ii) $x_{i}^{t}<\tilde{x}_{i}^{t}$ and $x_{i}^{e}\leq\tilde{x}_{i}^{e}$. Moreover, $x_{i}$ is said to be pareto optimal if there does not exist $\tilde{x}_{i}\in X_{i}$ that pareto dominates $x_{i}$. Then, the pareto front of the feasible $X_{i}$ is defined as

which will be a subset of $X_{i}$’s boundary.

In light of the above, we have $x_{i}^{\text{nom}}\in\text{PF}(X_{i})$, where $x_{i}^{\text{nom}}$ is the solution of the convex problem (2). To prove this claim, assume $x_{i}^{\text{nom}}\notin\text{PF}(X_{i})$. Then, $x_{i}^{\text{nom}}$ is not pareto optimal and there exists $v\in\mathbb{R}_{\geq 0}^{2}$, $v\neq 0$, such that $x_{i}^{\text{nom}}-v$ pareto dominates $x_{i}^{\text{nom}}$ and

which is a contradiction becausue $x_{i}^{\text{nom}}$ being the solution of (2) is the minimizer of $c_{i}(\cdot)$.

Some might argue that reporting the emissions vs. travel time trade-off parameter, $\vartheta_{i}$, can be challenging for users in reality. Aside from its vague and technical interpretation, it is possible that users may not know the exact value of their parameters, let alone report them truthfully. Instead, the eco-planner may ask the user to report their preferred (i.e., nominal) travel time $x_{i}^{t,\text{nom}}\in X_{i}$ between $o_{i}$ and $d_{i}$. Notice that this report has to correspond to achievable travel time on $(o_{i},d_{i})$ at the time of report. Since we know $x_{i}^{\text{nom}}\in\text{PF}(X_{i})$, we can find the corresponding emissions $x_{i}^{e,\text{nom}}$ that $i$ would incur for their nominal route selection and driving style. Then, the question is how to estimate $\theta_{i}=[\begin{array}[]{cc}\vartheta_{i}&1-\vartheta_{i}\end{array}]^{\top}$ given that $x_{i}^{\text{nom}}$ is the minimizer of (1)?

A simple algorithm to estimate $\theta_{i}$ is as follows. Sample $\vartheta_{i}\in[0,1]$ and obtain $0=\vartheta_{i}^{1}<\vartheta_{i}^{2}<\dots<\vartheta_{i}^{s}=1$ for some sufficiently large $s\in\mathbb{N}$. For every $\vartheta_{i}^{j}$, solve (2) and obtain the solution $x_{i}^{\text{PF}_{j}}\in\text{PF}(X_{i})$. Then,

and

One can refine this solution arbitrarily by subsequently sampling again around $x_{i}^{\text{PF}_{s^{*}}}$, where the idea is to coarsely sample initially and then keep on refining the samples around the closest solutions in the next iteration.

When users report their preferred travel times instead of their emissions vs. travel time trade-off parameters, the steps involved in the incentive mechanism can be modified accordingly and the linear program (7) is written as

where

with $\hat{\theta}^{\top}=[\begin{array}[]{ccc}\hat{\theta}_{1}&\dots&\hat{\theta}_{n}\end{array}]$. $\mathsf{P}$ then proposes incentives $\gamma_{1},\dots,\gamma_{n}$ to the users, where

The incentives are conditioned on the recommended emission-travel time outcomes $x_{1}^{\text{rec}},\dots,x_{n}^{\text{rec}}$, respectively, which are achieved by complying with the recommended routes and eco-driving strategies

We set up a controlled experiment with a simple road network using the Simulation of Urban MObility (SUMO) [11]. The road network consists of two routes for one origin-destination pair: the first route through the urban area is shorter but includes two stop signs, while the second route using a boulevard/highway, although longer, is uninterrupted by stop signs (Fig. 2). The speed limit for both routes is set to be the same. The first route, with two stop signs and one static traffic signal, is shorter and takes shorter travel time, but it emits larger amounts of carbon emissions because of stop-and-go traffic behavior. The second route is longer and may take longer travel time, but it is more eco-friendly because of a smoother traffic.

Our experiment design is structured to analyze the trade-offs between travel time and carbon emissions, directly informed by the route choice for a given OD pair. We computationally generated free-flow traffic conditions for both routes, ensuring an unbiased assessment of their inherent characteristics. All vehicles follow the Intelligent Driver Model (IDM), which is a time-continuous car-following model proposed by [12]. The emission model used in the simulation is based on the Handbook Emission Factors for Road Transport (HBEFA). Route 1, while shorter, was observed to produce higher CO emissions because of the stops imposed by the stop signs and a traffic signal. In contrast, Route 2, despite its longer distance, resulted in lower emissions by benefiting from a continuous driving flow without interruptions.

The collected data points, representative of the distinct travel times and emissions outcomes for each route, helped construct a convex hull that represents the feasible region of outcomes (Fig. 3). This convex hull is instrumental in visualizing the potential impact of different driving behaviors and route selections on travel time and carbon monoxide emissions. For each type, the nominal (circle) and recommended (diamond) outcome points are distinctly marked, providing insight into the specific eco-driving recommendations by the incentive mechanism. This visual representation underscores the emission-saving potential of Route 2 despite its longer travel times, aligning with the eco-driving principles encouraged by the study’s incentive mechanism. Our approach allows us to evaluate the effectiveness of the proposed incentive mechanism in guiding drivers towards choices that align better with eco-friendly driving principles.

As described in Section II-D, we consider two incentive mechanisms: baseline and optimal (proposed). In the baseline, we propose equal incentive $\gamma_{i}^{\text{BL}}=B/n$ to all the users. Let $x_{i}^{\text{rec},r2}\in X_{i}$ be a recommendation to users that corresponds to the least travel time on feasible points corresponding to route 2. Then, user $i$ complies with this recommendation under baseline incentive if and only if

Similarly, given budget $B$, the optimal incentive mechanism yields $\gamma_{1},\dots,\gamma_{n}$, where the user $i$ complies with the recommendation $x_{i}^{\text{rec},r2}$ if and only if

In Fig. 4a, we illustrate the correlation between budget allocation and driver compliance with eco-driving recommendations. It compares the result of the linear program in (9) and baseline incentive across different budget levels. It is apparent that under baseline incentives, compliance escalates swiftly with a slight increase in budget, plateauing at a compliance ratio of 0.5. Beyond this point, the compliance rate remains constant, indicating that additional incentives under this model do not further motivate drivers. In contrast, under optimal incentives, we observe a gradual yet consistent increase in compliance as the budget grows, eventually surpassing the baseline once half of the drivers are compliant. This trend suggests that the optimal incentive structure is more effective at progressively encouraging a larger proportion of drivers to adopt eco-driving practices, particularly in scenarios where the budget is ample enough to support such incentivization.

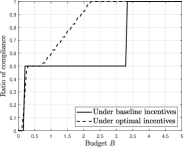
Fig. 4b illustrates the relationship between the budget allocated for incentives and the total CO emissions and average travel time from vehicles within the simulation. Both are normalized for comparative purposes. The graph compares the efficacy of baseline incentives to that of the proposed optimal incentives. As shown in Fig. 4b, both incentive schemes initially cause a sharp decrease in emissions as the budget is increased, demonstrating that even minimal financial motivation can significantly alter driving behaviors. However, the baseline incentives exhibit a more extended plateau compared to the optimal incentives, indicating a point where additional funds cease to yield proportional reductions in emissions. Conversely, the optimal incentives lead to a more consistent and prolonged decline in emissions with increasing budgets, highlighting their effectiveness in continuously promoting eco-friendly driving practices. Meanwhile, Fig. 4b reveals an increase in average travel time concurrent with efforts to reduce carbon emissions, emphasizing the importance of a balanced strategy that judiciously weighs budget spending against both environmental impact and time-savings.