Improving Knowledge Graph Representation Learning by Structure Contextual Pre-training
Abstract.
Representation learning models for Knowledge Graphs (KG) have proven to be effective in encoding structural information and performing reasoning over KGs. In this paper, we propose a novel pre-training-then-fine-tuning framework for knowledge graph representation learning, in which a KG model is firstly pre-trained with triple classification task, followed by discriminative fine-tuning on specific downstream tasks such as entity type prediction and entity alignment. Drawing on the general ideas of learning deep contextualized word representations in typical pre-trained language models, we propose SCoP to learn pre-trained KG representations with structural and contextual triples of the target triple encoded. Experimental results demonstrate that fine-tuning SCoP not only outperforms results of baselines on a portfolio of downstream tasks but also avoids tedious task-specific model design and parameter training.
1. Introduction
Knowledge Graphs (KGs) can be regarded as directed labeled graphs in which facts are represented as triples in the form of (head entity, relation, tail entity), abbreviated as (h,r,t). In recent years, KGs gain rapid development on both construction and applications, proven to be useful in artificial intelligence tasks such as semantic search (Berant and Liang, 2014), information extraction (Daiber et al., 2013), and question answering (Diefenbach et al., 2018).
Graph structure in KGs contains a lot of valuable information (Cao et al., 2015; Hamilton et al., 2017), thus representation learning methods, embedding entities and relations into continuous vector spaces, are proposed to extract these structural features (Bordes et al., 2013; Wang et al., 2014; Lin et al., 2015).
Various representation learning methods are specially proposed for different tasks, such as entity type prediction (Yaghoobzadeh and Schütze, 2015), entity alignment (Zhu et al., 2017) and link prediction (Kazemi and Poole, 2018). In our opinion, though tasks are different, KGs might be the same. Thus a general way to encode KGs is necessary. And the challenge is to make structural and contextual information into consideration, since they varies in different tasks.
Inspired by Pre-trained Language Models (PLM) such as BERT (Devlin et al., 2019), which learn deep contextual representations for words and has achieved significant improvement in a variety of NLP tasks, we propose a novel knowledge graph representation learning method by Structure Contextual Pre-training (SCoP) model, to extract deep structural features and context for different knowledge graph tasks automatically. Similar to PLMs, there are two steps for using SCoP, pre-training and fine-tuning. Pre-training step enables the model to extract various deep structural contextualized information of entities and relations in knowledge graph and fine-tuning step makes the model adapt to specific downstream tasks.
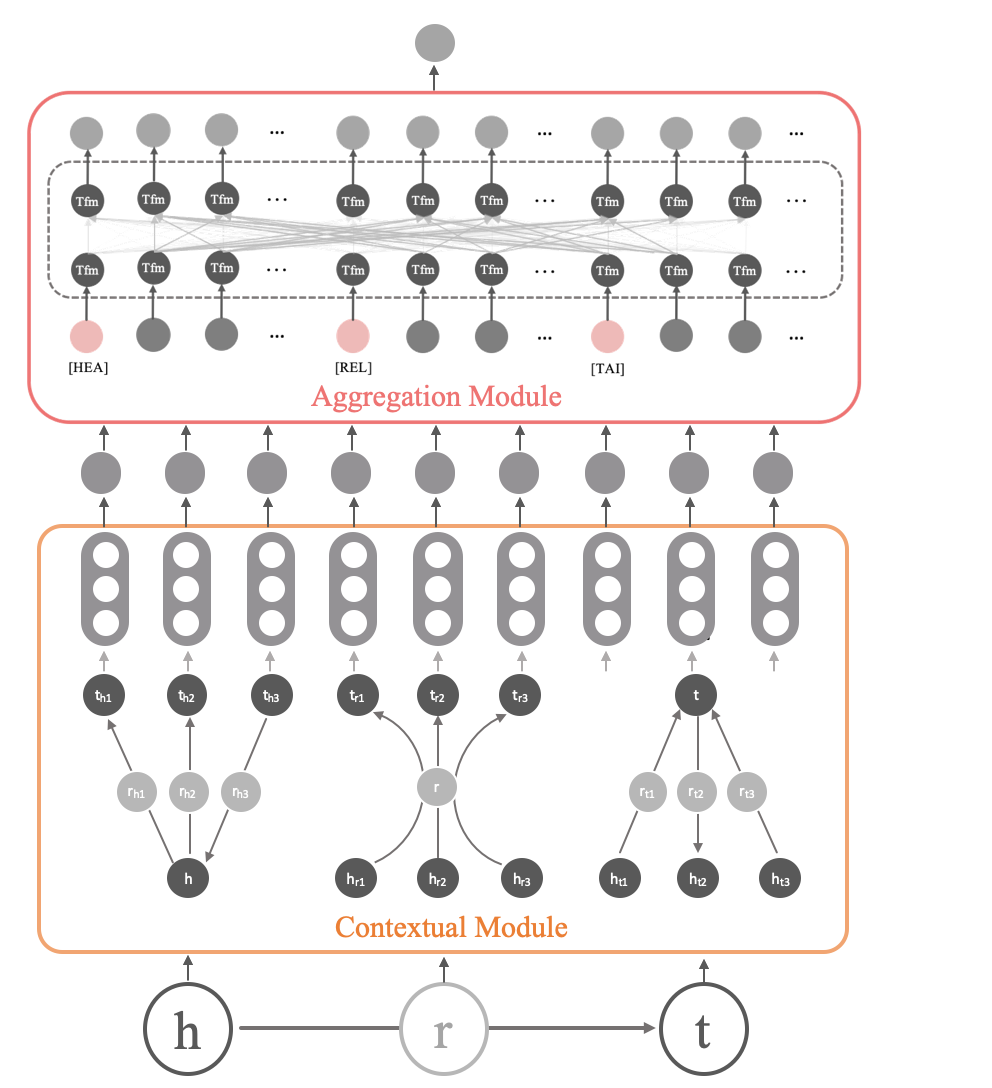
With a target triple as input, SCoP mainly includes two parts, in which contextual module generates representations for and ’s contextual triples, and aggregation module uses Transformer (Vaswani et al., 2017) to learn structural features with all contextual triples and fully interacted and generates a task-specific output vector.
We construct a new KG dataset, WN-all, which contains all the triple from WordNet and is suitable for KG pre-training model. We experimentally prove that SCoP is capable of doing different downstream tasks including entity type prediction, entity alignment and triple classification, and it could achieve better results in an efficient way. What’s more, SCoP exhibits good prediction and classification performance and the importance of structural and contextual information in KG.
2. SCoP
2.1. SCoP overview
Similar to pre-trained language model, SCoP model in this paper includes two steps: pre-training and fine-tuning. The SCoP model is based on structure contextual triples to learn the structural information of knowledge graph.
From the perspective of model structure, SCoP consists two modules that integrate and extract the deep structure information of KG. In this paper, bold characters denote vector representations, for example, is the vector representation of entity .
| Method | Entity Type Prediction | Entity Alignment | ||||||
|---|---|---|---|---|---|---|---|---|
| MRR | Hit@1 | Hit@3 | Hit@10 | MRR | Hit@1 | Hit@3 | Hit@10 | |
| TransE-pr | 0.8499 | 83.11 | 86.35 | 87.75 | 0.8964 | 88.65 | 90.08 | 91.06 |
| TransE-ft | 0.8386 | 81.99 | 85.10 | 86.92 | 0.8943 | 88.63 | 89.76 | 90.89 |
| ComplEx-pr | 0.8396 | 80.30 | 86.77 | 89.15 | 0.8636 | 82.27 | 90.03 | 90.94 |
| ComplEx-ft | 0.7809 | 72.09 | 77.49 | 82.72 | 0.8772 | 84.26 | 89.56 | 90.23 |
| RotatE-pr | 0.8941 | 88.12 | 90.93 | 91.62 | 0.9066 | 89.78 | 91.34 | 92.20 |
| RotatE-ft | 0.8814 | 86.60 | 90.05 | 90.88 | 0.9035 | 89.75 | 90.77 | 91.36 |
| SCoP-pr | 0.9018 | 89.73 | 90.11 | 90.37 | 0.9271 | 92.61 | 92.78 | 92.88 |
| SCoP-ft | 0.9208 | 91.98 | 92.06 | 92.51 | 0.9319 | 93.15 | 93.21 | 93.39 |
2.2. Structure Contextual Triples
Given a KG , , and are the set of entities, relations and triples respectively. And .
Entity contextual triples
For an entity , contextual triples of it are triples containing either as head or tail entity. Specifically, given an entity , the contextual triple set of is
Relation contextual triples
Similarly, triples that contain the same relation are the contextual triples of . Unlike entity contextual triples, relation contextual triples are not directly adjacent. Given a relation , is
2.3. Two Steps: Pre-training and Fine-tuning
At the pre-training step, all parameters of the model are first trained on a general task which is triple classification in this paper, as the existence of a triple is the most widely available information in a knowledge graph.
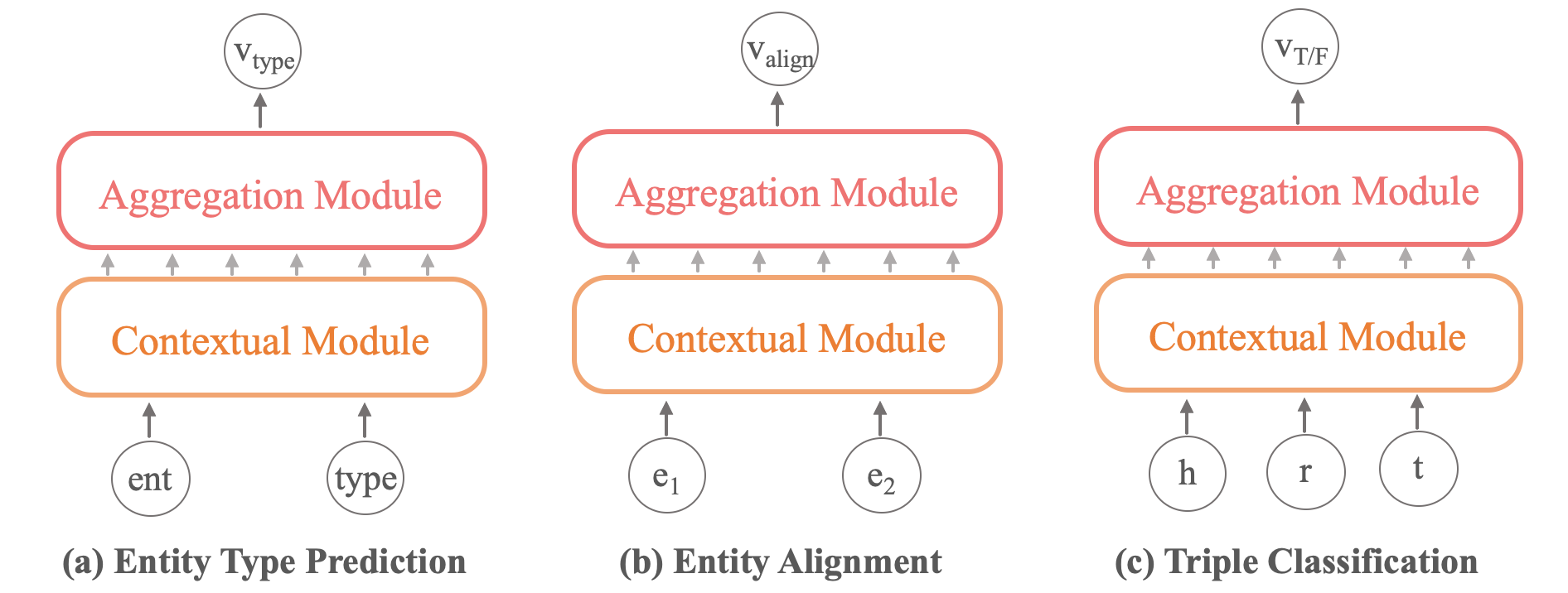
At the fine-tuning step, we generate model variants based on the specific downstream task and the parameters in SCoP are fine-tuned with its dataset, as shown in Figure 2. This process is lightweight and fast to better results.
2.4. Two Modules
Contextual module
Given a target triple , Contextual Module (C-Mod) first finds contextual triples of , and , and then encodes each contextual triple into a triple representation . Thus
where denotes a sequence of and . We implement the triple module based on a single layer feed-forward neural network.
Aggregation module
Aggregation Module (A-Mod) takes contextual triple representation sequences and outputs an aggregation representation , so A-Mod can be expressed as
where are the sequence of contextual triples of represented as follows
and is the -th contextual triples of where is one of . is the number of contextual triples.
We introduce segment vector into the current contextual triple sequences as Bert (Devlin et al., 2019), indicating whether it belongs to head entity , relation or tail entity . Besides, three types of triple token [HEA], [REL] and [TAI] are added in front of each contextual triple of and their representations are denoted as . Consequently, the updated input sequence can be represented as
where is the sequence of updated contextual triple representations . A-Mod encodes the input sequence with multi-layer bidirectional Transformer encoder, referred to the key idea of Bert.
Eventually, based on the three structure representations, , and , the scoring function can be written as
where denotes the concatenation vector , and . and are weights while is a bias vector. is a 2-dimensional real vector with after softmax function. Given the positive triple set and a negative triple set constructed accordingly, we compute a cross-entropy loss with and triple labels:
where is the label of , and is if while if . The negative triple set is simply generated by replacing head entity or tail entity with another random entity or replacing relation with another random relation .
| Dataset | # Ent | # Rel | # Train | # Dev | # Test |
|---|---|---|---|---|---|
| WN-all | 116,377 | 26 | 302,074 | 37,759 | 37,759 |
| Type-Prediction | 87,875 | - | 72,076 | 8,431 | 8,582 |
| Entity-Alignment | 13,205 | - | 17,725 | 1,805 | 1,856 |
3. Experiments
3.1. Datasets
To prove the effective of pre-training knowledge graph, we conduct experiments on the whole knowledge graph WordNet, named WN-all. We also construct two downstream datasets for fine-tuning. Detailed statistics of datasets are shown in Table 2.
3.2. Pre-training SCoP
We pre-train SCoP on WN-all via triple classification task, aiming to judge whether the triple is correct with label . The loss is defined as .
We fix the length of input contextual triple sequence with 256 and the length of each contextual triple of , , is 84. We set the self-attention with 6 layers, 3 heads and the hidden dimension of representation vectors of 192 in Transformer in A-Mod, and learning rate of , training batch size of 32, learning rate warm-up over the first 1,000 steps and a dropout probability of 0.1 on all layers.
3.3. Entity type prediction
Entity type prediction concentrates to complete a pair (entity, entity type) when its type is missing, which aims to verify the capability of our model for inferring missing entity type instances. Under this definition, we extract entity and its type from triples with relation in WN-all as the dataset for this task, shown in Table 2.
To fine-tune on entity type prediction task and its dataset, we input the structure contextual triples sequence of entity type pair and use the output vector of A-Mod to compute the score function and entity type classification loss: , where is the classification weight and is a 2-dimensional real vector. Label is if entity type pair is positive while if negative. The Figure 2 (a) shows the structure of fine-tuning SCoP for entity type prediction task.
We adopt the Mean Reciprocal Rank(MRR) and percentage of triples ranked in top (Hit@) where as evaluation metrics, which are commonly adopted in previous KG works. See Section 4 for details of baseline models.
Experimental results are presented in the left part of Table 1. Compared with the results of fine-tuning stage (even rows with ”-ft” suffix in table), SCoP-ft outperforms other models on all evaluation metrics, especially obtaining 3.8% prediction accuracy improvement on Hit@1 over the prior state of the art. Besides, we observe that SCoP-ft model has better performance than SCoP-pr while on the contrary, the results of other models after fine-tuning decreased. It proves that the structure contextual triples, and the structural information that they represent in essence, can effectively improve the effect of entity type prediction.
3.4. Entity alignment
Entity alignment task aims to find two entities that refer to the same thing in the real world. Similarly, we generate the dataset for entity alignment consisting of two entities with the same meaning from triples with relation , such as (nascent, emergent) and (sleep, slumber). Similar to the fine-tuning progress of entity type prediction, we compute the score function for alignment entity pair and its classification loss in the same way. Figure 2 (b) shows its model structure and the right part of Table 1 shows the results.
The experimental results show that SCoP model still has the greatest advantage in Hit@1 metric, which is 93.15% and surpasses the second result by 3.3%. On the entity type prediction task, the results from pre-training step of SCoP model are not always optimal. For example, RotatE-pr has a better result with Hit@10 metric on entity type prediction task. However, those results of SCoP model outperform all other models at pre-training step on entity alignment task, let alone the overwhelming results after fine-tuning.
3.5. Triple classification and prob-distribution
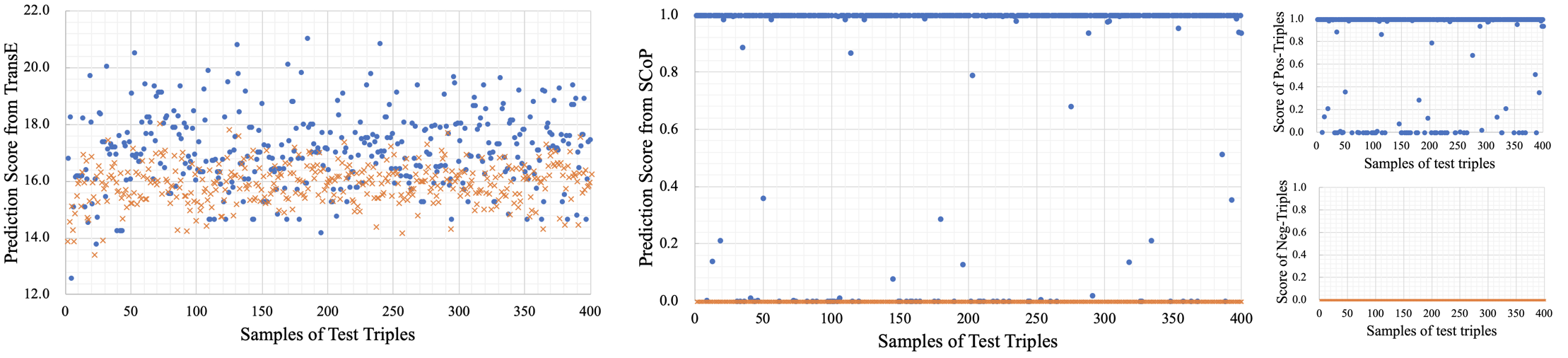
We observed that the data of Hit@1, Hit@3, and Hit@10 in SCoP model are very close, and the interval between them is less than 1% while those of other models have clear gaps. Therefore, we further investigated the distribution of prediction score and the triple classification task, whose aim is to judge whether a given triple () is correct or not, as shown in Figure 2 (c).
From Figure 3, it is not difficult to see that the prediction scores of the positive samples and negative samples are relatively evenly distributed in the whole score space predicted by the baseline model like TransE, and most of the positive examples are in the upper part of the space while the negative in the lower part. The score distribution of ComplE and RotatE resembles TransE, so these similar figures are not repeatedly shown. However, The prediction scores of positive and negative samples in SCoP model are close to their upper and lower boundaries respectively and only a small part of the predicted values are distributed in the middle region. Figure 3 shows that structural information can bring significant gains to triple classification tasks, and it is easier to set the margin to distinguish between positive and negative samples. The experiment shows that, different margins among percent of maximum prediction score, hardly affect the prediction accuracy of SCOP with 92.6% numerically, while that of TransE varies greatly, from 13.6% to 91.1%.
4. Related Work
Knowledge Graph Embedding (KGE)
With the introduction of the embedding vector into Knowledge Graph by TransE model (Bordes et al., 2013), the method of KGE has made great progress. The key idea is to transform entities and relations in triple into continuous vector space. ComplEx (Trouillon et al., 2016) introduces complex embeddings so as to better model asymmetric relations and RotatE (Sun et al., 2019) further infers the composition pattern.
Pre-train Language Models (PLM)
The PLMs have achieved excellent results in many natural language processing (NLP) tasks, such as BERT (Devlin et al., 2019). Later studies have proposed variants of BERT combined with KG, like K-BERT (Liu et al., 2019), KG-BERT (Liang Yao, 2019), ERNIE (Zhang et al., 2019) and KnowBert (Peters et al., 2019), paying attention to the combination of knowledge graph and pre-trained language model. However, these methods aim at adjusting the PLM by injecting knowledge bases or their text representations. Whereas, our SCoP model mainly focuses on encoding knowledge graph instead of texts in sentences, so as to extract deep structural information to apply to various downstream tasks in knowledge graph.
5. Conclusion
In this work, we construct a new dataset WN-all from complete triples in WordNet and introduce SCoP, a pre-training knowledge graph representation learning method that achieves state-of-the-art results on three various knowledge graph downstream tasks on this dataset. SCoP shows good prediction and classification performance, due to its ability to capture the structural information in KG dynamically. In the future, we plan to evaluate SCoP in more scenarios and to fine-tune it in more different ways.
Acknowledgements.
This work is funded by national key research program 2018YFB1402800, and NSFC91846204/U19B2027.References
- (1)
- Berant and Liang (2014) Jonathan Berant and Percy Liang. 2014. Semantic Parsing via Paraphrasing. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, ACL 2014, June 22-27, 2014, Baltimore, MD, USA, Volume 1: Long Papers. The Association for Computer Linguistics, 1415–1425. https://doi.org/10.3115/v1/p14-1133
- Bordes et al. (2013) Antoine Bordes, Nicolas Usunier, Alberto García-Durán, Jason Weston, and Oksana Yakhnenko. 2013. Translating Embeddings for Modeling Multi-relational Data. In Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013. Proceedings of a meeting held December 5-8, 2013, Lake Tahoe, Nevada, United States, Christopher J. C. Burges, Léon Bottou, Zoubin Ghahramani, and Kilian Q. Weinberger (Eds.). 2787–2795. https://proceedings.neurips.cc/paper/2013/hash/1cecc7a77928ca8133fa24680a88d2f9-Abstract.html
- Cao et al. (2015) Shaosheng Cao, Wei Lu, and Qiongkai Xu. 2015. GraRep: Learning Graph Representations with Global Structural Information. In Proceedings of the 24th ACM International Conference on Information and Knowledge Management, CIKM 2015, Melbourne, VIC, Australia, October 19 - 23, 2015, James Bailey, Alistair Moffat, Charu C. Aggarwal, Maarten de Rijke, Ravi Kumar, Vanessa Murdock, Timos K. Sellis, and Jeffrey Xu Yu (Eds.). ACM, 891–900. https://doi.org/10.1145/2806416.2806512
- Daiber et al. (2013) Joachim Daiber, Max Jakob, Chris Hokamp, and Pablo N. Mendes. 2013. Improving efficiency and accuracy in multilingual entity extraction. In I-SEMANTICS 2013 - 9th International Conference on Semantic Systems, ISEM ’13, Graz, Austria, September 4-6, 2013, Marta Sabou, Eva Blomqvist, Tommaso Di Noia, Harald Sack, and Tassilo Pellegrini (Eds.). ACM, 121–124. https://doi.org/10.1145/2506182.2506198
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), Jill Burstein, Christy Doran, and Thamar Solorio (Eds.). Association for Computational Linguistics, 4171–4186. https://doi.org/10.18653/v1/n19-1423
- Diefenbach et al. (2018) Dennis Diefenbach, Kamal Deep Singh, and Pierre Maret. 2018. WDAqua-core1: A Question Answering service for RDF Knowledge Bases. In Companion of the The Web Conference 2018 on The Web Conference 2018, WWW 2018, Lyon , France, April 23-27, 2018, Pierre-Antoine Champin, Fabien Gandon, Mounia Lalmas, and Panagiotis G. Ipeirotis (Eds.). ACM, 1087–1091. https://doi.org/10.1145/3184558.3191541
- Hamilton et al. (2017) William L. Hamilton, Rex Ying, and Jure Leskovec. 2017. Representation Learning on Graphs: Methods and Applications. IEEE Data Eng. Bull. 40, 3 (2017), 52–74. http://sites.computer.org/debull/A17sept/p52.pdf
- Kazemi and Poole (2018) Seyed Mehran Kazemi and David Poole. 2018. SimplE Embedding for Link Prediction in Knowledge Graphs. In Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, December 3-8, 2018, Montréal, Canada, Samy Bengio, Hanna M. Wallach, Hugo Larochelle, Kristen Grauman, Nicolò Cesa-Bianchi, and Roman Garnett (Eds.). 4289–4300. https://proceedings.neurips.cc/paper/2018/hash/b2ab001909a8a6f04b51920306046ce5-Abstract.html
- Liang Yao (2019) Yuan Luo Liang Yao, Chengsheng Mao. 2019. KG-BERT: BERT for Knowledge Graph Completion. arXiv:1909.03193 (2019).
- Lin et al. (2015) Yankai Lin, Zhiyuan Liu, Maosong Sun, Yang Liu, and Xuan Zhu. 2015. Learning Entity and Relation Embeddings for Knowledge Graph Completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, January 25-30, 2015, Austin, Texas, USA, Blai Bonet and Sven Koenig (Eds.). AAAI Press, 2181–2187. http://www.aaai.org/ocs/index.php/AAAI/AAAI15/paper/view/9571
- Liu et al. (2019) Weijie Liu, Peng Zhou, Zhe Zhao, Zhiruo Wang, Qi Ju, Haotang Deng, and Ping Wang. 2019. K-BERT: Enabling Language Representation with Knowledge Graph. arXiv:1909.07606 (2019).
- Peters et al. (2019) Matthew E Peters, Mark Neumann, IV Logan, L Robert, Roy Schwartz, Vidur Joshi, Sameer Singh, and Noah A Smith. 2019. Knowledge Enhanced Contextual Word Representations. arXiv preprint arXiv:1909.04164 (2019).
- Sun et al. (2019) Zhiqing Sun, Zhi-Hong Deng, Jian-Yun Nie, and Jian Tang. 2019. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv preprint arXiv:1902.10197 (2019).
- Trouillon et al. (2016) Théo Trouillon, Johannes Welbl, Sebastian Riedel, Éric Gaussier, and Guillaume Bouchard. 2016. Complex embeddings for simple link prediction. International Conference on Machine Learning (ICML).
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention is All you Need. In Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, Isabelle Guyon, Ulrike von Luxburg, Samy Bengio, Hanna M. Wallach, Rob Fergus, S. V. N. Vishwanathan, and Roman Garnett (Eds.). 5998–6008. https://proceedings.neurips.cc/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html
- Wang et al. (2014) Zhen Wang, Jianwen Zhang, Jianlin Feng, and Zheng Chen. 2014. Knowledge Graph Embedding by Translating on Hyperplanes. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, July 27 -31, 2014, Québec City, Québec, Canada, Carla E. Brodley and Peter Stone (Eds.). AAAI Press, 1112–1119. http://www.aaai.org/ocs/index.php/AAAI/AAAI14/paper/view/8531
- Yaghoobzadeh and Schütze (2015) Yadollah Yaghoobzadeh and Hinrich Schütze. 2015. Corpus-level Fine-grained Entity Typing Using Contextual Information. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, EMNLP 2015, Lisbon, Portugal, September 17-21, 2015, Lluís Màrquez, Chris Callison-Burch, Jian Su, Daniele Pighin, and Yuval Marton (Eds.). The Association for Computational Linguistics, 715–725. https://doi.org/10.18653/v1/d15-1083
- Zhang et al. (2019) Zhengyan Zhang, Xu Han, Zhiyuan Liu, Xin Jiang, Maosong Sun, and Qun Liu. 2019. ERNIE: Enhanced Language Representation with Informative Entities. arXiv preprint arXiv:1905.07129 (2019).
- Zhu et al. (2017) Hao Zhu, Ruobing Xie, Zhiyuan Liu, and Maosong Sun. 2017. Iterative Entity Alignment via Joint Knowledge Embeddings. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI 2017, Melbourne, Australia, August 19-25, 2017, Carles Sierra (Ed.). ijcai.org, 4258–4264. https://doi.org/10.24963/ijcai.2017/595