Improving Dither Modulation based Robust Steganography by Overflow Suppression

Throughout the paper, matrices, vectors and sets are written in capital letters. Unless otherwise indicated, we use symbol $\boldsymbol{D}$ to denote the matrices of quantized DCT coefficients, $\boldsymbol{Q}$ to denote the matrices of quantization table, $\boldsymbol{S}$ to denote the matrices of spatial values derived from $\boldsymbol{D}$ by IDCT and $\boldsymbol{X}$ to denote the matrices of pixels. Elements in the matrix are denoted by corresponding lowercase letters, for example $\boldsymbol{D}=(d_{u,v})$, $\boldsymbol{Q}=(q_{u,v})$, $\boldsymbol{S}=(s_{i,j})$, $\boldsymbol{X}=(x_{i,j})$, where the subscripts mean their position. Considering the way JPEG compression chunking operates we normally use $8\times 8$ block, namely, $u,v,i,j\in\{1,2,\cdots,8\}$. Also considering the storage limitations in JPEG, $d_{u,v}\;(or\;d)\in\{-1024,\cdots,1023\}$, $q_{u,v}\;(or\;q)\in\{1,\cdots,255\}$, $s_{i,j}\;(or\;s)\in\{-128,\cdots,127\}$ and $x_{i,j}\;(or\;x)\in\{0,\cdots,255\}$. The transformation functions are denoted by bold symbols, additionally, $\left[\;\cdot\;\right]$, $\left\lceil\;\cdot\;\right\rceil$ and $\left\lfloor\;\cdot\;\right\rfloor$ are denote rounding methods round, ceil and floor in mathematics. The aforesaid notations and the relationship among the above elements can be briefly explained through the JPEG compression process as follows.

The JPEG recompression process first converts the DCT coefficients to spatial values, then truncates and rounds them to obtain spatial image, finally converts spatial image into quantized DCT coefficients with the QF of channel. For detail, the process of recompressing an $8\times 8$ DCT block $\boldsymbol{D}$ from quality factor $q_{1}$ to $q_{2}$ is as follows:

• •

  coefficients dequantization:

  $$\boldsymbol{\widetilde{D}}_{q_{1}}=\boldsymbol{D}_{q_{1}}\times\boldsymbol{Q}_{q_{1}},$$

  (1)

• •

  inverse discrete cosine transformation:

  $$\boldsymbol{S}=\textbf{IDCT}(\boldsymbol{\widetilde{D}}),$$

  (2)

• •

  spatial truncation:

  $$\boldsymbol{\dot{S}}=\textbf{TRU}(\boldsymbol{S}),$$

  (3)

• •

  spatial rounding:

  $$\boldsymbol{X}=\left[\boldsymbol{\dot{S}}+128\right],$$

  (4)

• •

  spatial shift:

  $$\boldsymbol{\ddot{S}}=\boldsymbol{X}-128,$$

  (5)

• •

  discrete cosine transformation:

  $$\boldsymbol{\widetilde{D}}_{q_{2}}=\textbf{DCT}(\boldsymbol{\ddot{S}}),$$

  (6)

• •

  coefficients quantization:

  $$\boldsymbol{D}_{q_{2}}=\left[\boldsymbol{\widetilde{D}}_{q_{2}}/\boldsymbol{Q}_{q_{2}}\right].$$

  (7)

We use $\boldsymbol{\widetilde{D}}$ to denote the matrices of unquantized DCT coefficients. The function TRU$(\;\cdot\;)$ is truncation of the pixel which value is out of the spatial range thus called overflow:

Notably, DCT coefficient quantization referred to in this paper usually includes both quantization and rounding operations unless specified. Greek letters denote costs of the coefficients and parameters. Specific explanations of the notations, or elements not mentioned, will be elaborated on later.

Dither modulation is an extension of the original uniform quantized index modulation (QIM) algorithm [29]. Since dither modulation can be robust in embedding while maintaining high visual quality of the image, it is widely used in watermarking algorithms. In the below, we briefly introduce the embedding process of dither modification on DCT coefficients in [30].

The modification method of algorithm [30] is shown in Figure 1(a). We use $d_{1}$ and $d_{2}$ to represent the unquantized DCT coefficients and the quantization step associated with them is $q$. The axes which represent the unquantized DCT coefficients can be divided into many segments by quantization step $q$. As seen in the Figure 1(a), $d_{1}$ in the odd segment represents the message bit ‘1’, and $d_{2}$ in the even segment represents the message bit ‘0’. If we want $d_{2}$ to represent the message bit ‘0’, we will add $h_{2}$ to it and adjust it to the center of the nearest even segment. A similar modification will be performed if the message represented by $d_{1}$ is changed.

Dither Modulation-based robust Adaptive Steganography (DMAS) [20] is a recent robust steganographic algorithm under the “Robust Domain Selection + ECC-STCs Codes” framework. It constructs compression-resistant domain mainly by choosing middle frequency DCT coefficients as the embedding domain in conjunction with dither modulation. DMAS can be applied in either spatial or DCT domain.

Generalized dither Modulation-based robust Adaptive Steganography (GMAS) [22] improves resistance to detection and compression by generalized dither modulation and expanding the embedding domain of DMAS. The embedding scheme of generalized dither modulation is illustrated in the Figure 1(b). Unlike DMAS, which modifies the coefficients to the center of the nearest interval. GMAS considers the possibility of modifying to both sides as well as introduces ternary embedding and asymmetric distortion for hiding message. We will only describe GMAS in detail here:

1. i.

   Select Cover Elements from Expended Robust Domain. The expended embedding domain are composed of coefficients $d_{i,j}$ satisfying the $(i+j=7,8,9)$. These coefficients are selected as steganographic cover and embedded using generalized dither modulation.

2. ii.

   Calculate Asymmetric Distortion. Calculate the spatial pixels that eliminate the JPEG compression block effect.

   $$\boldsymbol{X^{\prime}}=\boldsymbol{X}\otimes\boldsymbol{F},$$

   (9)

   $$\boldsymbol{F}=\begin{bmatrix}1/9&1/9&1/9\\ 1/9&1/9&1/9\\ 1/9&1/9&1/9\end{bmatrix}.$$

   (10)

   To improve the performance, use this $\boldsymbol{X^{\prime}}$ as a reference and define asymmetric distortion to encourage modifications toward the reference image. In detail, a block DCT transformation of $\boldsymbol{X^{\prime}}$ yields unquantized DCT coefficients ${\overline{d}}_{i,j}$, calculate symmetric costs $\rho_{i,j}$ with existing distortion functions then asymmetric costs of the quantized DCT coefficients can be defined as follows:

   $$\rho_{i,j}^{+}=\left\{\begin{array}[]{l}\lambda\cdot\rho_{i,j}\;,\;d_{i,j}<{\overline{d}}_{i,j}/q_{i,j}\\ \rho_{i,j}\;,\;else\end{array}\right.,$$

   (11)

   $$\rho_{i,j}^{-}=\left\{\begin{array}[]{l}\lambda\cdot\rho_{i,j}\;,\;d_{i,j}>{\overline{d}}_{i,j}/q_{i,j}\\ \rho_{i,j}\;,\;else\end{array}\right.,$$

   (12)

   where $d_{i,j}$ denotes the quantized DCT coefficients and $\lambda\in(0,1)$ controls the intensity of the adjustment. The final asymmetric costs $\xi_{i,j}^{+}$ and $\xi_{i,j}^{-}$ for the unquantized DCT coefficients are calculated as follow:

   	$\displaystyle\zeta_{i,j}^{+}$	$\displaystyle=\rho_{i,j}^{+}/q_{i,j},$		(13)
   	$\displaystyle h_{i,j}^{+}$	$\displaystyle=(k+1)q_{i,j}-\tilde{d}_{i,j},$
   	$\displaystyle\xi_{i,j}^{+}$	$\displaystyle=\zeta_{i,j}^{+}\times h_{i,j}^{+},$

   	$\displaystyle\zeta_{i,j}^{-}$	$\displaystyle=\rho_{i,j}^{-}/q_{i,j},$		(14)
   	$\displaystyle h_{i,j}^{-}$	$\displaystyle=\tilde{d}_{i,j}-(k-1)q_{i,j},$
   	$\displaystyle\xi_{i,j}^{-}$	$\displaystyle=\zeta_{i,j}^{-}\times h_{i,j}^{-},$

   where $k\in N$ is an integer. $\tilde{d}_{i,j}\in((k-1/2)q_{i,j},(k+1/2)q_{i,j})$ and $q_{i,j}$ denote the unquantized DCT coefficients and the corresponding quantization step, respectively.

3. iii.

   RS Encoding and Ternary STC Embedding. Utilizing RS codes to encode the messages. A modifiable ternary sequence can be obtained from the selected coefficients using generalized dither modulation so ternary STC is used to embed to attain a lower bit error rate and stronger security. Specifically, ternary STC can be implemented using double-layered STCs [31].

After receiving the compressed stego image, the receiver first converts JPEG images to spatial values, then obtains the unquantized DCT coefficients derived from spatial images, finally calculates the quantized DCT coefficients with the same quantization table as that used for embedding, and we call this entire operation “DCT Coefficients Restoration”. After that, the same middle frequency DCT coefficients are chosen to gain the message using STCs and RS decoding.

Yu et al. [22] experimentally found that steganographic algorithms using dither modulation for embedding (such as DMAS and GMAS) generally behave excellently when the QF of channel compression is larger than that of the cover image and called this phenomenon “Upward Robust”. This part will provide a theoretical analysis of this phenomenon.

Generally, we denote the unquantized DCT coefficient of a stego JPEG image by $\tilde{d}$. Then the relation among $\tilde{d}$ , the corresponding quantized coefficients $d$, and quantization steps $q$ is as follows:

This means that the unquantized DCT coefficients of the JPEG image are exactly at the center of the region divided by the quantization step. If the quantization step used for this coefficient in channel compression is $q^{\prime}$, the maximum modifications caused by channel compression is $q^{\prime}/2$ without considering the processing of the spatial pixels. So after channel compression we have:

where $\tilde{d}_{q^{\prime}}$ is unquantized DCT coefficient after channel compression. As described in the Section 2.3, it is necessary to perform DCT coefficients restoration. Denote the coefficient after restoration at this situation as $d_{q^{\prime}}$. When the channel compression QF is larger than the cover QF (the corresponding quantization step of channel compression is less than that of the cover), it is obvious from the Figure 1(c) that

In this case, the coefficients after coefficients restoration are the same as the original ones, so the message can be extracted accurately. If the QF of channel compression is smaller than the QF of cover, the corresponding quantization steps $q^{\prime\prime}$ will produce a contrary consequence. Also as shown in Figure 1(c):

where $\tilde{d}_{q^{\prime\prime}}$ and $d_{q^{\prime\prime}}$ are unquantized and quantized coefficients in this situation. Such cases usually involve extraction errors and error propagation due to the utilization of STCs. Here we consider the generalized dither modulation.The above analysis explained the fundamental principle of dither modulation to achieve upward robustness. So dither modulation based algorithms (DMAS and GMAS) require the selection of the image with a lower QF to meet the real-world application scenarios.

In summary, the embedding using dither modulation is theoretically error-free when the channel compression QF is larger than the cover QF (Upward Robust). But this method still has errors in a real-world implementation even if the QF meets the requirement of Upward Robust. The reason is that we have considered only one of the three lossy processes in the recompression (coefficients quantization). The influences of spatial truncation and rounding were not considered, which will be discussed in the next subsection.

According to the inference of Section 3.1, dither modulation-based algorithms are unaffected by coefficients quantization. However, when considering the impact of spatial operations, Equation (16) will not necessarily be true. So we will explore this below.

To measure the effect of the spatial truncation and rounding, we summarize the JPEG recompression process in Section 2.1 as follows,

First we investigate the impact of spatial rounding. We ignore the truncation operations on the spatial domain. Then the recompression process is represented as follows,

where $\boldsymbol{E}$ is a rounding error block and all the elements $(e_{i,j})_{8\times 8}$ of $\boldsymbol{E}$ belong to $[-0.5,0.5)$. Here, we assume that $e_{i,j}$ in $\boldsymbol{E}$ is an independent identically distributed (i.i.d.) random variable with uniform distribution in the range of $[-0.5,0.5)$. Then, based on the central limit theorem, for each element $w_{i,j}$ in $\boldsymbol{W}$, $w_{i,j}$ can be approximately regarded as a Gaussian distribution $\mathcal{N}(0,1/12)$ [33]. Consequently, we see that

where $q_{i,j}$ is the quantization step corresponding to the recompression quality factor $q_{2}$. Therefore, spatial rounding has almost no effect on the recompressed DCT coefficients with recompression $\text{QF}\leqslant 92$, since each element of the quantization matrix is larger than 1. This way we can exclude the effect of the spatial rounding operation on the robust steganography algorithm. As a conclusion, in the case where the recompression QF is larger than the cover QF, spatial truncation operation is the primary cause of the error. Here is an experiment to verify the above conclusion. We characterize the magnitude to which the DCT coefficient is affected by spatial operations as the stability of the coefficient. From Figure 2, we can observe experimentally that truncation operations in the spatial values are the major contributor to the instability of the DCT coefficients, and that rounding operations in the spatial values contribute only relatively small effects.

The specific operation of spatial truncation is shown in Equation (8). Compared to spatial rounding, truncation operations usually cause larger variation, correspondingly also have a greater impact on DCT coefficients, as shown in Figure 2. Obviously, the exact extent of the impact caused by the truncation operation is related to the magnitude of the corresponding block overflow. And the cause of spatial overflow is that the DCT coefficient derived from the unoverflowed spatial value becomes a coefficient with a larger absolute value during quantization when the image is saved in JPEG format. From the cause of overflow, it is known that the magnitude of overflow depends on the size of the corresponding quantization step. Notably, this quantization step is a save-time one, which is in the quantization table of the cover for the steganographer. We counted the overflow extent of the images in BOSSbase 1.01 [32] with different QFs and the results are shown in Figure 3. The smaller the QF of the cover image, the larger the quantization step, the greater the degree of overflow, and the greater the impact suffered from the spatial truncation operation. For robustness, dither modulation based steganography need to choose the image with long quantization step as cover, but this makes them subject to the spatial truncation, even if GMAS chooses to embed in the middle frequency regions with large quantization steps, it is impossible to avoid errors. The reason why repeatedly processing the images through channels can improve the robustness is also that the spatial overflow of the images can be reduced in repeated compression, making the instability of the DCT coefficients diminished. But repeated uploads and downloads are behaviorally insecure. Through the above analysis, we can fundamentally improve the robustness and security by dealing with the image overflow.

In conclusion, coefficient quantization results in the primary effect among the three lossy operations, but the application of dither modulation solves this problem. In the two remaining problems, spatial truncation plays a major role, while the effect of spatial rounding is almost negligible. Consequently, in the procedure of channel compressing, the DCT coefficients of the blocks with the overflow spatial values tend to change dramatically. Inspired by the above discoveries, we have designed a strategy called Removing Overflow based Adaptive robuSt sTeganography (ROAST) to effectively remove the spatial overflow of cover images, which strengthens the stability of the DCT coefficients, thus we do not need to select the robust domain as previous steganography algorithms and can embed on the entire image, which not only significantly enlarges the embedding capacity, but also improves the anti-detection performance remarkably. The proposed strategy ROAST can resist compression primarily because of the removal of spatial overflow, which can be accomplished in two methods: Overall Scale and Specific Truncation. We designed corresponding steganography schemes based on the respective properties of the two approaches. Each is described in detail later.

The first method of removing spatial overflow is Overall Scale (OS). This method is primarily concerned with theoretical rigor and enabling greater removal of spatial overflow in particular. The concrete process can be outlined in Figure 4, and the subsequent part will describe the details and prove the feasibility of this approach.

1. i.

   Inverse DCT and Inspection. The object of the algorithm is an $8\times 8$ DCT coefficient block $\boldsymbol{D}$ of a JPEG image. Convert it to spatial block $\boldsymbol{S}$ with inverse DCT. Denote the unquantized DCT coefficients of row $u$ column $v$ in the DCT block by $\tilde{d}_{u,v}$ and the spatial values of row $i$ column $j$ in the spatial block by $s_{i,j}$. Note that the spatial value here is not a pixel, an shifting is required to convert it to a pixel. The relationship between the DCT coefficient and the spatial value can be obtained by the formula of DCT:

   	$\displaystyle\tilde{d}_{u,v}\!=\!\frac{1}{4}\cdot$	$\displaystyle\boldsymbol{C}(u)\!\cdot\!\boldsymbol{C}(v)[\sum_{i=0}^{7}\!\sum_{j=0}^{7}\!s_{i,j}\!\cdot\!\cos\!\frac{(2i\!+\!1)u\pi}{16}\!\cdot\!\cos\!\frac{(2j\!+\!1)v\pi}{16}]\;,$		(22)
   		$\displaystyle\boldsymbol{C}(u)=\left\{\begin{array}[]{lc}\sqrt{\frac{1}{N}}&u=0\\ \sqrt{\frac{2}{N}}&u\neq 0\end{array}\right.,$

   where $N=8$ denotes the side length of the block. For a more intuitive description, we rewrite Equation (22) to the following form:

   $$\tilde{d}_{u,v}=\sum_{i,j}s_{i,j}\cdot\Phi_{i,j;u,v}\;,\;i,j,u,v\in\{0,1,\cdots,7\},$$

   (23)

   where $\Phi_{i,j;u,v}$ denotes the value of $\tilde{d}_{u,v}$ when $s_{i,j}=1$, which is the variation caused by a single spatial value on this DCT coefficient. Once the conversion is complete, the overflow can be observed via the spatial value, namely, check if $s_{i,j}$ satisfies $s_{i,j}>127$ or $s_{i,j}<-128$. If there exists an overflow in a block, then this block will be processed to remove the overflow. If not, then the block will be skipped.

2. ii.

   Scale of Spatial Values. Remove spatial overflow by scaling the whole block to a block without overflow:

   $$s^{\prime}_{i,j}=\alpha\cdot s_{i,j}\;,\;i,j\in\{0,1,\cdots,7\},$$

   (24)

   where $s^{\prime}_{i,j}$ denotes the spatial value after scaling and $\alpha$ is the parameter. The amount of $\alpha$ depends on the degree of spatial overflow of the block:

   $$\alpha=\frac{s_{\text{0}}}{\left|s_{\left|\text{max}\right|}\right|}\;,\;\;s_{\text{0}}=\left\{\begin{array}[]{lc}127,&s_{\left|\text{max}\right|}>0\\ 128\;,&\;else\end{array}\right.,$$

   (25)

   where $s_{\left|\text{max}\right|}$ denotes the spatial value with the maximum absolute value. So that $\alpha$ calculated in this way makes the scaled block without overflow.

3. iii.

   DCT and Quantization. Convert the block which has been removed overflow into DCT coefficients. The DCT coefficients corresponding to the scaled block are $\tilde{d}^{\prime}_{u,v}$:

   $$\tilde{d}^{\prime}_{u,v}=\sum_{i,j}s^{\prime}_{i,j}\cdot\Phi_{i,j;u,v}\;=\alpha\sum_{i,j}s_{i,j}\cdot\Phi_{i,j;u,v}\;=\alpha\cdot\tilde{d}_{u,v}.$$

   (26)

   At this time, this block gets rid of overflow. Thereafter, the DCT coefficients will be quantized to integer. Generally, the round function “$\left[\;\cdot\;\right]$” is adopted which modifies a number to the nearest integer for quantization. However, the round operation will cause undesirable changes, e.g. the coefficient increases. The former scaling changes intend to reduce the amplitude of DCT coefficients, therefore FIX$(\;\cdot\;)$ which modifies the number to the nearest integer with a smaller absolute value is utilized here for quantization.

   $$\textbf{FIX}(x)=\left\{\begin{array}[]{lc}\left\lfloor x\right\rfloor&x\geqslant 0\\ \left\lceil x\right\rceil&else\end{array}\right..$$

   (27)

   The final processed DCT coefficient is $d_{u,v}^{*}$,

   $$d_{u,v}^{*}=\textbf{FIX}(\tilde{d}^{\prime}_{u,v}/q_{u,v}),$$

   (28)

   where $q_{u,v}$ is the corresponding quantization step.

Here gives the proof that the processed block is without the overflow. The unquantized DCT coefficient corresponding to the finally stored DCT coefficient is $\tilde{d}_{u,v}^{*}$:

where $\beta_{u,v}$ is a parameter jointly determined by quantization and overall scale. It is obvious from the above process that $\beta_{u,v}\leqslant\alpha$. Similar to the way the DCT formula in Equation (23), rewrite the inverse DCT in the following format:

where $\Psi_{u,v;i,j}$ denotes the value of $s_{i,j}$ when $d_{u,v}=1$. The spatial value corresponding to the adjusted coefficients is $s_{i,j}^{*}$ :

Apparently, $s_{i,j}^{*}\leqslant s^{\prime}_{i,j}$ as a result of $\beta_{u,v}\leqslant\alpha<1$. Hence, the corresponding spatial values diminish spatial overflow after adjusting the DCT coefficients. Even though it may occasionally cause overflow after steganography, the effect will be minimal compared to before.

The stability of the coefficients can be significantly improved via the Overall Scale method introduced in the previous section, so we use this method and generalized dither modulation to design an upward robust steganography scheme named ROAST-OS. Figure 5 illustrates the procedure of the scheme. The process and details are described hereunder:

1. i.

   Preprocessing of Cover Image. Removing the spatial overflow of cover image by the Overall Scale method. The cover after preprocessing is generally considered to be sufficiently robust that the whole image can be regarded as a robust region, which we called robust cover.

2. ii.

   Define Distortion for Robust Cover. Define the asymmetric distortion of robust cover using the Equation (11) and Equation (12). Here the distortion of the quantized DCT coefficients instead of the unquantized DCT coefficients are calculated, that is, Equation (13) and Equation (14) are not required here. This is according to the Equation (15) which means the unquantized DCT coefficients of the JPEG image are exactly at the center of the region divided by the quantization step.

3. iii.

   RS Encoding and Ternary STC Embedding. Utilizing RS codes to encode the messages and ternary STC to embed.

The receiver first performs the DCT coefficients restoration introduced in Section 2.3 on the compressed stego image. The message is then decoded with the RS code and STCs.

Although the aforesaid Overall Scale method can remove the overflow to produce a robust cover and is also outstanding in practical steganography schemes, we need to consider the anti-detection performance while pursuing robustness in robust steganography. The employment of the Overall Scale generates a large number of modifications, which greatly affects the anti-detection performance, so we devised a method named Specific Truncation (ST) for targeted tuning of the overflow location and parameterizing the processing intensity to remove spatial overflow with relatively fewer modifications. The concrete procedure of the method is shown in Figure 4, and the details are presented as follows.

1. i.

   Inverse DCT and Inspection. Convert the DCT block to spatial values and detect whether the block is overflowing or not, namely, check if there is $s_{i,j}$ satisfying $s_{i,j}>127$ or $s_{i,j}<-128$. If there exists an overflow, then the block will be processed to remove the overflow. If not, then it will be ignored.

2. ii.

   Specific Truncation of Overflow Values. For all out-of-range positions, denoted as $\hat{s}_{i,j}$ ($\hat{s}_{i,j}>127$ or $\hat{s}_{i,j}<-128$), the truncation operation is performed as follows:

   $$\hat{s}_{i,j}=\left\{\begin{array}[]{lc}127-T_{1},&\hat{s}_{i,j}>127\\ -128+T_{1},&\hat{s}_{i,j}<-128\end{array}\right.,$$

   (32)

   $T_{1}$ is a parameter to control the intensity of the truncation operation and the magnitude of the modification, which pursues a better trade-off between robustness and resistance to detection. Denote the processed spatial block as $\boldsymbol{\widehat{S}}$.

3. iii.

   DCT and Quantization. Convert the processed spatial block $\boldsymbol{\widehat{S}}$ to coefficients $\boldsymbol{\widetilde{D}}$ using DCT:

   $$\boldsymbol{\widetilde{D}}=\textbf{DCT}(\boldsymbol{\widehat{S}}).$$

   (33)

   Following the setting in section Section 4.1, we apply FIX() in the quantization phase as well.

   $$\boldsymbol{D}=\textbf{FIX}(\boldsymbol{\widetilde{D}}/\boldsymbol{Q})=\textbf{FIX}(\textbf{DCT}(\boldsymbol{\widehat{S}})/\boldsymbol{Q}),$$

   (34)

   $\boldsymbol{D}$ is the robust block after the removal of the spatial overflow.

Specific Truncation is a de-overflow method with relatively smaller modifications compared to Overall Scale, but it also unavoidably weakens the performance of overflow removing. The steganographic scheme called ROAST-ST is designed to enhance the robustness by using robust asymmetric distortion. As shown in Figure 6, it consists of three parts: preprocessing, calculate robust asymmetric distortion, and STCs embedding. Each step of the scheme is described in detail below:

1. i.

   Preprocessing. The preprocess is designed to enhance the stability of the DCT coefficients by removing the spatial overflow with Specific Truncation operations. When determining whether a block is overflowed or not, it is not as straightforward as before, but instead first calculates the extent of the overflow. Because the preprocessing always has a more significant impact on the image compared to the embedding process and an intuitive way to improve security is to make fewer changes. The overflow of a block is measured by $\Omega$, which is calculated as follow:

   $$\Omega=\sum_{i,j}\delta_{i,j}\;,\;\delta_{i,j}=\left\{\begin{array}[]{lc}\left|s_{i,j}\right|-127\;,&s_{i,j}>127\\ \left|s_{i,j}\right|-128\;,&s_{i,j}<-128\\ 0\;,&else\end{array}\right..$$

   (35)

   Actually, it is the de-overflow operation rather than steganographic modification impacts on the security of the block. We therefore introduce $T_{2}$ to control whether or not the block is considered overflow. The block will be considered as overflow block if $\Omega>T_{2}$ or not if $\Omega\leq T_{2}$. This way we can divide the blocks of cover $\boldsymbol{C}$ into two groups: $\boldsymbol{A}$ with overflow and $\boldsymbol{B}$ without overflow. A de-overflow operation on $\boldsymbol{A}$ yields $\boldsymbol{A^{\prime}}$ and $\boldsymbol{B}$ doesn’t do the processing, thus obtain a robust cover $\boldsymbol{C_{\text{o}}}$ for steganography. While reducing the magnitude of the modification in the Specific Truncation, it also leads to the consequence that it is difficult to completely remove all spatial overflow with this method used only once. So we expect to remove spatial overflow further during embedding. A de-overflow operation on $\boldsymbol{A^{\prime}}$ again yields $\boldsymbol{A^{\prime\prime}}$ and twice de-overflow operations on $\boldsymbol{B}$ yields $\boldsymbol{B^{\prime\prime}}$, thus obtain a reference cover $\boldsymbol{C_{\text{e}}}$ with less overflow than robust cover. Making $\boldsymbol{C_{\text{o}}}$ close to $\boldsymbol{C_{\text{e}}}$ in the process of embedding modifications can enhance coefficient stability.

2. ii.

   Define Robust Asymmetric Distortion. In the aforementioned preprocessing, not only a robust cover is prepared, but also a reference image is given for designing asymmetric distortion. Therefore we can combine the de-overflow into the process of message embedding. In detail, we employ the distortions $\rho_{i,j}^{+}$ and $\rho_{i,j}^{-}$ calculated by the Equation (11) and Equation (12) on the robust cover as the basic distortions. Denote the quantized DCT coefficient of the robust cover and the reference image as $d_{i,j}^{\text{o}}$ and $d_{i,j}^{\text{e}}$, respectively. Robust asymmetric distortion is calculated as follows:

   $$\varepsilon_{i,j}^{+}=\left\{\begin{array}[]{lc}\mu\cdot\rho_{i,j}^{+},&d_{i,j}^{\text{e}}>d_{i,j}^{\text{o}}\\ \rho_{i,j}^{+},&else\end{array}\right.,$$

   (36)

   $$\varepsilon_{i,j}^{-}=\left\{\begin{array}[]{lc}\mu\cdot\rho_{i,j}^{-},&d_{i,j}^{\text{e}}<d_{i,j}^{\text{o}}\\ \rho_{i,j}^{-},&else\end{array}\right.,$$

   (37)

   $\varepsilon_{i,j}^{+}$ and $\varepsilon_{i,j}^{-}$ are asymmetric distortion after performing robustness adjustment. $0<\mu\leqslant 1$ is a parameter for adjusting distortion. This defines a smaller “+1” cost for locations where the coefficient of the reference image is larger than that of the robust cover and a smaller “-1” cost for locations where the coefficient of the reference image is less than that of the robust cover.

3. iii.

   RS Encoding and Ternary STC Embedding. This part is the same as mentioned before.

The receiver extracts the message in the same way as Section 4.2, which is not repeated here.

All experiments in this paper are conducted on BOSSbase 1.01 [32] containing 10,000 grayscale $512\times 512$ images. We randomly selected 2000 of them and the original images are JPEG compressed using quality factor 65 as the cover image. From Section 3 we know that the dither modulation based algorithm needs to choose a cover with a relatively low QF to achieve robustness. Therefore, we use 65 as an example in our experiments. The relative payload is $n_{\textrm{m}}/n_{\textrm{nzac}}$, where $n_{\textrm{m}}$ is the length of the original embedded messages rather than the encoded messages by RS codes and $n_{\textrm{nzac}}$ is the number of non-zero AC DCT coefficients of the original cover image rather than the robust cover after de-overflow processing. Previous steganographic algorithms typically set the range of the relative payloads of robust adaptive steganography from $0.05$ to $0.15$ bits per non-zero AC DCT coefficients (bpnzac) due to their limited performance. We refer to such payloads as low payloads and perform experiments with high payload from $0.1$ to $0.5$ (bpnzac) in this paper. The extraction error rate $R_{\textrm{error}}=n_{\textrm{error}}/n_{\textrm{m}}$, where $n_{\textrm{error}}$ is the number of wrong message bits. The QF of the cover image and channel JPEG compression is denoted as $Q_{\textrm{cover}}$ and $Q_{\textrm{channel}}$, respectively. Two effective feature sets (CCPEV [26], DCTR [27]) and SRNet [28] are selected for steganalysis of JPEG image. We will set the secure parameter $h=10$ of STCs, and RS (31,15) will be adopted in the following experiments. As for ($n^{*}$, $k^{*}$) RS codes, $n^{*}$ and $k^{*}$ denote the code length and message length respectively, and the greater the ratio of $k^{*}$ to $n^{*}$, the stronger the error correction ability of RS codes.

The detectors are trained as binary classifiers implemented using the FLD ensemble with default settings [34]. The ensemble by default minimizes the total classification error probability under equal priors $P_{\textrm{E}}=\min_{P_{\textrm{FA}}}\frac{1}{2}(P_{\textrm{FA}}+P_{\textrm{MD}})$, where $P_{\textrm{FA}}$ and $P_{\textrm{MD}}$ are the false-alarm probability and the missed-detection probability respectively. SRNet is fed the cover and stego images. The training first runs for 300 epocks with an initial learning rate of $r_{1}=0.001$ and then for an additional 100 epochs with a learning rate of $r_{2}=0.0001$. A separate classifier and a deep network are trained for each embedding algorithm and payload. The ultimate security is qualified by average error rate $\overline{P}_{\textrm{E}}$, and larger $\overline{P}_{\textrm{E}}$ means stronger security.

The preprocessing improves the stability of the DCT coefficients by removing the spatial overflow of the cover image. It is an operation that has a relatively high impact on security and robustness therefore we use parameters to find a trade-off between them. Subsequently, we will explore these in detail through experiments.

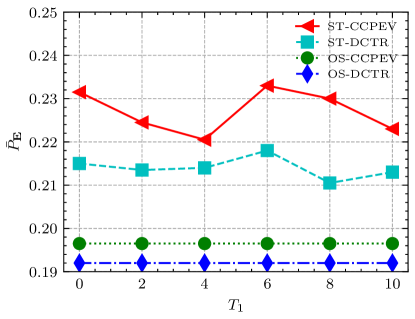
In this section, we compare the proposed algorithms with state-of-the-art algorithms. First of all, in terms of applicability, the algorithm proposed by Tao et al. [23] only works in the scenario that the QF of channel compression is less than that of cover images (Downward Robust). TCM [19] works well only if the channel parameters are known or if the channel can be used at will. Therefore, we compare the proposed algorithms to GMAS [22] and DMAS [20] that have the same application environment. After that, we choose parameters for ROAST-ST that make it perform comparable to ROAST-OS according to the results of the previous experiment. The specific values are $T_{1}=8$ , $T_{2}=0$ , $\mu=0.5$.

The comparison of robustness is shown in Figure 13 and the security is shown in Figure 14. In terms of robustness, except for $Q_{\text{channel}}=85$ with payloads near $0.1$ bpnzac, both algorithms proposed in this paper have significant advantages over the previous algorithms. Comparing robustness at $Q_{\text{channel}}=85$ and $Q_{\text{channel}}=95$, we can obtain that as the recompression QF decreases, the robustness performance of the algorithm decreases. This is consistent with the inference in Section 3.1 regarding the recompression QF. In terms of security, it is also the proposed algorithms that have significant advantages, except when using CCPEV feature and the payload is near $0.1$ bpnzac. Representatively, average detection error rate $\overline{P}_{\textrm{E}}$ is increased by +18% when utilizing DCTR features with $payload=0.1$ bpnzac and +14% when utilizing CCPEV features with $payload=0.3$ bpnzac. It is worth mentioning that both DMAS and GMAS almost fail to resist detection at $payload\geqslant 0.2\;\;(\text{bpnzac})$ when utilizing more powerful DCTR features, and the proposed algorithms are even more outstanding in this situation. We also compare the security when using the popular CNN-based steganalysis in Figure 15. The security of the proposed method is enhanced at low embedding rate compared with DMAS and GMAS. Average detection error rate $\overline{P}_{\textrm{E}}$ is increased by +5% when utilizing SRNet with $payload=0.12$ bpnzac. Overall ROAST-ST and ROAST-OS achieve notable robustness and security.

The two algorithms proposed in this paper have their strengths and weaknesses, due to the use of de-overflow operations and corresponding steganographic strategies. From Figure 14, roughly divided by $payload=0.3\;\;(\text{bpnzac})$, ROAST-ST has superiority in both robustness and security when the payload is small, and ROAST-OS has superiority in both when the payload is large. With smaller payloads, the security of the algorithm is substantially determined by the method of preprocessing, so this case can demonstrate the benefits of fewer preprocessing modifications and robust asymmetric distortions in ROAST-ST. When the payload is large, the modifications caused by embedding also progressively take effect, and therefore the strengths of fewer modifications in preprocessing operations are not so much, instead, the stable robustness of more preprocessing modifications and the security of distortion without robust adjustment will be exhibited. Consequently, both of these two algorithms are characterized by their properties.