AMoRE Collaboration
Improved Limit on Neutrinoless Double Beta Decay of from AMoRE-I
Abstract
AMoRE searches for the neutrinoless double beta decay of with 100 kg of enriched . Scintillating molybdate crystals coupled with a metallic magnetic calorimeter operate at milli-Kelvin temperatures to measure the energy of electrons emitted in the decay. AMoRE-I is a demonstrator for the full-scale AMoRE, operated at the Yangyang Underground Laboratory for over two years. The exposure was 8.02 kgyear (or 3.89 kgyear), and the total background rate near the value was 0.025 0.002 counts/keV/kg/year. We observed no indication of decay and report a new lower limit of the half-life of decay as at 90% confidence level. The effective Majorana mass limit range is (210–610) meV using nuclear matrix elements estimated in the framework of different models, including the recent shell model calculations.
Experiments with solar and atmospheric neutrinos [1, 2] have found that neutrinos are massive. Various oscillation experiments [3, 4, 5, 6] have measured the three mixing angles and two mass differences. Although the absolute masses of neutrinos have not yet been measured, we know they are very small, less than 1 eV/ based on measurements ofthe tritium -spectrum endpoint [7, 8].
The small neutrino masses and the absence of right-handed neutrinos in the Standard Model motivated the introduction of Majorana masses for neutrinos, as opposed to charged leptons that have Dirac masses. Small Majorana neutrino mass can be generated via the seesaw mechanism in which the masses of active neutrinos are suppressed by heavy right-handed sterile neutrinos [9], and the mass terms violate lepton number conservation [10].
The currently well-established method for determining if neutrinos are Majorana fermions is to search for neutrinoless double beta ) decay of nuclei [11]. Regardless of the underlying mechanism, the observation of decay would prove that lepton number is violated [12], which is necessary for the seesaw mechanism and leptogenesis [13]. The amplitude of decay is proportional to the effective Majorana mass, defined by the charged-current couplings of Majorana neutrinos. A decay experiment requires monitoring a large mass of isotopes with a detector having an ultralow background and a high energy resolution to reach the true effective Majorana mass. In spite of more than seventy years of experimental efforts [14], no signal for decay has been observed. The best half-life limit has been established by KamLAND-Zen for with yr, limiting the effective Majorana mass to (28–122) meV [15]. For other isotopes, the () limits are: yr (90–305 meV) for by CUORE using cryogenic techniques [16], yr (79–180 meV) for by GERDA using high purity germanium detectors [17], and yr (280–490 meV) for by CUPID-Mo using cryogenic scintillating crystal detectors [18, 19].
AMoRE aims to search for the decays using molybdate-based crystal detectors operating at milli-Kelvin (mK) temperatures [20, 21], similar to CUPID-Mo. AMoRE intends to achieve quasifree of background, defined as having less than one count in the region of interest (ROI) near =3034.4 keV for the five-year experiment with about 100 kg of 100Mo isotope.
The AMoRE project is progressing in three phases. The first two, AMoRE-Pilot and AMoRE-I, were completed at the 700-meter-deep Yangyang Underground Laboratory (Y2L). AMoRE-II will run at the newly built Yemilab for five years. We have reported a half-life limit of yr at a 90% confidence level (CL) using six 48deplCa100MoO4 crystals in the AMoRE-Pilot stage [22, 23, 24]. To confirm the performance and long-term stability of the detection system and determine the background level achievable with the existing setup at Y2L, we operated AMoRE-I from 2019 to 2023. This report describes the experimental setup, data analysis, and a new half-life limit of .
AMoRE-I was carried out in the same cryostat that was used for AMoRE-Pilot [22, 23, 24, 25], but with a larger number of detectors. We made a few modifications to the detector modules and shielding enhancements. The AMoRE-I system used a two-stage temperature control system to maintain the detector tower at a constant temperature [26]. The datasets used for this report were taken at a temperature of 12 mK.
The AMoRE-I detector array consists of eighteen crystals with a total mass of 6.2 kg, including 3.0 kg of 100Mo, comprising five (LMO) crystals, and thirteen 48deplCa100MoO4 (CMO) crystals, six of which were inherited from AMoRE-Pilot. The molybdenum in the crystals was enriched in 100Mo to 95.70.2%. Each detector module consisted of a crystal surrounded by a Vikuiti reflector film, an MMC sensor connected to the crystal, and a light detector made of an absorber with an MMC sensor. The mass-spring vibration damping system [27] was removed to accommodate the increased number of detector modules. The stainless steel screws in the detector modules were replaced with copper and brass for lower radioactive contamination. Additionally, Si wafers with SiO2 antireflection coating were used for the light absorber instead of Ge wafers [28]. One flat surface of the LMO crystal, upon which the gold phonon collector was evaporated, was ground with 1500-grit SiC sandpaper to enhance the gold film bond at the interface. Each crystal had a stabilization heater attached to the flat surface to measure and correct the gain drift of the heat signal [29].Pulses of fixed current and duration were injected through the heater every 10 seconds. Detailed descriptions of the detector module can be found in [30, 26].
An additional 5 cm of lead was added outside of the cryostat vacuum chamber to further reduce high-energy environmental ’s. Initially, aluminum plates were used to support the lead bricks, but these plates were found to be highly contaminated by and were removed in May 2021. Ten additional muon counters made of plastic-scintillator panels were installed to extend the solid-angle coverage for the detector array.
Heat and light signals from the SQUID electronics were continuously digitized without an event trigger and stored using flash analog-to-digital converter modules with an 18-bit resolution for a 10-volt peak-to-peak dynamic range at a 100 kHz sampling frequency. Data acquisition (DAQ) with the full eighteen-crystal detector array started in December 2020 and ended in April 2023, with a 93% live time. About 78% of the DAQ live time was dedicated to physics measurement, while calibration and other commissioning data took up the remaining time. Thorium-containing welding rods were placed between the outer vacuum chamber and the external lead shielding to calibrate the energy scale every 4–8 weeks, depending on the detector’s stability.
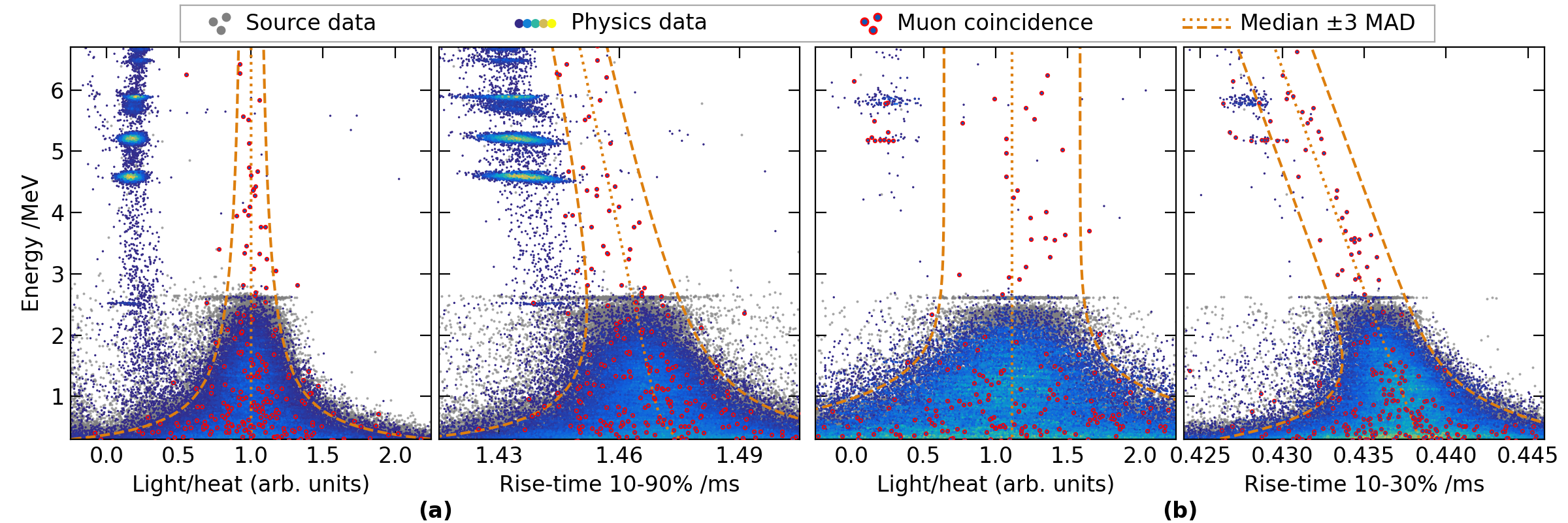
To suppress noise, the heat signal of each detector was processed using a Butterworth bandpass filter for the offline analysis. For most detectors, the trigger thresholds were set below 100 keV. Two modules that suffered from a significant vibration or electric noise had higher thresholds. The amplitudes of the heat and light signals were determined by fitting template waveforms to the data using a least-squares fit [31]. The fit was applied to the filtered waveforms and the bandwidths of the Butterworth filters were optimized to provide the highest energy resolutions. A template signal was constructed by averaging 2615 keV events accumulated in calibration runs. The rise and fall times were derived from the raw signals, defined as the time elapsed between specific points on the pulse. Unlike the AMoRE-pilot analysis, which used the time difference between the 10% and 90% levels of the signal, this analysis defined rise time (RT) variably for each detector, optimizing the pulse shape discrimination (PSD) power. One LMO detector had a noisy light signal, making it impossible to calculate the light signal amplitude accurately. Data from this detector were excluded from the analysis because of the limited PSD power. Examples of the RT versus signal amplitudes for a CMO and an LMO detector are shown in Fig 1.
The detector response change over time, mainly caused by temperature variations, influenced the pulse amplitudes and shapes of both physics and heater signals. Correlations between the heater signal’s RT and the amplitude of 2615 keV events were determined with calibration data and used for drift correction in the corresponding dataset. Each dataset consists of a calibration run followed by physics runs before the next calibration.
The energy scale was initially calibrated using four prominent peaks at 511.0 keV, 583.2 keV, 911.2 keV, and 2614.5 keV in the calibration-run spectrum for each dataset. As in the previous analysis, signal amplitudes for each detector were all well described as a quadratic function of true energy values, without a constant term [32, 22]. Secondary energy calibration was performed using another quadratic function with a constant term, including more peaks from the calibration data.
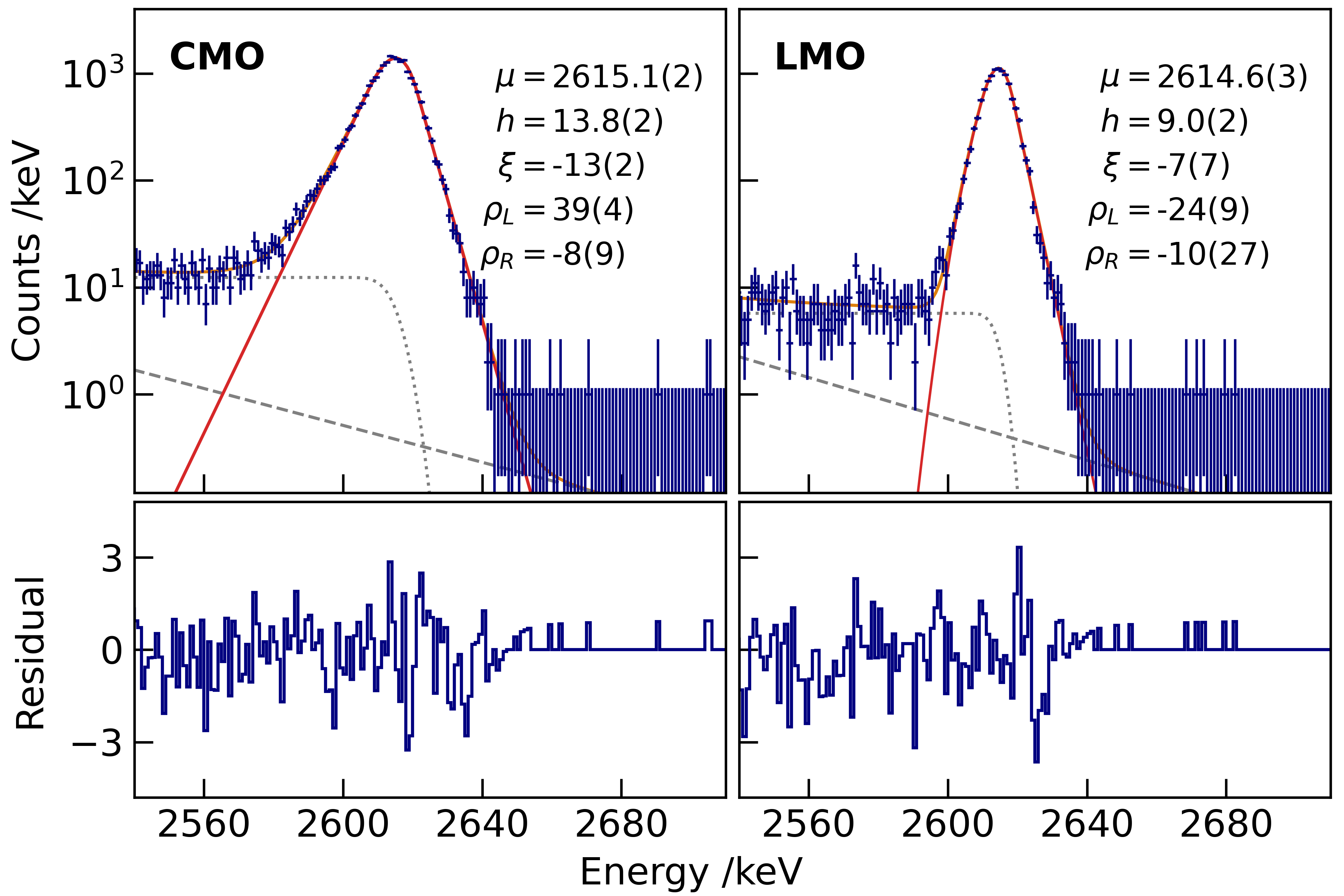
Owing to nonuniform, position-dependent detector responses, peaks in the energy spectra were asymmetric, showing tails on both the lower and upper sides. Among various peak-fitting functions, the Bukin function [33] was found to be well suited for the peaks in the calibration spectrum. The spectra around the 2615 keV peak in the calibration data for a CMO and an LMO detector are shown in Fig. 2. Shape parameters that were determined from fitting below 2615 keV were extrapolated to to estimate the signal shape. The squares of energy resolutions () were well fitted to a quadratic function of energy. The energy resolution at differs for each detector, varying from 10 to 28 keV of full width at half maximum with a weighted average 13 keV. Other shape parameters for asymmetry (), left tail (), and right tail () varied slowly with energy, and their uncertainties were extrapolated using a linear function or were left constant, depending on each detector’s characteristics.
The event-selection criteria for background reduction were divided into two categories. The first category was particle identification to remove the continuous background around the ROI due to radioactive contamination on the crystal surface or surrounding materials. Two parameters were adopted for each detector: PSD using RT of the heat signal, and the light-to-heat ratio (L/H), which leverages the differences in scintillation quenching for and particles. Fig. 1 shows the RT and L/H versus energy for the calibration runs, background runs, and events that were coincident with muons for one CMO and one LMO detector. Here, the events are clustered at higher energies and at smaller RT and L/H values, while most of the events without muon coincidence lie below 2.6 MeV.
The median-absolute-deviation (MAD) values were determined using source data at the energy range of 465–2665 keV and fitted using a function of energy. Events within the 3 MAD bands for RT and L/H, denoted as the dashed-orange curves in Fig. 1 were selected as events. The selection efficiencies at the calibration -peak energies were determined by comparing the event counts at each peak before and after the selection using the Bukin function on top of a simple exponential or linear background to extract the peak from the resulting spectra. These selection efficiencies, when extrapolated to , varied among detectors and ranged between 80% and 95% with uncertainties on the 1% level. Generally, CMO detectors showed a much better discrimination power than LMO, for both RT and L/H parameters, due to the higher light yield and the correlation of light yield with the pulse shape [34, 35]. The alpha backgrounds for the six CMO detectors used in AMoRE-Pilot were reported in [23]. The activities of () for the AMoRE-I dataset were determined by analysis of coincident events from the sequential decay of 222Rn and 218Po (224Ra and 220Rn). These were 5–59 Bq/kg (1–13 Bq/kg) in the CMO detectors, except for one highly contaminated CMO crystal, and 1–2 Bq/kg for both and in the LMO detectors. Detailed background modeling of AMoRE-I is in progress.
The second event-selection category involved a series of anticoincidence cuts. First, events occurring within 10 ms after a muon candidate event were rejected. About ten thousand muon candidate events were registered daily, resulting in an inefficiency of only 0.1% with negligible uncertainty. Secondly, we imposed a single-hit cut in which the signal candidate is the only hit that occurred within a 2 ms time window. Since the trigger rate of the background runs was typically 1 Hz, the efficiency of this single-hit requirement was about 99.8%. The final anticoincidence condition, called tagging, targeted one of the major backgrounds in the ROI from the decay of 208Tl with 4.998 MeV. These background events follow an event emitted in 212Bi decay to 208Tl. Since the half-life of 208Tl is 3.053 minutes and the energy released in the decay of 212Bi is 6.207 MeV, all events within 20 minutes after an event in the same crystal with 6.2 0.1 MeV energy were rejected. Two detectors with exceptionally high rates had a narrower energy window of 40 keV [23]. The efficiency of this veto was about 98% on average: 78% for the most -contaminated CMO and higher than 99% for LMOs. The cut efficiencies are summarized in Table 1.
| Parameters/selection | Efficiency (%) | Uncertainty (%) | |
|---|---|---|---|
| Particle identification | |||
| PSDL/H (3 MAD) | 78.8–95.4 (89.9) | 1.6 | |
| Anti-coincidences | |||
| Multiplicity () | 99.8 | 0.1 | |
| Muon veto (10 ms) | 99.9 | 0.1 | |
| 212Bi veto (20 min) | 77.6–99.8 (97.8) | 0.6 | |
| containment | 78.4–82.4 (81.1) | 1.0 | |
| Total detection efficiency | 49.1–76.1 (70.9) | 1.6 | |
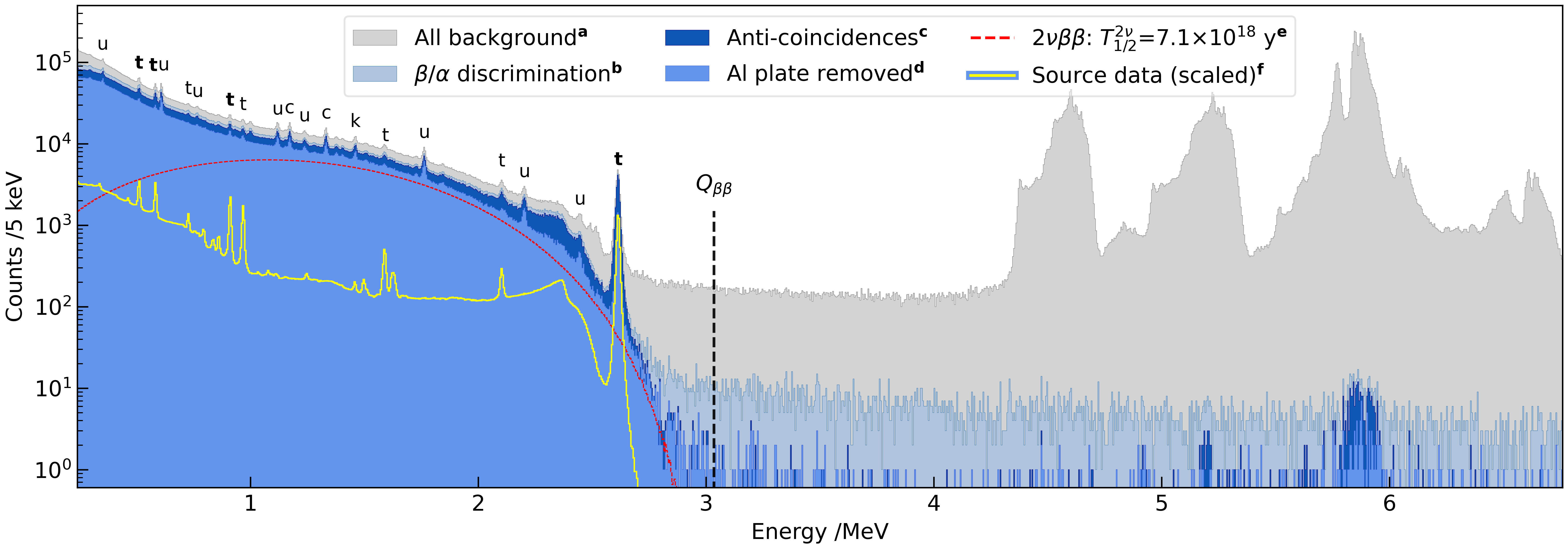
Figure 3 shows the resulting background energy spectra accumulated for 8.02 kgyear (or 3.89 kgyear) exposure, following the step-by-step selections, overlaid with the calibration spectrum. The first dataset taken with the aluminum support plate, shown as the dark blue shaded area, represents about 14% of the total exposure but contains about 20% of the events in the energy range below 2.7 MeV, including about 60% of 2615 keV events. Despite this, the background due to the contaminated aluminum plate is mainly confined to energies below 2.7 MeV, so these data were included in the analysis. As shown in the previous studies [22], the relationship between the signal amplitude and energy differs for events compared to events due to pulse shape differences, which vary across detectors. Consequently, energies, which were determined separately, are not reported in this work. As a result, the energy spectrum for all detectors and datasets shown in Fig. 3 has many peaks above 4 MeV electron-equivalent energy that are distributed incoherently when they are calibrated with the functions for events.
Events in the 2.7–3.6 MeV energy range were selected for the study. The background energy distribution was approximated as a linear combination of flat and exponential background components. The exponential component includes high-energy -decay events and background from internal and surface contamination of the crystal [23]. The flat component is introduced to describe high energy s from neutron capture, external sources such as rock and radon in the air, and residual and events due to incomplete rejection. A more detailed background modeling based on the measurements of detector components’ radioactivities is in progress.
Considering the background () and the decay signal () can be expressed in terms of the decay rate (=), the number of 100Mo nuclei (), the detection efficiency () for the decay of (shown in Table 1), and the DAQ live time () as =. An unbinned likelihood function was constructed as follows:
| (1) |
where and are indices of the detector and its events, respectively, and is the number of observed events in the th detector. The expected spectral shape was described by the probability density function, , that includes a background model, with flat and exponential components, plus a signal peak in the form of a Bukin function for fully contained events. Efficiency () and peak shape parameters () were treated as nuisance parameters with Gaussian priors ().
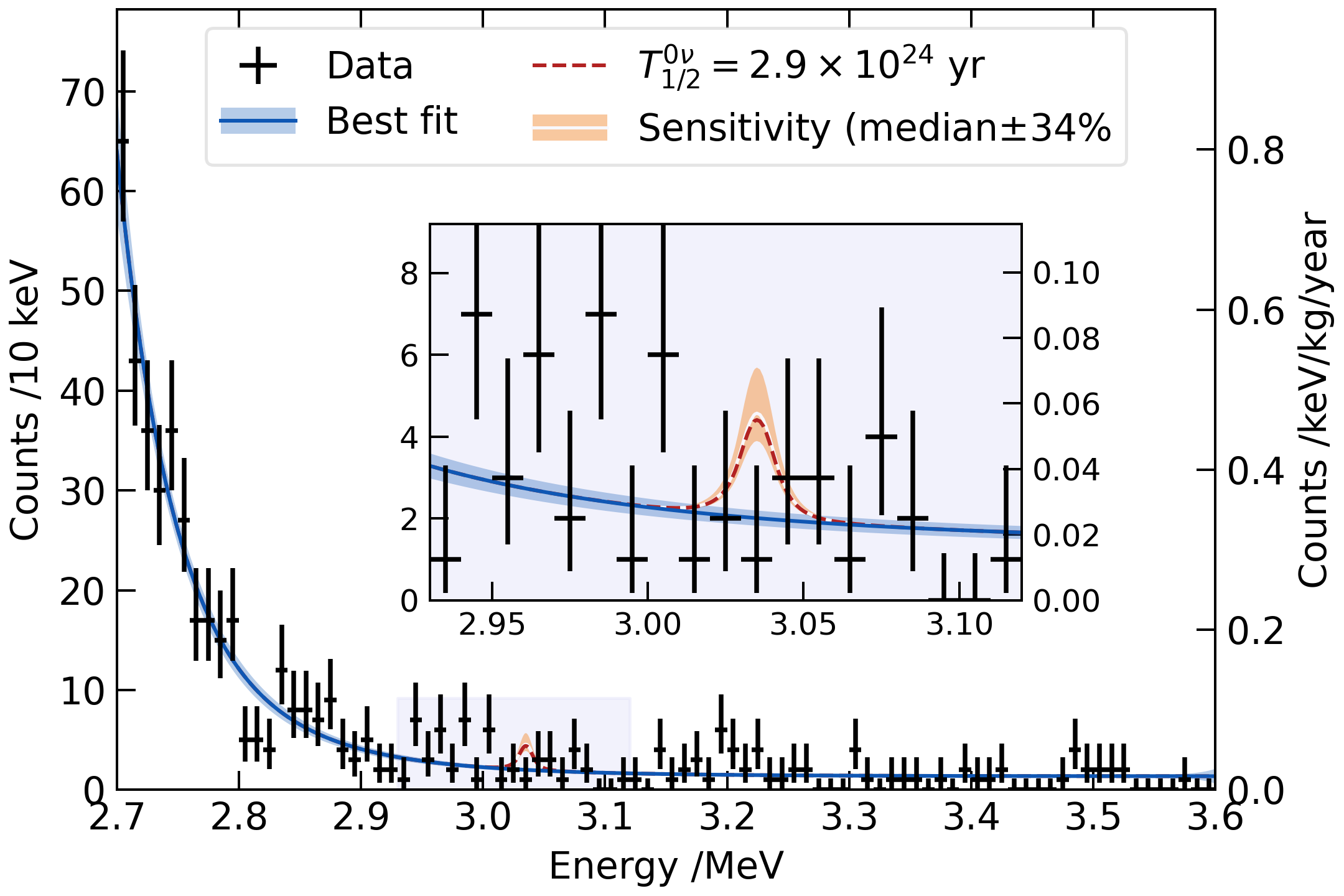
The minimized negative log likelihood was profiled over the sensitive range of from 0 to year-1, and the best fit was found at year-1, meaning that no event excess was found over the assumed background shape, as shown in Fig. 4. The corresponding limit on the half-life of the decay of 100Mo was evaluated at a 90% CL to be:
| (2) |
which extends the CUPID-Mo limit [19]. The limit matched well to the sensitivity determined by numbers of pseudodatasets with the given exposure, peak shapes and sideband background levels. The median 34% sensitivity of 90% CL limit is 2.8 yr, as shown in Fig. 4.
The posterior analysis leads to a total background level of counts/keV/kg/yr. The LMO detectors showed a slightly lower background rate of counts/keV/kg/yr on average, while the background counting rate of the CMO detectors is counts/keV/kg/yr. The total background rate in AMoRE-I was reduced by 15 times compared to that of AMoRE-pilot.
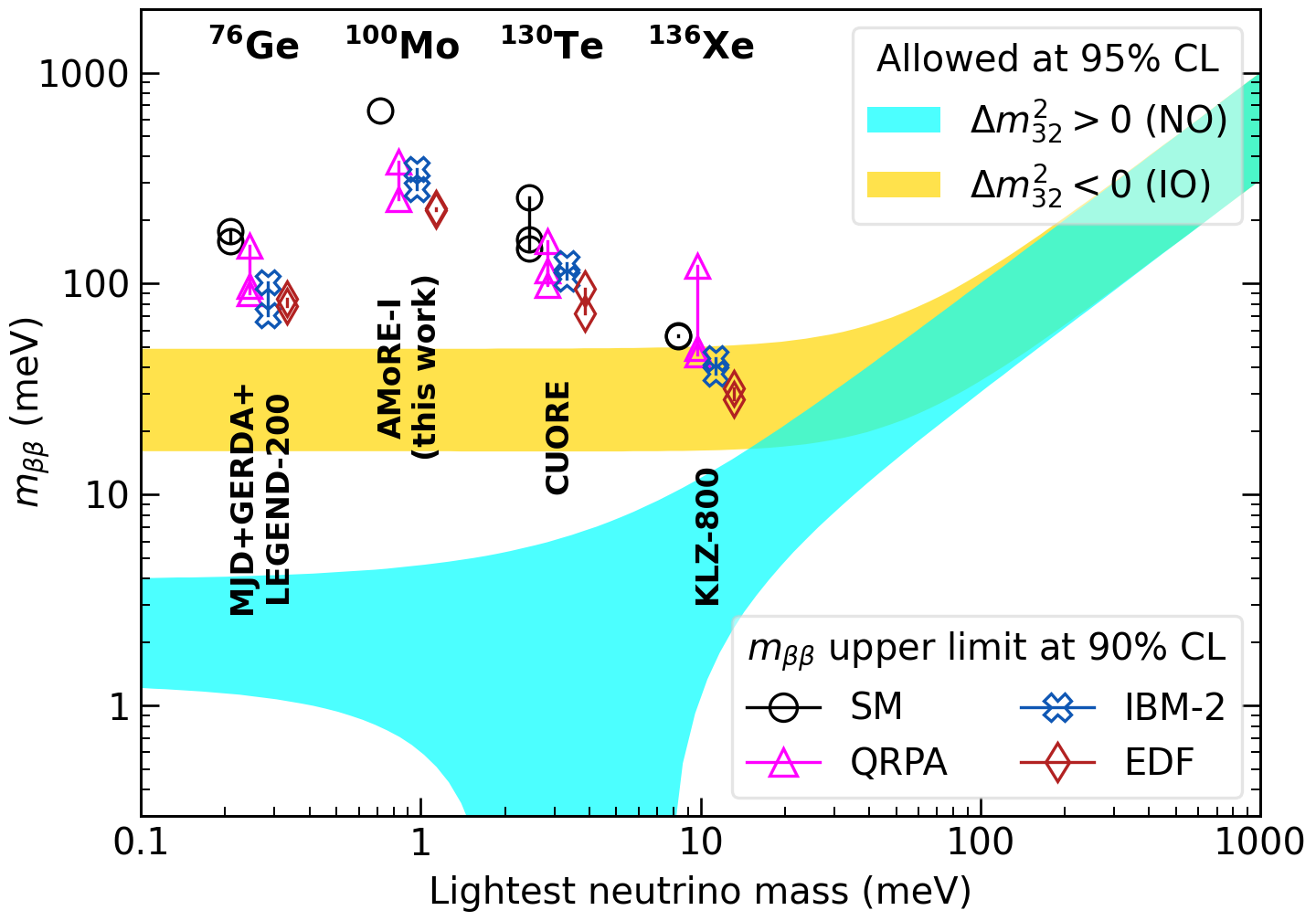
We calculated the effective Majorana mass within the theoretical framework of the light neutrino exchange model, incorporating the phase space factor [39, 40, 41] and nuclear matrix elements (NMEs) [42, 43, 44, 45, 46, 47, 48, 49]. The range of inferred upper limits on the effective Majorana mass is (210–350) meV assuming an axial vector coupling constant . If we include the first shell model calculation recently published for [50], the range of limits extends to (210–610) meV. The lower limit is derived from an energy density functional considering the nuclear deformation and pairing fluctuation [44], while the upper limit is based on a shell model that explicitly includes the short-range correlations [50]. Upper limits on the effective Majorana mass from existing experimental data and NMEs are shown in Fig. 5.
AMoRE-II is under preparation at Yemilab [53] with a muon rate about a quarter of that at Y2L [54]. We have developed an LMO detector module with improved energy resolution and alpha background rejection [55, 56]. The background level for AMoRE-II is projected to be less than counts/keV/kg/yr based on radioassay data and GEANT4 simulations [57]. The discovery sensitivity is projected to be approximately yr for five years of data collection.
Acknowledgements–This research is supported by Grants No. IBS-R016-D1 and No. IBS-R016-A2. It is also supported by the National Research Foundation of Korea (NRF-2021R1I1A3041453, NRF-2021R1I1A6A1A03043957) and the National Research Facilities & Equipment Center (NFEC) of Korea (No. 2019R1A6C1010027). We appreciate the support by the Ministry of Science and Higher Education of the Russian Federation (N121031700314-5), the MEPhI Program Priority 2030. The group from the Institute for Nuclear Research (Kyiv, Ukraine) was supported in part by the National Research Foundation of Ukraine under Grant No. 2023.03/0213. We thank the Korea Hydro and Nuclear Power (KHNP) Company for providing underground laboratory space at Yangyang and the IBS Research Solution Center (RSC) for providing high-performance computing resources. These acknowledgements are not to be interpreted as an endorsement of any statement made by any of our institutes, funding agencies, governments, or their representatives.
References
- Fukuda et al. [1998] Y. Fukuda et al. (Super-Kamiokande Collaboration), Evidence for oscillation of atmospheric neutrinos, Phys. Rev. Lett. 81, 1562 (1998) .
- Ahmad et al. [2002] Q. R. Ahmad et al. (SNO Collaboration), Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory, Phys. Rev. Lett. 89, 011301 (2002) .
- Bak et al. [2018] G. Bak et al. (RENO Collaboration), Measurement of reactor antineutrino oscillation amplitude and frequency at RENO, Phys. Rev. Lett. 121, 201801 (2018) .
- Adey et al. [2018] D. Adey et al. (Daya Bay Collaboration), Measurement of the electron antineutrino oscillation with 1958 Days of operation at Daya Bay, Phys. Rev. Lett. 121, 241805 (2018) .
- Acero et al. [2022] M. A. Acero et al. (NOvA Collaboration), Improved measurement of neutrino oscillation parameters by the NOvA experiment, Phys. Rev. D 106, 032004 (2022) .
- Abe et al. [2023] K. Abe et al. (T2K Collaboration), Measurements of neutrino oscillation parameters from the T2K experiment using protons on target, Eur. Phys. J. C 83, 782 (2023) .
- Aker et al. [2024] M. Aker et al. (Katrin Collaboration), Direct neutrino-mass measurement based on 259 days of KATRIN data, (2024), .
- Aghanim et al. [2020] N. Aghanim et al. (Planck Collaboration), Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641, A6 (2020); 652, C4(E) (2021) .
- Mohapatra and Senjanovic [1980] R. N. Mohapatra and G. Senjanovic, Neutrino Mass and Spontaneous Parity Nonconservation, Phys. Rev. Lett. 44, 912 (1980).
- Majorana [1937] E. Majorana, Teoria simmetrica dell’elettrone e del positrone, Nuovo Cim. 14, 171 (1937) .
- Agostini et al. [2023] M. Agostini, G. Benato, J. A. Detwiler, J. Menéndez, and F. Vissani, Toward the discovery of matter creation with neutrinoless decay, Rev. Mod. Phys. 95, 025002 (2023) .
- Schechter and Valle [1982] J. Schechter and J. W. F. Valle, Neutrinoless double beta decay in SU(2) x U(1) theories, Phys. Rev. D 25, 2951 (1982).
- Fukugita and Yanagida [1986] M. Fukugita and T. Yanagida, Baryogenesis Without Grand Unification, Phys. Lett. B 174, 45 (1986).
- Fireman [1949] E. L. Fireman, A measurement of the half-life of double beta-decay from (50)Sn-124, Phys. Rev. 75, 323 (1949).
- Abe et al. [2024] S. Abe et al. (KamLAND-Zen Collaboration), Search for Majorana neutrinos with the complete KamLAND-Zen dataset, (2024), arXiv:2406.11438 .
- Campani [2024] A. Campani, New results on 0 decay from the CUORE experiment, LHEP 2024, 516 (2024).
- Agostini et al. [2020] M. Agostini et al. (GERDA Collaboration), Final results of GERDA on the search for neutrinoless double- decay, Phys. Rev. Lett. 125, 252502 (2020) .
- Armengaud et al. [2021] E. Armengaud et al. (CUPID Collaboration), New limit for neutrinoless double-beta Decay of 100Mo from the CUPID-Mo experiment, Phys. Rev. Lett. 126, 181802 (2021) .
- Augier et al. [2022] C. Augier et al., Final results on the decay half-life limit of 100Mo from the CUPID-Mo experiment, Eur. Phys. J. C 82, 1033 (2022) .
- Bhang et al. [2012] H. Bhang et al., AMoRE experiment: a search for neutrinoless double beta decay of 100Mo isotope with 40Ca100MoO4 cryogenic scintillation detector, J. Phys. Conf. Ser. 375, 042023 (2012).
- Alenkov et al. [2015] V. Alenkov et al. (AMoRE Collaboration), Technical design report for the AMoRE decay search experiment, (2015) .
- Alenkov et al. [2019] V. Alenkov et al. (AMoRE Collaboration), First results from the AMoRE-Pilot neutrinoless double beta decay experiment, Eur. Phys. J. C79, 791 (2019) .
- Alenkov et al. [2022] V. Alenkov et al. (AMoRE Collaboration), Alpha backgrounds in the AMoRE-Pilot experiment, Eur. Phys. J. C 82, 1140 (2022) .
- Agrawal et al. [2024a] A. Agrawal et al. (AMoRE Collaboration), Background study of the AMoRE-pilot experiment, Astroparticle Physics 162, 102991 (2024a) .
- Kang et al. [2017] C. S. Kang, J. A. Jeon, H. S. Jo, G. B. Kim, H. L. Kim, I. Kim, S. R. Kim, Y. H. Kim, D. H. Kwon, C. Lee, H. J. Lee, M. K. Lee, S. H. Lee, S. Y. Oh, J. H. So, and Y. S. Yoon, MMC-based low-temperature detector system of the AMoRE-Pilot experiment, Superconductor Science and Technology 30, 084011 (2017).
- Woo et al. [2022] K. R. Woo, H. B. Kim, H. L. Kim, Y. H. Kim, D. H. Kwon, D. Y. Lee, H. J. Lee, S. H. Lee, Y. C. Lee, and H. S. Lim, An MMC-based temperature control 0 system for a long-term data collection, J. Low Temp. Phys. 209, 1218 (2022).
- Lee et al. [2018] C. Lee, H. S. Jo, C. S. Kang, G. B. Kim, I. Kim, Y. H. Kim, H. J. Lee, and J. H. So, Vibration mitigation for a cryogen-free dilution refrigerator for the AMoRE-Pilot experiment, J. Low Temp. Phys. 193, 786 (2018).
- Kim et al. [2023] M. B. Kim, J. S. Chung, 0 J. A. Jeon, C. S. Kang, H. B. Kim, H. L. Kim, S. C. Kim, S. G. Kim, S. R. Kim, W. T. Kim, Y. H. Kim, D. H. Kwon, D. Y. Lee, H. J. Lee, M. K. Lee, S. H. Lee, Y. C. Lee, H. S. Lim, and K. R. Woo, Large area light detectors with MMC readouts, IEEE Transactions on Applied Superconductivity 33, 1 (2023).
- Kwon et al. [2020] D. H. Kwon, J. A. Jeon, H. S. Jo, H. B. Kim, H. L. Kim, I. Kim, S. R. Kim, Y. H. Kim, H. Lee, M. K. Lee, et al., Stabilization heaters for low-temperature thermal calorimeters, J. Low Temp. Phys. 200, 312 (2020).
- Kim et al. [2022a] H. B. Kim et al., Status and performance of the AMoRE-I experiment on neutrinoless double beta decay, J. Low Temp. Phys. 209, 962 (2022a), .
- Lim et al. [tted] H. S. Lim, J. S. Chung, H. S. Jo, et al., An analysis method of heat and light detection with scintillating crystals, J. Low Temp. Phys. 217, 374 (2024) .
- Kim et al. [2017] G. B. Kim, J. H. Choi, H. S. Jo, et al., Novel measurement method of heat and light detection for neutrinoless double beta decay, Astroparticle Physics 91, 105 (2017).
- [33] RooBukinPdf Class Reference, https://root.cern.ch/doc/master/classRooBukinPdf.html.
- Mailyan et al. [2023] B. Mailyan, B. Sharma, H. J. Kim, S. C. Kim, W. T. Kim, Y. D. Kim, Y. H. Kim, M. H. Lee, and K. R. Woo, Light collection of some molybdate crystal absorbers for cryogenic calorimeters at millikelvin temperatures, IEEE Trans. Nucl. Sci. 70, 1307 (2023).
- Woo et al. [2024] K. R. Woo, J. S. Chung, D. H. Hwang, et al., Thermal model improvement in phonon detection channels using a scintillating crystal, J. Low Temp. Phys. https://doi.org/10.1007/s10909-024-03089-y (2024).
- Agostinelli et al. [2003] S. Agostinelli et al. (GEANT4 Collaboration), GEANT4–a simulation toolkit, Nucl. Instrum. Meth. A 506, 250 (2003).
- Ponkratenko et al. [2000] O. A. Ponkratenko, V. I. Tretyak, and Y. G. Zdesenko, The Event generator DECAY4 for simulation of double beta processes and decay of radioactive nuclei, Phys. Atom. Nucl. 63, 1282 (2000) .
- Augier et al. [2023] C. Augier et al. (CUPID-Mo Collaboration), Measurement of the 2 decay rate and spectral shape of Mo100 from the CUPID-Mo experiment, Phys. Rev. Lett. 131, 162501 (2023) .
- Kotila and Iachello [2012] J. Kotila and F. Iachello, Phase space factors for double- decay, Phys. Rev. C 85, 034316 (2012) .
- Mirea et al. [2015] M. Mirea, T. Pahomi, and S. Stoica, Values of the phase space factors involved in double beta decay, Rom. Rep. Phys. 67, 872 (2015) .
- Stoica and Mirea [2019] S. Stoica and M. Mirea, Phase space factors for double-beta decays, Front. in Phys. 7, 12 (2019).
- Rath et al. [2013] P. K. Rath, R. Chandra, K. Chaturvedi, P. Lohani, P. K. Raina, and J. G. Hirsch, Neutrinoless decay transition matrix elements within mechanisms involving light Majorana neutrinos, classical Majorons, and sterile neutrinos, Phys. Rev. C 88, 064322 (2013) .
- Šimkovic et al. [2013] F. Šimkovic, V. Rodin, A. Faessler, and P. Vogel, 0 and 2 nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration, Phys. Rev. C 87, 045501 (2013) .
- López Vaquero et al. [2013] N. López Vaquero, T. R. Rodríguez, and J. L. Egido, Shape and pairing fluctuations effects on neutrinoless double beta decay nuclear matrix elements, Phys. Rev. Lett. 111, 142501 (2013) .
- Barea et al. [2015] J. Barea, J. Kotila, and F. Iachello, and nuclear matrix elements in the interacting boson model with isospin restoration, Phys. Rev. C 91, 034304 (2015) .
- Hyvärinen and Suhonen [2015] J. Hyvärinen and J. Suhonen, Nuclear matrix elements for decays with light or heavy Majorana-neutrino exchange, Phys. Rev. C 91, 024613 (2015).
- Song et al. [2017] L. S. Song, J. M. Yao, P. Ring, and J. Meng, Nuclear matrix element of neutrinoless double- decay: relativity and short-range correlations, Phys. Rev. C 95, 024305 (2017) .
- Šimkovic et al. [2018] F. Šimkovic, A. Smetana, and P. Vogel, nuclear matrix elements, neutrino potentials and symmetry, Phys. Rev. C 98, 064325 (2018) .
- Rath et al. [2019] P. K. Rath, R. Chandra, K. Chaturvedi, and P. K. Raina, Nuclear Transition Matrix Elements for Double- Decay Within PHFB Model, Front. in Phys. 7, 64 (2019).
- Coraggio et al. [2022] L. Coraggio, N. Itaco, G. De Gregorio, A. Gargano, R. Mancino, and F. Nowacki, Shell-model calculation of 100Mo double- decay, Phys. Rev. C 105, 034312 (2022) .
- Pertoldi [2024] L. Pertoldi (LEGEND Collaboration), The first year of LEGEND-200 physics data in the quest for decay, in Presentatino at Neutrino 2024 conference, Milano, Italy (2024) .
- Adams et al. [2024] D. Q. Adams et al. (CUORE Collaboration), With or without ? Hunting for the seed of the matter-antimatter asymmetry, arXiv:2404.04453 .
- Park et al. [2024] K. S. Park, Y. D. Kim, K. M. Bang, H. K. Park, M. H. Lee, J. So, S. H. Kim, J. H. Jang, J. H. Kim, and S. B. Kim, Construction of Yemilab, Front. in Phys. 12, 1323991 (2024) .
- Prihtiadi [2018] H. Prihtiadi (COSINE-100), Muon detector and muon flux measurement at Yangyang Underground Laboratory for the COSINE-100 Experiment, PoS ICRC2017, 883 (2018).
- Kim et al. [2022b] W. T. Kim et al., Optimization of cryogenic calorimetric detection with lithium molybdate crystals for AMoRE-II experiments, JINST 17 (07), P07034.
- Kim et al. [2022c] W. T. Kim et al., Test Measurements of an MMC-Based 516-g Lithium Molybdate Crystal Detector for the AMoRE-II Experiment, J. Low Temp. Phys. 209, 299 (2022c).
- Agrawal et al. [2024b] A. Agrawal et al. (AMoRE), Projected background and sensitivity of AMoRE-II, Eur. Phys. J. C 85, 9 (2024b).