Improved description of di-lepton production in decays
Abstract Recently, the Belle collaboration reported the first measurements of the branching fraction and the spectrum of the pion-dielectron system. In an analysis previous to Belle’s results, we evaluated this branching fraction which turned out to be compatible with that reported by Belle, although with a large uncertainty. This is the motivation to seek for improvements on our previous evaluation of decays (). In this paper we improve our calculation of the vertex by including flavor symmetry breaking effects in the framework of the Resonance Chiral Theory. We impose QCD short-distance behavior to constrain most parameters and data on the spectrum reported by Belle to fix the remaining free ones. As a result, improved predictions for the branching ratios and hadronic/leptonic spectra are reported, in good agreement with observations. Analogous calculations for the strangeness-changing transitions are reported for the first time. Albeit one expects the spectrum to be measured in Belle-II and the observables with can be improved, it is rather unlikely that the channels can be measured due to the suppression factor .
1 Introduction
The search for signals of physics beyond the Standard Model (SM) requires a good understanding of SM processes either to discard possible backgrounds coming from it, such as large radiative corrections [1, 2, 3] or to have under good control hadronic contamination in precision tests of the SM [4]. In addition to offering a clean laboratory to test the hadronization of the weak currents, some semileptonic lepton decays, such as for , provide a good example where SM effects can be reliably calculated to disentangle possible New Physics signals hidden in precision observables.
In Ref. [5] we reported the first prediction of and the corresponding di-lepton spectrum where (this can be viewed as the crossed channels of lepton pairs produced in decays [6] in a larger kinematical domain); later on the Belle collaboration [7] announced the first searches of these decays. Recently, some of us have also reported similar studies of decays [8]. Together with the five lepton decays of tau leptons [9], they provide a better description of possible backgrounds in Lepton Number- or Lepton Flavor Violation searches in decays. Motivated by the Belle Collaboration studies [7], in this work we revisit our predictions for decays with the aim of improving the theoretical description of structure-dependent effects and to get reduced uncertainties. In addition, we make for the first time an analogous analysis of the strangeness-changing processes as well.
In these phenomena, the vertex plays a central role and its description is necessary to understand the radiative corrections to the decays [10].
This vertex also involves
parameters which are needed to describe the pion transition form factor (TFF),
which is required to compute the dominant piece (the pion pole) of the hadronic light-by-light contribution to
the anomalous magnetic moment of the lepton, . (The TFF can be obtained by our vector form factor (see section 3.2) by considering Bosé symmetry.) Although knowledge on these parameters could in principle help reduce the uncertainty on the hadronic part of [11], the data does not (and is not foreseeable to) have the necessary precision to improve actual predictions on the -pole contribution to .
The problem with the description of these effective vertices arises when one tries to describe them in terms of the fundamental fields of the Standard Model, since at energies below the scale, one can not give a proper perturbative description of color interactions.
However, the decay amplitude involving these vertices can be, for the sake of convenience, split into a part where the hadronic current and the electromagnetic interactions are computed using scalar QED (sQED), which we call structure-independent, and a part where more involved hadronic interactions are computed using an Effective Field Theory, called structure-dependent.
Thus, we try to surpass the difficulties of calculating the structure-dependent part using Resonance Chiral Theory (RT) [12, 13], which is an extension of Chiral Perturbation Theory (PT) [14, 15, 16] that includes resonances as active degrees of freedom. PT relies on the chiral symmetry group of the massless QCD Lagrangian. After it gets spontaneously broken, , the remaining symmetry gets explicitly broken when the masses of the light quarks are considered to be non-vanishing. The and di-lepton spectrum were computed previously in ref. [5] using such techniques, however, the novelty in the present treatment is that we include the effects of finite different light-quark masses as done for the Transition Form Factor of the pseudo Goldstone bosons for the Hadronic Light-by-Light part of the in ref. [17] (over [18], where these were neglected). We also give a more thorough treatment of the uncertainties than those in ref. [5], thus obtaining consistent results comparing with the corresponding form factors given in ref. [19]. Furthermore, the recent measurement of the branching fraction with a lower limit in the invariant mass of the pion and di-lepton pair [7], , motivates further this re-analysis, since in the GeV region the branching fraction gets saturated by the structure-dependent contribution. While most of the parameters of the model can be constrained by means of the high-energy behavior of QCD, some of them remain loose.
We fit these to the measured invariant mass spectra and also to the measurement of the branching fraction [7]. Despite the access to the invariant mass spectra data for the decay, we will only make use of the data for the decay. The reason not to use both sets is that the spectra have incompatibilities in several bins; also, when fitting individually the data set leads to unphysical conditions (see discussion in subsection 4.2). As a result, we improve our predictions, with correspondingly reduced uncertainties.
The outline of the paper is as follows. In section 2 the different contributions to the matrix element are collected. In section 3 we introduce the Lagrangian used for computing the structure-dependent corrections, calculate the corresponding form factors (including flavor-breaking corrections to our previous results) and derive the short-distance constraints among resonance couplings. In section 4 we carry out our phenomenological analysis, including a fit to Belle data and predicting the partner modes, yet to be discovered. We give our conclusions in section 5.
2 Amplitudes
For convenience, we take three kinds of contributions to the decay amplitude: the first called inner bremsstrahlung (IB) or structure independent (SI). The other two are the structure dependent (SD) ones, namely the polar- (V) and axial-vector (A) parts of the left-handed weak charged current. The IB amplitude can be obtained using the sQED Lagrangian, where the photon is either radiated by the lepton, off the pseudo Goldstone boson ( or ) or by the longitudinal propagation mode of the boson, a contribution which is needed to achieve gauge invariance of the total IB amplitude. The total IB contribution is shown in eq. (1), along with the parametrization of the SD parts as given in ref. [5]. The momenta definition is given in Figure 1.

The different contributions to the matrix element are ( for )
| (1a) | ||||
| (1b) | ||||
| (1c) | ||||
Here, and are the lepton electromagnetic and weak charged currents, respectively. We use and as the two independent Lorentz-invariants upon which the form factors () depend. In ref. [5] the axial amplitude was given only in terms of three form factors ( and a combination of and called ), since at chiral order , the and form factors are linearly dependent and can be written in terms of the pseudo Goldstone electromagnetic form factor [6]. Here, and cannot be recast in terms of , since we are considering contributions of chiral order . Furthermore, including the complete set of leading-order chiral symmetry breaking contributions will change the pion pole for the massive pion propagator. As a result, the and form factors become linearly independent and the axial-vector part of the left hadronic current cannot be expressed in terms of the two form factors and of refs. [19, 20, 21] (see discussion after eq. (24)).
3 Structure dependent form factors
3.1 The relevant operators
In this section we will present, for the sake of simplicity, only the relevant operators in the RT Lagrangian needed to compute the form factors, which are given in the next subsection. We will be concise here, for a more extended discussion see eg. ref. [17]. RT extends the domain of applicability of Chiral Perturbation Theory [16, 14, 15] (PT) by adding the light-flavored resonances as active degrees of freedom.
We start with operators involving no resonances, these being 111Although these terms also appear in the PT Lagrangian, their couplings get shifted in the presence of resonance contributions (see for instance [22, 23, 24]).
| (2) |
where the first term is given by the leading PT Lagrangian operators of chiral order [16, 14, 15], the second one is the anomalous Wess-Zumino-Witten Lagrangian of [25, 26] and the last three operators belong to the subleading odd-intrinsic parity sector Lagrangian [27]. We neglect operators not included in this Lagrangian. Congruently with refs. [19], [21] and [28], we will not consider any contribution whatsoever. In the first term, is the decay constant in the chiral limit, which we will set to MeV, and are chiral tensors [29], the former containing derivatives of the fields and external spin-one currents and the latter scalar currents involving the previous fields masses squared, , times even powers of such fields.
The equations of motion of the resonances give their classical fields in terms of series of chiral tensors of different order. The resonances are said to be integrated out (tree-level integration) when the classic fields are substituted in favor of chiral tensors in the resonant Lagrangian. Integrating the resonances out using the leading-order terms of the equations of motion very approximately saturates the (and leading ) contributions in the even-intrinsic parity sector [12, 13, 19]; therefore, we will not use the non-resonant set of operators for the sake of simplicity, since they are considered to yield negligible contributions. Since we will only consider leading-order terms in the resonances equations of motion, the chiral low-energy constants in the odd-intrinsic parity sector cannot be saturated upon resonance exchange [28], therefore we have to include the three contributing terms [27]:
| (3) | |||||
where the following chiral tensors [29] enter: gives odd powers of the fields with factors involving or , is the covariant derivative and includes spin-one left and vector external currents through the connection and yields the field-strength tensors of the charged-weak or electromagnetic fields.
We turn next to those operators with one resonance field, in either intrinsic parity sector,
| (4) |
In turn, the first piece can be further divided according to the quantum numbers of this resonance
| (5) |
The contributions with one vector resonance read 222 (analogously for axial resonances below) is a matrix in flavor () space and we use the antisymmetric tensor formalism for spin-one fields for convenience [12, 13]. [12, 19]
| (6) |
where the field (we assume ideal mixing of neutral mesons) has an analogous flavor structure as the pseudo Goldstone field , namely
| (7) |
In eq. (6), the first two operators give the contribution from the coupling of vector resonances to external fields in the chiral limit and the last term gives the flavor-breaking corrections to such couplings. Our , using the notation in ref. [19]. This last operator is the only one included from the full basis of even-intrinsic parity operators in ref. [19] since it is the single one that can contribute to the breaking in the coupling. There are, however, two reason to disregard basis of operators in the even-intrinsic parity sector: The operators that are relevant to the process can be dismissed on the basis of resonance field redefinitions333Through the redefinition of the vector resonance field it is possible to cancel the operator [19],
however, we keep it in order to show the full basis of possible breaking operators since we do not consider the full even-intrinsic parity basis of ref. [19]. We will show later that this is consistent, since the short distance constraints give .; if we, however, keep such operators, they will only give subleading contributions to those from the first two operators in eq. (6) with no contribution to -breaking vertices.
The axial resonance operators present a similar feature and an analogous flavor-space structure to that of the vector mesons. This is, the one-resonance even-intrinsic parity operators for axial resonances in ref. [19] can be absorbed through field redefinitions. We will therefore disregard any contribution from this part of the Lagrangian, including the breaking terms to the axial-vector resonance coupling to external currents, namely, the vertex. The remaining contributions with one resonance field are [12]
| (8) |
with a matrix in three-flavors space containing the lightest pseudoscalar resonances. The inclusion of the pseudoscalar resonance is necessary in order to obtain consistent short-distance constraints in and Green’s functions [19, 28, 30, 31]. All Feynman diagrams involving these resonances will give breaking contributions to the amplitude due to the last term in eq. (8). We have neglected other spin-zero resonance contributions (scalar and heavier pseudoscalar resonances [5]), which are not needed for theoretical consistency and are irrelevant phenomenologically. The odd-intrinsic parity contributions to are [32] 444Since we are only considering operators with one field, these constitute a basis. In the general case, the basis is given in ref. [28]. The translation between them can be read from ref. [30].
| (9) |
with the operators
| (10) | |||||
In the following, we quote those terms bilinear in resonance fields (we do not display the kinetic terms for the resonances, which can be found in ref. [12], as they do not contribute to the effective vertices).
| (11) |
with [19, 33, 34, 35] 555The operator with coefficient allows to account for breaking effects in the vector resonance masses, in agreement with phenomenology.
| (12) |
| (13) |
The operators appearing in the two previous equations are ()
| (14) | |||||
There is only one relevant operator with three resonance fields in either parity sector
| (15) |
Operators with a higer number of resonant fields will not be included, since otherwise one has to include subleading diagrams with loops where some of the internal lines are given by resonances. The present analysis is restricted to tree-level diagrams, which should already capture the leading effects associated with resonance exchange. One-loop diagrams with resonances are expected to be a numerically small correction since these would be subleading in the expansion [4]. Such corrections will be neglected due to the already sizeable number of parameters involved in the tree-level analysis and the current precision of the experimental data.
3.2 Form Factors
In this section we quote our results for the different contributions to the , , , form factors, for . All resonance propagators are to be understood as provided with an energy-dependent width (, ) computed within , using those in refs. [36] (), [37] () and [38, 39] (, including the cuts [40]). A constant width will suffice for the very narrow and mesons (their PDG [41] values will be taken). For the states we will follow [42].

The vector form factors are ( in QCD)
| (16) |
| (17) |
where and we have used the combinations of coupling constants [43]
| (18) | |||
and starred coefficients absorb breaking contributions induced by in eq. (6) and pseudoscalar resonances, respectively. Their expressions are given at the end of this subsection, after eq. (24).

The axial form factors are 666We note two mistakes in writing in ref. [5], see Appendix A. The result written here agrees with the one in ref. [44] for .
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
It is worth to notice that by replacing the propagator in and with the massless pole propagator, one recovers the linear dependence between both form factors, thus getting a congruent expression with those in reference [19]. Therefore, the short-distance constraints obtained in this reference can be used as shown there if the Weinberg’s sum rules are imposed. We, however, do not make use of these sum rules, as are fitted to data (see discussion in sections 3.3 and 4.2).
We introduced the short-hand notation
| (25) | |||
for the shifts appearing also in [17]. 777As mentioned in section 3.1, a similar shift can be introduced in , however, the operator responsible for such shift can be absorbed through axial resonance field redefinitions [19].
We employed several starred coefficients including breaking contributions, as given below:
| (27) |
implying
| (28) | |||
| (29) |
yielding
| (30) |
We have first shown here the correction to appearing in , while the remaining starred couplings were already introduced in ref. [17].
3.3 Short-distance constraints
We will demand that the different form factors have an asymptotic behaviour in agreement with QCD [45, 46]. Specifically, we will require their vanishing for large in the and cases. We will do this first in the chiral limit and then at 888Since we are considering a complete basis of chiral symmetry breaking operators at order , we neglect higher-order chiral corrections., paralleling the discussion in ref. [17] for the neutral pseudoscalar transition form factors. In this way, we find the following relations:
-
•
, :
(31) (32) (33) (34) -
•
, :
(35) (36) -
•
, : Same constraints as for the case, since both form factors 999 and form factors are also identical in this limit for or , obviously. are identical in the symmetry limit.
-
•
, :
(37)
For the sake of predictability and in order to further constrain the parameters in the form factor, we use the Green function, , constraints [28] obtained from the high-energy behaviour when and and matching to the Operator Product Expansion (OPE) leading terms in the chiral and large- limits. These give
| (38) |
Notice that these constraints coincide with our expressions in eqs. (31-34) and that they imply
| (39) |
One can see that from the definition of (eqs. (27) and (28)) combined with the last expression and the short-distance constraints eqs. (34), (36) and (38) would imply a relation of in terms of and , namely
| (40) |
however, we do not rely on this relation since comparison with previous phenomenology [34, 35] shows that the absolute value of eq. (40) obtained for MeV and GeV is an order of magnitude smaller than required by phenomenology.
On the other hand, no relation among parameters of the axial form factors can be obtained by taking the infinite virtualities limit, since it already has the right asymptotic behavior. Instead, we will rely on the relations obtained using the Green Function101010See, however, the discussion in section 6.2 of [47] comparing these short-distance constraints to the results in refs. [48, 20]. [21] in an analogous manner to that done for the Green Function.
We recall that the simultaneous analysis of the scalar form factor [49, 50] and the SS-PP sum rules [51] yields . Additionally, notice that depend on . In turn, depends on and . The appropriate short-distance behaviour of the Green Function [21] fixes all of them but or, in other words , as noted in ref. [19]
| (41) |
Despite the relation for from the scalar form factor and the SS-PP Green’s function, notice that there is no need for one since always appears multiplied by one of the other parameters to be constrained. We will also make use of the constraint [12]
| (42) |
In order to gain predictability, we will use the values of , and given for the best fit of reference [17], namely (their correlations are given in the quoted reference)
| (43) | |||||
4 Phenomenological analysis
4.1 Phase space
In order to compare our results with those of ref. [5] we use the same phase space configuration. We recall that the variables in ref. [5] are the invariant mass squared of the pseudo Goldstone and the neutrino, , the invariant mass squared of the charged lepton pair, , two polar angles and one azimuthal angle , with the integration limits given by
| (44a) | ||||
| (44b) | ||||
| (44c) | ||||
If we identify the particle with tag 1 with , the invariant mass of the weak gauge boson can be related to the Lorentz invariants of eqs. (44) via
| (45) |
where and , being , the Källén lambda function. Eq. (45) allows us to eliminate in favor of . The importance of the phase space configuration with instead of relies on the need to compute the spectrum in order to fit unconstrained parameters to the Belle invariant mass spectrum [7]. The kinematic limits on the non-angular variables for this phase space configuration read
| (46a) | ||||
| (46b) | ||||
| (46c) | ||||
where
| (47) | |||||
With this, the differential decay rate is given as
| (48) | |||||
4.2 Fit to data
Short-distance QCD behaviour [17, 19] does not constrain all parameters. Thus, we fit some of the remaining unknowns using the invariant mass spectra of the boson, , measured by the Belle collaboration [7]. We start with a four parameters fit (, , and , the branching fraction, are floated). Despite the fact that the whole spectrum has been measured, not all the data is available for this minimization since points below GeV were used as a control region to validate the Monte Carlo simulation, leaving thus the most sensitive part to SD contributions as the signal region [7]; therefore we use for the minimization the data above the cut GeV.
We use only the data set for the mode 111111This is the one shown in the plots of ref. [7]. We have checked better agreement with the Monte Carlo simulation (based on our previous paper [5], see also [52, 53]) for this mode with respect to its charge-conjugated mode.. Comparison of this with the expected signal events distribution in this reference allows us to roughly quantify the deconvolution of signal from detector, which we ignore. We have assumed this to be an energy-independent effect for simplicity, and taken it into account as a systematic uncertainty in the data. This error turns out to be comparable to the one reported by Belle for the branching fraction measured above the cut. In addition to this, the Belle collaboration used the expressions of our ref. [5]; which however had typos in some of the terms (see Appendix A). Besides, trying to keep our previous analysis as simple as possible, it resulted incomplete in the sense of Green’s function analysis121212Pseudoscalar resonance exchange and operators in the and form factors are lacking in our ref. [5]. This leads to relating both form factors to the electromagnetic form factor [6]., which altogether could lead to biased estimations of the decay observables. Both reasons motivate our choice of fitting the total branching fraction, , as an additional parameter instead of simply computing it from the decay width expression in eq. (48).
We used the relation
| (49) |
where is the total number of events, is the number of events in a given bin and is the bin width. We thus minimize the given by
| (50) |
where is the experimental uncertainty in a given bin, is the branching ratio for GeV reported by Belle [7], its error and the one obtained integrating our differential decay width above this cut. We recall that [7], where the first uncertainty is statistical, the second is systematic, and the third is due to the model dependence. In our fits, we have first realized that, varying all four parameters, there happen to be many quasidegenerate best fits and that the correlations among the fit parameters (, , and ) are always large. We interpret this as the data not being precise enough to disentangle the physical solutions among all close to the global minimum. Then, we proceeded to further simplify the fits by making constant one of these four parameters (not , as our systematic error due to unfolding is comparable to the overall uncertainty of ).
We present two sets of fits as our reference results. One fixing MeV (, in agreement with [30]), and the other setting (which is in the ballpark of previous estimates for , and neglects the contribution of pseudoscalar resonances to the starred coupling, see [54] and refs. therein). Considering individually the or sets we find that, apart from the incompatibility among both sets in several bins, the data set leads to the unphysical condition . Also, fixing to its short-distance prediction MeV [30], yields fits with larger that we disregard.
One way of interpreting this feature would be that excited resonances (at least the state and its interference with the resonance) are needed for an improved description of the data. However, given the errors of the measurement and the lack of invariant mass distribution data we are not able to test such more sophisticated theory input, which introduces several additional parameters that remain unconstrained after applying the short-distance conditions (see, e. g. ref. [55]). We thus understand that our fitted values of are effectively capturing missing dynamics in our description (such as the excitations).

Considering the Weinberg sum rules [56]
| (51a) | ||||
| (51b) | ||||
and taking only the contributions from the lightest nonet of resonances (along with ), one finds that the fitted value for approaches the prediction from these relations, namely that131313Also found from short distance constrictions of vector and axial form factors considering only one multiplet [12, 13]. . However, and as has been stated above, the consistent short distance limit when operators contributing to 2 and 3-point Green’s Functions are considered should be [30] . This makes us believe that the dynamics from heavier copies of the meson must be affecting the constraints on the decay constant . Of course, these copies will undoubtedly affect the contribution to the chiral-order LECs of the non-resonant Lagrangian when integrating the resonances out, however, we still assume they approximately saturate them and neglect the operators of such Lagrangian.141414Since the copies of the must have analogous dynamics, the operators contributing to the LECs of must be the same with the sustitution (and so on for heavier copies). Thus, their contributions must read (52) with and .
Our results are shown in table 1, the corresponding is reasonably good and is in agreement with the Belle data within less than 1 standard deviation in both cases. According to these results, we cannot exclude that pseudoscalar resonances give sizeable contributions to . We consider both fit results in table 1 as benchmarks for our predictions in the remainder of this work (we will refer to them as ’the two sets’). The difference among the corresponding two results can be taken as a first, rough estimate of our model-dependent error.
| set 1 | set 2 | |
| MeV | ||
| 130 MeV | () MeV | |
| (135.5) MeV | () MeV | |
| 102 | ||
| 31.1/26 | 31.4/26 |
4.3 Predictions for the decays
| set 1 | set 2 | IB | |
|---|---|---|---|
By generating 2400 points in the parameter space making a Gaussian variation of parameters, taking into account the correlations among them, we computed the sum of the SD and the SD-SI interference contributions to the branching fractions for the full phase space. We also computed for the and channel the SI contribution to with the cut GeV,
| (53) |
As expected, it is a factor smaller than the Belle measurement, which confirms GeV is a good cut to study structure-dependent effects.


Thus, the adding the SI contribution gives the total branching ratios shown in table 2, where the first (dominant) error includes the uncertainty from unfolding and from the difference between and BR and the second error was obtained from the Gaussian distribution of the fitted parameters. Also, in the same table, we show the SI contributions to the branching fractions for the different decay channels in the complete phase space.


From the discussion at the beginning of section 4.2 and from the results shown in table 2, we take the of each decay channel to be within the range obtained from the union of the intervals given by each set of fitted parameters, the latter ranges defined as the intervals given by each central value of Table 2 and its uncertainties. Also, we computed the spectra for the different decay channels shown in Figures 5 and 6 using both sets of fitted parameters, where the error band was obtained by taking the difference between them. The same was done for the dilepton spectra in Figures 7 and 8. Measurement of these observables at Belle-II [57] will be crucial for further reducing the uncertainties shown.




5 Conclusions
Motivated by recent measurements of the Belle Collaboration [7], in this paper we present an improved prediction of the decay.
This includes a more accurate description of the structure-dependent parts of the decay amplitudes, by taking into account the first order flavor-breaking corrections to the form factors involved in the vertex. As done for the Green’s function [30], we found that the inclusion of the pseudoscalar resonance is needed in order to obtain compatible expressions between the Green’s function and the form factors. In the high-energy limit we find that these expressions give the same constraints on the parameters of the resonance Lagrangians, as happens in the case.
We have obtained a reasonably good fit of the parameters that remain unconstrained after applying the SD behaviour to the form factors. A better set of data for the invariant mass spectrum of the hadronic current would allow to determine physically meaningful parameters in a unique way. It is worth to recall that despite the fact that we had access to the spectra obtained from Belle, we found some inconsistencies that make unreliable the fits to data from both positive and negative tau decays (see discussion in section 4.2). We have therefore only considered the data set of the decays. From the results in Table 2, we conclude that our best result for the branching fractions is the union of ranges given for both fitting sets. This is shown in Table 3, where the central value is the mean of the union of these intervals. The results for the case agree with those in ref. [5], where for and for were predicted. Thus, we have reached a more precise determination of the branching ratios for the decay channels than the previous ones in ref. [5]. Also, similar observables for the channels are predicted for the first time.
Despite the great achievement of the Belle collaboration [7] discovering the decays, our study shows the need for better data (hopefully from Belle-II [57] and forthcoming facilities) in order to increase our knowledge of these decay modes. The spectrum shown in Figure 4 is consistent with the destructive interference of the and resonances; however, current data uncertainties prevent investigating the dynamics involved in the interplay of such resonances. The effect of excitations does not seem, however, negligible, since by imposing the known behaviour [30] to the fit gives a far worse than those in Table 1, which are closer to (which holds with a minimal resonance Lagrangian beyond which we go in this and in our previous work on the subject). We assume that the effect of these heavier copies of the meson are responsible for this shift in the value of .
Acknowledgements
We are indebted to Denis Epifanov and Yifan Jin for leading the Belle analysis of these decays, and measuring for the first time the decays. We specially acknowledge Yifan Jin for sharing with us detailed information on their study and providing us with the simulated Monte Carlo generation. We also aknowledge Pablo Sánchez Puertas for usefull comments on short distance constraints. A.G. was supported partly by the Spanish MINECO and European FEDER funds (grant FIS2017-85053-C2-1-P) and Junta de Andalucía (grant FQM-225) and partly by the Generalitat Valenciana (grant Prometeo/2017/053). G.L.C. ackowledges funding from Ciencia de Frontera Conacyt project No. 428218 and perfil PRODEP IDPTC 162336, and P.R. by the SEP-Cinvestav Fund (project number 142), grant PID2020-114473GB-I00 funded by MCIN/AEI/10.13039/501100011033 and by Cátedras Marcos Moshinsky (Fundación Marcos Moshinsky), that also supported A. G.
Appendix A Previous and current expressions of axial form factors
When we compare the expressions for the axial part of the decay amplitude we see that the following relations should be fulfilled
| (54a) | |||
| (54b) | |||
| (54c) | |||
where . There is, however, some mistakes in the form factors of reference [5]. There we have
| (55) |
where and are the propagators of the and respectively. However, when we neglect the contributions stemming from the -breaking contributions in eq. (19) we get
| (56) |
where we show in red the factors and terms missing in the expression for of ref. [5].
Furthermore, since ref. [5] works in the chiral limit and are linearly dependent and are replace with the form factor , such that
| (57a) | ||||
| (57b) | ||||
As said previously, ref. [5] works on the chiral limit, therefore the term in eqs. (21) and eqs. (23) do not contribute. Nevertheless and for the sake of simplicity, ref. [5] gives in terms entirely of the part of the vector form factor. This means that the contribution from the meson is being neglected.

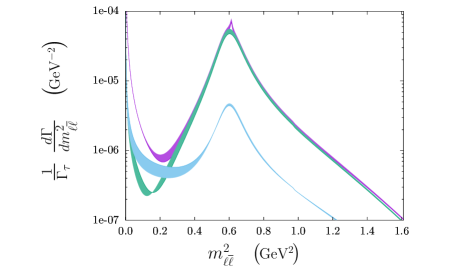
As a consequence of all this, we can see that the total spectrum gets really affected by such differences: We computed only the contribution of the axial amplitude to the spectrum (i.e., turning off the SI and vector contributions in eqs. (1) and keeping only that of eq. (1c)), and computed also such spectrum but with the axial form factors of reference [5]. The complete spectrum is shown in Figure 9 with a double logarithmic scale and a zoom with a logarithmic scale for the vertical axis in Figure 10.
As shown in ref. [5], the importance of the SD contributions start at . Thus, as shown in Figures 9 and 10, the total invariant mass spectrum (purple band) gets almost completely saturated by the axial contribution151515at lower energies, the total invariant mass spectrum gets saturated by the SI contribution (green band) at . In these Figures we also show the spectrum obtained with the mistakes shown in eq. (A) (pale-blue band), keeping our constrained couplings and values for fitted parameters, we see that there is an important difference between the spectra with the new and old form factors. Their contribution to the branching fraction of the decay obtained from the spectra are an order of magnitude away
| (58a) | ||||
| (58b) | ||||
In contrast, we computed also the contribution from the axial amplitude to the branching ratio of the decay as done for the complete in Table 2 for the new form factors both, considering (fb) and neglecting (fc) the breaking terms
| (59a) | ||||
| (59b) | ||||
showing thus that the difference between our results and those in ref. [5] stems from the differences between eqs. (A) and (A), and not from the breaking terms.
References
- [1] A. Guevara, G. López-Castro and P. Roig, Phys. Rev. D 95 (2017) no.5, 054015.
- [2] T. Husek, K. Kampf, S. Leupold and J. Novotny, Phys. Rev. D 97 (2018) no.9, 096013.
- [3] K. Kampf, J. Novotný and P. Sánchez-Puertas, Phys. Rev. D 97 (2018) no.5, 056010.
- [4] A. Guevara, G. López Castro, P. Roig and S. L. Tostado, Phys. Rev. D 92 (2015) no.5, 054035.
- [5] P. Roig, A. Guevara and G. López Castro, Phys. Rev. D 88 (2013) no.3, 033007.
- [6] J. Bijnens, G. Ecker and J. Gasser, Nucl. Phys. B 396 (1993), 81-118.
- [7] Y. Jin et al. [Belle], Phys. Rev. D 100 (2019) no.7, 071101.
- [8] J. L. Gutiérrez Santiago, G. López Castro and P. Roig, Phys. Rev. D 103 (2021) no.1, 014027.
- [9] A. Flores-Tlalpa, G. Lopez Castro and P. Roig, J. High Energ. Phys. 2016, 185 (2016).
- [10] M. A. Arroyo-Ureña, G. Hernández-Tomé, G. López-Castro, P. Roig and I. Rosell, [arXiv:2107.04603 [hep-ph]], to be published in Phys. Rev. D, and work in progress.
- [11] T. Aoyama et al., The Muon g-2 Theory Initiative, Phys. Rept. 887 (2020) 1-166.
- [12] G. Ecker, J. Gasser, A. Pich and E. de Rafael, Nucl. Phys. B 321 (1989), 311-342.
- [13] G. Ecker, J. Gasser, H. Leutwyler, A. Pich and E. de Rafael, Phys. Lett. B 223 (1989), 425-432.
- [14] J. Gasser and H. Leutwyler, Annals Phys. 158 (1984), 142.
- [15] J. Gasser and H. Leutwyler, Nucl. Phys. B 250 (1985), 465-516.
- [16] S. Weinberg, Physica A 96 (1979) no.1-2, 327-340.
- [17] A. Guevara, P. Roig and J. J. Sanz-Cillero, JHEP 06 (2018), 160.
- [18] P. Roig, A. Guevara and G. López Castro, Phys. Rev. D 89 (2014) no.7, 073016.
- [19] V. Cirigliano, G. Ecker, M. Eidemüller, R. Kaiser, A. Pich and J. Portolés, Nucl. Phys. B 753 (2006), 139-177.
- [20] M. Knecht and A. Nyffeler, Eur. Phys. J. C 21 (2001), 659-678.
- [21] V. Cirigliano, G. Ecker, M. Eidemüller, A. Pich and J. Portolés, Phys. Lett. B 596 (2004), 96-106.
- [22] V. Bernard, N. Kaiser and U. G. Meissner, Nucl. Phys. B 364 (1991), 283-320.
- [23] J. J. Sanz-Cillero, Phys. Rev. D 70 (2004), 094033.
- [24] Z. H. Guo and J. J. Sanz-Cillero, Phys. Rev. D 89 (2014) no.9, 094024.
- [25] J. Wess and B. Zumino, Phys. Lett. B 37 (1971), 95-97.
- [26] E. Witten, Nucl. Phys. B 223 (1983), 422-432.
- [27] J. Bijnens, L. Girlanda and P. Talavera, Eur. Phys. J. C 23 (2002), 539-544.
- [28] K. Kampf and J. Novotny, Phys. Rev. D 84 (2011), 014036.
- [29] J. Bijnens, G. Colangelo and G. Ecker, JHEP 02 (1999), 020.
- [30] P. Roig and J. J. Sanz Cillero, Phys. Lett. B 733 (2014), 158-163.
- [31] T. Kadavý, K. Kampf and J. Novotny, JHEP 10 (2020), 142.
- [32] P. D. Ruiz-Femenía, A. Pich and J. Portolés, JHEP 07 (2003), 003.
- [33] D. Gómez Dumm, A. Pich and J. Portolés, Phys. Rev. D 69 (2004), 073002.
- [34] V. Cirigliano, G. Ecker, H. Neufeld and A. Pich, JHEP 06 (2003), 012.
- [35] Z. H. Guo and J. J. Sanz-Cillero, Phys. Rev. D 79 (2009), 096006.
- [36] D. Gómez Dumm, A. Pich and J. Portolés, Phys. Rev. D 62 (2000), 054014.
- [37] M. Jamin, A. Pich and J. Portolés, Phys. Lett. B 640 (2006), 176-181.
- [38] D. G. Dumm, P. Roig, A. Pich and J. Portolés, Phys. Lett. B 685 (2010), 158-164.
- [39] I. M. Nugent, T. Przedzinski, P. Roig, O. Shekhovtsova and Z. Was, Phys. Rev. D 88 (2013), 093012.
- [40] D. G. Dumm, P. Roig, A. Pich and J. Portolés, Phys. Rev. D 81 (2010), 034031.
- [41] P. A. Zyla et al. [Particle Data Group], PTEP 2020 (2020) no.8, 083C01.
- [42] Z. H. Guo, Phys. Rev. D 78 (2008), 033004.
- [43] D. Gómez Dumm and P. Roig, Phys. Rev. D 86 (2012), 076009.
- [44] Z. H. Guo and P. Roig, Phys. Rev. D 82 (2010), 113016.
- [45] G. P. Lepage and S. J. Brodsky, Phys. Rev. D 22 (1980), 2157.
- [46] S. J. Brodsky and G. R. Farrar, Phys. Rev. Lett. 31 (1973), 1153-1156.
- [47] V. Cirigliano and I. Rosell, JHEP 10 (2007), 005.
- [48] B. Moussallam, Nucl. Phys. B 504 (1997), 381-414.
- [49] M. Jamin, J. A. Oller and A. Pich, Nucl. Phys. B 587 (2000), 331-362.
- [50] M. Jamin, J. A. Oller and A. Pich, Nucl. Phys. B 622 (2002), 279-308.
- [51] M. F. L. Golterman and S. Peris, Phys. Rev. D 61 (2000), 034018.
- [52] O. Shekhovtsova, T. Przedzinski, P. Roig and Z. Was, Phys. Rev. D 86 (2012), 113008.
- [53] S. Antropov, S. Banerjee, Z. Was and J. Zaremba, [arXiv:1912.11376 [hep-ph]].
- [54] J. A. Miranda and P. Roig, Phys. Rev. D 102 (2020), 114017.
- [55] V. Mateu and J. Portolés, Eur. Phys. J. C 52 (2007), 325-338.
- [56] S. Weinberg, Phys. Rev. Lett. 18 (1967), 507-509
- [57] E. Kou et al. [Belle-II], PTEP 2019 (2019) no.12, 123C01; PTEP 2020 (2020) 2, 029201 (erratum).