Implication of for generic neutrino interactions in effective field theories
Abstract
In this work we investigate the implication of from the recent KOTO and NA62 measurements for generic neutrino interactions and the new physics scale in effective field theories. The interactions between quarks and left-handed Standard Model (SM) neutrinos are first described by the low energy effective field theory (LEFT) below the electroweak scale. We match them to the chiral perturbation theory (PT) at the chiral symmetry breaking scale to calculate the branching fractions of Kaon semi-invisible decays and match them up to the SM effective field theory (SMEFT) to constrain new physics above the electroweak scale. In the framework of effective field theories, we prove that the Grossman-Nir bound is valid for both dim-6 and dim-7 LEFT operators, and the dim-6 vector and scalar operators dominantly contribute to Kaon semi-invisible decays based on LEFT and chiral power counting rules. They are induced by multiple dim-6 lepton-number-conserving operators and one dim-7 lepton-number-violating operator in the SMEFT, respectively. In the lepton-number-conserving transition, the decays provide the most sensitive probe for the operators with component and point to a corresponding new physics scale of associated with a single effective coefficient. The lepton-number-violating operator can also explain the observed discrepancy with the SM prediction within a narrow range , which is consistent with constraints from Kaon invisible decays.
I Introduction
Recently, the KOTO experiment at J-PARC Shinohara ; Lin and the NA62 experiment at CERN Ruggiero announced preliminary results of Kaon semi-invisible decays Kitahara et al. (2019)
| (1) | |||||
| (2) |
at the 95% confidence level (CL). They update the upper limit on the decay rate of from BNL E949 Artamonov et al. (2008, 2009) and the limit on the branching ratio from the 2015 run at KOTO itself Ahn et al. (2019)
| (3) | |||||
| (4) |
at the 90% CL. These decays are mediated by flavor changing neutral currents (FCNC) and thus are suppressed by the GIM mechanism in the Standard Model (SM), giving and , respectively Buras et al. (2006); Brod et al. (2011); Buras et al. (2015). In the SM no events are expected from the above Kaon rare decays, but KOTO reported three signal events in the search of . There exist quite a few works trying to explain these intriguing events reported by KOTO Kitahara et al. (2019); Fabbrichesi and Gabrielli (2019); Egana-Ugrinovic et al. (2019); Dev et al. (2019) (or constrain particular new physics (NP) models Fuyuto et al. (2015); Mandal and Pich (2019); Calibbi et al. (2019)) and meanwhile avoid the violation of its relation with the decay, that is the Grossman-Nir bound Grossman and Nir (1997). These efforts require the introduction of a new invisible degree of freedom with the mass scale being around MeV.
The interpretation of the KOTO result depends on not only whether the invisible particles are viewed as neutrinos, but also the experimental uncertainties. Even if we only take into account the statistical uncertainties at 95% CL for neutrino final states, there is allowed space for heavy NP beyond the SM consistent with both and measurements and satisfying the Grossman-Nir bound. As one can see from the Fig. 1 in Ref. Kitahara et al. (2019), the allowed region is rather delimited and not far away from the SM prediction. It can provide a constraint on the relevant quark-neutrino interactions and shed light on the search for generic neutrino interactions in the future. Thus, without introducing any new light particles, we focus on heavy NP contributing to the generic quark-neutrino interactions and generically confine the NP scale from the allowed region of and measurements. As the neutrino flavor is not measured and the fermionic nature of neutrinos is not determined, the semi-invisible Kaon decays are sensitive probes for a range of interactions.
In this work, we will use an effective field theory approach, where NP is described by a set of non-renormalizable operators which are added to the SM Lagrangian
| (5) |
Here are the dimension- (dim- in short below) effective operators. Each Wilson coefficient is associated with a NP scale . We first use the low energy effective field theory (LEFT) Jenkins et al. (2018a, b) to describe the interactions between quarks and left-handed SM neutrinos below the electroweak scale. Then, in order to calculate the Kaon decay rate, we match the LEFT operators to chiral perturbation theory (PT) Gasser and Leutwyler (1984, 1985) at the chiral symmetry breaking scale to take into account non-perturbative QCD effects. The branching fractions of Kaon semi-invisible decays are evaluated in terms of the Wilson coefficients and neutrino bilinears as external sources. Finally, we match them up to the Standard Model effective field theory (SMEFT) to constrain new physics above the electroweak scale Buchmuller and Wyler (1986); Grzadkowski et al. (2010); Lehman (2014); Liao and Ma (2016); Henning et al. (2017); Liao and Ma (2017).
The paper is outlined as follows. In Sec. II, we describe the LEFT basis and give the quark-neutrino operators relevant for our study. The LEFT operators are matched to PT and we show the general expressions for the branching fractions of Kaon semi-invisible decays. We then match the results to the SMEFT in Sec. III. In Sec. IV we show the implication of for new physics and discuss other constraints. Our conclusions and some discussions are drawn in Sec. V. Some calculation details for Kaon decays are collected in the Appendix.
II Generic neutrino interactions and calculation in PT
II.1 Generic quark-neutrino operators in LEFT basis
We consider the effective operators for neutrino bilinears coupled to SM quarks in the framework of LEFT obeying SUU gauge symmetry. In the basis of LEFT for neutrinos, the only dim-5 operator contributing to the neutrino magnetic moments is Canas et al. (2016)
| (6) |
where is the electromagnetic field strength tensor and denote left-handed active SM neutrinos. Its SMEFT completion has been investigated by Cirigliano et al. in Ref. Cirigliano et al. (2017). In principle, the neutrino magnetic moment operator can yield the process through a long-distance contribution with one vertex connecting to the transition operator . The corresponding coefficient is estimated to be in the SM Tandean (2000). There also exists a strong constraint on Canas et al. (2016). We thus conclude that the contribution from this operator to transition is negligible. There are also the dim-6 operators Jenkins et al. (2018a) with lepton number conservation (LNC, )
| (7) | ||||||
| (8) |
and those with lepton number violation (LNV, )
| (9) | ||||||
| (10) | ||||||
| (11) |
where and denote the left- (right-) handed up-type and down-type quark fields in mass basis, respectively. Note that the tensor operator vanishes for identical neutrino flavors (with ). The flavors of the two quarks and those of the two neutrinos in the above operators can be different although we do not specify their flavor indexes here. For the notation of the Wilson coefficients, we use the same subscripts as the operators, for instance together with , where denote the down-type quark flavors and are the neutrino flavors. In the following we will study the transition and thus only consider the operators with down-type quarks and .
II.2 Matching to the leading order of PT
The dim-6 quark-neutrino operators can be matched onto the meson-lepton interactions through the PT formalism by treating the lepton currents together with the accompanied Wilson coefficients as proper external sources. The QCD-like Lagrangian with external sources for the first three light quarks () can be described as
| (12) |
where the flavor space 3 matrices are the external sources related with the corresponding quark currents. One can extract the relevant external sources from the above dim-6 effective operators. On the other hand, based on Weinberg’s power-counting scheme, the most general chiral Lagrangian can be expanded according to the momentum and quark mass. The chiral Lagrangian with external sources at leading order reads Gasser and Leutwyler (1984, 1985)
| (13) |
where is the standard matrix for the Nambu-Goldstone bosons
| (17) |
with the constant being referred to the pion decay constant in the chiral limit. The covariant derivative of and are expressed in terms of the external sources
| (18) |
where the constant is related to the quark condensate and by . For the later numerical estimation, we take Colangelo and Durr (2004) and Cirigliano et al. (2017); Patrignani et al. (2016). The Nambu-Goldstone bosons parameterized by and the (pseudo-)scalar sources transform as and , where () is () transformation.
By inspecting the dim-6 operators related to the transition (the symbol ‘ ’ here indicating the neutrino pair can be either LNC or LNV 111Below we use to generally denote the experimental processes. appears when both and final states can occur in the analytical expressions of the theoretical calculation unless a LNC or LNV process is specified in our discussion.), we find that only the LNC operators and LNV operators can contribute to the leading order chiral Lagrangian. The tensor operator only contributes to the next-to-leading order chiral Lagrangian at . They lead to the following external sources
| (19) | |||||
| (20) | |||||
| (21) | |||||
| (22) | |||||
| (23) | |||||
| (24) | |||||
| (25) | |||||
| (26) |
After expanding , i.e. and the insertion of the above external sources into the Lagrangian in Eq. (13), we obtain the effective Lagrangians for and at the leading order
| (27) | |||||
| (28) | |||||
The above Lagrangians fit to the relation
| (29) |
This relation is the result of the transition operators that change isospin by . By neglecting the small CP violation in mixing, for the transition, the relevant effective Lagrangian becomes
where the flavor indices are summed over all three neutrino generations. Note that the Wilson coefficients for the scalar operators are symmetric in the neutrino flavor indices. From the effective Lagrangian we derive the branching ratios for the decays and
| (31) | |||||
| (32) | |||||
The details of the calculation are collected in Appendix A. The functions parameterize the kinematics of the three-body decay and are defined as
| (33) | |||||
| (34) | |||||
| (35) | |||||
| (36) |
where and denote the physical mass and decay width of , respectively. is the mass of , is the Fermi constant and is the invariant squared mass of the final-state neutrino pair. From the hermiticity of the effective Lagrangian and the Cauchy-Schwarz inequality we derive the following relations for the Wilson coefficients in LEFT
Note that in the second inequality we used from the fact that the vector operator itself is hermitian. If we sum over neutrino flavors, the second relation above turns out to be
| (39) |
Based on the above inequalities, the branching ratios in Eq. (31) and Eq. (32) lead to
| (40) |
where is defined by
| (41) |
The upper bound on the ratio of branching ratios in Eq. (40) holds independent of the value of , because and agree to two significant figures. This result is nothing but the Grossman-Nir bound Grossman and Nir (1997) expected from the isospin relation in Eq. (29) and the CP-conserving limit for neutral Kaon system. The numerical value slightly differs from the standard G-N bound value of 4.3, because we do not consider isospin breaking and electroweak correction effects beyond the mass difference in the phase space integration Marciano and Parsa (1996). We obtain the G-N bound from the matching of LEFT to PT. Thus, as expected, the Grossman-Nir bound holds for dim-6 LEFT operators in leading order PT.
II.3 Dim-6 tensor operators and dim-7 operators in the chiral Lagrangian
For the tensor currents in Eqs. (11), we have to go beyond the leading order of chiral Lagrangian. The relevant Lagrangian at next-to-leading order is Cata and Mateu (2007)
| (42) |
where denotes the low-energy constant. In terms of the dim-6 tensor operator , the relevant tensor sources are
| (43) | ||||||
| (44) |
After inserting these external sources into the Lagrangian (42), we obtain the following interactions for transitions
| (45) | |||||
where .
We also investigate dim-7 tensor operators in LEFT. There happens to be only one such operator related with the transition under consideration, that is
| (46) |
which leads to the tensor sources to be
| (47) | ||||||
| (48) |
By analogy we expand the Lagrangian (42) to obtain the interactions with mesons
One can see that, for the next-to-leading order chiral Lagrangian with dim-6 and dim-7 tensor operators in LEFT, the isospin relation in Eq. (29) and thus the Grossman-Nir bound still hold. Note that the Eq. (II.3) vanishes for massless neutrinos. This implies that the non-zero contribution from dim-7 tensor operator appears at level, and therefore is further suppressed by additional factor. In addition, there are also two dim-7 vector-like LNV operators related to , which we list for completeness
| (50) |
These dim-7 operators are suppressed by compared with dim-6 operators and, like the above tensor operators, lead to sub-leading contributions. Thus, we neglect them in the following calculation and restrict us to only consider the scalar and vector dim-6 operators in LEFT.
III Matching to the SMEFT
Next we need to match the Wilson coefficients relevant for the processes in LEFT to those in SMEFT at the electroweak scale , by integrating out heavy SM particles. First of all, the SM contribution to the transition occurs at loop-level and it only matches to the LEFT operator by integrating out heavy SM particles at the one-loop level Buchalla and Buras (1994, 1999)
| (51) | |||||
| (52) | |||||
| (53) |
where the loop function can be found in Refs. Buchalla and Buras (1994, 1999) and higher order corrections are given in Ref. Brod et al. (2011). We take the central values for CKM elements from CKMfitter CKMfitter , and from Ref. He et al. (2018), and the rest from the PDG book Tanabashi et al. (2018). Then, to the leading order in PT, the analytical expressions in Eqs. (31) and (32) with the Wilson coefficients in Eqs. (51) predict the branching ratios of Kaon semi-invisible decays in the SM
| (54) |
which are consistent with SM predictions quoted in the literature Buras et al. (2006); Brod et al. (2011); Buras et al. (2015).
Secondly, the dim-6 SMEFT operators in the Warsaw basis Grzadkowski et al. (2010) and the dim-7 SMEFT operators in the basis given in Refs. Liao and Ma (2016); Lehman (2014) can induce the operators in the LEFT by integrating out the SM particles at tree-level. The LNC operators are obtained through matching with the dim-6 SMEFT operators in addition to the SM contribution in Eq. (51). To linear order in the SMEFT Wilson coefficients, the matching results are
| (55) | |||||
| (56) | |||||
| (57) | |||||
| (58) |
where is the unitary matrix transforming left-handed down-type quarks between flavor and mass eigenstates , . We choose to be approximately the identity matrix and neglect its effect in the following, i.e. the weak interaction eigenstates are the same as the mass eigenstates and the mixing originates from the up-type quarks. The convention for the Wilson coefficients is taken from Ref. Grzadkowski et al. (2010), with the corresponding SMEFT operators being
| (59) | ||||||||
| (60) |
The are the Pauli matrices, and .
For the LNV operators the leading contribution comes from dim-7 SMEFT operators, since dim-6 operators in SMEFT do not violate lepton number by two units and the dim-5 Weinberg operator is strongly constrained from neutrino masses and only indirectly contributes to the LEFT operators. The only dim-7 SMEFT operator which induces at tree-level is Liao and Ma (2016)
| (61) |
with the matching result for the Wilson coefficients at the electroweak scale
| (62) | |||||
| (63) |
We use subscripts , , and to represent the SM quark generation. The indices or denote the SM lepton flavor. As the operator violates quark flavor, the contribution to neutrino masses is suppressed and does not pose a stringent constraint. Note that the operator cannot be induced at tree-level from SMEFT. In the following we derive constraints on the SMEFT operators from and compare to the existing measurements of other related processes.
A brief comment on renormalization group corrections in LEFT is in order. As neutrinos neither couple to gluons nor photons, we only have to consider QCD corrections. Due to the QCD Ward identity, there are no QCD corrections to the vector operators at one-loop order and the running of the scalar operator can be simply obtained by noting that is invariant under QCD renormalization group corrections. Hence, the running of the scalar operator can be directly related to the QCD correction to the quark masses, .
IV Implication of for new physics and other constraints
In this section, based on the above LEFT coefficients in the leading-order chiral Lagrangian and the matching to SMEFT, we evaluate the constraints on new physics above the electroweak scale from the measurements and other rare decays. According to the decay branching ratios in Eqs. (31) and (32), to the leading order of the chiral Lagrangian, both vector and scalar LEFT operators contribute to the decays . They correspond to dim-6 LNC operators and one dim-7 LNV operator in the SMEFT, respectively. We will separately discuss the constraints on them below.
IV.1 Constraint on the LNC operators
From the branching ratios in Eqs. (31-32), and the matching results in Eqs. (55-58), we split the contributions to the amplitude into the SM part given in Eq. (51) and the NP part as follows
| (64) |
where the NP part is the linear combination of the Wilson coefficients of dim-6 LNC operators in the SMEFT in Eqs. (55-58)
| (65) | |||||
Taking the splitting in Eq. (64) and the experimental results in Eqs. (1, 2), we find
| (66) | |||||
| (67) |
The following generic relations can be immediately obtained
| (68) | |||
| (69) |
Now we first consider the lepton-flavor-conserving (LFC) case and ignore the lepton-flavor-violating (LFV) contributions for the time being. After electroweak symmetry breaking, the SMEFT operators in Eqs. (59-60) will yield FCNC processes with charged leptons at tree level. In particular, the leptonic Kaon decays provide a complementary probe of these operators. Thus, there are constraints on the coefficients with and from the Kaon decay modes . Although the matching conditions are not exactly the same for Kaon decays into neutrinos and charged leptons, we can evaluate a rough estimate on the NP scale associated with the linear combination of the coefficients responsible for both and . Under the assumption that the SM contribution has no interference with the NP contribution, there is a lower limit on the new physics scale of 83 TeV for from and 20 TeV for from . The detailed derivation of these constraints is reported in Appendix B.
More importantly, as the component with does not participate in any tau lepton rare decays or leptonic charged Kaon decays at tree-level, provides a unique opportunity to probe the SMEFT Wilson coefficients entering . If the NP contribution to Kaon semi-invisible decays originates only from the operator with , we have
| (70) | ||||
| (71) | ||||
| (72) |
The first term describes the SM contribution from decays to electron and muon neutrinos and the second term describes the decay to tau neutrinos and receives contributions from both the SM and NP. The LFV contributions are neglected as stated above.
We further require the above results fall within the KOTO and NA62 sensitivity in Eqs. (1,2)
| (73) | |||
| (74) |
If we denote the Wilson coefficient as
| (75) |
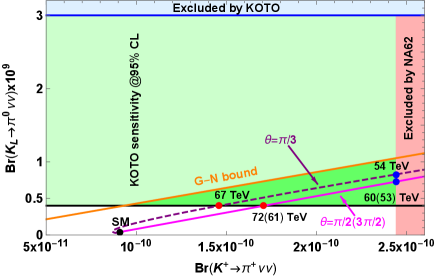
where denotes the phase of the Wilson coefficient. Note that the running from the electroweak scale to the chiral symmetry breaking scale vanishes, as the dim-6 vector operators are not renormalized at one-loop level due to QCD Ward identity. The allowed range in the plane of is given in the left panel of Fig. 1. From this plot, we can see that the phase is nonzero and the NP scale is limited to
| (76) |
For specific choices of or , the real part of vanishes and both branching ratios are only governed by . Thus, in the plane of two branching ratios shown in the right panel of Fig. 1, the correlation lines for these two choices coincide with each other. The NP scale resides in the range of for or for . We also display the case of resulting in a different line in the plane of two branching ratios.

On the other hand, for the LFV case, a similar analysis can be carried out based on Eqs. (68, 69). The SM has no interference with LFV contribution in this case. After neglecting the above LFC contribution from NP and assuming the coefficient with only one set of lepton flavors is switched on at a time, a lower limit on the NP scale associated with the LFV Wilson coefficients can be obtained as
| (77) |
where the NA62 result for at 95 (90)% CL is taken. A stronger bound can be set if we assume the same magnitude for all LFV Wilson coefficients, that is
| (78) |
In Refs. Carpentier and Davidson (2010); He et al. (2019a, b), there are similar analyses for LFV coefficients using the limit on from PDG. Their limits can be translated into a bound on NP scale in our convention as 56.8 TeV in Ref. Carpentier and Davidson (2010) and 50 TeV in Refs. He et al. (2019a, b). We can see that the new NA62 result pushes the NP scale higher. The bound obtained above is the most stringent one for the coefficients with flavor, compared to the bound from lepton LFV rare decays He et al. (2019b). For the coefficients with or , the most stringent bound with is from the charged lepton decay modes of Kaon, i.e. . See also the derivation in Appendix B.
IV.2 Constraint on the LNV operator
In this section we assume the NP contribution from dim-6 LNC operators is negligible and therefore only keep the SM contribution in the LNC case. Under this assumption, we focus on the LNV NP contribution. As discussed above, the scalar LEFT operators from one dim-7 LNV operator in the SMEFT play an important role in the Kaon semi-invisible decays.
The Kaon invisible decays can entail constraint on the above Wilson coefficients. The effective Lagrangian for at the leading order is
| (79) | |||||
and that for decay is
| (80) | |||||
One can see that the processes are only induced by dim-6 operators in LEFT since they flip the helicity of one of neutrinos to allow the pseudoscalar Kaon to decay invisibly. The dim-6 operators are severely suppressed by the neutrino mass because they are subject to helicity-suppression. As seen in the above subsection, only the operator is induced by one dim-7 SMEFT operator at tree-level. By including the one-loop QCD running result for from electroweak scale to the chiral symmetry breaking scale , we obtain
| (81) |
We further assume the Wilson coefficients in Eqs. (62-63) at scale as
| (82) |
where denotes the NP scale above the electroweak scale. Combining Eqs. (79-80), the matching results in Eqs. (62-63), and the naive assumption in Eq. (82), we find that there is no tree-level contribution to decay. For invisible decay, we obtain the branching ratio of invisible decay
| (83) |
where the factor 2 accounts for the anti-neutrino case, the factor 3 for the 3 generations of neutrinos, the factor for the identical neutrinos in final states, and for the phase space, respectively. The experimental bounds for the Kaon invisible decay were estimated in Ref. Gninenko (2015) as
| (84) | |||||
| (85) |
The above bound translates into a rather weak lower limit on the new physics scale
| (86) |
Given the matching results in Eqs. (62) and (63) together with the assumption in Eq. (82), the branching ratios of in Eqs. (31) and (32) can be simplified as
| (87) | |||||
| (88) | |||||
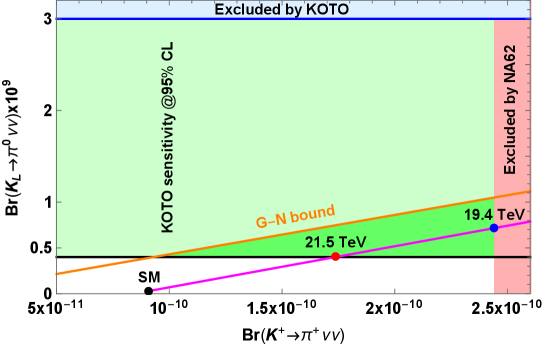
There is obviously no interference between the SM contribution and the LNV contribution. If we require those results to satisfy the region allowed by the KOTO and NA62 upper bounds, the NP contribution resides along the pink line in Fig. 2 and the NP scale is highly constrained to a narrow range
| (89) |
See Fig. 2 for a more detailed illustration. This is an appealing scale both for LHC experiments and TeV scale seesaw mechanism yielding Majorana neutrino mass. This interpretation highly depends on the precision of the measurements and the simple assumption in Eq. (82). If we take the upper bound on from the NA62 experiment at 90% CL, that is Ruggiero , the contribution of the LNV operator together with the assumed Wilson coefficients in Eq. (82) is almost excluded. The analysis of the 2018 NA62 data would indicate if LNV operator can precipitate the discrepancy under the assumption.
The operator in Eq. (61) can also contribute to neutrinoless double beta () decay. The NP scale from this process is constrained to be larger than Cirigliano et al. (2017); Liao and Ma (2019). Constraints from are complementary and provide a similar sensitivity, because they constrain the quark flavor violating Wilson coefficients with an - and a -quark and any arbitrary generations of the lepton fields in the operator after relaxing the assumption in Eq. (82).
V Discussions and Conclusions
In the above analysis, we focus on the contact interactions from effective operators composed of quarks and two neutrinos for transition, that is the so-called short-distance (SD) contribution. In addition, there exist the long-distance (LD) contributions to from the heavy NP parameterized by the dim-6 LNC operators in SMEFT. The LD contributions are mediated by light charged leptons, neutrinos or light meson propagators in the PT picture. In the processes, it turns out that the LD contributions are negligible compared to the SD contribution and can be safely ignored. The detailed analysis is included in Appendix C.
In summary, we investigate the implication of from the recent KOTO and NA62 measurements for generic neutrino interactions in effective field theories. The interactions between quarks and left-handed SM neutrinos are first described by the LEFT below electroweak scale. We match them to PT at the chiral symmetry breaking scale to calculate the branching fractions of Kaon semi-invisible decays and match them up to the SMEFT to constrain new physics above the electroweak scale.
In the framework of effective field theories, we prove that the Grossman-Nir bound is valid for both dim-6 and dim-7 LEFT operators in PT, and the dim-6 scalar and vector operators dominantly contribute to the transition. They are induced by multiple dim-6 LNC operators and one dim-7 LNV operator in the SMEFT, respectively. After providing a generic constraint on the relevant Wilson coefficients, we separately discuss the constraints on the two kinds of operators. The LNC vector operators lead to interference with the SM contribution. We consider the lepton-flavor-conserving case and evaluate the constraints from Kaon leptonic decay modes . For the component in the transition, the decays provide the only sensitive probe. We find the NP scale associated with the Wilson coefficient is limited to be .
One the other hand, we assume the NP contribution from dim-6 LNC operators is negligible and therefore only keep the SM prediction in the LNC case. As a result, the scalar LEFT operators from one dim-7 LNV operator in the SMEFT dominates the decay. We find that the invisible decay places a weak bound on the new physics scale for the LNV operator. As there is no interference with the SM contribution, the constraint on the NP scale from is rather precise and resides in a narrow range .
Appendix A The amplitudes and partial widths of
In this appendix we present details of the calculation of . For the process of , the amplitudes for decay are
| (90) |
and those for decay are
| (91) |
with . The factor of comes from the symmetry property of the operators and the corresponding Wilson coefficients for . We neglect the masses of final state neutrinos and thus the different amplitudes do not interfere. After summing over all possible flavors, the flavor- and spin- summed squared matrix elements read
| (93) | |||||
where and . Here means that for we take flavor configurations. One should note that the flavor indices are implicitly summed over in the Lagrangian, while in the above amplitudes they denote the specific neutrino flavors in final states. The overall factor 2 in the second line for decay is because the contributions from and are the same for any pair of . The accounts for the double counting of final state phase space for identical particles.
The partial decay width can be expressed as
| (94) |
where the integration interval of is
| (95) |
with
| (96) |
The partial widths of Kaon semi-invisible decays are obtained by performing the integral
| (97) | |||||
| (98) | |||||
Appendix B The constraints from leptonic Kaon decays
The current experimental constraints on the branching ratios of Ambrosino et al. (2009) and Collaboration (2019) are
| (99) |
at 90% CL. The lepton-flavor-conserving modes of decays have been measured Tanabashi et al. (2018)
| (100) |
Their SM predictions are Valencia (1998); Gomez Dumm and Pich (1998); D’Ambrosio and Kitahara (2017)
| (101) |
We match the SMEFT Wilson coefficients in Eq. (59), relevant for Kaon physics, to the four vector operators in LEFT
| (102) | ||||||
| (103) |
The matching condition is given by222We do not include tensor operators and which are suppressed in PT power counting relative to the vector-type operators, and also the scalar operators which are suppressed by the SM Yukawa couplings.
| (104) | |||||
| (105) | |||||
| (106) | |||||
| (107) |
The lepton-flavor-conserving decay widths are
| (108) |
where and is the physical Kaon decay constant. I.T. stands for the interference term between the SM part and the NP part. Here the I.T. contribution is larger than the pure NP squared term in the above equation. To make a conservative estimation of the NP scale, we simply neglect the interference term below. Note that, once including the additional interference term, we should obtain a more stringent limit on the NP scale for and coefficients. The NP contribution is the linear combination of Wilson coefficients in Eqs. (104-107) and takes the form as
| (109) | ||||
| (110) |
Considering the physical lifetime of and and the experimental constraints in Eqs. (99, 100), the stronger limit on NP scale is set by the decays. After neglecting the interference term in Eq. (108) and subtracting the SM contribution in Eq. (101), the NP scales associated with the and coefficients are constrained to be
| (111) | |||
| (112) |
Finally, we quote the result for the LFV mode
| (113) | ||||
| (114) |
| (115) |
The upper limit on the lepton-flavor-violating decay of at 90% CL Tanabashi et al. (2018) leads to a constraint on the NP scale of
| (116) |
with or .
Appendix C Long-distance contributions from dim-6 operators
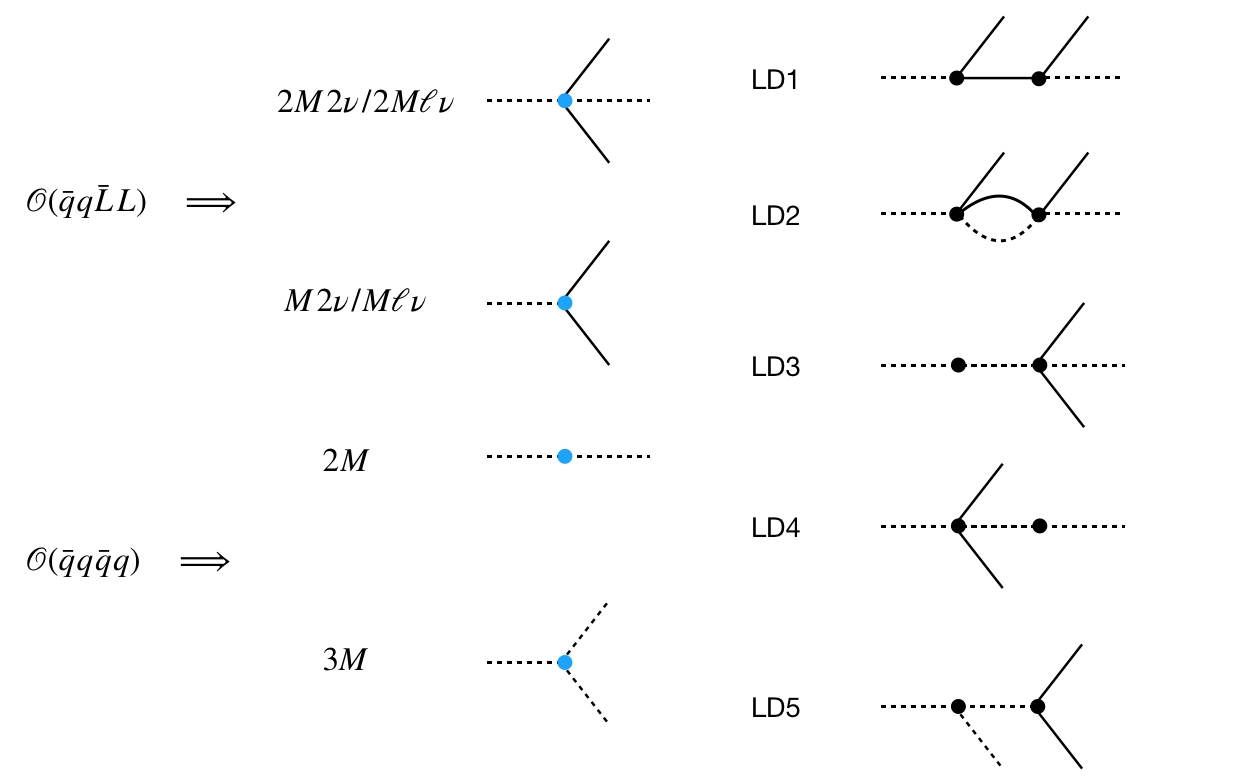
In this Appendix, we estimate the long distance (LD) contributions to from the heavy NP parameterized by the dim-6 LNC operators in SMEFT. The LD contributions are mediated by light charged leptons, neutrinos or light meson propagators in the PT picture. In Fig. 3 we categorize the possible topologies for the LD contribution from the dim-6 two-quark-two-lepton operators and four-quark operators in SMEFT. The dashed and solid lines represent the possible meson and lepton fields, respectively.
The LD contributions mediated by neutrinos are suppressed compared to the SD contribution. In the Feynman diagrams for this kind of LD contribution, the vertex connecting the Kaon state involves the same Wilson coefficients as the SD case and the other vertex leads to one additional suppression factor . Hence, we find that they are suppressed by .
The LD contributions mediated by charged leptons can be induced by charged-current vector and/or scalar operators. The contribution from scalar operators is strongly constrained by charged pseudoscalar meson decays. The branching ratio for is
| (117) |
where we sum over neutrino flavor and () denotes the scalar (vector) operator contribution. The SM contribution is helicity-suppressed and given by , while NP scalar contributions do not suffer from helicity-suppression. Requiring that the NP scalar contribution can be at most as large as the SM contribution translates into . The same scalar contribution enters the LD contribution to mediated by a charged lepton. After considering the phase space, the squared matrix element is determined in terms of
| (118) |
The second term is suppressed by a factor of and consequently the LD scalar contribution is sub-dominant.
In the SM, the LD contribution induced by vector operators is suppressed by relative to the SD contribution Hagelin and Littenberg (1989). As the NP contribution to charged current operators is at most of the same order as the SM contribution, the LD contribution from vector operators is negligible.
Similarly, the meson-mediated tree-level contributions (LD3 and LD4) are suppressed by with respect to the SD contribution Hagelin and Littenberg (1989); Lu and Wise (1994) in the SM, while the one-loop contribution LD2 is of the same order as the LD1 contribution in the SM Rein and Sehgal (1989); Buchalla and Isidori (1998). To our knowledge, there is no general LEFT analysis of LD contributions to . As four quark operators with directly contribute to hadronic Kaon decays of which many have been measured at sub-percent level precision, we expect that similar conclusions hold for NP contributions mediated by meson exchange. In summary, currently it is safe to neglect long-distance contributions to .
Acknowledgements.
We would like to thank Xiao-Gang He, Yi Liao, Jusak Tandean and Jian Zhang for very useful discussions and communication. TL is supported by the National Natural Science Foundation of China (Grant No. 11975129) and “the Fundamental Research Funds for the Central Universities”, Nankai University (Grants No. 63191522, 63196013). XDM is supported by the MOST (Grant No. MOST 106-2112-M-002-003-MY3).References
- (1) S. Shinohara, Search for the rare decay , KAON2019, Perugia, Italy, September 2019 .
- (2) C. Lin, Recent Result on the Measurement of at the J-PARC KOTO Experiment, J-PARC Symposium 2019 .
- (3) G. Ruggiero, New Result on from the NA62 Experiment, KAON2019, Perugia, Italy, September 2019 .
- Kitahara et al. (2019) T. Kitahara, T. Okui, G. Perez, Y. Soreq, and K. Tobioka, (2019), arXiv:1909.11111 [hep-ph] .
- Artamonov et al. (2008) A. V. Artamonov et al. (E949), Phys. Rev. Lett. 101, 191802 (2008), arXiv:0808.2459 [hep-ex] .
- Artamonov et al. (2009) A. V. Artamonov et al. (BNL-E949), Phys. Rev. D79, 092004 (2009), arXiv:0903.0030 [hep-ex] .
- Ahn et al. (2019) J. K. Ahn et al. (KOTO), Phys. Rev. Lett. 122, 021802 (2019), arXiv:1810.09655 [hep-ex] .
- Buras et al. (2006) A. J. Buras, M. Gorbahn, U. Haisch, and U. Nierste, JHEP 11, 002 (2006), [Erratum: JHEP11,167(2012)], arXiv:hep-ph/0603079 [hep-ph] .
- Brod et al. (2011) J. Brod, M. Gorbahn, and E. Stamou, Phys. Rev. D83, 034030 (2011), arXiv:1009.0947 [hep-ph] .
- Buras et al. (2015) A. J. Buras, D. Buttazzo, J. Girrbach-Noe, and R. Knegjens, JHEP 11, 033 (2015), arXiv:1503.02693 [hep-ph] .
- Fabbrichesi and Gabrielli (2019) M. Fabbrichesi and E. Gabrielli, (2019), arXiv:1911.03755 [hep-ph] .
- Egana-Ugrinovic et al. (2019) D. Egana-Ugrinovic, S. Homiller, and P. Meade, (2019), arXiv:1911.10203 [hep-ph] .
- Dev et al. (2019) P. S. B. Dev, R. N. Mohapatra, and Y. Zhang, (2019), arXiv:1911.12334 [hep-ph] .
- Fuyuto et al. (2015) K. Fuyuto, W.-S. Hou, and M. Kohda, Phys. Rev. Lett. 114, 171802 (2015), arXiv:1412.4397 [hep-ph] .
- Mandal and Pich (2019) R. Mandal and A. Pich, (2019), arXiv:1908.11155 [hep-ph] .
- Calibbi et al. (2019) L. Calibbi, A. Crivellin, F. Kirk, C. A. Manzari, and L. Vernazza, (2019), arXiv:1910.00014 [hep-ph] .
- Grossman and Nir (1997) Y. Grossman and Y. Nir, Phys. Lett. B398, 163 (1997), arXiv:hep-ph/9701313 [hep-ph] .
- Jenkins et al. (2018a) E. E. Jenkins, A. V. Manohar, and P. Stoffer, JHEP 03, 016 (2018a), arXiv:1709.04486 [hep-ph] .
- Jenkins et al. (2018b) E. E. Jenkins, A. V. Manohar, and P. Stoffer, JHEP 01, 084 (2018b), arXiv:1711.05270 [hep-ph] .
- Gasser and Leutwyler (1984) J. Gasser and H. Leutwyler, Annals Phys. 158, 142 (1984).
- Gasser and Leutwyler (1985) J. Gasser and H. Leutwyler, Nucl. Phys. B250, 465 (1985).
- Buchmuller and Wyler (1986) W. Buchmuller and D. Wyler, Nucl. Phys. B268, 621 (1986).
- Grzadkowski et al. (2010) B. Grzadkowski, M. Iskrzynski, M. Misiak, and J. Rosiek, JHEP 10, 085 (2010), arXiv:1008.4884 [hep-ph] .
- Lehman (2014) L. Lehman, Phys. Rev. D90, 125023 (2014), arXiv:1410.4193 [hep-ph] .
- Liao and Ma (2016) Y. Liao and X.-D. Ma, JHEP 11, 043 (2016), arXiv:1607.07309 [hep-ph] .
- Henning et al. (2017) B. Henning, X. Lu, T. Melia, and H. Murayama, JHEP 08, 016 (2017), [Erratum: JHEP09,019(2019)], arXiv:1512.03433 [hep-ph] .
- Liao and Ma (2017) Y. Liao and X.-D. Ma, Phys. Rev. D96, 015012 (2017), arXiv:1612.04527 [hep-ph] .
- Canas et al. (2016) B. C. Canas, O. G. Miranda, A. Parada, M. Tortola, and J. W. F. Valle, Phys. Lett. B753, 191 (2016), [Addendum: Phys. Lett.B757,568(2016)], arXiv:1510.01684 [hep-ph] .
- Cirigliano et al. (2017) V. Cirigliano, W. Dekens, J. de Vries, M. L. Graesser, and E. Mereghetti, JHEP 12, 082 (2017), arXiv:1708.09390 [hep-ph] .
- Tandean (2000) J. Tandean, Phys. Rev. D61, 114022 (2000), arXiv:hep-ph/9912497 [hep-ph] .
- Colangelo and Durr (2004) G. Colangelo and S. Durr, Eur. Phys. J. C33, 543 (2004), arXiv:hep-lat/0311023 [hep-lat] .
- Patrignani et al. (2016) C. Patrignani et al. (Particle Data Group), Chin. Phys. C40, 100001 (2016).
- Marciano and Parsa (1996) W. J. Marciano and Z. Parsa, Phys. Rev. D53, R1 (1996).
- Cata and Mateu (2007) O. Cata and V. Mateu, JHEP 09, 078 (2007), arXiv:0705.2948 [hep-ph] .
- Buchalla and Buras (1994) G. Buchalla and A. J. Buras, Nucl. Phys. B412, 106 (1994), arXiv:hep-ph/9308272 [hep-ph] .
- Buchalla and Buras (1999) G. Buchalla and A. J. Buras, Nucl. Phys. B548, 309 (1999), arXiv:hep-ph/9901288 [hep-ph] .
- (37) CKMfitter, http://ckmfitter.in2p3.fr/www/results/plots_summer18/num/ckmEval_results_summer18.html.
- He et al. (2018) X.-G. He, G. Valencia, and K. Wong, Eur. Phys. J. C78, 472 (2018), arXiv:1804.07449 [hep-ph] .
- Tanabashi et al. (2018) M. Tanabashi et al. (Particle Data Group), Phys. Rev. D98, 030001 (2018).
- Carpentier and Davidson (2010) M. Carpentier and S. Davidson, Eur. Phys. J. C70, 1071 (2010), arXiv:1008.0280 [hep-ph] .
- He et al. (2019a) X.-G. He, J. Tandean, and G. Valencia, JHEP 07, 022 (2019a), arXiv:1903.01242 [hep-ph] .
- He et al. (2019b) X.-G. He, J. Tandean, and G. Valencia, Phys. Lett. B797, 134842 (2019b), arXiv:1904.04043 [hep-ph] .
- Gninenko (2015) S. N. Gninenko, Phys. Rev. D91, 015004 (2015), arXiv:1409.2288 [hep-ph] .
- Liao and Ma (2019) Y. Liao and X.-D. Ma, JHEP 03, 179 (2019), arXiv:1901.10302 [hep-ph] .
- Ambrosino et al. (2009) F. Ambrosino et al. (KLOE), Phys. Lett. B672, 203 (2009), arXiv:0811.1007 [hep-ex] .
- Collaboration (2019) T. L. Collaboration (LHCb), (2019).
- Valencia (1998) G. Valencia, Nucl. Phys. B517, 339 (1998), arXiv:hep-ph/9711377 [hep-ph] .
- Gomez Dumm and Pich (1998) D. Gomez Dumm and A. Pich, Phys. Rev. Lett. 80, 4633 (1998), arXiv:hep-ph/9801298 [hep-ph] .
- D’Ambrosio and Kitahara (2017) G. D’Ambrosio and T. Kitahara, Phys. Rev. Lett. 119, 201802 (2017), arXiv:1707.06999 [hep-ph] .
- Hagelin and Littenberg (1989) J. S. Hagelin and L. S. Littenberg, Prog. Part. Nucl. Phys. 23, 1 (1989).
- Lu and Wise (1994) M. Lu and M. B. Wise, Phys. Lett. B324, 461 (1994), arXiv:hep-ph/9401204 [hep-ph] .
- Rein and Sehgal (1989) D. Rein and L. M. Sehgal, Phys. Rev. D39, 3325 (1989).
- Buchalla and Isidori (1998) G. Buchalla and G. Isidori, Phys. Lett. B440, 170 (1998), arXiv:hep-ph/9806501 [hep-ph] .