Impact of the Fizeau drag effect on Goos-Hänchen shifts in graphene
Abstract
We investigate the Goos-Hänchen shifts in reflection for a light beam within a graphene structure, utilizing the Fizeau drag effect induced by its massless Dirac electrons in incident light. The magnitudes of spatial and angular shifts for a light beam propagating against the direction of drifting electrons are significantly enhanced, while shifts for a beam co-propagating with the drifting electrons are suppressed. The Goos-Hänchen shifts exhibit augmentation with increasing drift velocities of electrons in graphene. The impact of incident wavelength on the angular and spatial shifts in reflection is discussed. Furthermore, the study highlights the crucial roles of the density of charged particles in graphene, the particle relaxation time, and the thickness of the graphene in manipulating the drag-affected Goos-Hänchen shifts. This investigation offers valuable insights for efficiently guiding light in graphene structures under the influence of the Fizeau drag effect.
I Introduction
The optical phenomenon known as the Fizeau drag effect was first elucidated in 1851 by Armand Fizeau Fizeau (1851) and was later verified for light propagating in flowing water Banerjee et al. (2022); Davuluri and Rostovtsev (2012); Kuan et al. (2016). Under this effect, the speed of light can be modified when it is propagating in a moving medium. This effect arises when a moving optical element, such as a moving mirror or transparent material, partially entrains a medium. In the Fizeau experiment, light was directed through a tube containing a flowing liquid. The light beam was split, with one part moving in the direction of the liquid’s flow and the other against it. Upon recombining the two beams, interference fringes were observed. The experiment demonstrated that the motion of the medium through which light traveled influenced its speed. The beam moving with the flow of the liquid resulted in a slight increase in speed, while the beam moving against the flow led to a slight decrease in speed. This differential effect caused a shift in the interference fringes.
By utilizing the high electron mobility in graphene Geim and Novoselov (2007); Geim (2009) and the slow plasmon propagation of its massless Dirac fermions, Dong et al. Dong et al. (2021) and Zhao et al. Zhao et al. (2021) recently demonstrated experimentally Fizeau drag effect for graphene plasmons. They observed that the Dirac electrons in graphene possess the ability to effectively drag surface plasmons along their direction of propagation, a phenomenon highlighted by the observed wavelength change in these modes.
On the other hand, when light interacts with dielectric interfaces, reflection and transmission occur Saleh and Teich (2019). In the case of total internal reflection at the interface between two media, the reflected beam deviates laterally from the position predicted by geometrical optics. This lateral shift is known as the Goos-Hänchen (GH) shift Goos and Hänchen (1947) and arises due to the phase shift between the reflected and transmitted beams Wang et al. (2008a, 2013a); Wu et al. (2019a). In this phenomenon, each plane-wave component undergoes a unique phase change. This results in a reflected beam that experiences a lateral displacement due to the superposition of these components. Furthermore, the different reflective coefficients of each plane wave component contribute to an angular change Wan and Zubairy (2020). Widely applicable in angle measurements Yallapragada et al. (2016), beam splitters Song et al. (2012), sensors Wang et al. (2008b), and optical switches Wang et al. (2013b), the GH shift has been extensively studied in various media and structures, including metal and dielectric slabs Wan and Zubairy (2020); Li (2003), optical cavities or waveguides Kandammathe Valiyaveedu et al. (2018); Zhu et al. (2016), photonic crystals Soboleva et al. (2012); Din et al. (2022), metamaterials Wu et al. (2019b); Yallapragada et al. (2016), optomechanical systemsUllah et al. (2019); Khan et al. (2020), atomic media Wang et al. (2008a); Radmehr et al. (2016), surface plasmon resonance structures Yin et al. (2004); Salasnich (2012), graphene Li et al. (2014); Chen et al. (2017); Song et al. (2012); Wu et al. (2017); Grosche et al. (2016); Wu et al. (2011) and other 2D materials Shah (2022); Jahani et al. (2023). GH shifts in geometries containing graphene can be efficiently tuned by graphene, depending on its remarkable properties, such as adjusting its carrier density through the applied gate voltage Cheng et al. (2014); Zeng et al. (2017), varying its number of layers or thickness Li et al. (2014); Chen et al. (2017), using different substrates on which it is deposited Blake et al. (2007); Novoselov et al. (2012), and varying the direction of polarization of incident light Li et al. (2014). Valley-dependent GH shifts were also studied in graphene where electrons in different valleys were shown to have different shifts Wu et al. (2011). These investigations span both the fundamental understanding and practical aspects of the GH shift.
GH shift, although typically considered a subtle effect Jayaswal et al. (2013), holds significant implications in various optical applications, including precision measurement Chen et al. (2017); Mi et al. (2017) and sensing Wu et al. (2019a); Hashimoto and Yoshino (1989); Yin and Hesselink (2006). Hence, a crucial consideration is the exploration of strategies to enhance and improve the GH shifts. One potential avenue we identify is the incorporation of relativistic effects in graphene induced by its fast-moving, massless Dirac electrons. These electrons can effectively drag light along or against its propagation direction, leading to shifts that can be either enhanced or suppressed.
We explore the dependencies of the drag-affected GH shifts on the thickness of a two-dimensional (2D) graphene sheet, its carrier density, and the incident wavelength. Our findings reveal that depending upon the direction of propagation of the incoming light, the angular and spatial shifts of the reflected beam are significantly amplified or suppressed by the inclusion of Fizeau drag due to the swift motion of electrons in graphene. This dependency is demonstrated across various drift velocities of electrons in graphene. This study presents an efficient platform for guiding light through graphene in its current-carrying state. In our study, the Fizeau drag emerges as a relativistic phenomenon, exhibiting a pronounced dependence on the relative motion of the medium. This implies that a significant contrast in the dispersion characteristics of co-propagating and counter-propagating waves in graphene is induced only when relativistic electron drift velocities are present. It is crucial to note the distinction between light drag and plasmon drag in graphene, attributed to the broken Galilean invariance, as discussed in Dong et al. (2021).
The paper is organized as follows. In Sect. II, we define the geometry and revise the Fizeau drag effect based on the special relativity. Subsequently, we present the analytical expressions for the description of GH shifts. Then we present expressions for describing the transformations from a stationary frame to a moving frame, as well as for the optical response of graphene. The results are presented and discussed in Sect. III and the last section (Sect. IV), summarizes the results.
II Model and Expressions for GH Shift with Fizeau Drag
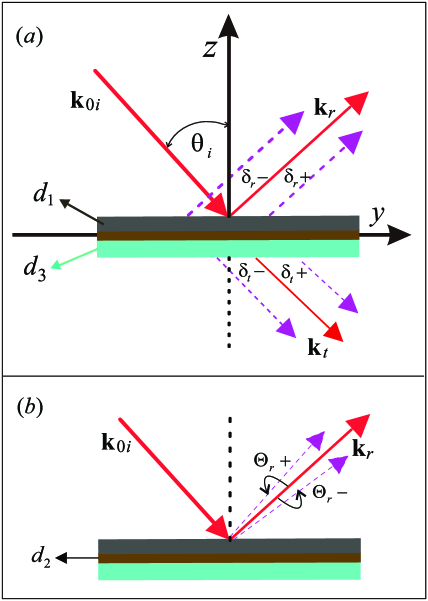
The geometry depicted in Fig. 1 illustrates our model for investigating GH shifts of a light beam under the influence of the Fizeau drag effect in graphene. A linearly polarized light impinges on a three-layered structure at an incident angle with the -axis. The three layers consist of a graphene sheet with relative electric permittivity positioned between a substrate with relative dielectric constant and an upper medium with relative electric permittivity . The parameters , , and represent the thicknesses of the top medium, the graphene layer, and the substrate, respectively. In this context, denotes the spatial GH shift, and represents the angular shift of the reflected wave, with indicating the corresponding positive and negative shifts. Vectors and denote the reflected and transmitted portions of the incident light. Further insights into such a three-layered model can be found in previous works discussing GH shift phenomena Wang et al. (2008a); Song et al. (2012); Din et al. (2022)
We aim to explore spatial and angular shifts in the depicted geometry by incorporating the influence of Fizeau drag caused by Dirac electrons in graphene. In subsequent sections, we outline the Fizeau drag effects of Dirac electrons in graphene on the incident light. Subsequently, we provide expressions for the GH shifts in both reflection and transmission.
II.1 Fizeau drag in graphene and the resulting expressions for drag-affected GH shifts
We make the assumption that the Fizeau drag that affects the incident light is solely a result of the drifting electrons in graphene. These drifting electrons are considered to propagate along the positive -axis. To explore the GH shifts in the current-carrying state, we begin our analysis with Lorentz transformations applied to various physical quantities of graphene Borgnia et al. (2015); Dong et al. (2021)
| (1) |
| (2) |
| (3) |
where represents the frequency of the incident light, is the wave vector of light in graphene, is the charge density, and denotes the drift velocity of the charged particles in graphene. The subscript “0” designates the quantities measured in the frame moving with velocity , and denotes the Lorentz factor Dong et al. (2021). Given our assumption that graphene possesses free electrons and an associated electric current, the effective relative optical permittivity of graphene, for a monochromatic light with angular momentum , can be derived from its optical conductivity using Maxwell’s equations as Saleh and Teich (2019)
| (4) |
where represents the vacuum permittivity. An essential parameter for an accurate depiction of the dielectric properties of graphene is its optical conductivity. This quantity is contingent on both the incoming frequency and the in-plane wave vector. Notably, the energy–momentum relationship for electrons in graphene is linear for energies below , as opposed to being quadratic. Consequently, the low-energy conductivity of graphene encompasses two components: intraband and interband contributions. The graphene conductivity, derived from the Kubo formula Gusynin et al. (2007) or the random phase approximation Platzman and Wolff (1973), is expressed as . These contributions arise from intraband electron-phonon scattering and interband electron transitions, given by Hanson (2008)
| (5) | |||||
Here, represents the Fermi energy, where is the Fermi wave vector, and is the Fermi velocity of the charged particles. The parameter denotes the relaxation time of the charge carriers with density , and is the Heaviside function. It is important to note that the presented formulas are applicable for highly doped or gated graphene, specifically when . In the long wavelength and high doping limit, i.e., , the interband contributions become negligible, and the intraband term dominates, defining the total conductivity of graphene.
We will see that the normal component of the incident light corresponding to the graphene sheet is
| (6) |
where is the wave vector propagating with velocity in graphene and the -component of the wave vector in vacuum. If we consider the Fizeau effect due to drifting electrons in graphene, the phase velocity of the wave becomes
| (7) |
where the and signs stand for a wave propagating along and against the drifting electrons in graphene, respectively. We call the former the forward (f) mode and the latter as backward (b) mode. in Eq. (7) is the drag coefficient of graphene and is obtained as
| (8) |
where represents the refractive index of graphene and is its group index. Rewriting Eq. (7) in terms of wave vectors and applying the transformations given by Eqs. (1) and (2), we obtain the following expression:
| (9) |
Notice that becomes for the upper sign and for the lower sign, the Fizeau drag-affected wave vectors of the backward mode and forward mode, respectively. Solving these equations, we get a quadratic equation in and for each mode whose solution is
| (10) | |||||
| (11) |
The component of this drag-affected wave vector becomes . Additionally, the Fermi energy in the current-carrying graphene channel is modified to , where is determined by the transformation given in Eq. (3). Substituting these values into the expressions for the GH shifts, we obtain the desired results for spatial and angular shifts of light under the Fizeau drag effect.
II.2 General expressions for GH shifts
The incident beam on the geometry presented in Fig. 1 undergoes partial transmission and partial reflection through the substrate layer to reach the graphene. The electric field of the incident beam can be expressed as Li (2003); Wang et al. (2008a). We assume a Gaussian beam with an angular spectrum = where with is the beam waist and is distributed around . Assuming that the incident wave has a sufficiently large width, that is, , the GH shifts for the reflected and transmitted beams can be obtained using stationary phase theory Wang et al. (2008a); Cheng et al. (2014), which has been demonstrated to be accurate for structures containing graphene Li et al. (2014); Song et al. (2012). To facilitate this, we start the analysis with the standard characteristic matrix approach Wang et al. (2008a, 2013a), where the input and output of the electric field propagating through each medium in the structure are related via the transfer matrix.
| (12) |
where , is the z-component of the incident wave vector in medium such that is the wave vector in vacuum. is the thickness of the th medium where =1,2,3. For the three-layered nanostructure in our model, the total transfer matrix is
| (13) |
The reflection (transmission) coefficient (), where denotes the phase of the reflection (transmission) coefficient, can be determined as
| (14) |
| (15) |
where such that is the z-component of the wave vector in vacuum and are the elements of transfer matrix given by Eq. (13). Having calculated and , the lateral shifts (GH shifts) for a monochromatic beam of wavelength can be calculated by using stationary phase theory Wang et al. (2008a); Cheng et al. (2014). The GH shift in reflection (transmission) is , where
| (16) |
However, we are interested in spatial and angular GH shifts independently that contribute to the total GH shifts via = Aiello et al. (2009), and represents the distance from the origin of the point at which the total beam shift is observed. The spatial and angular shifts in reflection and transmission are given, respectively, by Aiello et al. (2009); Cheng et al. (2014)
| (17) |
| (18) |
In the above expression, is the angular spread of the beam with its waist, () is the real (imaginary) part of the quantity. Notice that at this stage, we do need to substitute the Fizeau effect corrections into the expressions for the GH shifts so that we obtain the desired results for spatial and angular shifts for light. For the convenience of the reader, the modified expressions are provided in the appendix.
III Numerical results and discussions
In this section, we present numerical results for the spatial and angular shifts of the reflected part of the light beam in our model under the Fizeau effect. We assume the carrier density in graphene to be cm-2, and the relaxation time fs. The thicknesses of the different media in the structure are taken as m and nm. The waist of the incident beam is set to mm Wu et al. (2017), and the incident wavelength is nm unless otherwise stated. The relative dielectric constants for the media above and below graphene are assumed to be and throughout this work.
Here we explain how to solve the sets of equations mentioned above. We start with Eq. (5) since the optical properties of graphene are strongly dependent on its conductivity . We then substitute this expression into Eq. (4) and calculate the dielectric function of graphene. The dispersion characteristics of light propagating in graphene are obtained through and its normal component is obtained as in Eq. (6). At this stage, we are dealing with a normal graphene channel. To include the Fizeau effect, we make the transformation (1)-(3) to analyze the optical properties of graphene in the current-carrying state. Then, we consider the interaction of light with the structure. Depending upon the direction of propagation, the phase velocity of the incoming light is modified through Eq. (7). Making use of Eq. (9), we finally calculate the drag-affected wave numbers of light co- and counter-propagating with the drifting electrons in graphene by utilizing Eqs. (10) and (11). Subsequently, we calculate the transfer matrix of each medium in the geometry by using Eq. (12). However, the transfer matrix of the current-carrying graphene channel is modified as given in the appendix [Eq. (19)]. The reflection coefficient of light is obtained from Eq. (14) through Eq. (13). Finally, the spatial and angular shifts for the incoming light are calculated from Eqs. (17) and (18).
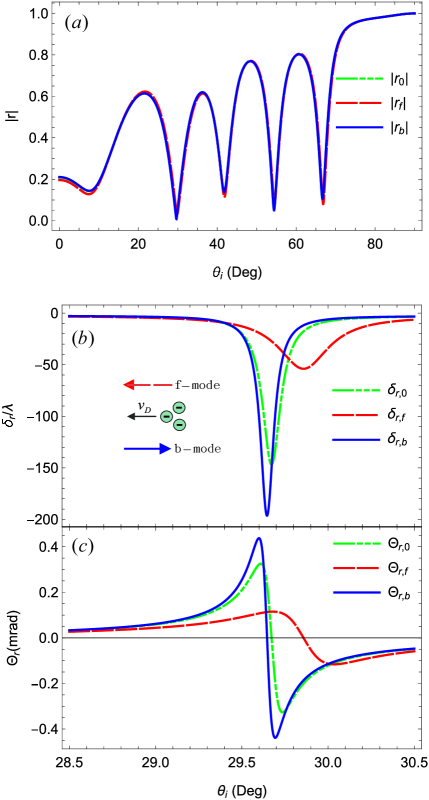
To initiate our analysis, we compare the results obtained for the GH shift of the reflected beam without drag and under the Fizeau drag effect. One of the three media is current carrying channel of graphene and is greatly modified as compared to a current-free graphene case. The comparison is presented in Fig. 2, where we illustrate () the reflection coefficients () spatial shifts, and () angular reflection shifts as functions of the incident angle . For the drag-affected GH shifts, we assume the drift velocity of the electrons in graphene to be . We find that the reflection coefficients are almost overlapping for the two cases, forward and backward waves because of its small magnitude that only varies between 0 and 1. The difference becomes clear in the case of GH shifts where the magnitudes are very high. The oscillation of the reflection coefficients originates from the trigonometric function of in the transfer matrix.
The dashed-dotted green curves depict the spatial and angular shifts of light without the Fizeau drag effect, i.e., in graphene. In comparison, we observe that the angular and spatial shifts for a light beam propagating along the direction of drifting electrons are significantly reduced, while those for a light beam propagating against the drifting electrons are markedly amplified. The modifications stem from the new momentum wave vectors in 2D graphene. The charge carriers acquire finite drift velocity which affects the dispersion characteristics of the interacting light. This observation aligns well with the experimental outcomes in Refs. Dong et al. (2021); Zhao et al. (2021) on the Fizeau drag of surface plasmons due to Dirac electrons in graphene. In those experiments, it was observed that the wavelength of surface plasmons co-propagating with the charge carriers in the current-carrying graphene channel increased, while that of the counter-propagating plasmon decreased.
In our proposed structure, the Fizeau drag due to Dirac electrons in graphene also results in an enhancement and reduction of the wave numbers of the backward and forward modes. Consequently, the curves for GH shifts of drag-free light in our model lie between those for the forward mode and the backward mode. This implies that GH shifts for a light beam under Fizeau drag are direction-dependent. This directional dependence will be further elucidated when wavelength dependence of the GH shifts of light beam interacting with the given geometry is analyzed.
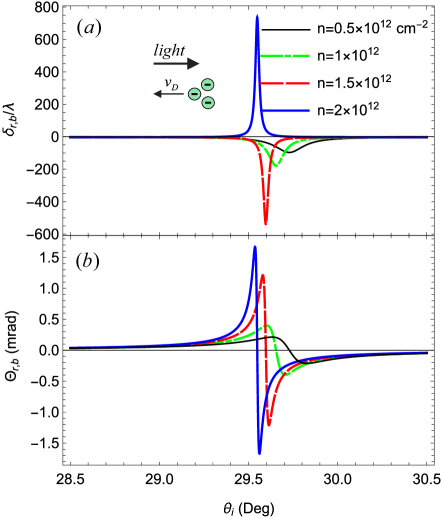
The point in Fig. 2 () where the magnitudes of the spatial shifts of the three modes are maximum corresponds to the resonant angles for the given wavelength in the structure, which happens to be around 29.7∘ for =600 nm. The angular shifts are also found to be maximum at this angle, as shown in Fig. 2 (). In addition to the magnitudes of the spatial and angular shifts, the peaks of the shifts also exhibit slight shifts toward higher (lower) incident angles for the forward (backward) mode. Additionally, we numerically examine that as approaches zero at certain , both and exhibit peaks. One point occurs at =29.7∘ where we noted higher magnitudes of GH shifts as compared to those at other minima peaks of . Besides, the difference between GH shifts of the forward and backward modes is also the greatest at this angle. Therefore, in our analysis of the drag-affected GH shifts, we mostly focus on the minimum peak of occurring at =29.7∘.
The observed phenomena can be explained through the understanding that Fizeau drag, as investigated in our study, is a relativistic phenomenon intricately linked to the relative motion of the medium. If we set to 0 in Eq. (7) and subsequent expressions, no drag effects on light are evident, reducing the analysis to a standard graphene channel. Under these conditions, the green curves in Fig. 2 for spatial and angular shifts are recovered.
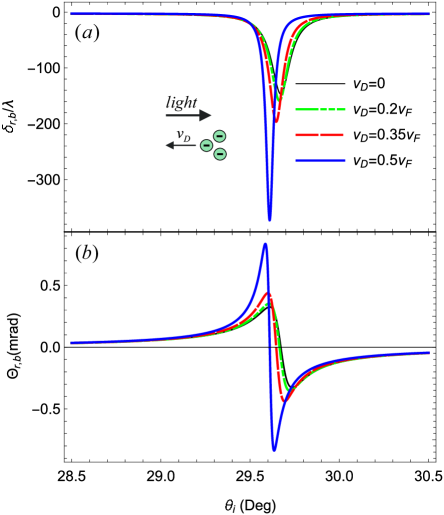
To further explore the impact of the Fizeau drag on GH shifts, we plot the spatial and angular shifts of the forward and backward modes with different drift velocities of the electrons in graphene in Fig. 3. The drift velocity of the electrons can be adjusted by applying a direct current (dc) from a source Dong et al. (2021). The GH shifts are depicted with three different drift velocities of the charged particles, as indicated. We observe a substantial amplification in both spatial and angular shifts as increases, particularly for the counter-propagating mode. Simultaneously, the resonant angle experiences a slight shift towards lower incident angles with the increasing value of . To provide context, we include the case where , corresponding to a normal graphene channel. It is evident that, under these conditions, the magnitudes of spatial and angular shifts, represented by the black curves in Fig. 3, mirror those given by the green curves in Fig. 2 at . This demonstrates that the application of Fizeau drag can significantly affect GH shifts of light and should be considered when guiding light through graphene or other 2D materials of interest in current-carrying state.
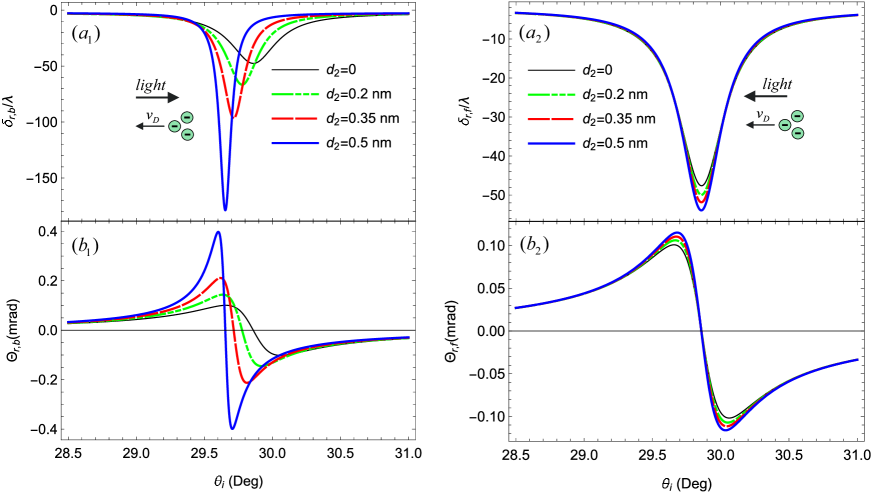
In our proposed geometry, the Fizeau drag-affected GH shifts also strongly depend on the effective thickness of the graphene sheet. The thickness of graphene can be varied by considering ripples or wrinkles on it. This dependence is shown in Fig. 4 for three different thicknesses of the graphene layer, as indicated in the figure. For comparison, the case of no graphene sheet is also demonstrated as shown by the black curves. In this case, the GH shifts are found to be very small and the role of graphene sheet in the geometry is clear. We observe that the magnitudes of GH shifts for the forward and backward reflected modes are significantly enhanced with increasing . Similarly, the curve peaks indicate that the resonant angle is slightly shifted towards lower incident angles as the thickness increases. This variation is independent of the propagation direction, as the spatial and angular shifts of both modes are equally enhanced with the increasing thickness of the graphene sheet. Moreover, the angle of TIR is the same for both modes. In a normal graphene channel, it has been demonstrated that the disparity between GH shift for TM and TE modes tends to grow as the thickness of the graphene material increases Li et al. (2014). Nevertheless, it was observed that the individual shifts were greater in the absence of a graphene sheet and diminished as the number of graphene layers increased.
The GH reflection shifts, influenced by the Fizeau drag, exhibit similar variations as depicted in Fig. 4, with an increase in the number density of charged particles in graphene. This relationship is illustrated in Fig. 5 across four different number densities. It is observed that both the spatial and angular shifts of the backward mode amplify with the rising within the range of 0.5 1012 to 2 1012 cm-2, as illustrated in Fig. 5 (a) and (b). We also see that the resonant angle for the given wavelength is slightly shifted toward low incident angles with increasing for both spatial and angular shifts of the backward modes. In a normal graphene channel, Cheng et al. Cheng et al. (2014) noted a comparable rise in angular shifts with the augmentation of Fermi energy for light of frequency = 5 THz. Given that in graphene, our results are compatible with those observed in Cheng et al. (2014). Nevertheless, is further modified by Eq. (3) to account for the Fizeau effect in our studied structure. Conversely, Wu et al. Wu et al. (2017) observed a reduction in angular shift as Fermi energy increased. It is important to note that their investigation focused on the quantum Hall regime, employing a beam with a waist of = 1 mm and a frequency of = 1 THz.
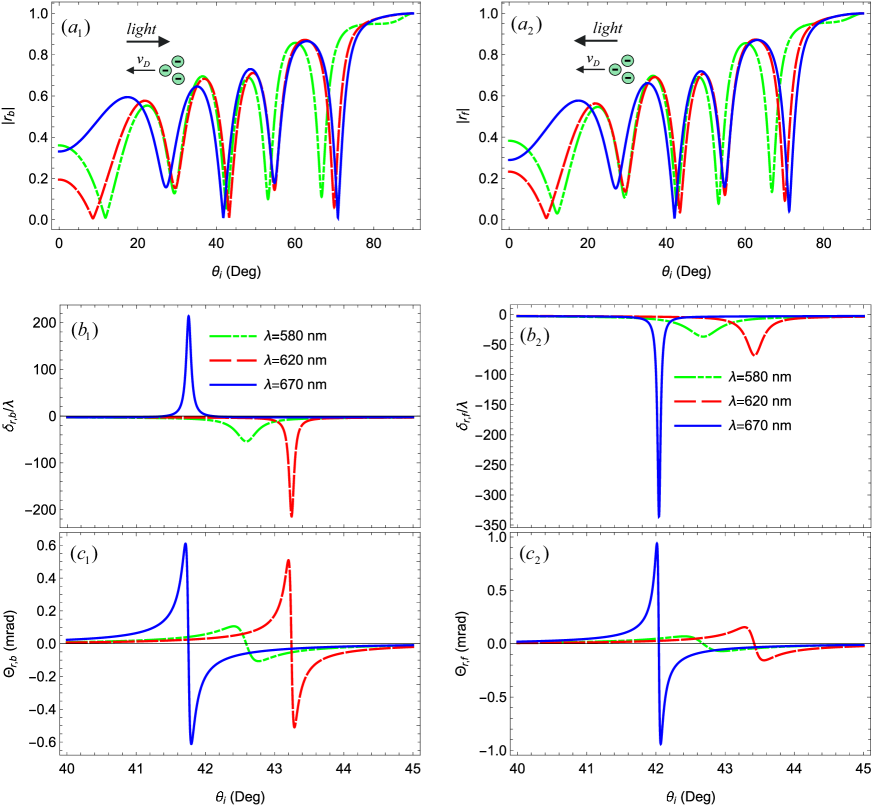
The profiles of GH shifts under the effect of Fizeau drag exhibit strong variations with changing incident wavelength . These variations are depicted in Fig. 6 for the reflection coefficients and GH reflection shifts of both forward and backward beams. Multiple peaks, due to the wavelength dependence of the transfer matrix, can be observed in the reflection coefficient of each mode, as illustrated in Fig. 6 (), corresponding to the angles at which the GH shifts of the reflected wave abruptly increase. We focus on a small range of angles between 40∘ and 45∘ to clearly observe the behavior of spatial and angular shifts for both modes. Moreover, the three wavelengths are chosen randomly to demonstrate that our model works well across the entire visible frequency range.
It is evident that both and are small for low incident wavelengths and increase with increasing as shown in Figs. 6 (bi-ci) for =1 and 2. Not only do the magnitudes of the spatial and angular shifts vary with varying , but the angles at which these shifts occur also shift towards different angles. We should notice that at higher wavelengths, the variations in GH shifts of the backward mode are comparatively smaller than those for the forward mode. Accordingly, the GH shifts can be modified depending on the choice of geometry and incident frequency.
In Fig. 6 (), an intriguing phenomenon is evident: the GH shift () for the backward mode undergoes a sign change at 670 nm. It becomes positive, whereas it is negative for two shorter wavelengths. This behavior is a result of the structural resonance occurring for different wavelengths at different angles. We will see shortly that, for given range, the curve for drag-free light is also positive around 670 nm.
In Fig. 6 (bi-ci), we note another intriguing feature: as we transition from shorter to longer wavelengths, the peaks in the curves shift to the right, but at the longest wavelength, there is a sudden jump back. A similar variation, not presented here without Fizeau drag, also occurs and is attributed to the resonance of the structure at different wavelengths and angles.
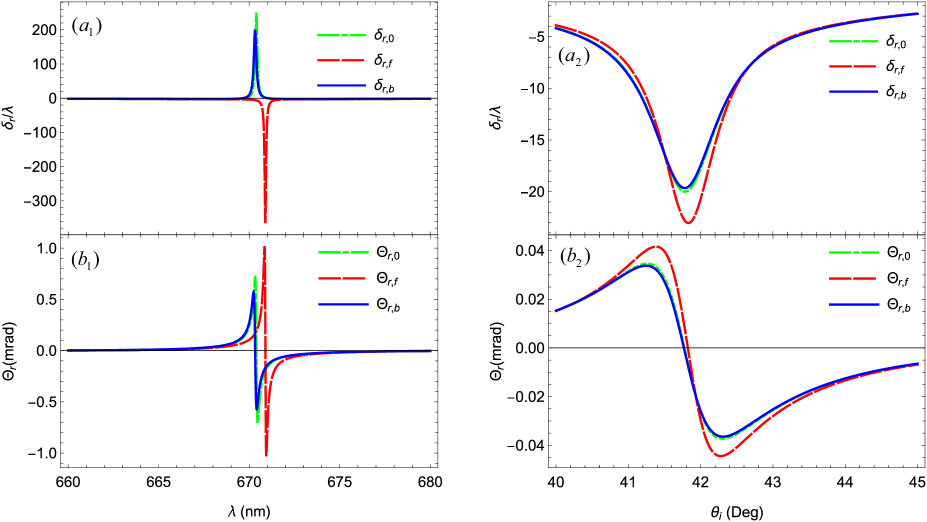
To delve further into this, we plot and in terms of the incident wavelength () at in Fig. 7 () and (), respectively. It is noteworthy that for the drag-free light turns positive around 669 nm at the given , as depicted in Fig. 7 (). Similarly, the backward mode exhibits variations akin to the drag-free mode within the specified range of . The GH shift () for this mode is also observed to be positive. However, the magnitudes of the GH shifts for the drag-free and forward modes differ, and remains negative.
Fig. 7 (), () further demonstrates that the magnitudes of the GH shifts increase for the forward mode and decrease for the backward mode compared to drag-free light, consistent with the results in Fig. 6. It is important to note that these findings differ from the results presented in Fig. 2, where increased GH shifts were observed for the backward mode and decreased shifts for the forward mode. To validate these outcomes, we plotted the GH shifts of the three modes at the same set of parameters as in Fig. 2 but with a different range of in Fig. 7 () and (). The reason behind the alternation of GH shifts for the forward and backward modes becomes apparent, and it is attributed to the varying range of incident angles considered. This observation is significant as it allows us to selectively enhance the shifts of either the forward or backward mode based on the angle of incidence. Additionally, it is worth noting that the magnitudes of and for the three modes obtained at = 600 nm in Fig. 7 () and () are smaller than those shown in Fig. 7 () and (). This aligns with the previous analysis, indicating that the GH shifts in the structure tend to increase with the wavelength.
IV Conclusion
In summary, we have investigated spatial and angular shifts in reflection for a light beam in a graphene structure under the effect of Fizeau drag due to Dirac electrons on incident light. Compared to the drag-free case, we have found that the magnitude of the GH shifts becomes directional, depending on the propagation direction of light concerning the dragging source. When the light is counter-propagating with the drifting electrons in graphene, the magnitudes of both the spatial and angular reflection shifts increase compared to the drag-free case at low incident angles. Conversely, the GH shifts were found to decrease for a light beam co-propagating with the drifting electrons. Interestingly, this varying behavior for the two modes can be reversed at slightly higher angles. The GH shift varies with the electron relaxation time because it influences conductivity and, consequently, the reflective index of graphene.
Furthermore, we have noted that irrespective of the propagation direction of the beam light, the GH shifts in reflection increase with the increasing velocity of the moving medium. In our case, the dragging source of light is the drifting electron cloud, leading to an enhancement of the spatial and angular shifts with greater speeds. The thickness of the 2D system was also found to significantly modify the GH shifts under Fizeau drag. Additionally, we have shown that with increasing Fermi energy of graphene, the magnitudes of the spatial and angular GH shifts in reflection can be increased.
The wavelength dependence of the GH shifts in our model was analyzed, where the GH shifts were shown to increase with the incident wavelength. These findings would be verified by current state-of-the-art experiments. Our results are computed for visible frequencies, offering a practical and experimentally accessible range. The distinct shifts observed for the co- and counter-propagating modes in our methodology suggest the potential for designing efficient light modulators Benea-Chelmus et al. (2021). The directional modulation of GH shifts could find applications in nonreciprocal and directional energy transport along interfaces Xu et al. (2022).
Future extensions of our study could involve the development of a more fundamental temperature sensor, leveraging the temperature-sensitive optical properties of graphene. Previous proposals for temperature sensors based on the GH shift and the Fizeau effect could be further explored Wu et al. (2019a); Xu et al. (2022). Additionally, there is potential to enhance the sensitivity of devices operating on the Doppler effect using insights gained from this study. Exploring applications in twisted bilayer graphene Tabert and Nicol (2013) represents another promising avenue for future research.
Moreover, considering the dependence of the GH effect at a p-n interface in graphene on the sublattice degree of freedom due to electrostatic potential Beenakker et al. (2009), incorporating sublattice effects could be an intriguing future insight, expanding the scope and applicability of the proposed ideas.
Acknowledgements.
We acknowledge the financial support from the postdoctoral research grant (ZC304023922) and the NSFC under grant No. 12174346. R. A. received partial funding from the Iran National Science Foundation (INSF) under project No. 4026871.Appendix A Expressions for GH shift under the effect of Fizeau drag in graphene
Under the effect of Fizeau drag due to drifting electrons in graphene, the wave vector of light in graphene modifies to where given by expressions (10) and (11). Using these, the transfer matrix of graphene from Eq. (12) becomes
| (19) |
where is the counterpart of in the moving frame. Under this substitution, the total transfer matrix in our model becomes
| (20) |
and the corresponding matrix elements are
| (21) |
| (22) |
| (23) |
| (24) |
and in the above expressions are defined in the main text. Using these in Eq. (14), the modified expression for the reflection coefficient of a light beam under the effect of Fizeau drag can be obtained. Having calculated the reflection coefficient, the spatial and angular GH shifts of the reflected beam under the effect of Fizeau drag can be obtained using expressions (17) and (18).
References
- Fizeau (1851) A.-H. Fizeau, Comptes Rendus de l’Académie des Sciences 33 (1851).
- Banerjee et al. (2022) C. Banerjee, Y. Solomons, A. N. Black, G. Marcucci, D. Eger, N. Davidson, O. Firstenberg, and R. W. Boyd, Phys. Rev. Res. 4, 033124 (2022).
- Davuluri and Rostovtsev (2012) S. Davuluri and Y. V. Rostovtsev, Phys. Rev. A 86, 013806 (2012).
- Kuan et al. (2016) P.-C. Kuan, C. Huang, W. Chan, S. Kosen, and S.-Y. Lan, Nature Commun. 7, 13030 (2016).
- Geim and Novoselov (2007) A. K. Geim and K. S. Novoselov, Nature Mater. 6, 183 (2007).
- Geim (2009) A. K. Geim, Science 324, 1530 (2009).
- Dong et al. (2021) Y. Dong, L. Xiong, I. Phinney, Z. Sun, R. Jing, A. McLeod, S. Zhang, S. Liu, F. Ruta, H. Gao, Z. Dong, R. Pan, J. Edgar, P. Jarillo-Herrero, L. Levitov, A. Millis, M. Fogler, D. Bandurin, and D. Basov, Nature 594, 513 (2021).
- Zhao et al. (2021) W. Zhao, S. Zhao, H. Li, S. Wang, S. Wang, M. Utama, S. Kahn, Y. Jiang, X. Xiao, S. Yoo, K. Watanabe, T. Taniguchi, A. Zettl, and F. Wang, Nature 594, 517 (2021).
- Saleh and Teich (2019) B. E. Saleh and M. C. Teich, Fundamentals of Photonics (John Wiley & sons, 2019).
- Goos and Hänchen (1947) F. Goos and H. Hänchen, Ann. Phys. 436 (1947).
- Wang et al. (2008a) L.-G. Wang, M. Ikram, and M. S. Zubairy, Phys. Rev. A 77, 023811 (2008a).
- Wang et al. (2013a) L.-G. Wang, S.-Y. Zhu, and M. S. Zubairy, Phys. Rev. Lett. 111, 223901 (2013a).
- Wu et al. (2019a) F. Wu, J. Wu, Z. Guo, H. Jiang, Y. Sun, Y. Li, J. Ren, and H. Chen, Phys. Rev. Appl. 12, 014028 (2019a).
- Wan and Zubairy (2020) R.-G. Wan and M. S. Zubairy, Phys. Rev. A 101, 023837 (2020).
- Yallapragada et al. (2016) V. J. Yallapragada, A. P. Ravishankar, G. L. Mulay, G. S. Agarwal, and V. G. Achanta, Sci. Rep. 6, 19319 (2016).
- Song et al. (2012) Y. Song, H.-C. Wu, and Y. Guo, Appl. Phys. Lett. 100, 253116 (2012).
- Wang et al. (2008b) Y. Wang, H. Li, Z. Cao, T. Yu, Q. Shen, and Y. He, Appl. Phys. Lett. 92, 061117 (2008b).
- Wang et al. (2013b) X. Wang, C. Yin, J. Sun, H. Li, M. Sang, W. Yuan, Z. Cao, and M. Huang, Appl. Phys. Lett. 103, 151113 (2013b).
- Li (2003) C.-F. Li, Phys. Rev. Lett. 91, 133903 (2003).
- Kandammathe Valiyaveedu et al. (2018) S. Kandammathe Valiyaveedu, Q. Ouyang, S. Han, K.-T. Yong, and R. Singh, Appl. Phys. Lett. 112, 161109 (2018).
- Zhu et al. (2016) B.-S. Zhu, Y. Wang, and Y.-Y. Lou, J. Appl. Phys. 119, 164304 (2016).
- Soboleva et al. (2012) I. V. Soboleva, V. V. Moskalenko, and A. A. Fedyanin, Phys. Rev. Lett. 108, 123901 (2012).
- Din et al. (2022) R. U. Din, X. Zeng, H. Ali, X.-F. Yang, and G.-Q. Ge, Physica E: Low-dimensional Systems and Nanostructures 135, 114989 (2022).
- Wu et al. (2019b) H. Wu, Q. Luo, H. Chen, Y. Han, X. Yu, and S. Liu, Phys. Rev. A 99, 033820 (2019b).
- Ullah et al. (2019) M. Ullah, A. Abbas, J. Jing, and L.-G. Wang, Phys. Rev. A 100, 063833 (2019).
- Khan et al. (2020) A. A. Khan, M. Abbas, Y.-L. Chaung, I. Ahmed, and Ziauddin, Phys. Rev. A 102, 053718 (2020).
- Radmehr et al. (2016) A. Radmehr, M. Sahrai, and H. Sattari, Appl. Opt. 55, 1946 (2016).
- Yin et al. (2004) X. Yin, L. Hesselink, Z. Liu, N. Fang, and a. Zhang, Appl. Phys. Lett. 85, 372 (2004).
- Salasnich (2012) L. Salasnich, Phys. Rev. A 86, 055801 (2012).
- Li et al. (2014) X. Li, P. Wang, F. Xing, X.-D. Chen, Z.-B. Liu, and J.-G. Tian, Opt. Lett. 39, 5574 (2014).
- Chen et al. (2017) S. Chen, C. Mi, L. Cai, M. Liu, H. Luo, and S. Wen, Appl. Phys. Lett. 110, 031105 (2017).
- Wu et al. (2017) W. Wu, S. Chen, C. Mi, W. Zhang, H. Luo, and S. Wen, Phys. Rev. A 96, 043814 (2017).
- Grosche et al. (2016) S. Grosche, A. Szameit, and M. Ornigotti, Phys. Rev. A 94, 063831 (2016).
- Wu et al. (2011) Z. Wu, F. Zhai, F. M. Peeters, H. Q. Xu, and K. Chang, Phys. Rev. Lett. 106, 176802 (2011).
- Shah (2022) M. Shah, Opt. Mater. Express 12, 421 (2022).
- Jahani et al. (2023) D. Jahani, O. Akhavan, A. Hayat, and M. Shah, J. Opt. Soc. Am. A 40, 21 (2023).
- Cheng et al. (2014) M. Cheng, P. Fu, X. Chen, X. Zeng, S. Feng, and R. Chen, J. Opt. Soc. Am. B 31, 2325 (2014).
- Zeng et al. (2017) X. Zeng, M. Al-Amri, and M. S. Zubairy, Opt. Express 25, 23579 (2017).
- Blake et al. (2007) P. Blake, E. W. Hill, A. H. Castro Neto, K. S. Novoselov, D. Jiang, R. Yang, T. J. Booth, and A. K. Geim, Appl. Phys. Lett. 91, 063124 (2007).
- Novoselov et al. (2012) K. S. Novoselov, V. I. Fal’ko, L. Colombo, P. R. Gellert, M. G. Schwab, and K. Kim, Nature 490, 192 (2012).
- Jayaswal et al. (2013) G. Jayaswal, G. Mistura, and M. Merano, Opt. Lett. 38, 1232 (2013).
- Mi et al. (2017) C. Mi, S. Chen, W. Wu, W. Zhang, X. Zhou, X. Ling, W. Shu, H. Luo, and S. Wen, Opt. Lett. 42, 4135 (2017).
- Hashimoto and Yoshino (1989) T. Hashimoto and T. Yoshino, Opt. Lett. 14, 913 (1989).
- Yin and Hesselink (2006) X. Yin and L. Hesselink, Appl. Phys. Lett. 89, 261108 (2006).
- Borgnia et al. (2015) D. S. Borgnia, T. V. Phan, and L. S. Levitov, arXiv preprint arXiv:1512.09044 (2015), 10.48550/arXiv.1512.09044.
- Gusynin et al. (2007) V. P. Gusynin, S. G. Sharapov, and J. P. Carbotte, J. Phys.: Condens. Matter 19, 026222 (2007).
- Platzman and Wolff (1973) P. M. Platzman and P. A. Wolff, Waves and interactions in solid state plasmas, Vol. 13 (Academic Press New York, 1973).
- Hanson (2008) G. W. Hanson, J. Appl. Phys. 104, 084314 (2008).
- Aiello et al. (2009) A. Aiello, M. Merano, and J. P. Woerdman, Phys. Rev. A 80, 061801 (2009).
- Benea-Chelmus et al. (2021) I.-C. Benea-Chelmus, M. Meretska, D. Elder, M. Tamagnone, L. Dalton, and F. Capasso, Nature Commun. 12, 5928 (2021).
- Xu et al. (2022) L. Xu, G. Xu, J. Huang, and C.-W. Qiu, Phys. Rev. Lett. 128, 145901 (2022).
- Tabert and Nicol (2013) C. J. Tabert and E. J. Nicol, Phys. Rev. B 87, 121402 (2013).
- Beenakker et al. (2009) C. W. J. Beenakker, R. A. Sepkhanov, A. R. Akhmerov, and J. Tworzydło, Phys. Rev. Lett. 102, 146804 (2009).