Impact of Postshock Turbulence on the Radio Spectrum of Radio Relic Shocks in Merging Clusters

As outlined in the introduction, downstream of the shock front, CR electrons further acquire energy through TTD resonance with compressive fast-mode waves and gyroresonant scattering off Alfvén waves. These waves might be present in small-scale, kinetic magnetic fluctuations that are cascaded down from MHD-scale turbulence (Brunetti & Jones, 2014) or excited by plasma microinstabilities in the shock transition zone (Guo & Giacalone, 2015; Trotta et al., 2023). However, the microphysics governing the excitation and evolution of MHD/plasma waves and Fermi-II acceleration of CR electrons in the high beta ICM plasmas are quite complex and relatively underexplored (e.g. Lazarian et al., 2012). This makes it hard to formulate accurate models for the momentum diffusion coefficient, $D_{pp}$.

The TA timescale due to the interaction with fast modes can be related with $D_{pp}$ as

where, in general, $\tau_{pp}(p)$ depends on the nature and amplitude of magnetic fluctuations, $\delta B(x,t)$, in the flow. As in many previous studies (e.g. Kang et al., 2017), we take a practical approach in which a constant value, $\tau_{pp}=0.1$ Gyr is assumed since the detail properties of the postshock turbulence are not well constrained. For instance, using cosmological structure formation simulations, Miniati (2015) found that in the ICM typically $t_{pp}\sim 0.1-1$ Gyr due to enhanced turbulence during the active phase of major mergers.

Based on the work of Fujita et al. (2015), we adopt $D_{pp}$ due to gyro-resonance with Alfvén waves as follows:

where $v_{A}=B/\sqrt{4\pi\rho}$ is the Alfvén speed, $D_{xx}\sim cl_{\rm mfp}/3$ is the spatial diffusion coefficient, $\eta_{m}\sim 5\times 10^{-4}$ is a reduction factor for waves on small kinetic scales, and $p_{0}=10^{-3}m_{e}c$ is the reference momentum. The slope $q_{K}=5/3$ is adopted since Alfvén modes of decaying MHD turbulence are expected to have a Kolmogorov spectrum (e.g., Cho & Lazarizn, 2003). As a result, $D_{\rm pp,A}/p^{2}\propto p^{-1/3}B^{2}$, so TA becomes increasingly inefficient at higher momentum. In addition, $D_{\rm pp,A}$ decreases as magnetic fluctuations decay in the postshock flow. The Coulomb mean free path for thermal electrons can be estimated as

where $\ln\Lambda\sim 40$ is the Coulomb logarithm (Brunetti & Lazarian, 2007).

Figure 2 shows the cooling timescales for Coulomb collisions, $\tau_{\rm Coul}$, and synchrotron plus IC losses, $\tau_{\rm sync+IC}$, for a representative set of parameters for the ICM, i.e., $n=10^{-4}{\rm cm^{-3}}$, $B=2~{}\mu G$, and the redshift, $z_{r}=0.2$. For radio emitting CR electrons with the Lorentz factor, $\gamma\sim 10^{3}-10^{4}$, typical cooling timescales range $\tau_{\rm cool}\sim 0.1-1$ Gyr. The figure also compares the TA timescales due to fast modes, $\tau_{\rm Dpf}$, and for Alfvén modes, $\tau_{\rm DpA}$. For the set of representative parameters considered here, TA with $D_{\rm pp,A}$ is more efficient compared to radiative losses for $\gamma\lesssim 3\times 10^{3}$, whereas TA with $D_{\rm pp,f}$ is more efficient for $\gamma\lesssim 10^{4}$.

The full consideration of the evolution of postshock turbulence, including the vorticity generation behind a rippled shock front, additional injection of turbulence driven by continuous subclump mergers, decompression of the postshock flows, and kinetic wave-particle interactions, is beyond the scope of this study. In anticipation of the dissipation of MHD turbulence energy, we employ an exponential function to model the decay of magnetic energy and the reduction of momentum diffusion:

where $t_{\rm dec}=0.1$ or 0.2 Gyr is considered (see Table 1). Although the functional forms for the two quantities could differ with separate values of $t_{\rm dec}$, we opt for this simple model to reduce the number of free parameters in our modeling. In addition, we note that non-driven MHD turbulence is known to decay as a power law in time, i.e., $E_{B}\propto(1+C_{B}t/t_{\rm dec})^{-\eta}$ with $\eta\sim 1$ and $C_{B}\sim 1$ (MacLow et el., 1998; Cho & Lazarizn, 2003). Within one eddy turnover time ($t_{\rm dec}$), the magnetic energy density decreases by a factor of $\sim 2.7^{2}$ in the exponential decay model given in equation (6), and by a factor of $\sim 2$ in the power-law decline model. We can justify our choice since our study primarily focuses on a qualitative examination of how turbulence decay influences postshock synchrotron emission. Considering that $t_{\rm dec}$ is a not-so-well constrained, free parameter in our model, the quantitative interpretation of our results should be taken with caution.

We follow the time evolution of the CR distribution function, $f(p,t)$, in the Lagrangian fluid element that advects downstream with the constant postshock speed. So the spatial advection distance of the fluid element from the shock front is given as $x=u_{2}t$. At the shock position ($t=0$), the shock-injected spectrum, $f_{\rm inj}(p)$, or the shock-reaccelerated spectrum, $f_{\rm RA}(p)$, are assigned as the initial spectrum (see Figure 3).

The spectrum of injected CR electrons is assumed to follow the DSA power-law for $p\geq p_{\rm min}$:

where $n_{2}$ and $T_{2}$ are the postshock gas density and temperature, respectively (Kang, 2020). In addition, $p_{\rm th}=\sqrt{2m_{e}k_{B}T_{2}}$, $p_{\rm min}=Q_{e}~{}p_{\rm th}$ with the injection parameter $Q_{e}=3.5$. Usual physical constants are used: $m_{e}$ for the electron mass, $c$ for the speed of light, and $k_{B}$ for the Boltzmann constant.

For the preshock population of CR electrons, we adopt a power-law spectrum with the slope $s$ for $p\geq p_{\rm min}$:

where $f_{\rm o}$ is the normalization factor and $p_{\rm cut}\approx 10^{3}m_{e}c$ is a cutoff momentum due to cooling. The preexisting CR electrons may consist of fossil electrons injected by relativistic jets from radio galaxies or residual electrons accelerated in previous shock passages. If these fossil electrons are accelerated by relativistic shocks contained in relativistic jets, the power-law slope could be $s\approx 4.3$ (Kirk et al., 2000). On the other hand, if they are accelerated by ICM shock with $M_{s}\approx 2.3-3$ in the cluster outskirts, $s\approx 4.5-4.9$ (Hong et al., 2014).

The reaccelerated population at the shock can be calculated by the following integration:

(Drury, 1983; Kang & Ryu, 2011). Except in the case of $q=s$, $f_{\rm RA}(p)\propto p^{-r}$ with $r=\min(q,s)$, meaning $f_{\rm RA}(p)$ adopts the harder spectrum between $p^{-q}$ and $p^{-s}$.

We choose shocks with Mach numbers $M_{s}=2.3$ and $M_{s}=3.0$ as the reference models. This selection is based on the observation that the Mach number of radio relic shocks detected in the cluster outskirts typically falls in the range of $2\lesssim M_{\rm rad}\lesssim 5$ (Wittor et al., 2021). Furthermore, numerous particle-in-cell (PIC) simulations have shown that only supercritical shocks with $M_{s}\gtrsim 2.3$ can effectively accelerate CR electrons in weakly magnetized ICM characterized by $\beta\sim 50-100$ (e.g., Kang et al., 2019; Ha et al., 2021; Boula et al., 2024).

The columns 1-4 of Table 1 list the model names for shocks with $M_{s}=3.0$, along with the various model parameters being considered. In M3In* models, the shock-injected population given in Equation (7) is deposited at the shock location, while the reaccelerated population given in Equation (9) is used in M3RA* models. Additionally, we will present the same set of models with $M_{s}=2.3$, denoted as M2.3*, in Section 3.

M3InDp0 corresponds to the conventional DSA model without TA ($D_{pp}=0$) in the postshock region with a constant magnetic field ($B_{2}$). The effects of decaying $B(t)$ is explored with the two values of the decay time, $t_{\rm dec}=100$ Myr and $200$ Myr. For M3In* models, the number in the parenthesis represents $t_{\rm dec}$ in units of Myr. Additionally, we investigate the dependence on the momentum diffusion models, namely $D_{\rm pp,f}$ and $D_{\rm pp,A}$. Note that for the models with nonzero $D_{\rm pp}$, the constant $B$ field case is not included, as it is incompatible with the decaying model for magnetic fluctuations.

For M3RA* models, we explore two values of the power-law slope, $s=4.3$ and $4.7$, considering the DSA slope $q=4.5$ for $M_{s}=3$ shocks. Note that the number in the parenthesis of the model names for M3RA* represents the value of $s$.

To follow the time evolution of $f(p,t)$ along the Lagrangian fluid element, we solve the following Fokker-Planck equation:

Here, the cooling rate, $b_{l}$, includes energy losses from Coulomb, synchrotron, and IC interactions. Standard formulas for these processes can be found in various previous papers, such as Brunetti & Jones (2014). Specifically, the Coulomb interaction depends on the density of thermal electrons, $n$, synchrotron losses depend on the magnetic field strength, $B$, and the inverse Compton scattering off the cosmic background radiation depends on the redshift, $z_{r}$ (see Figure 2). The divergence term becomes $\nabla\cdot\mathbf{u}=0$ in the postshock flow in 1D plane-parallel geometry, and the source term $S(p)$ accounts for $f_{\rm inj}(p)$ and $f_{\rm RA}(p)$ deposited at the shock position.

Figure 4 illustrates the evolution of the distribution function, $g(p)=p^{4}f(p)$, for M3In*(100) and M3RA*(4.3) models. Additionally, it presents the volume-integrated spectrum, $G(p)=p^{4}F(p)=p^{4}\cdot u_{2}\int_{0}^{t_{f}}f(p,t)dt$, where $t_{f}=0.2$ Gyr denotes the final advection time. The M3InDp0(100) model, which solely incorporates radiative cooling without TA, serves as a reference for comparison with other models. In Panel (a), it is evident that Coulomb loss is important only for low-energy electrons with $\gamma<10$, whereas synchrotron + IC losses are significant for $\gamma>10^{3}$. This panel demonstrates that the volume-integrated CR spectrum $F(p)$ steepens from $p^{-q}$ to $p^{-(q+1)}$ above the “break momentum” as expected:

where the effective magnetic field strength, $B_{\rm e}^{2}=B_{2}^{2}+B_{\rm rad}^{2}$, takes account for radiative losses due to both synchrotron and IC processes, and $B_{\rm rad}=3.24\mu{\rm G}(1+z_{r})^{2}$ corresponds to the cosmic background radiation at redshift $z_{r}$.

Figures 4(b-c) illustrate how TA with $D_{\rm pp,f}$ or $D_{\rm pp,A}$ delays or reduces the postshock cooling, enhancing $f(p)$. Consequently, the resulting spectrum, including both $f(p,t)$ and $F(p)$, deviates significantly from the simple DSA predictions that take into account only postshock cooling. As shown in Figure 2, TA with $D_{pp,A}$ is dominant for $\gamma<10^{2}$, while TA with $D_{\rm pp,f}$ becomes more effective for higher $\gamma$ for the parameters considered here. Regarding the parameter dependence, obviously, TA with $D_{\rm pp,f}$ becomes less efficient for a greater value of $\tau_{\rm Dpf}$. On the other hand, TA with $D_{pp,A}$ becomes more efficient with a stronger $B$ and a smaller $\eta_{m}$.

Figures 4(d-f) present similar results for the M3RA*(4.3) models, wherein the reaccelerated spectrum $f_{\rm RA}(p)$ with $s=4.3$ is introduced at $t=0$. For illustrative purposes, the normalization factor, $f_{\rm o}$, is set to be the same as that of $f_{\rm inj}(p)$ in Equation (7). Consequently, the resulting $f_{\rm RA}$ (depicted by the blue lines at $t=0$ in the lower panels) is larger than $f_{\rm inj}$ (represented by the blue lines at $t=0$ in the upper panels), as shown in the figure. For the M3RA*(4.7) models with $s=4.7$, only $f_{\rm pre}(p)$ and $G(p)$ are displayed in the magenta lines for comparison. In the case of the reacceleration models, both the postshock spectrum, $f(p,t)$, and the volume-integrated spectrum, $F(p)$, may not be represented by simple power-law forms, even without TA.

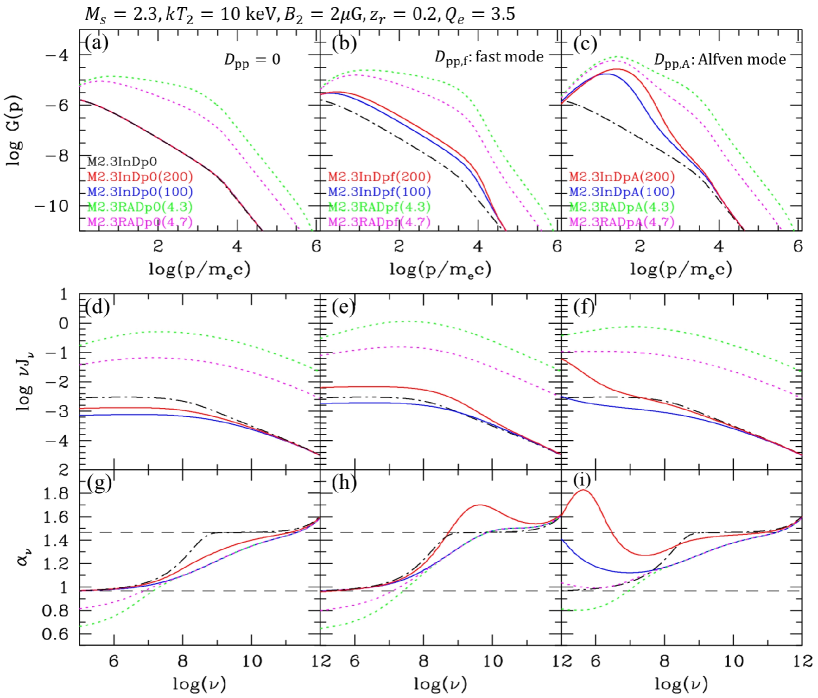
Figures 5(a-c) compare $G(p)$ for all $M_{s}=3$ models listed in Table 1. For the three models without TA but with different values of $t_{\rm dec}$, M3InDp0, M3InDp0(200), and M3InDp0(100), $G(p)$ is almost the same since the total cooling is dominated by the IC cooling, and the effects of decaying $B(t)$ are relatively minor. For comparison, $G(p)$ for M3InDp0 (no TA and a constant $B_{2}$) is displayed in the black dotted-dashed line in each panel. Panels (b) and (c) show the effects of TA with $D_{\rm pp,f}$ and $D_{\rm pp,A}$, respectively. Thus, compared with the conventional DSA model, TA due to postshock turbulence may enhance the CR electron population. In addition, the reaccelerated spectrum, $f_{\rm RA}$ (green and magenta dotted lines) could be higher than $f_{\rm inj}$, depending on the amplitude of the fossil electron population.

For the same thirteen models depicted in Figures 5(a-c), the volume-integrated synchrotron spectrum, $\nu J_{\nu}$, is shown in Figures 5(d-f), while its spectral index, $\alpha_{\nu}=-d\ln J_{\nu}/d\ln\nu$ is displayed in Figures 5(g-i). Again, in each panel, the black dotted-dashed line represents the results for M3InDp0, included for comparison. In Panels (d) and (g), the three models without TA, M3InDp0, M3InDp0(200) and M3InDp0(100), are depicted in the black, red, and blue lines, respectively. They demonstrate that the effects of decaying $B(t)$ are quite prominent due the strong dependence of the synchrotron emissivity on the magnetic field strength. For example, $j_{\nu}\propto B^{(q-1)/2}$ for the power-law spectrum of $f(p)\propto p^{-q}$.

In the conventional DSA model with a constant $B$ (M3InDp0), the transition from $\alpha_{\rm sh}$ to $\alpha_{\rm int}$ occur rather gradually around the break frequency,

So one should use radio observations at sufficiently high frequencies, $\nu\gg\nu_{\rm br}$, to estimate the Mach number given in Equation (2) using the integrated spectral index (Kang, 2015). However, as depicted in the red and blue solid lines in Panel (g), this transition takes place much more gradually in the case of decaying magnetic fields with smaller $t_{\rm dec}$. Thus, an accurate model for the postshock $B(x)$ is required to estimate the Mach number of radio relic shocks using Equation (2), considering the observational radio frequency range of $\sim 0.1-30$ GHz.

Figures 5(h-i) illustrate that TA with a large momentum diffusion coefficient, especially $D_{\rm pp,A}$, could lead to a significant deviation from the simple DSA prediction with a constant magnetic field strength. We also note that, in Panels (g)-(i), the blue, green, and magenta lines (all with $t_{\rm dec}=100$ Myr) overlap with each other, except for very low frequencies ($\nu<10$ MHz), whereas they differ significantly from the black ($t_{\rm dec}=\infty$) and red ($t_{\rm dec}=200$ Myr) lines. This implies that the magnetic field distribution plays a significant role in governing the integrated spectral index $\alpha_{\nu}$ of the volume-integrated radio spectrum.

In Table 1 for the M3* models, the columns 5-7 list the integrated spectral index, $\alpha_{\nu_{1}}^{\nu_{2}}$, between two frequencies, $\nu_{1}$ and $\nu_{2}$, where $\nu=0.15,~{}0.61,~{}3.0,~{}{\rm and}~{}16$ GHz are chosen as representative values. Moreover, the columns 8-10 list the integrated Mach number, $M_{\nu_{1}}^{\nu_{2}}$, estimated based on Equation (2) using $\alpha_{\nu_{1}}^{\nu_{2}}$. For M3InDp0, the results are consistent with conventional DSA predictions except for the low frequency case: i.e., $\alpha_{\nu_{1}}^{\nu_{2}}=1.25$ and $M_{\nu_{1}}^{\nu_{2}}=3$ for $\nu\gg\nu_{\rm br}$. In the case of $\alpha_{0.15}^{0.61}$, the frequencies are not sufficiently high, resulting in the overestimation of Mach number, $M_{0.15}^{0.61}=3.8$ for M3InDp0. In fact, for most other models, $\alpha_{0.15}^{0.61}<1$, so $M_{0.15}^{0.61}$ cannot be estimated. Both TA and reacceleration significantly influence the integrated spectrum $J_{\nu}$ and tend to generate smaller $\alpha_{\nu_{1}}^{\nu_{2}}$, resulting in higher $M_{\nu_{1}}^{\nu_{2}}$ except for M3InDpf(200) (see also Figures 5(g-i)).

The M2.3* models also exhibit similar results, as can be seen in Figure 6.

Using the geometrical configuration of the shock surface depicted in Figure 1, we estimate the surface brightness, $I_{\nu}(d)$, as a function of the projected distance, $d$. In brief, a radio relic has a coconut-shell-shaped, elongated surface with an axial ratio $a/b\sim 1-1.5$ and a thickness corresponding to the cooling length of electrons, $l_{\rm cool}$. Here, the radius of the spherical shell is set as $R_{s}=1$ Mpc. Then the surface brightness or intensity is calculated by

where $h_{\rm min}$ and $h_{\rm max}$ are determined by the extension angles, $\psi_{1}$ and $\psi_{2}$. As illustrated in Figure 1, the path length $h$ along the observer’s line of sight reaches its maximum at $d_{\rm peak}=R_{s}(1-\cos\psi_{1})$. So for the assumed model parameters, $R_{s}=1$ Mpc and $\psi_{1}=\psi_{2}=15^{\circ}$, the surface brightness peaks at $d_{\rm peak}\approx 34$ kpc.

Figure 7 presents the spatial profiles of $I_{\rm 0.15}(d)$ at 0.15 GHz and $I_{\rm 0.61}(d)$ at 0.61 GHz for the same thirteen models shown in Figure 5. The spectral index $\alpha_{0.15}^{0.61}(d)$ is calculated from the projected $I_{\nu}(d)$ between the two frequencies. Several points are noted:

1. 1.

   The postshock magnetic field plays a key role in determining the profile of $I_{\nu}(d)$ and $\alpha_{\nu}(d)$, as it governs the synchrotron emissivity $j_{\nu}$ and $D_{\rm pp,A}$. Consequently, the results depend sensitively on the decay of $B(t)$ in the postshock region.

2. 2.

   The models with postshock TA (middle and right columns) exhibit a slower decrease in $I_{\nu}(d)$ compared to the models without TA (left column). This occurs because TA delays the postshock cooling of electrons, resulting in a broader effective width of radio relics. In particular, the models with $D_{\rm pp,f}$ generate greater widths than those with $D_{\rm pp,A}$.

3. 3.

   In the models with $D_{\rm pp,A}$, the enhancement by TA is less significant due to the effects of decaying magnetic fields, distinguishing it from models with $D_{\rm pp,f}$.

4. 4.

   Panels (g-i) demonstrate that the postshock profile of $\alpha_{\nu}$ is independent of the injection spectrum (i.e., $f_{\rm inj}$ or $f_{\rm RA}$). The profile is mainly influenced by the decay profile of $B(x)$ and by TA due to $D_{\rm pp}(p,x)$.

5. 5.

   The spectral index is the smallest at the relic edge ($d=0$), while the intensity profile peaks at $d_{\rm peak}$ in our model set-up for the relic shock surface. Therefore, in observations of radio relics, the region $d<d_{\rm peak}$ corresponds to the postshock region rather than the preshock region.

The M2.3* models presented in Figure 8 also exhibit the similar behaviors.