Impact of Local Pressure Enhancements on Dust Concentration in Turbulent Protoplanetary Discs

We consider a global hydrodynamic model of a PPD consisting of gas and a single species of dust, governed by the set of dynamical equations

$$\left(\frac{\partial}{\partial t}+\@vec{v}_{g}\cdot\@vec{\nabla}\right)\,\rho_{g}=-\rho_{g}\left(\@vec{\nabla}\cdot\@vec{v}_{g}\right),$$

(1)

$$\left(\frac{\partial}{\partial t}+\@vec{v}_{g}\cdot\@vec{\nabla}\right)\,\@vec{v}_{g}=-\frac{1}{\rho_{g}}\@vec{\nabla}P+\frac{1}{\rho_{g}}\@vec{\nabla}\cdot\hat{T}-\@vec{\nabla}\Phi_{*}-\frac{\epsilon}{t_{s}}\left(\@vec{v}_{g}-\@vec{v}_{d}\right),$$

(2)

$$\left(\frac{\partial}{\partial t}+\@vec{v}_{d}\cdot\@vec{\nabla}\right)\,\rho_{d}=-\rho_{d}\left(\@vec{\nabla}\cdot\@vec{v_{d}}\right)+\@vec{\nabla}\cdot\left(\nu\rho\@vec{\nabla}f_{d}\right),$$

(3)

$$\left(\frac{\partial}{\partial t}+\@vec{v}_{d}\cdot\@vec{\nabla}\right)\,\@vec{v}_{d}=-\@vec{\nabla}\Phi_{*}-\frac{1}{t_{s}}\left(\@vec{v}_{d}-\@vec{v}_{g}\right),$$

(4)

where $\rho_{g}$, $\rho_{d}$, $\@vec{v}_{g}$ and $\@vec{v}_{d}$ are the gas and dust volume mass densities and three-dimensional gas and dust velocities, respectively, in a non-rotating frame with cylindrical coordinates $(r,\varphi,z)$ and with origin on a central star of mass $M_{*}$ with gravitational potential $\Phi_{*}=-GM_{*}/\sqrt{r^{2}+z^{2}}$, where $G$ is the gravitational constant. The indirect gravitational term, stemming from the fact that the center of mass of the system does not coincide with the center of the star, is omitted. Furthermore, we neglect self-gravity and magnetic fields. The remaining symbols in the above equations are explained below.

We adopt a locally isothermal equation of state for the gas such that the pressure

$$P=c_{s}^{2}\rho_{g},$$

(5)

where the squared sound-speed follows a power-law with constant index $-q$:

$$c_{s}^{2}(R)=c_{s0}^{2}\left(\frac{r}{r_{0}}\right)^{-q}.$$

(6)

The reference sound-speed $c_{s0}=c_{s}(r_{0})$, where $r_{0}$ is a reference radius. Unless otherwise stated, we take $q=1$. This value is a bit larger than what is typically expected at large radii in PPDs where the temperature profile is set by stellar irradiation [e.g. Andrews et al., (2009)]. However, our choice facilitates a comparison with the isothermal simulations by Nelson et al., (2013), Stoll and Kley, (2016), Richard et al., (2016) and Manger and Klahr, (2018); Manger et al., (2020) who used the same value. Moreover, it also has the advantage of a radially constant disc aspect ratio such that the required vertical resolution in our simulations is independent of radius. The characteristic gas pressure scale height $H_{g}=c_{s}/\Omega_{K}$, where $\Omega_{K}\equiv\sqrt{GM_{*}/r^{3}}$ is the Keplerian frequency.

The dust component is treated as a pressureless fluid that interacts with the gas through a friction force (Johansen et al.,, 2014) quantified by the stopping time¹¹1Strictly $c_{s}$ should be replaced by the mean thermal gas velocity (Weidenschilling,, 1977) which differs from $c_{s}$ by a factor $\sqrt{8/\pi}$. For convenience we absorb this factor in the particle size $r_{d}$.

$$t_{s}=\frac{r_{d}\rho_{d}}{\rho_{g}c_{s}},$$

(7)

where $r_{d}$ and $\rho_{d}$ stand for the particle radius and bulk density, respectively. The stopping time is the characteristic timescale for a grain to reach velocity equilibrium with its surrounding gas. The fluid approximation for dust is valid for sufficiently small $t_{s}$ (Jacquet et al.,, 2011). Usually we will work with the dimensionless Stokes number

$$\tau=\Omega_{K}t_{s}.$$

(8)

Grains with $\tau\ll 1$ are tightly (but not necessarily perfectly) coupled to the gas, which either corresponds to small grain sizes or to small distances to the star where the gas density is appreciably higher. The former case is the one that applies to this paper. The Stokes number at $r=r_{0}$, $z=0$, and time $t=0$, denoted by $\tau_{0}$, will be a freely specifiable parameter in our model. This means that, for a given particle radius and bulk density, its stopping time at a certain location and at a certain time is given by

$$t_{s}=\frac{\tau_{0}}{\Omega(r_{0})}\frac{\rho_{g}(r_{0},z=0,t=0)\,c_{s}(r_{0})}{\rho_{g}c_{s}}.$$

(9)

We also define

	$\displaystyle\epsilon$	$\displaystyle=\frac{\rho_{d}}{\rho_{g}},$		(10)
	$\displaystyle f_{d}$	$\displaystyle=\frac{\rho_{d}}{\rho},$		(11)

as the dust-to-gas density ratio and the dust fraction, respectively, with the total density $\rho=\rho_{g}+\rho_{d}$. Note that $f_{d}=\epsilon/(1+\epsilon)$.

Finally,

$$\hat{T}=\rho_{g}\nu\left[\@vec{\nabla}\@vec{v}_{g}+\left(\@vec{\nabla}\@vec{v}_{g}\right)^{\dagger}-\frac{2}{3}\hat{U}\@vec{\nabla}\cdot\@vec{v}_{g}\right]$$

is the viscous stress tensor with a (constant) kinematic viscosity $\nu$, which also describes dust diffusion via the diffusion term in Equation (3). The symbol $\dagger$ denotes the conjugate transpose and $\hat{U}$ stands for the unit tensor. Viscous terms are only included to ensure numerical stability. Hence, $\nu$ is chosen to be very small and in derivations which follow below viscous terms are neglected. In particular, $\nu$ is much smaller than the typical value of the $\alpha$-viscosity (defined in Section 2.5) measured in simulations.

Our numerical simulations evolve Equations 1–4 directly (Section 2.5). However, as shown by Lin and Youdin, (2017) many important aspects of dust-gas dynamics can be described within a reduced one-fluid model, governed by the set of equations

$$\left(\frac{\partial}{\partial t}+\@vec{v}\cdot\@vec{\nabla}\right)\,\rho=-\rho\left(\@vec{\nabla}\cdot\@vec{v}\right),$$

(12)

$$\left(\frac{\partial}{\partial t}+\@vec{v}\cdot\@vec{\nabla}\right)\,\@vec{v}=-\frac{1}{\rho}\@vec{\nabla}P-\@vec{\nabla}\Phi_{*},$$

(13)

$$\left(\frac{\partial}{\partial t}+\@vec{v}\cdot\@vec{\nabla}\right)\,\mathrm{S_{\mathrm{eff}}}=-\@vec{v}\cdot\@vec{\nabla}\ln\,c_{s}^{2}+\frac{c_{s}^{2}}{P}\@vec{\nabla}\cdot\left(t_{\mathrm{eff}}f_{d}\@vec{\nabla}P\right),$$

(14)

with density

$$\rho=\rho_{g}+\rho_{d},$$

the center of mass velocity

$$\@vec{v}=\frac{\rho_{g}\@vec{v}_{g}+\rho_{d}\@vec{v}_{d}}{\rho}$$

(15)

and where the effective (dimensionless) entropy of the dust-gas mixture is defined by

$$\mathrm{S_{\mathrm{eff}}}=\ln\frac{P}{\rho}$$

(16)

and the effective particle stopping time by

$$t_{\mathrm{eff}}=t_{s}\frac{\rho_{g}}{\rho}.$$

(17)

These equations can be derived from Equations (1)-(4) and (5) if dust and gas relative velocities are fixed by the terminal velocity approximation

$$\@vec{v}_{g}-\@vec{v}_{d}=-\frac{t_{\mathrm{eff}}}{\rho_{g}}\@vec{\nabla}P,$$

(18)

valid for small particles which are tightly coupled to the gas (Youdin and Goodman,, 2005). For a more general set of one-fluid equations, see Laibe and Price, (2014). We use (12)-(14) to motivate the ground state of our disc.

Within this formalism the dust fraction is related to the gas pressure (and temperature) via (5) and (11) such that

$$f_{d}=1-\frac{P}{c_{s}^{2}\rho}.$$

(19)

Similarly, one can define a reduced temperature of the dust-gas mixture

$$T_{\mathrm{red}}\equiv\frac{\mu}{\mathcal{R}}\frac{P}{\rho}=T\left(1-f_{d}\right),$$

(20)

with the gas constant $\mathcal{R}$ and the mean molecular weight $\mu$, such that an increased dust fraction corresponds to a reduced temperature. Furthermore, the flux term (second term on the right hand side of Equation (14)) stems from the fact that dust drifts into the direction of increasing pressure, as reflected by (18). Hence, the mixture of a locally isothermal gas with tightly coupled dust behaves as a single-component adiabatic fluid with a non-vanishing energy flux due to the exchange of dust between adjacent fluid parcels and an entropy source term resulting from the imposed global gas temperature profile.

A detailed derivation of this model and applications to various dusty analogs of pure gas instabilities can be found in Lin and Youdin, (2017). Here we merely summarize important quantities that govern the ground state of our disc and its stability, which can be directly derived from Equations (12)-(14). Following Lin, (2019) we assume a Gaussian dust-to-gas ratio distribution

$$\epsilon(r,z)=\epsilon_{mid}(r)\exp\left(-\frac{z^{2}}{2H_{\epsilon}^{2}}\right),$$

(21)

where the gas and dust scale heights are implicitly defined via

$$\frac{1}{H_{\epsilon}^{2}}=\frac{1}{H_{d}^{2}}-\frac{1}{H_{g}^{2}}.$$

(22)

This ansatz suggests that $\rho_{d}$ follows a Gaussian with scale height $H_{d}$ and $\rho_{g}$ follows a Gaussian with scale height $H_{g}$, which is indeed nearly the case as shown below. The initial mid-plane dust-to-gas ratio $\epsilon_{mid}(r)$ is chosen such that the radial contribution to the effective entropy source vanishes, i.e.

$$\frac{\partial}{\partial r}\left(t_{\mathrm{eff}}f_{d}\frac{\partial P}{\partial r}\right)=0$$

(23)

to reduce radial evolution of the initial state (see also Chen and Lin,, 2018). Of course, in a stratified disc the vertical contribution cannot be zero without diffusion, which results in dust settling (so strictly speaking $v_{z}\neq 0$). In practice we will set $H_{d}\lesssim H_{g}$ such that $H_{\epsilon}\gg H_{g}$. That is, the dust is initially well-mixed with the gas. This enables us to define the ground state metallicity

$$Z\equiv\left(\frac{\Sigma_{d}}{\Sigma_{g}}\right)_{0}=\epsilon_{mid}\left(\frac{H_{d}}{H_{g}}\right)_{0},$$

(24)

with the dust and gas surface mass densities $\Sigma_{d}$ and $\Sigma_{g}$, respectively. Since $H_{d}\lesssim H_{g}$ this also means that $\epsilon_{mid}(r=r_{0})\approx Z$. In addition to $\tau_{0}$ defined above, $Z$ will also be a used as an adjustable parameter in our simulations.

The radial and vertical components of Equation (13) at equilibrium and under the assumption of axisymmetry read

$$\Omega^{2}r=\Omega_{K}^{2}\left(1-\frac{3}{2}\frac{z^{2}}{r^{2}}\right)+\frac{1}{\rho}\frac{\partial P}{\partial r}$$

(25)

and

$$0=-\Omega_{K}^{2}z-\frac{1}{\rho}\frac{\partial P}{\partial z},$$

(26)

where we defined the orbital frequency $\Omega=v_{\phi}/R$ and applied the thin disc approximation, i.e. a Taylor expansion of the gravitational force term in (13) with respect to the quantity $z^{2}/r^{2}$ to next leading order and used the condition that the radial component of $\@vec{v}$ identically vanishes. Furthermore, we neglected the small contribution $\sim(f_{d}\,\tau)^{2}\Omega_{K}^{2}|z|\ll\Omega_{K}^{2}|z|$ due to dust settling²²2This term can be estimated from (4) and (15) in the limit of small $\tau$ and assuming $v_{gz}=0$.. From Equation (25) we obtain the orbital frequency

$$\Omega(r,z)=\Omega_{K}\left[1-\frac{3}{2}\frac{z^{2}}{r^{2}}-\frac{2\rho_{g}}{\rho}\eta\right]^{1/2},$$

(27)

where we defined

$$\eta=-\frac{1}{2\rho_{g}(\Omega_{K}r)^{2}}\frac{\partial P}{\partial\ln r},$$

(28)

which was also defined in Youdin and Goodman, (2005). Near the disc mid-plane we have $\eta>0$ such that the dusty gas rotates with sub-Keplerian frequency. Integration of Equation (26) using (21) yields the equilibrium gas density profile

$$\rho_{g}=\rho_{g,mid}\exp\left\{-\frac{z^{2}}{2H_{g}^{2}}-\epsilon_{mid}\frac{H_{\epsilon}^{2}}{H_{g}^{2}}\left[1-\exp\left(-\frac{z^{2}}{2H_{\epsilon}^{2}}\right)\right]\right\}.$$

(29)

As expected, for $\epsilon_{mid}\to 0$ we recover a Gaussian gas density profile with scale height $H_{g}$. In practice, deviations of the gas density from the latter are small, since we consider $\epsilon_{mid}\ll 1$, $H_{\epsilon}\gg H_{g}$, and $|z|$ is $O(H_{g})$.

We define

$$\rho_{g,mid}(r)=\frac{\Sigma_{g}(r)}{\sqrt{2\pi}H_{g}(r)},$$

(30)

such that the vertically integrated gas density yields the surface density $\Sigma_{g}(r)$, which we set to be

$$\Sigma_{g}(r)=\Sigma_{g,0}\left(\frac{r}{r_{0}}\right)^{-s},$$

(31)

with $s=3/2$. The total surface density is $\Sigma=\Sigma_{g}+\Sigma_{d}$.

Since our aim is to study the effect of a pressure bump on the dust evolution in the disc we modify the mid-plane density as

$$\begin{split}\rho_{g,mid}(r)&\to\rho_{g,mid}(r)\times\left[1+A\exp\left(-\frac{\left(r-r_{0}\right)^{2}}{2H_{g0}^{2}}\right)\right]\\ \quad&=\frac{\Sigma_{0}}{\sqrt{2\pi}H_{g0}}\left(\frac{r}{r_{0}}\right)^{-p}\left[1+A\exp\left(-\frac{\left(r-r_{0}\right)^{2}}{2H_{g0}^{2}}\right)\right]\end{split}$$

(32)

with $p\equiv s+(3-q)/2$. That is, we add a Gaussian density bump of amplitude $A$ and width $H_{g}(r_{0})=H_{g0}$ to the gas mid-plane density profile. While the width of the bump will be kept fixed throughout all simulations, its amplitude $A$ will be varried. Similar density bumps have been employed in numerous previous studies (e.g. Meheut et al., (2012); Taki et al., (2016); Carrera et al., 021a ). With (32) the equilibrium azimuthal velocity (27) now reads

$$\begin{split}\Omega(r,z)=\Omega_{K}&\left\{1-\frac{3}{2}\frac{z^{2}}{r^{2}}-\frac{\rho_{g}H^{2}}{\rho r^{2}}\left[p+q+r\frac{r-r_{0}}{H_{g0}^{2}}\right.\right.\\ \quad&\left.\left.\times\frac{A\exp\left(-\frac{\left(r-r_{0}\right)^{2}}{2H_{g0}^{2}}\right)}{1+A\exp\left(-\frac{\left(r-r_{0}\right)^{2}}{2H_{g0}^{2}}\right)}\right]\right\}^{1/2}.\end{split}$$

(33)

If we restrict our considerations to a narrow region about the mid-plane for the time being, we can neglect vertical gravity and the results of unstratified discs apply. In particular, since our disc is effectively inviscid the ground state planar velocities of dust and gas are those derived by Nakagawa et al., (1986), i.e.

$$\@vec{v}_{d}=\left[r\Omega-\frac{1}{2}\frac{\rho_{g}}{\rho}\tau\,v_{\mathrm{drift}}\right]\@vec{e_{\varphi}}+v_{\mathrm{drift}}\,\@vec{e}_{r},$$

(34)

$$\@vec{v}_{g}=\left[r\Omega+\frac{1}{2}\frac{\rho_{d}}{\rho}\tau\,v_{\mathrm{drift}}\right]\@vec{e_{\varphi}}-\frac{\rho_{d}}{\rho_{g}}v_{\mathrm{drift}}\,\@vec{e}_{r},$$

(35)

where we defined

$$v_{\mathrm{drift}}=-2\left(\frac{\rho_{g}}{\rho}\right)^{2}\frac{\eta\Omega_{K}r\tau}{1+\left(\tau\rho_{g}/\rho\right)^{2}}.$$

(36)

These ground state velocities can be derived from (2) and (4) under the neglect of vertical stratification. Solutions for $\alpha$-viscous discs that take into account the vertical disc structure can be found for instance in Takeuchi and Lin, (2002) and Kanagawa et al., (2017).

The effect of a pressure bump ($A>0$) in Eq. (33) has a profound effect on dust drift. This is illustrated in Figure 1 for different amplitudes $A$ and $\tau=10^{-2}$. This figure shows how $v_{\mathrm{drift}}$ is essentially controlled by the magnitude of $\eta$. Since $\eta\sim h^{2}\equiv(H_{g}/r)^{2}$ in PPDs ($h=H_{g}/r$ being the disc aspect ratio), typical values are $\eta\sim 10^{-2}-10^{-3}$. For the most part $\eta>0$ so dust drifts inwards, but $\eta$ is non-uniform. The bump thus leads to a ’traffic jam’-like accumulation of dust within a region $\Delta r\sim H_{g}$ surrounding the bump center. For the case $A=0.4$ the particle drift comes to a complete halt at a certain radius. This is one reason why pressure bumps in PPDs are expected to be preferred locations for planetesimal formation.

By combining Equations (25) and (26) we obtain

$$\begin{split}r\frac{\partial\Omega^{2}}{\partial z}=&\frac{c_{s}^{2}(r)}{\left(1+\epsilon\right)^{2}}\\ \quad&\times\left[\frac{\partial\epsilon}{\partial r}\frac{\partial\ln\rho_{g}}{\partial z}-\frac{\partial\epsilon}{\partial z}\frac{\partial\ln P}{\partial r}+\frac{q}{r}\left(1+\epsilon\right)\frac{\partial\ln\rho_{g}}{\partial z}\right].\end{split}$$

(37)

Hence, the disc’s equilibrium velocity profile is subjected to vertical shear, which constitutes the driving force of the VSI. As pointed out in Lin and Youdin, (2017) and Lin, (2019), in typical situations the main source of vertical shear is the disc’s global temperature gradient, quantified through $q$. However, in regions where sufficiently large gradients of $\epsilon$ occur, also the first two terms in the bracket may play a role. More on this follows below.

Another important quantity to characterize our disc is the vertical Buoyancy frequency

$$N_{z}^{2}\equiv-\frac{1}{\rho}\frac{\partial P}{\partial z}\frac{\partial S_{\mathrm{eff}}}{\partial z}=c_{s}^{2}\frac{\partial\ln\rho_{g}}{\partial z}\frac{\partial f_{d}}{\partial z},$$

(38)

which quantifies the stabilizing effect of vertical entropy stratification with respect to adiabatic perturbations. In our vertically isothermal disc this quantity is entirely due to dust-layering. As shown by Lin and Youdin, (2017), ‘dusty’ buoyancy mitigates the VSI by stabilizing vertical motions, similar to classical buoyancy if $N_{z}^{2}\gtrsim r\mathinner{\!\left\lvert\frac{\partial\Omega^{2}}{\partial z}\right\rvert}$, which is satisfied within sufficiently settled dust-layers. However, in the presence of strong VSI turbulence corrugation of the dust-layer can result in situations where $\partial f_{d}/\partial_{z}>0$ for $z>0$ and hence $N_{z}^{2}<0$, such that vertical convection may occur.

The occurrence of the VSI in a locally isothermal (dust-free) disc as the one considered here has been established analytically by Nelson et al., (2013), Barker and Latter, (2015) and Lin and Youdin, (2015). In addition, Nelson et al., (2013) conducted 3D hydrodynamical simulations. Linear stability analyses presented in these papers show that the VSI excites inertial waves that are destabilized by free energy extracted from the disc’s vertical shear. The dominant modes are so called “body modes”, which constitute vertically global ($l_{z}\sim hr$), radially local ($l_{x}\sim h^{2}r$) low frequency ($\sim h\Omega_{K}$) traveling inertial waves that result in either corrugation or ’breathing’ motion of the disc with respect to the mid-plane. The maximum linear growth rates $\sigma$ of the body modes in an isothermal disc are governed by the maximum shear in the domain under consideration, i.e.

$$\mathinner{\!\left\lvert\sigma\right\rvert}<\mathrm{max}\mathinner{\!\left\lvert r\frac{\mathrm{d}\Omega}{\mathrm{d}z}\right\rvert}\sim\Omega_{K}qh,$$

where the latter similarity assumes a domain $\mathinner{\!\left\lvert z\right\rvert}\lesssim H_{g}$. This approximation remains applicable even in the presence of dust (Lin and Youdin,, 2017). However, dust limits the amplitude of turbulent velocity perturbations wherever dust-induced buoyancy becomes significant.

Furthermore, Lin and Youdin, (2017) provided the corresponding Solberg-Høiland stability criteria for a dusty gas in the limit of perfect coupling $t_{\mathrm{eff}}=0$ and vanishing radial temperature gradient $q=0$, such that the source terms in Equation (14) vanish. These criteria read

$$\kappa^{2}+\frac{1}{\rho_{g}}\@vec{\nabla}P\cdot\@vec{\nabla}f_{d}>0,$$

(39)

$$-\frac{1}{\rho_{g}}\frac{\partial P}{\partial z}\left(-\kappa^{2}\frac{\partial f_{d}}{\partial z}+r\frac{\partial\Omega^{2}}{\partial z}\frac{\partial f_{d}}{\partial r}\right)>0,$$

(40)

where $\kappa^{2}=r^{-3}\partial_{r}\left(r^{4}\Omega^{2}\right)$ is the epicycle frequency squared, and determine the conditions for stability with respect to adiabatic perturbations (Tassoul,, 1978). These are appropriate since the dust-gas mixture under the aforementioned approximations behaves like an adiabatic gas that conserves the entropy (16). As discussed by Lin and Youdin, (2017), the first criterion (39) is expected to be fulfilled in typical situations due to alignment of the two gradients in the second term and since the disc is rotationally supported. The second criterion (40) can in principle be violated at locations where dust is well mixed vertically but $\epsilon$ undergoes sufficiently strong radial variations. Furthermore, if $\partial f_{d}/\partial_{z}>0$ occurs for $z>0$ the first term in the brackets in (40) is expected to be destabilizing. We will indeed see that both situations can be realized under certain circumstances in our simulations which involve strong corrugations of the dust-layer due to the VSI. However, this also means that the VSI is required in first place to violate any of the two criteria in our simulations. We will come back to this issue in Section 3.2.

Finally, an important instability that is directly involved in the nonlinear saturation of the VSI is the Rossby Wave Instability (RWI, Lovelace et al., (1999)) which can result in the formation of vortices. This instability can be expected when the generalised vortensity

$$\mathcal{L}=\frac{\Sigma}{2\omega_{z}}\left(\frac{\Pi}{\Sigma^{\gamma}}\right)^{2/\gamma}$$

(41)

possesses a local extremum, where $\Pi=c_{s}^{2}\Sigma_{g}$ denotes the vertically integrated pressure and where the $z$-component of vorticity defined in the inertial frame is

$$\omega_{z}=\@vec{e}_{z}\cdot\@vec{\nabla}\times(\@vec{v}+\Omega_{0}r\,\@vec{e}_{\varphi}),$$

(42)

and $\gamma$ is the adiabatic index. It should be noted that although (42) and other quantities above are defined using the center of mass velocity (15), the latter is nearly equal to both the dust and gas velocities since dust is tightly coupled to the gas in our model. Although the above condition was originally derived for gaseous discs, our locally isothermal gas with tightly coupled dust is equivalent to an adiabatic gas disc with $\gamma=1$ (Lin and Youdin,, 2017). We therefore expect $\mathcal{L}$ to also play a role in our simulations. Note that here, $\Pi$ arises from the gas only, but $\Sigma$ accounts for both gas and dust. For brevity we will simply refer to $\mathcal{L}$ as the vortensity.

As outlined in Richard et al., (2016) the VSI generates axisymmetric vortensity rings. These become unstable to the RWI, which consequently leads to the formation of vortices while the vortensity extrema are destroyed (see also Manger and Klahr,, 2018; Manger et al.,, 2020). Latter and Papaloizou, (2018) argue that in an isothermal disc where the vertical shear is strictly forced by the imposed global temperature gradient, the amplitude of the VSI-related velocity perturbations is limited by the emergence of Kelvin-Helmholtz parasitic modes that drain energy from the VSI modes and transfer it to smaller scales until viscous dissipation sets in. Based on theoretical arguments Latter and Papaloizou, (2018) estimate a maximal turbulent velocity amplitude of saturated VSI modes of a few percent to roughly ten percent of $c_{s}$. This is indeed in agreement with results from previous isothermal simulations of the VSI and also with results presented below. The parasitic modes may also result in the formation of small-scale vortices. Moreover, the mid-plane dustlayer can in principle undergo Kelvin Helmholtz Instability [KHI; Johansen et al., (2006); Lee et al., (2010)] but this is not expected to be resolved in our simulations. We also note that the pressure bump that is initially placed in our simulations is not expected to be Rossby Wave unstable when comparing the values of the width and amplitude used here with those applied in linear stability analyses of Ono et al., (2016) for a Gaussian density bump. That is, the largest amplitude bump considered here ($A=0.4$) might be marginally unstable to the RWI. However, in our

We solve Equations (1)-(4) with the multi-fluid code FARGO3D⁵⁵5http://fargo.in2p3.fr (Benítez-Llambay and Masset,, 2016; Benítez-Llambay et al.,, 2019). All quantities are subjected to periodic boundary conditions in azimuth. As for the radial and vertical boundary conditions equilibrium values of gas density and azimuthal velocity are extrapolated into the ghost zones, while gas radial and vertical velocities are set to zero at the boundaries. The only difference for the dust is that densities are subjected to symmetric boundary conditions. Simulations are carried out in spherical coordinates $(R,\varphi,\theta)$. Units are such that $R_{0}=\Omega_{0}=G=1$ ($R_{0}$ equals the radius $r_{0}$ defined in Section 2). We adopt $h_{0}=H_{g0}/R_{0}=0.05$ in all runs. The numerical grid covers $0.5\leq R\leq 1.5$, $-3H_{g}\leq z\leq+3H_{g}$, where $z=R\tan(\pi/2+\theta)$, and in 3D simulations $0\leq\varphi\leq\pi$. The grid resolution of most of our 2D simulations is $N_{R}\times N_{\theta}=2160\times 480$. Our 3D simulations are conducted on a grid with $N_{R}\times N_{\theta}\times N_{\varphi}=1088\times 256\times 512$. This corresponds to a resolution of $\sim(54\times 42\times 8)\,H_{g0}^{-1}$. While the radial and vertical resolutions are high compared to previous studies, we adopt a rather moderate azimuthal resolution for reasons of computational resources and since we expect structures to form in our simulations to be predominantly axisymmetric or elongated in azimuthal direction. Selected 2D simulations that are used for a direct comparison with 3D simulations have the same radial and vertical grid cells. The latter are carried out on a GPU cluster which is necessary to cover a substantial domain in parameter space while adopting a reasonable spatial resolution. All simulations are run for 1000 reference orbits. A list of all conducted 2D and 3D simulations with references to the corresponding sections is provided in Tables 1 and 2, respectively.

For analysis of our simulations we will often consider the diagnostic quantities defined as follows. Turbulent vertical momentum transport will be quantified through the Reynolds stress component

$$\langle\mathcal{R}_{\theta\varphi}(\theta,t)\rangle=\langle\mathrm{sgn}(z)\,\rho_{g}v_{g\theta}\Delta v_{g\varphi}\rangle_{R\varphi}$$

(43)

where $\Delta v_{g\varphi}$ denotes the azimuthal velocity deviation from its ground state value. Averages $\langle\,\rangle$ are in all cases taken over $R$, $\varphi$ (in 3D simulations) and in addition either $\theta$ or $t$. The additional factor $\mathrm{sgn}(z)$ is included here in order to facilitate averaging of values above and below the mid-plane $z=0$ when presenting its time evolution, which enables a better comparison with the radial stress component defined below. Positive values of $\langle\mathcal{R}_{\theta\varphi}\rangle$ correspond to angular momentum transport away from the mid-plane. Unless otherwise stated, the diagnostic domain of our simulation region is $0.8\leq R\leq 1.2$.

In 3D simulations the radial turbulent angular momentum transport is similarly described by

$$\langle\mathcal{R}_{R\varphi}(\theta,t)\rangle=\langle\rho_{g}v_{gR}\Delta v_{g\varphi}\rangle_{R\varphi}.$$

(44)

The turbulent $\alpha$-parameter (Shakura and Sunyaev,, 1973) is then defined through

$$\alpha(\theta,t)=\frac{\langle\mathcal{R}_{R\varphi}\rangle_{R\varphi}}{\langle P\rangle_{R\varphi}}.$$

(45)

Furthermore, the dust scale height $H_{d}$ is computed by fitting a Gaussian along the vertical grid $z$ to the distribution $\rho_{d}(z)$.

The settling of dust toward the mid-plane of a VSI-turbulent PPD in the absence of a pressure bump was studied in some detail

by Lin, (2019) who employed the one-fluid model to describe a dusty gas devised by Lin and Youdin, (2017) (Section 2.2). Figure 2 illustrates the effect of the particle size, i.e. the Stokes number $\tau_{0}$, as well as the background metallicity $Z$ on the dust’s ability to settle in the mid-plane of the disc. Shown is the time evolution of (from top to bottom) dust-to-gas scale height ratio, dust-to-gas mid-plane mass-density ratio, rms mid-plane vertical dust velocity, rms vertically averaged Reynolds stress as defined in section 2.5, averaged here over the radial domain $R_{0}-H_{0}<R<R_{0}+H_{0}$. The results in the left panels of Figure 2, which correspond to a Stokes number $\tau_{0}=10^{-3}$, show a clear systematic trend with increasing metallicity $Z$. That is, turbulence generated by the VSI is increasingly mitigated with increasing amount of dust in the system. As a result, the latter is able to settle to a layer of decreasing thickness, which is also reflected in decreased values of the mid-plane vertical dust velocity $\mathrm{rms}(v_{dz})$ and the vertical Reynolds stress parameter $\mathcal{R}_{\theta\phi}$. It can be seen from these curves that the VSI reaches nonlinear saturation after some 100 orbits, in agreement with previous studies (Nelson et al.,, 2013; Richard et al.,, 2016; Manger and Klahr,, 2018). Furthermore, these results agree well with those of Lin, (2019), although the impact of dust settling appears to be slightly weaker in our simulations. A substantially weaker trend is seen in the right panel, which shows the effect of an increasing particle size ($\tau_{0}$) for a fixed metallicity $Z=0.01$.

In agreement with Lin, (2019) the VSI growth rates are largely unaffected by dust. However, there appears to be a weak increase in the early values of $\mathrm{rms}(v_{dz})$ with increasing $\tau_{0}$ and also with increasing $Z$, the former increase being stronger. Since initially dust settles such that the center of mass velocity $v_{settle}\sim\tau_{0}f_{d}c_{s}$ (at $z\sim H_{g0}$) it can be expected that the collective vertical movement of dust and gas toward the mid-plane serves as a seed for VSI modes, which are hence stronger initially for larger $\tau_{0}$ and to a lesser extent for larger $\epsilon_{0}$ (recall that $f_{d}=\epsilon/(1+\epsilon)$), explaining the observed trends. Furthermore, since $v_{settle}$ roughly increases linearly with $\tau_{0}$, dust can consequently settle to a thinner layer before the VSI turbulence develops. In the thinner layer buoyancy (38) is increased so as to stabilize the VSI which reduces stirring of the dust-layer. Outside of the dust layer away from the mid-plane the VSI still drives turbulence, albeit weaker than in the dust-free case. The effect of particle size observed here is weaker than in the simulations of Lin, (2019). Thus, it appears that the overall impact of dust in the system is stronger in the latter study. One reason might be that the single fluid description implicitly assumes the terminal velocity approximation (Youdin and Goodman,, 2005; Lovascio and Paardekooper,, 2019) for the dust. Furthermore, the different numerical setup used in Lin, (2019) is possibly more dissipative such that the overall level of turbulence is expected to be slightly weaker. Nevertheless, the plots in Figure 2 demonstrate that the back-reaction force from the dust onto the gas is essential for the weakening of the VSI. The level of turbulent velocity perturbations of a few percent to about 10 percent in the nonlinear saturation of the VSI is consistent with the theoretical estimates by Latter and Papaloizou, (2018).

In the following we investigate the impact of a pressure bump on the accumulation of dust in 2D simulations which will be compared to results of 3D simulations in Section 4. Figure 3 summarizes a 2D simulation survey for the evolution of dust near a pressure bump over 1000 orbital periods. Results are presented for varying initial amplitude $A$ and for different Stokes numbers $\tau_{0}$ and ground state metallicities $Z$. Each solid circle represents a single simulation in terms of the radial location of the maximal

mid-plane dust-to gas ratio $\langle\epsilon_{max}\rangle_{t}\equiv\langle\mathrm{max}(\rho_{d}/\rho_{g})_{z=0}\rangle_{t}$ averaged over the last 100 orbits, which in all simulations with $A>0$ is the result of dust accumulation in the vicinity of the initially imposed pressure bump. The color of each circle represents the value of $\langle\epsilon_{max}\rangle_{t}$. This figure reveals several noteworthy features. First of all, in absence of a pressure bump ($A=0$) we find that in order to achieve mid-plane dust-to-gas ratios on the order unity or larger (and hence triggering of the SI and possibly planetesimal formation), a metallicity of at least $Z\approx 0.04$ and a Stokes number $\tau\gtrsim 0.01$ are necessary. On the other hand, for non-vanishing bump amplitude this can be achieved with solar metallicity ($Z\sim 0.01$) for the same Stokes number.

For lower metallicity ($Z=0.01-0.02$) we observe an increasing (radial) inward shift of the radial location of $\langle\epsilon_{max}\rangle_{t}$ with increasing $\tau_{0}$, while for higher metallicity ($Z\gtrsim 0.04$) this trend does not exist and $\langle\epsilon_{max}\rangle_{t}$ is in all cases located at $R\sim R_{0}$. The inward shift at lower metallicities implies that the gas pressure bump has drifted inward while dust accumulated within its vicinity and migrated along with the gas bump, in contrary to the cases with higher metallicity where the pressure bump remains at its origin.

In some cases with lower metallicity and larger bump amplitude ($A\gtrsim 0.3$) the resulting dust ring becomes unstable such that it gets disrupted (either partially or entirely) and a new dust ring forms just inside the original one. Thus, in the case of partial disruption two dust rings remain at the end of the simulation, both of which have resulted from the pressure bump. Such simulations are accordingly represented by two filled circles connected by a dotted line in Figure 3. For large parts of the considered parameter space though, the simulation outcomes show only a subtle dependence on the bump amplitude (as long as it not too small). A similar observation was also reported by Carrera et al., 021a .

The different outcomes of our simulations are illustrated in Figure 4 which displays the time evolution of $\epsilon$ (we plot its fourth root for improved visibility) for three simulations with $Z=0.01$, $Z=0.03$ and $Z=0.05$ (in all cases $A=0.4$), respectively.

The over-plotted profiles illustrate the gas pressure at different times which are indicated by horizontal dashed lines. Since our simulations are locally isothermal, these curves effectively correspond to the evolution of the gas density. The arrows indicate dust drift velocities as computed from (36), which, as expected describe the movement of dusty ‘clumps’ quite well. Interestingly, particle feedback seems to enhance the gas pressure bump for lower background metallicities, rendering the pressure bump unstable such that it eventually disrupts. In principle such an enhanced pressure bump could potentially be subjected to the RWI (Ono et al.,, 2016) which, however, is suppressed due to the imposed axisymmetry in these simulations. Disruption of the dust ring occurs much earlier for the case with intermediate metallicity $Z=0.03$. Whether the dust ring in the case $Z=0.01$ would disrupt in our simulation ultimately depends on the radial size of the domain since sufficient dust needs to be accumulated before the region outside the ring gets depleted of dust. On the other hand, no instability appears to occur for the case with $Z=0.05$. These findings are chiefly confirmed in full 3D simulations which will be presented in Section 4.

It turns out that the drifting, as well as the splitting of dust rings both are the result of a violation of at least one of the Solberg-Høiland criteria for a dusty gas [Eqs. (39), (40)]. In regions of low metallicity the VSI is sufficiently vigorous to strongly puff up the dust-layer such that dust adjacent to a high density ring possesses a substantially larger scale height than the former, such that a relatively strong radial gradient $\mathinner{\!\left\lvert\partial\epsilon/\partial R\right\rvert}\gg 0$ can occur away from the mid-plane and at the same time a small vertical gradient $\partial\epsilon/\partial z\approx 0$. If $\partial\epsilon/\partial R\ll/\gg 0$, accommodated by a vertical shear around the mid-plane $\partial\Omega^{2}/\partial z>/<0$, this results in a violation of (40).

VSI turbulence can also result in situations⁶⁶6in what follows we restrict to values $z>0$, keeping in mind that a similar argument applies to the case $z<0$. where $\partial\epsilon/\partial z>0$ for $z>0$, which, along with $\kappa^{2}>0$ leads to a violation of (40) provided $\partial\epsilon/\partial R\approx 0$. Such situations are realized for instance within the dust ”bubble” directly inside the dust ring in the simulation with $Z=0.03$. Moreover, a positive $\partial\epsilon/\partial z$ above the mid-plane translates to vertical convection since then $N_{z}^{2}<0$ [Equation (38)].

Furthermore, in low metallicity regions the VSI modes, when attaining sufficiently large amplitude, can directly violate the Rayleigh criterion such that (39) is violated since the first term on the right hand side of (39) dominates the second term practically everywhere in our simulated discs. In parts of such a region we also find (40) to be violated where $\partial\epsilon/\partial z<0$ for $z>0$, which is expected near the mid-plane. The dominance of the first term over the second in (39) is due to the system still being rotationally supported, so that the buoyancy term $\@vec{\nabla}P\cdot\@vec{\nabla}f_{d}$ is small in comparison. Radial profiles of $\kappa^{2}$ appear noisy on the grid level and they vary in time. It is not unexpected that $\kappa^{2}$ can drop to negative values. The VSI operates on small radial length scales and the linear modes are also nonlinear solutions, at least in the incompressible limit (Latter and Papaloizou,, 2018). Therefore one can assume that linear VSI modes are able to grow to large amplitudes. Specifically the vertical component of vorticity, which amounts to $\kappa^{2}/2\Omega$ in axisymmetric models. Therefore, this quantity can grow until the Rayleigh criterion is violated. In 3D simulations, however, linear modes will undergo KHI / RWI and the flow develops non-axisymmetry before the Rayleigh criterion is actually violated.

Figure 5 illustrates the unstable behavior of dust rings in the same simulations as those shown in Figure 4. The upper panels display the dust-to-gas ratios for a time near 450 orbits, which is just prior to the dust ring in the simulation with $Z=0.03$ being disrupted at the expense of a new dust ring, which subsequently drifts inward. This is also when the dust ring in the simulation with $Z=0.01$ starts to drift inward. The remaining panels from top to bottom are the two time-averaged (over the range 350-450 orbits) Solberg-Høiland expressions $\langle\textrm{SH}_{1}\rangle$, $\langle\textrm{SH}_{2}\rangle$, corresponding to (39), (40), and the rms averaged Reynolds stress $\mathrm{rms}(\mathcal{R}_{\theta\varphi})$, corresponding to (43). What these plots mainly show is that the Solberg-Høiland criteria are violated in various places, mostly away from the mid-plane. However, both stability criteria are most severely violated in the puffed up dust-layers adjacent to the dust ring of each simulation. In the unstable regions just inside of the dust rings for the cases $Z=0.01$ and $Z=0.03$ we find a substantially increased Reynolds stress $R_{\theta\varphi}$ and hence an increased vertical angular momentum transport (away from the mid-plane). We expect this to be responsible for the inward drift / disruption of the dust rings in these simulations.

Previous works that investigated the evolution of dust in the vicinity of a pressure bump ( Taki et al., (2016); Onishi and Sekiya, (2017); Huang et al., (2020); Carrera et al., 021a ) did not report unstable behavior of dust rings that formed at a pressure bump, as described in the previous sections. Although Taki et al., (2016) found that the pressure bump gets destroyed by the particle feedback within hundreds of orbital periods without sufficient reforcing, this turned out to be caused by the neglect of vertical stellar gravity and hence dust sedimentation in the mid-plane (Onishi and Sekiya,, 2017). Also, for the parameters used by Taki et al., (2016) ($Z=0.1$, $\tau_{0}=1$) or Huang et al., (2020) ($Z=0.05$, $\tau_{0}\sim 0.25$) we do not expect drifting or disruption in our simulations to occur as well, based on Figure 3.

Huang et al., (2020) found an instability of dust rings with dust-to-gas ratios of order unity, but their simulations were 2D (vertically integrated) and thus as well omitted the vertical disc

stratification. Furthermore, the instability found by Huang et al., (2020) does in principle only require a dust ring with sufficiently sharp edges and order unity dust-to-gas ratio such that gas within the dust ring is forced to attain Keplerian velocity, and they speculate that the edges of the ring could be unstable to the RWI due to a sharp drop of the vorticity $\omega_{z}$, which is not captured in our 2D axisymmetric simulations. Also the finding that our simulation with $Z=0.05$ does not show unstable behaviour despite having developed a dense sharp dust ring would then be hard to explain.

We have verified that neither drifting nor disruption of dust rings occurs in 1D radial simulations or 2D vertically unstratified, axisymmetric simulations. Furthermore, we ran simulations with reduced temperature gradient (i.e. smaller values of $|q|$) and found that the unstable behavior diminishes, the dust rings behaving essentially laminar, with decreasing $|q|$. These findings, which are presented in Appendix A, support our picture of a dusty gas instability that is triggered by the VSI turbulent motions and which lead to the phenomena described above. Indeed, the VSI does not occur in an unstratified disc as there is no vertical shear. Also a reduction of $|q|$ weakens the vertical shear and hence the VSI.

We start by comparing the strength of VSI turbulence as it occurs in 3D and 2D simulations without an initial pressure bump. Figure 6 shows the time evolution of the spatially averaged vertical Reynolds stress (43), which represents a running time-average to smooth out strong fluctuations (upper panels), as well as its time-averaged vertical profile (lower panels). Time-averages have in the lower panel been taken over the last 400 orbits. Overall, turbulence takes comparable magnitudes in 2D and 3D simulations. The influence of dust on the strength of turbulence appears to be complicated. At low metallicity and small Stokes number, the presence of dust appears to result in additional stirring of the gas such that the stress $\mathcal{R}_{\theta\varphi}$ is enhanced as compared to the dust free case. This applies to both 2D and 3D simulations, although the effect is stronger in 2D. We conjecture that this increased turbulent activity in the low metallicity and Stokes number cases shares its origin with the dusty gas instability discussed in Section 3.3. This is illustrated in Figure 7, where the plots correspond to $\leavevmode\nobreak\ 900$ orbits. In the plots of the dust-to-gas ratios small-scale vortices are visible along the edges of the strongly corrugated dust-layers in the lower metallicity case. The second row displays, similarly as in Figure 5 the time-averaged (900-1000 orbits) expression $\langle\textrm{SH}_{2}\rangle$, corresponding to (40). The third row represents the time-average of the gas-vorticity component $\omega_{\varphi}\equiv\@vec{e}_{\varphi}\cdot\left(\@vec{\nabla}\times\@vec{v}_{g}\right)$. The last two rows show the radial and vertical gradients of the dust fraction $f_{d}$. This figure underlines that increased vorticity production stems mainly from radial structuring and to a smaller extent from vertical structuring of the dust-layer, which we verified by inspection of the two terms within the brackets on the right hand side of (40). This structuring of the dust-layer is caused by corrugation (an idea first put forward by Lorén-Aguilar and Bate, (2015)). In principle, since there are locations where $\partial\epsilon/\partial z>0$ for $z>0$ and hence $N_{z}^{2}<0$, the condition for vertical convection is locally fulfilled at these locations during some time. It is unclear if the latter has a notable influence on the disc turbulence. The figure also shows how the vertical gradient $\partial f_{d}/\partial z$ has a strongly stabilizing effect in the case $Z=0.05$ that overcompensates potentially destabilizing effects of the radial gradient $\partial f_{d}/\partial R$. Thus, at larger metallicity dust sufficiently weakens the VSI such that dust can settle to a thinner and denser layer which is less prone to corrugation motions. This leads to a strongly reduced production of vorticity $\omega_{\varphi}$ around the mid-plane. Subsequently, the Reynolds stresses fall below the dust-free values. In principle an increased vorticity could also be due to KHI as adjacent dusty gas layers shear past each other in the vertical direction due to corrugation. However, if KHI were the reason for the observed increased vorticity and Reynolds stress we would expect this effect to be strongest in the dust-free case since the KHI does not rely on the presence of dust and the VSI is causing the corrugation which would be the origin of the KHI. The observed strong increase in $R_{\theta\varphi}$ when adding small amounts of dust would not be expected in this scenario. Also the finding that the Solberg-Høiland criteria are actually violated in the corrugated dusty layer points to the dusty gas instability for being the origin of the increased hydrodynamic activity. Moreover, our resolution is likely not sufficiently high to resolve such parasitic KHI modes (C. Cui, private communication).

Interestingly, Lorén-Aguilar and Bate, (2015), who conducted smoothed particle hydrodynamics simulations of a PPD with very similar setup (3D, locally isothermal) found a similar corrugation of the mid-plane dust-layer. However, they concluded this to be the result of a baroclinic instability which arises in response to a violation of (40) which they defined for a pure gas with an entropy $S\sim\log\left(P/\rho_{g}^{\gamma}\right)$ in contrast to our definition (16), which is also that of Lin and Youdin, (2017) and where $\rho_{g}$ is replaced by the total density $\rho$. This subtle difference in the definition of $S$ leads to a change of sign in the criterion for the onset of vertical convection, i.e. $\partial\epsilon/\partial z>0$ for $z>0$ in contrast to Equation (7) of Lorén-Aguilar and Bate, (2015). From the results presented in Figure 7 we conclude that the criterion adopted here is adequate since the settled dust-layer itself is stable, whereas regions above and below it are marginally unstable. Corrugation of the dust-layer in our simulations is a direct result of velocity perturbations of VSI modes and it is the corrugation that facilitates the conditions for a violation the second Solberg-Høiland criterion or a locally unstable vertical entropy stratification. Furthermore, it remains questionable that the VSI did not develop in the simulations of Lorén-Aguilar and Bate, (2015) despite the required physical conditions being fulfilled.

To further illustrate the impact of dust on the turbulent properties of the disc we compare in Figure 8 the vertical dependence of the time and radially/azimuthaly averaged radial mass flow and radial velocity of gas and dust in 2D and 3D simulations, respectively. At low metallicity (lower panels in all cases) we recover the results of Stoll and Kley, (2016) and Manger and Klahr, (2018). That is, gas flows inward near the disc’s mid-plane, whereas at larger heights it flows outward. A similar flow pattern is also found in our 2D simulations, albeit of slightly different magnitude, which, in some cases exceed the 3D values. The observation that inflow velocities near the mid-plane for low metallicities in 2D and 3D simulations take comparable values most likely stems from the anisotropic (Reynolds) stress generated by the VSI and that the most prominent perturbations excited by the VSI are vertically global modes of relatively short radial wavelength $\lesssim H_{g}$. This anisotropy was studied by Stoll et al., (2017) who attempted to model the turbulent accretion flow induced by the VSI in 3D simulations by a laminar viscous accretion flow in 2D axisymmetric simulations and found that the vertical viscosity coefficient (characterizing $\mathcal{R}_{\theta\varphi}$) in their models needed to be 650 times larger than the radial component (characterizing $\mathcal{R}_{r\varphi}$) in order to make the vertical structure of the accretion flow pattern in the two simulations agree. In passing, we note that we obtained a total gas accretion rate of $\sim-1.2\cdot 10^{-5}\,\Sigma_{g0}\Omega_{K}$ for the dust-free 3D simulation by vertically integrating the mass flow

profile shown in the bottom left panel of Figure 8. This value seems consistent with the value $\sim-2.4\cdot 10^{-5}\,\Sigma_{g0}\Omega_{K}$ reported by Manger and Klahr, (2018) who adopted a larger disc aspect ratio of $h=0.1$. However, a quantitative study of accretion rates requires carefully defined boundary conditions and will not be considered here.

Many aspects of the profiles plotted in Figure 8 can be understood by considering basic aspects of dust-gas drag (Section 2.3). Considering the 3D results for the time being, for small Stokes numbers $\tau_{0}=10^{-3}$ dust and gas averaged velocities are essentially equivalent, regardless of $Z$, which is also in agreement with results in Figure 17 of Stoll et al., (2017). For larger $\tau_{0}$, dust velocities become increasingly negative and gas velocities increasingly positive, which is also expected. Moreover, In the dense dusty mid-plane layer that forms in simulations with higher values of $\tau_{0}$ and $Z$, radial drift velocities become small as $\rho_{d}>\rho_{g}$. However, with increasing metallicity and Stokes numbers the gas and dust radial velocity profiles change substantially. For instance, for $Z=0.1$ and $\tau_{0}=10^{-3}$ (actually this is already observed for $Z=0.05$ which is not shown here) or for $Z=0.03$ and $\tau_{0}=5\cdot 10^{-3}$ the profiles have changed such that material is flowing inward away from the mid-plane while it flows outward in narrow regions close to the mid-plane. Interestingly this flow profile resembles to some extent the standard laminar isotropic $\alpha$-viscosity case (e.g. Takeuchi and Lin, (2002)). The reason for this change is due to different VSI modes being dominant in the different cases. This is illustrated for the examples $Z=0.01,0.1$ with $\tau_{0}=10^{-3}$ in Figure 9 and can also be seen in the vertical profiles of the Reynolds stress for these parameters in Figure 6. At low metallicity and for increasing Stokes number, we find that the radial mass fluxes qualitatively agree with those of Stoll and Kley, (2016) (their Figure 18). Departures occur for

the radial dust velocities at larger Stokes numbers where they found that the radial dust velocity away from the mid-plane is always directed outward and larger in magnitude than the radial gas velocities. In contrast, we find that the dust velocities become negative for larger Stokes numbers, as mentioned above. These discrepancies with Stoll and Kley, (2016) are most likely due to the neglect of particle feedback in their simulations. Moreover, they added particles at a time at which the VSI had reached a quasi steady state whereas we simulate both dust and gas coevally. However, the overall qualitative agreement between 2D and 3D simulations lends additional credibility to our results. Comparing averaged velocities with averaged mass fluxes for the gas is generally straight forward. The gas is nearly incompressible such that its averaged mass flow is essentially the averaged gas velocity multiplied with the initial Gaussian density profile. This does not, however, apply to the dust whose mid-plane density can exhibit complex time variations owing to corrugation, and a detailed analysis of the dust mass flow profiles is beyond the scope of this paper.

Figure 10 compares the dust settling process in 2D and 3D simulations with metallicities $Z=0.01-0.1$ and Stokes numbers $\tau=10^{-3}-10^{-2}$. Shown are the dust-to-gas scale height ratio and the mid-plane dust-to-gas density ratio. Overall the results compare quite well. For both the 2D and 3D simulations averages are taken within a radial domain of $0.8\leq R\leq 1.2$. For the 3D simulations an additional averaging over azimuth has been performed. Apart from the smallest metallicity and Stokes number cases, dust settling is somewhat stronger in 2D simulations, which is expected from the results in Figure 6. All simulations shown were run with the same radial and vertical resolution and domain sizes. For the 3D simulation with $Z=0.01$ and $\tau=10^{-2}$ the disc region under consideration already becomes significantly depleted of dust by the end of the simulation. This is in part due to vortices that form and collect inward drifting dust and eventually leave the considered disc region. This will be discussed in more detail in Section 5.

Furthermore, Figure 11 illustrates the effect of dust on the VSI’s ability to transport angular momentum in radial direction

in 3D simulations. Shown is the time evolution, which again are a running time-average, as well as time-averaged vertical profiles of the $\alpha$-viscosity parameter (45). The averages are taken in the same fashion as in Figure 6. In contrast to the behavior of $\mathcal{R}_{\theta\varphi}$ (Figure 6) which describes vertical angular momentum transport, $\alpha$ decreases steadily with increasing metallicity, even at low metallicity. The reason is that the main driver of an increased $\mathcal{R}_{\theta\varphi}$ is corrugation of the dust-layer which can only occur in vertical direction. The values $\alpha\lesssim 10^{-3}$ extracted from our dust-free reference simulation are in good agreement with those of Nelson et al., (2013), but almost a factor 10 larger than those reported by Manger et al., (2020) for the same disc aspect ratio $h=0.05$. Several other studies report smaller values (Stoll and Kley,, 2016; Pfeil and Klahr,, 2021; Flock et al.,, 2020), mainly due to adopting a more realistic equation of state, improved by at least a finite cooling time (compared to the isothermal approximation) which is known to mitigate the VSI (Lin and Youdin,, 2015). The most likely reason for the difference to the values of Manger et al., (2020) is the higher radial and vertical grid resolution adopted in our simulations. Furthermore, Manger et al., (2020) found that the resolution in azimuthal direction has a subdominant effect on the VSI activity, in contrary to the strong dependence on the azimuthal domain size (Manger and Klahr,, 2018).

One class of prominent substructures in PPDs that ALMA has revealed in recent years are rings and gaps, visible in the dust’s mm continuum or spectral line emission (e.g. van der Marel et al., (2013); ALMA Partnership et al., (2015); Andrews, (2020); van der Marel et al., (2021)). A fraction of the well-observed dust rings exhibit more or less strong (typically crescent shaped) non-axisymmetries whose origin is still topic of debate. One generally assumes that there are two main mechanisms which can generate these structures. These are so called ‘horseshoes’, which constitute non-axisymmetric gas enhancements in discs just outside the inner cavity which has been cleared by a stellar binary (Ragusa et al.,, 2017), or vortices generated at a pressure bump adjacent to a gap which is assumed to be created by a planet of sufficiently high mass (e.g. Zhu and Stone, (2014)). The latter mechanism is the one relevant to this work and here we wish to investigate if and under which conditions dust rings that form at a pressure bump in an VSI turbulent disc can attain dust to gas ratios that could result in planetesimal formation and if dust rings can be subjected to any persistent non-axisymmetries.

Figures 12-15 show dust rings that formed in 3D simulations in response to an initially seeded pressure bump, for different background metallicities $Z$, Stokes numbers ($\tau_{0}=0.001$, $\tau_{0}=0.005$ and $\tau_{0}=0.01$) and bump amplitudes ($A=0.2$ and $A=0.4$), respectively. The dotted and dashed curves illustrate the azimuthally averaged final and initial gas pressure profile, respectively.

We verified by means of test simulations that the pressure bumps in these simulations are not subjected to the RWI⁷⁷7In these test simulations we adopted a very small temperature gradient $q\to 0$ such that the VSI was extinguished.. It should be kept in mind that our resolution is not sufficient to resolve small-scale instabilities such as the SI, which may disrupt the dust rings, although the SI might be less efficient in a turbulent disc. That being said, what Figures 12-15 reveal is that an increase of the parameters $Z$ and $\tau_{0}$ (and to some extent also $A$) results in a transition from a preference to form dusty vortices toward a preference to form dusty rings. Generally speaking, we find an increasing axisymmetry of formed dust enhancements when increasing these parameters. We hypothesize that the reason for this transition is the same as that for the increased stability of dust rings found in our 2D simulations when increasing the same parameters, since essentially this weakens the VSI. When comparing the results presented in this section with those of our 2D simulations which are summarized in Figure 3, we find many similarities. For instance, the cases with the smallest Stokes number $\tau_{0}=10^{-3}$ and lower metallicity $Z\lesssim 0.03$ are lacking any notable dust enhancements at the pressure bump site, although we observe the formation of weak dusty vortices in 3D. Furthermore, in Section 3.2 we discussed the occurrence of a dusty gas instability and how it results in disruption and/or inward drift of dust rings. The parameter regime within which this happens can be directly determined from Figure 3. Indeed, Figures 12-15 show that also in 3D simulations dust rings undergo inward drift and the magnitude of this drift is larger for

larger/smaller Stokes number/metallicity. For illustration, Figure 16 compares the radial locations of dust rings as observed in 2D and 3D simulations for two metallicities ($Z=0.01,0.03$) and bump amplitudes ($A=0.2,0.4$) and Stokes number $\tau_{0}=10^{-2}$. For the case $Z=0.01$ dust rings in 2D simulations (dashed curves) drift slightly faster than in 3D simulations (solid curves), whereas the opposite is the case for $Z=0.03$. The behavior for $Z=0.01$ can be explained considering that the dusty gas instability which causes the inward drift is somewhat stronger in 2D than in 3D (cf. Figure 6). On the other hand, the negligible inward drift in the 2D simulations with $Z=0.03$ is a consequence of the much larger value of $\epsilon$ attained in the corresponding dust rings (cf. Figure 3). For the same reason (i.e. increased $\epsilon$) drift speeds for the cases with $A=0.4$ are generally smaller than for the corresponding cases with $A=0.2$. That being said, drift speeds of dust rings according to Figure 16 can get as fast as $\sim 0.2H_{g0}$/(100 orbits) in 3D simulations and $\sim 0.3H_{g0}$/(100 orbits) in 2D simulations.

Moreover, the dust rings formed in simulations with $Z\leq 0.03$ are subject to strong turbulent distortions, whereas those

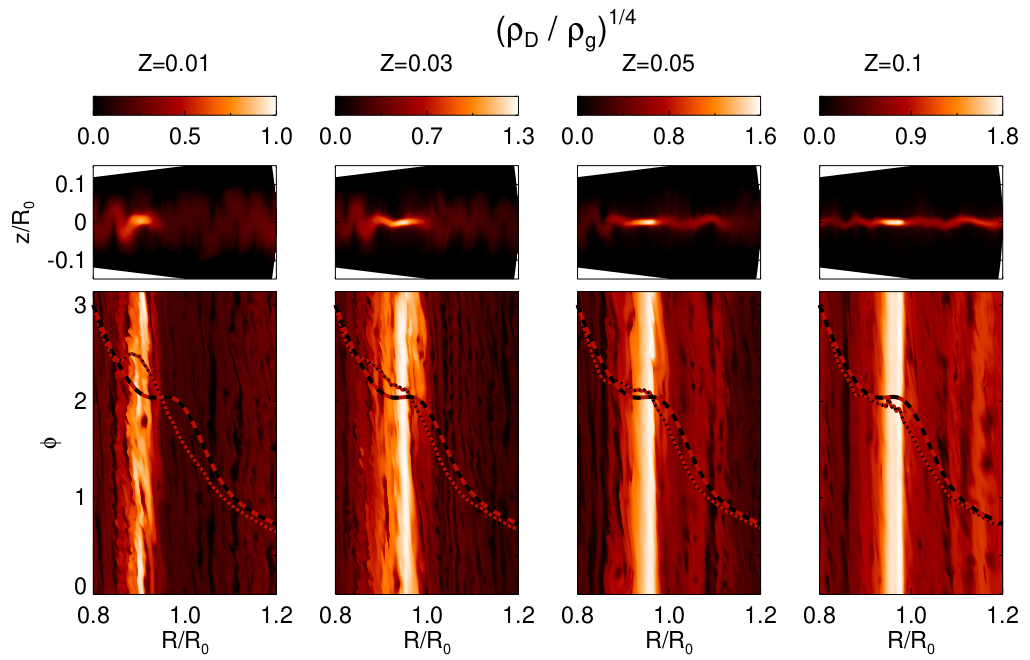
corresponding to larger $Z$ are nearly axisymmetric. In the former cases the gas pressure bump is dragged along with the dust ring and in some cases even amplified, similar as in corresponding 2D simulations (Figure 4). Also one can clearly see strong corrugation of the dust-layer adjacent to the ring for these cases in the upper panels which show meridional contour plots. This corrugation facilitates the dusty gas instability discussed in Section 3.3.

One difference is that in 3D simulations instability leads to vortex formation, which is suppressed in 2D axisymmetric simulations. An example for the evolution of an unstable dust ring in a 3D simulation is presented in Figure 17. In this case the dust ring continuously produces new vortices that split off and drift inward. The driving force of this unstable behaviour is, similarly to the 2D simulations, the VSI. The attained dust-to-gas density ratios in 3D dust rings are not nearly as high as in 2D, which is due to planar turbulent diffusion generated by the VSI and quantified through $\alpha$ (as discussed in Section 4.1) in 3D simulations.

Figure 18 shows the mid-plane vorticity (42) after around 600 reference orbits in 3D dust-free simulations with an initially seeded pressure bump of varying amplitude $A$. The lower left panel corresponds to the run presented in the lower left frame of Figure 8 in Manger et al., (2020) and we find good agreement between the sizes $\Delta R\sim H_{g0}$ and aspect ratios $R\Delta\varphi/\Delta R\sim 8-10$ of the largest vortices appearing in these simulations. Moreover, the size of these vortices appears to increase with increasing bump amplitude $A$. They appear after $\sim 200-400$ orbits, where earlier times correspond to larger values of $A$. Numerous small-scale vortices are present as well. These are short-lived and cannot be tracked in our simulations since our time resolution is $\sim 50$ orbits. In previous works (Richard et al.,, 2016; Manger and Klahr,, 2018) similarly small vortices were found and their survival times were estimated to be several orbits. Although it is not entirely clear if the correspondence between vortex size and bump amplitude is physical or a coincidental outcome of our simulations, a possible explanation is that large vortices grow by absorption of small-scale vortices and that this can happen more efficiently in the vicinity of a pressure bump. Paardekooper et al., (2010) have shown that in razor-thin disc models, vortices undergo migration by emitting sound waves inwards and outwards in an asymmetrical fashion, similar (but not identical) to planets embedded in a disc. The direction of migration is related to the background surface density gradient, such that vortices migrate toward regions of larger surface density. This should also imply migration towards the mild pressure maximum corresponding to a large vortex. However, since the small-scale vortices have a small vertical extent of considerably less than one scaleheight (Richard et al., (2016)) the vertically-averaged results of Paardekooper et al., (2010) potentially do not apply to these vortices. It is therefore not clear whether or not they can migrate over any significant distance and be absorbed by a large vortex before they dissipate. On the other hand, migration and also merging of larger vortices is directly observed in our simulations, similar to what was reported by Manger et al., (2020).

Figure 19 shows the time evolution of the radial gas density profile (azimuthally averaged) at the mid-plane for the same simulations as in Figure 18. The dashed vertical lines indicate the radial location of the large vortex for the three latest times. In all simulations the vortex survives for hundreds of orbits and migrates inwards. This is in agreement with the results reported by Manger and Klahr, (2018), Manger et al., (2020) and also Pfeil and Klahr, (2021). In addition, the density bump smears out through turbulent diffusion and redistribution of mass within the disc in response to the (turbulent) angular momentum transport generated by the VSI, an aspect recently considered by Manger et al., (2021). Indeed, we find a pileup of mass around $R\sim 0.6R_{0}$ (outside the diagnostic domain) in a similar manner as shown in Figure 9 (bottom left panel) of Manger et al., (2021).

Apart from the size of the vortices, the results in Figure 19 do not provide evidence that the pressure bump has an effect on migration of large vortices, or that it is a preferred location for the formation of the latter, since also the vortex in the simulation with $A=0$ forms at a very similar radius as in all other simulations with $A>0$. Nevertheless, we hypothesize that large vortices result from merging of smaller vortices and that this is more likely to occur if vortex radial migration is mitigated. The latter is expected to depend on the surface density gradient ((Paardekooper et al.,, 2010)) and we therefore expect a more efficient growth of vortices at a pressure bump. To further test this hypothesis we ran additional simulations with different surface density slopes $s$ (and hence different mid-plane gas density slopes $p$). The results of these simulations, which are presented in Appendix B, show that a flatter mid-plane density profile leads to slower migration speeds and larger vortices, supporting our hypothesis.

Our dusty 3D simulations reveal that large ($\Delta R\sim H_{g0}$) vortices collect dust and survive for typically hundreds of orbital periods, which is similar to the survival time of pure gas vortices discussed above. Within a simulation time of 1000 reference orbits, we find large, long-lived vortices only for metallicities $Z\lesssim 0.03$ and if $Z=0.03$ only for small Stokes numbers $\tau_{0}\sim 10^{-3}$. We generally do not observe larger, long-lived vortices in simulations with $Z\geq 0.05$. The exception is in a simulation with $Z=0.05$ and $\tau_{0}=10^{-3}$, where at late simulation times past 1000 orbits we find the formation of a large vortex, but its dust content is negligible compared to ambient turbulent dust lanes that are present in the simulation region as well. We attribute the absence of long-lived vortices at high metallicities and Stokes numbers to the corresponding weakening of the VSI by dust feedback and its ability to form vortices. Therefore we also expect weaker vortensity perturbations in simulations with larger $Z$, which is illustrated in Figure 20, where the vortensity $\mathcal{L}$ is given by (42).

None of the vortices that formed in our simulations without an initial pressure bump attained dust-to-gas ratios of unity or larger. The largest value we find is $\epsilon\sim 0.7$ in a vortex by the end of the simulation with $Z=0.01$ and $\tau_{0}=10^{-2}$. This is in strong contrast to the values of $\epsilon$ attained in vortices that formed in the 3D shearing box simulations of the COS by Raettig et al., (2021), where even for an initial value $Z\sim 10^{-4}$ vortices formed rapidly and after tens of orbits values of $\epsilon\sim 10$ were reached within the vortices. The main reason for these differences is certainly the much weaker vertical turbulent velocities generated by the COS ($\sim 10-100$ times smaller than for the VSI) and perhaps to some extent the larger Stokes numbers $\tau_{0}\geq 5\cdot 10^{-2}$ considered in that work. That being said, we cannot rule out that larger dust-to-gas ratios could be obtained with Stokes numbers $>10^{-2}$, a larger radial domain, or both; the latter of which would supply more dust for trapping. (An inflow outer boundary condition would have the same effect.) Because of dust drift, we already find significant dust depletion in the diagnostic domain $0.8\leq R\leq 1.2$ by the end of the aforementioned simulation with $\tau_{0}=10^{-2}$, such that the collection of dust in the vortex is already hampered. This effect will be even more severe in simulations with larger Stokes numbers such that these would either require a substantially larger radial domain size or inflow of dust at the outer boundary.

In the presence of dust the evolution of a pressure bump can differ significantly from the dust-free evolution discussed in Section 5.1, which is illustrated in Figure 21. In Section 4.2, we had seen that pressure bumps give rise to the formation of dust rings, vortices, or a combination of both. While pressure bumps are expected to either trap dust or cause ‘traffic jams’ to produce dust rings (see §2.3), the frequent formation of vortices at the pressure bump is less obvious based on above dust-free results in Section 5.1. (Recall that our initial pressure bumps are stable against the vortex-forming RWI.) However, in Section 3.3 we found that dust rings at low and intermediate metallicities are locations of increased hydrodynamic activity due to violations of one of the Solberg-Høiland criteria [Eqs. (39)-(40)], which are associated with corrugations of the dust-layer by the VSI. In 3D, we can therefore expect such dust rings to be preferred locations for the formation of vortices, for a given range of dust-parameters. Similar to 2D simulations shown in Figure 4, such unstable dust rings also go along with an increased gas density such that the pressure bump is effectively being amplified, which is clearly seen in the lower right and upper left panel of Figure 21. Within this scenario, it is also consistent that no vortices form at dust rings in simulations with sufficiently large $Z\gtrsim 0.05$, due to effective weakening of the VSI by dusty buoyancy. This can clearly be seen by comparing Figure 5 with Figure 14.

Examples of dusty vortices that form at a pressure bump are found in Figures 14, 17, and 23. The latter figure also demonstrates that dust is more settled in the vortex core, which is clearly seen in the contour plot of scale height ratio $H_{d}/H_{g}$. Unlike bump-free simulations, for moderate initial pressure bumps ($A=0.2-0.4$) we do find vortices that collect sufficient amounts of dust such that the SI should be triggered within these, would it be resolved. Figure 22 illustrates the evolution of large, long-lived vortices that form at a pressure bump with an amplitude $A=0.4$⁸⁸8A similar result is obtained with $A=0.2$. in simulations with metallicity $Z=0.01$ and Stokes numbers $\tau_{0}=10^{-3}$ and $\tau_{0}=10^{-2}$, respectively. These vortices survive a considerable time span of about 500 orbits. For $\tau_{0}=10^{-3}$ the vortex core does not attain unity dust-to-gas ratios within the simulation timescale and steadily migrates inward with a rate $\sim 0.4H_{g0}$/(100 orbits), comparable to that of dust-free vortices (cf. Appendix B), until it eventually dissolves in the background flow.

On the other hand, the vortex formed in the simulation with $\tau_{0}=10^{-2}$ reaches unity dust-to-gas ratio at about 200 orbits following its formation and a maximum value of almost 4 after 400 orbits. Therefore it can be expected that the SI would be triggered with higher grid resolutions. Due to the larger dust-to-gas ratio the inward drift of the vortex is substantially slower in this case. Furthermore, the shape of the dust distribution within the vortex is more elongated in the case of larger Stokes number (or equivalently, larger particle size). By the end of the simulation the vortex dissolves into a turbulent, non-axisymmetric circumferential dust ring. A similar trend in the distribution of dust particles of different sizes in vortices was reported by Crnkovic-Rubsamen et al., (2015) and Surville and Mayer, (2019) for vortices in 2D shearing sheet simulations.

The small-scale, compact vortices found in our simulations and those of Richard et al., (2016) and Manger et al., (2020) are assumed to be the result of parasitic KHI that inflict the VSI modes, thereby controlling their nonlinear saturation amplitudes (Latter and Papaloizou,, 2018). The rapid dissipation of these vortices is likely caused by the elliptic instability (Lesur and Papaloizou,, 2009; Railton and Papaloizou,, 2014), which is more vigorous for small vortex aspect-ratios. Larger vortices with aspect ratios of around 5 or larger do not fit in the scenario just described. First of all, their properties are different from the vortices that were described in Latter and Papaloizou, (2018). For instance, the large scale vortices found here are vertically extended structures where the vorticity perturbation extends over more than one gas scale height, which is illustrated in Figure 23. Moreover, these elongated vortices are likely less affected by the elliptic instability in our simulations since for such vortices this instability grows slowly and requires high radial resolution.

Richard et al., (2016) found that long-lived vortices with larger aspect ratios can form in their simulations if the disc possesses relatively long cooling times $\gtrsim 0.5\Omega^{-1}$ and steep temperature profiles with $q=2$. They argued that for such disc-parameters the SBI (Petersen et al., 2007a, ; Petersen et al., 2007b, ; Lesur and Papaloizou,, 2010) can amplify the vortices, whereas the SBI is inactive for shorter cooling times (such as our locally isothermal discs), shallower temperature profiles, or both. However, since the VSI most likely appears in disc regions that are not expected to fulfill the criteria for the SBI (although the simulations of Pfeil and Klahr, (2021) suggest that the VSI can exist in the inner, optically thick part of a PPD, where also the SBI is expected to be active) Richard et al., (2016) concluded that the vortices resulting from the VSI are unlikely to promote planetesimal formation on global scales. It was later shown by Manger and Klahr, (2018) that the VSI can generate large, long-lived vortices in an isothermal disc and that the reason for the absence of such vortices in the simulations of Richard et al., (2016) was a too small azimuthal simulation domain.

Furthermore, it is unlikely that the mechanism which eventually destroys the large-scale vortices in our simulations is the same as that in previous 2D simulations of dusty vortices (Fu et al.,, 2014; Crnkovic-Rubsamen et al.,, 2015; Raettig et al.,, 2015; Surville and Mayer,, 2019) , which might be the heavy core instability (Chang and Oishi,, 2010). The results presented in Figure 22 rather suggest that the lifetime of the large scale vortices in our simulations is independent of the amount of dust concentrated within them. It can be expected that whatever instability attacked vortices in the aforementioned high resolution shearing sheet simulations is not resolved here. Since the vortices do disappear on time scales that are in agreement with the lifetimes of dust-free vortices as discussed in Section 5.1, this suggests that the mechanism of destruction is also the same. Most likely this is a combination of turbulent diffusion and Keplerian shear that disrupts large vortices in our simulations. The influence of the elliptical instability (Lesur and Papaloizou,, 2009), the parasitic KHI (Latter and Papaloizou,, 2018), or the VSI itself in the vortex core must be clarified in future high resolution 3D simulations.