Imaging coupled vibrational, rotational, and electronic wave packet dynamics in a triatomic molecule

Recording molecular movies of an isolated molecule undergoing ultrafast structure changes with sufficient spatiotemporal resolution has been a longstanding goal in molecular optical sciences [1, 2, 3, 4]. Remarkable progress towards this goal has been demonstrated recently, including the development of gas-phase ultrafast electron diffraction (UED) [5, 6] and ultrafast X-ray scattering (UXS) techniques [7, 8, 9]. These techniques have provided novel insight into many photochemical reactions. However, the former still has limited time resolution, and the latter requires powerful X-ray sources due to low scattering cross sections. Both methods are insensitive to light atoms and often need access to large-scale facilities. They also project structural information (pairwise distances) onto a single coordinate (the momentum transfer), which makes unambiguous imaging of complex molecular dynamics difficult. Directly observing atomic motion during photochemical processes remains challenging [2, 4].

Another method used for making such movies is time-resolved Coulomb explosion imaging [10, 11, 12, 13, 14, 15, 16]. While CEI does not yield interatomic distances directly, it provides excellent temporal resolution, high sensitivity to light atoms, and accessibility in university-scale laboratories. Most importantly, coincidence imaging techniques [17, 18, 19, 20, 21, 22, 23] generate multidimensional CEI data that possesses an advantage in separating different reaction pathways, even for rare stochastic processes such as roaming [24].

Previously, all three methods have been employed to directly image light-induced vibrational wave packets (see, for instance, [19, 25, 26, 27, 8]), which play a critical role in many types of molecular dynamics [28, 29, 30, 31, 32, 33, 34, 35, 36]. However, most experimental movies of molecular vibrations have been limited to diatomic molecules (such as $\mathrm{H_{2}^{+}}$ [37, 19], $\mathrm{D_{2}^{+}}$ [38, 39], $\mathrm{N_{2}^{+}}$ [40], $\mathrm{O_{2}^{+}}$ [41, 40], $\mathrm{CO^{+}}$ [42, 40], and $\mathrm{I_{2}}$ [25, 26, 27]) or the stretching of only one bond in polyatomic molecules [43, 44, 45]. Due to the fast timescale and complexity of rovibronic motions in polyatomic molecules, only a limited number of direct structural measurements of other vibrations has been reported [46, 47, 8].

In this Letter, we demonstrate that laser-induced Coulomb explosion can directly image ultrafast coherent wave packets in a small polyatomic molecule and produce movies that show the motion of individual atoms even in the presence of coupled nuclear and electronic motion. We investigate sulfur dioxide (SO₂), a bent triatomic molecule that has been studied extensively (see, for instance, [48, 49, 18, 12, 50, 51, 52, 53, 54, 55, 56]) due to its significance in atmospheric processes and its intriguing photochemistry, including the efficient formation of neutral and ionic molecular oxygen [57, 58, 59, 60]. We first demonstrate the use of pump-probe CEI and coincident measurement of ion momenta to image the coherent vibrational wave packet in SO${}_{2}^{+}$ generated by ionization. These observations are supported by quantum mechanical wave packet calculations and classical Coulomb explosion simulations. We then show that, although recoil-frame ion momenta best represent this vibrational wave packet, laboratory-frame momenta reveal the importance of rotational motion in determining the overall dynamics. Finally, we show that a secondary wave packet resulting from a resonant dipole coupling between two ionic states traverses a conical intersection and leaves signatures of the nonadiabatic coupling in the ion momentum distributions.

Our experiment utilized a Ti:Sapphire laser operating at 10 kHz, generating near-infrared (NIR) pulses with a central wavelength of approximately 790 nm and a pulse duration of about 28 fs. We split this output into pump and probe pulses, with independently controlled power, and scan their relative delay using a motorized linear stage. As depicted in Fig. 1, we use a 3.4$\times 10^{14}$ W/cm² pump pulse to ionize SO₂ and a 8$\times 10^{14}$ W/cm² probe pulse to further ionize and dissociate (i.e., Coulomb explode) it. The ions are then detected in coincidence using a COLTRIMS apparatus [61]. The momenta of these ions, determined from their measured time of flight and impact position, are used to deduce information about the induced wave packets.

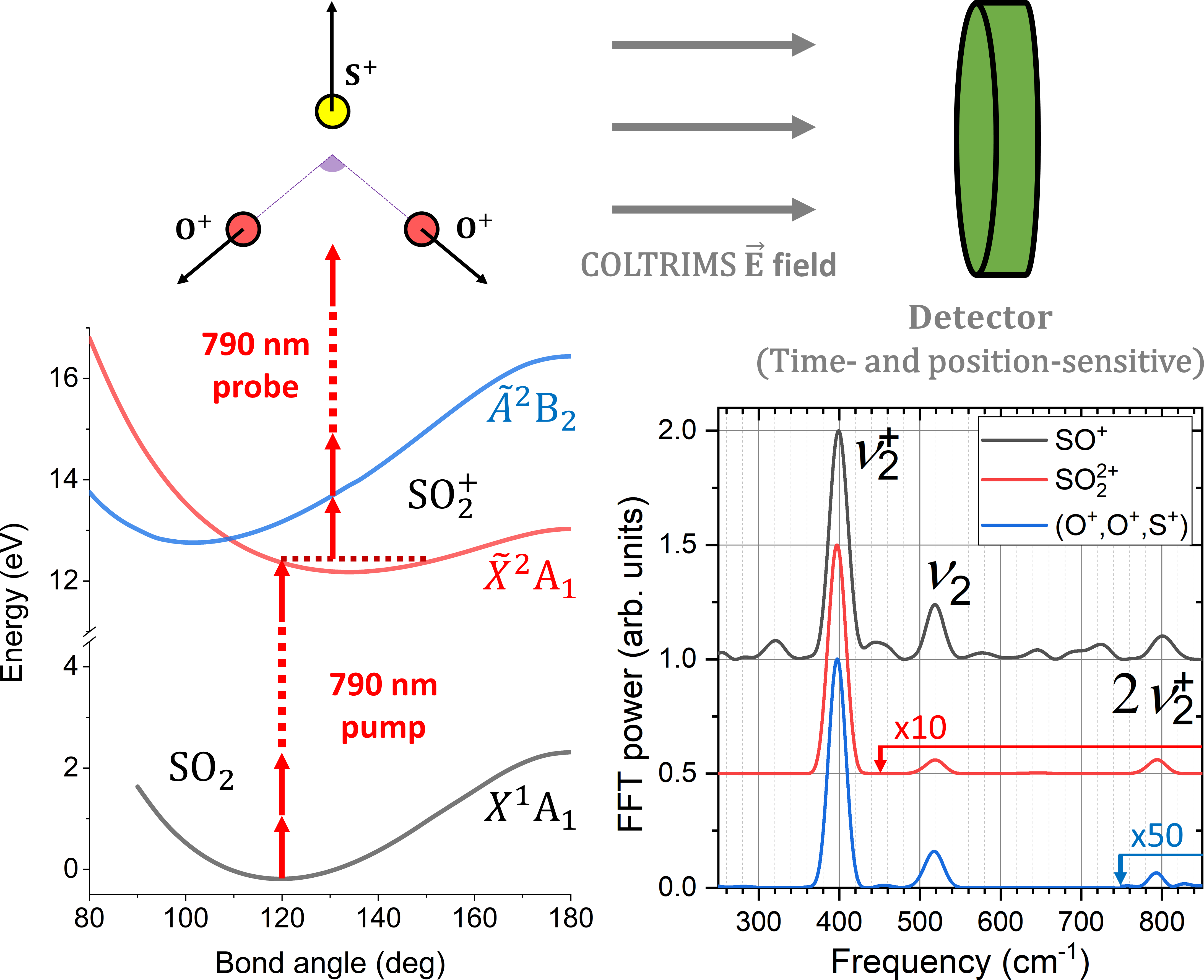
Previous studies [62, 63, 64, 65] have reported that the bending mode progression dominates the SO${}_{2}^{+}$ ($\tilde{X}^{2}A_{1}$) $\leftarrow$ SO₂ ($X^{1}A_{1}$) photoelectron spectra because the equilibrium geometries in the electronic ground state of the neutral SO₂ ($X^{1}A_{1}$) and ionic SO${}_{2}^{+}$ ($\tilde{X}^{2}A_{1}$) have almost identical bond lengths but different bond angles [62, 66]. This leads to a strong excitation into the bending mode ($\nu_{2}^{+}$) and very weak excitation into the symmetric ($\nu_{1}^{+})$ and asymmetric ($\nu_{3}^{+}$) stretch modes. The first seven bending-mode energies are approximately equally spaced with a nearest-neighbor separation of $\approx 400$ cm^-1. In our experiment, which has a 17 cm^-1 frequency resolution, oscillations at this frequency (and its first overtone at $\approx 800$ cm^-1) are observed in different observables for various ionization and fragmentation channels. This indicates that these channels involve the population of SO${}_{2}^{+}$ ground state by the pump pulse and subsequent ionization and/or fragmentation by the probe. For example, as shown in Fig. 1, the fast Fourier transform (FFT) spectra of the delay-dependent yields of SO⁺ and SO${}_{2}^{2+}$ ions and the three-body triply-charged final-state channel $\mathrm{(O^{+},O^{+},S^{+})}$ show a strong peak at the bending frequency and a much smaller one at the overtone. They also show a weak but clear signature of the bending vibration in the ground state of neutral SO₂ (at 520 cm^-1) [67]. In this Letter, we focus on the three-body channel to directly visualize the bending vibrations of the cation via delay-dependent kinetic energy (KE) spectra and angle correlations between the fragment ions.

In Fig. 2, we present experimental data from the $\mathrm{(O^{+},O^{+},S^{+})}$ channel illustrating the delay dependence of several key observables: (a) the angle between the momentum vectors of two O⁺ ions [ $\mathrm{\angle(O^{+},O^{+})}$], (b) the kinetic energy of S⁺ fragment [KE($\mathrm{S^{+}}$)], and (c) the total kinetic energy of two O⁺ fragments [KEsum($\mathrm{O^{+},O^{+}}$)]. Simulation results for these observables are depicted in panels (d-f) and their delay-dependent mean values are shown in panel (g). Panel (h) features distributions of the ions at 250 fs (scatter plot) and 210 fs (contour line) when the bending wave packet is at the inner and outer turning points, respectively.

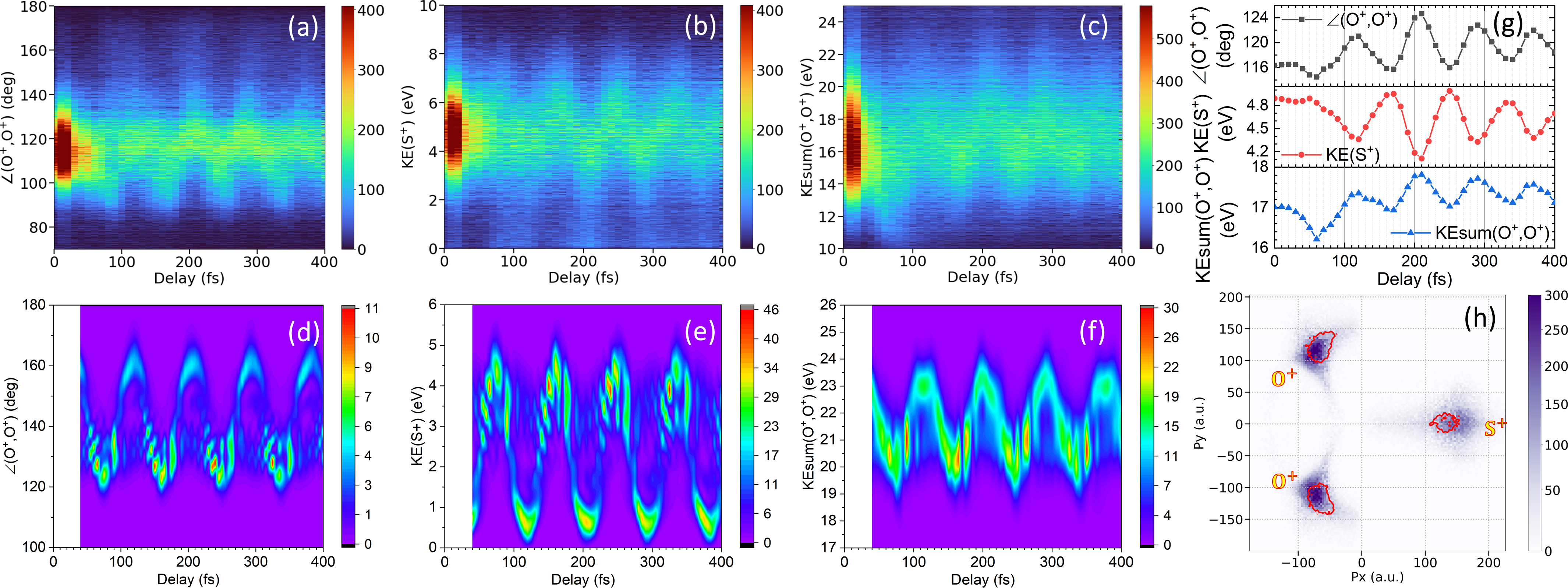
There are two distinguished features in the experimental data shown in Fig. 2(a-c). First, all the observables, namely $\mathrm{\angle(O^{+},O^{+})}$, KE($\mathrm{S^{+}}$), and KEsum($\mathrm{O^{+},O^{+}}$), show pronounced oscillations. The periodicity of these observed oscillations is about 83 fs (or 400 cm^-1), clearly indicating that we mainly image the vibrational wave packet in the ground state of SO${}_{2}^{+}$ [63]. Second, there is a clear correlation between these observables: $\mathrm{\angle(O^{+},O^{+})}$ and KEsum($\mathrm{O^{+},O^{+}}$) oscillate in-phase with each other and out-of-phase with KE(S⁺). This can be explained in terms of Coulomb forces between point charges (see Fig. S3 in the SM): near the equilibrium geometry, the net force on the S⁺ (O⁺) fragment due to the other two decreases (increases) with increasing bond angle. Moreover, $\mathrm{\angle(O^{+},O^{+})}$ also increases monotonically with the real-space bond angle.

We numerically model the experimental observables in Figs. 2(a-c) by solving the time-dependent Schrödinger equation for the coupled nuclear motion on the Born-Oppenheimer potential energy surfaces of the SO₂ ($X$) and SO${}_{2}^{+}$ ($\tilde{X}$) electronic ground states, including all vibronic degrees of freedom (symmetric stretch, bending, and antisymmetric stretch modes) [74]. We calculated the molecular electronic states ab initio by applying the multi-configurational self-consistent-field method as implemented in the quantum chemistry code GAMESS [75], based on seven frozen inner orbitals and 12 active orbitals expanded in the correlation consistent-polarized valence triple zeta (cc-pVTZ) basis set. Following the dipole coupling of the nuclear motion in the neutral and ionic ground states by the pump pulse, we model the delayed probe pulse by vertically projecting the nuclear motion onto the potential energy surface of the triply-charged molecule, approximated as purely Coulombic, and propagate the nuclear wave packet to sufficiently large internuclear distances on the (O⁺, O⁺, S⁺) asymptote to achieve numerical convergence. We obtain the fragment kinetic energy releases by Fourier transformation of the real-space nuclear wave function to momentum space [76].

Our simulations in Figs. 2(d-f) closely resemble the experimental data in Figs. 2(a-c), manifesting similar periodicity, phases, and correlations between the delay-dependent fragment angles $\mathrm{\angle(O^{+},O^{+})}$ and fragment kinetic energies KE($\mathrm{S^{+}}$) and KEsum($\mathrm{O^{+},O^{+}}$). However, we note that each pair of experiment-simulation plots shows a mismatch in absolute value because vertical projection to and propagation on the Coulomb potential do not adequately describe the ionization and fragmentation process caused by the probe pulse. Nevertheless, these results provide a direct intuitive picture of the strong-field-induced vibrational wave packet motion in a triatomic molecule. Modulations of this three-body channel are dominated by the ionic ground-state vibrations, with a weak contribution from bending vibrations in the ground state of neutral SO₂ as revealed by Fourier transformation of the delay-dependent data (see Fig. 1 and Fig. S2 of the SM).

Besides revealing the states involved in the vibrational wave packet, coincidence momentum imaging also allows us to visualize the correlated motion of individual atoms. To achieve this, we plot the data for all ions from the $\mathrm{(O^{+},O^{+},S^{+})}$ channel in a 2D momentum image (Newton plot). Fig. 2(h) features a representative image at 250 fs with a contour for data at 210 fs (the inner and outer turning points of the bending wave packet). Because the $\mathrm{\angle(O^{+},O^{+})}$ and KE($\mathrm{S^{+}}$) manifest the same behavior as the OSO bond angle and the displacement of S from the center of mass (see Fig. 2 and Fig. S3), movies comprising a timed sequence of these images (as provided in the SM) are a striking and intuitive representation of the bending vibration of the molecule. These molecular movies illustrate that during the first 400 fs, the wave packet is well localized and mimics the motion of a “ball-and-stick” model.

While bending vibrations are responsible for the most pronounced features of the observables shown in Figs. 1 and 2, the experimental data contain more information about the molecular wave packet launched by the pump pulse. One hint of other dynamics is found in the total yield of the (O⁺, O⁺, S⁺) channel, which does not exhibit oscillations at the frequency of the bending vibration. This suggests that double ionization probability of the cation is insensitive to this mode. However, as depicted in Fig. 3(a), the yield initially decreases by approximately 15% within the first few hundred femtoseconds before flattening out. To explain this behavior, we also plot $\langle\cos^{2}{\theta}\rangle$ for this channel in Fig. 3(a). Here, $\theta$ is the angle between the laser polarization and $\Delta\vec{p}(\mathrm{O}^{+})=\vec{p_{1}}(\mathrm{O}^{+})-\vec{p_{2}}(\mathrm{O}^{+})$, representing the direction of the O-O axis. The strong correlation between these two quantities (except near the overlap region) indicates that the observed yield variation is due to the initial alignment of the pump-induced rotational wave packet. The time scale is consistent with the rotational dynamics of the two-body breakup channels shown in Fig. S4 (SM). Although the O-O axis is the most polarizable axis of the molecule, strong-field ionization of neutral SO₂ is more likely to occur along the symmetry axis (see [54] and SM, Fig. S5). Thus, SO${}_{2}^{+}$ ions are most likely created near the peak of the pump pulse with their symmetry axes aligned with the laser polarization. They then rotate due to the angular momentum accumulated in the pump pulse and reach peak alignment (of the O-O axis) around 200 fs. After the peak, the rotational wave packet dephases and exhibits long-term incoherent alignment.

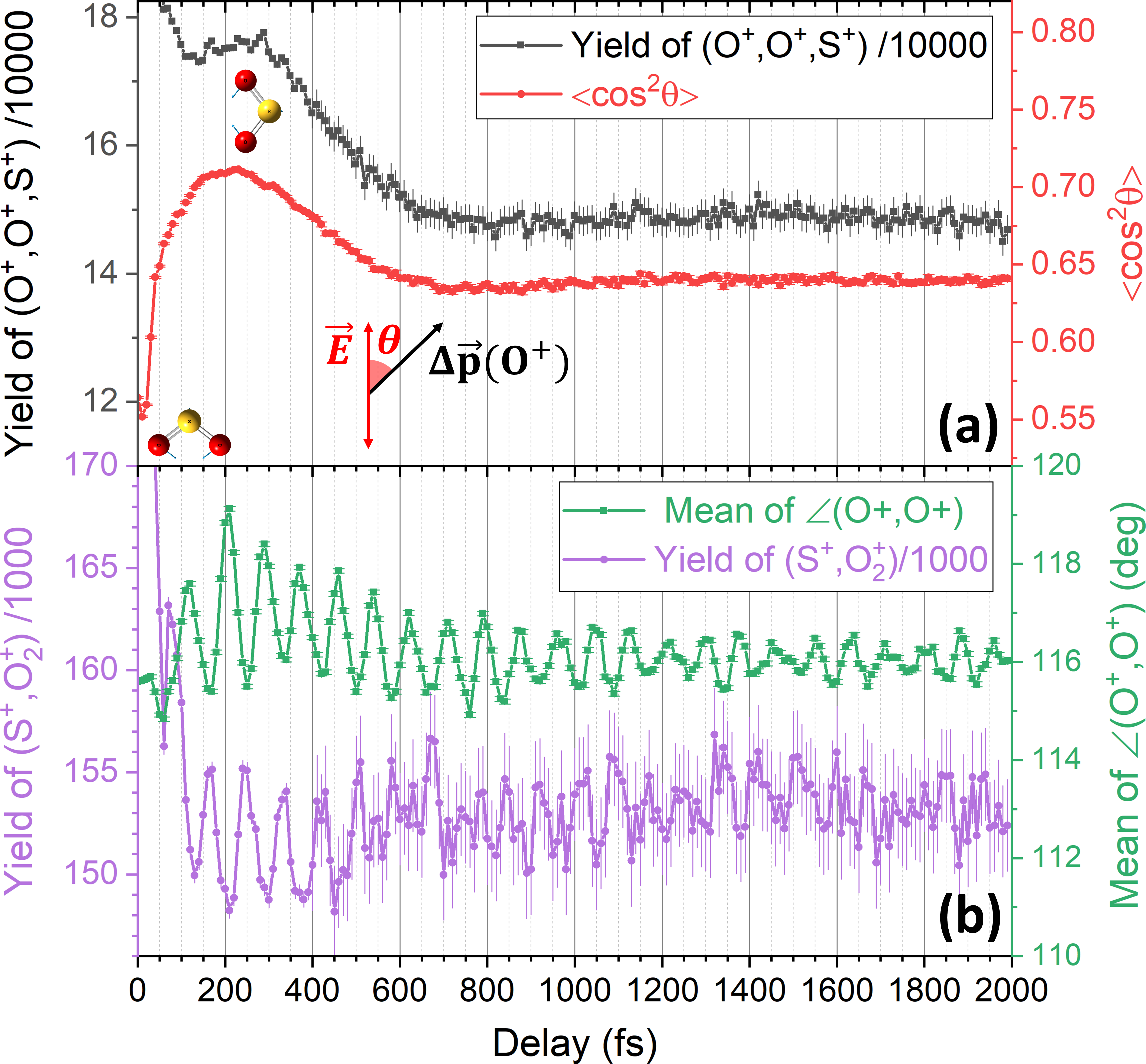
This rovibrational wave packet motion in SO${}_{2}^{+}$ has other manifestations that can be elucidated by multi-coincidence momentum imaging. One example is the formation of O${}_{2}^{+}$, which can be traced by analyzing the (S⁺,O${}_{2}^{+}$) coincidence channel. The delay-dependent yield of this channel is shown in Fig. 3(b) along with the mean value of $\mathrm{\angle(O^{+},O^{+})}$ in the three-body channel. Clearly, the two oscillate out of phase, suggesting an intuitive picture of O${}_{2}^{+}$ formation by the probe pulse: O${}_{2}^{+}$ is more likely to be formed if the probe pulse finds the cation at smaller OSO angles, where the two oxygen atoms are closer to each other. The alignment and bending angle dependence of O${}_{2}^{+}$ production may help improve our understanding of a potential source of abiotic oxygen in SO₂-rich planetary atmospheres [58].

The rovibrational wave packet also controls the excitation of the ground-state cations to the first excited state in the probe pulse. This single-photon transition is energetically allowed for $\phi\lesssim 134^{\circ}$ and its dipole moment is along the O-O axis. Thus, when ground state cations have rotated into alignment with the probe laser polarization and bending mode vibration has pushed the nuclear probability density to smaller-then-equilibrium bond angles (i.e., $\phi<134^{\circ}$), a single photon in the leading edge of the probe can resonantly transfer population from $\tilde{X}^{2}A_{1}$ to $\tilde{A}^{2}B_{2}$ (see Fig. 1 for PE curves). These two states have a symmetry-allowed conical intersection (CI) at $\approx 108^{\circ}$ with the branching space comprised of the bending and asymmetric stretching coordinates [53]. After excitation to $\tilde{A}^{2}B_{2}$ the wave packet travels towards the CI where it is nonadiabatically coupled to the asymmetric stretch mode and returns to $\tilde{X}^{2}A_{1}$ within 20 fs [53]. Since our probe pulse width is 28 fs, these cations can still be ionized at the peak of the probe and appear in the (O⁺, O⁺, S⁺) channel. On the other hand, if the excitation occurs in the trailing edge of the pump pulse, the wave packet should dephase rapidly as it traverses the CI and not exhibit periodic oscillations at 400 cm^-1.

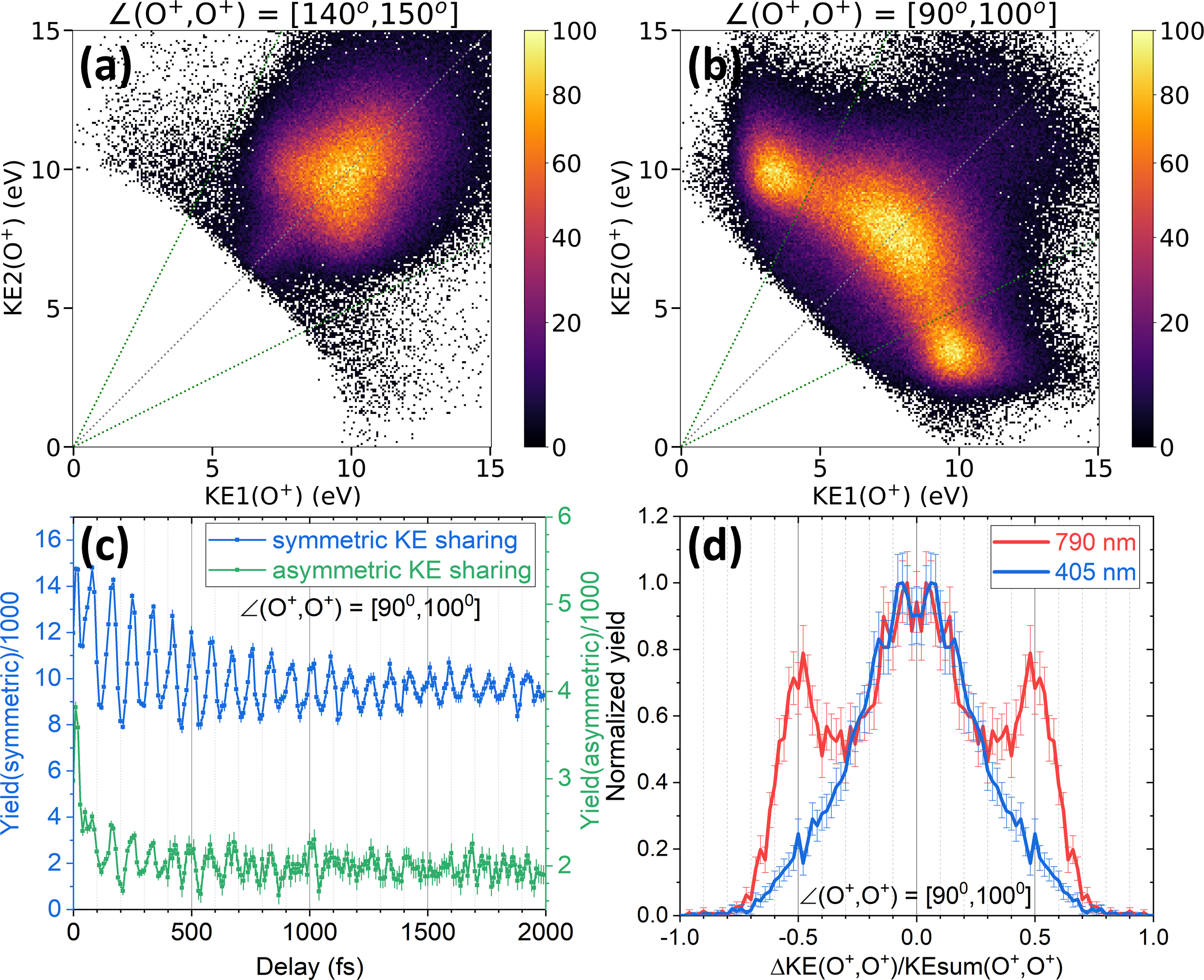
In the experimental data, signatures of a wave packet in $\tilde{A}$ state are seen in the KE sharing plot for the O⁺ ions. We separate events with $\mathrm{\angle(O^{+},O^{+})}\in[140^{\circ},150^{\circ}]$ and $\mathrm{\angle(O^{+},O^{+})}\in[90^{\circ},100^{\circ}]$ in Fig. 4(a,b), respectively, with the expectation that the population excited to $\tilde{A}$ can travel to smaller bending angles than the inner turning point of bending wave packet in $\tilde{X}$ but not to the outer turning point within the probe pulse. The strong component with asymmetric KE sharing seen in Fig. 4(b) but not in Fig. 4(a) confirms the dipole coupling to $\tilde{A}$ and nonadiabatic coupling to asymmetric stretch mode. Fig. 4(c) shows the delay-dependent yields of events with symmetric (blue) and asymmetric (green) KE sharing [all with small $\mathrm{\angle(O^{+},O^{+})}$]. The in-phase oscillation of the two curves is consistent with population transfer by the probe to the SO${}_{2}^{+}$ ($\tilde{A}$) state near the inner turning point of the ground state bending vibration. To further test this hypothesis of resonant inter-state coupling, we use a single laser pulse at 405 nm to ionize SO₂ into (O⁺, O⁺, S⁺). The absence of asymmetric KE sharing peaks in the 405-nm case [Fig. 4(d)] confirms a resonant coupling near 790 nm, corroborating our conclusion that we see signatures of mode-coupling at the CI in our pump-probe experiment.

In conclusion, our work highlights the direct sensitivity of CEI to changes in the spatial density of the nuclear wave packet, demonstrating the feasibility of tracking the correlated motion of individual atoms within a molecule. This approach offers intuitive mechanistic insights into various molecular dynamics. The high-dimensional measurement allows us to observe and interpret the interplay between rotational, vibrational, and electronic motion in determining the molecular wave packet evolution and the experimental outcomes. Our simulations successfully capture the periodicity and phase behavior of different observables and their correlations, strongly supporting our interpretations. In view of recent advancements demonstrating that CEI can image detailed 3D structures of gas-phase molecules with about ten atoms [21, 23], this work paves the way for tracking dynamics of medium-size polyatomic molecules with unprecedented detail.