Images of hairy Reissner-Nordström black hole illuminated by static accretions
Abstract
In this paper, we investigate the shadow and optical appearance of the hairy Reissner-Nordström (RN) black hole illuminated by two toy models of static accretion. The hairy RN black hole was constructed in the gravitation decoupling approach to describe the deformation of a Schwarzschild black hole due to the inclusion of additional arbitrary source (scalar field, tensor field, fluidlike dark matter, etc.). So it is characterized by the parameters: mass (), deformation factor (), electric charge () and the additional hairy charge ()., differentiating from the case in RN black hole. Though the specific background theory that results in this hairy RN black hole is still tricky, here we shall focus on the novel observable features introduced by the hair of this black hole. First, we find that for the hairy RN black hole, the event horizon, radius of photon sphere and critical impact parameter all increase as the increasings of and , but decrease as grows. Furthermore, the three characterized parameters are found to have significant effects on the photon trajectories, and shadows as well as images of the hairy RN black hole surrounded by the static accretion disk and spherical accretion, respectively. In particular, both and have mutually reinforcing effects on the optical appearance and shadows of the hairy RN black hole, which implies that we may not distinguish the electric charge and hairy charge from the shadow and image of black hole in this scenario. Additionally, because of the competing effects of the charge parameters () and the deviation parameter on the observed intensities of brightness, the optical appearance between the hairy RN black hole and RN black hole could have degeneracies, indicating the indistinguishability. Our current results contribute more to the phenomenal aspects which could be helpful to build the background theory of this hairy RN black hole.
I Introduction
Recently, the Event Horizon Telescope (EHT) has made significant achievements, providing us with a new window to test the essence of gravity in the strong field regime. One of the most impressive achievement among them is the release of images of the supermassive black hole M87* Akiyama et al. (2019a, b, c, d, e, f) and the central black hole of our Milky Way Akiyama et al. (2022a, b, c, d, e, f). The dark regions in the center of the images are the shadow of black hole, which are related to the strong gravitational lensing of photons around the black hole Virbhadra and Ellis (2000, 2002); Virbhadra and Keeton (2008); Synge (1966); Bardeen et al. (1972); Bozza (2010). The unstable photon orbit (photon sphere) in the innermost layer around the black hole define the radius of shadow, and the bright rings in the images are related to the outer photon orbits. Moreover, the bright ring-shaped construction is the product of various light rays as the black hole is always illuminated by complex accretion flows.
In fact, early on, the black hole shadow was known as the escaping cone of photon Synge (1966), which is defined as the impact parameter corresponding to the critical curve. Furthermore, the expression of the angular radius of the photon capture region for the Schwarzschild black hole was proposed Luminet (1979), and later Bardeen investigated the D-type shadow of the Kerr black hole Bardeen et al. (1972), which is caused by the dragging effect of the rotating black hole on the light rays. This has inspired a wave of research on the shadow of black hole, and numerous simulations of various black hole shadows have been widely discussed, see for examples Shen et al. (2005); Yumoto et al. (2012); Atamurotov et al. (2013); Papnoi et al. (2014); Abdujabbarov et al. (2015); Kumar and Ghosh (2020) and references therein. Those studies indicate that the properties of black hole shadows closely depend on the spacetime background. The shadows of black holes in different spacetime dimensions and modified theories of gravity have also been attracted extensive discussion, such as conformal gravity Meng et al. (2022), Gauss-Bonnet theory Ma and Lu (2020); Guo and Li (2020), the Chern-Simons type theory Meng et al. (2023a); Ayzenberg and Yunes (2018); Amarilla et al. (2010), f(R) gravity Addazi et al. (2021); Dastan et al. (2022), and so on Amarilla and Eiroa (2012, 2013); Amir et al. (2018); Mizuno et al. (2018); Eiroa and Sendra (2018); Vagnozzi and Visinelli (2019); Banerjee et al. (2020); Chowdhuri and Bhattacharyya (2021); Konoplya and Zhidenko (2019); Younsi et al. (2016); Olmo et al. (2023). In addition, the shadows of naked singularities have been studied in Shaikh et al. (2019a); Joshi et al. (2020); Dey et al. (2021), and the wormholes shadows were also explored in Rahaman et al. (2021); Kasuya and Kobayashi (2021); Shaikh et al. (2019b); Wielgus et al. (2020); Peng et al. (2021a); Neto et al. (2023); Tsukamoto et al. (2012) and references therein. On the other hand, images from EHT collaboration are simulated via Kerr black holes in general relativity (GR). However, due to the finite resolution of EHT, this also provides some space for alternative theories beyond GR. Therefore, plenty of works have been carried out to use the shadow observations of the EHT to test or constrain modified theories of gravity Vagnozzi et al. (2023); Afrin et al. (2021); Kuang et al. (2022); Tang et al. (2022, 2023); Kuang and Övgün (2022); Kumar et al. (2019); Shaikh et al. (2021); Wu et al. (2023a); Capozziello et al. (2023); Sui et al. (2023); Pantig et al. (2023); Ghosh et al. (2023); Tsukamoto et al. (2014).
The bright ring-shaped constructions in the EHT images are closely related to the accretion flow radiation around the black hole, and the geometric features of the accretion flow determine the optical appearance of the black hole. However, in the realistic astrophysical environments, the accretion flows around black holes are always very complex such that one need numerical simulation using general relativistic magnetohydrodynamic (GRMHD) to extract the black hole images Porth et al. (2019). It is worth noting that usually in order to investigate the main characteristics of black hole images and the gravity in strong field regime, giving some toy models of accretion structures is enough to put forward. Thus, Wald et al. first proposed an optically and geometrically thin toy accretion disk around Schwarzschild black holes, and defined direct , lensed ring and photon ring emissions by the number of times () light intersecting with the accretion disk Gralla et al. (2019). They found that the total observed brightness of black hole images mainly comes from the direct emissions, while the contribution of lensed ring emissions is small and photon ring emissions can even be ignored. Subsequently, toy accretion disk models around various black holes have been extensively studied Dokuchaev and Nazarova (2019); Peng et al. (2021b); He et al. (2022); Eichhorn and Held (2021); Li and He (2021); Wang et al. (2023). The spherical accretions, as another toy accretion model, have also been attracted great interest Zeng et al. (2020); Saurabh and Jusufi (2021); Zeng and Zhang (2020); Qin et al. (2021); Narayan et al. (2019), in which the size and shape of shadows are mainly determined by the spacetime geometry of the black hole, rather than the details of the accretions. Moreover, the accretion constructions around black holes with two unstable photon spheres were also analyzed in Gan et al. (2021a, b); Meng et al. (2023b). Compared to black hole with single photon sphere, the black hole with double photon spheres could have additional photon rings in the image, and the photon ring and lensed ring emissions will contribute significantly to the total observed brightness. In general, the optical appearance is a potential probe to distinguish GR black holes from other alternative compact objects Boshkayev et al. (2022); Xavier et al. (2023); Sakai et al. (2014); Bacchini et al. (2021); Destounis et al. (2023) or black holes in alternative theories beyond GR Guo et al. (2023a, b); Archer-Smith and Zhang (2021); Okyay and Övgün (2022); Uniyal et al. (2023a); Hou et al. (2022); Uniyal et al. (2023b); Akbarieh et al. (2023); Gao et al. (2023); Theodosopoulos et al. (2023); Zeng et al. (2023); Meng et al. (2023c), but this does not always work, as even in GR, the images of black holes may exhibit degeneracies. For example, sufficiently dense boson stars Liebling and Palenzuela (2023); Rosa et al. (2023) may have shadows similar to those of classical black holes Rosa and Rubiera-Garcia (2022) and images of very relativistic rotating boson stars may resemble Kerr black holes Vincent et al. (2016).
On the other hand, when there are other additional sources around the black hole, the interaction between spacetime and additional sources can cause the black hole to carry global charge. This charge is also known as the hair of black hole, and in this case the spacetime usually will deviate from that in GR. In this scenario, Ovalle and Casadio first proposed the gravitational decoupling (GD) approach Ovalle et al. (2021); Contreras et al. (2021) to introduce additional sources, and obtain hairy black holes which describes deformations of the black holes in GR. Due to the fact that in the GD approach, the additional sources can be dark matter, scalar fields, tensor fields etc., so the GD approach can be used to study the general existence problem of solutions for hairy black holes. In particular, they take the Schwarzschild black hole as the seed black hole, and use the GD approach to construct the hairy Schwarzschild black hole which obtain extensive attention, such as the thermodynamics of rotating hairy black holes Mahapatra and Banerjee (2023), scalar perturbations and quasinormal modes of hairy black holes Cavalcanti et al. (2022); Yang et al. (2023a); Li (2023), strong gravitational lensing, black hole shadow and image Afrin et al. (2021); Islam and Ghosh (2021); Meng et al. (2023b), precession and Lense-Thirring effect Wu et al. (2023b) and gravitational waves from extreme mass ratio inspirals Zi and Li (2023).
In this work, we will focus on the optical features of the hairy RN black hole, which was also constructed via the GD approach by taking the Schwarzschild black hole in GR as the seed black hole. Since the hairy RN black hole includes electric charge and additional arbitrary hairy charge, thus, the aim of this work to investigate if the black hole shadow and image can probe the different charges in this scenario. In details, we will firstly explore the effects of characterized parameters of the hairy RN black hole on the light rays, and on the black hole rings and images when it is surrounded by the optically and geometrically thin accretion disks and spherical accretion. Then we shall discuss the possible distinguishable effects of the charges on the hairy RN black hole shadows and images, and potentially differentiate the hairy RN black hole from RN black hole.
This paper is organized as follows. In Sec. II, we will study the radius of photon sphere and impact parameters by analyzing the effective potential of photons around the hairy RN black hole. In Sec. III, we use the ray-tracing method to discuss the distribution of the light rays around the hairy RN black hole, and then investigate the optical appearance of hairy RN black hole illuminated by the optically and geometrically thin accretion disk. In Sec. IV, we present the black hole shadows and images illuminated by static spherical accretions. Sec. V gives our conclusions.
II Photons sphere of the hairy RN black hole
Black holes in classical GR are only described by mass, electric charge and spin because of the no-hair theorem Ruffini and Wheeler (1971). But the interaction between black hole spacetime and matters may introduce other charges, so the black hole could carry additional hairy charges and the physical effects of these hairy charges can modify the original background spacetime, namely, hairy black holes may form. Recently, Ovalle et.al used the GD approach to obtain a spherically symmetric black hole with additional hairy charges Ovalle et al. (2021); Contreras et al. (2021), which has the metric
| (1) |
with
| (2) |
This metric describes the deformation of the Schwarzschild black hole solution due to the introduction of additional sources, which can be dark matter, scalar fields, tensor fields, etc. Here and represent potential charges, and both of them are proportional to , such that the above solution reduces to Schwarzschild case as . In appendix A, we review how the hairy RN black hole (1) is solved out from the seed metric via the GD approach. The technics of this approach to obtain the deformed solutions sound good, but the specific background theory, which can give the additional required tensor field in the approach, remains open. The authors of Ovalle et al. (2021) briefly discussed the potential background theories which still call for further investigations. Nevertheless, the uncertainty of the background theories did not hinder physicists’ attention on this type of deformed black hole, and lots of theoretical and observable properties of the deformed black hole have been investigated Mahapatra and Banerjee (2023); Cavalcanti et al. (2022); Yang et al. (2023a); Li (2023); Afrin et al. (2021); Islam and Ghosh (2021); Meng et al. (2023b); Wu et al. (2023b); Zi and Li (2023). The reasons may stem from two aspects: (i) Due to the uncertainty of the ingredients in our Universe and the dispute on no-hair theorem of black hole, people can temporarily suspend the unclear background theory and go ahead to study its possible outputs. (ii) More complete understanding of the hairy black hole could give more information to build its background theories, at least from bottom-up perspective. In particular, as addressed in Ovalle et al. (2021), can be an electric charge, or a tidal charge of extradimensional origin or any other source depending on the specific background theory. When represents an electric charge, the electrovacuum of the RN geometry also contains a tensor-vacuum whose components are those explicitly proportional to . In this paper, taking our motivations mentioned in the Introduction into account, we will treat as the electric charge differentiating from the additional hairy charge , and instead of clarifying its corresponding background theory, we shall discuss their possible probe from black hole shadow and images. So we denote the above geometry (1) as the hairy RN spacetime. Thus, in the following studies, , , and are the parameters related with the mass, electric charge and hairy charge of the black hole, respectively. In addition, should satisfy to ensure the asymptotic flatness of spacetime.
Here we focus on the properties of motions of photon in the vicinity of the hairy RN black hole. Before proceeding, we briefly discuss the event horizon of hairy RN black hole, which can be solved out from
| (3) |
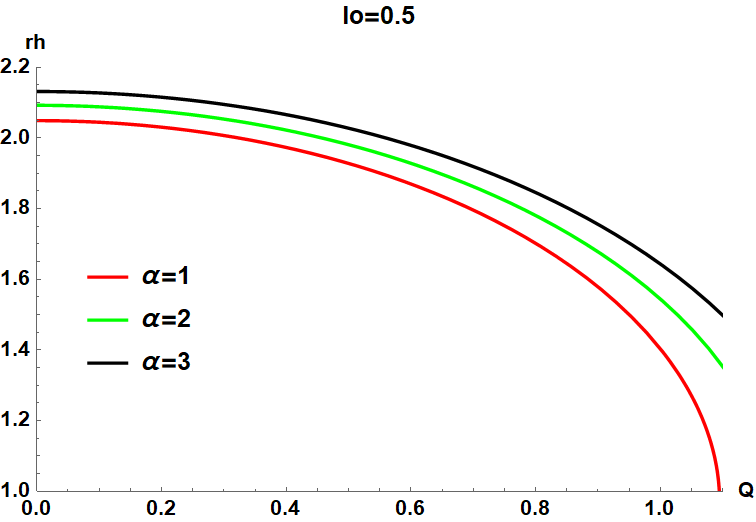
After numerical calculation, we show how the event horizon is affected by the parameters , , and with the others fixed in FIG.1. Obviously, with fixed , both the charge parameters and will suppress the event horizon , but as the deformation parameter increases, the event horizon of the hairy RN black hole becomes larger.


Next, we will investigate the null geodesic motion in the hairy RN black holes. The motions of photons are described by the Euler-Lagrange equation,
| (4) |
where represents the four-velocity of the photon and is the affine parameter. In the static spherically symmetric hairy RN black hole, the Lagrangian of the photon takes the form
| (5) |
Since and are Killing vector fields of the hairy RN spacetime, we can define the conserved energy, , and the component of the angular momentum, , of the photon as
| (6) |
Furthermore, due to the spherical symmetry of the spacetime, we can focus on the motions of photons on the equatorial plane without losing generality. Moreover, by considering for photon and defining the impact parameter , we can obtain three first-order differential equations of motion for the photons
| (7) |
where the effective potential is given as
| (8) |
The sign in (7) represent the clockwise and counterclockwise direction of photons’ trajectories, respectively. Then the fate of a photon is determined by the radial geodesic equation. In particular, the circular orbit should satisfy and , which will be translated to
| (9) |
where is the radius of the photon sphere satisfying , and is the critical impact parameter which is related with the shadow radius of the black hole. As shown in the leftmost plot of FIG. 2, the light rays with , will be deflected by the black hole and escape to infinity; on the contrary, the light rays with will be captured into the event horizon of the black hole. The light rays with will circle around the black hole all the time with the radius . The effects of the two charges on the and are shown in the middle and rightmost plot of FIG. 2. It shows that as both charge parameters increase, both and become smaller, similar to what occurs for the event horizon, as shown in FIG. 1, as expected.



Based on the preliminary analysis, we shall study the optical appearance of the hairy RN black hole in various illumination conditions. It is known that the hot, optically thin accretion flows are surrounding M87*, Sgr A* and many other supermassive black holes in our Universe Yuan and Narayan (2014). Here we will consider the hairy RN black hole illuminated by statically thin disk accretions and spherical accretions, respectively, which are simple toy accretion models but enough for the purpose of this paper.
III Images of hairy RN black hole illuminated by thin accretions disk
In this section, we shall use the ray-tracing method to analyze the distribution of light rays in the vicinity of the hairy RN black hole and further investigate the optical appearance of the black hole illuminated by an optically and geometrically thin accretion disk. For simplicity, we consider that the accretion disk is fixed at the equatorial plane and the observer is located at the North pole. Due to the strong gravitational lensing effect, the light rays around the black hole may intersect with the accretion disk arbitrary times before falling into the black hole or escaping to infinity, which brings different contributions to the total intensity received by the observer. For this purpose, we should first classify the light rays in terms of the number of times they intersect with the thin accretion disk, and then figure out the images of the hairy RN black hole.
III.1 Classification of the light rays
The motion trajectories of photons around the hairy RN black holes are controlled by the trajectory equation
| (10) |
derived from (7). It is obvious that the trajectory of light ray is closely related to the impact parameter . As addressed in Gralla et al. (2019), the regions of impact parameters are divided into three types based on the total number of orbits , where is the total change in azimuthal angle. More specifically, the light ray from the North pole only intersects with the equatorial plane once, which corresponds to direct emission with . For the second type with , the light ray intersects with the equatorial plane twice, which corresponds to the lensed ring emission. The third type is photon ring emission with , where the light rays intersect with the equatorial plane at least three times.
In order to better understand how the charges affect the photon trajectories and their classification, we use the ray-tracing method to solve the trajectory equation (10) with selected parameters of the hairy RN black hole. The total number of orbits as function of impact parameters , and the photon trajectories in panel are shown in FIG. 3. We see from the plots (FIG. 3a, 3e, 3i) that in all cases, as the impact parameter increases, the total number of photon orbits first increases to be an infinity at , and then gradually decreases. Moreover, the parameters all affect the width of various emissions we defined previously.



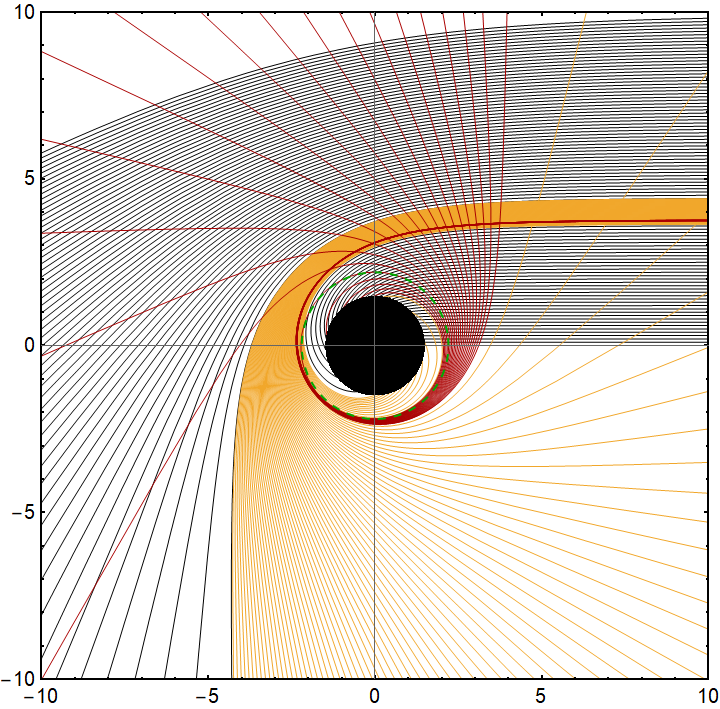








By further careful calculation, we determine the borders of for each emissions, and list the results in Table 1-Table 3 in which we also show the results of black hole’s event horizon , photon sphere radius , and critical impact parameters . As both charge parameters and increase, , , all decrease, but the widths of the lensed ring and photon ring emissions both increase. However, the effects of on all those quantities obey the opposite rules. Furthermore, we mark the light rays from the direct, lensed ring, and photon ring emissions into black, gold, and red, respectively and figure out photon trajectories around the hairy RN black hole into FIG. 3, where the green dashed circle and black disk represent the photon sphere and the black hole, respectively. The effects of , and on all physical quantities listed in Table 1-Table 3 are explicit if we compare the trajectories of photons in each row of FIG. 3. In particular, larger both charges enlarge the width of lensed ring and photon ring structure of the black hole in observations. On the contrary, for larger , the lensed ring and photon ring emissions may be less likely to be observed. We expect to verify these phenomena in the optical appearance of the black hole in the next subsection.
| Direct emission | Lensed ring emission | Photon ring emission | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 0.1 | 0.1 | 2.38260 | 3.42178 | 5.56182 | ; | ; | |
| 5 | 1 | 0.1 | 2.05833 | 2.96629 | 4.88403 | ; | ; | |
| 5 | 1.5 | 0.1 | 1.47998 | 2.20043 | 3.75803 | ; | ; |
| Direct emission | Lensed ring emission | Photon ring emission | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 1 | 0.1 | 2.05833 | 2.96629 | 4.88403 | ; | ; | |
| 5 | 1 | 1 | 1.44737 | 2.02571 | 4.13132 | ; | ; | |
| 5 | 1 | 1.9 | 1.00002 | 2.00000 | 4.00000 | ; | ; |
| Direct emission | Lensed ring emission | Photon ring emission | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.1 | 2.00651 | 3.00572 | 5.19796 | ; | ; | |
| 5 | 0.1 | 0.1 | 2.38260 | 3.42178 | 5.56182 | ; | ; | |
| 20 | 0.1 | 0.1 | 2.89692 | 4.00597 | 6.09891 | ; | ; |
III.2 Observed intensities and optical appearances
The light rays will extract energy when they intersect with the accretion disk each time, which will directly affect the contribution of the direct, lensed ring, and photon ring emissions to the observed brightness. Since the parameters and have obvious influences on the emission widths of the three types. Therefore, it is interesting to examine their effects on the optical appearance of the hairy RN black hole. Considering that the thin accretion disk emits isotropically in the rest frame of static worldlines, the specific intensity received by the observer with emission frequency is
| (11) |
where is the redshift factor, and are the frequency of the observed light and the specific intensity of the accretion disk, respectively Bromley et al. (1997). The total observed intensity is then evaluated by integrating over all the observed frequencies of as
| (12) |
where we denote as the total emitted intensity. Therefore, since the reverse light ray from the observer may intersect the accretion disk multiple times, depending on the type of emission, so the total intensity received by the observer is the sum of the intensities from each intersection Gralla et al. (2019)
| (13) |
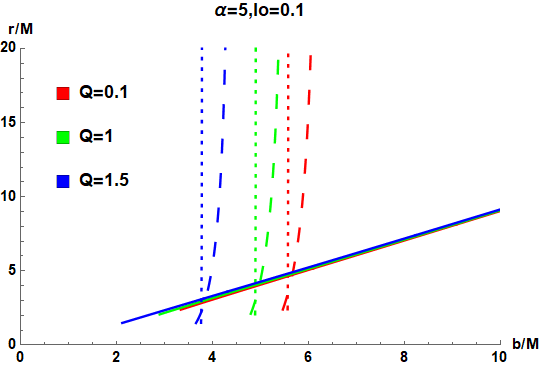
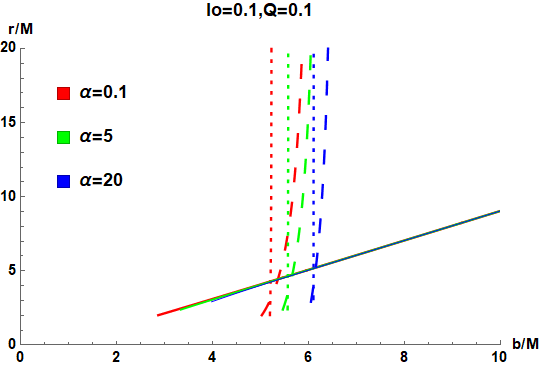
where is known as the transfer function, which represents the radial coordinate of the th intersection of the light ray with impact parameter and the accretion disk. Thus, the slope describes the demagnification factor, and the case with larger corresponds to strong demagnification so as to contribute much less to the total luminosity. Moreover, as we illustrated in Wang et al. (2023), the first transfer function corresponds to the direct image originating from direct, lensed and photon ring emission; the second transfer function can origin from lensed ring and photon ring emission; while the third transfer function can only origin from photon ring emission. We show the first three transfer functions for the selected parameters in FIG. 4, where the solid, dashed, and dotted curves denote , and , respectively. We see that as the charge parameters or increases (FIG. 4a and FIG. 4b), the three transfer functions areas become wider and move toward the smaller , while the parameter gives opposite influence (FIG. 4c). However, there are still some common properties in all cases: (i) the slope of is almost 1, because the direct image corresponds to the source profile after redshift. (ii) and are highly steeper comparing to , and is steeper than . This feature means that will dominate in the total luminosity and other transfer functions contribute very little.

We proceed to investigate the optical appearance of the hairy RN black hole by considering a specific toy model emission function of the accretion disk, which gradually decays from the event horizon in the form Wang et al. (2022); Yang et al. (2023b)
| (14) | ||||
Here, is the maximum intensity and the innermost stable circular orbit can be computed by Wang et al. (2023)
| (15) |
in which is the metric function of the hairy RN black hole, and the prime represents the derivative with respect to the radial coordinate .

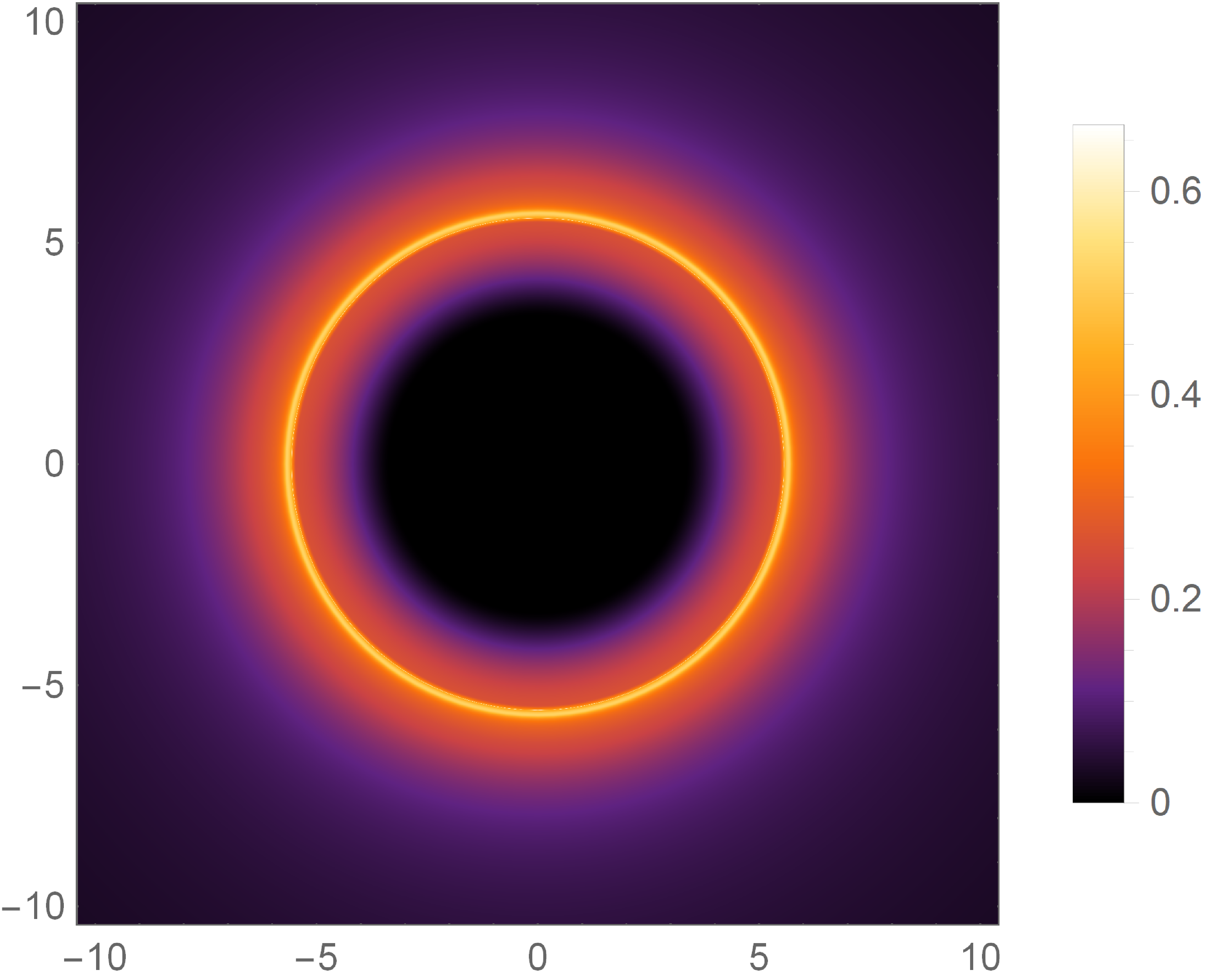









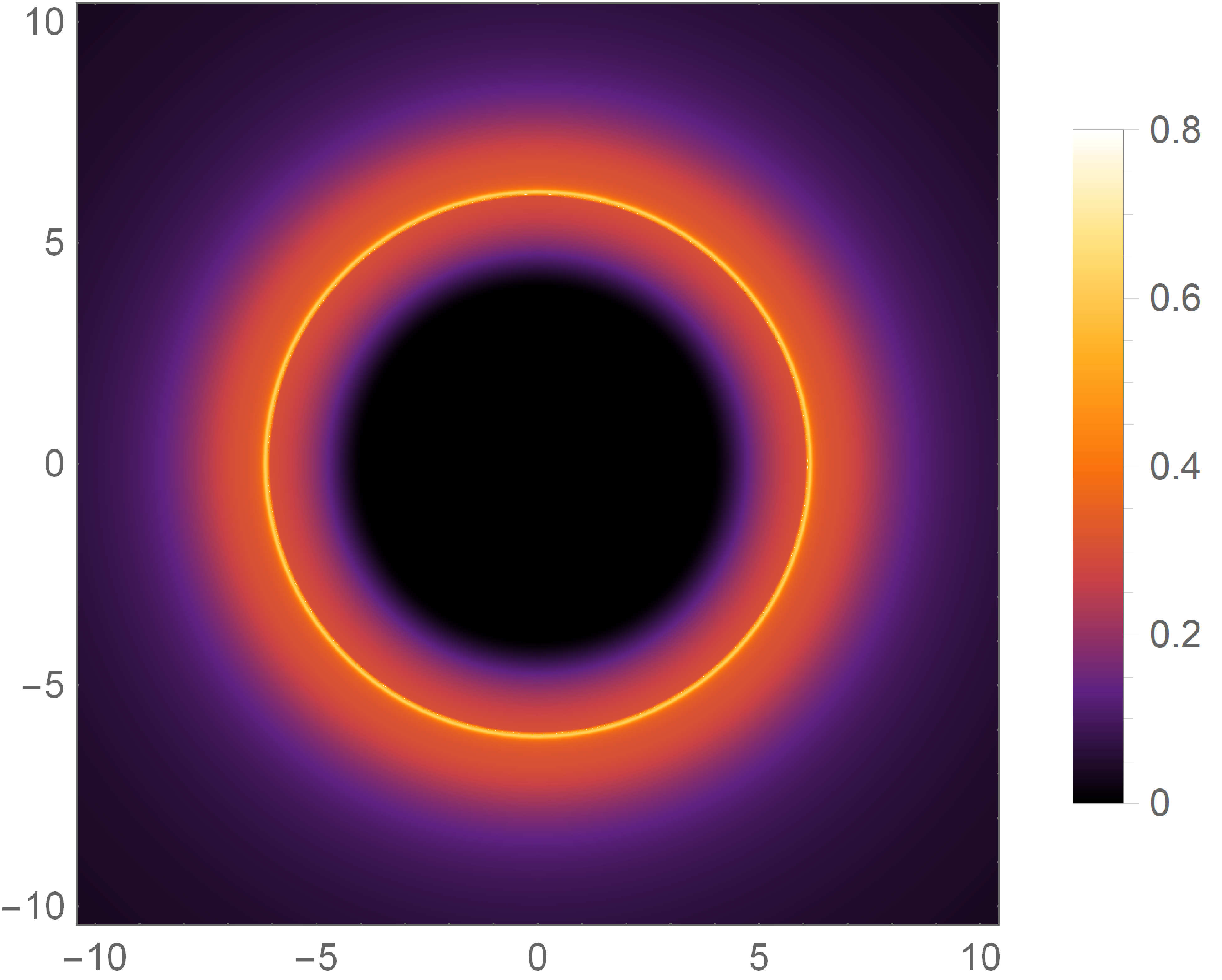
Having both the transfer and emission functions of the accretion disk in hands, we can evaluate the observed intensities via (13) and figure out the black hole images. Our results for the selected parameters are shown in FIG. 5. In each row, we first show the total observed intensities as a function of impact parameter for different parameters, and then project them into a two dimensional plane to explicitly present the optical appearance of the accretion disk. In all cases, we can see two obvious peaks in the total observed intensities, corresponding to two rings in the images. Moreover, for larger () with fixed () and , the two peaks of are both smaller and shift to smaller . On the contrary, for larger with fixed and , the peaks are enhanced and occur at larger . In addition, it is obvious from the images that larger ( ) corresponds to smaller shadow region while larger deviation parameter gives larger shadow region as we illustrated in section II. Consequently, our results imply that one may not be able to tell which kind of charge the hairy RN black hole carry through the rings and images of the accretion disk, since the two charge parameters, and , have similar influence on the observed intensities of the black hole surrounded by the accretion disk. Moreover, there are potential degeneracies in the hairy RN black hole images because and may counteract their effects. This may also result in the optical appearance of the hairy RN black hole being undistinguished from that of the RN black hole.
IV Images of hairy RN black hole illuminated by static spherical accretions
In this section, we will investigate the images of hairy RN black holes surrounded by a static spherical accretion. When the materials in the Universe are trapped by a black hole, the disk-shaped accretion flow usually forms around the black hole and rotates with a large angular momentum, but the matter will flow radially to the black hole and form a spherically symmetric accretion when the angular momentum is extremely small Yuan and Narayan (2014). For an optically and geometrically thin static accretion with spherical symmetry, the observed specific intensity detected by an observer at infinity (measured in erg s-1 cm-2 str-1 Hz-1) is evaluated by integrating the specific emissivity along the photon path Bambi (2013)
| (16) |
Here, and are the emitted photon frequency and the observed photon frequency, respectively. is the redshift factor. is the emissivity per unit volume in the rest frame and usually taken the form with the emitter’s rest-frame frequency Bambi (2013). And is the infinitesimal proper length given by
| (17) |
where the is expressed in (10). Subsequently, by further integrating (16) over all the observed frequencies, we obtain the total observed intensity as
| (18) |












Then we calculate the total observed intensities, and depict them into a two dimensional plane as the images of hairy RN black hole with the same selected parameters as previous sections. The results are presented in FIG. 6. For the total observed intensities in each case, there exists a peak which corresponds to the bright ring in the images of the black hole. As the increasing of both and (FIG.6a and 6e), the peak is enhanced and shifts to smaller impact parameters, indicating that the ring becomes brighter but the faint illuminating region in the center is smaller for larger (Fig. 6b-6d) or (Fig. 6f-6h). In addition, FIG. 6i-6l show that the effect of increasing of obeys a completely different rule from that of the charges. Namely, increasing suppresses the peak but enlarges the corresponding impact parameters, thus, we see larger faint illuminating region in the images of black hole with larger . Thus, comparing to the RN black hole, the introduction of additional field can enlarge/suppress or keep the brightness as well as the size of photon ring, depending on the competition between the parameters and . This implies the possible degeneracies in the optical appearances of the hairy RN black hole and RN black hole surrounded by the static spherical accretion.
V Conclusion and discussion
The black hole images released by the EHT collaborators open a new window for testing gravity in strong field regime and provide new inspiration for testing possible hairs around the black hole. In this paper, taking the hairy RN black hole constructed by GD proposal Ovalle et al. (2021), which could contain electric charge and additional arbitrary hairy charge, as the central object, we investigated its optical appearance illuminated by some toy accretion models to discuss the possible probes of the two charges.
As the preparation, we first analyzed the effects of electric charge, additional hairy charge and the deviation parameter on the photon sphere and critical impact parameters. We found that as both charges increase, the photon sphere and critical impact parameters of the hairy RN black hole both decrease, but the deviation parameter enlarges them. Then, using the back ray-tracing method, we studied the photon trajectories around the hairy RN black hole and found that the charges have a significant influence on the distributions and classification of light rays. In particular, for the hairy RN black hole with larger electric charge or additional hairy charge, the widths of the lensed ring and photon ring emissions of light rays is larger, on the contrary, the one with larger deviation parameter corresponds to narrower widths of the lensed ring and photon ring emissions. This phenomena would indeed have been printed on the black hole images.
We then investigated the optical appearance of the hairy RN black holes illuminated by an optically and geometrically thin accretion disk, which is radiated in the form (14). There always exist two explicit peaks in the total observed intensity, which correspond to two bright rings in the image of the hairy RN black hole as we project the total observed intensity into a two dimensional plane. We found that hairy RN black hole with larger charge parameter () gives rings with weaker brightness, while that with larger has brighter rings. In addition, for larger charge parameter (), the central black hole shadow is smaller, but the larger deviation parameter tends to enlarge the central shadow size. Finally, we figured out the optical appearances of hairy RN black holes illuminated by a static spherical accretion. The observed intensity shows a peak at critical impact parameter, indicating that in the optical appearance of the hairy RN black hole, a bright ring enclosing a shaded region appears and the brightness becomes weaker as the impact parameter increase due to the redshift effect. Moreover, we found that as the charge parameter () increases, the ring becomes brighter but the enclosed shaded region in the center is smaller. While the stronger deviation parameter corresponds to a darker ring but larger faint illuminated region in the central of black hole images, which are completely opposite to the influence of charge parameter or .
In conclusion, we investigated the effects of electric charge , additional hairy charge and the deviation parameter on the accretion images of the hairy RN black holes in the scenario of GD proposal. Our results show that the electric charge and additional hairy charge have similar effects on the rings and images of the hairy RN black hole, while the deviation parameters show completely different influences. Thus, we discussed that one may not be able to distinguish the electric charge and additional hairy charge via the rings and images of the black hole in this scenario. Besides, there could be degeneracies in the optical appearances of the hairy RN black hole, caused by the competing effects of the charge parameters and the deviation parameter. This could also produce the undistinguished images between the hairy RN black holes and RN black holes.
The significance of the current study could exist in two aspects. From observable point, our study chooses the hairy RN black hole as a first attempt to utilize ring and image of black holes as potential probes to seek the possible distinguishing of electric charge and other charges. We hope that our study can inspire more related researches in this direction. From theoretical point, as previously mentioned, the complete background theory that generates the hairy RN black hole is unclear now, so our results may give some beneficial hints for building the background theory of hairy RN black hole from the phenomena besides for the existed thermodynamics Mahapatra and Banerjee (2023), quasinormal modes Cavalcanti et al. (2022); Yang et al. (2023a); Li (2023), strong gravitational lensing Afrin et al. (2021); Islam and Ghosh (2021); Meng et al. (2023b), precession and Lense-Thirring effect Wu et al. (2023b) and gravitational waves Zi and Li (2023).
Acknowledgements.
This work is partly supported by the Natural Science Foundation of China under Grants Nos. 12375054 and 12375055, Natural Science Foundation of Jiangsu Province under Grant No. BK20211601, and the Postgraduate Research Practice Innovation Program of Jiangsu Province under Grants Nos. KYCX22-3452 and KYCX21-3192.Appendix A Brief derivation of the hairy RN black hole via GD approach
Recently, Ovalle et al. used the GD approach to obtain a spherically symmetric metric with electric charge and additional hairy charge Ovalle et al. (2021), in which the corresponding Einstein equation is expressed by
| (19) |
The total energy momentum tensor contains two parts: is the energy momentum tensor associated with a known solution of GR and is introduced by new matter fields or a new gravitational sector. The Bianchi identity requires . In the GD approach proposed in Ovalle (2017), is always assumed to be decoupled from Contreras et al. (2021); Ovalle et al. (2021). We will review the main steps to better understand how the GD approach works in the construction of a deformed solution from a seed metric. As we will show that under the decoupling assumption, we can decouple the equations of motion for the two sectors.
Firstly, we write the static spherically symmetric solution to (19) as
| (20) |
and the corresponding Einstein tensor is denoted as . Secondly, we consider that the above solution is generated by the seed metric
| (21) |
which only sources from (i.e. ), and the introduction of additional source is equivalent to deforming the seed metric by
| (22) |
Here the parameter is introduced to keep track of the deformations. Subsequently, we can check that the Einstein equation (19) can be decomposed into the standard Einstein equation and an additional equation =, respectively. It is obvious that the tensor will vanish for the vanishing of the metric deformations. Also, under the transformation (22), the Einstein tensor will be transformed by
| (23) |
which is a linear combination, originated from two sources added linearly in the r.h.s of (19). In fact, this is the key point existing in GD approach to analytically construct the deforming metric from the seed solution.
Then, the authors of Ovalle et al. (2021) consider the seed metric (21) as the Schwarzschild one (with ), and treat the additional source as the anisotropic fluid satisfying dominant energy condition. They solve out the Einstein equation and obtain the hairy charged solution deformed from the Schwarzschild metric, and the metric for the hairy charged black hole reads as
| (24) |
This metric describes certain deformation of the Schwarzschild solution due to the introduction of additional material sources.
References
- Akiyama et al. (2019a) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 875, L1 (2019a), eprint 1906.11238.
- Akiyama et al. (2019b) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 875, L2 (2019b), eprint 1906.11239.
- Akiyama et al. (2019c) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 875, L3 (2019c), eprint 1906.11240.
- Akiyama et al. (2019d) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 875, L4 (2019d), eprint 1906.11241.
- Akiyama et al. (2019e) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 875, L5 (2019e), eprint 1906.11242.
- Akiyama et al. (2019f) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 875, L6 (2019f), eprint 1906.11243.
- Akiyama et al. (2022a) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 930, L12 (2022a).
- Akiyama et al. (2022b) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 930, L13 (2022b).
- Akiyama et al. (2022c) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 930, L14 (2022c).
- Akiyama et al. (2022d) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 930, L15 (2022d).
- Akiyama et al. (2022e) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 930, L16 (2022e).
- Akiyama et al. (2022f) K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. Lett. 930, L17 (2022f).
- Virbhadra and Ellis (2000) K. S. Virbhadra and G. F. R. Ellis, Phys. Rev. D 62, 084003 (2000), eprint astro-ph/9904193.
- Virbhadra and Ellis (2002) K. S. Virbhadra and G. F. R. Ellis, Phys. Rev. D 65, 103004 (2002).
- Virbhadra and Keeton (2008) K. S. Virbhadra and C. R. Keeton, Phys. Rev. D 77, 124014 (2008), eprint 0710.2333.
- Synge (1966) J. L. Synge, Mon. Not. Roy. Astron. Soc. 131, 463 (1966).
- Bardeen et al. (1972) J. M. Bardeen, W. H. Press, and S. A. Teukolsky, Astrophys. J. 178, 347 (1972).
- Bozza (2010) V. Bozza, Gen. Rel. Grav. 42, 2269 (2010), eprint 0911.2187.
- Luminet (1979) J. P. Luminet, Astron. Astrophys. 75, 228 (1979).
- Shen et al. (2005) Z.-Q. Shen, K. Y. Lo, M. C. Liang, P. T. P. Ho, and J. H. Zhao, Nature 438, 62 (2005), eprint astro-ph/0512515.
- Yumoto et al. (2012) A. Yumoto, D. Nitta, T. Chiba, and N. Sugiyama, Phys. Rev. D 86, 103001 (2012), eprint 1208.0635.
- Atamurotov et al. (2013) F. Atamurotov, A. Abdujabbarov, and B. Ahmedov, Phys. Rev. D 88, 064004 (2013).
- Papnoi et al. (2014) U. Papnoi, F. Atamurotov, S. G. Ghosh, and B. Ahmedov, Phys. Rev. D 90, 024073 (2014), eprint 1407.0834.
- Abdujabbarov et al. (2015) A. A. Abdujabbarov, L. Rezzolla, and B. J. Ahmedov, Mon. Not. Roy. Astron. Soc. 454, 2423 (2015), eprint 1503.09054.
- Kumar and Ghosh (2020) R. Kumar and S. G. Ghosh, Astrophys. J. 892, 78 (2020), eprint 1811.01260.
- Meng et al. (2022) Y. Meng, X.-M. Kuang, and Z.-Y. Tang, Phys. Rev. D 106, 064006 (2022), eprint 2204.00897.
- Ma and Lu (2020) L. Ma and H. Lu, Phys. Lett. B 807, 135535 (2020), eprint 1912.05569.
- Guo and Li (2020) M. Guo and P.-C. Li, Eur. Phys. J. C 80, 588 (2020), eprint 2003.02523.
- Meng et al. (2023a) Y. Meng, X.-M. Kuang, X.-J. Wang, and J.-P. Wu, Phys. Lett. B 841, 137940 (2023a), eprint 2305.04210.
- Ayzenberg and Yunes (2018) D. Ayzenberg and N. Yunes, Class. Quant. Grav. 35, 235002 (2018), eprint 1807.08422.
- Amarilla et al. (2010) L. Amarilla, E. F. Eiroa, and G. Giribet, Phys. Rev. D 81, 124045 (2010), eprint 1005.0607.
- Addazi et al. (2021) A. Addazi, S. Capozziello, and S. Odintsov, Phys. Lett. B 816, 136257 (2021), eprint 2103.16856.
- Dastan et al. (2022) S. Dastan, R. Saffari, and S. Soroushfar, Eur. Phys. J. Plus 137, 1002 (2022), eprint 1606.06994.
- Amarilla and Eiroa (2012) L. Amarilla and E. F. Eiroa, Phys. Rev. D 85, 064019 (2012), eprint 1112.6349.
- Amarilla and Eiroa (2013) L. Amarilla and E. F. Eiroa, Phys. Rev. D 87, 044057 (2013), eprint 1301.0532.
- Amir et al. (2018) M. Amir, B. P. Singh, and S. G. Ghosh, Eur. Phys. J. C 78, 399 (2018), eprint 1707.09521.
- Mizuno et al. (2018) Y. Mizuno, Z. Younsi, C. M. Fromm, O. Porth, M. De Laurentis, H. Olivares, H. Falcke, M. Kramer, and L. Rezzolla, Nature Astron. 2, 585 (2018), eprint 1804.05812.
- Eiroa and Sendra (2018) E. F. Eiroa and C. M. Sendra, Eur. Phys. J. C 78, 91 (2018), eprint 1711.08380.
- Vagnozzi and Visinelli (2019) S. Vagnozzi and L. Visinelli, Phys. Rev. D 100, 024020 (2019), eprint 1905.12421.
- Banerjee et al. (2020) I. Banerjee, S. Chakraborty, and S. SenGupta, Phys. Rev. D 101, 041301 (2020), eprint 1909.09385.
- Chowdhuri and Bhattacharyya (2021) A. Chowdhuri and A. Bhattacharyya, Phys. Rev. D 104, 064039 (2021), eprint 2012.12914.
- Konoplya and Zhidenko (2019) R. A. Konoplya and A. Zhidenko, Phys. Rev. D 100, 044015 (2019), eprint 1907.05551.
- Younsi et al. (2016) Z. Younsi, A. Zhidenko, L. Rezzolla, R. Konoplya, and Y. Mizuno, Phys. Rev. D 94, 084025 (2016), eprint 1607.05767.
- Olmo et al. (2023) G. J. Olmo, J. L. Rosa, D. Rubiera-Garcia, and D. Saez-Chillon Gomez, Class. Quant. Grav. 40, 174002 (2023), eprint 2302.12064.
- Shaikh et al. (2019a) R. Shaikh, P. Kocherlakota, R. Narayan, and P. S. Joshi, Mon. Not. Roy. Astron. Soc. 482, 52 (2019a), eprint 1802.08060.
- Joshi et al. (2020) A. B. Joshi, D. Dey, P. S. Joshi, and P. Bambhaniya, Phys. Rev. D 102, 024022 (2020), eprint 2004.06525.
- Dey et al. (2021) D. Dey, R. Shaikh, and P. S. Joshi, Phys. Rev. D 103, 024015 (2021), eprint 2009.07487.
- Rahaman et al. (2021) F. Rahaman, K. N. Singh, R. Shaikh, T. Manna, and S. Aktar, Class. Quant. Grav. 38, 215007 (2021), eprint 2108.09930.
- Kasuya and Kobayashi (2021) S. Kasuya and M. Kobayashi, Phys. Rev. D 103, 104050 (2021), eprint 2103.13086.
- Shaikh et al. (2019b) R. Shaikh, P. Banerjee, S. Paul, and T. Sarkar, Phys. Lett. B 789, 270 (2019b), [Erratum: Phys.Lett.B 791, 422–423 (2019)], eprint 1811.08245.
- Wielgus et al. (2020) M. Wielgus, J. Horak, F. Vincent, and M. Abramowicz, Phys. Rev. D 102, 084044 (2020), eprint 2008.10130.
- Peng et al. (2021a) J. Peng, M. Guo, and X.-H. Feng, Phys. Rev. D 104, 124010 (2021a), eprint 2102.05488.
- Neto et al. (2023) M. R. Neto, D. Pérez, and J. Pelle, Int. J. Mod. Phys. D 32, 2250137 (2023), eprint 2210.14106.
- Tsukamoto et al. (2012) N. Tsukamoto, T. Harada, and K. Yajima, Phys. Rev. D 86, 104062 (2012), eprint 1207.0047.
- Vagnozzi et al. (2023) S. Vagnozzi et al., Class. Quant. Grav. 40, 165007 (2023), eprint 2205.07787.
- Afrin et al. (2021) M. Afrin, R. Kumar, and S. G. Ghosh, Mon. Not. Roy. Astron. Soc. 504, 5927 (2021), eprint 2103.11417.
- Kuang et al. (2022) X.-M. Kuang, Z.-Y. Tang, B. Wang, and A. Wang, Phys. Rev. D 106, 064012 (2022), eprint 2206.05878.
- Tang et al. (2022) Z.-Y. Tang, X.-M. Kuang, B. Wang, and W.-L. Qian, Sci. Bull. 67, 2272 (2022), eprint 2206.08608.
- Tang et al. (2023) Z.-Y. Tang, X.-M. Kuang, B. Wang, and W.-L. Qian, Eur. Phys. J. C 83, 837 (2023), eprint 2211.08137.
- Kuang and Övgün (2022) X.-M. Kuang and A. Övgün, Annals Phys. 447, 169147 (2022), eprint 2205.11003.
- Kumar et al. (2019) R. Kumar, S. G. Ghosh, and A. Wang, Phys. Rev. D 100, 124024 (2019), eprint 1912.05154.
- Shaikh et al. (2021) R. Shaikh, K. Pal, K. Pal, and T. Sarkar, Mon. Not. Roy. Astron. Soc. 506, 1229 (2021), eprint 2102.04299.
- Wu et al. (2023a) W.-H. Wu, C.-Y. Zhang, C.-G. Shao, and W.-L. Qian, Chin. Phys. C 47, 085102 (2023a), eprint 2303.04907.
- Capozziello et al. (2023) S. Capozziello, S. Zare, and H. Hassanabadi (2023), eprint 2311.12896.
- Sui et al. (2023) T.-T. Sui, Q.-M. Fu, and W.-D. Guo, Phys. Lett. B 845, 138135 (2023), eprint 2311.10930.
- Pantig et al. (2023) R. C. Pantig, A. Övgün, and D. Demir, Eur. Phys. J. C 83, 250 (2023), eprint 2208.02969.
- Ghosh et al. (2023) R. Ghosh, S. Sk, and S. Sarkar, Phys. Rev. D 108, L041501 (2023), eprint 2306.14193.
- Tsukamoto et al. (2014) N. Tsukamoto, Z. Li, and C. Bambi, JCAP 06, 043 (2014), eprint 1403.0371.
- Porth et al. (2019) O. Porth et al. (Event Horizon Telescope), Astrophys. J. Suppl. 243, 26 (2019), eprint 1904.04923.
- Gralla et al. (2019) S. E. Gralla, D. E. Holz, and R. M. Wald, Phys. Rev. D 100, 024018 (2019), eprint 1906.00873.
- Dokuchaev and Nazarova (2019) V. I. Dokuchaev and N. O. Nazarova, Universe 5, 183 (2019), eprint 1906.07171.
- Peng et al. (2021b) J. Peng, M. Guo, and X.-H. Feng, Chin. Phys. C 45, 085103 (2021b), eprint 2008.00657.
- He et al. (2022) K.-J. He, S. Guo, S.-C. Tan, and G.-P. Li, Chin. Phys. C 46, 085106 (2022), eprint 2103.13664.
- Eichhorn and Held (2021) A. Eichhorn and A. Held, JCAP 05, 073 (2021), eprint 2103.13163.
- Li and He (2021) G.-P. Li and K.-J. He, JCAP 06, 037 (2021), eprint 2105.08521.
- Wang et al. (2023) X.-J. Wang, X.-M. Kuang, Y. Meng, B. Wang, and J.-P. Wu, Phys. Rev. D 107, 124052 (2023), eprint 2304.10015.
- Zeng et al. (2020) X.-X. Zeng, H.-Q. Zhang, and H. Zhang, Eur. Phys. J. C 80, 872 (2020), eprint 2004.12074.
- Saurabh and Jusufi (2021) K. Saurabh and K. Jusufi, Eur. Phys. J. C 81, 490 (2021), eprint 2009.10599.
- Zeng and Zhang (2020) X.-X. Zeng and H.-Q. Zhang, Eur. Phys. J. C 80, 1058 (2020), eprint 2007.06333.
- Qin et al. (2021) X. Qin, S. Chen, and J. Jing, Class. Quant. Grav. 38, 115008 (2021), eprint 2011.04310.
- Narayan et al. (2019) R. Narayan, M. D. Johnson, and C. F. Gammie, Astrophys. J. Lett. 885, L33 (2019), eprint 1910.02957.
- Gan et al. (2021a) Q. Gan, P. Wang, H. Wu, and H. Yang, Phys. Rev. D 104, 044049 (2021a), eprint 2105.11770.
- Gan et al. (2021b) Q. Gan, P. Wang, H. Wu, and H. Yang, Phys. Rev. D 104, 024003 (2021b), eprint 2104.08703.
- Meng et al. (2023b) Y. Meng, X.-M. Kuang, X.-J. Wang, B. Wang, and J.-P. Wu, Phys. Rev. D 108, 064013 (2023b), eprint 2306.10459.
- Boshkayev et al. (2022) K. Boshkayev, T. Konysbayev, Y. Kurmanov, O. Luongo, and D. Malafarina, Astrophys. J. 936, 96 (2022), eprint 2205.04208.
- Xavier et al. (2023) S. V. M. C. B. Xavier, H. C. D. Lima, Junior., and L. C. B. Crispino, Phys. Rev. D 107, 064040 (2023), eprint 2303.17666.
- Sakai et al. (2014) N. Sakai, H. Saida, and T. Tamaki, Phys. Rev. D 90, 104013 (2014), eprint 1408.6929.
- Bacchini et al. (2021) F. Bacchini, D. R. Mayerson, B. Ripperda, J. Davelaar, H. Olivares, T. Hertog, and B. Vercnocke, Phys. Rev. Lett. 127, 171601 (2021), eprint 2103.12075.
- Destounis et al. (2023) K. Destounis, F. Angeloni, M. Vaglio, and P. Pani, Phys. Rev. D 108, 084062 (2023), eprint 2305.05691.
- Guo et al. (2023a) S. Guo, G.-R. Li, and E.-W. Liang, Eur. Phys. J. C 83, 663 (2023a), eprint 2210.03010.
- Guo et al. (2023b) G. Guo, Y. Lu, P. Wang, H. Wu, and H. Yang, Phys. Rev. D 107, 124037 (2023b), eprint 2212.12901.
- Archer-Smith and Zhang (2021) P. Archer-Smith and Y. Zhang, Phys. Lett. B 817, 136309 (2021), eprint 2005.08980.
- Okyay and Övgün (2022) M. Okyay and A. Övgün, JCAP 01, 009 (2022), eprint 2108.07766.
- Uniyal et al. (2023a) A. Uniyal, R. C. Pantig, and A. Övgün, Phys. Dark Univ. 40, 101178 (2023a), eprint 2205.11072.
- Hou et al. (2022) Y. Hou, Z. Zhang, H. Yan, M. Guo, and B. Chen, Phys. Rev. D 106, 064058 (2022), eprint 2206.13744.
- Uniyal et al. (2023b) A. Uniyal, S. Chakrabarti, R. C. Pantig, and A. Övgün (2023b), eprint 2303.07174.
- Akbarieh et al. (2023) A. R. Akbarieh, M. Khoshragbaf, and M. Atazadeh (2023), eprint 2302.02784.
- Gao et al. (2023) X.-J. Gao, T.-T. Sui, X.-X. Zeng, Y.-S. An, and Y.-P. Hu, Eur. Phys. J. C 83, 1052 (2023), eprint 2311.11780.
- Theodosopoulos et al. (2023) D. P. Theodosopoulos, T. Karakasis, G. Koutsoumbas, and E. Papantonopoulos (2023), eprint 2311.02740.
- Zeng et al. (2023) W. Zeng, Y. Ling, Q.-Q. Jiang, and G.-P. Li, Phys. Rev. D 108, 104072 (2023), eprint 2308.00976.
- Meng et al. (2023c) K. Meng, X.-L. Fan, S. Li, W.-B. Han, and H. Zhang, JHEP 11, 141 (2023c), eprint 2307.08953.
- Liebling and Palenzuela (2023) S. L. Liebling and C. Palenzuela, Living Rev. Rel. 26, 1 (2023), eprint 1202.5809.
- Rosa et al. (2023) J. a. L. Rosa, C. F. B. Macedo, and D. Rubiera-Garcia, Phys. Rev. D 108, 044021 (2023), eprint 2303.17296.
- Rosa and Rubiera-Garcia (2022) J. a. L. Rosa and D. Rubiera-Garcia, Phys. Rev. D 106, 084004 (2022), eprint 2204.12949.
- Vincent et al. (2016) F. H. Vincent, Z. Meliani, P. Grandclement, E. Gourgoulhon, and O. Straub, Class. Quant. Grav. 33, 105015 (2016), eprint 1510.04170.
- Ovalle et al. (2021) J. Ovalle, R. Casadio, E. Contreras, and A. Sotomayor, Phys. Dark Univ. 31, 100744 (2021), eprint 2006.06735.
- Contreras et al. (2021) E. Contreras, J. Ovalle, and R. Casadio, Phys. Rev. D 103, 044020 (2021), eprint 2101.08569.
- Mahapatra and Banerjee (2023) S. Mahapatra and I. Banerjee, Phys. Dark Univ. 39, 101172 (2023), eprint 2208.05796.
- Cavalcanti et al. (2022) R. T. Cavalcanti, R. C. de Paiva, and R. da Rocha, Eur. Phys. J. Plus 137, 1185 (2022), eprint 2203.08740.
- Yang et al. (2023a) Y. Yang, D. Liu, A. Övgün, Z.-W. Long, and Z. Xu, Phys. Rev. D 107, 064042 (2023a), eprint 2203.11551.
- Li (2023) Z. Li, Phys. Lett. B 841, 137902 (2023), eprint 2212.08112.
- Islam and Ghosh (2021) S. U. Islam and S. G. Ghosh, Phys. Rev. D 103, 124052 (2021), eprint 2102.08289.
- Wu et al. (2023b) M.-H. Wu, H. Guo, and X.-M. Kuang, Phys. Rev. D 107, 064033 (2023b), eprint 2306.10467.
- Zi and Li (2023) T. Zi and P.-C. Li, Phys. Rev. D 108, 084001 (2023), eprint 2306.02683.
- Ruffini and Wheeler (1971) R. Ruffini and J. A. Wheeler, Phys. Today 24, 30 (1971).
- Yuan and Narayan (2014) F. Yuan and R. Narayan, Ann. Rev. Astron. Astrophys. 52, 529 (2014), eprint 1401.0586.
- Bromley et al. (1997) B. C. Bromley, K. Chen, and W. A. Miller, Astrophys. J. 475, 57 (1997), eprint astro-ph/9601106.
- Wang et al. (2022) H.-M. Wang, Z.-C. Lin, and S.-W. Wei, Nucl. Phys. B 985, 116026 (2022), eprint 2205.13174.
- Yang et al. (2023b) J. Yang, C. Zhang, and Y. Ma, Eur. Phys. J. C 83, 619 (2023b), eprint 2211.04263.
- Bambi (2013) C. Bambi, Phys. Rev. D 87, 107501 (2013), eprint 1304.5691.
- Ovalle (2017) J. Ovalle, Phys. Rev. D 95, 104019 (2017), eprint 1704.05899.