\journaltitle

JFP \cprCambridge University Press \jnlDoiYr2023

\doival

10.1017/xxxxx

\totalpg

References

{authgrp}

Idris TyRE: a dependently typed regex parser

Ohad Kammar Katarzyna Marek {kmarek,ohad.kammar}@ed.ac.uk University of Edinburgh, Scotland

Abstract

Regular expressions — regexes — are widely used not only for validating, but also for parsing textual data. Generally, regex parsers output a loose structure, e.g. an unstructured list of matches, leaving it up to the user to validate the output’s properties and transform it into the desired structure. Since the regex itself carries information about the structure, this design leads to unnecessary repetition.

Radanne introduced typed regexes — TyRE — a type-indexed combinator layer that can be added on top of an existing regex engine. We extend Radanne’s design, and implement a parser which maintains type-safety throughout all layers: the user-facing regexes; their internal, desugared, representation; its compiled finite-state automaton; and the automaton’s associated instruction-set for constructing the parse-trees. We implemented TyRE in the dependently-typed language Idris 2.

1 Introduction

Regular expressions are an old and well researched subject. They have become a standard way to validate or parse textual data for a class of use cases. Yet, in statically typed languages regex parsers do not have the same type-induced safety as handwritten parsers or combinator-based parsing may offer. Even though the pattern — the regex — is known at compile time, the type system takes no advantage of the information contained in the regex to constrain the result. For example, take the regex parser in the standard library of the programming language Scala 2. Parsing a string using a regex results in a tuple of matches, which the user can reshape by pattern matching. However, it is up to the user to make sure that the tuple multiplicity is correct, even though all the necessary information to check this multiplicity is provided at compile time.

Here we describe a regex parser which produces a result of a pattern-dependent type. This design eliminates errors such as tuple multiplicity mistakes. As with parser combinators, the shape of the result reflects the structure of the parser. This typing provides a level of safety both for correctness of the parser itself and correctness of the pattern. Additionally, the user can write result-data transformations, as with combinators, to obtain the desired data structure, without any repetition of the information contained in the pattern. But unlike parser combinator designs, the parser is guaranteed to be linear in time and space complexity with respect to the length of the parsed string.

This work is based on Radanne’s (2019) design of a typed regex parser. Radanne takes advantage of an existing regex engine and adds a typed layer on top of it. This layer adds a level of safety and allows for convenient data transformation. He implements this design in the OCaml programming language (Leroy et al., 1996) and uses Vouillon’s regex engine¹¹1Jérôme Vouillon’s ocaml-re is available from https://github.com/ocaml/ocaml-re ..

Idris 2 (Brady, 2021) is a new strict dependently-typed programming language. Idris 2 does not have a standard regex parser library, providing an opportunity to revisit Radanne’s design. The new design maintains type safety throughout all the layers, which makes the type constraints become an additional safety check for the parser itself.

We make the following contributions:

•

a typed instruction language for a Moore machine;
•

a compilation scheme into this machine language accompanying Thompson’s regex-to-non-deterministic finite-state automaton construction;
•

a user-facing regex literal layer that uses a type-level parser; and
•

a use-case stream editing library — sedris — that uses the new TyRE library for its search and replace operations.

The source-code for both the regex²²2TyRE is available from https://github.com/kasiamarek/tyre . and stream editing³³3Sedris is available from https://github.com/kasiamarek/sedris . libraries is publicly available.

We proceed as follows. Sec. 2 briefly presents the core functionality of the library. Sec. 3 overviews our design and how its implementation layers fit. Sec. 4 describes the regex layer and its implementation in detail. Sec. 5 describes the automata-based parser and its Moore-machine typed instruction language. Sec. 6 evaluates the library: while space and time complexity is linear w.r.t the length of the parsed stream, the size of the regex literal and its structure make the size of the parser scale non-linearly. We measure TyRE’s performance compared with Idris 2’s parser combinator library on discriminating, but pathological, examples. We also describe our experience in using TyRE when developing the stream editing library sedris. Sec. 7 surveys immediately related work. Sec. 8 concludes.

Aside.

Idris 2 is a relatively new language. To make this manuscript self-contained but brief, we explain Idris’s syntax and semantics as the need arises, formatted like so. [Uncaptioned image]

2 Library overview

TyRE provides two kinds of constructors for typed regexes: string literals, which implicitly define the shape of the output parse tree; and combinator-style regex constructors, that give a fine-grained control over the shape of the parse tree. To see TyRE’s string literals in action, we’ll look at a regex for time-stamps in the format hh:mm.

There are two related ways to use regexes:

•

matching: determining whether the string matches the regex:

match : TyRE a -> String -> Bool
•

parsing: returning a parse-tree when the string matches the regex:

parse : TyRE a -> String -> Maybe a

The type of the result parse-tree, a in both cases, is only relevant for parsing, not matching.

Aside.

Idris expects type declarations for all top-level definitions, such as match and parse. If you’re reading this manuscript in colour, we use semantic highlighting distinguishing between: defined functions or constants; bound/binding occurrences of variables; type constructors; and data constructors (not shown). [Uncaptioned image]

The following code defines a regex literal: a string encoding of the regular expression, in a variation on the standard notation present in Unix-like systems:

-- (range from 0 to 9)time1 : TyRE Unit -- v v-(matches exactly `:’)time1 = r "(([01][0-9])|([2][0-3])):[0-5][0-9]"-- ^ ^ ^(alternation of expressions)-- | (one of the characters ’0’ and ’1’})-- (smart constructor for typed regex from a string literal)

Aside.

Comments begin with a double-dash (--). [Uncaptioned image]

The comments point at the syntax with ASCII-art arrows (^,v). Regex literals match characters verbatim, with a few key characters having a special role:

•
Brackets ([]) enumerate alternatives, either through:
- –
  
  exhaustive enumeration ([01]); or
- –
  
  a character range ([0-9]).
•

Pipes (|) specify alternation between two sub-regexes; and
•

Parentheses (()) help the regex-literal parser parse the literal.

To validate a chosen string against the regex, use match:

validateTimestamp : String -> BoolvalidateTimestamp str = match time1 str

Fig. 1 includes a TyRE for parsing a timestamp into a more structured format: a pair of arbitrary precision integer value representing the hours and minutes.

-- v----------------v-(the shape of the result parse tree)time2 : TyRE (Integer, Integer)time2 = -- (map : (a -> b) -> TyRE a -> TyRE b) -- v v-(TyRE’s notation for a capture group) map f (r "([01][0-9])!" `or` r "([2][0-3])!") <*> map f (r ":([0-5][0-9])!") -- ^(or : TyRE a -> TyRE a -> TyRE a) --^((<*>) : TyRE a -> TyRE b -> TyRE (a, b)) where digit : Char -> Integer digit c = cast c - cast ’0’ f : (Char, Char) -> Integer f (c1, c2) = 10 * digit c1 + digit c2

Figure 1: A structured timestamp parser.

Aside.

Idris pairs (c1, c2) and pair types (Char, Char), like Haskell’s, use a bracketed sequence notation. The TyRE type-constructor has the structure of a Functor, providing the function map (see below). Infix operators, are either sequences of lexically-designated operator characters (<*>) or any function name surrounded by back-ticks (`or`). Idris supports where clauses for local definitions. [Uncaptioned image]

The exclamation mark (!) in this regex literal is a TyRE-specific special character that works as a typed capture group. We will produce parse-trees for sub-strings matching the sub-regexes marked with the exclamation mark, while other sub-strings will parse as the Unit value (). The regex time1 is of type TyRE Unit exactly because it has no capture groups. The TyRE library parses the string literal and computes its shape: its parse-trees’ type. Smart constructors mixed with regex literals exert fine-grained control over the shape:

•

We transform the result using the Functor instance of TyRE:

map : (a -> b) -> TyRE a -> TyRE b
•

Uniform alternation works the same as alternation, but both sub-regexes have the same shape, and the result does not track which alternative regex matched:

or : TyRE a -> TyRE a -> TyRE a

We pass the regex to parse, which returns either Just a parse tree consisting of a pair of integers, if the string matches the regex, or Nothing otherwise:

parsedTimestamp : String -> Maybe (Integer, Integer)parsedTimestamp str = parse time2 str

TyRE provides other string-parsing functions:

•

Prefix parsing: parse the longest or shortest matching prefix, depending on the greedy flag, also returning the unparsed remainder of the string:

parsePrefix : TyRE a -> String -> (greedy : Bool) -> (Maybe a, String)
•

Disjoint matching: some text processing tasks require finding all matching occurrences of a regex in a string:

disjointMatches : (tyre : TyRE a) -> {auto 0 consuming : IsConsuming tyre} -> String -> (greedy : Bool) -> (List (List Char, a), List Char)The given tyre must be consuming — only match non-empty strings, and we require a (runtime-erased) witness of type IsConsuming tyre.

Aside.

The auto argument in braces ({}) means Idris will search for this argument using a process called proof search. It follows user-defined hints, attempts visible data constructors, and prioritises bound variables of appropriate types. Idris implements type-classes by desugaring instance resolution to proof search.
•

Substitution: replace all found disjoint matches in a string:

substitute : (tyre: TyRE a) -> {auto 0 consuming : IsConsuming tyre} -> (a -> String) -> String -> StringFor example, we change the format in which the time is given in some text.

changeTimeFormat : String -> String changeTimeFormat = substitute time2 (\case (h, m) => show m ++ " past " ++ show h) -- ^-(pattern matching anonymous function)

Aside.

The keyword \case expresses an anonymous function that immediately matches on its argument.

The call changeTimeFormat "Look, it is 11:15." evaluates to "Look, it is 15 past 11.".
•

Streams: The TyRE library can be used not only for parsing strings but also for tokenizing a Stream Char using the function:

getToken : (greedy : Bool) -> TyRE a -> Stream Char -> (Maybe a, Stream Char)
Aside.

Idris Streams are infinite lazy lists.

Here is a simple lexer, tokenizing a semicolon-separated stream of digits:
getDigits : Stream Char -> Stream (Maybe Integer) getDigits = -- v-(match : Char -> TyRE ()) unfoldr (getToken True (match ’;’ *> digit)) --((*>) : TyRE a -> TyRE b -> TyRE b)-^ ^(digit : TyRE Integer)We used three smart constructors:
- –
  
  match exactly the chosen character:
  
  match : Char -> TyRE ()
- –
  
  a digit TyRE:
  
  digit : TyRE Integer
- –
  
  a regex combinator that discards the first parse-tree and returns only the second:
  
  (*>) : TyRE a -> TyRE b -> TyRE b

3 Architecture

TyRE is composed of two main parts:

•
A regex layer, which contains typed regular expressions and user-facing interface:
- –
  
  smart constructors;
- –
  
  regexes with computed/inferred shape, which we call untyped regexes; and
- –
  
  regex literals.
•

A typed Moore machine that builds the parse-tree while executing a nondeterministic finite-state automaton for the regex.

Fig. 2 depicts TyRE’s architecture. Users may construct typed or untyped regexes directly, or as regex literals, and the regex layer will translate them into the core typed regex representation. A variant of Thompson’s construction then generates a typed Moore machine, i.e., a non-deterministic finite state automaton whose transitions also emit action in a typed language of low-level routines. Given the input text, we execute this Moore machine, either reporting failure to match the regex, or a result parse tree.

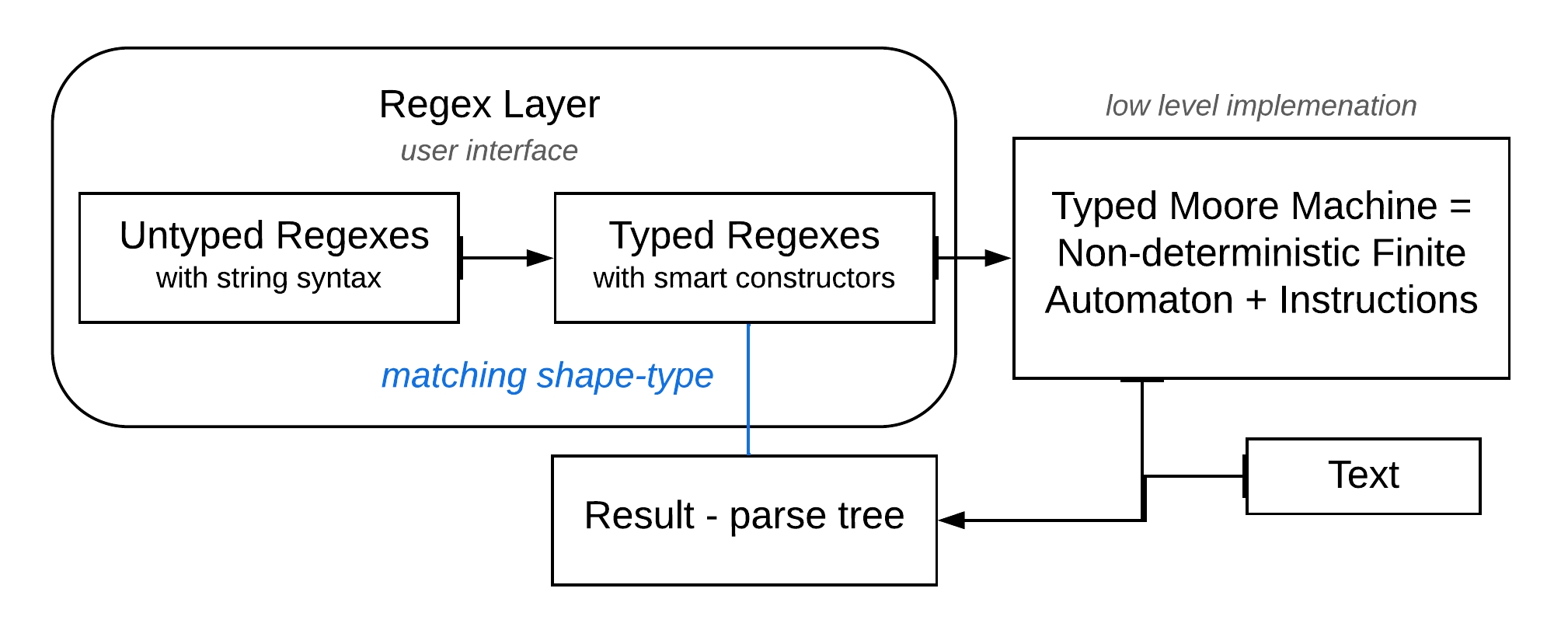
Refer to caption — Figure 2: Overview of the parser’s architecture.

Fig. 3 demonstrates the connections between the components and their responsibilities. We parse the string "A3" using r "A[0-9]!". TyRE first parses the regex string literal to a typed regex $r_{0}$ : TyRE Char. From there, we build a typed Moore machine using a variant of Thompson’s construction (McNaughton & Yamada, 1960; Thompson, 1968). Fig. 3(a) shows the resulting typed machine. It is a non-deterministic finite automaton for the regex literal "A[0-9]": the labels under the arrows are a Char-predicate determining when to take this transition. The labels over the arrows are code-routines to execute in each transition that will result in a correct parse-tree when we reach an accepting state.

We feed the Moore machine with our chosen string "A3". As we traverse the NFA, we collect parts of the parse tree on a stack⁴⁴4Although the Moore-machine uses a stack in its auxiliary state, this stack does not affect the control-flow of execution, which is governed solely by the current state and current character. Thus the model of computation is still a regular non-deterministic finite state automaton, and not a push-down automaton.. Fig. 3(b) traces the stack during the execution of this Moore machine, interleaving the current NFA state — the currently read character and the condition guarding the next transition — with the Moore machine code over this transition and its effect on the auxiliary stack. To ensure the content of the stack can produce a well-formed parse-tree, we associate to each state a stack shape. It describes what must be the shape of the stack at this point. Concretely, the stack shape is a sequence of types, describing which parts of the result parse-tree have already been constructed on the stack. We implement the stack shape by a SnocList of types. Each code-routine instruction is typed by the assumed stack shapes before and after its execution, thus its typing judgements are a form of a Hoare triple. The stack shape we associate to the unique accepting state is the singleton [< Char] : SnocList Type, matching the input shape TyRE Char. Thus a successful path through the Moore machines guarantees we can extract a parse-tree of the correct shape.

Aside.

Idris supports the following syntactic sugar for left-nested lists, where:

[< x1, x2, $\ldots$ , xn] desugars into (((Lin :< x1) :< x2) $\cdots$ ) :< xn [Uncaptioned image]

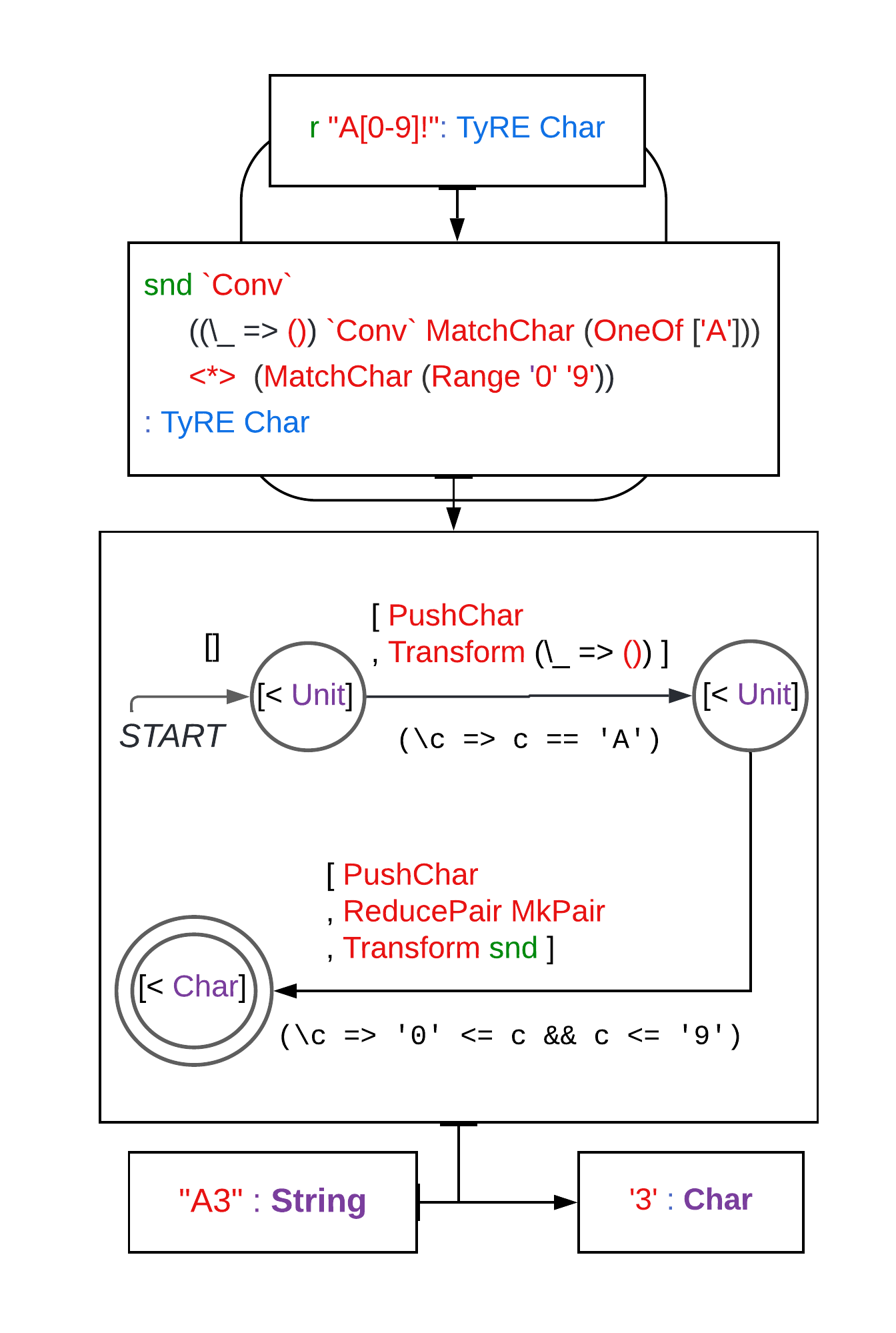
ROUTINE	STACK
	[ $<$ ]
Current character: ’A’.
Condition check: ${}^{\prime}A^{\prime}==^{\prime}A^{\prime}$
PushChar	[ $<$ ’A’]
Transform ( $\backslash\_=>$ ())	[ $<$ ()]
Current character: ’3’.
Condition check:
’0’ <= ’3’ && ’3’ <= ’9’
PushChar	[ $<$ (), ’3’]
ReducePair MkPair	[ $<$ ((), ’3’)]
Transfrom snd	[ $<$ ’3’]
Accept.

4 Regex layer

The regex layer provides the user-facing abstractions that we will now describe in detail. When users use the smart-constructor r,

•

the regex literal is parsed at compile into an
•

untyped regex (RE), whose inferred shape is also computed at compile time, and then translated into a
•

typed regex (TyRE).

4.1 Regex literals

TyRE provides string literals to create typed regexes. Taking advantage of Idris’s type-level computation we parse string literals into typed regexes at compile time. This feature both ensures that the string is a valid regex expression and calculates the type of the result parse tree. We parse regex literals in two steps. First, we parse the string literal into an untyped regex data structure (RE) using a parser combinator library⁵⁵5The formal language of well-formed regex literals is context-free, and not regular, and so we need the additional expressiveness parser combinators offer.. In the second step, we translate this untyped regex to typed ones using one-to-one mappings between parse-trees and shape simplification rules.

Table 1 shows the mapping between the string regex and RE and defines an approximation to the expected untyped regex’s shape. However, the actual regex’s shape calculation is more complex:

•

Every sub-regex that is not wrapped in the Keep constructor, marked by an exclamation mark (!) in regex literals, gets flattened into a Unit, for example:

r "((([a-z])+)!)|(hj)" has the shape Either (List Char) Unit
•
We eliminate redundancy Unit types in kept sub-regexes. Concretely, we simplify:
- –
  
  a pair of Units to a Unit;
- –
  
  a List Unit to a Nat, representing the list’s length;
- –
  
  an Either Unit Unit to a Boolean.
For example:

r"((([a-z])+)!)|(hj)" has shape List Char

r"((ab*[vkw]([a-z])+)|(hj))!" has shape Maybe (Nat, (Char, List Char))

r"((([a-z])+)!)\|(hj)" has shape	List Char
r"((ab*[vkw]([a-z])+)\|(hj))!" has shape	Maybe (Nat, (Char, List Char))

To parse regex literals at compile time, we use a copy of the parser combinator library in Idris’s standard library. In our copy of the parser combinator library, all the functions are qualified as public export. Thus the type-checker evaluates well-formed regex literals into a value of type RE.

String regex	RE	Shape	Keep Shape (KS)
r "a"	Exactly a	Unit	Unit
r "[ab]"	OneOf [’a’, ’b’]	Unit	Char
r "[a-c]"	To ’a’ ’c’	Unit	Char
r "."	Any	Unit	Char
r "AB"	Concat A B	(Shape A, Shape B)	(KS A, KS B)
r "A $\|$ B"	Alt A B	Either (Shape A) (Shape B)	Either (KS A) (KS B)
r "A?"	Maybe A	Maybe (Shape A)	Maybe (KS A)
r "A*"	Rep0 A	List (Shape A)	List (KS A)
r "A+"	Rep1 A	List (Shape A)	List (KS A)
r "A!"	Keep A	KS A	KS A

Table 1: Regex literal syntax, RE and associated shape

Aside.

Idris’s definitions have visibility qualifiers:

•

export: client modules can use the definition with its associated type;
•

public export: client modules types can also rely on the body of this definition;
•

private (the default): client modules may not refer to this definition directly.

4.2 Typed Regexes

Typed regexes express the parse-tree shape explicitly. For a typed regex of type TyRE a the result of parsing will be a parse tree of type a or nothing (Maybe a). Fig. 5 defines the TyRE data structure. It has constructors of two kinds.

The first kind are the usual Kleene-algebra operations: empty string regex, conditional character regex — where Fig. 4 defines the operations on single-character conditional, concatenation, alternation and repetition. There is no constructor for an empty language. We can express the empty language by passing an impossible predicate to the CharPred constructor, e.g. CharPred (Pred (\ _ => False)).

The second kind of constructors manipulate the parse-tree shape without changing the regex. The Conversion constructor transforms the parse-tree according to the given function. It is this constructor that allows us to implement the Functor TyRE instance we mentioned in Sec. 2. The Group constructor forgets the parse-tree shape and will result in simply returning the sub-string of matching characters. By forfeiting structured-parsing, we replace regex parsing with regex matching. Matching enables automata minimisation techniques, resulting in faster parsers.

data CharCond : Type where ||| Matches if the character is contained in the set OneOf : SortedSet Char -> CharCond ||| Matches if the character is in the range (inclusive) Range : (Char, Char) -> CharCond ||| Matches if the character matches the predicate Pred : (Char -> Bool) -> CharCond

Figure 4: Single character conditionals.

data TyRE : Type -> Type where ||| Regex for an empty word (epsilon) Empty : TyRE () ||| Single character regex MatchChar : CharCond -> TyRE Char ||| Concatenation. A word matches when it can be divided into ||| two subsequent parts matching the sub-regexes in order. (<*>) : TyRE a -> TyRE b -> TyRE (a, b) ||| Alternation. A word matches when it matches either sub-regex. (<|>) : TyRE a -> TyRE b -> TyRE (Either a b) ||| Kleene star. A word matches when it can be divided ||| into n subsequent parts each matching the argument. Rep : TyRE a -> TyRE (SnocList a) ||| Shape transformation. ||| Maintain the underlying regex, and converse the result parse-tree ||| according to the given function. Conv : TyRE a -> (a -> b) -> TyRE b ||| Forfeit structured parsing and return matched sub-string. ||| The resulting parser only collects the consumed characters. May ||| generate a smaller (= faster) parser. Group : TyRE a -> TyRE String

Figure 5: Typed Regexes

5 Moore machine

We parse by executing a typed Moore machine. Typed machine code maintains semantic invariants that may otherwise require substantial proofs to guarantee (Morrisett et al., 1999). In a dependently-typed language, it is straightforward to embed such typed machine-languages (McKinna & Wright, 2006). We divide the machine into two conceptually-distinct parts:

•

NFA: a non-deterministic finite automaton executing the matching; and
•

routines: lists of instructions labelling the transitions of the NFA, and executing these instructions along an accepting path is guaranteed to construct a valid parse-tree.

The NFA component governs be the control flow of the Moore machine, and its routines component governs the machine’s cumulative side-effects.

5.1 Abstractions

The Moore-machine layer manipulates several key programming abstractions. We describe these abstractions in this subsection, and the data types implementing them in §5.3.

NFAs.

A non-deterministic finite-state automaton over a set of input symbols $\Sigma$ — called the alphabet — is a tuple $(Q,S,q_{acc},next,P)$ consisting of:

•

$Q$ : a finite set of states;
•

$S\subseteq Q$ : a set of starting/initial states;
•

$\mathrm{acc}\in Q$ : a distinguished accepting state;
•

$next:(Q\setminus\{\mathrm{acc}\})\times\Sigma\rightarrow\mathcal{P}Q$ : a relation, the transition relation.
(We denote the power set by $\mathcal{P}$ .)

Each $q_{2}\in next(q_{1},a)$ represents a transition $q_{1}\xrightarrow{a}q_{2}$ from state $q_{1}$ to $q_{2}$ labelled by the symbol $a$ . In this formulation, the accepting state has no arrows out of it, and we disallow silent transitions, often known as epsilon transitions. This choice does not affect the class of parsers we can express. We restrict attention to automata over Characters.

Runtime model.

As we traverse the NFA, we build parts of the parse tree, collecting them on a heterogeneous stack. More precisely:

•

To ensure that the stack’s values form a valid parse-tree upon acceptance, we index types by the stack shape — a left-nested list of types, one for each stack position:

Shape : Type Shape = SnocList Type
•

We execute a pool of threads transitioning through the NFA state:

ThreadData : Shape -> Type
•

Each thread-data may record the currently matched sub-string, and maintains a stack of the partially constructed parse-tree:

Stack : Shape -> Type

Routines.

A routine is a list of instructions, each affecting the thread data. To ensure that instructions produce parse-trees of the correct type, we index each instruction, and therefore each routine, by an assumption about the stack shape before its execution and the stack shape it guarantees after its execution:

Instruction : (pre, post : Shape) -> Type -- ^---------------^

-- (stack shape before and after executing the instruction/routine) -- v---------------v Routine : (pre, post : Shape) -> TypeOne of the instructions — pushing the last-read symbol onto the stack — is not valid before the machine has consumed a symbol. We therefore also designate which instructions can execute when we initialise the machine:

IsInitRoutine : Routine xs ys -> Type

Typed Moore Machines.

Since our NFAs include a single, distinguished, accepting state, we will implement the states of the Moore machine using the Maybe type constructor, with the distinguished state Nothing representing the accepting state. We will index Moore machines by their result parse-tree type:

MooreMachine : (t : Type) -> TypeEach MooreMachine assigns expected stack shapes to each non-accepting state:

lookup : s -> Shapeand so together with the result parse-tree type t, we associate a stack shape to every state:

shapeOf : (lookup : s -> Shape) -> (t : Type) -> Maybe s -> Shape shapeOf lookup t (Just s) = lookup s -- non-accepting state shapeOf lookup t Nothing = [< t ] -- accepting state

5.2 Aside: Idris preliminaries

We need some more Idris features to discuss the Moore machine layer implementation.

Quantities.

A substantial innovation in Idris 2 (Brady, 2021) is its quantity annotations, following McBride’s (unpublished) and Atkey’s (2018) quantitative type theory. For example, we may define the following semi-erased sum type:

data EitherErased : Type -> Type -> Type where Left : ( x : a) -> EitherErased a b Right : (0 y : b) -> EitherErased a bIts Left constructor is similar to the more familiar, standard, constructor of the Either type constructor. However, the argument to its Right constructor is annotated with the quantity 0, meaning this argument will be erased at runtime. Thus, Right y is represented at runtime as a tag, meaning values of EitherErased a b have the same runtime representation as values of the type Maybe a. Idris 2 supports the quantities:

•

runtime-erased (0);
•

linear (1): the variable must be used exactly once at run-time; and
•

any (unannotated, the default): the variable may be used any number of times.

Records.

Idris 2’s records desugar into one-constructor data declarations together with projection functions for each field. For example, here is the definition of a dependent pair:

record DPair a (b : a -> Type) where constructor MkDPair fst : a snd : b fstwhich desugars⁶⁶6Agda cognoscenti might expect records to support $\eta$ -equality, meaning the judgemental equality:
rec = (MkDPair rec.fst rec.snd)
Since ordinary data declarations don’t support such $\eta$ -equality judgementally, Agda records can’t be simply desugared into single-constructor data declaractions. While Idris may in the future support $\eta$ -equality for records, it does not do so at the moment, and desugars records accordingly. into a data declaration:

data DPair : (a : Type) -> (b : a -> Type) -> Type where MkDPair : (fst : a) -> (snd : b fst) -> DPair a band two definitions, called projections, that use Idris’s post-fix notation:

(.fst) : DPair a b -> a (MkDPair x y).fst = x (.snd) : (rec : DPair a b) -> b rec.fst (MkDPair x y).snd = y Idris includes special syntax for dependent pairs, where the type:

(shape : Shape ** Stack shape)desugars into the dependent pair type:

DPair Shape (\shape => Stack shape)and the tuple of a Shape and an appropriately-shaped Stack:

([< Nat, Bool] ** [< 42, True])desugars into the dependent pair:

MkDPair [< Nat, Bool] [< 42, True]

Record fields may include quantity annotations, for example, Idris’s standard library includes records where one field is erased at runtime:

record Subset a (b : a -> Type) where constructor Element fst : a 0 snd : b fstWe will use this dependent pair to exclude some values from a given type, by requiring a dependent pair whose (.snd) field contains a proof the value is allowed. For example, the type IsInitInstruction of initialisation-safe instructions. Since this field is erased at run-time, we will only be passing around the instruction, not its safety proof.

Implicit arguments.

Idris supports two kinds of implicit arguments, which it tries to construct during elaboration:

•

Ordinary implicit arguments will be elaborated using its dynamic pattern unification algorithm (Miller, 1992; Reed, 2009; Gundry, 2013). We declare them using braces, for example, we will later define the runtime state of a thread to be the following record, namely its NFA state and associated ThreadData:
record Thread {t : Type} (machine : MooreMachine t) where constructor MkThread state : Maybe machine.s tddata : ThreadData (shapeOf machine.lookup t state)Users need only mention Thread machine, since the elaborator can deduce the expected result parse-tree type t from the type of the given Moore machine machine. Idris adopts by default two conventions for implicit arguments:
- –
  
  the keyword forall a. binds an implicit argument called a at quantity 0, trying to infer its type using unification;
- –
  
  unbound implicit arguments in type declarations are implicitly bound as implicit arguments at quantity 0 in the beginning of the declaration. This feature, which may be turned off, can produce more succinct type-declaration, similar to the ones found in languages with prenex polymorphism.
•

Proof-search implicit arguments will be elaborated, in addition to unification, by following user-declared unification hints (Asperti et al., 2009), attempting to use data/type constructors and record projections, and to plug-in bound variables. We declare proof-search implicit arguments using the auto keyword we mentioned on page • ‣ 2. For example, we will later define the Moore machines as a record with a proof-search implicit argument:

record MooreMachine (shape : Type) where constructor MkMooreMachine 0 s : Type 0 lookup : s -> Shape {auto isEq : Eq s} init : InitStatesType shape s lookup next : TransitionRelation shape s lookup The type Eq s is a record with a field for an equality-predicate on the machine’s state type s:

(==) : s -> s -> BoolBy designating a proof-search argument to the record’s constructor, the elaborator will search for values of Eq t, expressing a form of type-class resolution using proof-search implicits (Sozeau & Oury, 2008).

5.3 Implementation data types

We can now define the data-structures we use to represent Moore machines in TyRE.

Stacks.

We use heterogeneous stacks, indexed by their shape:

data Stack : Shape -> Type where Lin : Stack [<] (:<) : Stack tps -> (e : t) -> Stack (tps :< t)Thus a stack is either empty, or a snoc-cell consisting of a stack of a given shape (tps) with a value on top.

Aside.

Idris’s desugaring convention for snoc-list notation is purely syntactic⁷⁷7 If you’re reading this manuscript in colour, you might enjoy this puzzle: construct the following term so that each character has the designated semantic role: [ n , m , n ], i.e.: type constructor, bound variable, data constructor, definition, type constructor, bound variable, and data constructor, respectively. , and we can use snoc-list notation to implicitly left-nest sequences of any constructors or functions called Lin and snoc (:<). [Uncaptioned image]

Thread-local state.

The state of each thread consists of a stack indexed by the thread data’s shape, together with a bit, rec that determines whether the thread needs to record the currently parsed sub-string. In that case, the update the field dedicated to containing the characters recorded so far:

record ThreadData (shape : Shape) where constructor MkThreadData stack : Stack shape recorded : SnocList Char rec : Bool

Instruction set.

data Instruction : (pre, post : Shape) -> Type where ||| Pushes chosen symbol on the stack Push : {0 x : Type} -> x -> Instruction tps (tps :< x) ||| Pushes currently consumed character on the stack PushChar : Instruction tps (tps :< Char) ||| Reduces two last symbols from the stack ||| according to the specified function ReducePair : {0 x, y, z : Type} -> (x -> y -> z) -> Instruction (tps :< x :< y) (tps :< z) ||| Maps the top element of stack Transform : {0 x, y : Type} -> (x -> y) -> Instruction (tps :< x) (tps :< y) ||| Pushes collected string on the stack EmitString : Instruction tps (tps :< String) ||| Raises record flag and starts collecting characters Record : Instruction tps tps

Figure 6: Moore machine instruction set

Fig. 6 presents the Moore machine instructions, i.e., the instructions that may appear in labels for the NFA’s transition routines. These instructions will operate on the appropriate ThreadData record. As we traverse the Moore machine we usually collect the information about the parse tree on the stack. There is one exception to this rule. When executing the Moore machine we can enter a special mode enabled by raising the record flag using the Record instruction. When the record flag is raised, we will also record the consumed characters in the dedicated buffer recorded. The recorded characters can be pushed on the stack using the EmitString instruction, which also lowers the record flag, reverts the machine to the non-recording mode, and flushes the buffer. We will use the recording mode when creating the parse tree for a Group sub-regex. All the other instructions change the stack by either pushing onto it or transforming it. We define the predicate IsInitInstruction to include all instructions but Push.

The stack shapes pre and post that index each instruction rely on the thread’s stack to have an appropriate shape before execution, and then guarantee a given shape after execution. We can then execute an instruction on a stack with the appropriate shape by implementing a function with this type:

execInstruction : (r : Instruction pre post) -> EitherErased Char (IsInitInstruction r) -> ThreadData (p ++ pre) -> ThreadData (p ++ post)It requires either the last-read character, or a runtime-erased proof that the instruction does not require this character. It will then take a ThreadData whose stack’s top layer adheres to the instruction stack shape pre-condition, and will produce ThreadData guaranteeing the post-condition.

We label the Moore machine’s transition with routines: cons-lists of instructions, collapsing the intermediate stack shapes telescopically in their indices:

data Routine : (pre, post : Shape) -> Type where ||| Empty routine Nil : Routine shape shape ||| Prepend an instruction to a routine (::) : Instruction pre mid -> Routine mid post -> Routine pre postIt is straightforward to extend execution from instructions to routines inductively.

Typed Moore machines.

To represent the NFA abstraction from §5.1 while easing our type-safety proofs, we pair each transition in the NFA with its labelling routine. We will represent transition relations, using a list to represent the set of outgoing edges, as follows:

TransitionRelation : (shape : Type) -> (state : Type) -> (stateShape : state -> Shape) -> Type TransitionRelation shape state stateShape = (st : state) -> (c : Char) -> List (st’ : Maybe state ** Routine (stateShape st) (shapeOf stateShape shape st’))Thus, we parameterise the type of transition relations by:

•

shape: the result parse-tree type;
•

state: the type of the non-accepting NFA states; and
•

stateShape: the assumed stack-shape for each state.

Given these parameters, a transition relation, given input

•

st: starting state; and
•

c: Character

maps them to a list, representing a finite set, of transitions st ${}\xrightarrow[\text{{{\color[rgb]{1,0.42578125,0.71484375}{c}}}}]{\text{{{\color[rgb]{1,0.42578125,0.71484375}{r}}}}}{}$ st’:

•

st’: the target state, which may be the accepting state Nothing; and
•
r: the labelling routine for this transition, which assumes the stack shape associated to st and guarantees the stack shape associated to st’, given by shapeOf (cf. page 5.1):
- –
  
  When st’ is a non-accepting state Just s’, it is stateShape s’.
- –
  
  When st’ is a the state Nothing, it is the given shape.

Similarly, if we view a starting state as being the target state for a transition without a source, then we represent a subset, represented as a list, of initial states as follows:

InitStatesType : (shape : Type) -> (state : Type) -> (stateShape : state -> Shape) -> Type InitStatesType shape state stateShape = List (st : Maybe state ** Subset (Routine [<] (shapeOf stateShape shape st)) IsInitRoutine)Thus, we represent each initial state $\mathsf{Start}\xrightarrow{\text{{{\color[rgb]{1,0.42578125,0.71484375}{r}}}}}{}$ st by:

•

st: a state, which may be the accepting state Nothing; and
•

r: an initialisation routine, and so we require a runtime-erased proof that the routine contains only initialisation-safe instructions.

record MooreMachine (shape : Type) where constructor MkMooreMachine 0 s : Type 0 lookup : s -> Shape {auto isEq : Eq s} init : InitStatesType shape s lookup next : TransitionRelation shape s lookup

Figure 7: TyRE’s Moore machine type

Fig. 7 presents the TyRE’s record declaration for Moore machines. Its fields:

•

s: a runtime-erased type of non-accepting states
•

lookup: a runtime-erased association of a shape to each non-accepting state;
•

isEq: an implicit equality-predicate on non-accepting states, elaborated using Idris’s proof-search mechanism;
•

init: the initial states with their initialisation routines;
•

next: the transition relation labelled with the parsing routines;

We use the equality-predicate isEq in two places:

•

during automata minimisation; and
•

during execution, to maintain a bounded number of threads. In detail, if two threads meet in the same state, that means both have parsed the same substring and have the same paths available to them going forward. They may only differ in the parts of the parse tree constructed so far. Being in the same state means that the parse trees constructed so far must have the same shape. Since we aren’t striving to construct all the possible parse trees but return one possibility, we keep only one of such two threads going forward. Doing so ensures the number of thread is bounded by the number of states in the automaton, guaranteeing linear time and space complexity.

5.4 Thompson’s construction

McNaughton & Yamada (1960) and Thompson (1968) describe algorithms for turning a regex into an equivalent automaton. Our compilation scheme is a standard variation on these well-known constructions, augmented with code routine labels to perform the parsing. When compiling a Group sub-regex, we use a separate mechanism to build the Moore machine for regexes wrapped in a group. Figure 8 shows how we build a state machine for all TyRE constructors except Group. We describe this remaining case in §5.5.

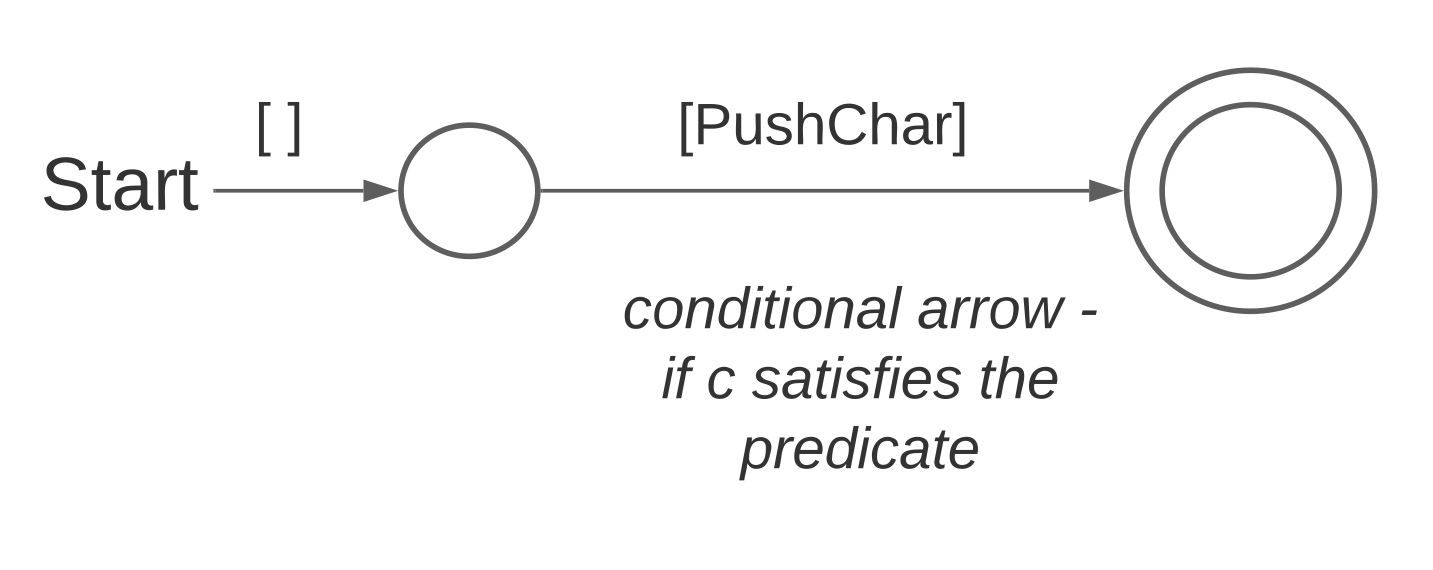
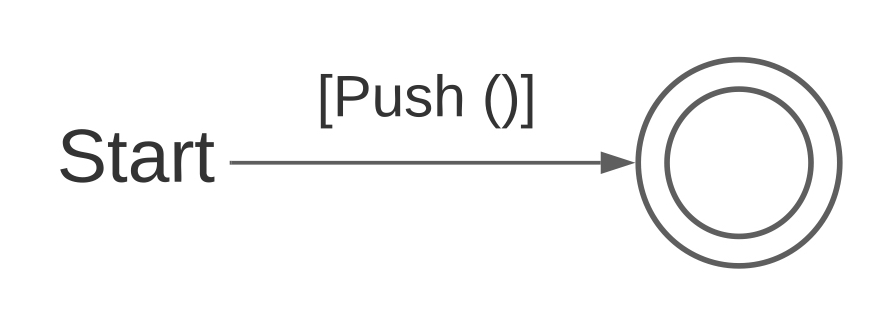
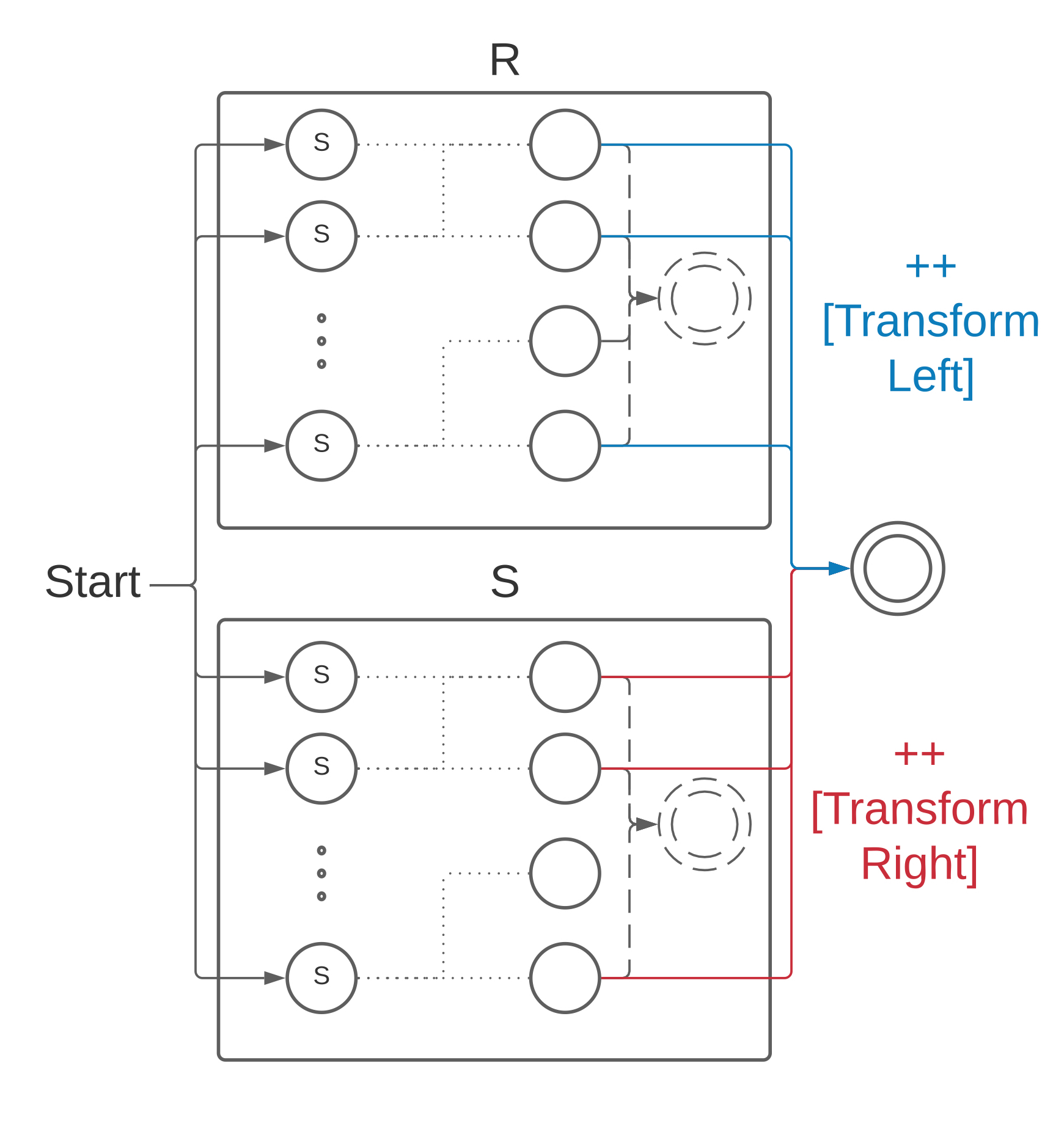
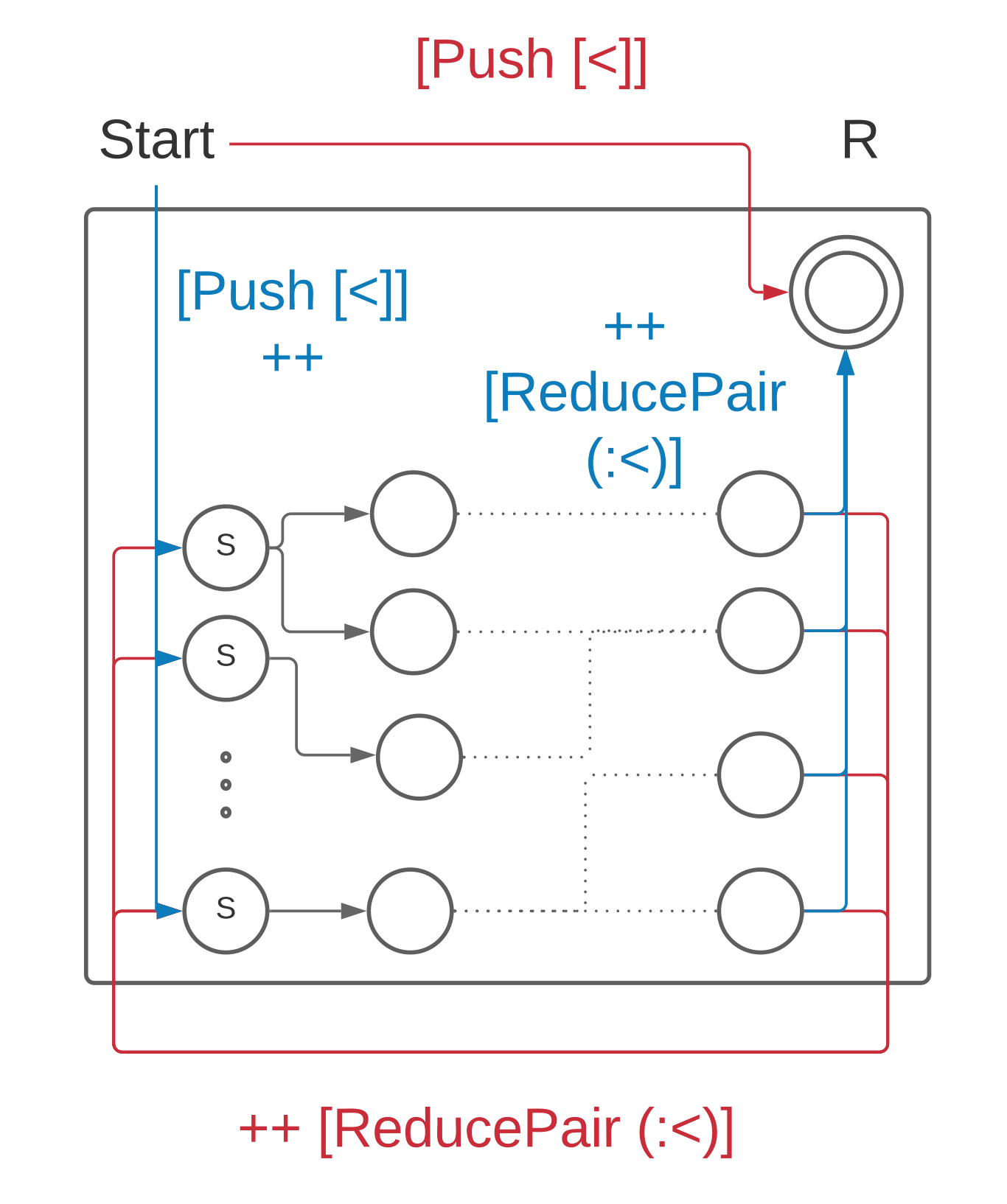
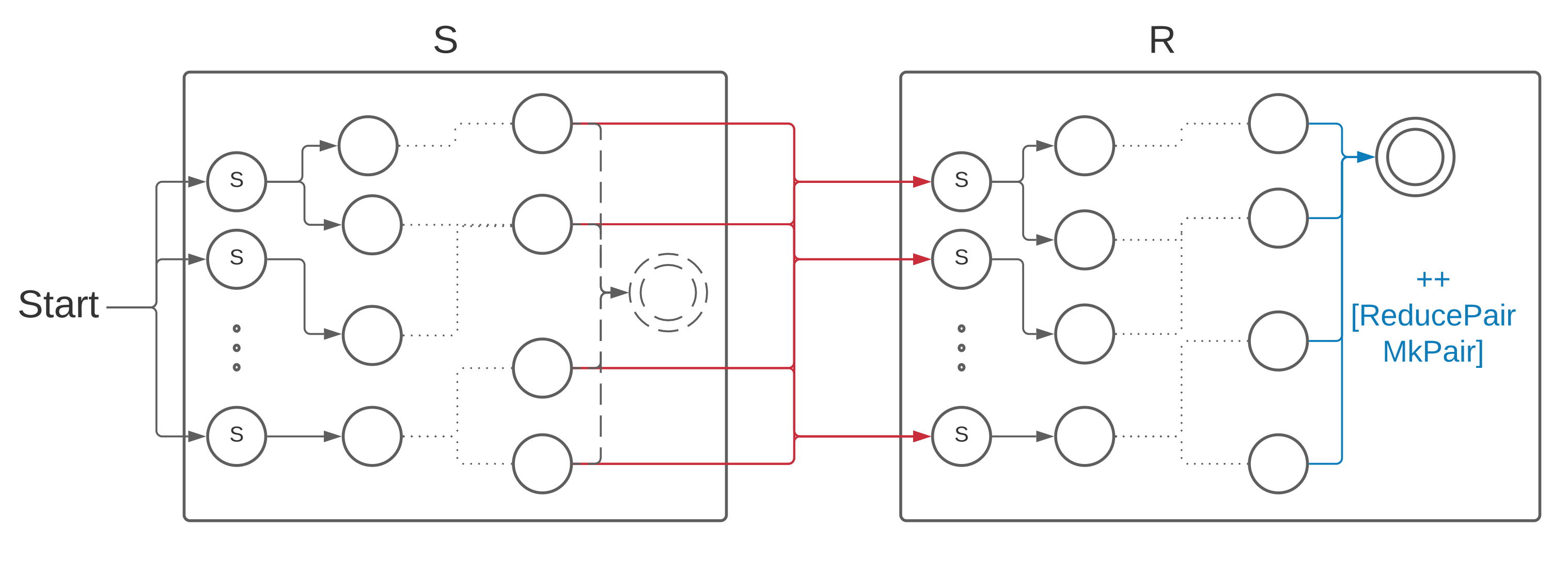
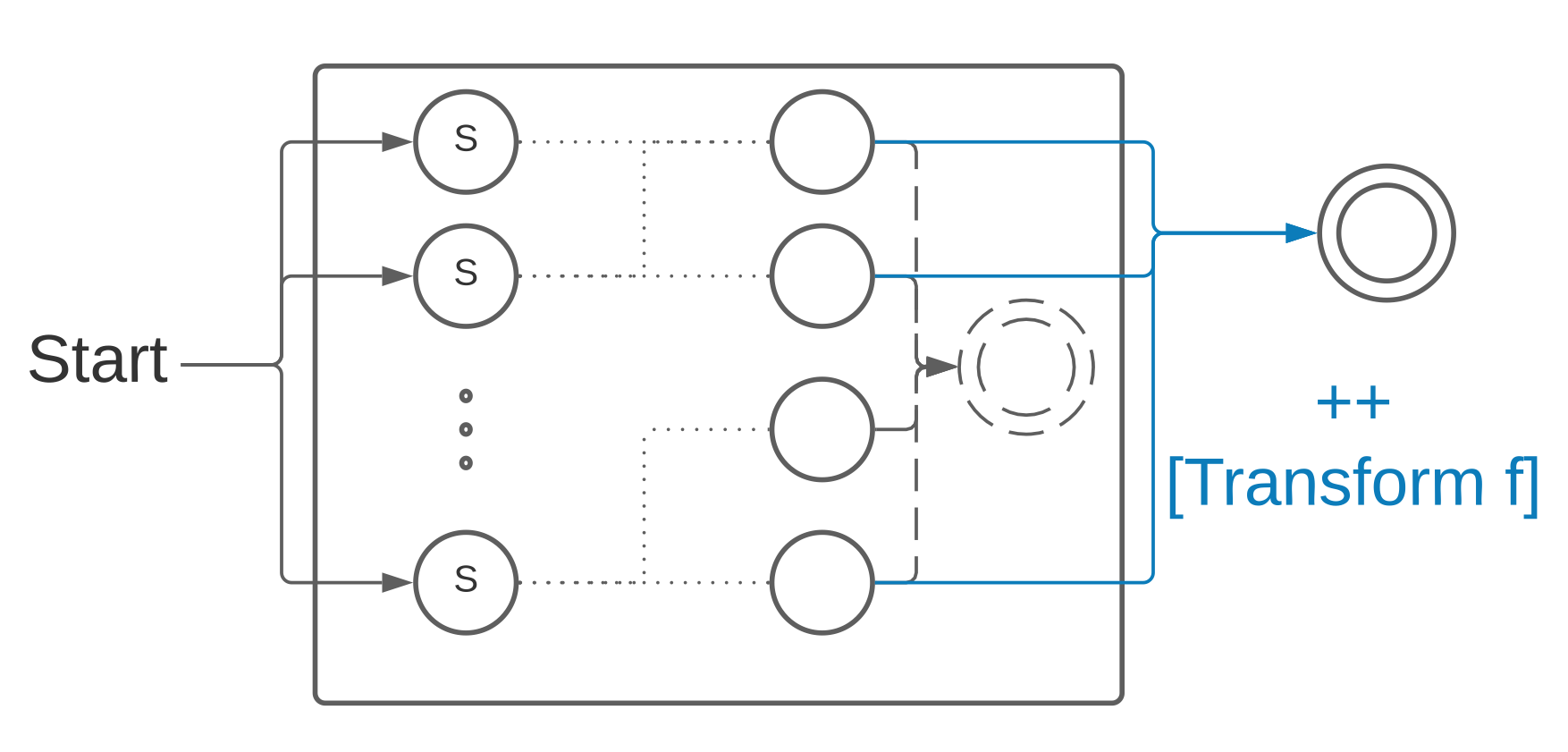
Fig. 8(a): Predicate.

The state machine accepting a language of single character words has:

•

a single start state with an empty list of initial instructions;
•

a single transition to the accepting state, guarded by the given predicate; and
•

a single instruction labelling this transition: PushChar.

We use this contruction uniformly by defining when each CharCond is satisfied:

satisfies : CharCond -> Char -> Bool satisfies (OneOf xs ) = \c => contains c xs satisfies (Range (x, y)) = \c => x <= c && c <= y satisfies (Pred f ) = \c => f c

Fig. 8(b): Empty string.

In the state machine for the Empty string $\epsilon$ , the accepting state is a starting state and the only existing state. It has a single initialisation instruction: Push ().

Fig. 8(c): Alternation.

To build a state machine for $R|S$ (Alt R S), first we build the state machines $R_{\mathrm{m}}$ and $S_{\mathrm{m}}$ for $R$ and $S$ , respectively. The starting states in the alternation state machine will be the union of the starting states from both $R_{\mathrm{m}}$ and $S_{\mathrm{m}}$ . We will keep all the transitions and merge the accepting states into a single one, so to get to the accepting state we traverse either $R_{\mathrm{m}}$ or $S_{\mathrm{m}}$ . We track which one we have traversed and lift collected parse tree to the Either type for all the transitions from $R_{\mathrm{m}}$ to the accepting state. To do so, we add a Transform Left instruction at the end of the routine, and, similarly, a Transform Rigth instruction for transitions from $S_{\mathrm{m}}$ to the accepting state.

Fig. 8(d): Kleene star.

We start building a state machine for $R^{*}$ (Star R) by building the state machine $R_{\mathrm{m}}$ for $R$ . The starting states in the new state machine are the starting states from $R_{\mathrm{m}}$ together with the accepting state. We prepend a Push [<] instruction to each initialisation routine, pushing an accumulating empty SnocList on the stack. Thus, if we go straight to the accepting state the parse tree will be the empty SnocList. We keep all the transitions from the prefix parser $R_{\mathrm{m}}$ . For each transition into the accepting state, we:

•

add a (potentially new) transition back to the starting states; and
•

for both the existing and new transitions, append a ReducePair (:<) instruction to the routine, pushing the newest $R$ -parse tree on the accumulating SnocList.

Fig. 8(e): Concatenation.

To build a state machine for $RS$ (Concat R S) we start by building the state machines $R_{\mathrm{m}}$ and $S_{\mathrm{m}}$ for $R$ and $S$ , respectively. The starting states in the state machine for concatenation will be the starting states from $R_{\mathrm{m}}$ . We keep all the transitions from $R_{\mathrm{m}}$ , except for the ones that lead to the accepting state. For each of these latter transitions, we also add new transitions to each of the starting states from $S_{\mathrm{m}}$ , leaving all the $S_{\mathrm{m}}$ unchanged. So now we will first traverse $R_{\mathrm{m}}$ and then $S_{\mathrm{m}}$ , and at the end the top of the stack will contain a parse tree for $R$ and a parse tree for $S$ . We combine them by prepending a ReducePair MkPair instruction to each routine label.

Fig. 8(f): Conversion.

The state machine for the conversion operation (Conv $R$ f) is the machine for $R$ , with a Transform f instruction appended to each accepting transition.

An optimization.

Often, when recursively constructing the Moore machine we add an instruction at the very end of an existing routine. This happens for <|>, <*>, Rep, and Conv. On the other hand we add an element to the begining of a routine only for Rep (initial [Push [<]]). Adding to the end of a list requires traversing the whole list, which is suboptimal. For this reason we actually use snoc-list accumulators for routines while constructing the Moore machine, ensuring the pre and post stack-shapes of their constituent instructions are aligned, and reverse the lists into Routines for execution.

5.5 Group Minimization

For a typed regex Group a the shape of the parse tree is a String. The corresponding state machine is then a regex matcher rather than a parser. We take advantage of this property and create a completely separate mechanism for building a state machine for groups. First we build an NFA; then we perform some optimizations that shrink the NFA; and at last we build a MooreMachine String from the NFA.

In the deterministic case, automata minimisation can be solved efficiently (Hopcroft, 1971). However, in the non-deterministic case, Jiang & Ravikumar (1993) show that NFA minimisation is hard. Specifically, they show it is pspace-complete. We therefore use some simple heuristic to minimise the NFA, and we leave to future work the task of implementing optimal minimisation, such as Kameda & Weiner’s algorithm (1970).

We build the NFA using a variant of Thompson’s construction for our type of NFA. This is the same construction as used for building Moore machine for other typed regexes, but without the routines. To represent an NFA here we use a dedicated data structure, which has a list of the starting states and a mapping, for each state, of a list of pairs consisting of:

•

a neighbouring state in the automaton; and
•

a CharCond character-predicate guarding the transition to this neighbouring state.

This is a simplification to a normal NFA, grouping the transition relation by the target state.

Optimizations.

We shrink the size of the NFA by merging states that have the same outgoing transitions, meaning that under the same condition we get the same set of next states. We repeat this operation until there are no more states that can be merged. We compare conditions by comparing the constructor and arguments. Mind that we compare only the arguments in OneOf and Range, but we cannot compare functions passed to Pred, thus we always assume them to be different. This choice can be optimised in the future using more efficient data structures such as binary decision diagrams (Lee, 1959).

Building a Moore machine from the NFA.

We build a state machine from the NFA. Each state, except the accepting state, has the shape [<]. We define the following code routines:

•

We initialise each starting state with the routine [Record]
•

We label all the transitions leading to the accepting state with [EmitString].
•

If the accepting state is a starting state, we initialise it with [Record, EmitString].
•

We label all other transitions with the empty routine [].

6 Evaluation

We evaluate the TyRE library in two ways. Our first evaluation is a quantitative comparison with the existing parser combinator library and whether and how the TyRE design improves the state-of-the-art in the Idris 2 ecosystem. We use pathological tests that emphasise performance trade-offs between TyRE and Idris 2’s parser combinator library. Our second evaluation is qualitative, reporting on our experience using TyRE as part of a bigger application: a stream editing library.

6.1 Comparing TyRE with Idris 2 parser combinators

Since Idris 2 has no existing regex parser library, we evaluate TyRE by comparing it with Idris 2’s standard parser combinator library. Idris 2’s standard parser combinator library parses context free languages, making it more powerful than a regex parser, although without the same run-time complexity guarantees.

We have compared run-time for both TyRE and Idris 2’s standard parser combinator library for equivalent regex parsers and the same inputs, for four pathological example regexes. These pathological examples highlight the strengths and weaknesses of the two libraries. Note that in the examples in which we increase the size of the regex along the horizontal axis, the resulting NFA is larger, and TyRE’s run-time scales non-linearly. For a fixed regex, execution is guaranteed to be linear in the size of the parsed string.

We ran⁸⁸8We used an Intel Core i7 8700 3.2 2666MHz 6C, 65W CPU with 32GB (2x16GB) DDR4 2666 DIMM RAM and 7200RPM SATA-6G ROM. the test files from a Python program, timing the execution for each input size from the moment we supply the input until the parser produces output. Each measurement for each input size consists of 20 samples.

Figure 9 compares parsing times for the parser combinator library and TyRE. On each chart, we plot the mean execution time for Idris 2 stdlib parser combinators (orange) and for TyRE (blue). We add a fainter band of the same colour, whose magnitude is $1$ standard deviation of the sampled run-time for this input size to each side.

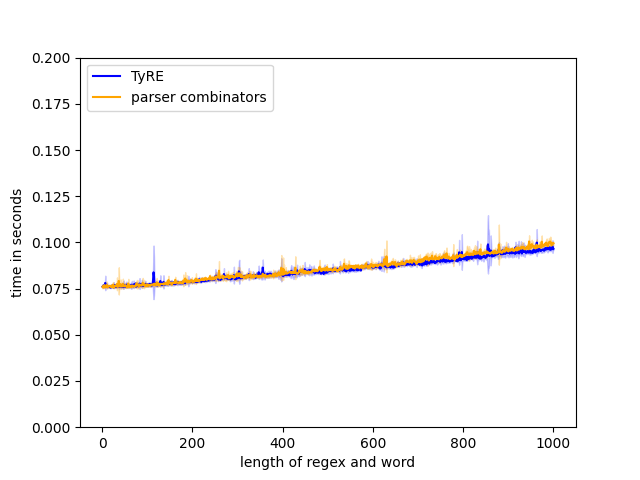
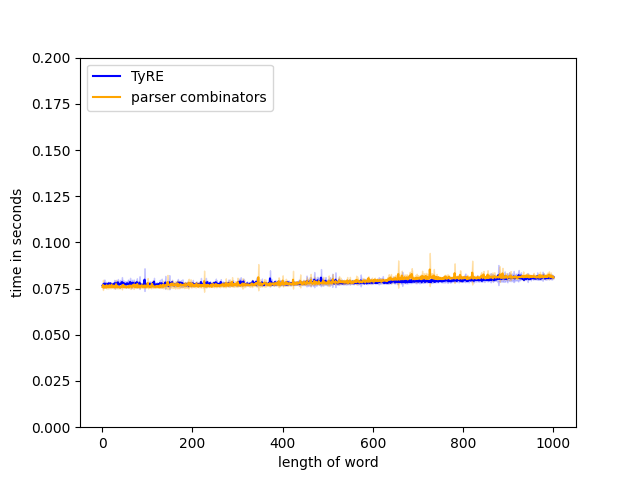
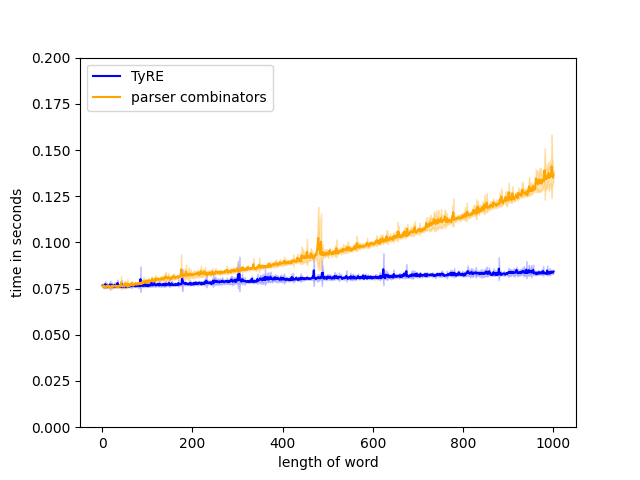
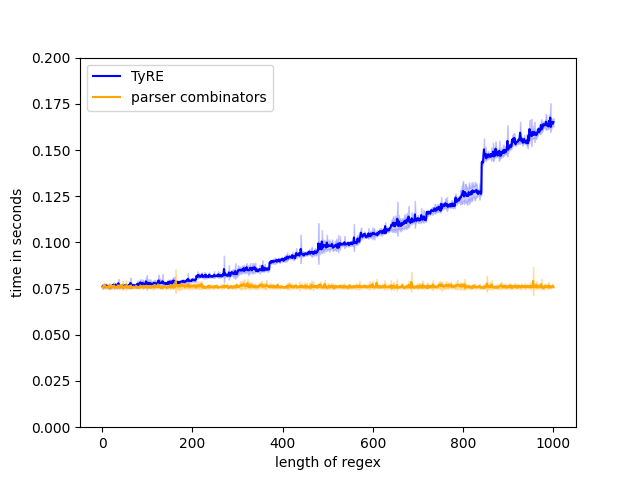
Figure 9(a): regex: $a^{n}$ parsee: $a^{n}$ .

We compare the times for parsing a string of $n$ consecutive $a$ ’s with a the regex $a^{n}$ for $n$ from $1$ to $1000$ . The execution times are similar for both libraries and approximately linear with respect to the length $n$ of the regex and string. Since at each step there is only one possible next state, TyRE maintains a single thread as it traverses the Moore machine. Similarly, the parser-combinator parser consume characters one by one without any need for backtracking.

Figure 9(b): regex: $a*$ parsee: $a^{n}$ .

Here we parse the same family of strings $a^{n}$ , but uniformly with the regex $a*$ . Again both libraries run in approximately linear time with respect to $n$ and the execution times are similar across the two libraries.

Figure 9(c): regex: $((ac)|a)b$ parsee: $a^{n}b$ .

In this test TyRE scales better than Idris 2’s parser combinator library. The parser that we built with parser combinators will always first choose the left branch when presented with alternation, which for this example is always the incorrect choice. This example thus forces the parser to backtrack repeatedly, resulting in a quadratic complexity. TyRE searches both branches simultaneously. Thanks to the trimming of the search space by merging threads, TyRE maintains only a constant number of threads resulting in the linear complexity.

To highlight TyRE’s limitations, here is a pathological case for TyRE:

Figure 9(d): regex: $a(|a)^{n-1}$ parsee: $a$ .

TyRE searching all possibilities at once is not always the best option. Here, we parse a single character word $a$ with $a(|a)^{n-1}$ . The parser that we built with parser combinators parses this string in an almost constant time. It chooses one of the possible branches and quickly finds a match for the single character. On the other hand, TyRE creates $n$ threads for each possible path and creates a parse tree for each one. Because each choice is encoded by the Either type, the built parse tree has up to $O(n)$ -many Either constructors. This simultaneous traversal results in the quadratic execution time of TyRE in this test.

This example is however pathological, and we created it by meta programming the regex and its associated type. Figure 10 evaluates three workarounds for this issue. We repeat (blue) the evaluation from Figure 9(d): an unbalanced spine of regex alternations.

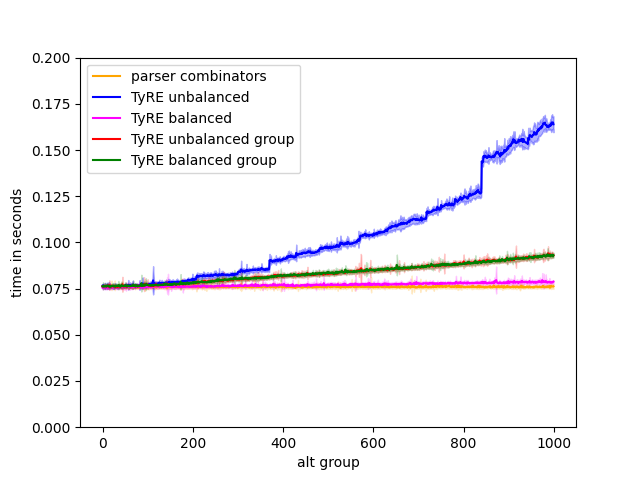
We can instead balance the alternation in the regex to get shorter encoding of the chosen branch. For example, for $n=8$ :

$\left(\left(a\mathbin{|}a\right)\mathbin{|}\left(a\mathbin{|}a\right)\right)\mathbin{|}\left(\left(a\mathbin{|}a\right)\mathbin{|}\left(a\mathbin{|}a\right)\right)$ instead of $\left(\left(\left(\left(\left(\left(a\mathbin{|}a\right)\mathbin{|}a\right)\mathbin{|}a\right)\mathbin{|}a\right)\mathbin{|}a\right)\mathbin{|}a\right)\mathbin{|}a$ .

This balancing (magenta) improves the runtime to O( $n\log n$ ). This improved performance is slower than the non-backtracking parser combinator counterpart (orange).

An easier ‘fix’ is to disregard tracking the matching alternative. We apply the ignore smart constructor to the regex, which applies the Group constructor to the resulting TyRE. Grouping the unbalanced regex (red) improves the parsing time significantly. This grouping means that the NFA will be minimized and all the alternations will collapse into a single path. However, grouping the balanced regex (green) degrades its performance in this case. This visible overhead is the cost of minimization, where at one point or another during NFA traversal we compare each state with all the other ones, again getting a flatter quadratic slope. The real benefit of the Group constructor is in minimizing the NFA automatically, staging the minimized NFA and reusing it.

More qualitatively, a big difference for users in practice is the interface to both libraries. To support regex literals, TyRE only parses character strings, whereas the parser combinator library is much more generic. On the other hand, writing even a simple regex matcher with the parser combinator library requires the user to define more entities, e.g. a set of tokens and a lexer. In fact, Idris 2’s stdlib supports a copy of the parser combinator library for dealing solely with strings for this reason. In addition, the interface to the parser combinator library, even the streamlined character string one, might be less familiar to newcomers compared to the more familiar regex literals.

6.2 Sedris

We used TyRE in a stream-editing embedded DSL — sedris. We base sedris on the GNU sed program⁹⁹9Lee E. McMahon first developed sed around 1973 (Hauben & Hauben, 1997, Ch. 9). (Pizzini et al., 2020). A sedris script is a list of commands executed from top to bottom. A script can invoke ‘file scripts’. A file script operates on a file and is executed for each consecutive line.

We demonstrate how to use sedris to rename variables in code¹⁰¹⁰10We use this example for demonstration purposes only. We do not condone the use of simple regex-based text substitution for renaming binding and bound occurrences of program variables. We firmly believe substitution ought to be done by scope-aware tools that are well-equipped for this task. We only recommend regex-based substitution in the absence of convenient scope-aware tools.. For example, in a hypothetical previous version of TyRE, we call the typed ‘Moore machine’ a ‘state machine’. We can use sedris to substitute in all the variables the substrings ‘sm’/‘SM’ — standing for state machine — to the substrings ‘mm’/‘MM’ — standing for Moore machine. For example, ‘asSM’ $\mapsto$ ‘asMM’ and ‘sm’ $\mapsto$ ‘mm’. We’ll match all the words that either end with capital ‘SM’ (endsWithSM) or begin with ‘sm’ or ‘SM’ followed by an optional string that starts with a capital letter (startsWithSM). To match only whole words our pattern must be delimited by a space. To deal with the first and last word of a line we’ll artificially add spaces on both ends of each line before matching and later strip them before writing the line to the file.

1rename : Script [<] IO2rename =3 -- TyRE for capturing the matching variables’ names.4 let tyre : TyRE (Either (Bool, String) String)5 tyre = let endsWithSM = r " `([a-z]|[A-Z])+`SM "6 startsWithSM = r " ((sm)|(SM))!`([A-Z]([a-z]|[A-Z])*)?` "7 in startsWithSM <|> endsWithSM8 -- File script performing line by line substitutions.9 fileScript : String -> FileScript [<] IO10 fileScript fileOut =11 -- for the first line clean the output file12 [ Line 1 ?> ClearFile fileOut13 -- add spaces on both ends of the line14 , > Exec (\str => " " ++ str ++ " ")15 -- replace all the matches in the line according to `toStr’16 , > Replace (AllRe tyre toStr)17 -- strip the additional spaces18 , > Exec ( fastPack . reverse19 . dropHead . reverse20 . dropHead . fastUnpack)21 -- write the line to the output file22 , > WriteTo fileOut]23 in24 -- the script with all the files for which we perform the substitutions25 [ ["SM.idr"] * fileScript "MM.idr"26 , ["SMConstruction.idr"] * fileScript "MMConstruction.idr"27 , ["SMGroup.idr"] * fileScript "MMGroup.idr"28 ] where29 dropHead : List Char -> List Char30 dropHead [] = []31 dropHead (x :: xs) = xs32 ||| A function that creates a substitution string for a match33 toStr : Either (Bool, String) String -> String34 -- `sm’ at the beginning of the name, e.g. smToNFA35 toStr (Left (True, str)) = " mm" ++ str ++ " "36 -- `SM’ at the beginning of the name, e.g. SMConstruction37 toStr (Left (False, str)) = " MM" ++ str ++ " "38 -- `SM’ at the end of the name, e.g. asSM39 toStr (Right str) = " " ++ str ++ "MM "

Figure 11: Sedris script replacing occurrences of ‘sm’ to ‘mm’.

Sedris with TyRE.

Figure 11 presents the example sedris script. The full sedris DSL is beyond the scope of this manuscript, and we explain only the relevant sedris fragments.

At the heart of sedris is the type ReplaceCommand whose values tell sedris how to replace substrings. Here (line 16) we use the following variant, which takes a TyRE to match and a substitution sending each match to its replacement string:

AllRe : (re : TyRE a) -> {auto 0 consuming : IsConsuming re} -> (a -> String) -> ReplaceCommand To guarantee productivity, AllRe also requires a proof that the TyRE is consuming, i.e., successful matches consume at least one input character.

Sedris applies these transformations by storing each consecutive line from its input in a designated pattern space. Some sedris commands only make sense in the context of such line-by-line processing, and so we index commands by the following type:

data ScriptType = Total | LineByLine More sophisticated sedris commands may bind and refer to sedris variables — which we will not discuss here. We index commands by their relationship to the variables in context: their scope, whose type is Variables — a SnocList of Variables; and the List of Variables that they bind. Some commands assume they interact with a file in memory or on disk, and we express this type of assumption using the type FileScriptType. Thus, sedris indexes its Command type by four arguments:

data Command : (scope : Variables) -> (binding : List Variable) -> ScriptType -> FileScriptType -> Type We call replacement commands such as AllRe (line 15) with the Replace constructor:

Replace : ReplaceCommand -> Command sx [] st iowhose indices express the following guarantees:

•

sx: the command assumes nothing about its enclosing variable scope, and so this command is valid in any scope;
•

[]: the command does not bind any new variables;
•

st: this command may appear in any script type; and
•

io: this command may interact with any kind of file.

Sedris file scripts may also invoke arbitrary Idris string transformations (lines 14 and 18):

Exec : (String -> String) -> Command sx [] st io

We write the pattern space out to a file with the following command (line 22), which requires the file script’s stream to support output:

WriteTo : {0 t : FileScriptType} -> {auto isIO : NeedsIO t} -> IOFile -> Command sx [] LineByLine t

We can create a new output file/delete an existing output file’s contents in preparation for writing to it line-by-line (line 10):

ClearFile : {0 t : FileScriptType} -> {auto isIO : NeedsIO t} -> IOFile -> Command sx [] LineByLine t As we compose commands into file scripts, we can contextualise some of them to only take effect in specific addresses:

•

explicitly given line numbers;
•

explicit line ranges;
•

lines that match a regex guard — given by a TyRE; or
•

the last line in the file.

We specify an address by tagging the command with it:

data CommandWithAddress : (scope : Variables) -> (binding : List Variable) -> FileScriptType -> Type where (>) : Command sx ys LineByLine t -> CommandWithAddress sx ys t (?>) : Address -> Command sx [] LineByLine t -> CommandWithAddress sx [] t In our example, we only clear the output file on the first line of the input file (line 12) and we use the Line address constructor. All other file script commands apply every line.

We compose these potentially contextualised commands together to form scripts that apply to a file using ornate lists:

data FileScript : Variables -> FileScriptType -> Type where Nil : FileScript sx t (::) : CommandWithAddress sx ys t -> FileScript (sx <>< ys) t -> FileScript sx t The cons constructor (::) uses the ‘fish’ operator — the action of Lists on SnocLists:

(<><) : SnocList a -> List a -> SnocList aA script comprises of ScriptCommands:

data ScriptCommand : (scope : Variables) -> (binding : List Variable) -> FileScriptType -> Type For example, we apply a file script to a file using this constructor:

(*) : List IOFile -> FileScript sx IO -> ScriptCommand sx [] IO We compose top-level script commands into scripts using another type of ornate lists:

data Script : Variables -> FileScriptType -> Type where Nil : Script sx t (::) : ScriptCommand sx ys t -> Script (sx <>< ys) t -> Script sx t

Experience report.

When writing this small sedris script, we had no issues with expressing the desired substitution using TyRE. Seeing that the computed regex type matches the expected one gave us confidence in the pattern. Later, when writing the toStr function, we used type-driven style, interactively covering all the cases.

There were two inconvenient aspects to TyRE. First, the lack of special marks matching end or beginning of a string in TyRE tokens. Such tokens are a common extension in regexes engines. In this case they would have allow us to skip artificially adding spaces on both sides of each line. Second is the number of brackets needed in the pattern. For example, in "((sm)|(SM))!" all the brackets are needed, because in TyRE alternation and concatenation have the same precedence, though commonly concatenation binds stronger.

7 Related work

Our work is based directly on Radanne’s tyre design (2019). Radanne presents a typed regex layer that can be added on top of an existing regex parser to ensure safety. He implements his design in the OCaml tyre library. We extend his work by ensuring type safety throughout the layers, including our custom regex engine. An feature in Radanne’s design that we have excluded is the parse-tree unparsing. To support unparsing, we can use Radanne’s original Conversion constructor that has bi-directional conversion functions.

Other work also ensure safety for regex matching by adding a safety layer for an existing regex engine. Spishak et al. (2012) implement a type system for regular expressions in Java. The type system checks the validity of a regex statically and ensures the correct number of capture group results, eliminating an ‘IndexOutOfBoundsException’ exception. The implementation is available as a part of the Checker Framework – a plugin for the JVM. Blanvillain (2022) provides similar safety guarantees while also lifting possible null’s coming from optinal parts into an Option type. Blanvillain takes advantage of Scala 3’s match types (Blanvillain et al., 2022) to perform the neccassary type level computation. Nair (2021) takes a similar approach in the Typescript ‘typed-regex’ library which provides a safety layer for an existing regex engine. This design uses conditional types (Typescript Handbook, 2023) for type level computation. This libary provides named capture groups, and it guarantees to return a directory with the relevant names.

Weirich (2017-2018) implements a type-safe regex parser in Haskell. While her work is a proof of concept that aims to show possible uses of dependent types in Haskell, her aims are similar to ours. Her implementation uses Brzozowski derivatives for matching. Cheplyaka (2011–2022) implements ‘regex-applicative’, a Haskell type-safe regex parser. It uses parser combinators, allowing for an easy transformation of the result. It does not yet support regex string literals.

Willis et al. (2022) implement Oregano, a typed regex parser in Haskell. Like our implementation, Oregano parses using a typed Moore machine with a heterogenous stack. Oregano implements the Moore machine by generating a function that guarantees to return the correct shape, rather than an explicit virtual-machine implementation. One concrete difference is that TyRE removes duplicate threads that meet in the same state and thus ensures linear performance. In comparison, Oregano implements a backtracking parser, and counts all possible ambiguous results. Oregano also uses more advanced staging techniques to improve performance.

While TyRE is type safe, its types do not ensure neither:

•

soundness: only matches return a parse-tree;
•

completeness: all matches will parse correctly.

We believe our design is not far from achieving soundess of parsing for core untyped regexes. If we deleted the ‘Group’ constructor and the condition for character predicates changed to matching exactly one character, we believe we could implement unparsing for core untyped regexes and prove soundness. For implementations of certified regex parsers that do not focus on performance, see Firsov & Uustalu (2013), Ribeiro & Du Bois (2017), and Lopes et al. (2016).

8 Conclusion and further work

We described a typed regex parser library. Using dependent types we take advantage of the information in regex patterns at compile time to create additional safety layers, both facing users and at the level of the state machine. Static analysis of regex literals to validate the literal is well-formed and compute its result type has been recently a subject of interests (Blanvillain, 2022; Spishak et al., 2012; Willis et al., 2022; Nair, 2021). Often, the safety checks are bolted onto an untyped parser. We maintain the parse-tree shape as an intrinsic characteristic of the built parser.

Interestingly, such powerful type system characteristics as dependent types are not necessary to provide all of these guarantees. Haskell’s Oregano parser (Willis et al., 2022) monitors the result type. It seems type-level computation, extensive preprocessing or macro capabilities, or bespoke language support seem necessary to support regex literals with static guarantees. Finally, as we traverse the NFA in TyRE, when two threads are in the same state we merge them. This kind of analysis uses a deep-embedding of the typed NFA, which is particularly straightforward with dependent types. This optimisation is an important performance improvement, that guarantees linear time parsing for all patterns.

There are many possible extensions to this work. First, we could prove soundness or even completeness of the parser. We conjecture soundness to be straightforward to achive with our architecture under some restriction. These would exclude user-defined transformations, groups, and non-equality predicates on characters. We would keep proofs in the parse tree that the character satisfies the predicate. As a consequence, the parse tree itself would almost be the soundness proof. We would only have to prove additionally that the parse tree really represents the input word. This fact should naturally follow from the Moore machine construction. Achieving completeness would require much more effort. Not only we would have to prove that if there is no accepting path in our Moore machine, then the word doesn’t match the pattern, but also that getting rid of some threads as we do doesn’t affect completeness.

There’s a useful consequence to proving soudness — it provides an unparsing feature for free. Unparsing is possible in Radanne’s design. However, we can achieve unparsing more directly. One adds a bi-directional conversion constructor for TyRE shape transformations. Then, parse trees for TyREs without uni-directional conversion support unparsing.

Finally, it could be interesing to integrate TyRE with Idris 2’s stdandard library parser combinators, both for tokenizing, and parsing, or extending the family of languages that TyRE supports to $\mu$ -regular expressions (Krishnaswami & Yallop, 2019) or nested words (Alur & Madhusudan, 2009). These extensions would allow us for bootstraping TyRE and use the integrated parser library or TyRE itself for parsing regex literals.

Acknowledgements.

Supported by a Royal Society University Research Fellowship and Enhancement Award, and an Alan Turing Institute seed-funding grant. We are grateful to Guillaume X. Allais, Edwin C. Brady, Donovan Crichton, Paul Jackson, James McKinna, Michel Steuwer, and Jeremy Yallop for helpful suggestions and fruitful discussions.

References

(1)
Alur & Madhusudan (2009) Alur, R. & Madhusudan, P. (2009), ‘Adding nesting structure to words’, Journal of the ACM 56(3), 1–43.
https://dl.acm.org/doi/10.1145/1516512.1516518
Asperti et al. (2009) Asperti, A., Ricciotti, W., Sacerdoti Coen, C. & Tassi, E. (2009), Hints in unification, in S. Berghofer, T. Nipkow, C. Urban & M. Wenzel, eds, ‘Theorem Proving in Higher Order Logics’, Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 84–98.
Atkey (2018) Atkey, R. (2018), Syntax and semantics of quantitative type theory, in ‘Proceedings - Symposium on Logic in Computer Science’.
Blanvillain (2022) Blanvillain, O. (2022), Type-Safe Regular Expressions, in ‘13th ACM SIGPLAN Scala Symposium, Preprint’.
https://github.com/OlivierBlanvillain/regsafe
Blanvillain et al. (2022) Blanvillain, O., Brachthäuser, J. I., Kjaer, M. & Odersky, M. (2022), ‘Type-level programming with match types’, Proc. ACM Program. Lang. 6(POPL).
https://doi.org/10.1145/3498698
Brady (2021) Brady, E. (2021), Idris 2: Quantitative Type Theory in Practice, in A. Møller & M. Sridharan, eds, ‘35th European Conference on Object-Oriented Programming (ECOOP 2021)’, Vol. 194 of Leibniz International Proceedings in Informatics (LIPIcs), Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Dagstuhl, Germany, pp. 9:1–9:26.
https://drops.dagstuhl.de/opus/volltexte/2021/14052
Cheplyaka (2011–2022) Cheplyaka, R. (2011–2022), regex-applicative, Gihub repository.
https://github.com/UnkindPartition/regex-applicative
Firsov & Uustalu (2013) Firsov, D. & Uustalu, T. (2013), Certified parsing of regular languages, in ‘Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics)’, Vol. 8307 LNCS.
Gundry (2013) Gundry, A. (2013), Type Inference, Haskell and Dependent Types, PhD thesis.
https://personal.cis.strath.ac.uk/adam.gundry/thesis/thesis-2013-07-24.pdf
Hauben & Hauben (1997) Hauben, M. & Hauben, R. (1997), Netizens: On the History and Impact of Usenet and the Internet, Wiley-IEEE Computer Society Pr.
Hopcroft (1971) Hopcroft, J. (1971), An $n\log n$ algorithm for minimizing states in a finite automaton, in Z. Kohavi & A. Paz, eds, ‘Theory of Machines and Computations’, Academic Press, pp. 189–196.
https://www.sciencedirect.com/science/article/pii/B9780124177505500221
Jiang & Ravikumar (1993) Jiang, T. & Ravikumar, B. (1993), ‘Minimal nfa problems are hard’, SIAM Journal on Computing 22(6), 1117–1141.
https://doi.org/10.1137/0222067
Kameda & Weiner (1970) Kameda, T. & Weiner, P. (1970), ‘On the state minimization of nondeterministic finite automata’, IEEE Transactions on Computers C-19(7), 617–627.
Krishnaswami & Yallop (2019) Krishnaswami, N. R. & Yallop, J. (2019), A typed, algebraic approach to parsing, in K. S. McKinley & K. Fisher, eds, ‘Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2019, Phoenix, AZ, USA, June 22-26, 2019’, ACM, pp. 379–393.
https://doi.org/10.1145/3314221.3314625
Lee (1959) Lee, C. Y. (1959), ‘Representation of switching circuits by binary-decision programs’, The Bell System Technical Journal 38(4), 985–999.
Leroy et al. (1996) Leroy, X., Vouillon, J. & Doligez, D. (1996), The Objective Caml system.
Lopes et al. (2016) Lopes, R., Ribeiro, R. & Camarão, C. (2016), Certified derivative-based parsing of regular expressions, in F. Castor & Y. D. Liu, eds, ‘Programming Languages’, Springer International Publishing, Cham, pp. 95–109.
McKinna & Wright (2006) McKinna, J. & Wright, J. (2006), A type-correct, stack-safe, provably correct, expression compiler in epigram.
McNaughton & Yamada (1960) McNaughton, R. & Yamada, H. (1960), ‘Regular expressions and state graphs for automata’, IRE Transactions on Electronic Computers EC-9(1), 39–47.
Mic (2023) Mic (2023), Typescript Handbook, Conditional Types.
https://www.typescriptlang.org/docs/handbook/2/conditional-types.html
Miller (1992) Miller, D. (1992), ‘Unification under a mixed prefix’, Journal of Symbolic Computation .
http://www.sciencedirect.com/science/article/pii/074771719290011R
Morrisett et al. (1999) Morrisett, G., Walker, D., Crary, K. & Glew, N. (1999), ‘From system f to typed assembly language’, ACM Trans. Program. Lang. Syst. 21(3), 527–568.
https://doi.org/10.1145/319301.319345
Nair (2021) Nair, A. (2021), typed-regex, Github repository.
https://github.com/phenax/typed-regex
Pizzini et al. (2020) Pizzini, K., Bonzini, P., Meyering, J. & Gordon, A. (2020), GNU sed: a stream editor, Free Software Foundation.
Radanne (2019) Radanne, G. (2019), Typed parsing and unparsing for untyped regular expression engines, in ‘PEPM 2019 - Proceedings of the 2019 ACM SIGPLAN Workshop on Partial Evaluation and Program Manipulation, Co-located with POPL 2019’.
Reed (2009) Reed, J. (2009), ‘Higher-order constraint simplification in dependent type theory’, ACM International Conference Proceeding Series pp. 49–56.
Ribeiro & Du Bois (2017) Ribeiro, R. & Du Bois, A. (2017), Certified bit-coded regular expression parsing, in ‘ACM International Conference Proceeding Series’, Vol. Part F130805.
Sozeau & Oury (2008) Sozeau, M. & Oury, N. (2008), First-class type classes, in O. A. Mohamed, C. Muñoz & S. Tahar, eds, ‘Theorem Proving in Higher Order Logics’, Springer Berlin Heidelberg, Berlin, Heidelberg, pp. 278–293.
Spishak et al. (2012) Spishak, E., Dietl, W. & Ernst, M. D. (2012), A type system for regular expressions, in ‘Proceedings of the 14th Workshop on Formal Techniques for Java-like Programs’, FTfJP ’12, Association for Computing Machinery, New York, NY, USA, p. 20–26.
https://doi.org/10.1145/2318202.2318207
Thompson (1968) Thompson, K. (1968), ‘Programming techniques: Regular expression search algorithm’, Commun. ACM 11(6), 419–422.
https://doi.org/10.1145/363347.363387
Weirich (2017-2018) Weirich, S. (2017-2018), Dependently-Typed Regular Expression Submatching.
https://github.com/sweirich/dth/tree/master/regexp
Willis et al. (2022) Willis, J., Wu, N. & Schrijvers, T. (2022), Oregano: Staging regular expressions with moore cayley fusion, in ‘Proceedings of the 15th ACM SIGPLAN International Haskell Symposium’, Haskell 2022, Association for Computing Machinery, New York, NY, USA, p. 66–80.
https://doi.org/10.1145/3546189.3549916

Idris TyRE: a dependently typed regex parser

Abstract

1 Introduction

Aside.

2 Library overview

Aside.

Aside.

Aside.

Aside.

Aside.

Aside.

3 Architecture

Aside.

4 Regex layer

4.1 Regex literals

Aside.

4.2 Typed Regexes

5 Moore machine

5.1 Abstractions

NFAs.

Runtime model.

Routines.

Typed Moore Machines.

5.2 Aside: Idris preliminaries

Quantities.

Records.

Implicit arguments.

5.3 Implementation data types

Stacks.

Aside.

Thread-local state.

Instruction set.

Typed Moore machines.

5.4 Thompson’s construction

Fig. 8(a): Predicate.

Fig. 8(b): Empty string.

Fig. 8(c): Alternation.

Fig. 8(d): Kleene star.

Fig. 8(e): Concatenation.

Fig. 8(f): Conversion.

An optimization.

5.5 Group Minimization

Optimizations.

Building a Moore machine from the NFA.

6 Evaluation

6.1 Comparing TyRE with Idris 2 parser combinators

Figure 9(a): regex: ana^{n} parsee: ana^{n}.

Figure 9(b): regex: a∗a* parsee: ana^{n}.

Figure 9(c): regex: ((a∗c)|a)∗b((a*c)|a)*b parsee: an​ba^{n}b.

Figure 9(d): regex: a(|a)n−1a(|a)^{n-1} parsee: aa.

6.2 Sedris

Sedris with TyRE.

Experience report.

7 Related work

8 Conclusion and further work

Acknowledgements.

References

Figure 9(a): regex: $a^{n}$ parsee: $a^{n}$ .

Figure 9(b): regex: $a*$ parsee: $a^{n}$ .

Figure 9(c): regex: $((ac)|a)b$ parsee: $a^{n}b$ .

Figure 9(d): regex: $a(|a)^{n-1}$ parsee: $a$ .