Ideal Quantum Tele-amplification up to a Selected Energy Cut-off using Linear Optics

The ability to amplify an arbitrary state in a linear, or phase insensitive, manner is useful for a wide variety of quantum protocols. Unfortunately, the uncertainty principle means deterministic linear amplification will always introduce noise, which diminishes the output state’s quantum characteristics [1, 2]. However, noiseless linear amplification (NLA) is possible for non-deterministic amplifiers, which work with some success probability $\mathbb{P}<1$ [3, 4, 5]. Applications of NLA include quantum secure communication [6, 7, 8, 9, 10, 11], quantum repeaters [12, 13, 14], entanglement distillation [15, 16], quantum sensing [17, 18, 19], and quantum error correction [20, 21].

Quantum tele-amplification protocols implement quantum teleportation [22] and NLA simultaneously. In this regard, Pegg et al. proposed a non-deterministic teleporter for low-energy states called the one-photon quantum scissor ($1$-QS), named for its ability to cut or truncate an arbitrary state up to its one-photon Fock state $|\psi\rangle\equiv\sum_{j=0}^{\infty}c_{j}|j\rangle\rightarrow\sum_{j=0}^{1}c_{j}|j\rangle$ [23]. Ralph and Lund later realised adjusting a beam-splitter in the $1$-QS modified the output state’s amplitudes $|\psi\rangle\xrightarrow{1\text{-QS}}\sum_{j=0}^{1}g^{j}c_{j}|j\rangle$ [3]. Hence, for low-energy states, the $1$-QS can also perform an ideal NLA operation $g^{a^{\dagger}a}$ up to the one-photon Fock state with $g\in(0,\infty)$ gain; this was subsequently experimentally verified [4, 5]. To overcome the low-energy limitation, it was proposed to split up the input state, before applying multiple $1$-QS in parallel [3, 4]. However, for a finite number of $1$-QS, this protocol introduces extra undesirable factors to the Fock states, distorting the output state away from the ideal. Other NLA proposals are similarly non-ideal [24, 25, 26].

Rather than multiple $1$-QS in parallel, here we propose to generalise the $1$-QS to the $n$-photons quantum scissor ($n$-QS), for any $n\in\mathbb{N}^{+}$. Previous generalisations of the QS were only for specific sizes $n\in\{1,3,7\}$ [27], and our fully generalised $n$-QS protocol contains these previous results ¹¹1See Supplemental Material at [URL will be inserted by publisher] for the details about the technical proofs for the $n$-QS operations, probability of success with improvements, fidelity of output state, comparisons with other NLA protocols, loss-tolerant entanglement distillation analysis, and experimental imperfections analysis, which includes Ref. [54, 55, 56, 57, 58, 3, 27, 51, 59, 38, 60, 61, 62, 63, 64, 65, 4, 37]. Our $n$-QS protocol is a fully scalable linear optical scheme, which can perform tele-amplification on an arbitrary state perfectly up to the $n^{\mathrm{th}}$ Fock state. Other tele-amplification proposals are restricted to specific types of input states [29]. The $2$-QS case is of particular experimental interest, as it should be immediately accessible with current technology.

In this Letter, we first describe our $n$-QS protocol, including its operational mechanism and probability of success. We show that as an NLA it can produce amplified states with fidelities that are unreachable by previous linear-optical NLA protocols. Next, we explain how the $n$-QS is also useful as a high-fidelity continuous-variable teleporter, with orders of magnitude advantages over current alternatives. We then show that the $n$-QS can be used as a loss-tolerant relay for entanglement distillation. Finally, we discuss how our scheme is tolerant to standard resource and detector imperfections, and hence remains advantageous under practical conditions.

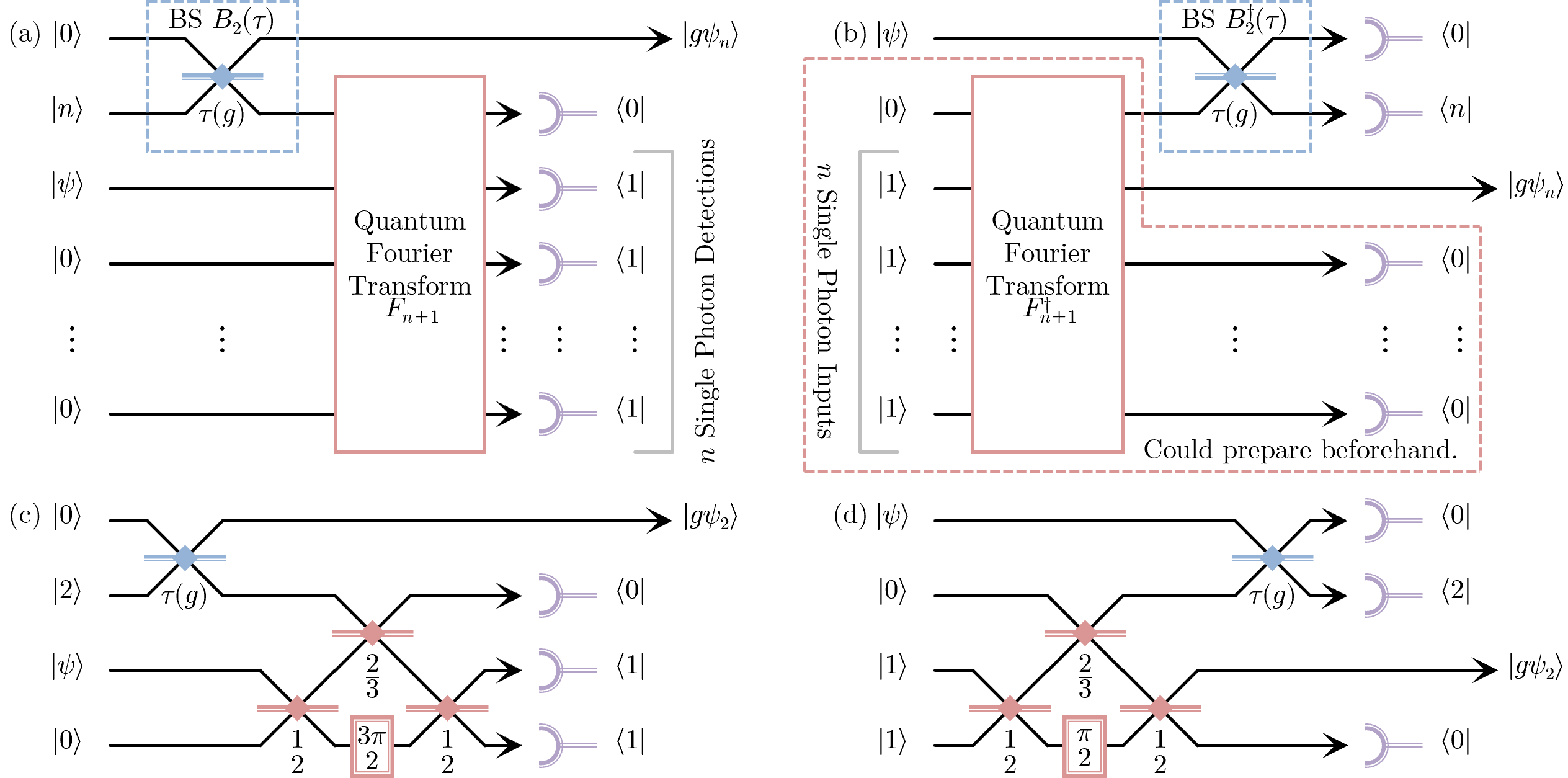
Noiseless linear amplifier.—The $n$-QS operation on an arbitrary bosonic state $|\psi\rangle$ truncates the Fock components after $n$ and performs NLA $g^{a^{\dagger}a}$ as follows

This is implemented via Fig. 1 using a beam-splitter (BS) and a fixed coherent $(n+1)$-splitter called the Quantum Fourier Transform (QFT), with $n$ extra resource photons and $n$ photon detections. The amount of amplification or de-amplification gain $g\in(0,\infty)$ can be freely chosen by setting the BS transmissivity to $\tau=g^{2}/(1+g^{2})$. The $n$-QS operation only occurs if the correct outcomes are measured. Two different architectures are shown in Fig. 1, with (a) requiring $|n\rangle$ bunched photons ($n$-QSBP or BP), while (b) requiring $\otimes^{n}|1\rangle$ single photons ($n$-QSSP or SP); we will differentiate these devices by their state resources. Due to recent experimental advances, such as in boson sampling, $n$-QSSP may be easier to implement; for example, Ref. [30] experimentally implements the QFT up to fourth order with single-photon inputs.

The action of the BS $B_{2}(\tau)$ is $a_{1}^{\dagger}\rightarrow\sqrt{1-\tau}a_{2}^{\dagger}-\sqrt{\tau}a_{1}^{\dagger}$, which describes how the photons are scattered for a given transmissivity $\tau$. Similarly, the action of an $m$ mode linear optical network $\vec{a}^{\dagger}\rightarrow U_{m}\vec{a}^{\dagger}$ is captured by an $m\times m$ unitary scattering matrix $U_{m}$. The QFT optical device has the scattering matrix $(F_{n+1})_{j,k}\equiv e^{-\frac{2i\pi(j-1)(k-1)}{n+1}}/\sqrt{n+1}$. This definition justifies the interpretation of the QFT as a coherent $(n+1)$-splitter, as it scatters photons equally amongst its $n+1$ output ports with fixed phases. An arbitrary unitary $U_{m}$ can always be decomposed into a network of at most $m(m-1)/2$ beam-splitters and phase shifts [31, 32]; however, only around half of the QFT network is needed since only the first two ports are used. As an example, we use Ref. [32] to decompose $2$-QS into a four BS network, as shown in Fig. 1 for either (c) BP $|2\rangle$, or (d) SP $|1\rangle|1\rangle$ resources. The $2$-QS is the smallest network whose useful tele-amplification properties were previously not known.

Here we will highlight the key elements which prove Fig. 1 implements the $n$-QS transformation in Eq. (1) $\forall n\in\mathbb{N}^{+}$. Firstly, one can show that $B_{2}(g)|0\rangle|n\rangle=\frac{1}{(g^{2}+1)^{n/2}}\sum_{j=0}^{n}g^{j}(-1)^{j}\sqrt{\binom{n}{j}}|j\rangle|n-j\rangle$, which already has the gain $g^{j}$ coefficients, though with unwanted $(-1)^{j}\sqrt{\binom{n}{j}}$ factors. The red dashed box in (b) produces the two-mode output $|R_{n}\rangle=\otimes^{n-1}\langle 0|F_{n+1}^{\dagger}|0\rangle\otimes^{n}|1\rangle=\frac{\sqrt{n!}}{(n+1)^{n/2}}\sum_{j=0}^{n}(-1)^{j}\sqrt{\binom{n}{j}^{-1}}|n-j\rangle|j\rangle$. In other words, the state $|R_{n}\rangle$ distorts the Fock states in an inverse manner to $B_{2}|0\rangle|n\rangle$. Hence, by combining one mode from each of these states, the overall action of the $n$-QSSP is

The $n$-QSBP is described by the same operator, since it is the conjugate transpose of this expression. The $n$-QS therefore applies ideal $g^{a^{\dagger}a}$ up to the $n^{\mathrm{th}}$ Fock state

The Supplemental Material contains the full proof [28].

The $n$-QS has a success probability of $\mathbb{P}=\langle g\psi_{n}|g\psi_{n}\rangle$, which can be improved depending on whether we are considering the BP or SP configuration. For $n$-QSBP, it is not required that the vacuum state $\langle 0|$ be detected at the first output port of $F_{n+1}$, since the QFT is highly symmetric. If $\langle 0|$ was instead detected in the $(m_{0}+1)^{\mathrm{th}}$ output port $\otimes^{m_{0}}\langle 1|\otimes\langle 0|\otimes^{n-m_{0}}\langle 1|$, $m_{0}\in\{0,\cdots,n\}$, the output state will be $|g\psi_{n}\rangle$ with an extra phase shift that can be corrected by $C_{1}(m_{0})=e^{\frac{2i\pi m_{0}}{n+1}a^{\dagger}a}$ [28]. Utilizing all $n+1$ heralding events enhances the success probability by $\mathbb{P}_{\text{BP}}=(n+1)\mathbb{P}$. For $n$-QSSP, the $|R_{n}\rangle$ resource state from the red dashed box in Fig. 1(b) could be prepared and stored beforehand; assuming $|R_{n}\rangle$ is deterministically available increases the success probability $\mathbb{P}_{\text{SP}}$ to at least $\frac{(n+1)^{n}}{(n+1)!}\mathbb{P}$ [28]. Note that $\mathbb{P}_{\text{SP}}<\mathbb{P}_{\text{BP}}$ for $n\in\{1,2\}$, $\mathbb{P}_{\text{SP}}=\mathbb{P}_{\text{BP}}$ for $n=3$, and $\mathbb{P}_{\text{SP}}>\mathbb{P}_{\text{BP}}$ for $n>3$ [28]. Since there is no difference between the output states of these configurations, we will use $\mathbb{P}_{\text{XP}}=\max(\mathbb{P}_{\text{SP}},\mathbb{P}_{\text{BP}})$ depending on the size $n$ under consideration.

We will now contrast our protocol with Xiang, et al. 2010 (X10) linear optical NLA protocol [4]. An $n$ sized X10 network has $n$ copies of $1$-QS in parallel between two $n$-splitters, hence requires approximately the same amount of physical resources as an $n$-QS. One advantage of the simplified $n$-QS structure is that setting a particular gain requires changing just one BS, while $n$-X10 requires changing $n$ BS concurrently. The output state from $n$-X10 has both the cut-off and distorted coefficients

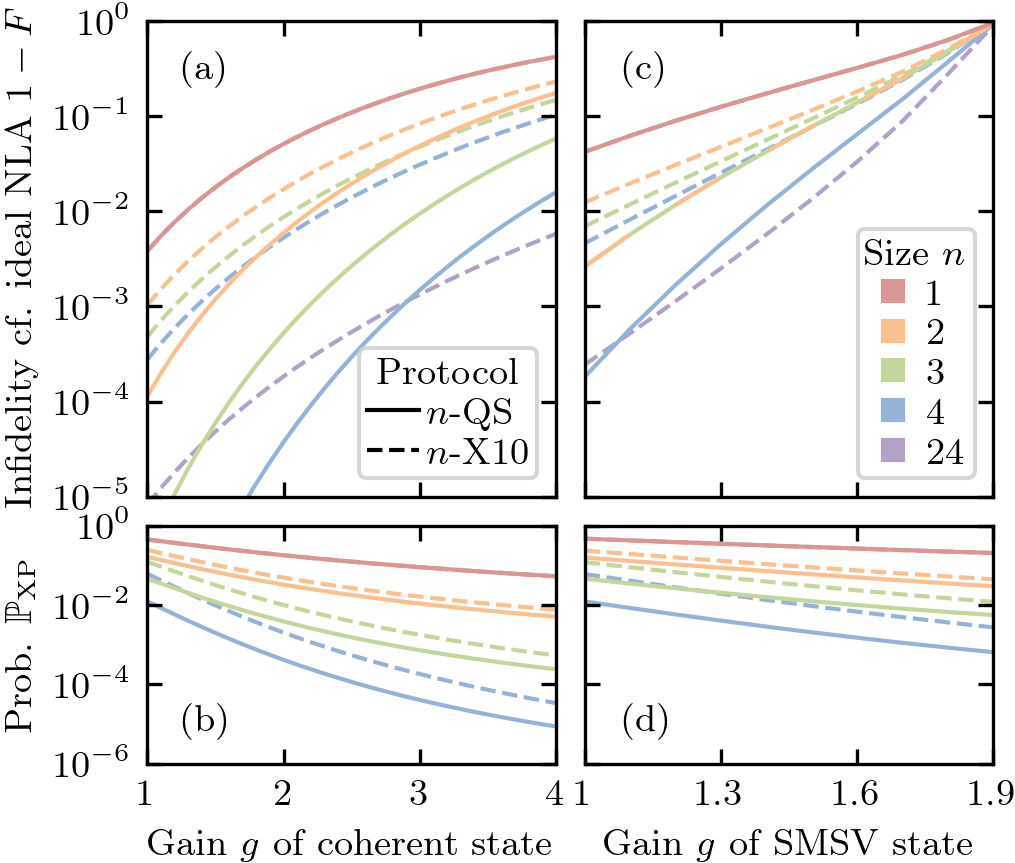
hence the NLA is not ideal in general [3]. The fidelity $F$ can quantify how far away these output states are from the ideal NLA output state $g^{a^{\dagger}a}|\psi\rangle=|g\psi\rangle$ [28]. It is clear an $n_{\text{max}}$-QS can amplify any arbitrary state with a $n_{\text{max}}$ upper energy limit with perfect fidelity. This feat cannot be replicated by any finite sized $n$-X10, or by any previous linear-optical NLA protocol [24, 25].

In Fig. 2 we consider amplifying a coherent state and a single-mode squeezed vacuum (SMSV) state. Our $n$-QS has superior fidelity scaling, and hence for a required target fidelity needs much less resources with better success probability than the $n$-X10. For example, Fig. 2(a) and (b) shows amplifying the coherent state by $g\approx 3$ with 99.9% fidelity requires only an $4$-QS with $10^{-5}$ success probability, as opposed to a much larger $24$-X10 with $10^{-24}$ success probability. Fig. 2(c) and (d) emphasize the flexibility of our $n$-QS protocol, in that we can choose the best $n$ size for a given input; since SMSV states contain only even photon numbers, it is best to use even sized $n$-QS (odd sizes will give the same fidelity as one size down). These graphs also show the $n$-QS has fidelity advantages even with amplifying SMSV states near maximum squeezing given by $g_{\text{max}}^{2}\ s=1$ (here $g_{\text{max}}\approx 1.9$).

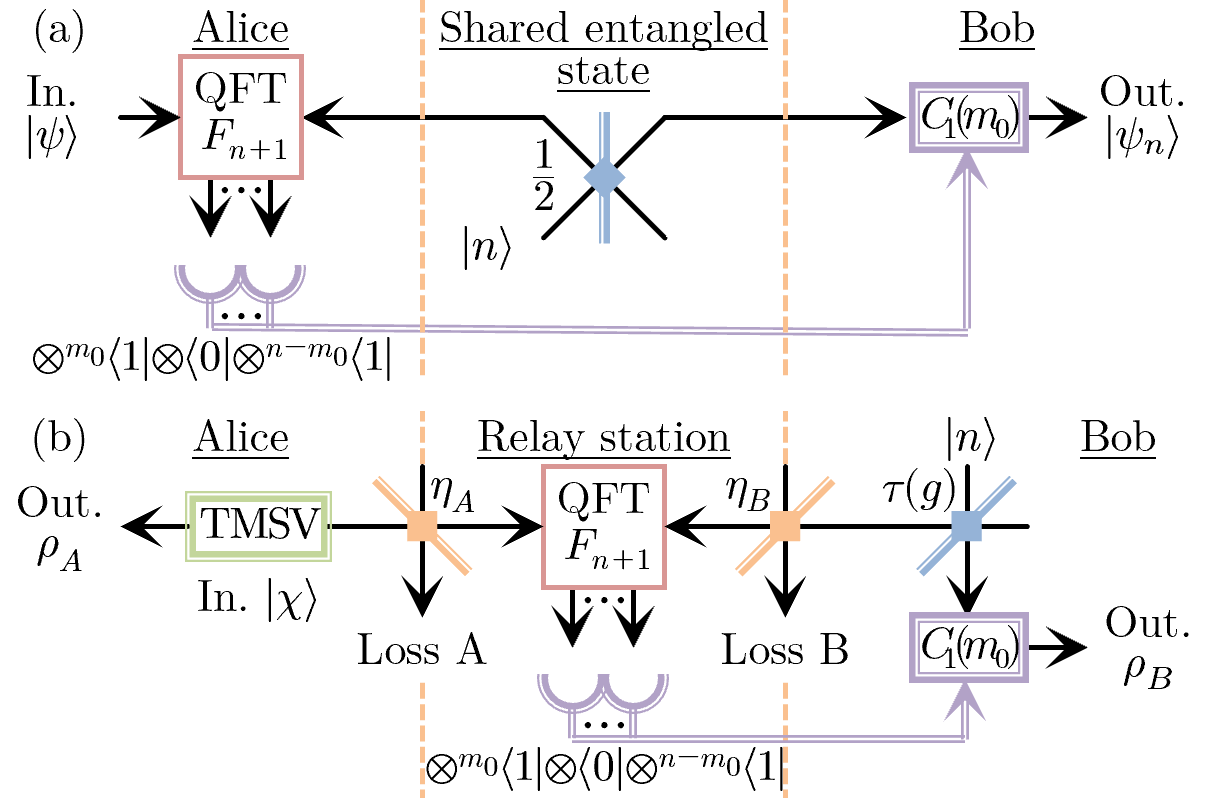
Quantum teleporter.—Quantum teleportation is a key primitive in quantum protocols [33, 34, 35], since it allows for the transfer and manipulation of quantum information through a shared entangled state; this is possible in both discrete variable [22] and continuous variable (CV) [36] regimes. Andersen and Ralph in 2013 (AR13) proposed a CV teleportation scheme [37], which could in principle reach high fidelities with lower energy requirements than standard CV teleportation [36]. However, in a similar manner as X10, a finite sized AR13 protocol distorts the output state. We will demonstrate our $n$-QS with $g=1$, as in Fig. 3(a), is a better protocol for high-fidelity teleportation. We restrict ourselves to linear-optical systems, hence both $n$-AR13 and $n$-QS are non-deterministic, and require a comparable amount of physical resources.

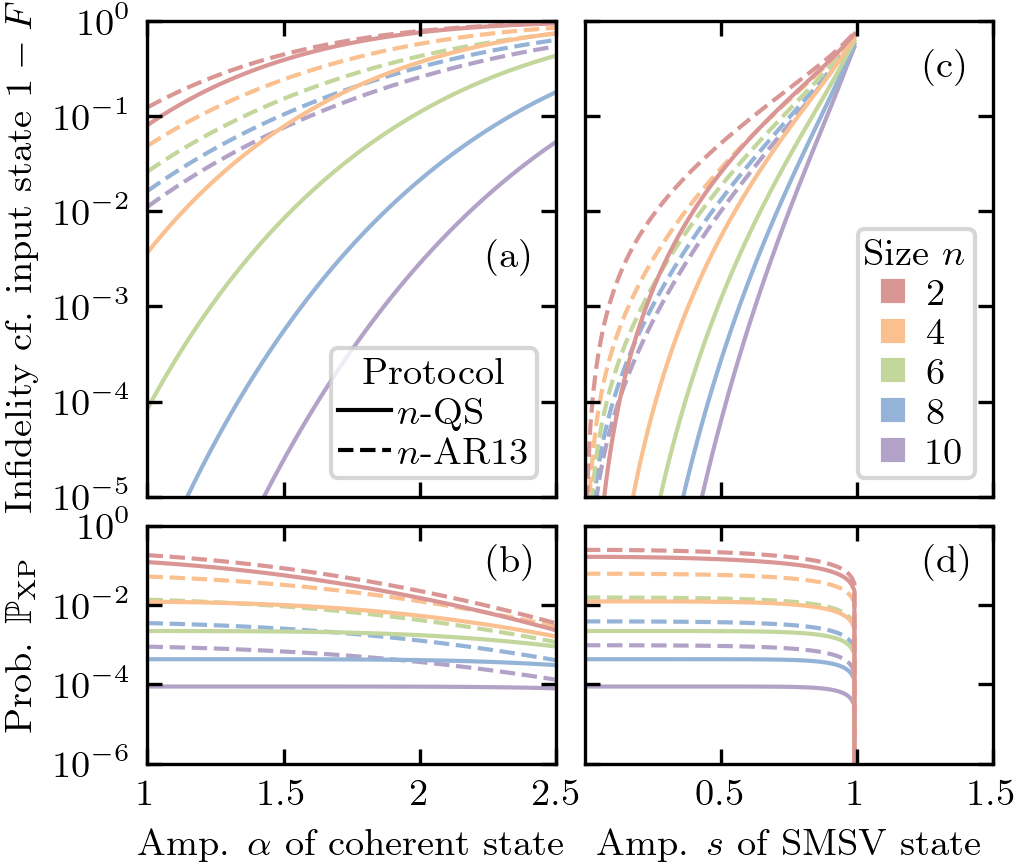
We consider teleporting coherent and SMSV states with various amplitudes in Fig. 4; we chose higher valued energy states to show the advantage of our scheme for larger $n$. It is clear our $n$-QS scales with many orders of magnitude better fidelity in comparison to $n$-AR13, while the probability of success scales comparatively. For example, teleporting an SMSV using a $4$-QS results in superior fidelity and success probability, while requiring less resources compared to a $10$-AR13.

The AR13 paper illustrated the effectiveness of their protocol by analysing the teleportation of a coherent state superposition $|\alpha\rangle+|-\alpha\rangle$ with $\alpha=2$. The authors note that to achieve just over 99% fidelity, the standard teleportation approach requires 500 average photons (30 dB of squeezing) [36], while $n$-AR13 requires an $n=100$ photon entangled state [37]. To reach the same fidelity, our $n$-QS protocol requires just $n=10$ photons.

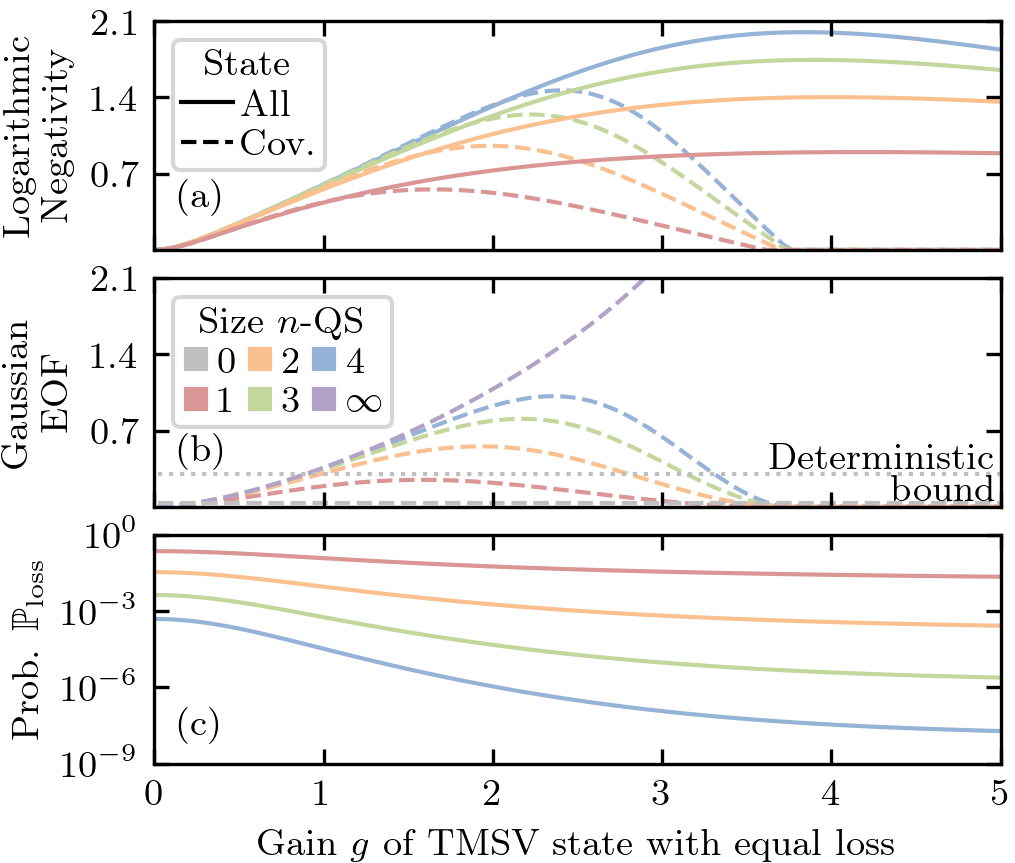
Loss-tolerant quantum relay.—Here we consider distilling entanglement through a loss channel with $\eta\in[0,1]$ total transmissivity. The $n$-QS can function as a quantum relay by distributing the QFT measurement component over the channel, as shown in Fig. 3(b), such that $\eta_{A}\eta_{B}=\eta$. The distributed $1$-QS has previously been shown to be uniquely loss tolerant, in that it can overcome the repeaterless PLOB bound without quantum memories [38]; the only other known scheme that can also do this feat is the twin-field QKD protocol and its variants [39, 40, 41, 42]. We confirm that the complete set of distributed $n$-QS are also loss tolerant with improved usage rates. In other words, instead of having the entire NLA at Bob’s side ($\eta_{A}=\eta,\eta_{B}=1$), by placing the QFT measurement half way ($\eta_{A}=\sqrt{\eta},\eta_{B}=\sqrt{\eta}$), we improve success probability scaling from $\eta^{n}$ to $\eta^{n/2}$ [28]. Note here we consider distilling a two-mode squeezed vacuum (TMSV) or EPR state with $\chi=0.25$ squeezing.

The logarithmic negativity (LN) is an entanglement monotone [43, 44], and an upper bound for distillable entanglement [45]. The LN is shown by the solid lines in Fig. 5(a), which increases with larger $n$ sizes. Maximum LN occurs with gain approximately $g_{\text{max}}\chi\sqrt{\eta_{A}/\eta_{B}}\approx 1$ (here $g_{\text{max}}\approx 4$), which corresponds to an output state that is uniformly distributed in the Fock basis [28]. The dashed lines in these graphs only considers the second moment covariance correlations, which are more relevant for Gaussian and CV protocols [46].

The entanglement of formation (EOF) is an entanglement metric [47], whose properties for multi-mode Gaussian states are known [48, 49, 50, 51, 52]. Fig 5(b) is the Gaussian EOF, which closely resembles the covariance-based LN, as expected. The gray horizontal lines are pure loss channels with no QS, where the dashed line has the same initial squeezing $\chi=0.25$, and the dotted line is the deterministic bound with infinite squeezing $\chi=1$; it’s clear this bound can be beaten by small sized $n$-QS. Increasing loss doesn’t significantly change the maximum amount of distillable entanglement, which is another experimental appealing feature of this loss tolerant protocol [28].

Experimental imperfections.—Finally, we examined the effect of noisy, inefficient photon detectors and sources. We showed that our $n$-QSBP protocol is tolerant to experimental imperfections, in the same sense as the already experimentally verified $1$-QS [4]. In other words, an imperfect $n$-QSBP as an amplifier, teleporter or relay results in relative improvements with increased $n$, in a similar fashion as the ideal graphs in this Letter. Unfortunately, the $n$-QSSP is not tolerant to experimental imperfections. This is because of how the entanglement resource is prepared, and a different preparation scheme could help to improve an imperfect $n$-QSSP. See the Supplemental Material for more details [28].

Conclusion.—We introduced the generalised $n\in\mathbb{N}^{+}$ quantum scissors, which can perform perfect fidelity tele-amplification up to the $n^{\mathrm{th}}$ Fock state. We proved that this operation can be implemented using two simple scalable linear-optical networks, with either $n$ single or $n$ bunched ancillary photons. As a consequence, our $n$-QS protocol is shown to have substantial advantages over existing NLA and teleportation schemes, in terms of fidelity scaling, success probability and physical resources. Finally, we showed that a distributed $n$-QS quantum relay is loss-tolerant with fast rates, hence is useful as building blocks for quantum repeater networks.

Note added.—The authors recently became aware of a new related work which investigated noiseless quantum tele-amplifiers from a different angle [53], based on the continuous-variable teleportation protocol [36].