Hypergraph Clustering for Finding
Diverse and Experienced Groups

Our work on diversity in clustering is partly related to the recent research on algorithmic fairness and fair clustering, which we briefly review. These results are based ideas that machine learning algorithms may make decisions that are biased or unfair towards a subset of a population [8, 17, 18]. There are now a variety of algorithmic fairness techniques to combat this issue [19, 28, 37]. For clustering problems, fairness is typically formulated in terms of protected attributes on data points — a cluster is “fair” if it exhibits a proper balance between nodes from different protected classes, and the goal is to optimize classical clustering objectives while also adhering to constraints ensuring a balance on the protected attributes [2, 4, 3, 10, 15, 16, 20, 30]. These approaches are similar to our notion of diverse clustering, since in both cases, the resulting clusters are more heterogeneous with respect to node attributes. While the primary attribute addressed in fair clustering is the protected status of a data point, in our case it is the “experience” of that point, which is derived from an edge-labeled hypergraph. In this sense, we have similar algorithmic goals, but we present our approach as a general framework for finding clusters of nodes with experience and diversity, as there are many reasons why one may wish to organize a dataset into clusters that are diverse with respect to past experience.

Furthermore, there exists some literature on algorithmic diverse team formation [6, 13, 29, 36, 41, 45]. However, this research has thus far largely focused on frameworks for forming teams which exhibit diversity with respect to inherent node-level attributes, without an emphasis on diversity of expertise, making our work the first to explicitly address this issue.

Our framework also facilitates a novel take on diversity within recommender systems. A potential application which we study in Section 4 is to select expert, yet diverse sets of reviews for different product categories. This differs from existing recommender systems paradigms on two fronts: First, the literature focuses almost exclusively on user-centric recommendations, with content tailored to an individual’s preferences; for us, a set of reviews is curated for a category of products that allows any user to glean both expert and diverse opinions regarding it. Further, the classic recommender systems literature defines diversity for a set of objects based on dissimilarity derived from pairwise relations among people and objects [12, 31, 35, 43, 46]. While some set-level proxies for diverse recommendations exist [14, 40], they do not deal explicitly with higher-order interactions among objects. Our work, on the other hand, encourages diversity in recommendations through an objective that captures higher-order information about relations between subsets of objects, providing a native framework for hypergraph-based diverse recommendations.

We start with an illustrative (but ultimately flawed) clustering objective whose characteristics will be useful in the rest of the paper. For this, we first define diversity and experience scores for a color $i$, denoted $D(i)$ and $E(i)$, as follows:

In words, $D(i)$ measures how much nodes in cluster $i$ have participated in hyperedges that are not color $i$, and $E(i)$ measures how much nodes in cluster $i$ have participated in hyperedges of color $i$. A seemingly natural but ultimately naive objective for balancing experience and diversity is:

The regularization parameter $\beta$ determines the relative importance of the diversity and experience scores. It turns out that the optimal solutions to this objective are overly-simplistic, with a phase transition at $\beta=1$. We define two simple types of clusterings as follows:

• •

  Majority vote clustering: Node $v$ is placed in cluster $\mathcal{C}(i)$ where $i\in\operatorname{argmax}_{c\in L}d_{v}^{c}$, i.e., node $v$ is placed in a cluster for which it has the most experience.

• •

  Minority vote clustering: Node $v$ is placed in cluster $\mathcal{C}(i)$ where $i\in\operatorname{argmin}_{c\in L}d_{v}^{c}$, i.e., node $v$ is placed in a cluster for which it has the least experience.

Proof  For node $i$, assume without loss of generality that the colors $1,2,\ldots,k$ are ordered so that $d_{i}^{1}\geq\dots\geq d_{i}^{k}$. Clustering $i$ with cluster 1 gives a contribution of $d_{i}^{1}+\beta\sum_{j=2}^{k}d_{i}^{j}$ to the objective, while clustering it with color $c\neq i$ gives contribution $d_{i}^{c}+\beta\sum_{j\neq c}d_{i}^{j}$. Because $d_{i}^{1}\geq\dots\geq d_{i}^{k}$, the first contribution is greater than or equal to the second if and only if $\beta\leq 1$. Hence, majority vote is optimal when $\beta\geq 1$. A similar argument proves optimality for minority vote when $\beta\leq 1$. $\Box$

We will use this observation when developing our clustering framework in the next section.

We now turn to a more sophisticated approach: a regularized version of the categorical edge clustering objective [5]. For a clustering $\mathcal{C}$, the objective accumulates a penalty of 1 for each hyperedge of color $c$ that is not completely contained in the cluster $\mathcal{C}(c)$. More formally, the objective is:

where $x_{e}$ is an indicator variable equal to 1 if hyperedge $e\in E_{c}$ is not contained in cluster $\mathcal{C}(c)$, but is zero otherwise. This penalty encourages entire hyperedges to be contained inside clusters of the corresponding color. For our context, this objective can be interpreted as promoting group experience in cluster formation: if a group of people have participated together in task $c$, this is an indication they could work well together on task $c$ in the future. However, we want to avoid the scenario where groups of people endlessly work on the same type of task without the benefiting from the perspective of others with different experiences. Therefore, we regularize objective (3) with a penalty term $\beta\sum_{c\in L}E(c)$. Since $\sum_{c\in L}[E(c)+D(c)]$ is a constant (Observation 2), this regularization encourages higher diversity scores $D(c)$ for each cluster $\mathcal{C}(c)$.

While the “all-or-nothing” penalty in (3) may seem restrictive at first, it is a natural choice for our objective function for several reasons. First, we are building on recent research showing applications of Objective (3) on datasets similar to ours, namely edge-labeled hypergraphs [5], and this type of penalty is a standard in hypergraph partitioning [9, 23, 25, 34, 32, 42]. Second, if we consider an alternative penalty which incurs a cost of one for every node that is split away from the color of the hyperedge, this reduces to the “flawed first approach” in the previous section, where there is no diversity-experience tradeoff. Developing algorithms that can optimize more complicated alternative hyperedge cut penalties is an active area of research [34, 44]. Translating these ideas to our setting constitutes an interesting open direction for future work, but comes with numerous challenges and is not the focus of the current manuscript. Finally, our experimental results indicate that even without considering generalized hyperedge cut penalties, our regularized objective produces meaningfully diverse clusters on real-world and synthetic data.

We now formalize our objective function, which we call diversity-regularized categorical edge clustering (DRCEC), which will be the focus for the remainder of the paper. We state the objective as an integer linear program (ILP):

The binary variable $x_{v}^{c}$ equals $1$ if node $v$ is not assigned label $c$, and is 0 otherwise. The first constraint guarantees every node is assigned to exactly one color, while the second constraint guarantees that if a single node $v\in e$ is not assigned to the cluster of the color of $e$, then $x_{e}=1$.

A polynomial-time 2-approximation algorithm.  Optimizing the case of $\beta=0$ is NP-hard [5], so DRCEC is also NP-hard. Although the optimal solution to (4) may vary with $\beta$, we develop a simple algorithm based on solving an LP relaxation of the ILP that rounds to a 2-approximation for every value of $\beta$. Our LP relaxation of the ILP in (4) replaces the binary constraints $x_{v}^{c},x_{e}\in\{0,1\}$ with linear constraints $x_{v}^{c},x_{e}\in[0,1]$. The LP can be solved in polynomial time, and the objective score is a lower bound on the optimal solution score to the NP-hard ILP. The values of $x_{v}^{c}$ can then be rounded into integer solutions to produce a clustering that is within a bounded factor of the LP lower bound, and therefore within a bounded factor of optimality. Our algorithm is simply stated:

$\begin{array}[]{l}\textbf{\text@underline{Algorithm 1}}\vspace{0.5mm}\\ \text{1. Solve the LP relaxation of the ILP in \eqref{eq:ccilp}.}\\ \text{2. For each $v\in V$, assign $v$ to any $c\in\operatorname{argmin}_{j}x_{v}^{j}$.}\end{array}$

Proof  Let the relaxed solution be $\{x_{e}^{*},x_{v}^{*c}\}_{e\in E,v\in V,c\in L}$ and the corresponding rounded solution $\{x_{e},x_{v}^{c}\}_{e\in E,v\in V,c\in L}$. Let $y_{v}^{c}=1-x_{v}^{c}$ and $y_{v}^{*c}=1-x_{v}^{*c}$. Our objective evaluated at the relaxed and rounded solutions respectively are

We will show that $S\leq 2S^{*}$ by comparing the first and second terms of $S$ and $S^{*}$ respectively. The first constraint in (4) ensures that $x_{v}^{c}<1/2$ for at most a single color $c$. Thus, for every edge $e$ with $x_{e}=1$, $x_{v}^{*c}\geq 1/2$ for some $v\in e$. In turn, $x_{e}^{*}\geq 1/2$, so $x_{e}\leq 2x_{e}^{*}$. If $x_{e}=0$, then $x_{e}\leq 2x_{e}^{*}$ holds trivially. Thus, $\sum_{e}x_{e}\leq 2\sum_{e}x_{e}^{*}$. Similarly, since $x_{v}^{c}=1$ ($y_{v}^{c}=0$) if and only if $x_{v}^{*c}\geq 1/2$ ($y_{v}^{c*}\leq 1/2$), and $x_{v}^{c}=0$ otherwise, it follows that $y_{v}^{c}\leq 2y_{v}^{*c}$. Thus, $\sum_{v\in V}\sum_{c\in L}d_{v}^{c}y_{v}^{c}\leq 2\sum_{v\in V}\sum_{c\in L}d_{v}^{c}y_{v}^{*c}$. $\Box$

In general, Objective (4) provides a meaningful way to balance group experience (the first term) and diversity (the regularization, via Observation 2). However, when $\beta\rightarrow\infty$, the objective corresponds to simply minimizing experience, (i.e., maximizing diversity), which is solved via the aforementioned minority vote assignment. We formally show that the optimal integral solution (4), as well as the relaxed LP solution under certain conditions, transitions from standard behavior to extremal behavior (specifically, the minority vote assignment) when $\beta$ becomes larger than the maximum degree in the hypergraph. In Section 3, we show how to bound these transition points numerically, so that we can determine values of the regularization parameter $\beta$ that produce meaningful solutions.

Proof  Let binary variables $\{x_{e},x_{v}^{c}\}$ encode a clustering for (4) that is not a minority vote solution. This means that there exists at least one node $v$ such that $x_{v}^{c}=0$ for some color $c\notin\operatorname{argmin}_{i\in L}d_{v}^{i}$. If we move node $v$ from cluster $c$ to some cluster $m\in\operatorname{argmin}_{i\in L}d_{v}^{i}$, then the regularization term in the objective would decrease (i.e., improve) by $\beta(d_{v}^{c}-d_{v}^{m})\geq\beta>d_{\mathit{max}}$, since degrees are integer-valued and $d_{v}^{c}>d_{v}^{m}$. Meanwhile, the first term in the objective would increase (i.e., become worse) by at most $\sum_{e:v\in e}x_{e}=d_{\mathit{max}}<\beta$. Therefore, an arbitrary clustering that is not a minority vote solution cannot be optimal when $\beta>d_{\mathit{max}}$. $\Box$

Proof  Let $\{x_{e},x_{v}^{c}\}$ encode an arbitrary solution to the LP relaxation of (4), and assume specifically that it is not a minority vote solution. For every $v\in V$ and $c\in L$, let $y_{v}^{c}=1-x_{v}^{c}$. The $y_{v}^{c}$ indicate the “weight” of $v$ placed on cluster $c$, with $\sum_{c\in L}y_{v}^{c}=1$. Since $\{x_{e},x_{v}^{c}\}$ is not a minority vote solution, there exists some $v\in V$ and $j\notin\mathcal{M}_{v}$ such that $y_{v}^{j}=\varepsilon>0$.

We will show that as long as $\beta>d_{\mathit{max}}$, we could obtain a strictly better solution by moving this weight of $\varepsilon$ from cluster $j$ to a cluster in $\mathcal{M}_{v}$. Choose an arbitrary $m\in\mathcal{M}_{v}$, and define a new set of variables $\hat{y}_{v}^{j}=0$, $\hat{y}_{v}^{m}=y_{v}^{m}+\varepsilon$, and $\hat{y}_{v}^{i}=y_{v}^{i}$ for all other $i\notin\{m,j\}$. Define $\hat{x}_{v}^{c}=1-\hat{y}_{v}^{c}$ for all $c\in L$. For any $u\in V$, $u\neq v$, we keep variables the same: $\hat{y}_{u}^{c}=y_{u}^{c}$ for all $c\in L$. Set edge variables $\hat{x}_{e}$ to minimize the LP objective subject to the $\hat{y}_{c}$ variables, i.e., for $c\in L$ and every $e\in E_{c}$, let $\hat{x}_{e}=\max_{u\in e}\hat{x}_{u}^{c}$.

Our new set of variables simply takes the $\varepsilon$ weight from cluster $j$ and moves it to $m\in\mathcal{M}_{v}$. This improves the regularization term in the objective by at least $\beta\varepsilon$:

Next, we will show that the first part of the objective increases by at most $\varepsilon d_{\mathit{max}}$. To see this, note that for $e\in E_{j}$ with $v\in e$, $\hat{x}_{e}\geq 1-\hat{y}_{v}^{j}=1\implies\hat{x}_{e}=1$ and $x_{e}\geq 1-y_{v}^{j}=1-\varepsilon$. Therefore, for $e\in E_{j}$, $v\in e$, we know that $\hat{x}_{e}-x_{e}=1-x_{e}\leq 1-(1-\varepsilon)=\varepsilon$. For $e\in E_{m}$ with $v\in e$ we know $\hat{x}_{e}-x_{e}\leq 0$, since $\hat{x}_{e}=\max_{u\in e}(1-\hat{y}_{u}^{m})$ and $x_{e}=\max_{u\in e}(1-y_{u}^{m})$, but the only difference between $y_{u}^{m}$ and $\hat{y}_{u}^{m}$ variables is that $\hat{y}_{v}^{m}=y_{v}^{m}+\varepsilon\implies(1-\hat{y}_{v}^{m})<(1-y_{v}^{m})$. For all other edge sets $E_{c}$ with $c\notin\{m,j\}$, $\hat{x}_{e}=x_{e}$. Therefore, $\sum_{e:v\in e}[\hat{x}_{e}-x_{e}]\leq\varepsilon d_{\mathit{max}}$. In other words, as long as $\beta>\varepsilon$, we can strictly improve the objective by moving around a positive weight $y_{v}^{j}=\varepsilon$ from a non-minority vote cluster $j\notin\mathcal{M}_{v}$ to some minority vote cluster $m\in\mathcal{M}_{v}$. Therefore, at optimality, for every $v\in V$, $\sum_{c\in\mathcal{M}_{v}}y_{v}^{c}=1$. $\Box$

Theorem 5 implies that if there is a unique minority vote clustering (i.e., each node has one color degree strictly lower than all others), then this clustering is optimal for both the original objective and the LP relaxation whenever $\beta>d_{\mathit{max}}$. Whether or not the the optimal solution to the LP relaxation is the same as the ILP one, the rounded solution still corresponds to some minority vote clustering that does not meaningfully balance diversity and experience. The bound $\beta>d_{\mathit{max}}$ is loose in practice; our numerical experiments show that the transition occurs for smaller $\beta$. In the next section, we use techniques in LP sensitivity analysis that allow us to better bound the phase transition computationally for a given labelled hypergraph. For this type of analysis, we still need the loose bound as a starting point.

Here, we examine the performance of Algorithm 1 for various regularization strengths $\beta$ and compare the results to the unregularized case (Figure 1). We observe that including the regularization term and using Algorithm 1 to solve the resulting objective only yields mild increases in cost compared to the optimal solution of the original unregularized objective. This “cost of diversity” ratio is always smaller than 3 and is especially small for the Math Overflow questions datasets (Figure 1, top left). Furthermore, the ratio between the LP relaxation of the regularized objective and the LP relaxation of the unregularized ($\beta=0$) objective has similar properties (Figure 1, top right). This is not surprising, given that every node in each of the datasets has a color degree of zero for some color, and thus for very large values of $\beta$, each node is put in a cluster where it has a zero color degree, so that the second term in the objective is zero. Also, the approximation factor of Algorithm 1 on the data is small (Figure 1, bottom left), which we obtain by solving the exact ILP, indicating that the relaxed LP performs very well. In fact, solving the relaxed LP often yields an integral solution, meaning that it is the solution to the ILP. The computed $\hat{\beta}$ bound also matches the plateau of the rounded solution (Figure 1, top left), which we would also expect from the small approximation factors and the fact that each node has at least one color degree of zero. We also examine the “edge satisfaction”, i.e., the fraction of hyperedges where all of the nodes in the hyperedge are clustered to the same color as the hyperedge [5] (Figure 1, bottom right). As regularization increases, more diversity is encouraged, and the edge satisfaction decreases. Finally, we note that the runtime of Algorithm 1 is small in practice, taking at most a couple of seconds in any problem instance.

Next, we examine the effect of regularization strength on diversity within clusters. To this end, we measure the average fraction of within-cluster reviews/posts. Formally, for a clustering of nodes $\mathcal{C},$ this measure, which we call $f_{\text{within}}$, is calculated as follows:

In computing the $f_{\text{within}}$ measure, within each cluster we compute the fraction of all user reviews/posts having the same category as the cluster. Then we average these fractions across all clusters, weighted by cluster size. Figure 2 shows that $f_{\text{within}}$ decreases with regularization strength, indicating that our clustering framework yields meaningfully diverse clusters.

Case Study I: Mexican restaurants in Madison, WI.

We now take a closer look at the output of Algorithm 1 on one dataset to better understand the way in which it encourages diversity within clusters. Taking the entire madison-restaurant-reviews dataset as a starting point, we cluster each reviewer to write reviews of restaurants falling into one of nine cuisine categories. After that, we examine the set of reviewers grouped by Algorithm 1 to review Mexican restaurants. To compare the diversity of experience for various regularization strengths, we plot the distribution of reviewers’ majority categories in Figure 3. Here, we take “majority category” to mean the majority vote assignment of each reviewer. In other words, the majority category is the one in which they have published the most reviews. We see that as $\beta$ increases, the cluster becomes more diverse, as the dominance of the Mexican majority category gradually subsides, and it is overtaken by the Chinese category. At $\beta=0$ (no regularization), 95% of nodes in the Mexican reviewer cluster have a majority category of Mexican, while at $\beta=0.04,$ only 20% still do. Thus, as regularization increases, we see greater diversity within the cluster, as “expert” reviewers from other cuisines are clustered to review Mexican restaurants.

Similarly, as $\beta$ increases we see a decrease in the fraction of users’ reviews that are for Mexican restaurants, when this fraction is averaged across all users assigned to the Mexican restaurant cluster (Figure 4). We refer to this ratio as the experience homogeneity score, which for a cluster $\mathcal{C}(i)$ is formally written as

This measure is similar to $f_{\text{within}}$ except that we look at only one cluster. However, this experience homogeneity score does not decrease as much as the corresponding fraction in Figure 3, falling from 91% to 38%, which illustrates that while the “new” reviewers added to the cluster with increasing $\beta$ have expertise in other areas, they nonetheless have written some reviews of Mexican restaurants in the past.

Case Study II: New York blues on Amazon.

We now perform an analogous analysis for reviews of blues vinyls on Amazon. We take the entire music-blues-reviews dataset and perform regularized clustering at different levels of regularization. Then, we keep track of the reviewers clustered to write reviews in the New York blues category. The fraction of users in the cluster whose majority category is New York decreases as we add more regularization, as seen in Figure 5. The percent share of all past New York blues reviews of reviewers within the cluster decreases with regularization, but not as much as the corresponding curve in the majority category distribution, as seen in Figure 6, indicating that while “new” reviewers added to the cluster with increasing $\beta$ have expertise in other types of blues music they nonetheless have written some reviews of New York blues vinyls in the past.

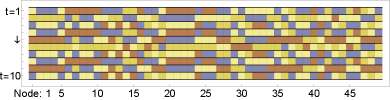
In this section we consider a dynamic variant of our framework in which we iteratively update the hypergraph. More specifically, given the hypergraph up to time $t$, we (i) solve our regularized objective to find a clustering $\mathcal{C}$ (ii) create a set of hyperedges at time $t+1$ corresponding to $\mathcal{C}$, i.e., all nodes of a given color create a hyperedge. At the next step, the experience levels of all nodes have changed. This mimics a scenario in which teams are repeatedly formed via Algorithm 1 for various tasks, where the type of the task corresponds to the color of the hyperedge. For our experiments, we only track the experiences from a window of the last $w$ time steps; in other words, the hypergraph just consists of the hyperedges appearing in the previous $w$ steps. To get an initial history for the nodes, we start with the hypergraph datasets used above. After, we run the iteration for $w$ steps to “warm start” the dynamical process, and consider this state to be the initial condition. Finally, we run the iterative procedure for $T$ times.

We can immediately analyze some limiting behavior of this process. When $\beta=0$ (i.e., no regularization), after the first step, the clustering will create new hyperedges that increase the experience levels of each node for some color. In the next step, no node has any incentive to cluster with a different color than the previous time step, so the clustering will be the same. Thus, the dynamical process is entirely static. At the other extreme, if $\beta>d_{max}$ at every step of the dynamical process, then the optimal solution at each step is a minority vote assignment by Theorem 5. In this case, after each step, each node $v$ will increase its color degree in one color, which may change its minority vote solution in the next iteration. Assuming ties are broken at random, this leads to uniformity in the historical cluster assignments of each node as $T\to\infty$.

For each of our datasets, we ran the dynamical process for $T=50$ time steps. We say that a node exchanges if it is clustered to different colors in consecutive time steps. Figure 8 shows the mean number of exchanges. As expected, for small enough $\beta$, nodes are always assigned the same color, resulting in no exchanges; for large enough $\beta$, nearly all nodes exchange in the minority vote regime. Figure 7 shows the clustering of nodes on a subset of the geometry-questions dataset for different regularization levels. For small $\beta$, nodes accumulate experience before exchanging. When $\beta$ is large, nodes exchange at every iteration. This corresponds to the scenario of large $\beta$ in Figure 8.