Hyperfine Structure of Transition Metal Defects in SiC
Abstract
Transition metal (TM) defects in silicon carbide (SiC) are a promising platform in quantum technology, especially because some TM defects emit in the telecom band. We develop a theory for the interaction of an active electron in the -shell of a TM defect in SiC with the TM nuclear spin and derive the effective hyperfine tensor within the Kramers doublets formed by the spin-orbit coupling. Based on our theory we discuss the possibility to exchange the nuclear and electron states with potential applications for nuclear spin manipulation and long-lived nunclear-spin based quantum memories.
For several applications in quantum technology, such as quantum networks, memories, emitters, and many more [1, 2, 3, 4], a quantum system needs to be coherently controlled and isolated from unwanted noise at the same time. Hybrid quantum systems [5, 6, 7], consisting of a part that can couple strongly to external fields as well as a part that is better shielded from its environment are promising platforms to fulfill this requirement. In these systems one can benefit from short gate times of one quantum system as well as long coherence times of the other. A much studied system of this type is the nitrogen vacancy center in diamond with its neighboring nuclear spins [8, 9, 10, 11, 12, 13, 14, 15, 16] (and Refs. [17, 18] for reviews).
Transition metal (TM) defects in silicon carbide (SiC) constitute a similar familiy of systems that have the benefit of being based on a well established host material as well as having accessible transitions in the telecommunication bands [19, 20, 21, 22, 23]. Recent studies made the first steps towards control of nuclear spins via transition metal defects in SiC [22]. While these results are highly promising, a complete theoretical framework is still needed. In this paper, we derive a model of the hyperfine coupling based on the underlying symmetry properties and relevant orbital configuration of the defect in the crystal, explaining the experimental data and leading to additional insights. In particular we derive a sensible form of the interaction of the defect nuclear spin with the spin and orbital angular momentum of the active electron as well as their combined interaction with external fields.
The prime examples for TM defects in SiC are created by neutral vanadium (V) and positively charged molybdenum (Mo) atoms substituting a Si atom in 6H- or 4H-SiC [24, 25, 19, 20, 21, 22, 23]. These defects have one active electron in the atomic -shell and are invariant under the transformations of the point group imposed by the crystal structure surrounding the defect. While the interaction with the nuclear spins of neighboring C and Si isotopes with non-zero nuclear spins is possible, the presence of such non-zero spin isotopes as a nearest neighbour is fairly improbable, because their natural abundances are about 1% for 13C (spin ) and 5% for 29Si (spin ) [26] and the abundance can be further reduced by using isotopically purified SiC [27, 28]. Here, we therefore concentrate on the interaction with the TM nuclear spin. The nuclear spin for the most common V isotope is () and for about of the stable Mo isotopes and for the remaining isotopes of Mo [29, 26].
In order to model the hyperfine coupling between the electron and nuclear spins in a TM defect in SiC, we start from the full Hamiltonian
| (1) |
where describes the electronic orbital and spin degrees of freedom without their interaction with the nuclear spin [30], while the remaining terms incorporate the nuclear spin and its interaction with the electron and external fields.
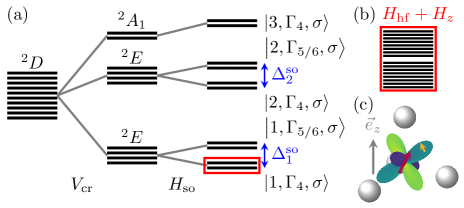
The first three terms in describe the zero-field spin-orbit level structure, as shown in Fig. 1. The defect atomic Hamiltonian localizes the active electron in the orbital; the crystal potential reduces the symmetry of the defect to due to the potentials of the surrounding crystal atoms, thereby splitting the -shell levels; the spin-orbit Hamiltonian takes the coupling of spin and orbital angular momentum into account and splits the levels further. In total, this leads to five doubly degenerate levels forming Kramers doublets (KD), pairs of states related by time-reversal symmetry [31]. The time-reversal symmetry protects KDs from coupling via operators that are invariant under time-reversal.
The Zeeman Hamiltonian describes the coupling to a static magnetic field which breaks time-reversal symmetry and thus energetically splits the KDs, the electric potential denotes the coupling to a static external electric field, and the driving Hamiltonian denotes oscillatory external fields. Because is invariant under time-inversion, electric fields cannot lift the degeneracy of the KDs, therefore we concentrate on static magnetic fields in the following.
Typically, the symmetric crystal potential is sufficiently large to approximate the spin-orbit coupled electronic system by five pseudo-spin subspaces (the KDs) with distinct zero-field energies where we label the orbital configuration with and and the irreducible representation (irrep) of pertaining to the KD with [30]. The effective Hamiltonian is already diagonal inside blocks of the same orbital configuration for static fields aligned with the crystal axis, i.e. the threefold rotation axis of which we refer to as the -axis in the following. The reason for this is that a parallel magnetic field only lifts the time-reversal symmetry but keeps the spacial symmetry intact. On the other hand, fields perpendicular to the crystal axis can mix KDs of the same orbital doublet (denoted in Fig. 1). The mixing is suppressed by the spin-orbit splitting
| (2) |
and therefore can be neglected for small fields . The coupling between states originating from different atomic orbitals is even smaller due to the large crystal field splitting .
In the following we assume a negligible mixing of the KDs, as we believe this is the most relevant case for experimental setups and further technical applications such as quantum memories, due to the better protection from noise via restricted coupling as a consequence of the intact symmetry. In this case we can treat each of the KDs as a separate pseudo-spin system, described by the Hamiltonians acting in the space of the pseudo-spin states and of the KD
| (3) |
with the vector of Pauli operators , the Bohr magneton , and the pseudo-spin -tensor . For all KDs is diagonal, for the KDs only , for the KDs with one finds [30] if the spin-orbit coupling strength is much smaller than the crystal level spacing. Using the projection on to the subspace of the KD we can combine these Hamiltonians to obtain the complete effective spin-orbit Hamiltonian as .
Now we incorporate the interaction with the nuclear spin given by Eq. (1). Taking both the Fermi contact and anisotropic hyperfine interaction as well as the orbital nuclear interaction into account [32, 33, 34, 35, 36], the total hyperfine Hamiltonian can be written as
| (4) |
with the electron (nuclear) spin () and orbital angular momentum in units of the reduced Planck constant , the electron direction operator , and the anisotropic hyperfine and Fermi contact coupling strengths and , with the electron (nuclear) -factor (), and the nuclear magneton . The anisotropic coupling strength depends on the electronic state via while the Fermi contact interaction depends on the spin polarization density at the position of the nucleus denoted using the delta distribution . The electron is mainly localized in a -shell but the mixing with -orbitals can still lead to a relevant Fermi contact interaction, which is known for TM complexes [32, 34, 35, 36].
The nuclear spin can couple to external magnetic fields described by the nuclear Zeeman Hamiltonian
| (5) |
and the corresponding driving term for oscillating magnetic fields. These terms are small in comparison to the KD Zeeman part [25, 37, 22] and diagonal for parallel to the crystal axis.
While the state describing the active electron shows the transformation properties of a orbital, due to effects such as the Jahn-Teller effect and covalency [23, 38, 39] there can be an admixture of other orbitals. The Wigner-Eckart theorem [40, 13] enables us to absorb these effects as well as the radial part of the wave-function in reduced matrix elements, in particular to find the minimal set of non-zero matrix elements of (mixed) square components of in Eq. (Hyperfine Structure of Transition Metal Defects in SiC), into the orbital basis. Here, we treat reduced matrix elements as parameters that can be obtained experimentally or via ab-inito calculations. Then we (perturbativly) transform to the block diagonal basis of the pure spin-orbit Hamiltonian, where spin and orbital states are entangled. More details are given in the supplemental material [41].
As we did for the mixing due to external fields we neglect off-diagonal blocks between different orbital configurations due to the crystal field splitting. We find for the effective hyperfine Hamiltonians inside the KDs,
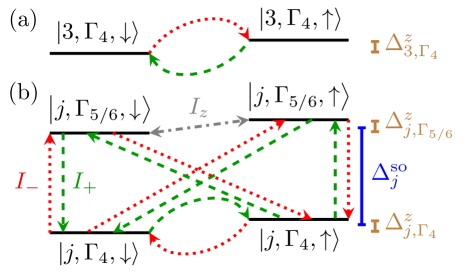
| (6) | ||||
| (7) | ||||
| (8) |
for and using the pseudo-spin as well as nuclear ladder operators. The diagonal part of the total effective hyperfine Hamiltonian can thus be written as . The terms mixing the KDs of the same orbital doublet are
| (9) |
where . Combined this leads to the effective hyperfine Hamiltonian . The resulting coupling structure is depicted in Fig. 2.
Combined with the effective spin-orbit Hamiltonians of the KDs (3) and nuclear Zeeman Hamiltonian (5), we obtain our first main result,
| (10) |
The immediate implications of Eq. (10) are given by its projection on the KDs, corresponding to the effective description for negligible inter-KD mixing . The importance of this is further underlined considering measurements by Wolfowicz et al. [22] where the hyperfine coupling strength is at least two orders of magnitude smaller than the spin-orbit splitting in all V defects in 4H- and 6H-SiC for the ground state ().
We now discuss the projection of Eq. (10) onto the KDs in more detail. Because the KDs transform in complete analogy to pure spin states, the coupling has a familiar form in this case. In particular the effective hyperfine coupling in the KD is the most similar to the simple diagonal dipolar coupling to the nuclear spin, because the crystal potential does not mix the orbital singlet () state with the remaining orbital states and the spin-orbit coupling vanishes in first order in the orbital singlet. Additionally, the form of the symmetry allowed part of the anisotropic hyperfine tensor in this case also agrees with that of the 14N NV--center which has the same symmetry but comprises spins [8, 12, 15].
The remaining KDs deviate significantly from this form because their two pseudo-spin states have a mixed spin and orbital wavefunction, due to the interplay of the crystal potential and the spin-orbit coupling. This leads to the (pseudo-)spin-non-conserving coupling, i.e. the non-diagonal coupling of the KDs as well as the coupling of the KDs for , see Fig. 2. Furthermore, the magnitude of can deviate significantly from the other two diagonal entries because it can have pure spin contributions.
Group theory further implies that the states cannot be coupled by operators transforming according to the representation of , e.g. . This follows from the requirement that in the spin-orbit operator part of has to transform according to the same basis vector of the same irrep as the corresponding nuclear spin operator, because as a whole has to transform according to . On the other hand the counterpart of (transforming according to ) can couple these states. Finally, we stress that the pseudo-spin matrices are not angular momentum type operators and, therefore, and can in part transform according to . For the relevant terms in the hyperfine Hamiltonian are .
We calculate the second order hyperfine interaction inside the KDs due to the interaction between KDs from the same orbital doublet with a Schrieffer-Wolff transformation [42]. The unperturbed Hamiltonian becomes perturbed inside the KDs by and between KDs with the same orbital origin by , leading to the first order of the Schrieffer-Wolff transformation
| (11) |
and the new effective Hamiltonian . We obtain the second-order correction with
| (12) |
for and , with the defect-configuration dependent constant . Combined with Eqs. (6)–(8) this leads to the second order of the effective hyperfine Hamiltonians for the KDs
| (13) |
We stress that the second order contribution of the hyperfine interaction is purely diagonal in the basis where points along the crystal axis.
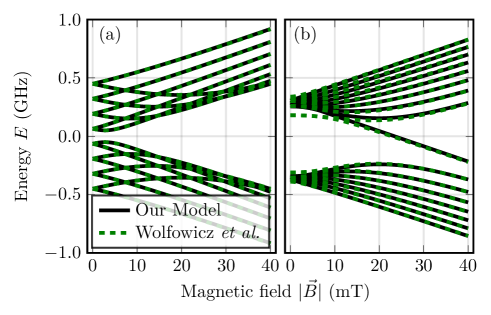
We now compare our results to the recent measurements by Wolfowicz et al. [22], concentrating on the two ground state KDs. In [22], a model for the KDs with a different form of the hyperfine coupling was used for all KDs, additionally allowing a tilt of the quantization axis of the pseudo-spin. The above-mentioned measurement in combination with our theoretical model suggests that the lowest-energy ground states (GS1) correspond to and GS2 to . The first point we want to highlight is that the measurement confirms that the KD states do not couple via and that a tilt of the pseudo-spin around the -axis corresponding to the coupling of to is found. We highlight that this artificial tilt of the quantization axis needs no further explanation in our theory where the coupling emerges naturally from the interplay of the crystal potential and the spin-orbit interaction. This can be seen via the transformation properties of the pseudo-spin operators as well as the form of the wavefunction of the KD states.
The second point is that our model provides a resort to explain the measurements [22] for GS1 without the need for an anisotropy in the hyperfine coupling tensor in the plane perpendicular to the crystal axis. Our model Eq. (7), shows good agreement with the transition frequencies in [22], despite a deviation of two energies in some configurations for small magnetic fields. For larger magnetic fields () indeed all energies are in agreement with the model in [22]. Not only does our model provide an explanation without the anisotropy, it furthermore reduces the number of free parameters. For the configuration of the V defect in -SiC we plot the comparison of the models in Fig. 3.
Additionally, the measurement of 6H-SiC in [22] includes all relevant electronic energy splittings allowing us to assign to the lowest energy excited state, for which we find that the form of the hyperfine interaction of our theory agrees with their measurement.
Finally we want to use the gained understanding of the effective hyperfine Hamiltonians within the KDs (13) and investigate the consequences. The effective Hamiltonians can be block diagonalised in blocks. In the KDs are mixed with each other but not with the nuclear spin, such that the resulting states are merely tilted around an axis perpendicular to the crystal axis. On the other hand, the KD electronic states are entangled with the nuclear spin, i.e.
| (14) | ||||
and similarly for the corresponding orthogonal states . The analytic diagonalization of the effective hyperfine Hamiltonian (13) including a static external magnetic field can be found in the supplemental material [41].
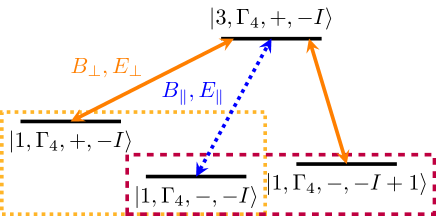
In combination with the selection rules for the electronic states [30], the mixing leads to the relevant allowed transitions. Here we concentrate on a set of transitions that can be used to transfer the pseudo-spin state of the ground-state KD to the nuclear spin and vice versa via a Lambda () system, i.e. . When constructing a system using a different KD we can neglect the nuclear driving term because transitions between the nuclear levels of the same KD pseudo-spin state are highly detuned. Because , we immediately see that this state can couple to as well as via a KD pseudo-spin conserving transition. Therefore, these levels can be used as a system driven by a magnetic or electric field perpendicular to the crystal axis, as shown in Fig. 4.
Analogously our effective theory shows that the hyperfine interaction opens the possibility to directly drive the pseudo-spin transition of the KDs for small magnetic fields due to the pseudo spin tilt or the pseudo-spin nuclear entanglement; this was studied using a different framework by Gilardoni et al. [43]. Lastly, when the spin-orbit splitting is sufficiently smal, the second order hyperfine interaction can enable optical driving inside the KDs by mixing the KDs of the same orbital doublet.
In summary, we introduced a theory to describe the hyperfine interacion in TM defects in SiC having a single electron in a -shell. The theory yields new insights on previous measurements and reduces the required number of fit parameters of the effective hyperfine coupling tensor. The newly gained insights can be used to construct a transition that can be exploited to create a nuclear spin quantum memory.
Acknowledgements.
We thank A. Csóré and A. Gali for useful discussions and acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 862721 (QuanTELCO).References
- Kimble [2008] H. J. Kimble, The quantum internet, Nature 453, 1023 (2008).
- Aharonovich et al. [2016] I. Aharonovich, D. Englund, and M. Toth, Solid-state single-photon emitters, Nature Photonics 10, 631 (2016).
- Heshami et al. [2016] K. Heshami, D. G. England, P. C. Humphreys, P. J. Bustard, V. M. Acosta, J. Nunn, and B. J. Sussman, Quantum memories: emerging applications and recent advances, J. Mod. Opt. 63, 2005 (2016).
- Awschalom et al. [2021] D. Awschalom, K. K. Berggren, H. Bernien, S. Bhave, L. D. Carr, P. Davids, S. E. Economou, D. Englund, A. Faraon, M. Fejer, S. Guha, M. V. Gustafsson, E. Hu, L. Jiang, J. Kim, B. Korzh, P. Kumar, P. G. Kwiat, M. Lončar, M. D. Lukin, D. A. Miller, C. Monroe, S. W. Nam, P. Narang, J. S. Orcutt, M. G. Raymer, A. H. Safavi-Naeini, M. Spiropulu, K. Srinivasan, S. Sun, J. Vučković, E. Waks, R. Walsworth, A. M. Weiner, and Z. Zhang, Development of quantum interconnects (quics) for next-generation information technologies, PRX Quantum 2, 017002 (2021).
- Clerk et al. [2020] A. A. Clerk, K. W. Lehnert, P. Bertet, J. R. Petta, and Y. Nakamura, Hybrid quantum systems with circuit quantum electrodynamics, Nature Phys. 16, 257 (2020).
- Smirnov et al. [2020] D. S. Smirnov, T. S. Shamirzaev, D. R. Yakovlev, and M. Bayer, Dynamic polarization of electron spins interacting with nuclei in semiconductor nanostructures, Phys. Rev. Lett. 125, 156801 (2020).
- Burkard et al. [2020] G. Burkard, M. J. Gullans, X. Mi, and J. R. Petta, Superconductor–semiconductor hybrid-circuit quantum electrodynamics, Nature Reviews Physics 2, 129 (2020).
- He et al. [1993] X.-F. He, N. B. Manson, and P. T. H. Fisk, Paramagnetic resonance of photoexcited N-V defects in diamond. I. level anticrossing in the 3A ground state, Phys. Rev. B 47, 8809 (1993).
- Gaebel et al. [2006] T. Gaebel, M. Domhan, I. Popa, C. Wittmann, P. Neumann, F. Jelezko, J. R. Rabeau, N. Stavrias, A. D. Greentree, S. Prawer, J. Meijer, J. Twamley, P. R. Hemmer, and J. Wrachtrup, Room-temperature coherent coupling of single spins in diamond, Nature Phys. 2, 408 (2006).
- Childress et al. [2006] L. Childress, M. V. G. Dutt, J. M. Taylor, A. S. Zibrov, F. Jelezko, J. Wrachtrup, P. R. Hemmer, and M. D. Lukin, Coherent dynamics of coupled electron and nuclear spin qubits in diamond, Science 314, 281 (2006).
- Gali et al. [2008] A. Gali, M. Fyta, and E. Kaxiras, Ab initiosupercell calculations on nitrogen-vacancy center in diamond: Electronic structure and hyperfine tensors, Phys. Rev. B 77, 155206 (2008).
- Felton et al. [2009] S. Felton, A. M. Edmonds, M. E. Newton, P. M. Martineau, D. Fisher, D. J. Twitchen, and J. M. Baker, Hyperfine interaction in the ground state of the negatively charged nitrogen vacancy center in diamond, Phys. Rev. B 79, 075203 (2009).
- Maze et al. [2011] J. R. Maze, A. Gali, E. Togan, Y. Chu, A. Trifonov, E. Kaxiras, and M. D. Lukin, Properties of nitrogen-vacancy centers in diamond: the group theoretic approach, New J. Phys. 13, 025025 (2011).
- Fuchs et al. [2011] G. D. Fuchs, G. Burkard, P. V. Klimov, and D. D. Awschalom, A quantum memory intrinsic to single nitrogen–vacancy centres in diamond, Nature Phys. 7, 789 (2011).
- Busaite et al. [2020] L. Busaite, R. Lazda, A. Berzins, M. Auzinsh, R. Ferber, and F. Gahbauer, Dynamic 14N nuclear spin polarization in nitrogen-vacancy centers in diamond, Phys. Rev. B 102, 224101 (2020).
- Hegde et al. [2020] S. S. Hegde, J. Zhang, and D. Suter, Efficient quantum gates for individual nuclear spin qubits by indirect control, Phys. Rev. Lett. 124, 220501 (2020).
- Doherty et al. [2013] M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup, and L. C. L. Hollenberg, The nitrogen-vacancy colour centre in diamond, Phys. Rep. 528, 1 (2013).
- Suter and Jelezko [2017] D. Suter and F. Jelezko, Single-spin magnetic resonance in the nitrogen-vacancy center of diamond, Prog. Nucl. Magn. Reson. Spectrosc. 98-99, 50 (2017).
- Bosma et al. [2018] T. Bosma, G. J. J. Lof, C. M. Gilardoni, O. V. Zwier, F. Hendriks, B. Magnusson, A. Ellison, A. Gällström, I. G. Ivanov, N. T. Son, R. W. A. Havenith, and C. H. van der Wal, Identification and tunable optical coherent control of transition-metal spins in silicon carbide, npj Quantum Inf. 4, 48 (2018).
- Spindlberger et al. [2019] L. Spindlberger, A. Csóré, G. Thiering, S. Putz, R. Karhu, J. Hassan, N. Son, T. Fromherz, A. Gali, and M. Trupke, Optical properties of vanadium in 4H silicon carbide for quantum technology, Phys. Rev. Appl. 12, 014015 (2019).
- Gilardoni et al. [2020] C. M. Gilardoni, T. Bosma, D. van Hien, F. Hendriks, B. Magnusson, A. Ellison, I. G. Ivanov, N. T. Son, and C. H. van der Wal, Spin-relaxation times exceeding seconds for color centers with strong spin–orbit coupling in SiC, New J. Phys. 22, 103051 (2020).
- Wolfowicz et al. [2020] G. Wolfowicz, C. P. Anderson, B. Diler, O. G. Poluektov, F. J. Heremans, and D. D. Awschalom, Vanadium spin qubits as telecom quantum emitters in silicon carbide, Sci. Adv. 6, eaaz1192 (2020).
- Csóré and Gali [2020] A. Csóré and A. Gali, Ab initio determination of pseudospin for paramagnetic defects in sic, Phys. Rev. B 102, 241201 (2020).
- Kaufmann et al. [1997] B. Kaufmann, A. Dörnen, and F. S. Ham, Crystal-field model of vanadium in 6H silicon carbide, Phys. Rev. B 55, 13009 (1997).
- Baur et al. [1997] J. Baur, M. Kunzer, and J. Schneider, Transition metals in SiC polytypes, as studied by magnetic resonance techniques, Phys. Status Solidi (a) 162, 153 (1997).
- Meija et al. [2016] J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. D. Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss, T. Walczyk, and T. Prohaska, Isotopic compositions of the elements 2013 (IUPAC technical report), Pure Appl. Chem. 88, 293 (2016).
- Barbouche et al. [2017] M. Barbouche, R. B. Zaghouani, N. Benammar, V. Aglieri, M. Mosca, R. Macaluso, K. Khirouni, and H. Ezzaouia, New process of silicon carbide purification intended for silicon passivation, Superlattices Microstruct. 101, 512 (2017).
- Mazzocchi et al. [2019] V. Mazzocchi, P. Sennikov, A. Bulanov, M. Churbanov, B. Bertrand, L. Hutin, J. Barnes, M. Drozdov, J. Hartmann, and M. Sanquer, 99.992 % 28si cvd-grown epilayer on 300mm substrates for large scale integration of silicon spin qubits, J. Cryst. Growth 509, 1 (2019).
- Audi et al. [2003] G. Audi, O. Bersillon, J. Blachot, and A. Wapstra, The NUBASE evaluation of nuclear and decay properties, Nucl. Phys. A 729, 3 (2003).
- Tissot and Burkard [2021] B. Tissot and G. Burkard, Spin structure and resonant driving of spin-1/2 defects in SiC, Phys. Rev. B 103, 064106 (2021).
- Dresselhaus et al. [2010] M. S. Dresselhaus, G. Dresselhaus, and A. Jorio, Group theory : application to the physics of condensed matter (Springer-Verlag, Berlin, 2010).
- Munzarová et al. [2000] M. L. Munzarová, P. Kubáček, and M. Kaupp, Mechanisms of EPR hyperfine coupling in transition metal complexes, J. Am. Chem. Soc. 122, 11900 (2000).
- Coish and Baugh [2009] W. A. Coish and J. Baugh, Nuclear spins in nanostructures, Phys. Status Solidi (b) 246, 2203 (2009).
- Micera and Garribba [2011] G. Micera and E. Garribba, Is the spin‐orbit coupling important in the prediction of the 51V hyperfine coupling constants of VO2+ species? ORCA versus gaussian performance and biological applications, J. Comput. Chem. 32, 2822 (2011).
- Vícha et al. [2014] J. Vícha, M. Straka, M. L. Munzarová, and R. Marek, Mechanism of spin-orbit effects on the ligand NMR chemical shift in transition-metal complexes: Linking NMR to EPR, J. Chem. Theory Comput. 10, 1489 (2014).
- Gohr et al. [2015] S. Gohr, P. Hrobárik, M. Repiský, S. Komorovský, K. Ruud, and M. Kaupp, Four-component relativistic density functional theory calculations of EPR g- and hyperfine-coupling tensors using hybrid functionals: Validation on transition-metal complexes with large tensor anisotropies and higher-order spin-orbit effects, J. Phys. Chem. A 119, 12892 (2015).
- Stone [2005] N. Stone, Table of nuclear magnetic dipole and electric quadrupole moments, At. Data Nucl. Data Tables 90, 75 (2005).
- Ham [1965] F. S. Ham, Dynamical Jahn-Teller effect in paramagnetic resonance spectra: Orbital reduction factors and partial quenching of spin-orbit interaction, Phys. Rev. 138, A1727 (1965).
- Ham [1968] F. S. Ham, Effect of linear Jahn-Teller coupling on paramagnetic resonance in a state, Phys. Rev. 166, 307 (1968).
- Cornwell [1997] J. F. Cornwell, Group theory in physics : an introduction (Academic Press, San Diego, Calif, 1997).
- SM [2021] See supplemental material at [URL will be inserted by publisher] for a more detailed derivation of the hyperfine Hamiltonian in the orbital constrained to symmetry of the crystal, the analytic diagonalization of the second order effective Hamiltonians for the KDs, and a table of hyperfine tensors for different V defects corresponding to data from Wolfowicz et al. (2021).
- Bravyi et al. [2011] S. Bravyi, D. P. DiVincenzo, and D. Loss, Schrieffer-Wolff transformation for quantum many-body systems, Ann. Phys. 326, 2793 (2011).
- Gilardoni et al. [2021] C. M. Gilardoni, I. Ion, F. Hendriks, M. Trupke, and C. H. van der Wal, Hyperfine-mediated transitions between electronic spin-1/2 levels of transition metal defects in SiC, in preparation (2021).