Hyperbolic Graph Neural Networks at Scale:
A Meta Learning Approach

Our problem consists of a group of tasks $\mathcal{T}_{i}\in\mathcal{T}$ which are divided into a support set $\mathcal{T}^{s}$ and query set $\mathcal{T}^{q}$, where $\mathcal{T}^{s}\cap\mathcal{T}^{q}=\phi$. Furthermore, each task $\mathcal{T}_{i}$ is a batch of node-centric subgraphs $S_{u}$ with a corresponding label $Y_{u}$ (class of root node in node classification or root link in link prediction). The subgraphs $S_{u}$ could be the partitions derived from a single graph or multiple graphs, both denoted by $\mathcal{G}^{\cup}=\mathcal{G}^{s}\cup\mathcal{G}^{q}$. We also define $Y_{s}=\{Y_{u}\in\mathcal{T}^{s}\}$ and $Y_{q}=\{Y_{u}\in\mathcal{T}^{q}\}$ as the set of labels in the support and query set respectively. The primary goal of meta-learning is to learn a predictor using the support set, $P_{\theta_{*}}(Y_{s}|\mathcal{T}^{s})$ such that the model can quickly learn a predictor $P_{\theta}(Y_{s}|\mathcal{T}^{s})$ on the query set. Following literature in this area [18], the problem categories are defined as follows:

1. 1.

   Single graph, shared labels $\langle SG,SL\rangle$: The objective is to learn the meta-learning model $P_{\theta_{*}\rightarrow\theta}$, where $Y_{s}=Y_{q}$ and $|\mathcal{G}^{s}|=|\mathcal{G}^{q}|=1$. It should be noted that the tasks are based on subgraphs, so $|\mathcal{G}^{s}|=|\mathcal{G}^{q}|=1\mathrel{{\ooalign{$\not\phantom{=}$\cr$\implies$}}}|\mathcal{T}^{s}|=|{T}^{q}|=1$. Also, this problem setup is identical to the standard node classification task considering $\mathcal{T}_{i}^{q}\in D_{test}$ to be the test set.

2. 2.

   Single graph, disjoint labels $\langle SG,DL\rangle$: This problem operates on the same graph in the support and query set, however unlike the previous one, the label sets are disjoint. The goal is to learn the model $P_{\theta_{*}\rightarrow\theta}$, where $|\mathcal{G}^{s}|=|\mathcal{G}^{q}|=1\text{ and }Y_{s}\cap Y_{q}=\phi$.

3. 3.

   Multiple graphs, shared labels $\langle MG,SL\rangle$: This problem setup varies in terms of the dataset it handles, i.e., the dataset can contain multiple graphs instead of a single one. However, our method focuses on tasks which contain node-centric subgraphs, and hence, the model’s aim is the same as problem 1. The aim is to learn the predictor model $P_{\theta_{*}\rightarrow\theta}$, where $Y_{s}=Y_{q}$ and $|\mathcal{G}^{s}|,|\mathcal{G}^{q}|>1$.

4. 4.

   Multiple graphs, disjoint labels $\langle MG,DL\rangle$: In this problem, the setup is similar to the previous one, but only with disjoint labels instead of shared ones, i.e., learn a predictor model $P_{\theta_{*}\rightarrow\theta}$, where $Y_{s}\cap Y_{q}=\phi$ and $|\mathcal{G}^{s}|,|\mathcal{G}^{q}|>1$.

From the problem setups, we observe that, while they handle different dataset variants, the base HNN model operates on the $(S_{u},Y_{u})$ pair. So, we utilize a hyperbolic subgraph encoder and prototypical labels to encode $S_{u}$ and get a continuous version of $Y_{u}$ for our meta-learning algorithm, respectively.

In previous methods [16, 18, 38], authors have shown that nodes’ local neighborhood provides some informative signals for the prediction task. While the theory is not trivially extensible, we use the local tangent space of Poincaré ball model to prove that the local neighborhood policy holds better for HNN models. The reason being that, while message propagation is linear in Euclidean GNNs [42], it is exponential in HNNs. Hence, a node’s influence, as given by Definition 1, outside its neighborhood decreases exponentially.

Theorem 1 shows that the influence of a node decreases exponent-of-exponentially ($exp_{u}^{c}=\mathcal{O}(e^{n})$) with increasing distance $\|p_{uv}\|$. Thus, we conclude that encoding the local neighborhood of a node is sufficient to encode its features for label prediction.

Theorem 2 shows that encoding the local subgraph is a $e^{\|p_{uv}\|}$ order approximation of encoding the entire graph, and thus, with high enough $\|p_{uv}\|$, the encodings are equivalent. Note that $\|p_{uv}\|$ is equivalent to the subgraph’s neighborhood size ($k$ in $k$-hop). This shows that encoding a node’s local neighborhood is sufficient to encode its features. Theorem proofs are provided in Appendix B. The above theorems provide us with the theoretical justification for encoding local subgraphs into our meta-learning framework. Hence, we partition the input $\mathcal{G}^{\cup}$ into subgraphs $S_{u}=V\times E$ centered at root node $u$, with $|V|$ nodes, $|E|$ edges, a neighborhood size $k$, and the corresponding label $Y_{u}$. The subgraphs are processed through an $k$-layer HGCN network and the Einstein midpoint [33] of all the node encodings are taken as the overall encoding of the subgraph $S_{u}$. For a given subgraph $S_{u}=(A,X)$, where $A\in\mathbb{H}^{\|V\|\times\|V\|}$ is the local adjacency matrix and $X\in\mathbb{H}^{\|V\|\times m}$ are the node feature vectors of $m$ dimension, the encoding procedure given can be formalized as:

where $HGCN(A,X)\in\mathbb{H}^{\|V\|\times d}$ is the output of k-layer HGCN with $d$ output units and $e_{u}\in\mathbb{H}^{d}$ is the final subgraph encoding of $S_{u}$. $\upgamma_{iu}$ is the Lorentz factor of the hyperbolic vector $h_{iu}$ that indicates its weightage towards the Einstein midpoint.

Label information is generally categorical in node classification tasks. However, this does not allow us to pass inductive biases from the support set to the query set. Hence, to circumvent this issue, we use prototypical networks [31] as our label encoding. Our approach constructs continuous label prototypes by using the mean of meta-training nodes’ features that belong to the label. These prototypes are then employed to classify meta-testing samples based on their similarity to the corresponding meta-training label prototypes. This enables our model to handle new, non-exhaustive labels in an inductive manner, without the need for additional training data. The primary idea is to form continuous label prototypes using the mean of nodes that belong to the label. To this end, the continuous label prototype of a label $y_{k}$ is defined as $c_{k}=\frac{\sum_{Y_{u}=y_{k}}\upgamma_{i}e_{i}}{\sum_{Y_{u}=y_{k}}\upgamma_{i}}\text{, where }\upgamma_{i}=\frac{1}{\sqrt{1-\|e_{i}\|^{2}}}$,and $e_{i}\in\mathbb{H}^{d}$ is encoding of subgraphs $S_{u}$ with labels $Y_{u}=y_{k}$. For each $S_{u}$ with class $y_{k}$, we compute the class distribution vector as $p_{k}=\frac{e^{(-d_{\mathbb{H}}^{c}(e_{u},c_{k}))}}{\sum_{k}e^{(-d_{\mathbb{H}}^{c}(e_{u},c_{k}))}}\text{, where }d_{\mathbb{H}}^{c}(e_{u},c_{k})=\frac{2}{\sqrt{c}}\tanh^{-1}\left(\sqrt{c}\|-e_{u}\oplus c_{k}\|\right)$ and the loss for HNN updates $\mathcal{L}(p,y)=\sum_{j}y_{i}\log{p_{j}}$, where $y_{i}$ is the one-hot encoding of the ground truth. The class distribution vector $p_{k}$ is a softmax over the hyperbolic distance of subgraph encoding to the label prototypes, which indicates the probability that the subgraph belongs to the class $y_{k}$. The loss function $\mathcal{L}(p,y)$ is the cross-entropy loss between ground truth labels $y$ and the class distribution vector $p$.

In the previous section, we learned a continuous label encoding that is able to capture inductive biases from the subgraph. In this section, we utilize the optimization-based MAML algorithm [12] to transfer the inductive biases from the support set to the query set. To this end, we sample a batch of tasks, where each task $\mathcal{T}_{i}=\{S_{i},Y_{i}\}_{i=1}^{\|\mathcal{T}_{i}\|}$. In the meta-training phase, we first optimize the HNN parameters using the Riemannian stochastic gradient descent (RSGD) [2] on support loss, i.e., for each $\mathcal{T}^{s}_{i}\in\mathcal{T}^{s}_{train}:\theta^{*}_{j}\leftarrow exp^{c}_{\theta^{*}_{j}}(-\alpha\nabla\mathcal{L}^{s})$, where $\alpha$ is the learning rate of RSGD. Using the updated parameters $\theta^{*}_{j}$, we record the evaluation results on the query set, i.e., loss on task $\mathcal{T}^{q}_{i}\in\mathcal{T}^{q}_{train}$ is $\mathcal{L}^{q}_{i}$. The above procedure is repeated $\eta$ times post which $\mathcal{L}^{q}_{i}$ over the batch of tasks $\mathcal{T}^{q}_{i}\in\mathcal{T}^{q}_{train}$ is accumulated for the meta update $\theta^{*}\leftarrow exp^{c}_{\theta^{*}}(-\beta\nabla\sum_{i}\mathcal{L}^{q}_{i})$. The above steps are repeated with the updated $\theta^{*}$ and a new batch of tasks till convergence. The final updated parameter set $\theta^{*}\rightarrow\theta$ is transferred to the meta-testing phase. In meta-testing, the tasks $\mathcal{T}^{s}_{i}\in\mathcal{T}^{s}_{test}$ are used for RSGD parameter updates, i.e., $\mathcal{T}^{s}_{i}\in\mathcal{T}^{s}_{test}:\theta_{j}\leftarrow exp^{c}_{\theta_{j}}(-\alpha\nabla\mathcal{L}^{s})$ until convergence. The updated parameters $\theta$ are used for the final evaluation on $\mathcal{T}^{q}_{i}\in\mathcal{T}^{q}_{test}$. Our meta-learning procedure is further detailed in Appendix C and the implementation code with our experiments is available at https://github.com/Akirato/HGRAM. Details on implementation and broader impacts are provided in Appendices 3.5 and E, respectively.

H-GRAM is primarily implemented in Pytorch [26], with geoopt [21] and GraphZoo [35] as support libraries for hyperbolic formulations. Our experiments are conducted on a Nvidia V100 GPU with 16 GB of VRAM. For gradient descent, we employ Riemannian Adam [28] with an initial learning rate of 0.01 and standard $\beta$ values of 0.9 and 0.999. The other hyper-parameters were selected based on the best performance on the validation set ($\mathcal{D}_{val}$) under the given computational constraints. In our experiments, we empirically set $k=2,d=32,h=4$, and $\eta=10$. We explore the following search space and tune our hyper-parameters for best performance. The number of tasks in each batch are varied among 4, 8, 16, 32, and 64. The learning rate explored for both HNN updates and meta updates are $10^{-2},5\times 10^{-3},10^{-3}$ and $5\times 10^{-4}$. The size of hidden dimensions are selected from among 64, 128, and 256. The final best-performing hyper-parameter setup for real-world datasets is presented in Table 5.

For the task of meta-learning, we utilize the experimental setup from earlier approaches [18]; two synthetic datasets to understand if H-GRAM is able to capture local graph information and five real-world datasets to evaluate our model’s performance in a few-shot setting.

• •

  Synthetic Cycle [18] contains multiple graphs with cycle as the basis with different topologies (House, Star, Diamond, and Fan) attached to the nodes on the cycle. The classes of the node are defined by their topology.

• •

  Synthetic BA [18] uses Barabási-Albert (BA) graph as the basis with different topologies planted within it. The nodes are labeled using spectral clustering over the Graphlet Distribution Vector [27] of each node.

• •

  ogbn-arxiv [17] is a large citation graph of papers, where titles are the node features and subject areas are the labels.

• •

  Tissue-PPI [43, 16] contains multiple protein-protein interaction (PPI) networks collected from different tissues, gene signatures and ontology functions as features and labels, respectively.

• •

  FirstMM-DB [25] is a standard 3D point cloud link prediction dataset.

• •

  Fold-PPI [43] is a set of tissue PPI networks, where the node features and labels are the conjoint triad protein descriptor [30] and protein structures, respectively.

• •

  Tree-of-Life [44] is a large collection of PPI networks, originating from different species.

For comparison with HNNs, we utilize the standard benchmark citation graphs of Cora [29], Pubmed [24], and Citeseer [29]. For the baselines, we select the following methods to understand H-GRAM’s performance compared to state-of-the-art models in the tasks of meta-learning and standard graph processing.

• •

  Meta-Graph [3], developed for few-shot link prediction over multiple graphs, utilizes VGAE [20] model with additional graph encoding signals.

• •

  Meta-GNN [40] is a MAML developed over simple graph convolution (SGC) network [36].

• •

  FS-GIN [37] runs Graph Isomorphism Network (GIN) on the entire graph and then uses the few-shot labelled nodes to propagate loss and learn.

• •

  FS-SGC [36] is the same as FS-GIN but uses SGC instead of GIN as the GNN network.

• •

  ProtoNet [31] learn a metric space over label prototypes to generalize over unseen classes.

• •

  MAML [12] is a Model-Agnostic Meta Learning (MAML) method that learns on multiple tasks to adapt the gradients faster on unseen tasks.

• •

  HMLP [13], HGCN [4], and HAT [15] are the hyperbolic variants of Euclidean multi-layer perceptron (MLP), Graph Convolution Network (GCN), and Attention (AT) networks that use hyperbolic gyrovector operations instead of the vector space model.

It should be noted that not all the baselines can be applied to both node classification and link prediction. Hence, we compare our model against the baselines only on the applicable scenarios.

To analyze the meta-learning capability of H-GRAM, we compare it against previous approaches in this area on a standard evaluation setup. We consider two experimental setups inline with previous evaluation in the literature [18]; (i) with synthetic datasets to analyze performance on different problem setups without altering the graph topology, and (ii) with real-world datasets to analyze performance for practical application. Based on the problem setup, the datasets are partitioned into node-centric subgraphs with corresonding root node’s label as the subgraph’s ground truth label. The subgraphs are subsequently batched into tasks which are further divided into support set and query set for meta-learning. The evaluation metric for both the tasks of node classification and link prediction is accuracy $\mathcal{A}=|Y=\hat{Y}|/|Y|$. For robust comparison, the metrics are computed over five folds of validation splits in a 2-shot setting for node classification and 32-shot setting for link prediction. Table 2 presents the five-fold average and 95% confidence interval of our experiments on synthetic and real-world datasets, respectively. From the results, we observe that H-GRAM consistently outperforms the baseline methods on a diverse set of datasets and meta-learning problem setups. For the disjoint labels setting, H-GRAM outperforms the best baseline in both the cases of single and multiple graphs. In the case of synthetic graphs, we observe that subgraph methods of H-GRAM and G-Meta outperform the entire graph encoding based approaches showing that subgraph methods are able to limit the over-smoothing problem [6] and improve performance. Also, we observe that meta-learning methods (ProtoNet and MAML) are unreliable in their results producing good results for some tasks and worse for others, whereas H-GRAM is consistently better across the board. Hence, we conclude that using label prototypes to learn inductive biases and transferring them using MAML meta updates is a more robust technique. We note that H-GRAM, unlike previous HNN models, is able to handle graphs with edges and nodes in the order of millions, as evident by the performance on large real-world datasets including ogbn-arxiv, Tissue-PPI, Fold-PPI, and Tree-of-Life. Our experiments clearly demonstrate the significant performance of H-GRAM in a wide-range of applications and prove the effectiveness of meta-learning in HNN models.

The current HNN formulations of HMLP, HAT, and HGCN do not scale to large datasets, and hence, we were not able to compare them against H-GRAM on large-scale datasets. However, it is necessary to compare the standard HNN formulations with H-GRAM to understand the importance of subgraph encoders and meta-learning.

Thus, we utilize the single graph and shared labels setup of H-GRAM to evaluate its performance on citation networks of Cora, Pubmed, and Citeseer for both tasks of node classification and link prediction. We also compare the time taken by our model and other HNNs on varying number of nodes $\left(|\mathcal{V}|=\{10^{i}\}_{i=1}^{7}\right)$ in the Synthetic BA graph. For this experiment, we also consider a multi-GPU version of H-GRAM that parallelizes the HNN update computations and accumulates them for meta update. From our results, presented in Table 3, we observe that H-GRAM is, on average, able to outperform the best baseline. This shows that our formulation of HNN models using meta-learning over node-centric subgraphs is more effective than the traditional models, while also being scalable over large datasets. The scalability allows for multi-GPU training and translates the performance gains of HNNs to larger datasets. In the results provided in Figure 3, we observe that the time taken by the models is inline with their parameter complexity (HMLP$\leq$HGCN$\leq$HAT$\leq$H-GRAM). However, the traditional HNNs are not able to scale beyond $|\mathcal{V}|=10^{4}$, whereas, H-GRAM is able to accommodate large graphs. Another point to note is that H-GRAM(multi) is able to parallelize well over multiple GPUs with its time taken showing stability after $10^{4}$ nodes (which is the size of nodes that a single GPU can accommodate).

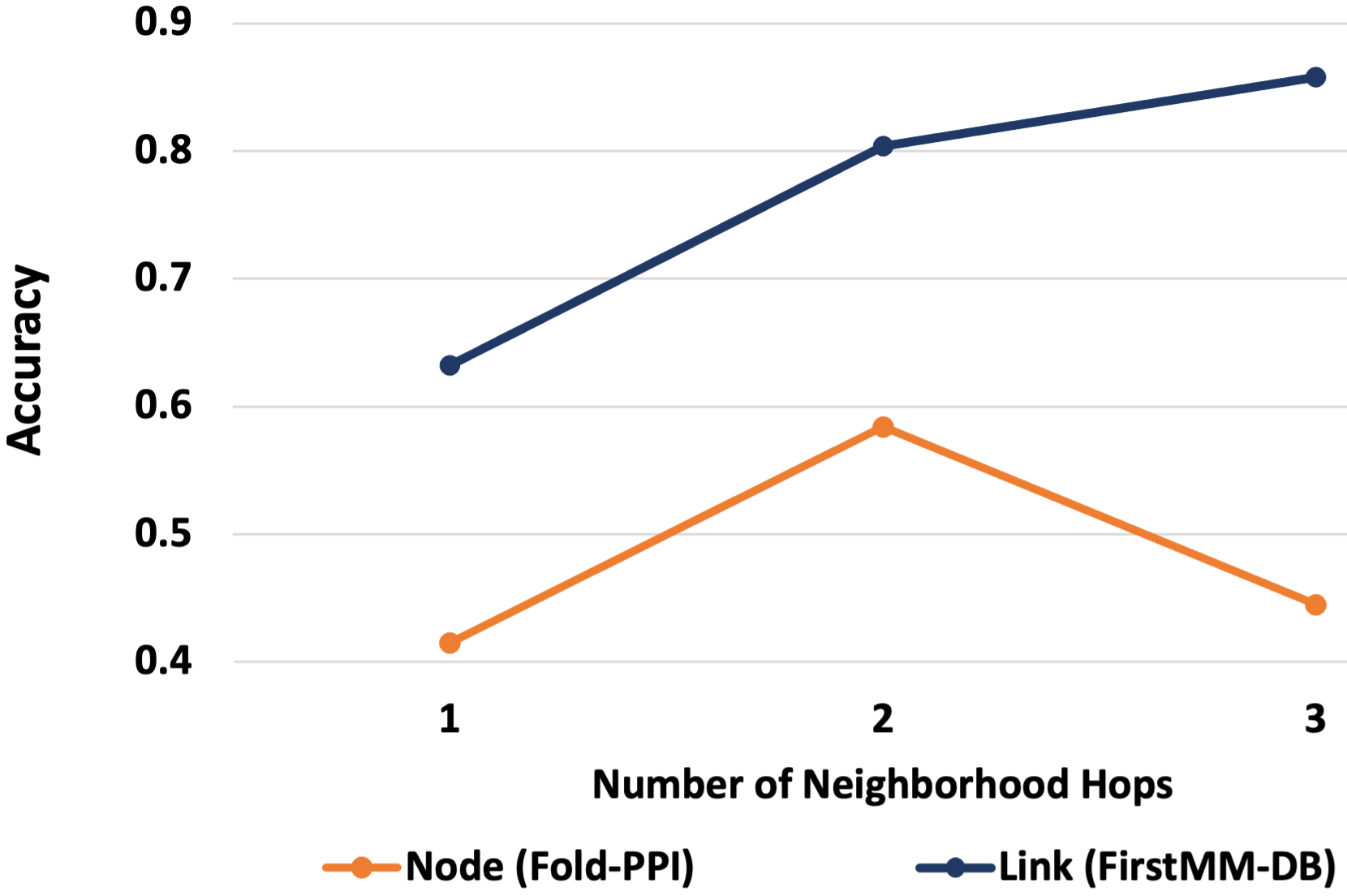
To understand the effect of different few-shot learning scenarios, we vary the number of few-shots $M$ and hops $K$ in the neighborhood. For the experiment on few-shot classification, we consider the problems of node classification on Fold-PPI dataset and link prediction on FirstMM-DB dataset. We vary $M=1,2,3$ and $M=16,32,64$ for node classification and link prediction, respectively, and calculate the corresponding accuracy and 95% confidence interval of H-GRAM. The results for this experiment are presented in Figures 4(a) and 4(b) for node classification and link prediction, respectively. To determine the effect of hops in the neighborhood, we vary $K=1,2,3$ for the same problem setting and compute the corresponding performance of our model. The results for varying neighborhood sizes are reported in Figure 4(c). In the results on varying the number of few-shots, we observe a linear trend in both the tasks of node classification and link prediction, i.e., a linear increase in H-GRAM’s accuracy with an increase in the number of shots in meta-testing. Thus, we conclude that H-GRAM, like other generic learning models, performs better with an increasing number of training samples. In the experiment on increasing the neighborhood size, we observe that in the task of node classification, $K=3$ shows the best performance, but in link prediction $K=2$ has the best performance, with a significant drop in $K=3$. Thus, for stability, we choose $K=2$ in our experiments. The trend in link prediction also shows that larger neighborhoods can lead to an increase in noise, which can negatively affect performance.

In this section, we aim to understand the contribution of the different components in our model. To this end, we compare variants of our model by (i) varying the base HNN model (HMLP, HAT, and HGCN), and (ii) deleting individual meta-learning components - H-ProtoNet implies H-GRAM without meta updates and H-MAML implies H-GRAM without prototypes. The model variants are compared on the real-world datasets and the results are presented in Table 4. The ablation study indicates that meta gradient updates and label prototypes contribute to $\approx$16% and $\approx$6% improvement in H-GRAM’s performance, respectively. This clearly demonstrates the ability of label prototypes in encoding inductive biases and that of meta gradients in transferring the knowledge from meta-training to the meta-testing phase. Additionally, from our study on different HNN bases for H-GRAM, we note that the HGCN base outperforms the other bases of HMLP and HAT by $\approx$19% and $\approx$2%, respectively. Thus, we choose HGCN as the base in our final model.