hyperbolic fibered slice knots with right-veering monodromy
Abstract.
We construct a hyperbolic fibered slice knot with right-veering monodromy, which disproves a conjecture posed in [HKK+21].
1. introduction
We give a negative answer to Question 8.2 posed in [HKK+21].
Question 1.1.
If K is a hyperbolic fibered slice knot, does the fractional Dehn twist coefficient (FDTC) of the monodromy vanish?
We construct a hyperbolic slice fibered knot with positive FDTC.
1.1. Motivation.
The authors [HKK+21] observes that many low-crossing slice fibered knots have zero FDTC. Any cable of slice fibered knot is still slice fibered, whereas FDTC of cable equals to . The authors therefore ask the above question about hyperbolic fibered slice knots.
Baldwin, Ni and Sivek [BNS22, Corollary 1.7] prove the following related proposition in terms of the invariant in Heegaard Floer homology:
Proposition 1.2.
If is a fibered knot with thin knot Floer homology such that , then FDTC vanishes.
The invariant vanishes for slice knots. Proposition 1.2 explains the case for low-crossing fibered slice knots because many of those are thin.
We have an immediate corollary:
Corollary 1.3.
The knot Floer homology of is not thin.
1.2. Organization.
We follow the recipe of Kazez and Roberts [KR13] to construct hyperbolic fibered knots with positive FDTC. The search for ribbon knot is inspired by the work of Hitt and Silver [HS91]. In section 2 we review Nielson-Thurston classification of surface automorphism and examples from Kazez and Roberts. We construct our example in section 3.
2. monodromies of fibered knots in
2.1. Surface automorphism.
We first recall Nielson-Thurston classfication of surface automorphisms:
Theorem 2.1.
[CCB88, Thu88] Let be an oriented hyperbolic surface with geodesic boundary, and let . Then is freely isotopic to either
-
(1)
a pseudo-Anosov homeomorphism that preserves a pair of geodesic laminations and ,
-
(2)
a periodic homeomorphism such that for some ,
-
(3)
a reducible homeomorphism that preserves a maximal collection of simple closed geodesic curves in . To avoid overlap, we consider reducible only when it is not periodic.
In particular, we only regard as reducible only if it is not periodic to avoid overlap. Let be an isotopy from to its Thurston representative . Considering the restriction of to the boundary , we have a homeomorphism:
defined by . The fractional Dehn twist coefficient can be defined as the winding number of the arc . Nielson-Thurston classification guarantees that .
Thurston proved that a fibered knot is hyperbolic if and only if its monodromy is pesudo-Anosov. Fractional Dehn twist coefficient is closely related to the following notion of right-veeringness.
Definition 2.2.
[HKM07] A homeomorphism is called right-veering if for every based point and every properly embedded arc starting at , is to the right of , after isotoping so that it intersects minimally. Similarly, is called left-veering if is to the left of .
Proposition 2.3.
[HKM07] is right-veering if and only if for every component of , and is left-veering if and only if for every component of .
If , one can find two arcs such that one is moved by to the right and the other to the left. The significance of right-veeringness is highlighted by the following theorem of Honda, Kazez and Matić:
Theorem 2.4.
[HKM09] Every open book that is compatible with a tight contact structure is right-veering.
A large source of examples of reducible right-veering homeomorphism comes from the class of fibered cable knots. Indeed, if is the monodromy of a fibered cable knot with Seifert surface , then and is reducible. Let be the collection of curves preserved by . partitions into subsurfaces permuted by . Let be the subsurface containing , then is periodic. Kazez and Roberts characterize the monodromy of a fibered knot in in the following theorem:
Theorem 2.5.
Corollary 2.6.
or for some integer , . In particular, .
In particular, the cable of a fibered knot in has its monodromy attaining maximum FDTC. We review hyperbolic case in the next section.
2.2. Stallings’ twist and (2,1)-cable.
Let be an unknot properly embedded in a surface . We say is untwisted relative to if bounds a disk transverse to along . A Stallings’ twist [Sta78] is a surgery along such an untwisted . Kazez and Roberts apply Stallings’ twist on cables to produce hyperbolic fibered knots with maximum FDTC .
Let be an open book decomposition of with connected binding , where is pseudo-Anosov and . Let be the cable of . The fibered surface of can be viewed as the union of two copies , of connected by a 1-handle. Let be the monodromy of this new open book.
We choose a simple closed curve in such that and are two essential arcs. Moreover, we require to be nonseparating in . Let be the right-handed Dehn twist along and .
Theorem 2.7.
[KR13] is pseudo-Anosov and .
3. ribbon fibered knot
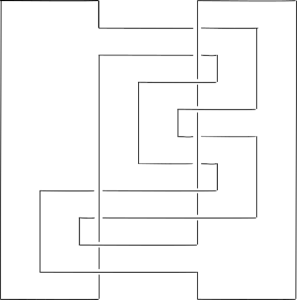
We are ready to construct a hyperbolic ribbon fibered knot with positive FDTC. Let be the knot from Rolfsen’s knot table. is a hyperbolic ribbon fibered knot with 3-genus 3. Figure 1 is a ribbon diagram for .
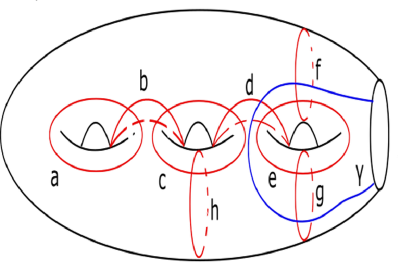
Let denote the monodromy. According to [CL], can be presented as decribed in Figure 2. One can see that is neither right-veering nor left-veering by choosing different endpoints of . Therefore, .
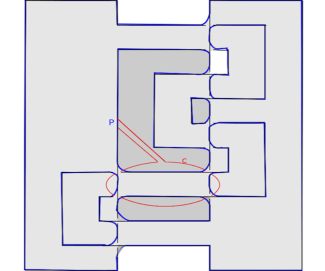
A Seifert surface of can be obtained by Seifert’s algorithm as explained in Figure 3. The genus of is 3 so that is the fibered surface.
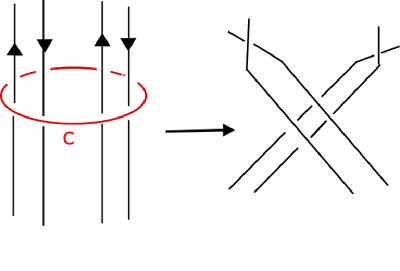
Let be the cable of (Figure 4). The twisted band connecting the two copies of is added at . is a nonseperating properly embedded arc on the fibered surface of . is also fibered whose fibered surface can be obtained by connecting two copies of with the same twisted band at . Then define a simple closed curve to be a band sum of the two copies of along an arc running across the twisted band.

Let denote the right-handed Dehn twist along , and denote the resulting fibered knot . By [KR13, Corollary 4.6], the monodromy is pseudo-Anosov and right-veering with .
Recall that is a ribbon knot, so is . is an unknotted untwisted curve. Performing a right-handed Dehn twist along has the same effect on applying a surgery along . The resulting manifold is still and we have a new knot . winds around two copies of a ribbon band (Figure 5).

.
Figure 6 illustrates the effect of surgery along to the ribbon bands. The resulting knot is still a ribbon knot.
Theorem 3.1.
is a hyperbolic ribbon fibered knot with FDTC. Hence, the monodromy is right-veering.
References
- [BNS22] John A Baldwin, Yi Ni, and Steven Sivek. Floer homology and right-veering monodromy, 2022. preprint, arXiv:2204.04093.
- [CCB88] Andrew J Casson, Andrew J Casson, and Steven A Bleiler. Automorphisms of surfaces after Nielsen and Thurston. Number 9. Cambridge University Press, 1988.
- [CL] Jae Choon Cha and Charles Livingston. Knotinfo: Table of knot invariants. http://www.indiana.edu/ knotinfo.
- [Gab97] David Gabai. Problems in foliations and laminations. Stud. in Adv. Math. AMS/IP, 2:1–34, 1997.
- [HKK+21] Diana Hubbard, Keiko Kawamuro, Feride Ceren Kose, Gage Martin, Olga Plamenevskaya, Katherine Raoux, Linh Truong, and Hannah Turner. Braids, fibered knots, and concordance questions. In Research Directions in Symplectic and Contact Geometry and Topology, pages 293–324. Springer, 2021.
- [HKM07] Ko Honda, William H. Kazez, and Gordana Matić. Right-veering diffeomorphisms of compact surfaces with boundary. Invent. Math., 169(2):427–449, 2007.
- [HKM09] Ko Honda, William H. Kazez, and Gordana Matić. On the contact class in Heegaard Floer homology. J. Differential Geom., 83(2):289–311, 2009.
- [HS91] L Richard Hitt and Daniel S Silver. Ribbon knot families via stallings’ twists. Journal of the Australian Mathematical Society, 50(3):356–372, 1991.
- [KR13] William H. Kazez and Rachel Roberts. Fractional Dehn twists in knot theory and contact topology. Algebr. Geom. Topol., 13(6):3603–3637, 2013.
- [Sta78] John R. Stallings. Constructions of fibred knots and links. In Algebraic and geometric topology (Proc. Sympos. Pure Math., Stanford Univ., Stanford, Calif., 1976), Part 2, Proc. Sympos. Pure Math., XXXII, pages 55–60. Amer. Math. Soc., Providence, R.I., 1978.
- [Thu88] William P Thurston. On the geometry and dynamics of diffeomorphisms of surfaces. Bulletin of the American mathematical society, 19(2):417–431, 1988.