Hybrid improper dipolar density wave in NaLaCoWO₆

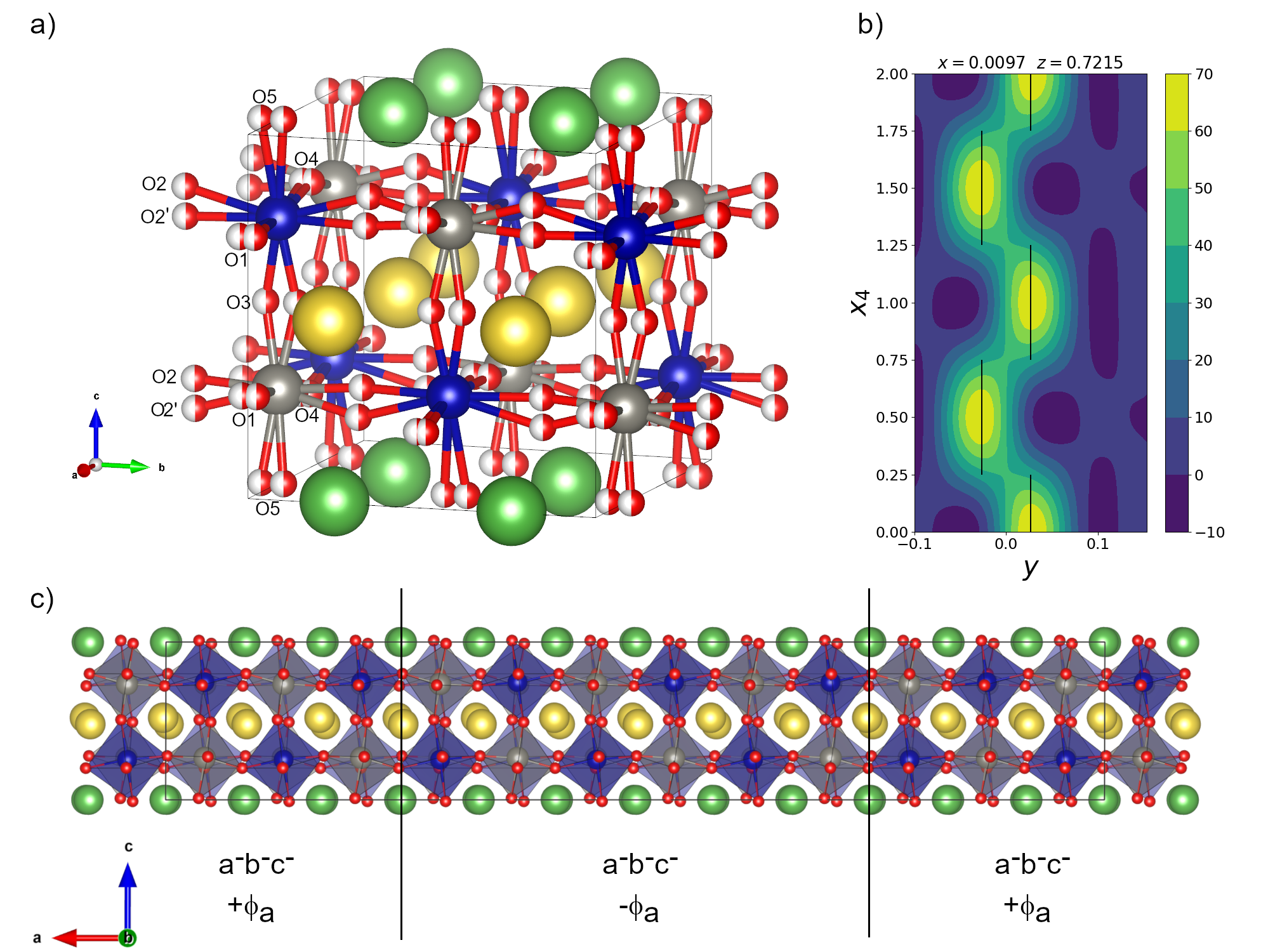
3D ED data collected on NaLaCoWO₆ nanocrystals (see Figure S1)[54] clearly show that the main reflections are accompanied by first order satellites (Figure 2a). The main reflections can be indexed with a pseudo-cubic cell with: a=7.83(3) Å, b=7.84(2) Å, c=7.89(8) Å and $\beta$ close to 90^∘ (the actual value refined against XRD data is 90.160(10)^∘). From the reconstruction of the reciprocal space, the extinction rule h+k=2n for the main reflections can be easily determined, indicating a C-centered lattice with no other extinctions observed. A reasonable model, with $C2/m$ symmetry, was found ab-initio using the charge flipping algorithm[55] on the 3D ED data. The average structure of the double ordered perovskite is in agreement with the one reported in literature,[32] with rock salt ordering of the CoO₆ and WO₆ octahedra, layer ordering of the Na and La cations and an average tilting pattern $a^{0}b^{-}c^{0}$.

Satellite reflections are observed in the 3D ED data along the $a^{*}$ direction, with a modulation vector q=0.172(2)$a^{*}$ . Some crystals show a strong twinning, which exchanges the $a^{*}$ and $b^{*}$ directions (see figure S2[54]). The collection of 3D ED data on a single crystalline domain allowed to determine the reflection conditions in four index notations as hklm: h+k=2n and h0lm: m=2n, which are consistent only with the superspace group $C2/m(\alpha 0\gamma)0s$. A first tentative refinement of the modulated structure against 3D ED data alone returned a structure with large displacive modulation of the La and Na atoms, clearly in contrast with the x-ray diffraction data where the satellite reflections are almost absent (Figure 2c). In earlier structural studies, aimed to disclose the nature of the incommensurate modulation in NaLaCoWO₆, it was suggested that the incommensurate distortions involve mainly the oxygen positions.[32] The authors indicated the presence of monoclinic twinned domains characterized by the inversion of the octahedral tilting, without providing a crystallographic description of such twinning.

To disclose the nature of the incommensurate distortions, high-resolution powder neutron diffraction, which is more sensitive to light ions, was carried out at room temperature. The simultaneous refinement of the average structure against the TOF-NPD data and the powder x-ray data results in a good fit. The average structural model is featured by elongated anisotropic ADPs for the oxygen positions suggesting a possible disorder or splitting of these sites. This possibility has been tested against the data with a clear improvement of the refinement and a normalization of the thermal parameters. The splitting of the equatorial oxygen (O1, O3, O4 and O5 see figure 3a) does not require additional atomic positions but can be obtained by shifting the ion from the 4i Wyckoff position sitting on the mirror plane. On the contrary, the splitting of the apical O2 site has been model with two symmetry-independent positions (O2 and O2’ see table S1[54]). The average splitting distance is $\approx$ 0.5 Å. A similar splitting, even if considerably smaller, has been observed for the cations in the structure. The disordered anion positions result in two possible octahedral orientations surrounding the Co²⁺ and W⁶⁺ cations. This suggests that two different tilting arrangements of the octahedral frameworks coexist in the crystal structure of NaLaCoWO₆, likely determining the incommensurate modulation.

To confirm this hypothesis, an incommensurate model was conceived starting from the unit cell, the modulation vector and the superspace group symmetry ($C2/m(\alpha 0\gamma)0s$) determined by 3D ED. In the structural refinement, based on TOF-NPD and XRD data, the modulation of the split oxygen positions has been described with the use of discontinuous crenel functions,[56] avoiding that in any point of the crystal both positions are simultaneously occupied. For the equatorial oxygen position (O1, O3, O4 and O5), to fulfill the latter requirement is sufficient to define a single crenel function. Indeed, the presence in the superspace group of the symmetry element $\{m_{y}|000s\}$ assures that only one position above or below the mirror plane is occupied throughout the crystal (see Figure 3b). On the contrary, for the two apical O2 and O2’, the absence of this symmetry element obliges to constrain the origin of the crenel function, x_4,0 ($x_{4}$ is the internal coordinate defined as $t+\stackrel{{\scriptstyle\rightarrow}}{{q}}\cdot\stackrel{{\scriptstyle\rightarrow}}{{r}}$ where t is the initial phase of the modulation function, $\stackrel{{\scriptstyle\rightarrow}}{{q}}$ is the modulation vector and $\stackrel{{\scriptstyle\rightarrow}}{{r}}$ is a position vector (x,y,z))[43, 50], for the two apical O2 and O2’ positions to have a 0.5 difference to fulfill the same physical requirement. A similar modulation function has been applied to the cation positions.

This model returns optimal agreement factors (see table S1)[54] for the simultaneous fitting of the powder data (TOF-NPD and XRD) as shown in Figure 2b-c. It is worth to underline that the superspace group allows the crenel origin parameter (x_4,0) for all positions to possess any value in the 0-0.5 range, nevertheless the refinement strongly suggests that the x_4,0 value for all atoms (except for the O2’ which is constrained to be the O2 value +0.5) to be zero within the uncertainty of the refinement. This is further confirmed by the absences of the 1111 and 110$\overline{1}$ reflections from the neutron pattern (indeed simulations with x_4,0 values different from 0 returns strong peaks at these positions). For this reason, the x_4,0 parameters were fixed to zero in the final refinement. It is worth to underline that the incommensurate model here proposed is very simple and the only refinable parameters, which influence the satellite intensities, are the positions of the split atoms in the average structure. To check if the refined model is compatible with 3D ED data, the incommensurate model obtained from the powder diffraction data has been refined against 3D ED data within the kinematical approximation. The refinement is stable and converges with agreement factor of wR=18.49%, R=17.59% and GOF=11.07. The final results of both refinement (3D ED data and powder neutron/x-ray data) are reported in table S1[54] showing good agreement.

The refined modulated structure is shown in Figure 3c. The incommensurate modulation can be described by an abrupt change of the tilting angle $\Phi$ along the a and c directions which resembles a twinning boundary. The tilting pattern in the structure remain constant as $a^{-}b^{-}c^{-}$, with the tilting angle $\Phi$ along the a and c direction abruptly changing its value but maintaining its antiphase character. Only at the boundary between the regions with $+\Phi$ and $-\Phi$ the tilting pattern is $a^{+}b^{-}c^{+}$. On the contrary, the value of the tilting angle along the b direction remain constant across the structure. The antiphase tilting along the c direction is a direct consequence of the x_4,0 parameter being 0 and we will see in section III-B its importance in the emergence of the dipolar density wave. The anion distortions are responsible for the modulation, which explains the weakness of satellite peaks in the XRD compared with NPD, and the smaller cations distortion follows the changes in octahedral tilting.

The crystallographic description of the modulated structure enables revisiting previous interpretation of this complex distortion. As remarked before, the structural modulation observed in systems like NaLaBB’O₆ has been interpreted in terms of irregular distribution of the A and A’ ion to form alternated off-stoichiometric domains composing the characteristic checkerboard contrast.[36, 57] In the combined XRD/TOF-NPD structural refinements, the La and Na sites resulted fully occupied and neither mixing of the two heterovalent ions nor randomly distributed vacancies are observed. Furthermore, the identified impurities are not in contrast with the occurrence of the 1:1 ratio of the La and Na in the doubly ordered perovskite. These assessments are, in general, supported by EDX analysis (see figure S3)[54], even if this measurement would suggests a small amount of Na vacancies in selected regions of the doubly ordered perovskite. This can be ascribed to Na evaporation induced by the electron irradiation documented in literature by the observation of the segregation of metallic Na and Na₂O.[58, 59]

Interestingly, the characteristic checkerboard contrast in the HREM images, which is usually interpreted as a cation ordering effect, has been explained as the occurrence of incommensurate oxygen displacement distortions in in Li_1-xNd_2/3-xTiO₃.[60] These displacements create region with different TiO₆ tilting patterns, which are at the basis of the observed bright and dark contrast in the HREM images.[60] In this regards, the crenel modulations functions used to describe the incommensurate tilting patterns in NaLaCoWO₆ can well describe the alternating region observed in the HREM images in different NaLaBB’O₆ systems.[36, 38, 57]

Before discussing the details of the coupling and of the dipolar ordering observed in the incommensurate phase of NaLaCoWO₆, it is worth to refresh the HIF mechanism observed in the commensurate $P2_{1}$ phase. In the remaining of the paper we will describe the distortion of all phases with respect to the parent $P4/nmm$ structure shown in Figure 1a. This will simplify the coupling terms and the group theory calculations, nevertheless it is still worth to underline some important points regarding the cation ordering and how this allows HIF in these system. The $P4/nmm$ phase is obtained from the parent simple perovskite structure (s.g. $Pm\overline{3}m$) by the action of the $R_{1}^{+}$ irreducible representation (irrep), which correspond to the chessboard ordering of the B site cations, and by the action of the $X_{3}^{-}$ irrep, which gives rise to the layer ordering on the A-site. The latter is important for HIF, as it removes the inversion symmetry from the B site point group allowing the octahedral tilting’s to break the macroscopic spatial inversion symmetry[13]

HIF in the $P2_{1}$ commensurate phases of the AA’BB’O₆ perovskites is strictly related to the $a^{-}a^{-}c^{+}$ octahedral tilting.[13, 28, 29, 34] In particular the out-of-phase tilting along the a and b directions is related to the $\Gamma_{5}^{+}$ irrep with order parameter $(\alpha,0)$, whereas the in-phase tilting around the c axis is due to the $\Gamma_{1}^{-}$ irrep with order parameter $\beta$. These two distortions acting together on the parent $P4/nmm$ structure will induce a secondary polar distortion, which transform as the $\Gamma_{5}^{-}$ irreps with order parameter $(\gamma,0)$, thanks to the trilinear free energy invariant $\alpha\beta\gamma$ (Figure 4). The polar $\Gamma_{5}^{-}$ distortion is a uniform opposite shift of the cation/anion in the structure that result in a net dipolar moment along the b-axis of the $P2_{1}$ structure. This induced polarization is switchable by an external electric field and the switching mechanism requires the change in sign of either the $\alpha$ or $\beta$ order parameters which correspond to a sign change of the $a^{-}a^{-}c^{0}$ or $a^{0}a^{0}c^{+}$ tilting respectively.

The scenario in the incommensurate phase of the NaLaCoWO₆ compound is similar but results in an incommensurate ordering of the induced dipoles. The $C2/m(\alpha 0\gamma)0s$ phase refined in this work can be obtained from the parent $P4/nmm$ structure by the action of two distortions related also in this case to the octahedral tilting’s. The first is the commensurate out-of-phase tilting along the b direction. This transform as the $\Gamma_{5}^{+}$ irrep as for the $a^{-}a^{-}c^{0}$ tilting in the $P2_{1}$ phase but with a different order parameter direction $(\alpha,-\alpha)$. The second distortion is the incommensurate out-of-phase tilting along the a and c directions which transform as the $\Sigma_{4}$ irrep with order parameter $(\delta,0,0,0)$ (this is a direct consequence of the $x_{4,0}$ parameter of the crenel function being equal to 0). These two distortions acting on the tetragonal parent structure induce, as secondary order parameter, an incommensurate displacement of the cation along the b direction which transform as the $\Sigma_{2}$ irrep $(\epsilon,0,0,0)$ thanks, also in this case, to a trilinear invariant $\alpha\delta\epsilon$ in the free energy as schematically shown in Figure 4. The analogies between the commensurate $P2_{1}$ case and the incommensurate $C2/m(\alpha 0\gamma)0s$ one let us to conclude that in the latter case we have observed the development of an incommensurate ordering of the induced dipoles with the same propagation vector as the incommensurate tilting. The induced dipoles are oriented along the b axis, in analogy with the $P2_{1}$ phase, and their amplitude is modulated with the period of the modulation vector, resembling the electric analog of a spin density wave. For the latter reason we describe the incommensurate dipolar ordering as a hybrid improper dipolar density wave.