Hundreds of new periodic signals detected in the first year of TESS with the weirddetector
Abstract
We apply the weirddetector, a nonparametric signal detection algorithm based on phase dispersion minimization, in a search for low duty-cycle periodic signals in the Transiting Exoplanet Survey Satellite (TESS) photometry. Our approach, in contrast to commonly used model-based approaches specifically for flagging transits, eclipsing binaries, or other similarly periodic events, makes minimal assumptions about the shape of a periodic signal, with the goal of finding “weird” signals of unexpected or arbitrary shape. In total, 248,301 TESS sources from the first-year Southern sky survey are run through the weirddetector, of which we manually inspect the top 21,500 for periodicity. To minimize false-positives, we here only report on the upper decile in terms of signal score, a sample for which we obtain 97% recall of TESS eclipsing binaries and 62% of the TOIs. In our sample, we find 377 previously unreported periodic signals, for which we make a first-pass assignment that 26 are ultra-short periods ( d), 313 are likely eclipsing binaries, 28 appear planet-like, and 10 are miscellaneous signals.
keywords:
eclipses — planets and satellites: detection — methods: numerical — stars: planetary systems1 Introduction
With the recently-launched Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) observing on the order of unique targets across the full sky and boasting an anticipated yield of thousands of novel exoplanets (Sullivan et al., 2015, 2017; Bouma et al., 2017; Barclay et al., 2018; Ballard, 2019), there is a need for varying approaches to the analysis of TESS data products to make full use of the survey’s wide scope and potential. The large survey size and all-sky nature of TESS make it particularly adept for catching uncommon signals, of potentially ill-classified or even unknown shape. These “needles in the haystack” may challenge our understanding of other stars and spark new theoretical developments, such as the case of Boyajian’s Star (Boyajian et al., 2016; Wright et al., 2016; Bodman & Quillen, 2016; Foukal, 2017; Katz, 2017; Neslusan & Budaj, 2017; Ballesteros et al., 2018; Wyatt et al., 2018; Martinez et al., 2019; Sucerquia et al., 2019). Accordingly, new methods to flag these signals for closer inspection have been developed in recent years to expedite their recovery (Giles & Walkowicz, 2019; Schmidt, 2019; Wheeler & Kipping, 2019).
The development of these new methods also serves to benefit the recovery of more conventional signals that may have been missed by more standard approaches, such as Box Least Squares (Kovács et al., 2002, 2006). For example, many of the known Kepler single- and double- transiting systems come from a myriad of independently developed search methods (Schmitt, 2017; Uehara et al., 2016; Wang et al., 2015; Foreman-Mackey et al., 2016; Kawahara & Masuda, 2019), including one specifically designed to find unusual signals (Wheeler & Kipping, 2019).
The latter approach, known as the weirddetector, was previously successfully run on the 161,786 Kepler sources, where it identified the 6 aforementioned missed mono/stereo transiters, but also another 18 previously missed periodic signals consistent with binary star systems. Given the similarities between the Kepler and TESS data products, this makes the weirddetector attractive as an automated search tool for TESS too. The weirddetector is a signal detection algorithm with the goal of relaxing assumptions about signal shape in order to detect events of abnormal morphology (Wheeler & Kipping, 2019). Whilst the weirddetector is not specifically intended for exoplanet transit detection, it is related to the more planet-specific search methods, in that it accounts for a different set of potential signals. Accordingly, the weirddetector is able to detect a wider variety of signals than just, say, transiting planets or eclipsing binaries (though it is also able to recover to those events), at the cost of lower sensitivity to signals of a-priori known shape.
In this work, we apply the weirddetector to 248,301 target light curves from sectors 1 through 13, which represents TESS’s first-year survey of the Southern sky. From these, we manually identify 468 significant periodic signals which appear to not have been previously reported, with particular attention given to the top 30 of these. In Section 2, we briefly describe the algorithm and the specific changes made for TESS. In Section 3, we discuss the application of the code, cross-reference the findings with those of other catalogues, and introduce the most likely signals detected which are previously undetected at the time of writing. In Section 4, we discuss further improvements and potential continuations of our work.
2 Methodology
The basic principle of the weirddetector is to identify high-likelihood periodic signals for manual inspection while abandoning any parametric function to describe the transit shape. We emphasize that the weirddetector algorithm cannot identify signals all on its own, but instead facilitates a subsequent informed manual search through the high-probability signals sorted by the algorithm; as such, it is most useful to consider usage of the weirddetector algorithm as one part in a larger search pipeline. A more in-depth discussion of the weirddetector is available in Wheeler & Kipping (2019), but we shall also include a brief description, highlighting in particular the points specific to our application on TESS data.
2.1 General principles of weirddetector
As the weirddetector searches for coherent, low duty-cycle periodic signals, the algorithm folds on many trial periods and searches for the period values which exhibit the smallest dispersion of fluxes. We note that phase dispersion minimization is not a novel concept–it has been used in other algorithms such as the Plavchan periodogram (Plavchan et al., 2008; Parks et al., 2014). In the case of TESS, which monitors each field for days, we opt for a period grid ranging from 0.25 days up to 15 days uniform in (24,567 total period values). Just as was found with Kepler though (Wheeler & Kipping, 2019), the algorithm is sensitive to periods outside the period grid if there is a harmonic of the true period within the grid (which is the case for some of our flagged signals later).
To quantify the relative success at phase dispersion minimization of a given trial period, the weirddetector examines the chi-squared (, which reflects how scattered the values are) and kurtosis (, which reflects the weight of a distribution’s tail relative to its peak). The algorithm then calculates excess kurtosis, and chi-squared less than the median, . These two metrics are multiplied to form a score strength, such that we require both perform well to yield a putative signal. To normalize the scores, we re-calculate along a grid of periods but for a scrambled version of the original data (which should have no periodicity), and evaluate a sliding standard deviation of the result, . Using these quantities, the algorithm defines a final merit function, , for each period value, given by .
The above value of the merit function gives us intuition about the ideal signal the weirddetector is searching for. To maximize the merit function of a period , the phase curve should be much more coherent at than at other “random" values of (i.e. large decrease in ); the phase curve should hover around a constant value with only one (or a few) short excursion(s) from the baseline (i.e. high excess kurtosis ); and these two conditions should otherwise have low variation at nearby -values not equal to , maintaining small values for and to demonstrate there is, in fact, a distinct signal with a specific period more likely than the rest (i.e. low ).
2.2 Differences between Kepler and TESS
The weirddetector is highly versatile and generalizable, and was able to run on TESS data after appropriate changes were made from the implementation for Kepler. Following are the details that are sensitive to the particular telescope gathering the data.
Kepler observed a 115 square-degree patch of sky, at a cadence of 30 minutes for 17 quarters of up to 90 days each. TESS, on the other hand, generates light curves with a cadence of 2 minutes and will observe 26 different sectors for 27 days each. TESS, while it spends only a month on the targets of each sector (barring targets that receive extra coverage as a result of overlap between sectors), will survey 85% of the sky, covering roughly 400 times as many unique stars as Kepler. As a result, there will be far more data to search through; however, by virtue of the shorter baseline, we are more limited in the range of periods for which we can detect signals.
In addition, having fewer data points means the weirddetector will be more sensitive to outlier events when calculating both and , such as stellar flares or instrument-caused deviations. As a result, we were more stringent in our outlier rejection when considering the phase-folding part of the algorithm to limit one-time events from inducing spurious signal detections or leading to false positives by unfavorably skewing . Additionally, while we do not expect or to change much, (and therefore ) is orders of magnitude lower in TESS because of the fewer points in the light curves. This means that drops accordingly; however, because the absolute values of do not matter as much as the relative values for determining the most promising period values, and we take the step of dividing by , our analysis is little-affected.
We also had to adjust the bandwidth used for our median-filter detrending algorithm to better reflect the duration of the signals we were searching for while considering the shorter range of trial periods we were folding on. In addition, the presence of TESS’s regular data gaps posed an issue, as Kepler data suffered far fewer gaps per unit time. However, as these changes did not require fundamentally altering the algorithm, their treatment is discussed in the beginning of Section 3.
2.3 Aliases
One major limitation of the weirddetector is its tendency to flag rational fractions or multiples (“aliases") of the true period of a signal. This is unavoidable when using a folding technique with such relaxed requirements for signal shape, and the issue is not specific to TESS light curves.
Here, we partially corrected for this error by attempting to automatically flag the correct period when an integer multiple was identified in the case of single-dip signals. It is important to note that a) our technique only accounts for flagged periods that are an integer multiple of the true period (which we chose to target because it is the most common case of aliasing); and b) we still need to manually examine the data to determine if the period detected is truly the correct one. Still, our technique helps us identify signals by suggesting the correct period more frequently.
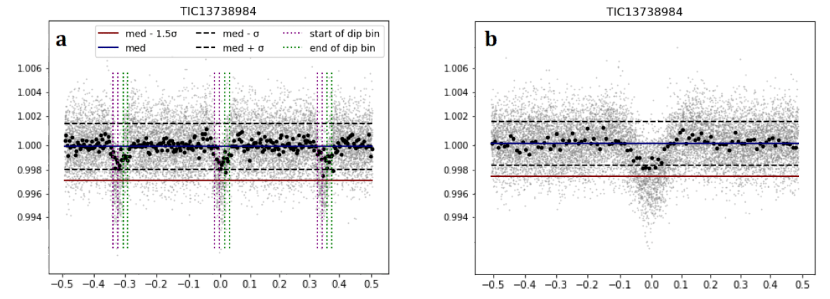
For a single-dip event with true period and flagged period , there will be dips in the phase curve folded with . By automatically detecting the number of dips , we can therefore retrieve the correct period by multiplying. We identify a dip by the following: examine the points in folded time-order in 200-point sliding windows. If greater than one-third of the points in this window have a flux value that falls under below the median, note the window as the beginning of a dip. Then, wait for the flux values to return to normal before looking for another dip by flagging the end of a dip when greater than three-quarters of the window has a value within of the median (see Figure 1). Note that the specific time picked out by the sliding window is not important, as this approach does not need to consider the duration or shape or the dip–only the number of significant dips .
The specific numerical values were chosen heuristically to handle the aforementioned case of aliasing– by far the most common case within our data. Though a similar approach may work in principle for regular increases in flux, there are too many confounding factors (particularly flares) to have a reliable solution to that problem.
3 Application to TESS data
3.1 Data preparation
We ran the weirddetector on all light curve files in sectors 1 through 13 available at MAST (248,301 not including overlap of targets between sectors; 223,087 unique targets after considering overlap). We remove probable outliers from each PDC light curve by removing points more than away from the median in an 11-point rolling window, where is the median absolute deviation: . (As one of the key assumptions of weirddetector is the presence of Gaussian noise, we can use as an estimator of the standard deviation with , meaning our threshold is also roughly equal to ). We also removed all points with non-zero quality flags in the FITS files.
In each sector, we split each PDC time series into two segments (“semi-sectors”) before and after the day data gap. Within each segment, we used linear interpolation to fill in missing data and detrended with a moving median filter, using a 1 day bandwidth, to remove long-term trends, following (Wheeler & Kipping, 2019). We decided on the 1-day window as it is both sufficiently shorter than the duration of observation (27 days per target) and longer than the duration of our signals of interest (most are of order days). This also acts to suppress long duty-cycle signals associated with stellar rotation. After detrending, we removed the interpolated points and recombined the segments. The weirddetector was then run on the trial periods for 248,301 unique light curves.
3.2 Filtering
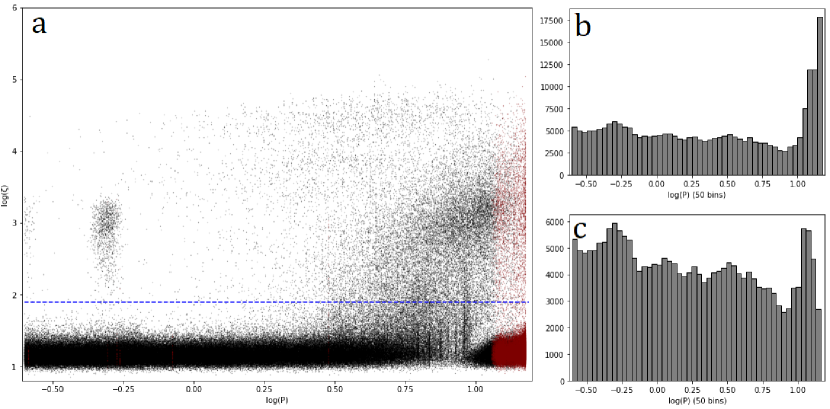
In order to preserve only the most likely signal candidates and remove artifacts of the data analysis, some cuts were made to the resultant data. The first one we note is that upon examining a scatter plot of a light curve’s versus , one immediately sees piling up a certain frequencies. A similar effect was reported by Wheeler & Kipping (2019) on the Kepler data. These are immediately suspicious as spurious common modes, rather than astrophysical signals. We therefore proceeded to design a means to filter out these suspicious periods.
Since the distribution of periods guessed by the weirddetector was at first not log-uniform (in particular with large saturation towards the upper end), we cut the 1,000 most commonly appearing periods to achieve a more uniform distribution (Figures 2b-c). Though the precise number chosen as a cutoff was somewhat ad-hoc, it accomplished the desired goal of picking out a set of signals with a more uniform distribution of .
Even after cuts, there are a few peculiarities in the distribution worth addressing. There is a low density of points at ; we posit these are caused by phasing of periods which are almost exactly half () of the 13-day semi-sector baseline, causing dips to frequently fall within the one-day gap. We also note a concentration of high- points close to ; these could be caused by a common mode, as they are unlikely to be astrophysical considering their distance from the rest of the distribution. The high- signals are denser at the higher end of -values even after cuts, which is likely due to lower values caused by the lesser dispersions associated with folding on longer periods; this trend contributes significantly to the aliasing effect of rational multiples as noted in Section 2.3
Since our goal is to find new signals, known variables from the Villanova eclipsing binary catalogue (Prsa, 2020), the ASAS-SN catalog of variable stars (Shappee, 2014; Jayasinghe et al., 2018, 2019), the International Variable Stars Index (VSX, Watson et al. (2006)), and the Tess Objects of Interest (TOIs) (NASA Exoplanet Archive list of current TOIs) were also removed. Altogether, these cuts comprised roughly 13% of the data, leaving 215,871 of the 248,301 targets intact.
We consider a signal to be “interesting” if its periodogram has a most-significant peak such that , again following Wheeler & Kipping (2019). We choose not independently at some fixed value, but set it to pick out the top decile of candidates, after cutting both common periods and already-discovered signals, for manual inspection. We look only at the most-significant peak (and rational fractions) as found by the previously described method, to generate phase curves with the highest likelihood of containing the correct period.
3.3 Data products
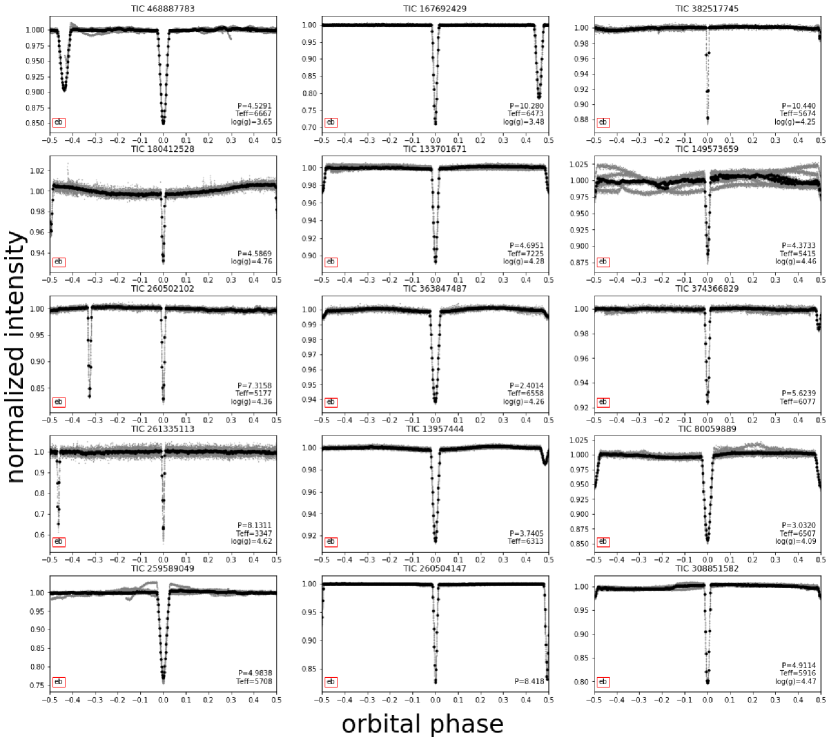
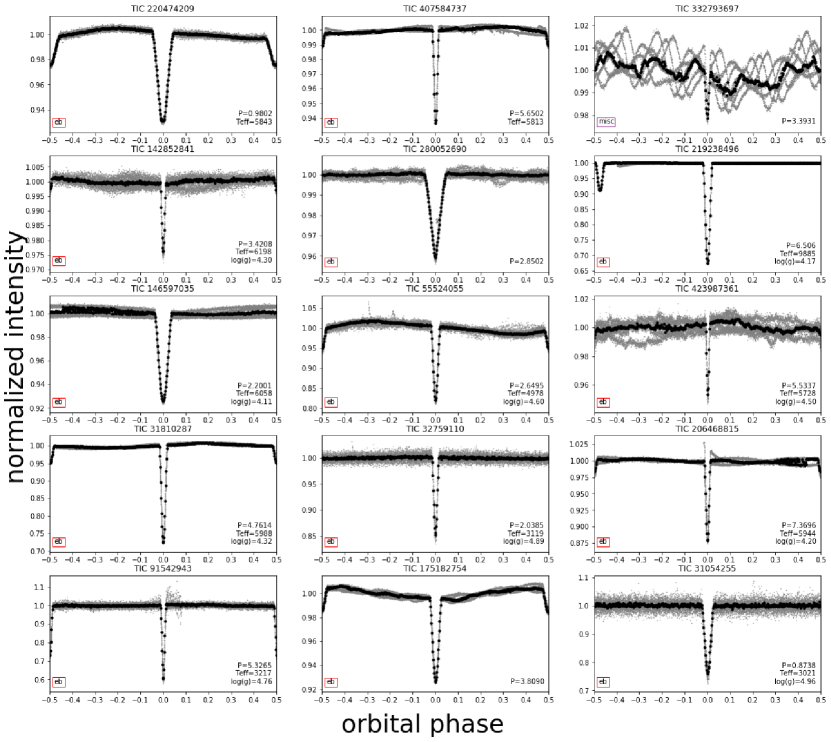
After filtering, we flag 377 previously-unidentified targets (dubbed Weird Objects of Interest, or WOIs) that appear to contain some periodic signal. The signals were selected manually based on whether their phase curves showed a clear signal (or multiple clear signals, in the case of aliases). values of the WOIs fall within the range of to , providing evidence that the selected periods are several orders of magnitude better than naive guessing. Additionally, we examined distributions of and for the WOIs, which showed no dependence on each other, assuring us that the high values are not artifacts. In Table LABEL:tab:WOIs, we present the and periods, along with accompanying information, for the WOI signals reported in this work.
To ensure each signal was not an artifact of the median-filter detrending, we applied different detrending algorithms to the raw light curves and re-folded on the flagged period. We applied the implementation of Cosine Filtering with Autocorrelation Minimization (CoFiAM; Kipping et al. 2013) found in the MoonPy Python library, as well as phasma, a non-parametric phase-folding algorithm (Jansen & Kipping, 2018). Example phase curves presented in Figures 3 & 4 have been detrended with phasma. We also queried the TIC-8 catalog (Stassun et al., 2018) for these objects to report their basic stellar properties, which is provided in the figure panels where available. We provide moving median, CoFiAM and phasma detrended phase curves for the 337 signals, as well as a CSV form of Table LABEL:tab:WOIs at this URL.
3.4 Performance
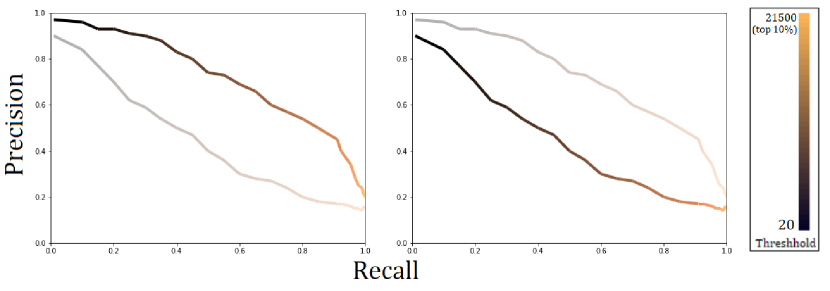
To quantify the weirddetector’s performance, we analyzed its effectiveness at recovering signals from the Villanova eclipsing binary and TOI catalogues. At the time of writing, 62% of currently-documented TOIs (1267/2044) and 97% (1801/1855) of Villanova eclipsing binaries fell within the top decile of values. The missing targets in each catalog are expected, as ideally a model-based approach would be best for finding transiting planets and eclipsing binaries, respectively, whereas the weirddetector is sensitive to all manner of periodic signals. We note also that all of the missing targets from the Villanova EB catalogue have periods falling outside our period grid ( days), explaining the algorithm’s failure to recover them. We maintained a high recall (the fraction of catalogued true signals recovered) percentage at the cost of precision (the fraction of flagged signals which we know or believe are real), as we wanted to minimize false negatives over false positives to find as many interesting signals as possible. Of course, one could vary the fraction of signals we consider from 10% to modify the precision and recall percentages (Figure 5).
4 Discussion
In this work, we have applied the weirddetector designed to flag high-likelihood periodic signals of arbitrary shape in time series photometry for subsequent manual inspection, to 248,301 unique TESS targets in Sectors 1-13 (the year-one Southern sky survey). Full frame image targets were not analyzed. Our work identifies 377 very high signal to noise periodic signals that have not been previously flagged in the literature or elsewhere to our knowledge. We have provided basic parameters and identifiers for these systems to enable community follow-up. The number of WOIs could surely be increased by relaxing our threshold to consider more than the top decile of events. This choice was made to allow us to quickly hone in on the most significant signals - the goal is to perform triage here and simply see if there is something glaringly obvious and exciting in the TESS data. Having done so, we can report that amongst the 377 WOIs identified, none of them appear to display the kind of remarkably unusual behaviour observed for Boyajian’s Star (Boyajian et al., 2016), despite the fact the weirddetector easily recovered that signal in the Kepler timeseries111Note that Boyajian’s Star is not strictly periodic, but like the detection of mono-transits by the weirddetector, the kurtosis aspect of its merit function provides sensitivity to even one-off events - although it is certainly not optimized to them.. This does not mean analogs do not exist amongst the target stars. While the new signals uncovered in this survey suggest gaps in the completeness functions of other detection methods, it remains unclear exactly what these gaps are. One could go about precisely identifying them with a detailed injection and recovery hare-and-hound exercise across several different search strategies, but that is beyond the scope of this work. By the same token, we cannot directly convert our lack of detection into an occurrence rate of Boyajian-like stars (nor is it immediately clear how one would define such events).
We also highlight that it is not the objective of this work to offer astrophysical interpretations of the identified signals. They are simply flagged periodic signals that have been apparently missed thus far, in the same vein as the Kepler study by Wheeler & Kipping (2019). Nevertheless, we will offer some simple classifications below.
We highlight that the periods in Table LABEL:tab:WOIs are only estimates and it is possible the true period is an alias. Still, in many cases we find extremely short flagged periods, less than 0.3 days, which we classify as “ultra short period” (USP). If correct, these are unlikely to be eclipses since for a Solar-like host the orbital period would be grazing or inside the star. A possible explanation is a rapidly rotating star, which could be checked with a measurement, or pulsations - which might be expected in the case of evolved stars with lower values. As an example, TIC 443494351 is a USP but also has an excessively long duty cycle for its “dip” (which is itself questionable in nature). This makes it unlikely to be an eclipse signal and more consistent with intrinsic stellar activity. We classify 26 of the cases as USPs.
The overwhelming majority of WOIs appear to be eclipsing binary systems, as evident from inspection of Figures 3 & 4. We can crudely classify an “EB” as one which displays a) two dips per period, or b) one dip and noticeable phase curve variations, or c) one dip with a depth greater than 2%. Using this criterion, and excluding the ultra short periods mentioned above, we classify 313 of the WOIs as likely EBs.
A third classification we offer is “planet-like” (PL). These are signals which appear consistent with a transiting planet from the phase curve morphology alone, but have not been subject to any further vetting. We classify signals as planet-like if they show no noticeable phase curve variations and have one-dip per period which is less than 2% in depth. We also impose the condition that the duration of the dip must be less than one-sixth of the orbital period (which corresponds to a planet with ). This results in 28 planet-like signals. This leaves 10 WOIs without a clear classification - within which we suspect stellar activity may be broadly responsible.
Amongst the WOIs, there are some curious signals, such as TIC 24347173. A 2% phase curve appears consistent with rotational modulation giving the phasing with respect to the dips, yet the strict coherence implies an apparent 2:1 commensurability between the rotation and orbital period. Béky et al. (2014) proposes an explanation to signals of this nature: if there is a latitude on the surface of a star with a period synchronous to its satellite, magnetic interactions between the objects may result in preferential spot formation at that latitude. The star would then exhibit photometric variations in resonance with its companion.
TIC 197886566 bares some resemblance to this but the phase curve is perhaps more plausibly consistent here with being caused by the companion, although this would require an offset in the phase curve.
Our work provides the first demonstration of an en-masse search for weird signals within the TESS photometric data. Although no clear examples of highly irregular signals manifest, the fact we recover 313 EB-like signals and 28 planet-like signals suggests gaps in the completeness functions of standard algorithms and demonstrates the utility of numerous algorithms being applied to photometric data sets such as this
Acknowledgments
DMK acknowledges support from the Simons Foundation and the Alfred P. Sloan Foundation. Special thanks to Tom Widdowson, Mark Sloan, Laura Sanborn, Douglas Daughaday, Andrew Jones, Jason Allen, Marc Lijoi, Elena West, Tristan Zajonc, Chuck Wolfred, Lasse Skov & Martin Kroebel.
Data Availability
The data underlying this article are publicly available at https://github.com/joheenc/woi_data.
References
- Ballard (2019) Ballard, S., 2019, AJ, 157, 113
- Ballesteros et al. (2018) Ballesteros, F. J., Arnalte-Mur, P., Fernandez-Soto, A., Martínez, V. J., 2018, MNRAS, 473, 21
- Barclay et al. (2018) Barclay, T., Pepper, J. & Quintana, E., 2018, ApJS, 239, 2
- Béky et al. (2014) Béky, B., Holman, M. J., Kipping, D. M., Noyes, R. W., 2014, ApJ, 788, 1
- Bodman & Quillen (2016) Bodman, E. H. L. & Quillen, A., 2016, ApJ, 819, 34
- Bouma et al. (2017) Bouma, L. G., Winn, J. N., Kosiarek, J., McCullough, P. R., 2017, arXiv e-prints:1705.08891
- Boyajian et al. (2016) Boyajian, T. S., LaCourse, D. M., Rappaport, S. A. et al., 2016, MNRAS, 457, 3988
- Foreman-Mackey et al. (2016) Foreman-Mackey, D., Morton, T. D., Hogg, D. W., Agol, E., Schölkopf, B., 2016, AJ, 152, 206
- Foukal (2017) Foukal, P., 2017, ApJ, 842, 3
- Giles & Walkowicz (2019) Giles, D. & Walkowicz, L., 2019, MNRAS, 484, 834
- Jansen & Kipping (2018) Jansen, T. & Kipping, D., 2018, MNRAS, 478, 3025
- Jayasinghe et al. (2018) Jayasinghe, T., Kochanek, C. S., Stanek, K. Z., Shappee, B. J., Holoien, T.W., Thompson, T. A., Prieto, J. L., Dong, S., Pawlak, M., Shields, J. V., Pojmanski, G., Otero, S., Britt, C. A., Will, D., 2018, MNRAS, 477, 3145
- Jayasinghe et al. (2019) Jayasinghe, T., Stanek, K. Z., Kochanek, C. S., Shappee, B. J., Holoien, T.W., Thompson, T.A., Prieto, J.L., Dong, S., Pawlak, M., Peicha, O., Shields, J. V., Pojmanski, G., Otero, S., Britt, C. A., Will, D., 2019, MNRAS, 486, 1907
- Katz (2017) Katz, J. I., 2017, MNRAS, 471, 3680
- Kawahara & Masuda (2019) Kawahara, H. & Masuda, K., 2019, ApJ, 157, 218
- Kipping et al. (2013) Kipping, D. M., Hartman, J., Buchhave, L. A., Schmitt, A. R., Bakos, G. Á. & Nesvorný, D., 2013, ApJ, 770, 101
- Kovács et al. (2002) Kovács, G., Zucker, S., & Mazeh, T., 2002, A&A, 391, 369
- Kovács et al. (2006) Kovćs, G., Zucker, S., & Mazeh, T., 2016, BLS: Box-fitting Least Squares, Astrophysics Source Code Library
- Martinez et al. (2019) Martinez, M. A. S., Stone, N. C., Metzger, B. D., 2019, MNRAS, 489, 5119
- Neslusan & Budaj (2017) Neslusan, L. & Budaj, J. 2017, A&A, 600, 86
- Parks et al. (2014) Parks, J. R., Plavchan, P., White, R. J., Gee, A. H., 2014, ApJS, 211, 1
- Plavchan et al. (2008) Plavchan, P., Jura, M., Kirkpatrick, J. D., Cutri, R. M., Gallagher, S. C., 2008, ApJS, 175, 1
- Prsa (2020) Prsa, A., 2020, “Eclipsing binary stars: Indispensableastrophysical labs”, TESS Program G011154, last accessed 24 June 2020 https://heasarc.gsfc.nasa.gov/docs/tess/data/approved-programs/G011154.txt
- Ricker et al. (2015) Ricker G. R. et al., 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003
- Schmidt (2019) Schmidt, E. G., 2019, ApJ, 880, 7
- Schmitt (2017) Schmitt, J. R., Jenkins, J. M. & Fischer, D. A., 2017, ApJ, 153, 180
- Shappee (2014) Shappee, B. J., Prieto, J. L., Grupe, D., Kochanek, C. S., Stanek, K. Z., De Rosa, G., Mathur, S., Zu, Y., Peterson, B. M., Pogge, R. W., Komossa, S., Im, M., Jencson, J., Holoien, T. W., Basu, U., Beacorn, J. F, Szczygiel, D. M., Brimacombe, J., Adams, S., Campillay, A., Choi, C., Contreras, C., Dietrich, M., Dubberley, M., Elphick, M., Foale, S., Giustini, M., Gonzalez, C., Hawkins, E., Howell, D. A., Hsiao, E. Y., Koss, M., Leighly, K. M., Morrell, N., Mudd, D., Mullins, D., Nugent, J. M., Parrent, J., Phillips, M. M., Pojmanski, G., Rosing, W., Ross, R., Sand, D., Terndrup, D. M., Valenti, S., Walker, Z., Yoon, Y., 2014, ApJ, 788, 1
- Stassun et al. (2018) Stassun, K. G., Oelkers, R. J., Pepper, J., et al., 2018, AJ, 156, 102
- Sucerquia et al. (2019) Sucerquia, M., Alvarado-Montes, J. A., Zuluaga, J. I., Cuello, N., Giuppone, C., 2019, MNRAS, 489, 2313
- Sullivan et al. (2015) Sullivan, P. W., Winn, J. N., Berta-Thompson, Z. K. et al., 2015, ApJ, 809, 77
- Sullivan et al. (2017) Sullivan, P. W., Winn, J. N., Berta-Thompson, Z. K. et al., 2017, ApJ, 837, 99
- Uehara et al. (2016) Uehara, S., Kawahara, H., Masuda, K., Yamada, S. & Aizawa, M., 2016, ApJ, 822, 2
- Wang et al. (2015) Wang, J., Fischer, D. A., Barclay, T., et al., 2015, ApJ, 815, 127
- Watson et al. (2006) Watson, C. L., Henden, A. A., & Price, A., 2006, The Society for Astronomical Sciences 25th Annual Symposium on Telescope Science, p.47
- Wheeler & Kipping (2019) Wheeler, A. & Kipping, D., 2019, MNRAS, 485, 5498
- Wright et al. (2016) Wright, J. T. & Sigurdsson, S., 2016, ApJL, 829, L3
- Wyatt et al. (2018) Wyatt, M. C., van Lieshout, R., Kennedy, G. M. & Boyajian, T. S., 2018, MNRAS, 473, 5286
Appendix
| TIC ID | [d] | [K] | dips | [%] | RA | Dec | Flat baseline | Class | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 468887783 | 4.5291 | 1.16e+05 | 8.20e+03 | 1.19e+02 | 6667 | 3.65 | 2 | 14.992 | 56.67 | 9.90 | y | eb |
| 167692429 | 10.280 | 1.07e+05 | 1.51e+03 | 1.63e+02 | 6473 | 3.48 | 2 | 28.962 | 102.71 | -63.43 | y | eb |
| 382517745 | 10.440 | 1.00e+05 | 4.85e+02 | 1.82e+02 | 5674 | 4.25 | 2 | 12.356 | 117.45 | -64.04 | y | eb |
| 180412528 | 4.5869 | 9.97e+04 | 6.50e+03 | 8.81e+01 | — | 4.76 | 2 | 6.7849 | 11.35 | -77.86 | y | eb |
| 133701671 | 4.6951 | 9.55e+04 | 1.55e+04 | 1.42e+02 | 7225 | 4.28 | 2 | 10.686 | 229.68 | -48.90 | y | eb |
| 149573659 | 4.3733 | 9.47e+04 | 3.70e+03 | 1.27e+02 | 5415 | 4.46 | 1 | 11.673 | 86.61 | -61.69 | n | eb |
| 260502102 | 7.3158 | 9.37e+04 | 6.17e+03 | 1.02e+02 | 5177 | 4.36 | 2 | 17.428 | 96.51 | -59.01 | y | eb |
| 363847487 | 2.4014 | 8.05e+04 | 1.12e+04 | 5.53e+01 | 6558 | 4.26 | 1 | 6.1775 | 200.43 | -42.62 | y | eb |
| 374366829 | 5.6239 | 7.86e+04 | 2.67e+03 | 1.46e+02 | 6077 | — | 2 | 7.6074 | 162.71 | 0.52 | y | eb |
| 261335113 | 8.1311 | 7.85e+04 | 1.45e+03 | 1.53e+02 | 3347 | 4.62 | 2 | 40.559 | 92.33 | -80.69 | y | eb |
| 13957444 | 3.7405 | 7.82e+04 | 2.45e+04 | 1.00e+02 | 6313 | — | 1 | 8.4917 | 75.48 | -37.03 | y | eb |
| 80059889 | 3.0320 | 7.74e+04 | 1.35e+04 | 7.07e+01 | 6507 | 4.09 | 2 | 14.450 | 297.89 | -43.37 | y | eb |
| 259589049 | 4.9838 | 7.67e+04 | 2.93e+03 | 1.37e+02 | 5708 | — | 1 | 22.989 | 72.43 | -53.00 | y | eb |
| 260504147 | 8.418 | 7.43e+04 | 5.35e+04 | 1.12e+02 | — | — | 1 | 17.577 | 96.43 | -55.16 | y | eb |
| 308851582 | 4.9114 | 7.05e+04 | 1.09e+03 | 1.18e+02 | 5916 | 4.47 | 2 | 20.297 | 122.58 | -63.74 | y | eb |
| 220474209 | 0.9802 | 6.84e+04 | 1.22e+05 | 3.09e+01 | 5843 | — | 2 | 6.9241 | 75.38 | -59.51 | y | eb |
| 407584737 | 5.6502 | 6.77e+04 | 1.80e+04 | 1.60e+02 | 5813 | — | 2 | 6.3343 | 352.77 | -74.13 | y | eb |
| 332793697 | 3.3931 | 6.64e+04 | 4.16e+03 | 5.97e+01 | — | — | 1 | 2.0910 | 215.98 | -50.49 | n | misc |
| 142852841 | 3.4208 | 6.54e+04 | 4.29e+03 | 8.79e+01 | 6198 | 4.30 | 2 | 2.4215 | 50.50 | -31.10 | y | eb |
| 280052690 | 2.8502 | 6.52e+04 | 4.10e+03 | 9.08e+01 | — | — | 1 | 4.0962 | 45.44 | -76.20 | y | eb |
| 219238496 | 6.506 | 6.49e+04 | 8.86e+03 | 2.06e+02 | 9885 | 4.17 | 2 | 32.689 | 64.49 | -48.39 | y | eb |
| 146597035 | 2.2001 | 6.37e+04 | 1.34e+04 | 8.37e+01 | 6058 | 4.11 | 1 | 7.3864 | 77.77 | -21.49 | y | eb |
| 55524055 | 2.6495 | 6.34e+04 | 1.16e+04 | 7.65e+01 | 4978 | 4.60 | 2 | 18.112 | 72.05 | -63.69 | y | eb |
| 423987361 | 5.5337 | 6.20e+04 | 3.27e+03 | 1.36e+02 | 5728 | 4.50 | 1 | 4.6543 | 235.84 | -63.66 | n | eb |
| 31810287 | 4.7614 | 5.85e+04 | 3.13e+04 | 1.21e+02 | 5988 | 4.32 | 2 | 27.721 | 136.65 | -47.06 | y | eb |
| 32759110 | 2.0385 | 5.79e+04 | 1.55e+04 | 8.20e+01 | 3119 | 4.89 | 1 | 14.696 | 86.24 | -24.93 | y | eb |
| 206468815 | 7.3696 | 5.77e+04 | 2.61e+03 | 1.43e+02 | 5944 | 4.20 | 2 | 12.202 | 57.01 | -53.60 | y | eb |
| 91542943 | 5.3265 | 5.67e+04 | 5.11e+03 | 1.05e+02 | 3217 | 4.76 | 1 | 40.042 | 43.82 | -33.74 | y | eb |
| 175182754 | 3.8090 | 5.65e+04 | 6.71e+03 | 1.08e+02 | — | — | 2 | 7.3807 | 115.96 | -37.72 | y | eb |
| 31054255 | 0.8738 | 5.52e+04 | 1.45e+04 | 2.74e+01 | 3021 | 4.96 | 1 | 24.747 | 80.57 | -25.11 | y | eb |
| 178938417 | 5.9747 | 5.48e+04 | 6.48e+03 | 1.98e+02 | 5405 | 4.51 | 2 | 0.8074 | 68.27 | -24.01 | n | eb |
| 142409400 | 1.3869 | 5.42e+04 | 1.74e+04 | 2.59e+01 | 3385 | 4.58 | 2 | 19.947 | 103.09 | -12.96 | y | eb |
| 178284729 | 2.2360 | 5.41e+04 | 2.78e+03 | 7.51e+01 | 3968 | 4.63 | 1 | 11.031 | 60.38 | -20.45 | y | eb |
| 32150630 | 1.4921 | 5.38e+04 | 1.84e+04 | 4.36e+01 | 4323 | — | 2 | 14.503 | 59.24 | -68.62 | n | eb |
| 143924219 | 2.8199 | 5.35e+04 | 4.54e+03 | 7.65e+01 | 6412 | 3.99 | 1 | 2.5442 | 332.70 | -48.89 | n | eb |
| 339607421 | 2.4381 | 5.25e+04 | 1.33e+04 | 8.03e+01 | 6327 | 4.33 | 1 | 5.4663 | 46.20 | -52.55 | y | eb |
| 238162238 | 1.2186 | 5.10e+04 | 3.65e+04 | 4.54e+01 | 6172 | 4.14 | 2 | 4.2458 | 106.39 | -48.84 | n | eb |
| 421285598 | 2.3578 | 5.07e+04 | 4.77e+03 | 4.61e+01 | 5745 | 4.15 | 2 | 13.222 | 261.92 | -54.11 | n | eb |
| 49534600 | 7.9529 | 5.06e+04 | 2.42e+03 | 1.52e+02 | — | — | 2 | 15.235 | 273.69 | -52.81 | y | eb |
| 301956407 | 1.8314 | 4.99e+04 | 2.86e+04 | 5.52e+01 | 6079 | 4.09 | 2 | 2.6056 | 260.05 | -70.04 | y | eb |
| 423530755 | 2.3421 | 4.97e+04 | 3.41e+04 | 8.64e+01 | 5547 | 4.27 | 1 | 7.2387 | 185.30 | -20.70 | n | eb |
| 365694569 | 9.0344 | 4.88e+04 | 3.69e+04 | 1.13e+02 | 6358 | 3.99 | 2 | 34.617 | 81.63 | 9.69 | y | eb |
| 147975720 | 2.8502 | 4.88e+04 | 1.37e+04 | 9.88e+01 | 3464 | 4.73 | 1 | 27.351 | 99.59 | -37.24 | y | eb |
| 33912852 | 1.7049 | 4.78e+04 | 6.74e+04 | 3.69e+01 | 6541 | 4.06 | 2 | 1.9524 | 356.14 | -26.47 | y | eb |
| 35349987 | 10.738 | 4.75e+04 | 1.33e+03 | 1.92e+02 | 3721 | 4.57 | 1 | 19.456 | 224.78 | -55.66 | y | eb |
| 101845679 | 1.2811 | 4.72e+04 | 3.69e+04 | 2.44e+01 | 6252 | 4.06 | 2 | 1.5564 | 304.00 | -50.13 | y | eb |
| 178171080 | 3.2501 | 4.71e+04 | 2.40e+03 | 1.00e+02 | — | — | 1 | 2.4862 | 43.26 | -31.40 | n | eb |
| 49558810 | 3.3543 | 4.58e+04 | 4.31e+03 | 8.50e+01 | 5209 | 4.34 | 1 | 7.8446 | 36.53 | -36.37 | y | eb |
| 290476605 | 5.7452 | 4.52e+04 | 1.24e+04 | 1.60e+02 | 6687 | 3.96 | 2 | 2.7871 | 139.16 | 0.72 | y | eb |
| 140659978 | 9.4407 | 4.46e+04 | 2.25e+03 | 1.41e+02 | 5221 | 4.20 | 2 | 29.384 | 72.45 | -72.46 | y | eb |
| 278784173 | 0.7473 | 4.45e+04 | 2.43e+04 | 3.31e+01 | — | — | 1 | 6.3155 | 335.73 | -37.52 | y | eb |
| 250387838 | 6.8863 | 4.40e+04 | 1.08e+04 | 1.09e+02 | 5871 | 3.80 | 2 | 3.7178 | 30.26 | -2.49 | y | eb |
| 371839073 | 3.7963 | 4.38e+04 | 2.74e+03 | 9.26e+01 | 6034 | 4.22 | 1 | 10.071 | 306.00 | -71.08 | y | eb |
| 269852699 | 5.1365 | 4.38e+04 | 2.12e+03 | 7.51e+01 | 6137 | 4.13 | 2 | 11.706 | 69.88 | -79.72 | y | eb |
| 220397947 | 1.7757 | 4.30e+04 | 3.94e+03 | 5.98e+01 | 6257 | 4.01 | 1 | 7.2456 | 69.01 | -58.07 | y | eb |
| 340100436 | 1.4689 | 4.30e+04 | 1.17e+04 | 5.98e+01 | 5297 | 4.43 | 1 | 3.9916 | 237.69 | -63.97 | y | eb |
| 379783522 | 2.4499 | 4.23e+04 | 1.91e+04 | 4.14e+01 | — | — | 2 | 1.6508 | 181.59 | -65.70 | n | eb |
| 255700967 | 3.4253 | 4.23e+04 | 2.56e+03 | 1.00e+02 | 6896 | 3.94 | 1 | 4.4857 | 98.90 | -52.33 | y | eb |
| 201747686 | 1.3457 | 4.20e+04 | 1.60e+04 | 3.02e+01 | 6233 | — | 2 | 2.2124 | 303.47 | -57.99 | n | eb |
| 273792220 | 1.9879 | 4.19e+04 | 2.99e+05 | 3.61e+01 | 5892 | 4.13 | 2 | 6.4483 | 30.55 | -62.59 | n | eb |
| 158150633 | 2.0783 | 4.13e+04 | 3.24e+03 | 5.82e+01 | 4525 | — | 2 | 11.701 | 162.13 | -38.90 | n | eb |
| 250196734 | 7.7037 | 4.11e+04 | 1.94e+05 | 1.41e+02 | 3962 | 4.41 | 2 | 50.505 | 65.21 | -2.62 | y | eb |
| 102691227 | 1.2097 | 4.10e+04 | 6.55e+04 | 4.60e+01 | 6457 | 4.05 | 1 | 7.4433 | 155.57 | -43.21 | y | eb |
| 146522930 | 1.0875 | 4.09e+04 | 8.56e+03 | 2.10e+01 | 5812 | — | 2 | 4.0696 | 76.69 | -19.96 | y | eb |
| 278706358 | 3.4512 | 4.08e+04 | 3.42e+04 | 1.15e+02 | 5619 | 4.11 | 2 | 36.414 | 334.81 | -40.53 | y | eb |
| 55369219 | 1.9793 | 4.06e+04 | 5.22e+03 | 4.54e+01 | 6821 | 3.82 | 1 | 7.4981 | 77.50 | -61.59 | y | eb |
| 348759510 | 3.7162 | 4.04e+04 | 2.43e+04 | 1.41e+02 | 6672 | 4.28 | 1 | 2.9118 | 134.20 | -17.43 | y | eb |
| 253715855 | 1.1317 | 4.02e+04 | 1.88e+04 | 3.82e+01 | 6138 | 4.20 | 2 | 4.3179 | 282.06 | -37.18 | n | eb |
| 158582801 | 1.0801 | 4.02e+04 | 4.98e+05 | 3.78e+01 | — | — | 1 | 43.263 | 21.86 | -49.47 | y | eb |
| 219362976 | 7.9768 | 4.01e+04 | 4.65e+03 | 2.11e+02 | 4387 | 4.29 | 1 | 20.637 | 75.11 | -49.42 | y | eb |
| 237944385 | 4.4247 | 4.00e+04 | 1.97e+03 | 1.52e+02 | 6304 | 4.03 | 1 | 1.7937 | 101.22 | -48.70 | y | pl |
| 201293780 | 0.9377 | 4.00e+04 | 3.04e+04 | 2.45e+01 | 5962 | 4.29 | 2 | 1.7623 | 3.23 | -57.35 | y | eb |
| 436158814 | 7.2141 | 3.99e+04 | 1.85e+03 | 1.27e+02 | 3510 | 4.64 | 2 | 19.849 | 83.94 | 9.76 | y | eb |
| 176591772 | 7.7591 | 3.94e+04 | 1.68e+03 | 1.03e+02 | 5626 | 4.19 | 2 | 6.9878 | 87.57 | -5.77 | y | eb |
| 148612685 | 5.0098 | 3.88e+04 | 6.32e+04 | 9.22e+01 | — | — | 2 | 12.547 | 165.34 | -11.89 | y | eb |
| 293081694 | 1.2540 | 3.83e+04 | 1.95e+04 | 3.80e+01 | 6335 | 4.19 | 2 | 3.1344 | 175.04 | -27.26 | n | eb |
| 92594505 | 11.435 | 3.79e+04 | 1.38e+03 | 1.72e+02 | 6302 | 3.75 | 1 | 7.8543 | 315.46 | -33.48 | y | eb |
| 231293332 | 1.7879 | 3.78e+04 | 5.31e+04 | 6.50e+01 | 6140 | 4.22 | 1 | 15.375 | 44.71 | -49.17 | y | eb |
| 88380001 | 4.4343 | 3.74e+04 | 2.42e+03 | 1.15e+02 | 6458 | 4.10 | 1 | 1.7522 | 44.79 | -25.23 | y | pl |
| 231809798 | 0.9057 | 3.63e+04 | 9.96e+04 | 1.99e+01 | 3520 | 4.74 | 2 | 18.734 | 85.53 | -52.11 | y | eb |
| 281494100 | 2.3076 | 3.63e+04 | 2.38e+05 | 6.51e+01 | 6427 | 4.17 | 2 | 43.686 | 112.19 | -56.40 | y | eb |
| 253657883 | 0.7908 | 3.62e+04 | 9.50e+03 | 2.08e+01 | 4316 | 4.51 | 2 | 8.2538 | 281.47 | -39.41 | n | eb |
| 140659980 | 9.4392 | 3.57e+04 | 1.88e+03 | 1.63e+02 | 5642 | 3.84 | 2 | 5.3466 | 72.47 | -72.46 | n | eb |
| 387544749 | 2.8185 | 3.55e+04 | 3.55e+04 | 6.12e+01 | 3711 | 4.59 | 2 | 9.5871 | 44.25 | 10.31 | n | eb |
| 143022688 | 1.5663 | 3.55e+04 | 2.12e+05 | 5.30e+01 | 4086 | — | 2 | 12.777 | 54.26 | -30.07 | y | eb |
| 117739806 | 5.6174 | 3.55e+04 | 8.52e+02 | 1.14e+02 | 5981 | 4.39 | 2 | 20.181 | 96.20 | -31.86 | y | eb |
| 278861826 | 0.5337 | 3.47e+04 | 2.79e+04 | 1.58e+01 | 6369 | 4.03 | 1 | 3.7808 | 100.65 | -56.54 | y | eb |
| 52641430 | 1.6715 | 3.47e+04 | 9.45e+03 | 2.90e+01 | — | — | 2 | 1.6214 | 101.11 | -33.98 | n | eb |
| 39818458 | 3.8154 | 3.44e+04 | 1.85e+04 | 1.25e+02 | 12561 | — | 1 | 5.3337 | 90.19 | -3.89 | y | eb |
| 211116547 | 1.2768 | 3.44e+04 | 1.43e+04 | 2.92e+01 | — | 4.74 | 2 | 36.378 | 280.43 | -31.67 | y | eb |
| 333642126 | 4.827 | 3.41e+04 | 1.45e+03 | 9.64e+01 | 5051 | 4.30 | 1 | 11.344 | 56.36 | -4.12 | y | eb |
| 48658291 | 1.5878 | 3.40e+04 | 2.00e+04 | 6.16e+01 | 6322 | 3.74 | 1 | 8.8601 | 96.92 | -25.83 | y | eb |
| 198076334 | 0.3913 | 3.39e+04 | 2.74e+05 | 1.53e+01 | 5854 | 3.61 | 1 | 2.4643 | 63.65 | -59.08 | y | eb |
| 3921749 | 5.6108 | 3.39e+04 | 5.66e+04 | 1.34e+02 | 4007 | 4.38 | 1 | 33.918 | 11.83 | -6.44 | y | eb |
| 253749178 | 1.8377 | 3.38e+04 | 4.19e+03 | 5.09e+01 | 5958 | — | 2 | 10.192 | 282.34 | -36.76 | n | eb |
| 310556491 | 1.5554 | 3.28e+04 | 6.39e+04 | 4.03e+01 | 6902 | 4.15 | 2 | 5.2244 | 185.28 | -65.83 | n | eb |
| 77437462 | 0.6079 | 3.27e+04 | 5.41e+03 | 3.11e+01 | 3588 | 4.77 | 1 | 1.8442 | 73.13 | -36.53 | n | pl |
| 294059372 | 0.6666 | 3.26e+04 | 3.27e+04 | 1.95e+01 | 6393 | — | 2 | 7.1110 | 263.93 | -71.40 | n | eb |
| 300972613 | 0.3880 | 3.25e+04 | 1.34e+05 | 1.30e+01 | — | — | 2 | 6.5351 | 10.77 | -47.30 | y | eb |
| 357911163 | 4.7821 | 3.22e+04 | 2.19e+04 | 8.52e+01 | 6682 | 4.42 | 2 | 15.130 | 192.89 | -79.02 | y | eb |
| 25188036 | 3.3930 | 3.18e+04 | 1.21e+03 | 4.41e+01 | 2868 | 5.05 | 2 | 1009.9 | 98.02 | -7.31 | y | eb |
| 268587594 | 9.1404 | 3.18e+04 | 2.40e+03 | 2.00e+02 | 5887 | 4.19 | 3 | 3.8126 | 15.73 | -23.88 | n | misc |
| 278826996 | 9.5834 | 3.16e+04 | 1.39e+03 | 1.77e+02 | 5800 | 4.03 | 2 | 35.039 | 100.33 | -54.02 | y | eb |
| 52641431 | 0.8358 | 3.16e+04 | 7.13e+03 | 2.25e+01 | — | — | 2 | 1.5964 | 101.11 | -33.98 | n | eb |
| 434664688 | 8.4292 | 3.09e+04 | 1.90e+03 | 1.54e+02 | — | — | 2 | 18.548 | 191.23 | -65.31 | y | eb |
| 142148228 | 0.7805 | 3.06e+04 | 9.43e+03 | 2.27e+01 | 6775 | 4.08 | 1 | 0.6429 | 100.36 | -74.67 | n | pl |
| 150357064 | 1.4894 | 3.03e+04 | 3.55e+03 | 4.98e+01 | 5722 | 4.13 | 1 | 5.8414 | 96.10 | -64.49 | n | eb |
| 243475355 | 1.0957 | 3.03e+04 | 1.26e+04 | 3.07e+01 | 13560 | — | 2 | 1.2504 | 205.91 | -42.06 | y | eb |
| 146439804 | 11.014 | 3.03e+04 | 6.27e+02 | 1.74e+02 | 3801 | 4.32 | 1 | 10.465 | 75.73 | -22.22 | y | eb |
| 262696097 | 0.9111 | 3.03e+04 | 7.64e+03 | 2.69e+01 | 6782 | 3.79 | 1 | 3.1139 | 107.78 | 7.45 | n | eb |
| 424992973 | 6.9254 | 3.02e+04 | 6.41e+03 | 1.83e+02 | 5171 | — | 2 | 35.136 | 81.80 | -18.57 | y | eb |
| 38937499 | 2.0276 | 3.00e+04 | 2.65e+03 | 5.70e+01 | 5199 | 4.32 | 2 | 0.3917 | 10.30 | -68.45 | y | eb |
| 79548760 | 7.9728 | 2.98e+04 | 9.98e+02 | 1.43e+02 | 6452 | 3.66 | 1 | 4.0596 | 51.07 | -45.09 | y | eb |
| 143171265 | 1.1410 | 2.97e+04 | 1.22e+04 | 3.72e+01 | 7333 | 4.31 | 2 | 1.7917 | 89.99 | -34.45 | n | eb |
| 294092960 | 0.9022 | 2.97e+04 | 1.54e+04 | 2.23e+01 | 5766 | 4.57 | 2 | 5.0331 | 107.35 | -57.50 | n | eb |
| 146688260 | 0.5030 | 2.94e+04 | 3.01e+04 | 1.53e+01 | 5551 | 4.28 | 2 | 1.3734 | 43.22 | -43.52 | n | eb |
| 58466459 | 3.8717 | 2.93e+04 | 6.87e+02 | 6.60e+01 | 6398 | 4.09 | 2 | 7.2758 | 201.66 | -27.14 | y | eb |
| 148544875 | 1.7441 | 2.92e+04 | 8.11e+03 | 6.30e+01 | 3159 | 4.88 | 1 | 24.273 | 164.12 | -9.83 | y | eb |
| 332488398 | 1.0416 | 2.92e+04 | 8.54e+04 | 2.70e+01 | 5458 | 4.29 | 1 | 4.7379 | 350.56 | -29.70 | y | eb |
| 281728376 | 11.177 | 2.91e+04 | 8.26e+02 | 1.73e+02 | 6656 | 4.00 | 1 | 2.6819 | 11.65 | -54.10 | y | eb |
| 317411334 | 1.4485 | 2.89e+04 | 1.48e+04 | 4.88e+01 | 6036 | 4.15 | 1 | 8.9622 | 87.71 | -12.15 | y | eb |
| 53997651 | 1.4587 | 2.86e+04 | 4.79e+04 | 6.27e+01 | 3418 | 4.71 | 1 | 73.489 | 159.57 | -33.26 | y | eb |
| 441422220 | 3.6995 | 2.81e+04 | 6.93e+03 | 1.13e+02 | 6348 | 4.26 | 2 | 28.628 | 311.36 | -34.64 | y | eb |
| 284196801 | 11.158 | 2.80e+04 | 1.03e+03 | 1.72e+02 | 6098 | 3.77 | 2 | 3.6876 | 105.54 | -71.12 | y | eb |
| 90716944 | 8.0234 | 2.79e+04 | 6.12e+03 | 2.12e+02 | 4900 | 4.55 | 2 | 15.891 | 277.08 | -45.49 | y | eb |
| 386262459 | 2.6672 | 2.79e+04 | 2.00e+03 | 8.05e+01 | 9557 | 4.15 | 2 | 1.9070 | 127.40 | -16.00 | n | eb |
| 91246422 | 9.4234 | 2.76e+04 | 2.73e+03 | 1.61e+02 | 12417 | — | 1 | 4.2674 | 277.93 | -45.91 | y | eb |
| 278826516 | 7.0430 | 2.75e+04 | 5.33e+02 | 1.24e+02 | 6248 | 4.10 | 1 | 10.377 | 100.47 | -54.81 | y | eb |
| 91636891 | 13.450 | 2.74e+04 | 9.44e+02 | 1.61e+02 | 6461 | 3.91 | 1 | 20.549 | 39.40 | -36.97 | y | eb |
| 153742549 | 6.0700 | 2.74e+04 | 2.10e+03 | 8.23e+01 | 5726 | 3.63 | 2 | 11.324 | 66.52 | -44.59 | y | eb |
| 178723395 | 1.7616 | 2.70e+04 | 2.30e+03 | 5.09e+01 | 6756 | 4.26 | 1 | 4.0281 | 166.14 | -43.24 | y | eb |
| 279949020 | 6.5493 | 2.65e+04 | 1.04e+03 | 1.37e+02 | 5860 | 3.77 | 2 | 14.611 | 40.39 | -59.98 | y | eb |
| 207080350 | 9.1069 | 2.65e+04 | 3.52e+05 | 1.93e+02 | 6978 | 3.98 | 2 | 33.987 | 320.91 | -39.77 | y | eb |
| 27654882 | 1.1156 | 2.65e+04 | 2.99e+03 | 3.74e+01 | 6447 | 3.88 | 1 | 3.4932 | 123.70 | 12.06 | y | eb |
| 270204401 | 2.2383 | 2.64e+04 | 3.58e+03 | 4.77e+01 | 9428 | 4.19 | 2 | 17.609 | 332.71 | -71.97 | y | eb |
| 350297040 | 10.874 | 2.63e+04 | 4.47e+02 | 1.27e+02 | 6294 | 4.45 | 2 | 19.383 | 83.71 | -55.93 | y | eb |
| 12158853 | 0.6311 | 2.61e+04 | 2.55e+05 | 2.17e+01 | 3465 | 4.69 | 2 | 18.312 | 91.55 | -3.61 | y | eb |
| 218152299 | 1.2597 | 2.59e+04 | 1.63e+04 | 3.65e+01 | 6225 | 3.83 | 1 | 7.6603 | 261.91 | -45.55 | y | eb |
| 2372579 | 9.9215 | 2.58e+04 | 2.30e+03 | 2.16e+02 | 5417 | 4.22 | 1 | 16.004 | 288.91 | -28.68 | y | eb |
| 32449963 | 6.5199 | 2.58e+04 | 5.22e+04 | 1.91e+02 | 5771 | 4.27 | 2 | 31.714 | 189.93 | -11.64 | y | eb |
| 70717462 | 2.9482 | 2.52e+04 | 2.18e+03 | 8.70e+01 | — | — | 1 | 2.2676 | 151.63 | -35.18 | n | eb |
| 426541180 | 4.6975 | 2.50e+04 | 1.15e+03 | 9.95e+01 | 5715 | 4.32 | 1 | 4.7776 | 244.93 | -72.21 | n | eb |
| 358108063 | 2.9858 | 2.49e+04 | 1.06e+03 | 7.24e+01 | 5723 | — | 2 | 8.8750 | 51.24 | -75.93 | y | eb |
| 394585218 | 3.9645 | 2.48e+04 | 1.46e+03 | 9.38e+01 | 6032 | 3.99 | 2 | 8.3107 | 341.02 | -65.76 | y | eb |
| 178996712 | 2.9828 | 2.46e+04 | 1.46e+04 | 4.16e+01 | 7188 | 4.10 | 2 | 3.6709 | 70.06 | -27.73 | n | eb |
| 220359766 | 1.7599 | 2.45e+04 | 2.14e+03 | 4.65e+01 | — | — | 1 | 2.2444 | 155.05 | -52.19 | y | eb |
| 341309569 | 7.3475 | 2.45e+04 | 6.00e+02 | 1.24e+02 | 4966 | — | 1 | 4.7958 | 315.92 | -64.13 | n | eb |
| 139188326 | 0.5883 | 2.42e+04 | 8.99e+04 | 1.08e+01 | 6506 | 3.67 | 2 | 0.7701 | 345.01 | -46.49 | n | eb |
| 270166263 | 7.6589 | 2.41e+04 | 2.03e+03 | 1.63e+02 | 4933 | 4.13 | 2 | 11.119 | 330.03 | -27.70 | y | eb |
| 317191077 | 2.1910 | 2.41e+04 | 4.85e+03 | 4.17e+01 | 6364 | — | 2 | 4.7310 | 87.14 | -13.05 | n | eb |
| 409900613 | 1.1032 | 2.40e+04 | 9.07e+03 | 4.67e+01 | 3194 | 4.83 | 1 | 9.5539 | 144.89 | -17.59 | y | eb |
| 118200081 | 0.9529 | 2.39e+04 | 1.01e+04 | 1.79e+01 | 5366 | — | 2 | 3.4996 | 272.18 | -56.78 | n | eb |
| 115275539 | 1.7630 | 2.37e+04 | 3.17e+03 | 5.11e+01 | 4913 | — | 1 | 2.3541 | 25.95 | -38.72 | y | eb |
| 46313508 | 1.0326 | 2.33e+04 | 6.23e+03 | 2.50e+01 | 6445 | 3.60 | 2 | 2.3889 | 83.10 | -14.97 | n | eb |
| 124350360 | 8.5580 | 2.33e+04 | 2.38e+04 | 2.33e+02 | 3471 | 4.62 | 1 | 14.902 | 227.66 | -52.80 | y | eb |
| 169316288 | 0.5589 | 2.33e+04 | 4.26e+04 | 1.42e+01 | 6290 | — | 2 | 5.4193 | 292.50 | -27.95 | n | eb |
| 222945452 | 0.7483 | 2.31e+04 | 1.41e+04 | 2.12e+01 | — | — | 2 | 0.9521 | 245.89 | -44.11 | n | eb |
| 228760807 | 0.7779 | 2.30e+04 | 9.22e+04 | 2.03e+01 | 5320 | — | 2 | 3.9835 | 194.10 | -27.39 | y | eb |
| 396655059 | 7.9781 | 2.30e+04 | 1.17e+03 | 1.00e+02 | 7909 | 4.16 | 2 | 12.262 | 214.77 | -77.09 | y | eb |
| 440788366 | 0.7742 | 2.28e+04 | 6.48e+03 | 2.05e+01 | 9079 | — | 1 | 2.6778 | 109.09 | 12.45 | n | eb |
| 18914916 | 11.287 | 2.27e+04 | 5.66e+02 | 1.51e+02 | 5486 | 4.57 | 2 | 15.729 | 118.92 | 13.80 | y | eb |
| 180943676 | 8.418 | 2.26e+04 | 8.62e+02 | 1.52e+02 | 6027 | 4.39 | 1 | 8.2751 | 88.72 | -46.42 | n | eb |
| 294197236 | 0.9672 | 2.24e+04 | 4.36e+03 | 3.07e+01 | 6372 | 3.60 | 1 | 5.6588 | 264.81 | -68.78 | n | eb |
| 312111256 | 1.1517 | 2.19e+04 | 1.01e+04 | 2.71e+01 | 7593 | 4.38 | 2 | 3.6697 | 140.66 | 6.23 | n | eb |
| 423524230 | 2.5815 | 2.18e+04 | 1.32e+03 | 6.25e+01 | 6564 | 4.33 | 2 | 2.7988 | 169.18 | -19.89 | n | eb |
| 30382918 | 0.5719 | 2.17e+04 | 2.86e+05 | 1.04e+01 | 5854 | 4.22 | 2 | 3.3986 | 198.43 | -41.27 | y | eb |
| 48063034 | 0.5863 | 2.16e+04 | 5.19e+04 | 1.52e+01 | 5304 | 4.20 | 2 | 6.5276 | 147.48 | -34.11 | n | eb |
| 67267845 | 1.0126 | 2.16e+04 | 4.29e+03 | 3.57e+01 | 6817 | 3.64 | 1 | 11.205 | 240.95 | -29.97 | n | eb |
| 35101462 | 4.1726 | 2.16e+04 | 1.76e+03 | 7.34e+01 | 6114 | 4.21 | 2 | 5.3038 | 35.41 | -14.78 | y | eb |
| 363933313 | 4.6865 | 2.13e+04 | 9.98e+02 | 9.37e+01 | 5428 | — | 1 | 11.931 | 251.32 | -71.05 | y | eb |
| 270411008 | 8.6657 | 2.11e+04 | 2.14e+04 | 2.31e+02 | 5492 | 4.24 | 1 | 41.883 | 349.40 | -29.17 | y | eb |
| 301247295 | 8.5054 | 2.10e+04 | 1.47e+03 | 9.64e+01 | 5933 | — | 2 | 15.232 | 255.08 | -69.56 | y | eb |
| 244163413 | 1.7879 | 2.09e+04 | 8.52e+04 | 6.67e+01 | 6098 | 4.29 | 2 | 14.971 | 5.16 | -5.14 | y | eb |
| 468958384 | 0.7675 | 2.07e+04 | 4.07e+03 | 2.16e+01 | 3478 | 4.81 | 1 | 35.711 | 107.70 | 7.90 | y | eb |
| 146761368 | 0.9176 | 2.05e+04 | 3.53e+03 | 2.83e+01 | 6597 | 3.58 | 1 | 6.5819 | 46.17 | -44.66 | n | eb |
| 191926695 | 1.9352 | 2.02e+04 | 9.92e+03 | 3.56e+01 | — | — | 2 | 2.2496 | 136.52 | -38.88 | y | eb |
| 303427297 | 4.2976 | 2.02e+04 | 1.29e+03 | 5.27e+01 | 5273 | — | 2 | 1.7764 | 164.18 | -57.75 | n | eb |
| 260659986 | 3.5699 | 2.01e+04 | 9.93e+02 | 9.34e+01 | 6107 | 3.90 | 1 | 16.691 | 98.48 | -59.96 | y | eb |
| 117879940 | 1.1311 | 2.00e+04 | 3.29e+03 | 2.72e+01 | 5559 | 3.92 | 2 | 3.8599 | 70.72 | -11.87 | n | eb |
| 380645083 | 4.3894 | 1.99e+04 | 1.95e+03 | 8.61e+01 | 5927 | 3.58 | 2 | 0.9681 | 285.20 | -34.88 | n | eb |
| 259864042 | 0.4607 | 1.99e+04 | 2.81e+03 | 3.90e+01 | 31000 | 5.59 | 1 | 14.676 | 40.32 | -68.92 | n | eb |
| 234494090 | 0.9726 | 1.96e+04 | 3.10e+03 | 2.98e+01 | — | — | 1 | 19.558 | 9.81 | -63.20 | y | eb |
| 319467578 | 2.3652 | 1.93e+04 | 1.48e+03 | 4.72e+01 | 6157 | 4.22 | 2 | 2.4735 | 100.22 | -52.69 | y | eb |
| 369966331 | 0.9128 | 1.92e+04 | 8.60e+03 | 1.77e+01 | 4686 | — | 2 | 0.9706 | 19.73 | -65.18 | y | eb |
| 291320884 | 0.3717 | 1.88e+04 | 3.30e+05 | 8.40e+00 | 3507 | 4.73 | 2 | 33.227 | 260.95 | -57.41 | n | eb |
| 410654298 | 8.2252 | 1.79e+04 | 1.91e+04 | 2.18e+02 | 5234 | — | 1 | 18.858 | 177.00 | -66.11 | y | eb |
| 66509654 | 2.6446 | 1.76e+04 | 3.45e+03 | 9.16e+01 | 3253 | 4.80 | 1 | 35.119 | 109.42 | -23.99 | y | eb |
| 22937402 | 1.3839 | 1.76e+04 | 1.59e+04 | 2.29e+01 | — | — | 2 | 0.6199 | 109.13 | -38.31 | n | eb |
| 94257578 | 1.1921 | 1.74e+04 | 2.43e+03 | 5.15e+01 | 5722 | — | 2 | 3.2446 | 241.41 | -30.64 | n | eb |
| 263925187 | 0.3330 | 1.73e+04 | 2.71e+04 | 1.21e+01 | 3944 | 4.59 | 1 | 21.136 | 269.99 | -30.07 | n | eb |
| 9053429 | 12.962 | 1.72e+04 | 6.14e+02 | 1.30e+02 | 31000 | 5.59 | 1 | 33.615 | 356.09 | -10.19 | y | eb |
| 197886566 | 0.8721 | 1.71e+04 | 1.32e+04 | 1.45e+01 | 6019 | 4.04 | 1 | 1.1038 | 57.31 | -58.44 | n | pl |
| 11756637 | 4.3061 | 1.70e+04 | 2.38e+04 | 9.04e+01 | 3436 | 4.60 | 2 | 53.312 | 90.61 | -1.31 | y | eb |
| 78450017 | 0.9438 | 1.70e+04 | 2.19e+03 | 2.75e+01 | 3524 | 4.60 | 1 | 11.030 | 102.58 | -21.46 | y | eb |
| 259543079 | 9.0208 | 1.69e+04 | 5.39e+02 | 1.24e+02 | 5241 | 4.31 | 1 | 17.720 | 71.63 | -53.12 | y | eb |
| 365570620 | 0.8584 | 1.69e+04 | 3.59e+03 | 2.69e+01 | 6505 | 3.73 | 1 | 4.8005 | 81.29 | 7.95 | n | eb |
| 142177867 | 1.4353 | 1.65e+04 | 7.92e+04 | 3.44e+01 | 5456 | 4.33 | 2 | 3.8672 | 37.41 | -47.22 | y | eb |
| 61724376 | 0.9538 | 1.64e+04 | 3.60e+03 | 2.46e+01 | 5780 | 3.82 | 1 | 5.1693 | 288.95 | -44.50 | n | eb |
| 220015845 | 54.515 | 1.64e+04 | 2.43e+03 | 2.10e+02 | 5950 | 4.12 | 1 | 33.659 | 32.36 | -49.55 | n | eb |
| 173038281 | 4.309 | 1.64e+04 | 1.00e+03 | 8.94e+01 | 6412 | 4.22 | 1 | 1.8536 | 102.27 | -27.34 | y | pl |
| 60479151 | 0.4189 | 1.63e+04 | 1.03e+04 | 1.46e+01 | 6210 | 3.99 | 1 | 1.6225 | 96.31 | -21.78 | y | pl |
| 164681172 | 4.9064 | 1.61e+04 | 4.12e+04 | 1.09e+02 | 5694 | 4.23 | 2 | 31.586 | 24.56 | -21.07 | y | eb |
| 91961 | 5.2823 | 1.56e+04 | 9.56e+02 | 8.55e+01 | — | 4.83 | 2 | 18.651 | 221.69 | -23.91 | y | eb |
| 31690845 | 1.1991 | 1.54e+04 | 6.68e+03 | 1.77e+01 | 6652 | 3.43 | 2 | 2.2371 | 289.12 | -31.40 | n | eb |
| 48063032 | 0.5863 | 1.54e+04 | 2.84e+04 | 1.51e+01 | 5824 | 4.39 | 2 | 5.3075 | 147.48 | -34.11 | n | eb |
| 162585282 | 0.5122 | 1.53e+04 | 1.02e+05 | 8.79e+00 | 3311 | 4.75 | 2 | 31.019 | 170.31 | -47.58 | n | eb |
| 4723156 | 9.4896 | 1.51e+04 | 4.85e+04 | 1.72e+02 | 3057 | 4.96 | 2 | 41.058 | 39.44 | -7.09 | y | eb |
| 323295967 | 0.4245 | 1.50e+04 | 1.59e+04 | 1.15e+01 | 5581 | — | 2 | 1.8769 | 52.64 | -39.24 | n | eb |
| 219328784 | 1.9687 | 1.47e+04 | 1.55e+03 | 4.42e+01 | 4539 | 4.30 | 1 | 1.0865 | 333.50 | -54.11 | n | eb |
| 18915591 | 3.4933 | 1.45e+04 | 8.48e+02 | 8.28e+01 | 7432 | 3.41 | 1 | 21.963 | 118.91 | 12.66 | y | eb |
| 12631605 | 0.7086 | 1.44e+04 | 1.28e+05 | 1.66e+01 | 5514 | 4.44 | 2 | 20.219 | 53.11 | -6.97 | y | eb |
| 147314529 | 0.4628 | 1.40e+04 | 1.08e+04 | 1.67e+01 | 11310 | 3.70 | 1 | 1.3431 | 104.69 | -17.63 | n | pl |
| 340633943 | 0.3757 | 1.40e+04 | 4.79e+04 | 9.30e+00 | 6031 | 4.41 | 1 | 6.0757 | 116.49 | -56.54 | n | eb |
| 412345587 | 0.5268 | 1.38e+04 | 3.06e+04 | 1.72e+01 | 3516 | 4.82 | 1 | 121.13 | 110.53 | -18.64 | n | eb |
| 114819301 | 4.8876 | 1.37e+04 | 8.06e+02 | 7.87e+01 | 3786 | 4.32 | 1 | 6.2994 | 2.30 | -18.91 | y | eb |
| 401926767 | 6.8009 | 1.36e+04 | 1.26e+05 | 1.20e+02 | 4342 | 4.25 | 2 | 48.278 | 57.35 | -1.24 | y | eb |
| 52924466 | 10.612 | 1.34e+04 | 3.99e+02 | 1.31e+02 | 5305 | 4.43 | 1 | 3.5125 | 102.38 | -33.70 | y | eb |
| 350298314 | 13.525 | 1.33e+04 | 3.58e+02 | 1.22e+02 | 5468 | 4.59 | 1 | 23.465 | 83.74 | -59.33 | y | eb |
| 183537458 | 0.2278 | 1.32e+04 | 2.00e+05 | 7.49e+00 | 6283 | 4.42 | 1 | 1.8545 | 357.79 | -39.86 | y | usp |
| 159897979 | 16.785 | 1.29e+04 | 1.29e+03 | 1.12e+02 | 6687 | 3.74 | 2 | 20.779 | 48.84 | -38.99 | y | eb |
| 343757299 | 5.8194 | 1.28e+04 | 9.17e+02 | 7.35e+01 | 9787 | 4.00 | 1 | 5.1452 | 273.21 | -74.28 | y | eb |
| 219201178 | 2.4170 | 1.28e+04 | 7.41e+02 | 4.50e+01 | 6760 | 4.03 | 2 | 3.6424 | 92.72 | -52.89 | n | eb |
| 148611095 | 4.8374 | 1.27e+04 | 1.01e+04 | 5.47e+01 | 3452 | 4.78 | 2 | 13.377 | 165.21 | -7.26 | y | eb |
| 143234741 | 1.9178 | 1.27e+04 | 7.46e+02 | 3.75e+01 | 5855 | 4.17 | 1 | 3.5656 | 90.62 | -32.38 | n | eb |
| 167812449 | 4.2356 | 1.25e+04 | 4.60e+02 | 7.52e+01 | 5799 | 4.28 | 2 | 1.7238 | 104.78 | -61.84 | n | eb |
| 269996393 | 10.381 | 1.25e+04 | 4.94e+02 | 1.28e+02 | 5711 | 4.51 | 1 | 0.5600 | 311.46 | -27.60 | n | misc |
| 358022169 | 0.3032 | 1.24e+04 | 3.48e+04 | 8.15e+00 | 5740 | 4.53 | 2 | 0.5261 | 193.65 | -80.07 | y | eb |
| 159803421 | 0.2761 | 1.24e+04 | 1.32e+04 | 1.23e+01 | 5708 | 4.37 | 1 | 0.2218 | 261.64 | -32.96 | y | usp |
| 120566395 | 1.7957 | 1.23e+04 | 1.72e+03 | 2.67e+01 | 6001 | 4.04 | 1 | 1.3061 | 3.84 | -39.52 | n | pl |
| 124712813 | 0.8256 | 1.23e+04 | 2.30e+03 | 2.07e+01 | 3592 | 4.68 | 2 | 7.0125 | 104.76 | -11.72 | n | eb |
| 326356701 | 1.1122 | 1.20e+04 | 4.50e+03 | 2.18e+01 | 4674 | — | 2 | 1.5596 | 325.59 | -21.76 | n | eb |
| 355357949 | 1.4604 | 1.17e+04 | 1.20e+03 | 3.51e+01 | 6714 | 4.17 | 1 | 3.5642 | 109.33 | -49.41 | n | eb |
| 47175622 | 1.5235 | 1.16e+04 | 2.62e+03 | 2.84e+01 | 6698 | — | 2 | 1.5101 | 145.35 | -7.65 | y | eb |
| 293480903 | 7.5701 | 1.11e+04 | 5.00e+02 | 7.90e+01 | 6180 | — | 2 | 3.4731 | 49.97 | -82.14 | n | eb |
| 63037741 | 12.295 | 1.09e+04 | 3.03e+02 | 1.52e+02 | 3341 | 4.84 | 1 | 6.5 | 336.86 | -35.01 | y | misc |
| 266769521 | 0.5362 | 1.07e+04 | 1.72e+06 | 7.77e+00 | 6659 | 4.06 | 2 | 36.167 | 29.75 | -22.91 | n | eb |
| 265551788 | 10.943 | 1.04e+04 | 3.55e+02 | 1.19e+02 | 5258 | — | 1 | 1.4161 | 94.75 | 5.93 | y | pl |
| 21184505 | 5.1777 | 1.02e+04 | 6.55e+02 | 1.01e+02 | 6146 | 4.23 | 3 | 0.7600 | 128.85 | 12.01 | n | eb |
| 443494351 | 0.2578 | 1.02e+04 | 3.05e+04 | 7.87e+00 | 7620 | 3.33 | 1 | 1.8084 | 146.78 | -54.20 | n | usp |
| 425864141 | 0.1091 | 1.01e+04 | 1.60e+05 | 6.38e+00 | 3039 | 4.92 | 1 | 15.052 | 352.08 | -45.91 | n | usp |
| 76698707 | 0.2639 | 1.01e+04 | 1.44e+04 | 9.62e+00 | 5845 | 3.61 | 1 | 1.1410 | 229.05 | -32.49 | y | usp |
| 300560295 | 10.292 | 1.00e+04 | 2.55e+02 | 1.00e+02 | 5885 | 4.25 | 1 | 2.3754 | 112.91 | -68.13 | n | eb |
| 274229418 | 9.6186 | 1.00e+04 | 1.16e+04 | 2.37e+02 | 3422 | 4.76 | 1 | 28.221 | 115.47 | 5.04 | y | eb |
| 278683641 | 4.2420 | 9.98e+03 | 1.09e+03 | 5.11e+01 | 6095 | 4.03 | 2 | 14.176 | 99.24 | -58.46 | y | eb |
| 349970685 | 1.2570 | 9.95e+03 | 1.15e+03 | 2.03e+01 | — | — | 2 | 9.6550 | 114.48 | -60.29 | y | eb |
| 75352949 | 0.4720 | 9.84e+03 | 5.46e+04 | 8.10e+00 | 4816 | — | 2 | 4.3822 | 6.41 | -17.81 | n | eb |
| 150357290 | 0.4926 | 9.81e+03 | 4.92e+03 | 1.36e+01 | 5650 | 4.39 | 1 | 0.6642 | 96.16 | -64.05 | n | misc |
| 224283342 | 0.8873 | 9.74e+03 | 6.83e+03 | 1.16e+01 | 3165 | 4.88 | 3 | 5.1680 | 356.35 | -40.33 | n | misc |
| 56128191 | 3.1118 | 9.72e+03 | 6.14e+02 | 5.59e+01 | 6798 | 4.20 | 2 | 2.9522 | 70.75 | -6.43 | y | eb |
| 133105082 | 0.4464 | 9.41e+03 | 3.23e+04 | 5.79e+00 | 3282 | 4.74 | 2 | 307.51 | 120.46 | -40.50 | n | eb |
| 309025566 | 8.8084 | 9.41e+03 | 5.13e+04 | 2.38e+02 | 6459 | — | 1 | 13.707 | 151.07 | -28.37 | y | eb |
| 384742846 | 6.3568 | 9.34e+03 | 6.43e+02 | 6.10e+01 | 6542 | 4.20 | 2 | 19.510 | 258.72 | -82.85 | y | eb |
| 173077938 | 1.2970 | 9.33e+03 | 3.07e+03 | 1.66e+01 | 7382 | 3.87 | 2 | 0.3219 | 111.05 | -40.86 | n | eb |
| 254039358 | 0.7477 | 9.16e+03 | 2.33e+03 | 1.60e+01 | 6124 | 4.10 | 1 | 0.4260 | 285.25 | -40.38 | y | pl |
| 121048789 | 0.6441 | 9.16e+03 | 4.15e+03 | 1.80e+01 | 5709 | 4.21 | 1 | 0.3975 | 56.19 | -21.29 | y | pl |
| 308184924 | 4.1283 | 8.89e+03 | 7.20e+02 | 4.39e+01 | 6082 | 3.99 | 2 | 26.963 | 130.43 | -69.78 | y | eb |
| 153709888 | 2.1663 | 8.85e+03 | 9.29e+02 | 3.93e+01 | 6720 | 4.22 | 1 | 6.3590 | 65.56 | -42.07 | y | eb |
| 304071827 | 1.5913 | 8.78e+03 | 2.92e+03 | 2.34e+01 | 6645 | 3.97 | 1 | 0.4086 | 258.45 | -65.68 | n | pl |
| 22146154 | 6.0609 | 8.58e+03 | 2.79e+02 | 8.65e+01 | 6874 | 3.97 | 1 | 2.9735 | 148.76 | -25.13 | y | eb |
| 189639080 | 1.5666 | 8.36e+03 | 4.35e+02 | 3.27e+01 | 8840 | — | 1 | 18.359 | 144.21 | -28.48 | y | eb |
| 32050581 | 1.5564 | 8.30e+03 | 5.09e+02 | 3.36e+01 | 5503 | 4.22 | 1 | 2.4356 | 57.07 | -69.15 | y | eb |
| 98658304 | 5.9320 | 8.29e+03 | 5.72e+02 | 7.09e+01 | 4996 | — | 2 | 15.442 | 8.93 | -22.74 | n | eb |
| 220569051 | 2.7779 | 8.25e+03 | 6.91e+02 | 4.67e+01 | 6025 | 3.73 | 2 | 6.6498 | 46.36 | -60.36 | y | eb |
| 55659311 | 5.595 | 7.96e+03 | 3.12e+02 | 6.63e+01 | 5103 | 4.45 | 2 | 20.880 | 74.11 | -64.48 | y | eb |
| 408512382 | 4.0311 | 7.96e+03 | 7.19e+02 | 6.06e+01 | 7126 | 3.32 | 2 | 5.8634 | 194.65 | -21.71 | y | eb |
| 219421171 | 8.3023 | 7.89e+03 | 3.44e+02 | 9.05e+01 | 6245 | 3.57 | 2 | 16.753 | 79.82 | -49.64 | y | eb |
| 146344020 | 2.4945 | 7.88e+03 | 7.28e+02 | 2.91e+01 | 5986 | 3.94 | 2 | 2.5643 | 74.34 | -20.96 | n | eb |
| 281053777 | 11.019 | 7.86e+03 | 3.55e+04 | 2.24e+02 | 6927 | — | 1 | 126.47 | 98.82 | 4.19 | y | eb |
| 409942986 | 0.2796 | 7.81e+03 | 2.22e+05 | 6.20e+00 | 5528 | 4.22 | 1 | 6.2729 | 145.00 | -17.16 | n | usp |
| 115693377 | 4.9269 | 7.67e+03 | 4.57e+02 | 6.05e+01 | 6136 | 4.13 | 2 | 3.7075 | 6.81 | -41.57 | n | eb |
| 460820330 | 5.0743 | 7.65e+03 | 4.49e+02 | 5.51e+01 | 6114 | 4.35 | 2 | 38.855 | 219.39 | -31.63 | y | eb |
| 270648838 | 7.6347 | 7.56e+03 | 3.17e+04 | 1.58e+02 | 6093 | 4.14 | 2 | 50.901 | 136.70 | 5.46 | y | eb |
| 140212820 | 0.7777 | 7.55e+03 | 1.34e+03 | 1.58e+01 | 6392 | 3.94 | 2 | 2.1021 | 84.96 | -30.76 | y | eb |
| 270348090 | 2.8190 | 7.55e+03 | 4.59e+02 | 4.96e+01 | — | — | 1 | 20.399 | 215.48 | -30.84 | y | eb |
| 269342892 | 0.2244 | 7.52e+03 | 1.31e+04 | 6.97e+00 | — | — | 1 | 0.5568 | 119.07 | -48.24 | n | usp |
| 82580956 | 0.9471 | 7.48e+03 | 1.95e+03 | 2.28e+01 | 5793 | 3.93 | 1 | 0.4057 | 169.62 | -53.71 | y | pl |
| 255548311 | 4.9631 | 7.45e+03 | 2.55e+02 | 5.80e+01 | — | — | 1 | 3.5553 | 95.48 | -50.92 | n | eb |
| 146559012 | 2.6411 | 7.43e+03 | 3.54e+04 | 8.64e+01 | 6216 | 4.39 | 1 | 17.012 | 77.51 | -23.67 | y | eb |
| 92628706 | 9.2030 | 7.42e+03 | 1.08e+05 | 2.30e+02 | 5547 | 4.20 | 1 | 30.235 | 315.74 | -32.58 | y | eb |
| 107012110 | 3.0334 | 7.34e+03 | 5.32e+02 | 5.40e+01 | 5994 | 4.14 | 1 | 1.4840 | 162.04 | -40.00 | n | pl |
| 451211626 | 2.4527 | 7.04e+03 | 6.29e+02 | 3.24e+01 | 3773 | 4.63 | 2 | 41.088 | 210.31 | -34.96 | y | eb |
| 279537689 | 5.7846 | 7.01e+03 | 5.36e+02 | 8.19e+01 | 5958 | 4.26 | 2 | 3.9806 | 59.40 | -14.16 | y | eb |
| 9172417 | 0.2451 | 6.89e+03 | 3.80e+05 | 5.19e+00 | 3551 | 4.67 | 2 | 6.4761 | 62.05 | -5.75 | n | usp |
| 405391996 | 1.2851 | 6.79e+03 | 1.38e+03 | 2.06e+01 | 5764 | — | 2 | 1.7041 | 128.78 | -13.75 | n | eb |
| 80025900 | 4.0594 | 6.71e+03 | 6.28e+02 | 6.11e+01 | 3876 | — | 2 | 8.6198 | 121.00 | -46.33 | y | eb |
| 231972938 | 1.5507 | 6.69e+03 | 5.75e+02 | 2.75e+01 | 6210 | 4.35 | 1 | 3.9200 | 95.47 | -46.21 | y | eb |
| 142677613 | 3.0912 | 6.64e+03 | 9.24e+02 | 5.28e+01 | 8357 | 4.16 | 2 | 16.442 | 103.60 | -14.45 | y | eb |
| 98064760 | 9.9000 | 6.60e+03 | 4.87e+02 | 7.64e+01 | — | — | 1 | 6.7401 | 289.91 | -40.81 | y | eb |
| 292293385 | 0.2694 | 6.50e+03 | 3.42e+04 | 5.26e+00 | 5492 | 4.48 | 1 | 3.3371 | 278.49 | -69.86 | n | usp |
| 167795859 | 3.1061 | 6.50e+03 | 2.75e+02 | 4.98e+01 | 5479 | 4.00 | 1 | 16.795 | 104.42 | -61.75 | y | eb |
| 387463207 | 0.1899 | 6.48e+03 | 9.64e+06 | 5.63e+00 | 6259 | 4.21 | 1 | 27.263 | 42.46 | 8.93 | n | usp |
| 437230910 | 0.3805 | 6.39e+03 | 3.01e+03 | 1.48e+01 | 5406 | 4.10 | 1 | 0.2367 | 164.77 | -21.70 | y | pl |
| 396934949 | 0.1887 | 6.36e+03 | 1.74e+04 | 6.15e+00 | 4340 | 4.29 | 1 | 4.5204 | 63.47 | 3.31 | n | usp |
| 96106862 | 5.3800 | 6.32e+03 | 6.05e+02 | 5.80e+01 | 6554 | 4.03 | 2 | 1.2424 | 147.20 | -8.49 | n | eb |
| 146601318 | 0.4935 | 6.27e+03 | 1.21e+03 | 1.39e+01 | 5257 | 3.75 | 1 | 1.9066 | 149.25 | -1.35 | y | pl |
| 456609929 | 4.5678 | 6.23e+03 | 1.15e+04 | 1.59e+01 | 7643 | 4.09 | 2 | 5.5403 | 282.35 | -59.42 | y | eb |
| 130942594 | 10.792 | 6.23e+03 | 1.09e+03 | 1.32e+02 | 6362 | — | 1 | 20.078 | 188.34 | -32.74 | y | eb |
| 87260967 | 0.5452 | 6.22e+03 | 7.45e+03 | 1.40e+01 | 4665 | — | 1 | 0.1441 | 272.76 | -47.51 | y | pl |
| 303811839 | 6.9220 | 6.18e+03 | 4.12e+02 | 7.14e+01 | 5938 | — | 1 | 2.0336 | 164.54 | -55.98 | n | eb |
| 220402290 | 0.7852 | 6.12e+03 | 2.36e+03 | 1.53e+01 | 5817 | 4.36 | 2 | 4.5066 | 69.57 | -57.20 | n | eb |
| 271225404 | 2.1195 | 6.11e+03 | 5.67e+02 | 3.20e+01 | 3764 | 4.62 | 2 | 47.344 | 211.10 | -31.31 | y | eb |
| 381948745 | 1.5953 | 6.02e+03 | 4.78e+03 | 1.37e+01 | 7084 | 3.55 | 1 | 7.1065 | 76.36 | -56.30 | n | eb |
| 128679896 | 11.130 | 5.99e+03 | 8.56e+04 | 2.35e+02 | 5594 | 4.20 | 2 | 19.882 | 299.25 | -43.61 | y | eb |
| 394657952 | 0.8723 | 5.94e+03 | 1.77e+03 | 2.02e+01 | 5725 | — | 1 | 2.7255 | 158.68 | -77.96 | y | eb |
| 105706808 | 0.1986 | 5.93e+03 | 8.48e+03 | 7.58e+00 | — | — | 1 | 0.4872 | 156.25 | -39.51 | n | usp |
| 231840927 | 1.6357 | 5.87e+03 | 1.46e+03 | 2.17e+01 | 5726 | 4.44 | 2 | 0.4241 | 25.17 | -65.41 | y | eb |
| 231833061 | 23.335 | 5.85e+03 | 1.17e+04 | 2.31e+02 | 4580 | 4.34 | 2 | 48.949 | 24.00 | -65.69 | y | eb |
| 294328887 | 0.3545 | 5.79e+03 | 1.89e+03 | 8.30e+00 | 3079 | 4.85 | 1 | 10.246 | 108.97 | -59.34 | n | eb |
| 124712820 | 0.8256 | 5.72e+03 | 1.08e+03 | 1.69e+01 | 3989 | 4.34 | 2 | 1.2622 | 104.76 | -11.72 | n | eb |
| 312907176 | 0.7580 | 5.71e+03 | 1.21e+03 | 1.47e+01 | 3260 | 5.00 | 1 | 43.759 | 182.91 | -68.82 | y | eb |
| 307033218 | 25.755 | 5.66e+03 | 1.92e+02 | 7.51e+01 | 5216 | 4.08 | 1 | 42.014 | 123.30 | -69.32 | y | eb |
| 438682877 | 0.9221 | 5.41e+03 | 1.65e+03 | 1.56e+01 | 5820 | — | 2 | 0.7677 | 202.22 | -44.68 | n | eb |
| 59038880 | 0.3053 | 5.29e+03 | 8.22e+07 | 4.70e+00 | 5325 | 4.62 | 2 | 79.385 | 57.36 | 12.90 | n | eb |
| 412942849 | 0.3806 | 5.18e+03 | 6.39e+03 | 8.75e+00 | 6222 | 3.43 | 1 | 0.5721 | 204.57 | -55.57 | n | pl |
| 168697816 | 0.6920 | 5.17e+03 | 1.91e+03 | 1.13e+01 | 6456 | 4.37 | 2 | 2.4111 | 61.66 | -34.96 | n | eb |
| 266816672 | 0.3031 | 5.03e+03 | 7.30e+06 | 4.92e+00 | 6064 | 4.32 | 2 | 21.483 | 30.93 | -19.88 | n | eb |
| 75818403 | 0.5635 | 4.94e+03 | 7.18e+03 | 6.93e+00 | 3669 | 4.75 | 2 | 62.353 | 139.52 | -46.08 | n | eb |
| 302038263 | 1.5474 | 4.93e+03 | 8.26e+02 | 1.96e+01 | — | — | 2 | 6.0819 | 131.95 | -69.39 | n | eb |
| 23328912 | 2.5639 | 4.83e+03 | 7.65e+02 | 3.80e+01 | 8690 | 4.15 | 2 | 0.8293 | 167.44 | -35.40 | n | eb |
| 1190662 | 0.4440 | 4.79e+03 | 1.30e+03 | 1.76e+01 | 3595 | 4.28 | 2 | 2.3930 | 136.03 | -16.49 | y | eb |
| 125501325 | 4.3858 | 4.77e+03 | 7.40e+02 | 4.11e+01 | — | — | 2 | 5.9093 | 105.85 | -10.70 | n | eb |
| 13738984 | 0.2769 | 4.76e+03 | 1.69e+04 | 6.68e+00 | 5818 | 4.35 | 2 | 0.5887 | 133.70 | -11.03 | n | usp |
| 89787749 | 0.5413 | 4.75e+03 | 6.98e+02 | 1.68e+01 | 3374 | 4.91 | 1 | 23.436 | 127.87 | -59.20 | n | eb |
| 92938279 | 0.2750 | 4.66e+03 | 2.92e+05 | 4.38e+00 | 3327 | 4.89 | 2 | 18.534 | 83.63 | -22.64 | n | usp |
| 92938280 | 0.2750 | 4.54e+03 | 1.20e+05 | 4.45e+00 | 3396 | 4.95 | 2 | 15.406 | 83.63 | -22.64 | n | usp |
| 29847695 | 4.9980 | 4.46e+03 | 7.29e+02 | 5.01e+01 | 6375 | — | 2 | 7.6000 | 23.58 | -8.45 | y | eb |
| 350740905 | 0.1555 | 4.37e+03 | 1.88e+05 | 4.22e+00 | 8181 | 3.86 | 1 | 0.8493 | 88.55 | -56.17 | n | usp |
| 436243444 | 0.6793 | 4.33e+03 | 9.70e+02 | 1.70e+01 | 5093 | 4.24 | 1 | 3.2989 | 84.13 | 8.43 | y | eb |
| 396953669 | 0.3327 | 4.30e+03 | 7.56e+03 | 6.55e+00 | 4719 | — | 2 | 0.3230 | 63.88 | 3.36 | n | eb |
| 30287190 | 3.1243 | 4.21e+03 | 3.17e+02 | 4.35e+01 | 6217 | 4.16 | 2 | 2.6468 | 207.60 | -31.23 | n | eb |
| 2353789 | 1.8718 | 4.20e+03 | 8.55e+02 | 1.98e+01 | 6969 | 3.91 | 1 | 3.0641 | 134.27 | -28.77 | n | eb |
| 279454212 | 11.762 | 4.17e+03 | 2.06e+02 | 7.62e+01 | 5951 | 4.42 | 1 | 4.1042 | 58.47 | -16.95 | y | eb |
| 425206178 | 0.1647 | 4.07e+03 | 1.41e+04 | 4.97e+00 | — | — | 1 | 6.2160 | 111.55 | 7.68 | n | usp |
| 161570793 | 0.2762 | 4.04e+03 | 4.21e+05 | 4.29e+00 | 6262 | 4.37 | 2 | 4.9210 | 74.44 | -42.89 | n | usp |
| 269762258 | 1.3247 | 3.99e+03 | 4.10e+04 | 2.63e+01 | 3358 | 4.67 | 2 | 11.874 | 66.47 | -81.31 | y | eb |
| 20095466 | 0.2118 | 3.97e+03 | 2.75e+03 | 7.97e+00 | 5966 | 4.49 | 1 | 0.2755 | 89.22 | -36.07 | y | usp |
| 284729177 | 0.2068 | 3.88e+03 | 6.91e+04 | 4.44e+00 | 7571 | 3.43 | 1 | 1.4845 | 67.66 | 10.60 | n | usp |
| 185805011 | 2.0054 | 3.78e+03 | 7.87e+02 | 1.85e+01 | 3477 | 4.83 | 2 | 27.171 | 130.69 | -31.03 | y | eb |
| 214299966 | 3.0675 | 3.64e+03 | 5.70e+02 | 3.30e+01 | 6181 | 4.14 | 1 | 1.7140 | 339.16 | -36.94 | n | pl |
| 147102369 | 2.0638 | 3.46e+03 | 4.47e+02 | 3.45e+01 | 7231 | 3.84 | 2 | 5.8315 | 124.80 | -30.42 | y | eb |
| 381854774 | 1.6447 | 3.45e+03 | 7.77e+02 | 2.21e+01 | 6375 | 4.12 | 1 | 1.0266 | 321.79 | -54.34 | y | pl |
| 178889597 | 1.8842 | 3.43e+03 | 7.90e+02 | 2.99e+01 | 4777 | — | 1 | 2.4647 | 195.12 | -38.84 | y | eb |
| 282051803 | 2.4625 | 3.41e+03 | 1.00e+03 | 2.24e+01 | 6246 | 3.87 | 2 | 7.0610 | 132.22 | -75.92 | y | eb |
| 186544053 | 8.9117 | 3.41e+03 | 2.15e+02 | 4.64e+01 | — | 4.67 | 1 | 1.7649 | 132.92 | -33.10 | y | pl |
| 198008281 | 0.2631 | 3.36e+03 | 3.04e+06 | 4.21e+00 | 7089 | 4.04 | 2 | 3.2852 | 60.26 | -54.40 | n | usp |
| 33689349 | 3.4974 | 3.25e+03 | 6.85e+02 | 2.50e+01 | 7098 | 4.10 | 2 | 24.721 | 92.93 | -17.68 | y | eb |
| 406276109 | 7.5474 | 3.23e+03 | 3.26e+02 | 4.51e+01 | 3200 | 4.82 | 2 | 10.415 | 325.64 | -64.21 | n | eb |
| 243391171 | 1.5167 | 3.18e+03 | 4.65e+03 | 1.52e+01 | 5943 | — | 1 | 2.3712 | 205.06 | -45.70 | n | eb |
| 335452175 | 7.7501 | 3.16e+03 | 4.01e+03 | 6.51e+01 | — | — | 1 | 0.8537 | 226.27 | -47.05 | n | pl |
| 360571125 | 2.4626 | 3.13e+03 | 7.99e+02 | 2.53e+01 | 9517 | 3.60 | 2 | 1.1710 | 263.87 | -55.76 | y | eb |
| 167007869 | 0.5509 | 3.10e+03 | 2.12e+03 | 1.06e+01 | 4949 | — | 1 | 0.1814 | 94.80 | -67.59 | n | misc |
| 9433212 | 5.0138 | 3.07e+03 | 1.45e+02 | 3.70e+01 | 5878 | 4.17 | 2 | 4.2410 | 73.54 | -9.49 | n | eb |
| 403136932 | 0.3028 | 3.05e+03 | 4.15e+05 | 3.93e+00 | 3391 | 4.82 | 2 | 46.579 | 333.76 | -54.27 | n | eb |
| 332003916 | 0.6461 | 3.02e+03 | 1.71e+04 | 5.50e+00 | 7458 | 3.54 | 4 | 0.7006 | 179.10 | -48.79 | n | misc |
| 349523518 | 0.1977 | 3.02e+03 | 2.61e+04 | 3.93e+00 | 6172 | 4.07 | 1 | 3.6427 | 111.49 | -63.22 | n | usp |
| 277912443 | 0.5379 | 3.01e+03 | 2.10e+03 | 9.50e+00 | 5964 | 4.04 | 1 | 0.6526 | 354.44 | -73.91 | n | misc |
| 129781743 | 0.2012 | 3.01e+03 | 9.79e+03 | 5.36e+00 | 6655 | 4.24 | 1 | 0.7832 | 36.24 | -38.68 | n | usp |
| 350518984 | 10.367 | 3.00e+03 | 1.40e+02 | 6.01e+01 | 7029 | — | 1 | 2.8731 | 86.18 | -56.71 | y | eb |
| 72229825 | 1.7954 | 2.99e+03 | 1.78e+02 | 2.11e+01 | 6415 | 4.41 | 1 | 1.5651 | 186.75 | -43.67 | n | pl |
| 350479101 | 5.9589 | 2.98e+03 | 2.65e+02 | 5.77e+01 | 6662 | 4.05 | 1 | 2.7658 | 85.79 | -59.14 | y | eb |
| 272086869 | 3.9823 | 2.97e+03 | 3.02e+02 | 3.20e+01 | 8799 | 4.03 | 2 | 1.7775 | 115.67 | -72.53 | y | eb |
| 349154435 | 4.4313 | 2.96e+03 | 2.13e+02 | 3.36e+01 | 5832 | 4.19 | 2 | 4.1264 | 108.18 | -62.01 | y | eb |
| 349911034 | 0.5385 | 2.92e+03 | 9.12e+02 | 1.17e+01 | 5799 | 4.20 | 1 | 1.6651 | 113.97 | -65.68 | y | pl |
| 270427198 | 2.5609 | 2.85e+03 | 2.07e+04 | 4.40e+00 | 6984 | 3.35 | 3 | 0.7279 | 96.35 | -78.57 | n | misc |
| 255567460 | 6.8989 | 2.84e+03 | 2.13e+02 | 4.38e+01 | 9984 | 4.35 | 1 | 1.3900 | 96.44 | -53.10 | y | pl |
| 312068854 | 7.1007 | 2.82e+03 | 1.38e+02 | 5.83e+01 | 5716 | 4.31 | 1 | 1.5401 | 140.02 | 8.44 | y | pl |
| 52382500 | 0.1968 | 2.80e+03 | 5.32e+04 | 3.97e+00 | 5944 | 3.61 | 1 | 1.7025 | 24.19 | -69.95 | n | usp |
| 48318875 | 0.3028 | 2.76e+03 | 7.34e+04 | 4.24e+00 | 5873 | 3.99 | 2 | 4.2039 | 223.30 | -31.62 | n | eb |
| 24347173 | 0.3516 | 2.75e+03 | 1.57e+03 | 1.16e+01 | 5744 | 4.22 | 2 | 0.8472 | 79.17 | -8.70 | n | eb |
| 289596375 | 7.2587 | 2.72e+03 | 4.74e+02 | 4.22e+01 | 6170 | 3.59 | 2 | 2.7868 | 131.79 | -13.06 | y | eb |
| 92743594 | 8.4461 | 2.70e+03 | 2.92e+02 | 3.26e+01 | 4835 | — | 4 | 1.9285 | 129.00 | -53.61 | y | eb |
| 453828066 | 9.1358 | 2.67e+03 | 4.58e+02 | 4.04e+01 | 6545 | 4.08 | 1 | 9.3237 | 53.36 | 0.11 | n | eb |
| 166319733 | 0.1410 | 2.66e+03 | 5.82e+04 | 4.09e+00 | 5425 | 3.86 | 1 | 5.0870 | 206.68 | -37.76 | n | usp |
| 372909935 | 3.6118 | 2.64e+03 | 2.09e+02 | 3.64e+01 | 7015 | 4.12 | 1 | 1.1117 | 119.45 | -64.21 | y | pl |
| 244252435 | 0.9435 | 2.62e+03 | 2.45e+04 | 3.39e+01 | 3675 | 4.57 | 2 | 5.4926 | 74.37 | -3.95 | n | eb |
| 23555025 | 4.7455 | 2.62e+03 | 2.34e+02 | 3.59e+01 | 6001 | 4.34 | 1 | 4.1329 | 169.03 | -32.65 | n | eb |
| 362086333 | 0.2828 | 2.61e+03 | 9.33e+03 | 5.41e+00 | 10440 | 4.18 | 1 | 1.0040 | 107.90 | -84.46 | n | usp |