Homoclinic puzzles and chaos in a nonlinear laser model
Abstract
We present a case study elaborating on the multiplicity and self-similarity of homoclinic and heteroclinic bifurcation structures in the 2D and 3D parameter spaces of a nonlinear laser model with a Lorenz-like chaotic attractor. In a symbiotic approach combining the traditional parameter continuation methods using MatCont and a newly developed technique called the Deterministic Chaos Prospector (DCP) utilizing symbolic dynamics on fast parallel computing hardware with graphics processing units (GPUs), we exhibit how specific codimension-two bifurcations originate and pattern regions of chaotic and simple dynamics in this classical model. We show detailed computational reconstructions of key bifurcation structures such as Bykov T-point spirals and inclination flips in 2D parameter space, as well as the spatial organization and 3D embedding of bifurcation surfaces, parametric saddles, and isolated closed curves (isolas).
1 Introduction
it is evident today the incorporation of complex mathematical elements in combination with the latest computational breakthroughs is the key drive that can further stimulate significant advances in fundamental sciences and cutting-edge engineering. The development of algorithmically simple and generalizable mathematical methods exploiting fast and comprehensive massively parallel simulations using graphics processing units (GPU) ensures better quantitative and, more importantly, qualitative understanding of the nature of complex nonlinear dynamics occurring in various multi-parametric models originating in applications of physical and living systems. The goal of this paper is to deepen our understanding of homoclinic bifurcation theory by demonstrating the universality of the causes and the rules underlying deterministic chaotic dynamics [1, 2, 3, 4, 5, 6] using a particular application from nonlinear optics – a reduced laser model [7, 8].
While basic transition mechanisms of oscillations emerging from stable equilibria through (homoclinic) saddle-node and Andronov-Hopf bifurcations are well presented in diverse applications, their higher dimensional analogues such as various homoclinic and torus bifurcations still remain poorly understood. One of the limiting factors behind such inadequacy is that expert tools for ODE models, i.e., the numerical continuation packages AUTO [9, 10] and MatCont [11], require advanced knowledge on a user’s part to be able to handle those bifurcations. These tools can detect and analyze the essential homoclinic and heteroclinic structure and bifurcations in the phase and parametric spaces of a system. This allows to identify the primary and codimension-two (cod-2) bifurcations, both local and non-local, and the corresponding curves to assess the skeleton of the bifurcation diagram for the system. The main shortcoming of this computational approach is that it requires particular skills and patience to perform a strenuous reconstruction of the “complete” bifurcation unfolding in the 2D parameter plane, by individually continuing a few dozens of principal bifurcation curves, one after another [12], as seen in Figs. 4,10b,12 in this paper. The recent MatCont releases have a strong built-in engine and support for numerical detection and analysis of typical low-codimension homoclinic bifurcations of saddle equilibria in autonomous systems [13]. Nevertheless, such studies involving even basic homoclinic structures remain state-of-the-art. One reason is that the built-in algorithms of a parameter-continuation software package must catch up with the rigorously developed theoretical results that are often rooted in or inspired by diverse applications with interesting dynamics. An alternative computational approach widely used in nonlinear dynamics is based on evaluating the maximal or several Lyapunov exponents [14]. Such a largest Lyapunov exponent approach computes some average rate of change, convergence or/and divergence, of the distance between two close, long-term transients. By definition, negative, zero and positive Lyapunov exponents are associated with stable equilibria, stable periodic orbits, and chaotic dynamics in the system, respectively. With a brute-force approach for sweeping 1D parametric pathways or 2D bi-parametric planes of the system, one can detect regions of regular/simple and complex/chaotic dynamics, as well as multistability, if it exists, by employing multiple initial conditions. While this brute-force approach based on the evaluation of Lyapunov exponents can effectively locate stability windows within regions of chaos [15, 16], it falls short in disclosing a variety of essential bifurcation structures in the parameter space that play a pivotal role to understand complex dynamics and their origin. Moreover, very long simulations are needed to reliably estimate the Lyapunov exponents. Given the current state-of-the-art, there is still a pressing need for tools and detailed evaluations of the global bifurcation unfolding of any system in question, to elucidate the contributions and multiplicity of the local and non-local bifurcations detected, and to determine how they shape regions of simple and complex dynamics in the corresponding 2D or even 3D parameter spaces. The objective of this paper is to somewhat remedy the situation by showcasing our know-how with an open source GPU-based computational toolkit based on symbolic dynamics, that should be accessible and practical for the nonlinear dynamics community.
Over the last several years, we developed a basis for new theoretical and computational approaches to explore the origin of complex dynamics and the characteristic bi-parametric patterns for so-called Lorenz-like systems [17, 18]. Our motivation is to extend the existing theory of homoclinic bifurcations of low-codimensions [1, 5, 19, 20, 21, 22, 3, 23, 24, 25, 26, 27, 28] and to make it accessible and practical for the nonlinear dynamics community. Recently, we have advanced an approach called the “Deterministic Chaos Prospector” (DCP) that utilizes symbolic representations of simple and chaotic dynamics [29, 30, 31, 32], based on our earlier works [18, 33]. This allows for fast and effective identification of bifurcation structures underlying and governing deterministic chaos in various systems. The ideas of this computational research trend are inspired by and based on the classical results of L.P. Shilnikov on homoclinic bifurcations [4, 24, 34]. We introduce and discuss the basic elements of homoclinic bifurcations in the text later, as well as how short-term symbolic dynamics can be introduced to disclose a stunning array of homoclinic structures and their organizing centers in all Lorenz-like systems, including the optically pumped laser (OPL) model under consideration in this paper. Some pilot results on the use of symbolic dynamics for the OPL model can be found in [17, 30]. In addition to simple dynamics associated with stable equilibria and periodic orbits, this system reveals a broad range of bifurcation structures that are typical for many ODE models from nonlinear optics and ones with the Lorenz attractor [18, 29, 33, 35, 36]. These include homoclinic orbits and heteroclinic connections between saddle equilibria that are the key building blocks of deterministic chaos in most systems. Their bifurcation curves with characteristic spirals around T(terminal)-points, along with other codimension-2 points, are the organizing centers that shape regions of complex and simple dynamics in the parameter space of such systems. Moreover, the latest advances in GPU and parallel computing techniques have empowered us to achieve a tremendous degree of parallelization to reconstruct highly detailed bi-parametric sweeps. A remarkable wealth of homoclinic bifurcations are disclosed in such a system, in a matter of just a few seconds on a desktop workstation powered by an Nvidia Tesla K40 GPU. It is fair to say that currently there is no other computational technique that is able to reveal the ordered intricacy in these bifurcation diagrams with such a stunning clarity and speed. Next, one can corroborate the type of homoclinic bifurcations using numerical continuation with AUTO or MatCont. While we do so in this paper, we underline that DCP performs impressively at just a fraction of the time taken for traditional continuation and other serial computational approaches. We also demonstrate how DCP can reveal intricate parametric regions of complex – structurally-unstable dynamics against those with simple – stable dynamics for a system, by exploiting the sensitivity of deterministic chaos for arbitrary long-term solutions whose symbolic descriptions are processed using periodicity-detection and Lempel-Ziv-complexity [30, 37] algorithms.
The multifarious set of complex dynamics exhibited by the OPL system makes it a prime candidate for this study, and enables us to demonstrate the versatility of our approach. In this paper, we employ the computational toolkit DCP and the numerical continuation package MatCont to disclose the remarkable features of the parameter space of the OPL model, due to various homoclinic and heteroclinic bifurcations that originate and underlie its complex, Lorenz-like dynamics. Specifically, using DCP we achieve the following objectives:
(1) We disclose the universal, self-similar fine organization of homoclinic and heteroclinic bifurcation structures in bi-parametric sweeps using short-term symbolic sequences. The key ones such as T-point spirals, saddles, inclination flips, and other codimension-2 bifurcation points, are also validated by MatCont-based numerical continuation, which provides all the necessary details, coordinates, eigenvalues etc.
(2) We elaborate on the spatial organization and embedding of the identified bifurcation structures in 3D parameter space, including two different types of parametric saddles and two different types of isolated closed curves (isolas for short). To our knowledge, this is the first elaborate 3D computational reconstruction of such bifurcation surfaces.
(3) We detect regions of simple and chaotic dynamics in the bi-parametric sweeps using a novel approach based on long-term symbolic sequences, combined with the periodicity-detection algorithms and the notion of Lempel-Ziv-complexity.
This paper is organized as follows. First, we introduce the OPL model, and present its key dynamical and bifurcational features. Next, we give a brief overview of the codimension-2 homoclinic inclination flip bifurcation, as well as a heteroclinic bifurcation involving all the three saddle equilibria in the phase space that corresponds to the so-called T(terminal)-point in the parameter plane of the model. This is followed by details of the numerical methods and the results of this study, which are presented in the order of (i) transient dynamics for global bifurcation structure, (ii) long term simple vs. complex dynamics, (iii) detailed examination of transient and long term behaviors near the organizing centers, and (iiii) 3D organization of special structures in the parametric space including branching and bridging saddles as well as annular and semi-annular isolas.
2 Optically pumped laser (OPL) model


The universality of characteristic chaotic oscillations that occur in various models with the Lorenz attractor, originating from hydrodynamics, magnetodynamics and nonlinear optics, was first shown by H. Haken in 1970s, followed by experimental demonstrations in , , and infrared gas lasers [38, 39, 40, 41, 42, 43]. Optically pumped, far infrared lasers are known to demonstrate a variety of nonlinear dynamic behaviors, including Lorenz-like chaos [44]. An acclaimed example of the modeling studies for chaos in nonlinear optics is the two-level laser model proposed by [38], to which the Lorenz equation can be reduced. The validity of Lorenz dynamics inherently persisting in three-level laser models was widely questioned back then. The reduced 6D model of a resonant three-level optically pumped laser (OPL) introduced in [7, 8, 45], and described by equations (2) below, was shown to possess a variety of dynamical and structural features of Lorenz-like systems, including stationary and periodic behaviors emerging through -pitchfork and Andronov-Hopf bifurcations. Specifically, the model demonstrates Lorenz-like chaotic behavior (see Fig. 1), with all the quintessential organizing structures, pivotal to understand its complex dynamics. These include various homoclinic and heteroclinic bifurcation structures of co-dimensions one and two, the so-called Bykov T-points with the associated spirals, as well as parametric saddles for switching branches in the parameter plane of this model, that are also seen in the classical Lorenz and Shimizu-Morioka models [1, 12, 16, 17, 18, 23, 33, 36, 46]. Similar structures were also discovered in another non-linear optics model describing a laser with a saturable absorber, which can be locally reduced to the Shimizu–Morioka model near a steady-state solution with triple zero Lyapunov exponents [47, 48].
The OPL model [8, 45] is given by the following six ODEs:
| (1) | |||||
where and are the Rabi flopping quantities representing the electric field amplitudes at pump and emission frequencies, respectively; is the ratio between population and polarization decay rates; represents the cavity loss parameter; is the unsaturated gain; ’s are the normalized density matrix elements for the transitions between levels and ; and ’s are the population differences between levels and . The system parameters , and can be manipulated experimentally. Furthermore, we set and . In this study, we treat and as the key bifurcation parameters for constructing biparametric scans and parameter continuations, at several fixed values of . Several such 2D scans may also be put together for 3D reconstructions of the parameter space of the model. Note that Eqs. (2) are –symmetric under the coordinate transformation , similar to other Lorenz-like systems.
2.1 Simple dynamics in the OPL-model


The OPL system (2) has either a single non-lasing steady state or an extra pair of equilibria that emerge following the loss of stability of through a pitchfork bifurcation. Some elements of the simple, Morse-Smale dynamics including stable equilibria and various periodic orbits are sampled in Fig. 2 at . It was shown in the original papers [8, 45], as well as recent ones [17, 30], that the OPL-model is quite rich in bifurcations – the list includes two super-critical Andronov-Hopf and pitchfork bifurcations, occurring respectively on the curves (for ), (for ), and in the bifurcation diagrams presented in Figs. 4,4. The description of simple dynamics starts off with the cod-2 point labeled as which stands for the Bogdanov-Takens bifurcation of an equilibrium state with two zero Lyapunov characteristic exponents. Given that the OPL-model is -symmetric, and so is the local central manifold containing such an equilibrium state, this should be referred to as a Khorozov-Takens bifurcation [5]. Its unfolding includes four bifurcation curves originating from the -point in the parameter plane, , , and , which we indeed retrieve all computationally using Matcont.
It is convenient to describe the bifurcation unfolding of simple solutions of the OPL model first, starting off with the trivial equilibrium state , where . This equilibrium remains stable in the parameter space to the right of the bifurcation curve labeled in Figs. 4,4. The curve corresponds to a supercritical Andronov-Hopf bifurcation that gives rise to a stable figure-8 periodic orbit shown in Fig. 2b (blue), existing for parameter values to the left of . The curve labeled corresponds to a pitchfork bifurcation that gives rise to a couple of additional equilibrium states with (see Fig. 2c blue and green dots) emerging from , which then becomes a saddle. This saddle is of (5,1)-type, i.e., has a pair of 1D unstable separatrices due to a single positive eigenvalue and a 5D stable manifold due to five eigenvalues with negative real parts (including a complex conjugate pair). The equilibrium states undergo another super-critical Andronov-Hopf bifurcation occurring on the curve (Figs.4,4) so that a pair of stable periodic orbits emerge from . In addition, the unfolding of the symmetric codimension-2 -point includes another bifurcation curve labeled . It corresponds to the occurrence of a homoclinic figure-8 pattern made up of two separatrix orbits of that each turn once around , respectively (see Fig. 2c red for ). This is a so-called “gluing” bifurcation: after the stable periodic orbits on either side become the separatrix loops of the saddle , they get “glued” to produce a stable figure-8 periodic orbit. Note that the saddle included into the homoclinic figure-8, has two leading eigenvalues, the positive and the largest negative (closest to the imaginary axis), whose sum, known as the saddle-value, remains negative near the -point. This condition assures the stability of the periodic orbits.
2.2 Cod-2 bifurcations: homoclinic and heteroclinic skeleton
The system (1) undergoes a homoclinic bifurcation when both unstable separatrices of the saddle equilibrium come back to itself, along the stable leading directions on the 5D stable manifold (Fig. 2c). The primary homoclinic bifurcation occurs on the curve in the 2D parameter diagrams represented in Figs. 4,4. The goal of this paper is to demonstrate the pivotal role of such bifurcations for Lorenz-like systems. Furthermore, we want to disclose the structure of global homoclinic unfoldings in the 3D parameter space of the OPL-model by illustrating different ways in which the homoclinic curves arrange themselves, morph, and switch branches across saddle points, as well as how such parametric saddles emerge/disappear as pairs of T-points merge together.
In his Ph.D. thesis, L.P. Shilnikov generalized the theory of homoclinic bifurcations of saddle and saddle-node equilibrium states, which would lead to the emergence of a single stable periodic orbit in , [49, 50]. Later, in 1968 he published another paper proving the existence and uniqueness conditions of a saddle periodic orbit emerging from a homoclinic loop of a plain saddle with a positive saddle value in and higher dimensions [34]. In it, he pointed out at three specific conditions giving rise to codimension-2 bifurcations code-named a zero saddle value, a zero separatrix value and the change of the leading direction at the saddle, that are, respectively, and alternatively known today as a resonant or neutral saddle, an inclination-flip and an orbit-switch (see Fig. 6). Furthermore, it was shown by L.P. Shilnikov that upon the fulfillment of certain conditions, these bifurcations can lead to the onset of complex dynamics in -symmetric systems, specifically, to the emergence of the Lorenz attractor in the phase space, right next to the homoclinic butterfly occurring near these cod-2 points on the bifurcation curves in the parameter diagram of such systems [51], see also [23, 52, 53, 48]. These results became a scientific folklore long time ago, i.e., lacking the proper acknowledgment of the original author, unlike his famous Shilnikov saddle-focus [24, 25, 54] and a lesser known Shilnikov saddle-node or saddle-saddle [55, 56, 20].
A salient feature of the OPL-model is the inclination-flip bifurcations (-points in Figs. 4 and 4) that occur on the primary homoclinic butterfly unlike the case of the Shimizu-Morioka (SM) model where it occurs on the double homoclinic loops; however, the SM-model shows the presence of a resonant homoclinic butterfly of the saddle with zero saddle value. Recall that the saddle value is the sum of the characteristic exponents (or their real values in the complex case) that are the closest (or leading) to the origin in the complex plane. Its sign determines whether a stable or unstable periodic orbit bifurcates from the homoclinic loop, or in the symmetric case, whether the homoclinic butterfly bifurcation glues two stable orbits into the stable figure-8 pattern, or can lead to the emergence of the Lorenz-like attractor near the resonant saddle in the parameter space.

| a | b | |
|---|---|---|
| 1.50 | 4.4309 | 0.6572 |
| 1.55 | 4.3394 | 0.6973 |
| 1.60 | 4.2382 | 0.7258 |
| 1.65 | 4.1333 | 0.7453 |
| 1.70 | 4.0291 | 0.7584 |
| 1.75 | 3.9285 | 0.7671 |
| 1.80 | 3.8325 | 0.7728 |
Let us go over the sequence of cod-2 bifurcations that occur along the primary homoclinic curve in the parameter space. For reference, see Figs. 4,4 at (as well as Figs.10,12 corresponding to different cuts at and ) in the parameter space of the OPL-model. The saddle is of (5,1)-type, i.e., has the eigenvalues that can be ordered as follows: . For such homoclinic saddles we need to evaluate the values of the following quantities: the saddle value whose sign determines the stability of a periodic orbit emerging from a homoclinic loop – negative/positive values imply stable/saddle orbits; alternatively, one can use the first saddle index or . Whenever , one needs to evaluate the second saddle index - the smallest quantity or . This holds true for the inclination flip case as well, when .
The homoclinic figure-8 connection stands for the case where both the unstable separatrices of the saddle come back to itself, opposite to each other along the leading -symmetric direction on the stable manifold, whereas in the homoclinic butterfly case, both come back tangent to each other and to the asymmetric leading direction – the vertical axis in Figs. 2 and 5. Near the cod-2 point , the homoclinic connection is initially of the figure-8 case, with a stable gluing bifurcation () occurring in a plane. As the bifurcation curve is continued further away from , Matcont detects the following sequence of singular homoclinic bifurcations depending on the -cut. In case of in Fig. 4, they are labeled as follows: corresponds to a resonant saddle with a neutral or zero saddle value or with a saddle index . After that the homoclinic connection is continued with , and hence gives rise to unstable/saddle periodic orbits. This should explain the reason for the presence of a Bautin bifurcation () point in this bifurcation puzzle, near the Bogdanov-Takens phenomenon. Recall that its unfolding includes the saddle-node bifurcation through which stable and unstable periodic orbits merge and annihilate. The following homoclinic cod-2 bifurcation detected by MatCont is the homoclinic orbit-switch () due to the change of the leading direction. In -symmetric systems like the OPL-model, this corresponds to the transition from the homoclinic figure-8 to the homoclinic butterfly with with . It follows from theory that a thin Lorenz-like attractor, hardly indistinguishable from the homoclinic butterfly without significant magnification, can already emerge near this point in the parameter space. One can see a loci of bifurcation curves emerging from the -point, in a vicinity of the -point, in Figs. 4 and 10, which will be further described later. Table 1 lists the coordinates of the cod-2 homoclinic orbit-switch points in the -parameter space of the OPL-model. Fig. 5a shows how the primary homoclinic loop morphs into a double loop as we move along the primary homoclinic bifurcation curve in Fig. 4 at . For a different parametric cut in Fig. 10 at , it forms a heteroclinic connection with the saddle foci as shown in Fig. 5b.
2.2.1 Inclination-flip homoclinic bifurcation


Of special interest in this paper is the role(s) of cod-2 inclination flip bifurcations (labeled as ) in the parameter space and how they shape and organize the global bifurcation unfolding of the OPL-model, see Figs. 4,4,15. The IF bifurcation occurs when an orientable stable or unstable manifold transitions to a non-orientable one, when followed along the homoclinic orbit. Unlike the Shimizu-Morioka model [18], this bifurcation in the OPL model involves the primary homoclinic butterfly and not the double homoclinic loops. As mentioned previously, L.P. Shilnikov pointed out the conditions under which the IF bifurcation gives rise to the onset of the Lorenz attractor in -symmetric systems. These conditions helped determine and verify the regions of existence of the Lorenz attractor, as well as enabled computer assisted proofs of chaotic dynamics in the canonical Lorenz model, without stable orbits and homoclinic tangencies [57, 58, 59, 60]. One such condition showed that the inclination-switch bifurcation can also lead to the onset of stable orbits nearby in the phase space, even in the case of an expanding saddle whose saddle index satisfies the condition . Below, we will highlight the essence of the inclination-switch bifurcation. Its in-depth analysis is given in [4, 5].
3D images in Figure 6 illustrate the concept of an inclination flip bifurcation that transforms an orientable homoclinic loop of the saddle (Figure 6a) into a non-orientable one (Figure 6b). This is depicted by a single twist of the surface traced out by a small, local section of the strongly stable direction, due to the smaller eigenvalue () of the saddle. Let us explore the global return map that takes a 2D cross-section, , transverse to the stable manifold of the saddle with a saddle index , onto itself along the homoclinic loop. The 1D outgoing separatrix of the saddle ( here ) comes back along the leading direction (vertical, due to ). Before the inclination-flip (Figure 6a), the section (the right half, relative to ) is mapped back on to the original (darker wedge), along the orientable primary homoclinic loop (in black). A nearby trajectory (red) is also shown. Post the inclination flip (Figure 6b), in the non-orientable or twisted case, the section is mapped onto the opposite section (dark yellow). This makes the surface “spanned” by the unstable (due to ) and the non-leading stable (due to ) eigenvectors look like a Möbius band.
Figure 6c depicts the action near an IF bifurcation using a 2D local Poincaré map. The map takes a small interval on into . For , the local map near the saddle is typically an expansion, stretching phase areas or volumes. Let us consider a small portion of the local manifold tangent to the span of the leading stable (due to ) and the leading unstable eigenvectors of the saddle . Near an IF bifurcation, as we take along the outgoing separatrix loop in a succession, it bends and hits the cross-section as a hook, narrowly squeezed due to the strongly stable eigenvalue . This hook of the pre-image looks like a Smale horseshoe on the cross-section (see Fig. 6c inset). This bending makes the image of shorter than the original , making the global map a contraction () as it overcomes the local expansion near the saddle (). Note that the global map is an expansion prior to the IF bifurcation. Figure 6d illustrates the onset of one of two “one-sided” chaotic attractors in the OPL-model near the inclination flip point on the primary homoclinic loop (at , next to the -point in Fig. 4) due to the presence of such a hook/Smale horseshoe (red), filled in with the points of intersection of transverse segments of the outgoing separatrix of the saddle on a nearby cross-section. The inset depicts a simulated analogue of the bending manifold sketched in Fig. 6c.
The geometric model of the Lorenz attractor (presented in [57]) can be elaborated using a 2D return map near the primary homoclinic butterfly of the two separatrix loops of the saddle. For a system to possess a genuine chaotic attractor devoid of homoclinic tangencies or stable orbits, this map should satisfy a few analytical conditions. The boundary of its existence region is marked by a violation of these criteria. The 2D map near the IF bifurcations can be further reduced to a simplified 1D map (Fig. 7) in the following form [5]:
| (2) |
where is the saddle index, is the separatrix value, and is the splitting parameter of the homoclinic loop [12]. Near the IF bifurcations when , the term is no longer negligible. Fig. 7 demonstrates the bent shape of such a return map, derived from the simulated 2D map, shown in Fig. 6d, for the “one-sided” chaotic attractor. As is decreased further, both “one-sided” (left/right) non-oriented attractors merge into a symmetric one. The map illustrates possible dynamics near the primary IF bifurcation due to period-doubling bifurcations in the 1D Poincaré map, leading to the emergence of multiple secondary homoclinic curves from this cod-2 point, as well as multiple stable periodic orbits (Figs. 8,9,15,16) when the return map starts bending again and again to resemble the return map of a Shilnikov saddle-focus but with a finite number of Smale horse-shoes [18].
2.2.2 Bykov “terminal” T-points
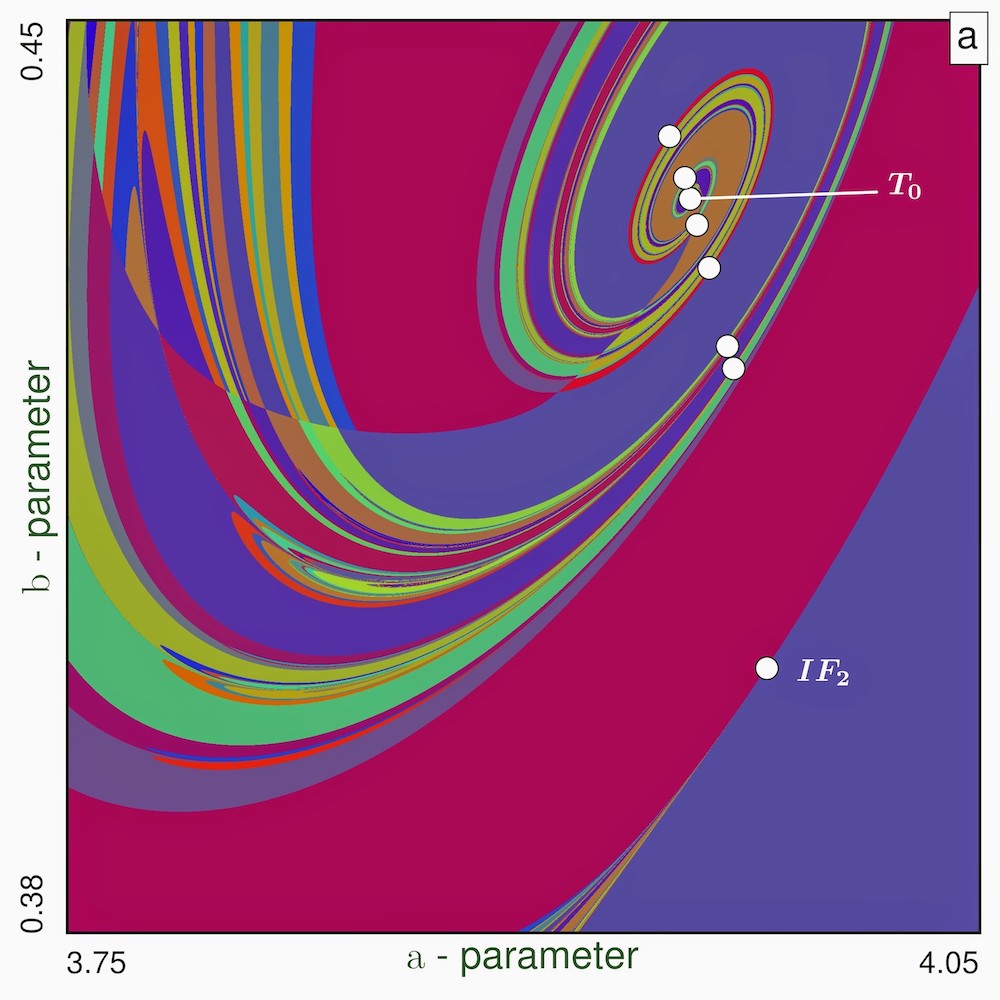



A typical signature for Lorenz-like systems is the complex universal and self-similar characteristic spirals in the parameter plane, organized around a central point called a Bykov terminal point (T-point) as seen in Figs. 4,4 and detailed magnifications are presented in Fig. 8 [30]. Each characteristic spiral around a T-point in the parameter plane corresponds to a homoclinic loop of the saddle in the phase space, such that with each turn of the spiral approaching the T-point, the outgoing separatrix of saddle makes increasing number of loops around a saddle-focus , before finally forming a closed heteroclinic connection between the saddle and the saddle focus at the T-point. Fig. 2d shows a one-way heteroclinic connection between the saddle and the saddle focus for parameter values near the T-point in Fig. 8b, with . Here, the unstable separatrix (red) of the saddle makes one loop around , followed by another loop around , then merges with the incoming separatrix of , thus effectively making infinite loops around before emerging out. The symmetric heteroclinic connection along from to , is shown in blue.
Near a T-point, there exist countably many secondary T-points with increasing complexity of heteroclinic connections in the phase space and with similar bifurcation structures as the central T-point in the parameter plane, although on a smaller scale (see Figs. 8, 9). Multiple inclination flip (IF) homoclinic bifurcations of the saddle occurring along the characteristic spirals of the T-points (detected with MatCont and shown as white dots in Figs. 8a,9) give rise to saddle-node and period-doubling bifurcations of periodic orbits [48, 5]. Fine organization of the structure of the chaotic regions and stability windows near the T-point and surrounding IF points is revealed in greater detail in 9b. In addition, the unfolding of a T-point also includes other curves corresponding to the homoclinic connections of the saddle-focus satisfying the Shilnikov condition [24, 54, 56] that give rise to a denumerable set of saddle periodic orbits nearby [25], as well as those corresponding to heteroclinic connections between both saddle-foci [19, 46, 61].
3 Numerical methods
3.1 Parametric continuation with MatCont
We constructed bifurcation diagrams such as Fig. 4 using numerical continuation with MatCont [11], including homotopy to initialize continuation of homoclinic and heteroclinic orbits, shown as blue and red curves, respectively [13]. First, we locate the local bifurcation curves of the symmetric and asymmetric equilibria. This also involves an Andronov-Hopf bifurcation. Following the limit cycle, we encounter a homoclinic bifurcation where the period explodes to infinity. In the region where the inclination flip occurs, has a single unstable direction. To determine these curves, we use homotopy to locate the connecting orbits, where we set the distances from the equilibrium to be at most, but typically . Once a connecting orbit has been located, we continue it with as free parameters and the “period” as auxiliary continuation parameter. During continuation, we monitor the test functions for various codimension-two bifurcations, including inclination flip and neutral homoclinic bifurcations.
While results have only been proven for three-dimensional vector fields, see [6, 46, 61], we follow these descriptions. We consider the following leading eigenvalues . To characterize the type of inclination flip, we define the quantities
| (3) |
If or , then there are infinitely many -homoclinic orbits emerging from this cod-2 bifurcation for each fixed .
3.2 Symbolic dynamics: Deterministic Chaos Prospector (DCP)
Our idea of symbolic dynamics is similar to the so-called kneadings [62, 63, 64], originally introduced for 1D continuous unimodal (with a single critical point) maps of an interval, and the binary description of their complex dynamics. A kneading invariant (see Eqs. (4,6)) was meant to serve as a modulus to topologically conjugate such maps and ODE systems generating such maps, see [3, 5, 18, 35, 65, 66, 67, 68]. In order to apply such a symbolic technique to a generic Lorenz-like system of higher dimensions, only wave forms of a symmetric variable progressing in time, that consistently start from the same initial condition near the saddle are required.
The system exhibits the presence of a Lorenz-like attractor which is both dynamically and structurally unstable (see Fig. 2c gray background), due to an abundance of homoclinic bifurcations of the saddle equilibrium . Both the outgoing separatrices of , and , densely fill out the two spatially symmetric wings of the Lorenz attractor in an unpredictable flip-flop pattern. In addition to this, as we vary the parameters of the system, the attractor itself undergoes bifurcations and reorganizes the flip-flop patterns, resulting in structural instability. Such changes are marked by homoclinic bifurcations of the saddle , where the outgoing separatrices, and , after a few flip-flops, merge with the stable manifold of (see Fig. 2c red curve). We make use of this property of homoclinic bifurcations to identify regions of topologically identical dynamics in parameter space by following the positive unstable separatrix of and converting the flip-flop patterns of the trajectory around into a binary sequence defined as:
| (4) |
This can be simplified by just considering complete or partial loops of the trajectory on the positive or negative side of , to be represented by the symbols 1 or 0, respectively. Therefore, the primary homoclinic bifurcation of Fig. 2c (red) is symbolically represented as since makes one loop around before returning to , while the blue and green curves are represented as and , respectively. Repetitive sequences are represented with an over-bar, as shown in Fig. 2a,b,d, showing convergence to a fixed point, periodic orbit, or heteroclinic connection, respectively. For example, the blue periodic orbit of Fig. 2b (transient omitted) generates the infinite sequence (), which is shortly represented as . We use the notation , to represent a sequence starting from the symbol up-to the symbol, with in and . As we always initiate trajectories along , we consider .
Since a single homoclinic loop, upon change of a parameter, can undergo transmutation into a double loop via an inclination flip, without an underlying homoclinic bifurcation (see Fig. 5), the above approach can give rise to artifacts near the IF bifurcations, e.g. Fig. 8a, where a single homoclinic loop starts to twist and then makes an extra loop on the left. We can avoid some of those artifacts by a slightly modified approach, given by:
| (5) |
With the former approach (4), the artifacts are confined to a small region near the IF bifurcations, while the modified approach (5) confines the artifacts to regions away from IF bifurcations. Therefore, we use approach (4) for most of the biparametric scans (Fig. 4,8 etc.), except for close zoom-ins near IF points (Fig. 15), for which we use approach (5).
3.2.1 2D/3D parametric scans
Topologically identical regions in the parametric plane can be identified by defining a formal convergent power series P [29, 62] for a sequence defined as:
| (6) |
For example, the value of this power series for the sequence with and can be computed as : The value of the sum lies between 0 (for the sequence ) and 1 (for the sequence in the limit as ). Two different sets of parameter values that show topologically identical behavior in their trajectories, result in identical sequences , and thus, have the same values. Therefore, serves as a dynamic invariant, which we can use in the construction of biparametric scans such as Fig. 4, as follows. The parameter is kept constant while we vary the parameters and (at a resolution of 2000x2000). For each set of values of these parameters, we follow the right unstable separatrix of to obtain the sequence and the power series . We then use a colormap to project the values onto the biparametric plane, where topological similarity between regions is identified by their equivalent colors, and the boundaries between adjacent regions represent homoclinic bifurcation curves. The colormap is constructed by discretizing the range of , i.e., [0,1], into bins, and assigning them RGB-color values from 0 through 1, for each of Red, Green and Blue colors in decreasing, random, and increasing fashion, respectively. Greater weight is assigned to the symbols towards the end of the sequences in the computation of , to maximize the color contrast between neighboring regions in a scan, that differ in the last symbol, separated by a homoclinic curve at their boundary. Numerical integration is performed using the classic Runge-Kutta method (RK4) with fixed step size . The computation of these trajectories is massively parallelized by running on separate GPU threads using CUDA. This allows for the construction of bi-parametric scans such as Fig. 12, in as little as 8 seconds on an Nvidia Tesla K40 GPU. Visualizations are done in Python. In order to construct complex bifurcation structures in the 3D parametric space, such as Figs. 17a,19,21, we obtain a large number of biparametric scans in the parametric plane, as we continuously vary the third parameter . Such arrays of scans are then rendered together using the open source volume exploration tool Drishti [69], which performed the best with our huge datasets, compared to other available tools for 3D rendering.
3.2.2 Long term behavior
The significance of our DCP tool is that not only can it reveal the short term transient dynamics and the underlying homoclinic, heteroclinic, saddle, and T-point spiral structures, but it can also be employed to reveal the long term behavior of the system (Fig. 14). When looking at the long term behavior of a trajectory after omitting a long transient, one should be aware of the shift-symmetry of periodic orbits. Depending on the length of the initial transient omitted, the same symmetric 8-shaped periodic orbit (Fig. 2b - blue) can be represented by either ) or ), and hence, needs to be normalized. In addition, if there is an asymmetric periodic orbit such as ), the symmetry of the system implies the existence of another periodic orbit which is its symmetric counterpart, ). This implies that all six of the periodic sequences ), ), ), ), ) and ) need to be normalized. We accomplish this by means of an algorithm we call Periodicity Correction (PC), where we identify the periodic structure within a sequence, along with its symmetric counterpart, and then normalize the sequence to the smallest valued circular permutation. Thus, both ) and ) are normalized to ) and all six of the asymmetric periodic orbits described previously are normalized to the lowest valued sequence ). PC helps in identifying regions of simple, Morse-Smale dynamics of stable fixed points and periodic orbits by eliminating artifacts arising from symmetries of the system or the symbolic sequence. Structurally unstable, chaotic regions are marked by the lack of periodicity in their symbolic representations. Alternatively, we can also employ a compression algorithm, like Lempel-Ziv-76 (LZ) [37], to find the complexity of a binary sequence. LZ scans a sequence from left to right, and adds a new word to the vocabulary every time a previously unencountered sub-string is detected. Since the circular permutations of a periodic orbit will have identical complexity, this approach can also detect windows of stability amidst structurally unstable chaotic regions.
While PC can detect stable periodic orbits efficiently even at short sequence lengths, LZ requires very long sequences and is not as effective. Within chaotic regions, on the other hand, PC cannot distinguish between different sequences while LZ separates very complex strings from not-so-complex strings, akin to Lyapunov exponents. To harness the best of both worlds, we therefore combine both PC and LZ. For a long term biparametric sweep, we first run the symbolic sequences through PC to detect the existence of, and to normalize, periodic orbits. The normalized sequences are then used to compute the power series sum and colored with the colormap as previously described. We then run the aperiodic sequences through LZ to detect their complexity. We color the LZ-complexity values in shades of gray, with darker gray representing greater complexity. Together, this results in long term bi-parametric sweeps such as Figs. 9,14,15b,16b,, where darker shades of gray represent greater structural instability and chaotic dynamics, while all other solid colors represent simple Morse-Smale dynamics of stable fixed points or periodic orbits. On the whole, we coin this collection of symbolic tools the ‘Deterministic Chaos Prospector (DCP)’. The open source software developed is available at https://bitbucket.org/pusuluri_krishna/deterministicchaosprospector/.
4 Results
Results are presented in the order of global transient dynamics, global long term dynamics, detailed magnifications near the organizing centers for both transient and long term behavior, followed by parametric saddles, isolas, and their 3D embedding.
4.1 Transient dynamics and global bifurcation structure
4.1.1 Case:
| a | b | |||||
| 1.50 | 3.8264 | 0.5189 | 1.8954 | -.5189 | -.7594 7.6491i | 0.4 |
| 3.9821 | 0.4011 | 1.5603 | -.4011 | -.6614 | 0.42 | |
| 1.55 | 3.7616 | 0.5436 | 1.9390 | -.5436 | -.77187.5199i | 0.4 |
| 3.8950 | 0.4160 | 1.6461 | -.4160 | -.70807.7845i | 0.43 | |
| 1.60 | 3.7011 | 0.5663 | 1.9754 | -.5663 | -.78317.3990i | 0.4 |
| 3.8127 | 0.4284 | 1.7197 | -.4284 | -.71427.6200i | 0.36 | |
| 1.65 | 3.6443 | 0.5872 | 2.0059 | -.5872 | -.79367.2856i | 0.4 |
| 3.7345 | 0.4386 | 1.7833 | -.4386 | -.6552 | 0.36 | |
| 1.70 | 3.5907 | 0.6065 | 2.0313 | -.6065 | -.80337.1788i | 0.4 |
| 3.6601 | 0.4470 | 1.8386 | -.4470 | -.6522 | 0.35 | |
| 1.75 | 3.5401 | 0.6246 | 2.0524 | -.6246 | -.81237.0778i | 0.4 |
| 3.5891 | 0.4536 | 1.8872 | -.4536 | -.6491 | 0.34 | |
| 1.80 | 3.4922 | 0.6414 | 2.0699 | -.6414 | -.82086.9820i | 0.4 |
| 3.5210 | 0.4588 | 1.9298 | -.4588 | -.6460 | 0.33 | |
| 1.90 | 3.4029 | 0.6719 | 2.0959 | -.6719 | -.8337 | 0.39 |
| 3.3928 | 0.4653 | 2.0008 | -.4653 | -.6401 | 0.32 | |
| 2.00 | 3.5705 | 0.8120 | 1.8373 | -.7615 | -.8120 | 0.44 |
| 3.3209 | 0.6988 | 2.1127 | -.6988 | -.8182 | 0.38 | |
| 3.5705 | 0.8120 | 1.8373 | -.7615 | -.8120 | 0.44 | |
| 10.0 | 1.2609 | 0.4956 | 0.5175 | -.4884 | -.4956 | 0.96 |
| 1.1570 | 0.1936 | 0.5710 | -.1936 | -.4444 | 0.77 | |
| 1.1247 | 0.1941 | 0.6225 | -.1941 | -.4987 | 0.79 | |
| 1.0681 | 0.1896 | 0.6969 | -.1896 | -.5765 | 0.82 |
We start this section with . Fig. 4 shows the bifurcation diagram in -parametric plane at using symbolic sequences . Two sets of parameters that result in topologically identical dynamics for the symbolic sequence under consideration, are colored identically in the bi-parametric sweep. Boundaries between such regions represent a shift in the dynamics due to homoclinic bifurcations. The corresponding bifurcation diagram obtained using continuation is shown in Fig. 4. Blue curves represent homoclinic bifurcation curves while heteroclinic bifurcation curves are shown in red.
A homoclinic bifurcation curve of the trivial equilibrium emerges from , which will be of primary interest as we vary . As we follow this primary curve we encounter a codim 2 point with two real stable eigenvalues and the leading stable direction changes. Here, a double, twisted homoclinic loop emerges. As we move along the primary homoclinic bifurcation curve from towards in the parametric plane (Fig. 4), in the phase space (Fig. 5a) the primary homoclinic loop is oriented and approaches from the right (light red curve). Moving on along , we find a first inclination flip bifurcation of complex type, where the primary homoclinic orbit approaches along its stable manifold (Fig. 5a - dark red). As we move further along , a twisted single loop approaches from the left (green), and and increase again when we find a second inclination flip point . Beyond , the homoclinic orbit changes its shape from a single loop around one non-trivial equilibrium to a double loop configuration around both non-trivial equilibria, that gradually grows bigger (light blue dark blue). Finally the primary curve gets close to the DRS point where the continuation terminates. This corroborates theoretical expectations although verification that the exact end point of this primary homoclinic curve is at the DRS point, is still open.
From the eigenvalues (see Table 2), we find that the inclination flip at and other cases are all of complex type so that infinitely many homoclinic bifurcation curves emerge from this point . The homoclinic bifurcation curves all spiral to the T-points such as (marked by the heteroclinic connection ). From the T-point , two heteroclinic bifurcation curves also emerge connecting the saddle-foci . These curves are rather straight and it may be appreciated that the homoclinic spirals to secondary T-points end up close to these heteroclinic curves. The inclination flip points, T-points, saddles() and closed loops are further explored in Sections 4.3,4.4.


4.1.2 Case:
The -parametric sweep for using symbolic sequences and continuation is shown in Fig. 10. We find results are globally quite similar for the pitchfork and AH curves. The primary homoclinic bifurcation curve has some marked differences though. First, the codimension-two neutral saddle point has disappeared simultaneously altering the nature of the BT point. Second, the primary homoclinic bifurcation curve no longer ends at the DRS point but spirals towards the T-point. In this case, as we sample parameters beyond , in the phase space the twisted loop starts making more and more revolutions around the stable manifold of , until it forms a heteroclinic connection to at the T-point. As shown in Fig. 5b, this transfiguration of the primary homoclinic orbit into a heteroclinic connection to happens through the orbits light red dark red green light blue as we move along . Detailed transition of the behavior of between and is explored further in Section.4.4. We also note that the second leading stable eigenvalue has changed from complex at to real for . This transition occurs at .
4.1.3 Case:


Moving on to , the bifurcation diagram using symbolic sequences is shown in Fig. 12. The corresponding diagram using parametric continuation is shown in Fig. 12. The inclination flip on the primary homoclinic is of a different type (type B), see Table 2 for the eigenvalues. This involves small regions with stable limit cycles. Indeed, we find a limit point of cycles bifurcation (LPC) indicating a small region with stable periodic orbits. These LPCs are only connected to the primary homoclinic bifurcation. This may not be apparent from Figure 12 as the primary curve does not seem to make a loop towards the T-point. Detailed calculations though suggest the primary curve makes a turn near , but accurate continuation did not succeed in that parameter region. All other inclination flip points are of type C. This implies that only the primary homoclinic bifurcation results in the emergence of additional stable periodic orbits nearby. The label stands for the neutral homoclinic saddle with a zero saddle value. Here, (), (), () and () represent various T-points. Note that the T-points and , above and below the saddle , have identical construction and the same heteroclinic connection . with the heteroclinic connection () is a special case. Although resembles a T-point, it falls in the region of the periodic orbit () which devours the spiral structure of , leaving behind a ghost of the T-point. and the semi-annular isolas near are detailed in Fig. 23. Further details of the special organizing structures are provided in the following sections.
4.1.4 Summary: variations

We conclude this section by presenting a summary of the bifurcation diagrams for varying -values. This also serves as a precursor for the construction of 3D parametric sweeps of Sec.4.4. Fig. 13(a-h) reveal variations in the bifurcation structure using for -values , , , , , , , and . See also supplementary Movie M1 that reveals these variations in further detail. Between (Fig. 13d) and (Fig. 13e), the primary homoclinic bifurcation curve branches and starts spiraling on to the primary T-point . As we increase further, the inclination flip and the homoclinic bifurcation curves from to change their orientation. Between (Fig. 13g) and (Fig. 13h), branches again to separate from .
4.2 Global long term dynamics

To study the long term behavior of the system with DCP, we use long symbolic sequences , omitting the first 999 symbols as transients. Fig. 14 shows such long term behavior at values: , , and in Panels (a)-(d), respectively. Simple, Morse-Smale dynamics of stable equilibria or periodic orbits are identified using Periodicity Correction and shown in solid colors. Distinct colors represent sequences with distinct periods. Structurally unstable, chaotic dynamics are identified by their lack of periodic structure, processed using LZ-complexity, and colored such that darker gray regions indicate greater LZ-complexity of the sequences, and therefore, increased structural instability and chaos. Between Fig. 14(a,b) vs. Fig. 14(c,)d note the change in orientation of the inclination flip and the stability windows emerging from it. This is also in agreement with the change in orientation of the transient dynamics as seen in Fig. 13 for the corresponding -values.
4.3 Transient and long term behavior near the organizing centers
In this section, we will present the detailed behavior of both short and long term dynamics near the organizing centers of T-points and inclination flips.
4.3.1 T-points
For all three sigma values of (Fig. 4), (Fig. 10) and (Fig. 12), the primary T-point is marked by the symbolic sequence . The phase trajectory at is as shown by the light blue curve of Fig. 5b, where makes one loop around , followed by a heteroclinic connection to . The trajectory effectively makes an infinite number of loops around , before leaving the neighborhood of . Fig. 8a shows a magnification near for using . It also shows multiple secondary T-points surrounding the primary T-point. Fig. 8b with shows a zoom of a small region with an analogous pair of T-points and , above and below , respectively, for (see Fig. 4 white box). The heteroclinic connection at is shown in Fig. 2d. Here makes one loop around , followed by one loop around , and then forms a heteroclinic connection to . Hence, the symbolic representation of . Similarly, the heteroclinic connection at is given by . Such T-points always come in pairs on either side of a homoclinic bifurcation curve. Such a T-point pair can also be seen for (Fig. 12), with () above , and ( )below it. The T-point below the saddle , also has the same structure in the parametric plane and the same heteroclinic connection () as . This is explored further in Sec.4.4.
4.3.2 Inclination flips




Next, we show how the inclination flip points serve not only as the confluence of infinitely many homoclinic bifurcation curves, but also as the originators of multiple windows of stability with respect to long term dynamics in the system. Fig. 8a () shows several inclination flips (white dots), starting from and leading all the way beyond , from which the homoclinic bifurcation curves arise leading up to the secondary T-points surrounding . The specific values of IF bifurcation points are obtained with continuation. Fig. 15 shows the behavior near the inclination flip point at for both transient (compare Fig. 4) and long term dynamics (compare Fig. 14b). Fig. 15a () reveals multiple homoclinic bifurcation curves that converge to , while Fig. 15b ( with DCP) shows the convergence of multiple stability windows (solid colors) towards , interspersed within regions of structural instability and chaos (darker gray implies greater LZ-complexity and less compressible binary sequences thus generated from the model equations). Similar transient and long term behavior near for (compare Fig. 12,14d) is summarized in Fig. 16a () and Fig. 16b ( with DCP), respectively.
4.3.3 Summary at
Finally, we magnify the behavior at which nicely summarizes the behavior of the inclination flips and secondary T-points for short term (Fig. 9a, ) and long term dynamics (Fig. 9b, with DCP). Several inclination flips (white dots) close to the primary T-point are clearly seen as the congregation centers of homoclinic curves leading up to secondary T-points vis-à-vis transient dynamics, while those same inclination flip points also give rise to stability windows in the long term, amidst regions of structurally unstable and chaotic dynamics. See Fig. 13a,14a for the corresponding global dynamics.
4.4 Parametric saddles and isolas
In this last section, we present a discussion of more complicated organizing structures in the parameter space. Specifically, we describe the 3D structures of two types of parametric saddles and two types of isolas (isolated closed curves). Such structures have been theoretically described previously [48, 70, 71, 72]. To our knowledge, this is the first detailed three dimensional computational reconstruction of such bifurcation surfaces in parameter space, made possible by the fast parallel computation of trajectories on GPUs.
4.4.1 Branching saddle for homoclinic bifurcation curves





In this section, we describe a saddle in the parameter space that causes branch switching between homoclinic bifurcation curves. As seen in Fig. 4 and Fig. 10, between and , the primary homoclinic bifurcation curve shifts from a complete loop towards the codimension-2 point , to a spiral organization around the primary T-point . This implies the existence of a saddle in between the two values that branches the primary homoclinic bifurcation curve , as seen in Fig. 13d,e. Fig. 17(left) shows a detailed 3D bifurcation diagram close to this saddle. It is constructed using 100 bi-parametric sweeps in the -plane with (top surface) (bottom surface), using and 3D volume is rendered with Drishti software [69]. This branching of occurs at and is marked by . Detailed zooms close to , shown in Fig. 19, further unravel this 3D organization of the homoclinic bifurcation surface at the homoclinic branching saddle . A similar 3D bifurcation surface with a saddle in the Shimizu-Morioka system is presented in [12] and shown in Fig. 19. Fig. 17(right) shows the homoclinic bifurcation curves close to the branching saddle obtained with continuation at values of (top), (middle) and (bottom).
4.4.2 Bridging saddle between T-points




We now focus on another kind of saddle ubiquitous to parametric sweeps, serving as a bridge between two identical T-points, marked in Figs.4,12. The interesting feature of such a saddle is that the T-point spirals above and below have identical construction and the same heteroclinic connections, as described previously in Fig. 12 for , with above and below . In order to see how such T-points on either side of a saddle are related to each other, we run multiple sweeps with closely varying values and observe the structural changes in the spiral organization. Fig. 20 shows such chaotic mixing close to the saddle as values are varied from (a) , (b) , (c) , and through (d) . As changes, the T-points above and below the saddle appear to be merging together, as depicted in the transitions: Fig. 20ab and Fig. 20cd.
The 3D scrolling structure of the bifurcation surface around the hyperbolic saddle for constructed using 2000 bi-parametric sweeps using and rendered with open-source scientific visualization software Drishti 222Drishti is available at https://github.com/nci/drishti is shown in Fig. 21. Fig. 21a,b,c reveal with gradually increasing depth, the continuous structural connections between the T-points on either side of this bridging saddle . As we move along the T-point curve by varying , the curve undergoes a change in orientation and re-enters the bifurcation planes of previous T-points, giving birth to the saddles in between them. Note that each sweep has the 2000x2000 resolution. All 2000 such produced slices imply a total computation of trajectories. Despite being computationally heavy, this was achieved in just about 8 hours on a single Nvidia Tesla-K40 GPU.
4.4.3 Annular isolas from a bridging saddle
As seen in Fig. 20, as the T-points on either side of a bridging saddle merge together with varying , it results in the formation of isolas of homoclinic bifurcation curves resembling concentric annular structures. This is due to the fact that the T-point curve changes its orientation with respect to the bifurcation planes and the T-point becomes non-transverse to this plane, which was described as a codimension-two-plus-one event [70, 71]. This also becomes clear in Fig. 22 which shows the top and bottom surfaces (rotated through ) of the 3D T-point curve in Fig. 21. As we slice several bi-parametric sweeps for changing -values, moving towards the bottom surface in Fig. 22b, the T-points appear to be merging as they become non-transverse to the bifurcation plane and we can only observe isolas made of homoclinic bifurcation curves.
4.4.4 Semi-annular isolas from the ghost of a T-point

We end this section with a description of isolas of a different nature with semi-annular structure as seen near the point of Fig. 12. The T-point (with the heteroclinic connection ) next to is of particular interest with respect to these isolas. To understand the relation between these isolas and , we vary in Fig. 23 through (a) 11.1253 (b) 11.2459 (c) 11.4501 and (d) 11.5522. As increases, starts crossing the boundary between the stable periodic orbit (green region) and structurally unstable chaotic regions in the parametric plane, the semi-annular isolas start merging around to gradually reveal the full spiral organization of homoclinic bifurcation curves around the T-point in Fig. 23(d). This explains how in Fig. 12, when the T-point falls inside the region of the periodic orbit, the spiral structure of is devoured by the periodic orbit, leaving behind the remnants of the spirals surrounding the ghost of the T-point , in the form of semi-annular isolas near the boundary. Note that when we say periodic orbit , for the sake of simplicity, we only mean an orbit that produces a periodic sequence in its symbolic representation. Its trajectory may still be chaotic but follow a periodic symbolic sequence as also seen in Fig. 6d for a one sided chaotic trajectory, whose symbolic representation would still be periodic . In fact, the region surrounding seems to be the two sided chaotic trajectory following the periodic sequence .
5 Conclusions
In this paper, we presented a novel framing combining applied dynamical systems, GPU-based parallel computation, and 2D and 3D parameter space visualization to extend the theory of non-local homoclinic bifurcations of lower codimensions. With this approach we explore and determine key universal rules of complex dynamics in diverse systems. Using the technique of symbolic dynamics with DCP, in corroboration with the parameter continuation methods powered by MatCont, we could identify regions of simple and chaotic dynamics in the parameter space of a classic nonlinear laser model with a Lorenz-like attractor, as well as disclose key underlying bifurcation structures, including Bykov T-point spirals and inclination flips. We performed detailed computational reconstruction and visualization of the three dimensional embedding of bifurcation surfaces, parametric saddles and isolas. The knowledge and the methodology created in this study should further advance new ideas and approaches for a better understanding of cross-disciplinary nonlinear phenomena at large, while the generality of our modeling approaches are also applicable to other biological, medical, and engineering systems [32].
Acknowledgements
This work was partly funded by the NSF grant IOS-1455527 and the RSF grant 14-41-00044 at Lobachevsky University of Nizhny Novgorod. We thank the Brains and Behavior initiative of Georgia State University for providing pilot grant support and the doctoral fellowship of K. Pusuluri. We thank NVIDIA Corporation for supporting us with the Tesla K40 GPUs used in this study. Finally, we acknowledge the support of all the current and past members of the Shilnikov NeurDS lab for enriching discussions.
References
- [1] V. S. Afraimovich, V. V. Bykov, L. P. Shilnikov, The origin and structure of the Lorenz attractor, Sov. Phys. Dokl. 22 (1977) 253–255.
- [2] V. S. Afraimovich, L. P. Shilnikov, Strange attractors and quasiattractors, in: Nonlinear dynamics and turbulence, Interaction Mech. Math. Ser., Pitman, Boston, MA, 1983, pp. 1–34.
- [3] J. Guckenheimer, R. F. Williams, Structural stability of Lorenz attractors, Inst. Hautes Études Sci. Publ. Math. 50 (50) (1979) 59–72.
- [4] L. P. Shilnikov, A. L. Shilnikov, D. V. Turaev, L. O. Chua, Methods of Qualitative Theory in Nonlinear Dynamics. Part I, World Scientific, Singapore, 1998.
- [5] L. P. Shilnikov, A. L. Shilnikov, D. Turaev, L. O. Chua, Methods of Qualitative Theory in Nonlinear Dynamics, Vol. 1-2, World Sci. Publ., Singapore, 1998, 2001.
- [6] A. J. Homburg, B. Sandstede, Homoclinic and heteroclinic bifurcations in vector fields, in: H. W. Broer, B. Hasselblatt, F. Takens (Eds.), Handbook of Dynamical Systems, Vol. 3, Elsevier Science, 2010, Ch. 8, pp. 379–524. doi:https://doi.org/10.1016/S1874-575X(10)00316-4.
- [7] J. V. Moloney, J. S. Uppal, R. G. Harrison, Origin of chaotic relaxation oscillations in an optically pumped molecular laser, PRL 59 (25) (1987) 2868. doi:10.1103/PhysRevLett.59.2868.
- [8] W. Forysiak, J. V. Moloney, R. G. Harrison, Bifurcations of an optically pumped three-level laser model, Physica D 53 (1) (1991) 162 – 186. doi:https://doi.org/10.1016/0167-2789(91)90170-E.
- [9] E. J. Doedel, A. R. Champneys, F. Dercole, T. F. Fairgrieve, Y. A. Kuznetsov, B. E. Oldeman, R. C. Paffenroth, B. Sandstede, X. J. Wang, C. H. Chang, Auto-07p: Continuation and bifurcation software for ordinary differential equations, , Concordia University, Canada (2007).
- [10] A. R. Champneys, Y. A. Kuznetsov, B. Sandstede, A numerical toolbox for homoclinic bifurcation analysis, Int. J. of Bifurcation and Chaos 6 (5) (1996) 867–887. doi:10.1142/S0218127496000485.
- [11] A. Dhooge, W. Govaerts, Y. Kuznetsov, H. G. E. Meijer, B. Sautois, New features of the software MatCont for bifurcation analysis of dynamical systems, Math. Comput. Model. Dyn. Syst. 14 (2) (2008) 147–175. doi:10.1080/13873950701742754.
- [12] A. L. Shilnikov, On bifurcations of the Lorenz attractor in the Shimizu-Morioka model, Physica D 62 (1-4) (1993) 338–346. doi:10.1016/0167-2789(93)90292-9.
- [13] V. De Witte, W. Govaerts, Y. A. Kuznetsov, M. Friedman, Interactive initialization and continuation of homoclinic and heteroclinic orbits in Matlab, ACM Trans. Math. Softw. 38 (3) (2012) 18:1–18:34. doi:10.1145/2168773.2168776.
- [14] A. Wolf, J. B. Swift, H. L. Swinney, J. A. Vastano, Determining Lyapunov exponents from a time series, Physica D 16 (3) (1985) 285–317. doi:10.1016/0167-2789(85)90011-9.
- [15] J. A. C. Gallas, The structure of infinite periodic and chaotic hub cascades in phase diagrams of simple autonomous flows, Int. J. Bif. & Chaos 20 (02) (2010) 197–211. doi:10.1142/S0218127410025636.
- [16] R. Barrio, F. Blesa, S. Serrano, A. Shilnikov, Global organization of spiral structures in biparameter space of dissipative systems with Shilnikov saddle-foci, Physical Review E 84 (3) (2011) 035201. doi:10.1103/PhysRevE.84.035201.
- [17] R. Barrio, A. Shilnikov, L. Shilnikov, Kneadings, symbolic dynamics and painting Lorenz chaos, Int. J. Bifurcation & Chaos 22 (04) (2012) 1230016. doi:10.1142/S0218127412300169.
- [18] T. Xing, R. Barrio, A. Shilnikov, Symbolic quest into homoclinic chaos, Int. J. Bifurcation & Chaos 24 (8) (2014) 1440004. doi:https://doi.org/10.1142/S0218127414400045.
- [19] V. V. Bykov, On the structure of bifurcations sets of synamical systems that are systems with a separatrix contour containing saddle-focus, Methods of Qualitative Theory of Differential Equations, Gorky University (in Russian). (1980) 44–72.
- [20] V. S. Afraimovich, S. V. Gonchenko, L. M. Lerman, A. L. Shilnikov, D. V. Turaev, Regular and chaotic dynamics, Scientific heritage of L.P. Shilnikov. Part 1 4 (19) (2014) 435–462. doi:10.1134/S1560354714040017.
- [21] D. Aubin, A. D. Dalmedico, Writing the history of dynamical systems and chaos: longue durée and revolution, disciplines and cultures, Historia Math. 29 (3) (2002) 273–339. doi:10.1006/hmat.2002.2351.
- [22] L. A. Belyakov, Bifurcations of systems with a homoclinic curve of the saddle-focus with a zero saddle value, Mat. Zametki 36 (5) (1984) 681–689, 798.
- [23] A. L. Shilnikov, Bifurcation and chaos in the Marioka-Shimizu system, Selecta Math. Soviet. 10(2) (1991) 105–117, originally published in Methods in qualitative theory and bifurcation theory (in Russian), Gorky State University, 1986, pp. 180–193.
- [24] L. P. Shilnikov, A case of the existence of a denumerable set of periodic motions, Dokl. Akad. Nauk SSSR 160 (1965) 558–561.
- [25] L. P. Shilnikov, The existence of a denumerable set of periodic motions in four-dimensional space in an extended neighborhood of a saddle-focus., Soviet Math. Dokl. 8(1) (1967) 54–58.
- [26] A. Shilnikov, Complete dynamical analysis of an interneuron model, J. Nonlinear Dynamics 68 (3) (2012) 305–328. doi:10.1007/s11071-011-0046-y.
- [27] S. Gonchenko, I. Ovsyannikov, C. Simo, D. Turaev, Three-dimensional Hénon-like maps and wild Lorenz-like attractors, Int. J. Bif. Chaos 15(11) (2005) 3493–3508. doi:10.1142/S0218127405014180.
- [28] V. V. Bykov, Bifurcations leading to chaos in Chua’s circuit, Inter. J. Bif. Chaos 8 (1998) 685–699. doi:10.1142/s0218127498000486.
- [29] K. Pusuluri, A. Pikovsky, A. Shilnikov, Unraveling the chaos-land and its organization in the rabinovich system, in: Advances in Dynamics, Patterns, Cognition, Springer, Cham, 2017, pp. 41–60. doi:10.1007/978-3-319-53673-6_4.
- [30] K. Pusuluri, A. Shilnikov, Homoclinic chaos and its organization in a nonlinear optics model, Physics Review E 98 (4) (2018) 040202. doi:10.1103/PhysRevE.98.040202.
- [31] K. Pusuluri, A. Shilnikov, Symbolic representation of neuronal dynamics, in: Advances on Nonlinear Dynamics of Electronic Systems, World Scientific, 2019, pp. 97–102. doi:10.1142/9789811201523_0018.
- [32] K. Pusuluri, H. Ju, A. Shilnikov, Chaotic dynamics in neural systems, in: R. A. Meyers (Ed.), Encyclopedia of Complexity and Systems Science, Springer Berlin Heidelberg, Berlin, Heidelberg, 2020, pp. 1–13. doi:10.1007/978-3-642-27737-5_738-1.
- [33] T. Xing, J. Wojcik, R. Barrio, A. Shilnikov, Symbolic toolkit for chaos explorations, in: Int. Conf. Theory and Application in Nonlinear Dynamics (ICAND 2012), Springer, 2014, pp. 129–140. doi:10.1007/978-3-319-02925-2_12.
- [34] L. P. Shilnikov, The generation of a periodic motion from a trajectory which is doubly asymptotic to a saddle type equilibrium state, Mat. Sb. (N.S.) 77 (119) (1968) 461–472.
- [35] R. Barrio, M. Angeles Martínez, S. Serrano, A. L. Shilnikov, Macro- and micro-chaotic structures in the Hindmarsh-Rose model of bursting neurons, Chaos 4 (2) (2014) 023128. doi:10.1063/1.4882171.
- [36] T. Xing, J. Wojcik, M. Zaks, A. L. Shilnikov, Fractal parameter space of lorenz-like attractors: A hierarchical approach, in: G. Nicolis, V. Basios (Eds.), Chaos, Information Processing and Paradoxical Games: The legacy of J.S. Nicolis, World Sci. Publ., Singapore, 2015, Ch. 5, pp. 87–104. doi:10.1142/9789814602136_0005.
- [37] A. Lempel, J. Ziv, On the complexity of finite sequences, IEEE Transactions on information theory 22 (1) (1976) 75–81. doi:10.1109/TIT.1976.1055501.
- [38] H. Haken, Analogy between higher instabilities in fluids and lasers, Physics Letters A 53 (1) (1975) 77–78. doi:10.1016/0375-9601(75)90353-9.
- [39] H. Haken, Laser Light Dynamics, North-Holland, Amsterdam, 1985.
- [40] L. Casperson, Spontaneous coherent pulsations in laser oscillators, IEEE Journal of Quantum Electronics 14 (10) (1978) 756–761. doi:10.1109/JQE.1978.1069683.
- [41] C. Weiss, H. King, Oscillation period doubling chaos in a laser, Optics Communications 44 (1) (1982) 59–61. doi:10.1016/0030-4018(82)90016-5.
- [42] C. Weiss, W. Klische, P. Ering, M. Cooper, Instabilities and chaos of a single mode NH3 ring laser, Optics communications 52 (6) (1985) 405–408. doi:10.1016/0030-4018(86)90339-1.
- [43] C. Weiss, J. Brock, Evidence for Lorenz-type chaos in a laser, Physical Review Letters 57 (22) (1986) 2804. doi:10.1103/PhysRevLett.57.2804.
- [44] C. Weiss, U. Hübner, N. Abraham, D. Tang, Lorenz-like chaos in NH3-FIR lasers, Infrared Physics & Technology 36 (1) (1995) 489–512. doi:https://doi.org/10.1016/1350-4495(94)00088-3.
- [45] J. V. Moloney, W. Forysiak, J. S. Uppal, R. G. Harrison, Regular and chaotic dynamics of optically pumped molecular lasers, Phys. Rev. A 39 (1989) 1277–1285. doi:10.1103/PhysRevA.39.1277.
- [46] V. Bykov, The bifurcations of separatrix contours and chaos, Physica D 62 (1–4) (1993) 290–299. doi:https://doi.org/10.1016/0167-2789(93)90288-C.
- [47] A. Vladimirov, D. Volkov, Low-intensity chaotic operations of a laser with a saturable absorber, Optics Communications 100 (1) (1993) 351–360. doi:https://doi.org/10.1016/0030-4018(93)90597-X.
- [48] A. L. Shil’nikov, L. P. Shil’nikov, D. V. Turaev, Normal forms and Lorenz attractors, Int. J. Bifurcation & Chaos 3 (1993) 1123–1123. doi:10.1142/S0218127493000933.
- [49] L. P. Shilnikov, Some instances of generation of periodic motions in -space, Dokl. Akad. Nauk SSSR 143 (1962) 289–292.
- [50] L. P. Shilnikov, Some cases of generation of period motions from singular trajectories, Mat. Sb. 61 (103) (1963) 443–466.
- [51] L. Shilnikov, The theory of bifurcations and quasiattractors, Uspeh. Math. Nauk 36(4) (1981) 240–242.
- [52] C. Robinson, Homoclinic bifurcation to a transitive attractor of Lorenz type, Nonlinearity 2 (1989) 495–518. doi:10.1088/0951-7715/2/4/001.
- [53] M. Rychlic, Lorenz attractor through Shil’nikov type bifurcation. Part I, Ergodic Theory and Dynamical Systems 10 (4) (1990) 793–821. doi:10.1017/S0143385700005915.
- [54] L. P. Shilnikov, A contribution to the problem of the structure of an extended neighborhood of a rough equilibrium state of saddle-focus type, Math. USSR-Sb 10 (1) (1970) 91–102. doi:10.1070/sm1970v010n01abeh001588.
-
[55]
L. P. Shilnikov, A certain new type of
bifurcation of multidimensional dynamic systems, Dokl. Akad. Nauk SSSR
189 (1) (1969) 59–62.
URL http://mi.mathnet.ru/eng/dan34997 - [56] L. P. Shilnikov, A. Shilnikov, Shilnikov bifurcation, Scholarpedia 2 (8) (2007) 1891, revision #153014. doi:10.4249/scholarpedia.1891.
- [57] V. S. Afraimovich, V. V. Bykov, L. P. Shilnikov, On structurally unstable attracting limit sets of Lorenz attractor type, Trans. Moscow Math. Soc. 44 (2) (1983) 153–216.
- [58] V. V. Bykov, A. L. Shilnikov, On the boundaries of the domain of existence of the Lorenz attractor, Selecta Math. Soviet. 11 (4) (1992) 375–382.
- [59] W. Tucker, The lorenz attractor exists, C.R. Acad. I - Math. 328 (12) (1999) 1197–1202. doi:https://doi.org/10.1016/S0764-4442(99)80439-X.
- [60] M. Viana, What’s new on Lorenz strange attractors?, Math. Intelligencer 22 (3) (2000) 6–19. doi:10.1007/BF03025276.
- [61] P. Glendinning, C. Sparrow, T-points: A codimension two heteroclinic bifurcation, Journal of Statistical Physics 43 (3) (1986) 479–488. doi:10.1007/BF01020649.
- [62] J. Milnor, W. Thurston, On iterated maps of the interval, in: J. Alexander (Ed.), Dynamical Systems: Proceedings of the Special Year held at the University of Maryland, College Park, 1986–87, Springer Berlin Heidelberg, Berlin, Heidelberg, 1988, pp. 465–563. doi:10.1007/BFb0082847.
- [63] P. Glendinning, C. Sparrow, Prime and renormalisable kneading invariants and the dynamics of expanding Lorenz maps, Physica D 62 (1–4) (1993) 22–50. doi:10.1016/0167-2789(93)90270-B.
- [64] P. Glendinning, T. Hall, Zeros of the kneading invariant and topological entropy for Lorenz maps, Nonlinearity 9 (4) (1996) 999–1014. doi:10.1088/0951-7715/9/4/010.
- [65] D. Rand, The topological classification of Lorenz attractors, Mathematical Proceedings of the Cambridge Philosophical Society 83 (3) (1978) 451–460. doi:10.1017/S0305004100054736.
- [66] M. I. Malkin, Rotation intervals and dynamics of Lorenz type mappings, Selecta Math. Sovietica 10 (1991) 265–275.
- [67] C. Tresser, R. F. Williams, Splitting words and Lorenz braids, Physica D 62 (1–4) (1993) 15–21. doi:10.1016/0167-2789(93)90269-7.
- [68] J. Guckenheimer, P. Holmes, Nonlinear oscillations, dynamical systems, and bifurcations of vector fields, Vol. 42 of Applied Mathematical Sciences, Springer-Verlag, New York, 1990.
- [69] A. Limaye, Drishti: a volume exploration and presentation tool, in: S. Stock (Ed.), Developments in X-Ray Tomography Viii, Vol. 8506 of SPIE Proceedings, International Society for Optics and Photonics, 2012, p. 85060X. doi:10.1117/12.935640.
- [70] S. Wieczorek, B. Krauskopf, Bifurcations of -homoclinic orbits in optically injected lasers, Nonlinearity 18 (3) (2005) 1095–1120. doi:10.1088/0951-7715/18/3/010.
- [71] A. Algaba, F. Fernández-Sánchez, M. Merino, A. Rodríguez-Luis, Structure of saddle-node and cusp bifurcations of periodic orbits near a non-transversal T-point, Nonlinear Dynamics 63 (3) (2011) 455–476. doi:10.1007/s11071-010-9815-2.
- [72] A. Algaba, F. Fernández-Sánchez, M. Merino, A. Rodríguez-Luis, Analysis of the T-point-Hopf bifurcation in the Lorenz system, Communications in Nonlinear Science and Numerical Simulation 22 (1-3) (2015) 676–691. doi:10.1016/j.cnsns.2014.09.025.