Higher-order Topological Phases of Magnons in van der Waals Honeycomb Ferromagnets
Abstract
We theoretically propose a second-order topological magnon insulator by stacking the van der Waals honeycomb ferromagnets with antiferromagnetic interlayer coupling. The system exhibits topological phase, protected by pseudo-time-reversal symmetry (PTRS). An easy-plane anisotropy term breaks PTRS and destroys the topological phase. Nevertheless, it respects a magnetic two-fold rotational symmetry which protects a second-order topological phase with corner modes in bilayer and hinge modes along stacking direction. Moreover, an introduced staggered interlayer coupling establishes a topology, giving rise to gapped topological surface modes carrying non-zero Chern numbers. Consequently, chiral hinge modes propagate along the horizontal hinges in a cuboid geometry and are robust against disorders. Our work bridges the higher-order topology and magnons in van der Waals platforms, and could be used for constructing topological magnonic devices.
In recent years, higher-order topological phases of matter have attracted much attention due to the unconventional bulk-boundary correspondence WABenalcazar ; ZSong ; JLangbehn ; WABenalcazar2 ; FSchindler ; MEzawa ; XZhu ; MGeier ; KKudo ; ZYan ; XWLuo ; YJWu ; CChen ; YRen ; WWang . Conventional topological insulator (TI) and superconductor (TSC) have one-dimensionally (1D) lower boundary or surface modes MZHasan ; XLQi . As a contrast, th-order TIs and TSCs in dimension host -dimensional topologically protected modes, dubbed corner or hinge modes. These higher-order topological phases are first proposed in the electronic systems, predicted and observed in quite a few materials CChen ; CYue ; ZWang ; YXu2 ; XLSheng ; BLiu ; YBChoi ; BJack , and then extended to the bosonic systems, such as photons JNoh ; XDChen ; BYXie , phonons MSGarcia ; XZhang ; LLuo , and the magnons ZLi ; ASil ; THirosawa ; ZXLi1 ; ZXLi2 ; AMook ; MJPark ; ZXLi3 in magnetic systems. For now, the works on higher-order topological phases of magnons are mainly distributed in the magnetic solitonic system. These works in the spin systems utilize either specially designed coupling AMook ; ASil or externally controlled antiferromagnetic noncollinear order MJPark , which are not realized experimentally due to technique difficulty.
Since the experimental discovery of two-dimensional (2D) ferromagnetism BHuang ; CGong ; ZFei , the van der Waals magnets provide new and versatile platforms to investigate the fundamental physics and also new opportunities for spintronic device design. Recent experimental progresses reveal topological phases in 2D magnetic materials, such as CrI3 and MnBi2Te4, etc LChen1 ; LChen2 ; FZhu ; YDeng ; DZhang ; CLiu ; BWei . The van der Waals magnets show a store of in-plane and out-of-plane magnetic orders. For example, in the collinear phase, there are four representative ground states, the combination of intralayer ferromagnetic (FM)/antiferromagnetic (AFM) and interlayer FM/AFM orders. When involving non-ferromagnetic orders, the magnon behavior usually does not have direct counterpart to electronic and other (quasi)particle systems YHLi ; CWang ; JSklenar ; HYYuan ; GChen ; HKondo ; YMLi . The interlayer magnetic orders and coupling strength can be even tuned by the external field, pressure, stacking and the interlayer distance PJiang ; XKong ; TLi ; TSong . As a result, the van der Waals magnets offer us more degrees of freedom to seek for intriguing properties of magnons, with experimental feasibility by use of the state-of-the-art van der Waals engineering.
In this Letter, motivated by the AFM interlayer coupling in chromium trihalides, we theoretically proposed that AA-stacked honeycomb ferromagnets with AFM interlayer coupling host second-order topological phases for magnons. The monolayer is a Chern insulator in the presence of next-nearest-neighboring (NNN) Dzyaloshinskii-Moriya interactions (DMI). The interlayer AFM coupling endows a pseudo-time-reversal symmetry (PTRS), realizes topological phases and supports helical edge states in bilayer and anisotropic topological surface modes (TSMs) in bulk located on the surfaces parallel to the stacking direction. An easy-plane anisotropic term breaks the PTRS and also the topological phase. But a magnetic two-fold rotational symmetry is preserved. Along the lines in the Brillouin zone leaving the system invariant under the rotational symmetry, the Hamiltonian can be decomposed into two parts with different eigenvalues of the symmetry operator. A half-quantized rotation-graded topological polarizations are obtained, indicating the system hosts a second-order topological phase with corner modes in bilayer and hinge modes along the stacking direction. Besides, a staggered interlayer coupling builds a topology, giving rise to gapped TSMs located on the surfaces perpendicular to the stacking direction, carrying non-zero Chern numbers. According to the bulk-boundary correspondence, chiral hinge modes propagate along the horizontal hinges with opposite chirality on the top and bottom horizontal hinges in a cuboid geometry. We would like to emphasize that our conclusion can be applied to different stacking, not limited to the AA stacking. This makes our proposal easier to be realized experimentally.
Model–We consider the AA-stacked van der Waals honeycomb ferromagnets for simplicity, as shown in Fig. 1 (a). The interlayer coupling is AFM-type, and the strength is staggered controlled by the interlayer distance. The minimal spin interaction Hamiltonian is given by
| (1) |
where is the layer index. describe the AFM coupling and the intralayer spin Hamiltonian
| (2) | |||||
characterizes FM intralayer coupling and represents the NNN DMI strength. with () for counterclockwise (clockwise) circulation. The last two terms denote the single-ion easy-plane (EPA) and easy-axis anisotropy. There are two ground states of the spin configuration, the down layer pointing up while the upper layer pointing down, or reversed. For convenience, we choose one of the two spin configurations without loss of generality. By applying the Holstein-Primakoff transformation , , for first layer and , , for second layer, and making the Fourier transformation , (, the sublattice index), the Hamiltonian in -space is expressed as with bosonic Bogoliubov-de Gennes (BdG) Hamiltonian in -space SM
| (3) |
The basis is with . , , . is identity matrix and the Pauli matrices. , , , , , , , intralyer NNN vectors. Diagonalizing the quadratic form in Eq. (3) invokes the Bogoliubov transformation, , with paraunitary eigenvectors satisfying and is the Pauli matrix acting on the particle-hole space RShindou . Typical magnon bands are shown in Fig. 2 (a).
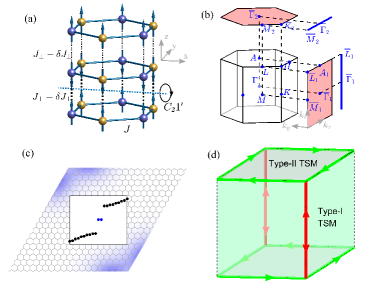
In the absence of EPA term, the Hamiltonian in Eq. (3) hosts a PTRS, with , where is Pauli matrix acting on the layer index and denotes the complex conjugation. We can see this PTRS coming from the AFM interlayer coupling, as the intralayer ferromagnetism breaks the TRS. As a result, the magnon bands show Kramers degeneracy (Fig. 2 (a)), and also host nontrivial Z2 topological phase. The previous work LFu on quantum spin Hall phase and topological crystalline insulators told us four Z2 invariants were needed to form the combination to describe the topological phase in 3D. As the bosonic Hamiltonian (3) does not host an inversion symmetry. We calculate the Z2 invariants by enlarging the unit cell along -direction to get a cuboid BZ RYu and obtain , , indicating the system is in a “weak” TI phase SM . Consequently, topological surface modes (TSMs) appear on the surfaces parallel to the stacking direction, i.e. the -axis, labelled as type-I. In Fig. 2 (b), we plot the magnon bands in the projected - plane with finite width along the axis. The anisotropic gapless TSMs emerge in the gap and show a nodal line along the axis, not even number of surface Dirac cones exhibited in the previous works LFu ; YYang ; SHKooi . The invariant for a bilayer such system should be equal to , indicating a 2D TI phase and gapless Dirac dispersive edge states SM .
Second-order topology–In the presence of EPA term, the PTRS is no longer kept. The magnon band degeneracy is lifted, as shown in Fig. 2 (a), thus the topological phase is broken. As a consequence, type-I TSMs at zigzag-terminated surfaces are gapped, as shown by the blue curves in Fig. 2 (b). Interestingly, when we consider a parallelogram pillar geometry with two zigzag-terminated surfaces encounter with an armchair connection, hinge modes arise in the surface gap, as shown by the red curves in Fig. 2 (c), where the magnon dispersion along direction is plotted. The local density distribution of the hinge modes is shown in the inset. Here these hinge modes come from nontrivial bulk band topology. Although the EPA breaks the PTRS and drives the 3D TI into a trivial insulator, it preserves various crystalline symmetries, i.e., a magnetic two-fold rotation symmetry in our case shown in Fig. 1 (a), which make the system to exhibit topological crystalline phase.
The magnetic two-fold rotational symmetric operation, illustrated in Fig. 1 (a), exchanges the A (B) sublattice in the first layer with the B(A) sublattice in the second layer and flips the spin. Acting on the magnon Hamiltonian ((3)), we have , with , behaving like a mirror symmetry changing to . As , has two eigenvalues . This indicates that we can decompose the Hamiltonian ((3)) into decoupled two parts labelled by the eigenvalues of along the lines in the BZ that leave the Hamiltonian invariant after applying . Here we regard the as a parameter. There are two types of lines: along at and . We mainly discuss the case , which is directly related to the hinge modes. The Hamiltonian at can be decomposed into two parts by using the eigenvectors
| (4) |
where and take the value of and at and denotes the subspace with eigenvalues.
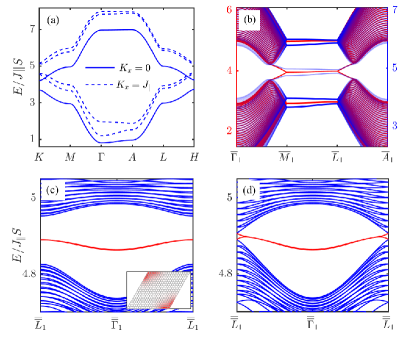
We can diagonalize the bosonic Hamiltonians by employing the Bogoliubov transformation, , with paraunitary eigenvectors satisfying . Then we have the rotation-graded Berry connection for n-th band, where is the diagonal matrix taking for n-th digaonal component and zero otherwise. The rotation-graded topological polarization . The summation is over the occupied particle bands. In our case, the integration interval is along at . We calculate numerically the topological polarization for rotation-graded mangnon bands and find that at any . This half-quantized polarization confirms that the system is in a topological crystalline phase TMLec . Gapless TSMs would exist on the armchair surface even at nonvanishing EPA, different from the TSMs at zigzag surfaces that are gapped by the EPA. Besides, when two zigzag surfaces encounter with an armchair connection, in-gap modes will emerge in the surface bandgap, as verified above in Fig. 2 (c). As the is independent on , the hinge modes are not chiral and are nearly flat due to the weak interlayer coupling. Thus they are not robust against disorders. But as long as the surface gap remains, these hinge modes retain. In Fig. 2 (d), we plot the magnon dispersion along at . The surface gap closes at , the hinge modes disappear near . The above discussions can also be applied to the bilayer case. The bilayer is also in second-order topological phase with corner modes SM , as shown in Fig. 1 (c). These corner modes are also protected by the magnetic rotational symmetry.
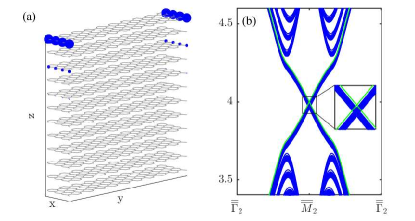
We now discuss the topology along the direction. The EPA term breaks the Z2 topology of the system and gives topological hinge modes. Here we show that at nonzero , there exists another Z2 topology along the stacking direction and will generate another type of TSMs and also chiral hinge modes. We start from the Bosonic BdG Hamiltonian in Eq. (3) and introduce the Berry connection and the Berry curvature . To characterize the bulk polarization along the stacking direction, we compute the Wannier bands . We find when , for all the bands and for all at any finite . We have checked for . This indicates a quantized bulk polarization along staking direction for all the bands, where is projected ontop BZ shown in Fig. 1 (b) and the area. The above analysis shows an additional invariant in our system, coming from the staggered interlayer coupling, which gives a Su-Schrieffer-Heeger (SSH) configuration of antiferomagnetic order.
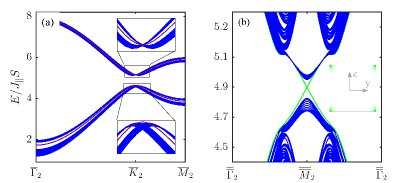
The quantized polarization will give rise to a different type of TSM, labelled by type-II. In Fig. 3 (a), we plot the magnon bands in plane with finite layers along stacking direction. Gapped TSMs emerge between the split bands, not in the bulk bandgap. These TSMs are doubly degenerate, distributed on the top and bottom surfaces, respectively. We calculate the Chern numbers for the type-II TSMs with lower energy and find the Chern number is () for type-II TSMs located at bottom (top) surface. Due to the nontrivial Chern numbers, a class of topology is established even the PTRS is broken. According to the bulk-boundary correspondence, there exists topological modes closing the TSM bandgap. In Fig. 3 (b), we further impose a finite width constraint on the -direction, and verified the existence of gapless states. These states are thus chiral hinges modes, robust against disorders, and propagate along the horizontal hinges in a cuboid geometry, shown in Fig. 1 (d) SM . As type-II TSMs at top and bottom surfaces host opposite Chern numbers, the corresponding chiral hinge modes show opposite chirality. Note that chiral hinges states coexist with the gapped type-I TSMs in the bulk bandgap. Although the topology is built at finite , where the PTRS is broken, the topology is still preserved at , as the bulk polarization along stacking direction is independent on . In this situation, both the type-I SMs and chiral hinge modes are gapless and coexist in the bandgap SM .
Discussions and summary–Finally, we discuss the possibility of experimental realization of our proposal. The CrI3, CrBr3 and other honeycomb ferromagnets with AFM interlayer coupling are promising candidates, and even the kagome ferromagnets. There are already experimental observations of the topology of magnons in monolayer honeycomb ferromagnets, due to the DM interaction LChen1 ; LChen2 ; FZhu , which is necessary in our proposal. The stacking type is not restricted in the AA-type. For example, the bilayer CrI3 have two stable stacking, i.e., rhombohedral stacking with FM interlayer coupling and monoclinic stacking with AFM interlayer coupling. The monoclinic stacking bilayer has an interlayer -glide along the zigzag direction compared to AA stacking. With the EPA term, we can also get the second-order topological phase SM when the two layers have an interlayer -glide, as the combined symmetry of and the glide plays as the effective mirror symmetry of in AA stacking. The topology is independent on the stacking type, the chiral hinge modes are maintained in any stacking type. In addition, the magnetic anisotropy terms, especially EPA term, can be controlled by light, mechanical strain and electronic gating DAfanasiev ; KNakamura ; YWang ; IAVerzhbitskiy in 2D monolayer and van der Waals magnets.
In summary, we find the second-order topological phases of magnons in van der Waals ferromagnets with AFM interlayer coupling. There are two different hinge modes coexisting arising from two different mechanisms. Firstly, the AFM interlayer coupling realizes a magnonic Z2 TI phase, protected by the PTRS. In the presence of the EPA, the PTRS is broken, but the magnetic two-fold rotational symmetry gives rise to rotation-graded topological polarization, which protects a second-order topological phase. Secondly, the introduced staggered AFM interlayer coupling brings a topology, giving rise to type-II gapped TSMs carrying finite Chern numbers, thus supporting chiral hinge modes along horizontal directions. Our work reveals the higher-order topological phase of magnons in 2D Van der Waals magnets, and paves an new way for dissipationless magnonic devices using van der Waals magnets.
Y.-M. Li thanks Dr. Weinan Lin for his helpful discussions. This work is partly supported by MOST of China (Grants No. 2017YFA0303400). Y.-M. Li is supported by the startup funding from Xiamen University.
References
- (1) W. A. Benalcazar, B. A. Bernevig, T. L. Hughes, Quantized electric multipole insulators, Science 357, 61 (2017).
- (2) Z. Song, Z. Fang, and C. Fang, (d-2)-Dimensional Edge States of Rotation Symmetry Protected Topological States, Phys. Rev. Lett. 119, 246402 (2017).
- (3) J. Langbehn, Y. Peng, L. Trifunovic, F. von Oppen, and P. W. Brouwer, Reflection-Symmetric Second-Order Topological Insulators and Superconductors, Phys. Rev. Lett. 119, 246401 (2017).
- (4) W. A. Benalcazar, B. A. Bernevig, and T. L. Hughes, Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators, Phys. Rev. B 96, 245115 (2017).
- (5) F. Schindler, A. M. Cook, M. G. Vergniory, Z. Wang, S. S. P. Parkin, B. A. Bernevig, and T. Neupert, Higher-order topological insulators, Sci. Adv. 4, eaat0346 (2018).
- (6) M. Ezawa, Higher-Order Topological Insulators and Semimetals on the Breathing Kagome and Pyrochlore Lattices, Phys. Rev. Lett. 120, 026801 (2018).
- (7) X. Zhu, Tunable Majorana corner states in a two-dimensional second-order topological superconductor induced by magnetic fields, Phys. Rev. B 97, 205134 (2018).
- (8) M. Geier, L. Trifunovic, M. Hoskam, and P. W. Brouwer, Second-order topological insulators and superconductors with an order-two crystalline symmetry, Phys. Rev. B 97, 205135 (2018).
- (9) K. Kudo, T. Yoshida, and Y. Hatsugai, Higher-order topological Mott insulators, Phys. Rev. Lett. 123, 196402 (2019).
- (10) Z. Yan, Higher-Order Topological Odd-Parity Superconductors, Phys. Rev. Lett. 123, 177001 (2019).
- (11) X.-W. Luo and C. Zhang, Higher-Order Topological Corner States Induced by Gain and Loss, Phys. Rev. Lett. 123, 073601 (2019).
- (12) Y.-J. Wu, J. Hou, Y.-M. Li, X.-W. Luo, X. Shi, and C. Zhang, In-Plane Zeeman-Field-Induced Majorana Corner and Hinge Modes in an s-Wave Superconductor Heterostructure, Phys. Rev. Lett. 124, 227001 (2020).
- (13) C. Chen, Z. Song, J.-Z. Zhao, Z. Chen, Z.-M. Yu, X.-L. Sheng, and S. A. Yang, Universal Approach to Magnetic Second-Order Topological Insulator Phys. Rev. Lett. 125, 056402 (2020).
- (14) Y. Ren, Z. Qiao, and Q. Niu, Engineering Corner States from Two-Dimensional Topological Insulators, Phys. Rev. Lett. 124, 166804 April (2020).
- (15) Wei Wang, Ze-Guo Chen, and Guancong Ma, Synthetic Three-Dimensional Topological Insulator in an Elastic Metacrystal, Phys. Rev. Lett. 127, 214302 (2021).
- (16) M. Z. Hasan and C. L. Kane, Colloquium: Topological insulators, Rev. Mod. Phys. 82, 3045 (2010).
- (17) X.-L. Qi and S.-C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys. 83, 1057 (2011).
- (18) C. Yue, Y. Xu, Z. Song, H. Weng, Y.-M. Lu, C. Fang, and X. Dai, Symmetry-enforced chiral hinge states and surface quantum anomalous hall effect in the magnetic axion insulator Bi2xSmxSe3, Nat. Phys. 15, 577 (2019).
- (19) Z. Wang, B. J. Wieder, J. Li, B. Yan, and B. A. Bernevig, Higher-order topology, monopole nodal lines, and the origin of large Fermi arcs in transition metal dichalcogenides XTe2 (X=Mo, W), Phys. Rev. Lett. 123, (2019).
- (20) Y. Xu, Z. Song, Z. Wang, H. Weng, and X. Dai, Higher-Order Topology of the Axion Insulator EuIn2As2, Phys. Rev. Lett. 122, 256402 (2019).
- (21) X.-L. Sheng, C. Chen, H. Liu, Z. Chen, Z.-M. Yu, Y. X. Zhao, and S. A. Yang, Two-Dimensional Second-Order Topological Insulator in Graphdiyne, Phys. Rev. Lett. 123, 256402 (2019).
- (22) B. Jäck, Y. Xie, J. Li, S. Jeon, B. A. Bernevig, and A. Yazdani, Observation of a Majorana zero mode in a topologically protected edge channel, Science 364, 1255 (2019).
- (23) Y.-B. Choi, Y. Xie, C.-Z. Chen, J. Park, S.-B. Song, J. Yoon, B. J. Kim, T. Taniguchi, K. Watanabe, J. Kim, K. C. Fong, M. N. Ali, K. T. Law, and G.-H. Lee, Evidence of higher-order topology in multilayer WTe2 from Josephson coupling through anisotropic hinge states, Nat. Mater. 19, 974 (2020).
- (24) B. Liu, L. Xian, H. Mu, G. Zhao, Z. Liu, A. Rubio, and Z. F. Wang, Higher-Order Band Topology in Twisted Moiré Superlattice, Phys. Rev. Lett. 126, 066401 (2021).
- (25) J. Noh, W. A. Benalcazar, S. Huang, M. J. Collins, K. P. Chen, T. L. Hughes, and M. C. Rechtsman, Topological protection of photonic mid-gap defect modes, Nat. Photon. 12, 408 (2018).
- (26) X.-D. Chen, W.-M. Deng, F.-L. Shi, F.-L. Zhao, M. Chen, and J.-W. Dong, Direct Observation of Corner States in Second-Order Topological Photonic Crystal Slabs, Phys. Rev. Lett. 122, 233902 (2019).
- (27) B.-Y. Xie, G.-X. Su, H.-F. Wang, H. Su, X.-P. Shen, P. Zhan, M.-H. Lu, Z.-L. Wang, and Y.-F. Chen, Visualization of Higher-Order Topological Insulating Phases in Two-Dimensional Dielectric Photonic Crystals, Phys. Rev. Lett. 122, 233903 (2019).
- (28) M. Serra-Garcia, V. Peri, R. Süsstrunk, O. R. Bilal, T. Larsen, L. G. Villanueva, and S. D. Huber, Observation of a phononic quadrupole topological insulator, Nature (London) 555, 342 (2018).
- (29) X. Zhang, L. Liu, M.-H. Lu, and Y.-F. Chen, Valley-Selective Topological Corner States in Sonic Crystals Phys. Rev. Lett. 126, 156401 (2021).
- (30) L. Luo, H.-X. Wang, Z.-K. Lin, B. Jiang, Y. Wu, F. Li, and J.-H. Jiang, Observation of a phononic higher-order Weyl semimetal, Nat. Mater. 20, 794 (2021).
- (31) Z. Li, Y. Cao, P. Yan, and X. Wang, Higher-order topological solitonic insulators, npj Comput. Mater. 5, 107 (2019).
- (32) A. Sil and A. K. Ghosh, First and second order topological phases on ferromagnetic breathing kagome lattice, J. Phys. Condens. Matter 32, 205601 (2020).
- (33) T. Hirosawa, S. A. Díaz, J. Klinovaja, and D. Loss, Magnonic Quadrupole Topological Insulator in Antiskyrmion Crystals, Phys. Rev. Lett. 125, 207204 (2020).
- (34) Z.-X. Li, Y. Cao, X. R. Wang, and P. Yan, Symmetry-Protected Zero Modes in Metamaterials Based on Topological Spin Texture, Phys. Rev. Applied 13, 064058 (2020).
- (35) Z.-X. Li, Y. Cao, X. R. Wang, and P. Yan, Second-order topological solitonic insulator in a breathing square lattice of magnetic vortices, Phys. Rev. B 101, 184404 (2020).
- (36) A. Mook, S. A. Díaz, J. Klinovaja, and D. Loss, Chiral hinge magnons in second-order topological magnon insulators, Phys. Rev. B 104, 024406 (2021).
- (37) M. J. Park, S. Lee, and Y. B. Kim, Hinge magnons from noncollinear magnetic order in a honeycomb antiferromagnet, Phys. Rev. B 104, L060401 (2021).
- (38) Z.-X. Li, Z. Wang, Z. Zhang, Y. Cao, and P. Yan, Third-order topological insulator in three-dimensional lattice of magnetic vortices, Phys. Rev. B 103, 214442 (2021).
- (39) B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero, and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature (London) 546, 270 (2017).
- (40) C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia, and X. Zhang, Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature (London) 546, 265 (2017).
- (41) Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J.-H. Chu, and X. Xu, Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2, Nat. Mater. 17, 778 (2018).
- (42) L. Chen, J.-H. Chung, B. Gao, T. Chen, M. B. Stone, A. I. Kolesnikov, Q. Huang, and P. Dai, Topological Spin Excitations in Honeycomb Ferromagnet CrI3, Phys. Rev. X 8, 041028 (2018).
- (43) L. Chen, J.-H. Chung, M. B. Stone, A. I. Kolesnikov, B. Winn, V. O. Garlea, D. L. Abernathy, B. Gao, M.Augustin, E. J. G. Santos, and P. Dai, Magnetic Field Effect on Topological Spin Excitations in CrI3, Phys. Rev. X 11, 031047 (2021).
- (44) F. Zhu, L. Zhang, X. Wang, F. J. dos Santos, J. Song, T. Mueller, K. Schmalzl, W. F. Schmidt, A. Ivanov, J. T. Park, J. Xu, J. Ma, S. Lounis, S. Blügel, Y. Mokrousov, Y. Su, T. Brückel, Topological magnon insulators in two-dimensional van der Waals ferromagnets CrSiTe3 and CrGeTe3: Toward intrinsic gap-tunability, Sci. Adv. 7, eabi7532 (2021).
- (45) Y. Deng, Y, Yu, M. Z. Shi, Z. Guo, Z. Xu, J. Wang, X. H. Chen, Y. Zhang, Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4, Science 367, 895 (2020).
- (46) D. Zhang, M. Shi, T. Zhu, D. Xing, H. Zhang, and J. Wang, Topological Axion States in the Magnetic Insulator MnBi2Te4 with the Quantized Magnetoelectric Effect, Phys. Rev. Lett. 122, 206401 (2019).
- (47) C. Liu, Y. Wang, H. Li, Y. Wu, Y. Li, J. Li, K. He, Y. Xu, J. Zhang, and Y. Wang, Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator, Nature Materials 19, 522 (2020).
- (48) B. Wei, J.-J. Zhu, Y. Song, and K. Chang, Renormalization of gapped magnon excitation in monolayer MnBi2Te4 by magnon-magnon interaction, Phys. Rev. B 104, 174436 (2021).
- (49) Y.-H. Li, and R. Cheng, Moiré magnons in twisted bilayer magnets with collinear order, Phys. Rev. B 102, 094404 (2020).
- (50) C. Wang, Y. Gao, H. Lv, X. Xu, and D. Xiao, Stacking Domain Wall Magnons in Twisted van der Waals Magnets, Phys. Rev. Lett. 125, 247201 (2020).
- (51) J. Sklenar and W. Zhang, Self-Hybridization and Tunable Magnon-Magnon Coupling in van der Waals Synthetic Magnets, Phys. Rev. Applied 15, 044008 (2021).
- (52) H. Y. Yuan, A. Kamra, D. M. F. Hartmann, and R. A. Duine, Electrically Switchable Entanglement Channel in van der Waals Magnets, Phys. Rev. Applied 16, 024047 (2021).
- (53) G. Chen, S. Qi, J. Liu, D. Chen, J. Wang, S. Yan, Y. Zhang, S. Cao, M. Lu, S. Tian, K. Chen, P. Yu, Z. Liu, X. C. Xie, J. Xiao, R. Shindou, and J.-H. Chen, Electrically switchable van der Waals magnon valves, Nat. Commun. 12, 6279 (2021).
- (54) H. Kondo, Y. Akagi, and H. Katsura, topological invariant for magnon spin Hall systems, Phys. Rev. B 99, 041110(R) (2019).
- (55) Y.-M. Li, J. Xiao, and K. Chang, Topological Magnon Modes in Patterned Ferrimagnetic Insulator Thin Films, Nano Lett. 2018, 18, 3032 (2018).
- (56) P. Jiang, C. Wang, D. Chen, Z. Zhong, Z. Yuan, Z.-Y. Lu, and W. Ji, Stacking tunable interlayer magnetism in bilayer CrI3, Phys. Rev. B 99, 144401 (2019).
- (57) T. Li, S. Jiang, N. Sivadas, Z. Wang, Y. Xu, D. Weber, J. E. Goldberger, K.Watanabe, T. Taniguchi, C. J. Fennie, K. F. Mak, and J. Shan, Pressure-controlled interlayer magnetism in atomically thin CrI3, Nat. Mater. 18, 1303 (2019).
- (58) T. Song, Z. Fei, M. Yankowitz, Z. Lin, Q. Jiang, K. Hwangbo, Q. Zhang, B. Sun, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Graf, T. Cao, J.-H. Chu, D. H. Cobden, C. R. Dean, D. Xiao, and X. Xu, Switching 2D magnetic states via pressure tuning of layer stacking, Nat. Mater. 18, 1298 (2019).
- (59) X. Kong, H. Yoon, M. J. Han, and L. Liang, Switching interlayer magnetic order in bilayer CrI3 by stacking reversal, Nanoscale 13, 16172 (2021).
- (60) See SupplementalMaterial for details of our calculation and derivation, which include Refs. RYu .
- (61) R. Shindou, R. Matsumoto, S. Murakami, and J.-ichiro Ohe, Topological chiral magnonic edge mode in a magnonic crystal, Phys. Rev. B 87, 174427 (2013).
- (62) L. Fu, C. L. Kane, and E. J. Mele, Topological Insulators in Three Dimensions, Phys. Rev. Lett. 98, 106803 (2007).
- (63) R. Yu, X. L. Qi, A. Bernevig, Z. Fang, and X. Dai, Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection, Phys. Rev. B 84, 075119 (2011).
- (64) Y. Yang, Z. Gao, H. Xue, L. Zhang, M. He, Z. Yang, R. Singh, Y. Chong, B. Zhang, and H. Chen, Realization of a three-dimensional photonic topological insulator, Nature 565, 622 (2019).
- (65) S. H. Kooi, G. van Miert, and C. Ortix, Hybrid-order topology of weak topological insulators, Phys. Rev. B 102, 041122(R) (2020).
- (66) Topological Matter: Lectures from the Topological Matter School 2017, edited by D. Bercioux, J. Cayssol, M. G. Vergniory, and M. Reyes Calvo (Springer Nature, Switzerland AG, 2018), Chap. 2.3.
- (67) K. Nakamura, R. Shimabukuro, Y. Fujiwara, T. Akiyama, T. Ito, and A. J. Freeman, Giant Modification of the Magnetocrystalline Anisotropy in Transition-Metal Monolayers by an External Electric Field, Phys. Rev. Lett. 102, 187201 (2009).
- (68) Y. Wang, C. Wang, S.-J. Liang, Z. Ma, K. Xu, X. Liu, L. Zhang, A. S. Admasu, S.-W. Cheong, L. Wang, M. Chen, Z. Liu, B. Cheng, W. Ji, F. Miao, Strain-Sensitive Magnetization Reversal of a van der Waals Magnet, Adv. Mater. 32, 2004533 (2020).
- (69) I. A. Verzhbitskiy, H. Kurebayashi, H. Cheng, J. Zhou, S. Khan, Y. Ping Feng, and G. Eda, Controlling the magnetic anisotropy in Cr2Ge2Te6 by electrostatic gating, Nat. Electron. 3, 460 (2020).
- (70) D. Afanasiev, J. R. Hortensius, M. Matthiesen, S. Mañas-Valero, M. Šiškins, M. Lee, E. Lesne, H. S. J. van der Zant, P. G. Steeneken, B. A. Ivanov, E. Coronado, and A. D. Caviglia, Controlling the anisotropy of a van der Waals antiferromagnet with light, Sci. Adv. 7, eabf3096 (2021).
I Supplementary Materials
I.1 S1. Bosonic Bogoliubov-de Gennes Hamiltonian
The spin interaction Hamiltonian is given by
| (S5) |
and the intralayer spin Hamiltonian
| (S6) | |||||
Due to interlayer antiferromagntic (AFM) order, we apply the Holstein-Primakoff transformation , , for first layer and , , for second layer, we can get the Hamiltonian up to the quadratic term
| (S7) |
where and , denote the Hermitian conjugate. Considering the AFM interlayer and FM intralayer coupling, we apply the Fourier transformation,
. Then we can get the Hamiltonian in momentum space with the Bosonic BdG Hamiltonian
| (S8) |
where the basis is . Note that appears in the subscript of basis and in hole part of the Hamiltonian. and . is the identity matrice and are the Pauli matrices. .
I.2 S2. Calculation of the Z2 number
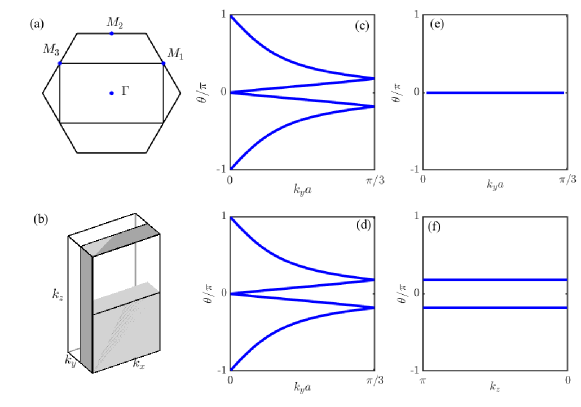
We first focus on the bilayer case. The Hamiltonian host a inversion symmetry: . The eigenvalues at four time-reversal-invariant momentum (TRIM), i.e. and three points (shown in Fig. S1 (a)), are , , , , respectively. So that indicate for bilayer system.
Now we focus on the 3D case. Four Z2 invariants are needed to form the combination [,(,,)] to describe the topological phase in 3D and distinguish the ”strong” and ”weak”. Here it is hard to directly calculate the four topological invariant as there is no inversion symmetry. We enlarge the unit cell along the direction and the Brillouin zone (BZ) is reduced to a rectangle in the - plane. We adopt the method introduced by Rui Yu, et al. RYu to calculate the evolution lines of Wannier centers to get the topological invariant indirectly. The effective BZ adopted is shown in Fig. S1 (b) as the shaded region. At and , the Wannier centers both winding one time, indicating , . at and , the Wannier centers both winding zero times, , . Thus the bulk system is in a ”weak” TI phase.
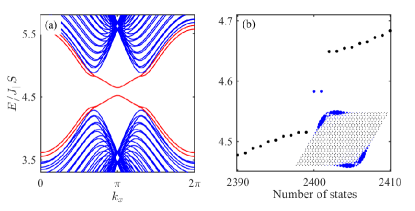
I.3 S3. Corner Modes in bilayer
The bilayer share a same Hamiltonian to Eq. (3) in the main text just by setting and . Then the bosonic Hamiltonian have an additional pseudo-inversion symmetry: with . When , the parity eigenvalues at and three M-points, i.e. the time-reversal invariant momentum (TRIM) points, are , , , , respectively, indicating invariant . The bilayer system is thus topologically nontrivial and supports gapless edge states with two-components propagating oppositely at each edge. The EPA breaks the pseudo-time-reversal symmetry and destroys the topological phase and opens gap for zigzag-edged ribbon, as shown in Fig. S2(a). The same to the bulk case, the magnetic two-fold rotational symmetry is preserved and rotation-graded topological invariant along the line at is half-quantized, makes the system a second-order topological insulator. The corner modes arise as a result, as shown in Fig. S2(b) in a parallelogram flake.
I.4 S4. The chiral Hinge modes at
In Fig. S2 (a), we plot the magnon local density distribution of the chiral hinge modes. In (b), we plot the magnon bands along -direction at . Without the EPA, there also exist the chiral hinge modes, coexisting with the gapless type-I TSMs, closing the gap.
I.5 S6. Magnons in Monoclinic stacked honeycomb ferromagnets
We first discuss the bilayer case to get an intuitive picture. The monoclinic stacking of bilayer CrI3 is a -glide along the Zigzag direction compared with AA stacking. Here we only consider the nearest interlayer AFM coupling. The bosonic BdG Hamiltonian in -space is given by
| (S9) |
in the basis with . Here ,
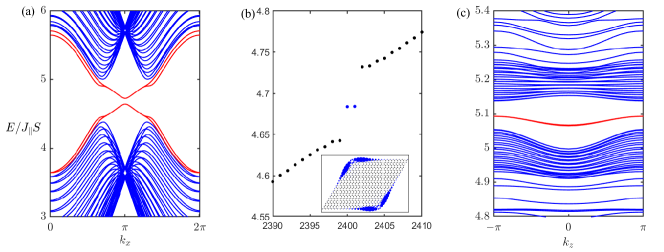
For above bosonic Hamiltonian, it is hard to find the pseudo-time-reversal-symmetry (PTRS). But the magnon bands are still doubly degenerate when . This is because in this case, the bosonic Hamiltonian can be divided into two sectors and and EPA describes the coupling between the two sectors. In two sectors, the interlayer coupling are the same with respect to a -dependent phase factor. This factor coming from the interlayer glide. For the AFM coupling, the obtained magnon bands are only dependent on the module of the coupling after Bogoliubov transformation. So the magnon bands are doubly degenerate when . The EPA term couples the two sectors and will breaks the degeneracy. In Fig. S4 (a) and (b), we can see the EPA opens gap for the degenerate edge states and gives us second-order topological magnons, i.e., corner modes.
For the bulk with monoclinic materials, there should be 6 layers in a primitive cell to build a period along -direction when considering the magnetic order. Here to simplify our calculation, we only consider a 2-layer period along -direction. That is to say, the first and third layer are in AA-stacking. The interlayer interaction Hamiltonian is
By considering a parallelogram pillar geometry, we can also get the hinge modes along the stacking direction, as shown in Fig. S4 (c) The bulk polarization along the stacking direction coming from the SSH configuration, independent on the stacking type. The topology is preserved and chiral hinge modes are expected to remain in the monoclinic stacking.