High Throughput Matrix-Matrix Multiplication between Asymmetric Bit-Width Operands
Abstract
Matrix multiplications between asymmetric bit-width operands, especially between - and -bit operands are likely to become a fundamental kernel of many important workloads including neural networks and machine learning. While existing SIMD matrix multiplication instructions for symmetric bit-width operands can support operands of mixed precision by zero- or sign-extending the narrow operand to match the size of the other operands, they cannot exploit the benefit of narrow bit-width of one of the operands. We propose a new SIMD matrix multiplication instruction that uses mixed precision on its inputs (- and -bit operands) and accumulates product values into narrower -bit output accumulators, in turn allowing the SIMD operation at -bit vector width to process a greater number of data elements per instruction to improve processing throughput and memory bandwidth utilization without increasing the register read- and write-port bandwidth in CPUs. The proposed asymmetric-operand-size SIMD instruction offers improvement in throughput of matrix multiplication in comparison to throughput obtained using existing symmetric-operand-size instructions while causing negligible () overflow from -bit accumulators for representative machine learning workloads. The asymmetric-operand-size instruction not only can improve matrix multiplication throughput in CPUs, but also can be effective to support multiply-and-accumulate (MAC) operation between - and -bit operands in state-of-the-art DNN hardware accelerators (e.g., systolic array microarchitecture in Google TPU, etc.) and offer similar improvement in matrix multiply performance seamlessly without violating the various implementation constraints. We demonstrate how a systolic array architecture designed for symmetric-operand-size instructions could be modified to support an asymmetric-operand-sized instruction.
Index Terms - Convolutional Neural Networks, Inference, Matrix Multiplication, Hardware Accelerators, GEMM, Systolic Array
I Introduction
Use of deeper and wider convolutional neural networks (CNNs) has led to impressive predictive performance in many machine learning applications, such as image classification, object detection, semantic segmentation, etc. However, the large model size and associated computational inefficiency of these deep neural networks often make it impossible to run many realtime machine learning tasks on resource-constrained mobile and embedded devices, such as smartphones, AR/VR devices, etc. One particularly effective approach has been the use of model quantization to enable this size and computation compression of CNN models. Quantization of model parameters to sub-byte values (i.e. numerical precision of bits), especially to -bits has shown minimal loss in predictive performance across a range of representative networks and datasets in recent works. As a result, some heavily quantized machine learning models may use kernel weights which have fewer bits than the corresponding activations which they are to be multiplied with. For example, there is an increasing interest in using -bit weights and -bit activations, which means that matrix multiplications between -bit weights and -bit activations are likely to become a fundamental kernel of many important workloads including neural networks and machine learning, although such multiplications may also be useful for other purposes. This is evident by the increasing interest and successful development of a large number of novel machine learning and linear algebra techniques [1, 11, 18, 2, 10] to preserve the predictive performance of deep neural networks with -bit weights and -bit activations in recent years.
However, in -bit-weight networks, the weights are encoded by bits, while the activation matrices are represented by more bits (e.g., bits in this example, although other examples could have larger activations). This creates a read width imbalance between -bit weights, -bit activations and outputs (accumulators) compared to previous technology. Ideally, we would like to sustain matched vector width of read and write operands while exploiting -bit weights for the best performance. In other words, we would like to utilize the full bandwidth of read and write ports while exploiting -bit weights for the best performance.
While existing instructions with a same operand size in both first and second operands already would support application to operations involving narrower data values for the second operand, they will not be able to exploit the narrower bit-width of the second operand for improving the MAC throughput of matrix multiply operation.
In contrast, by implementing an asymmetric-operand-size matrix multiplication instruction (or other similar operations) using -bit instead of -bit encoding for the weight matrix, twice as many values can be accessed for the same number of bits – this is by design and an intended consequence in order to get a speedup. Subsequently, part of the matrix multiplication hardware can be reused to do twice as many multiplies of narrower width, and the matrix architecture based on the narrower argument can be twice as wide to use all the bits available. While this improves the MAC throughput of the SIMD asymmetric-operand-size matrix multiply operation at -bit vector width by , the accumulation of product between - and -bit operands into -bit accumulators doubles the register read- and write-port bandwidth requirement of the output matrix owing to larger accumulator matrix. This is overcome by accumulating products into -bit accumulators. While this reduces the number of spare digits for carries, in practice for many common workloads (e.g., representative deep neural networks) overflows still do not occur often and so the concerns about overflows from -bit accumulators occurring too often are misplaced.
To summarize, we make the following contributions.
-
•
To the best of our knowledge, this is the first work to propose a SIMD matrix multiply operation between asymmetric bit-width operands that offers increase in MAC throughput without violating the register vector width requirements in CPUs while observing negligible () overflow from -bit accumulators for ResNet18-like architectures on ImageNet dataset.
-
•
This SIMD instruction addresses the challenges created by mismatch between the read bandwidth (vector width) of -bit weights, -bit activations, and write bandwidth of -bit accumulators.
-
•
The asymmetric-operand-size matrix multiply operation can be seamlessly integrated into a DNN accelerator (e.g., systolic array in Google TPUs, etc.) designed for symmetric-operand-size operation to achieve improvement in MAC throughput without violating the associated implementation constraints (e.g., the size of operand buffers and accumulator buffers).
II Background and Related Work
In recent years, numerous research efforts have been devoted to quantizing neural network architectures to sub-byte values while preserving the accuracy of full-precision model [17, 11, 18, 2, 10, 21, 20, 13, 19, 6, 3, 5, 4]. Furthermore, several approaches were proposed on developing compressed neural networks through the use of weight pruning [7], tensor decomposition [8, 16, 14, 15], compact network architecture design, etc. Learning quantization for numerical precision of -bits has been shown to be effective in recent works [1, 11, 18, 2, 10], in turn creating demand for efficient execution of matrix multiplication kernel between -bit weights and -bit activations on existing CPUs and DNN hardware accelerators. However, the mismatch between read bandwidth of -bit weights, -bit activations, and write bandwidth of accumulators poses major obstacles in implementing such an instruction for matrix multiplication hardware in CPUs and DNN hardware accelerators. The use of existing instructions (that execute MAC operations between symmetric bit-width operands) to perform such matrix multiplication between asymmetric bit-width operands will not be able to fully exploit the benefit of -bit weight quantization. On the other hand, failure to match the vector width of weights, activations, and accumulators by a matrix multiply instruction will either under-utilize expensive CPU resources (e.g., register file port bandwidth, etc.) or require significant increase in the DNN hardware accelerator resident SRAM resources (e.g., size of accumulator buffers, etc.) to realize any throughput benefit from -bit quantization. None of the recent works on -bit model quantization reports performance benefit on either existing CPUs or hardware accelerators.
III Overview of Matrix Multiplication between Symmetric Bit-Width Operands
Traditionally, the kernel weights would have the same number of bits as the corresponding activations which they are to be multiplied with. For example, it may be common for each activation value and kernel weight to comprise bits, bits or bits, with identical sizes for the activation and kernel values.
Figure 1 shows an example of implementing this matrix processing using a symmetric-operand-size matrix multiplication instruction which acts on first and second operands with identical data element sizes. In this example, the input activations and weights both comprise bits, so the result of any single multiplication operation on two -bit values will be -bits wide, and as machine learning processing requires the products of two or more different pairs of activations/weights to be added together (and possibly accumulated with previous elements calculated by earlier instructions), then to avoid loss of accuracy due to overflow, the -bit results are typically accumulated into -bit elements in the result matrix C. This means in a vector architecture for a same-element-size implementation the input-to-output width ratio of works well.
Furthermore, an additional source of performance improvement is matrix element reuse. Typically tiling (blocking) is used in software but can also be applied at an instruction level as well as seen in the proposed matrix multiplication instruction (demonstrated in Figure 1) by packing 2D matrices in vector registers. As shown in Figure 1, the registers can be loaded with a larger number of data elements than can be processed by a single instruction, so that the elements loaded by a single set of load operations can be reused across multiple instructions in different combinations. The portions of the activation and weight matrices indicated using the box in Figure 1 represent the portions processed by a single matrix multiplication instruction (e.g. each portion corresponds to a sub-matrix of elements of the -element matrix structure loaded into the registers), and the matrix multiplication instruction generates a output cell within the output matrix C (each element of the cell comprising a -bit element). The output of one instance of the matrix multiplication instruction only generates a partial value for that output cell – in this case corresponding to the multiplication of Atop and Btop shown in Figure 1. The final value for the output cell is computed across multiple matrix MAC instructions by adding the results of corresponding elements derived from matrix multiplications of Atop Btop, Atop Bbottom, Abottom Btop and Abottom Bbottom. The other output cells within the output matrix C can then be performed through similar calculations using different pairs of rows and columns from the loaded activation and weight matrix structures. By reusing the same set of inputs for multiple instructions, this can improve the overall load-to-compute ratio compared to an approach where separate load operations are required to load the operands for each individual instruction.
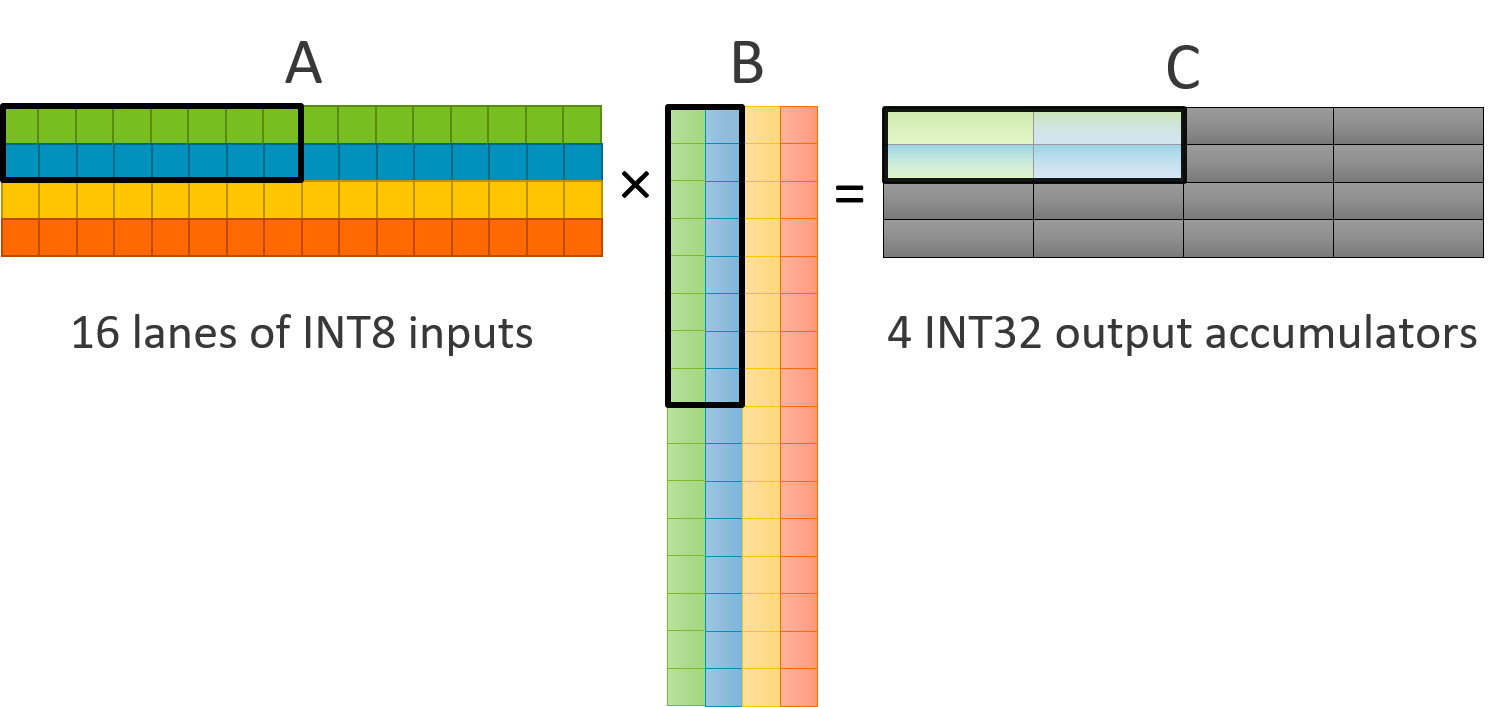
IV Matrix Multiplication between Asymmetric Bit-Width Operands
If a quantized neural network with -bit weights is executed using symmetric-operand-size matrix multiplication instructions similar to those shown in Figure 1, then the -bit weights stored in memory could be loaded into a number of -bit elements within the B operand registers, with each -bit weight value from memory sign-extended or zero-extended to fill the remaining bits of each -bit element of the B operand registers. This would mean that the -bit weights would not be packed contiguously into the input registers but would be dispersed into a number of non-contiguous -bit chunks with gaps between them corresponding to the locations of the sign-extension or zero-extension. Having extended the -bit weights from memory into -bit elements, the matrix multiplication could be performed in the same way as described above for Figure 1 to generate four -bit output accumulator values per instruction (based on the multiplication of () lanes of -bit activations and () lanes of -bit weights (expanded from the -bit weights in memory)). Hence, while this approach would allow the storage overhead of storing the weights in memory to be reduced compared to an approach using -bit weights, the processing throughput cost would be the same, as the number of elements processed per matrix multiply instruction would still be the same as in Figure 1.
In contrast, by implementing an asymmetric-operand-size matrix multiplication instruction using -bit elements instead of -bit elements for the operand used for the weight matrix, twice as many values can be accessed from memory per load instruction – this is by design and an intended consequence in order to get a speedup. Subsequently, part of the matrix multiplication hardware can be reused to do twice as many multiplies of narrower width.
Figure 2 shows the proposed asymmetric-operand-size matrix-matrix multiplication instruction processing - and -bit operands. The second operand has data elements contiguously packed into registers with a smaller data element size than the data element size of the elements of the first operand. The maximum possible result of any single multiplication operation between - and -bit operands is -bits wide. Due to the accumulative nature of a matrix multiplication operation, these -bit results can be accumulated into a -bit accumulator register. Furthermore, -bit weights can improve the virtual bandwidth (vector width) of register file by storing larger weight sub-matrices in the same limited-size register file. For example, with -bit vector width shown in Figure 2, the B input operand register corresponding to Btop that once held a sub-matrix of -bit elements can now hold a sub-matrix of -bit elements. Hence, in the example of Figure 2 the first operand A comprises the same sub-matrix of -bit activations as is represented by the portion Atop in Figure 1, but the second operand B comprises a sub-matrix of -bit weights and so corresponds to the top half of the matrix structure B shown in Figure 1 (rather than only comprising Btop). Hence the number of input elements in the second operand B that can be processed in one instruction is twice as many as in the symmetric-operand-size instruction shown in Figure 1. Similarly, the portion of the result matrix generated by an asymmetric-operand-size matrix multiply operation shown in Figure 2 includes twice as many elements as the portion generated by a symmetric-operand-size operation shown in Figure 1. The instruction in Figure 2 generates a matrix of -bit result elements, instead of generating a matrix of -bit elements, but can still use registers of the same size as Figure 1. Hence, while the symmetric-operand-size matrix multiply instruction shown in Figure 1 multiplies -bit activations by -bit weights to generate -bit output accumulators, the asymmetric-operand-size instruction shown in Figure 2 multiplies -bit activations by -bit weights to generate -bit output accumulators instead. This means that the asymmetric-operand-size instruction is able to process twice as many inputs and generate twice as many outputs per instruction as opposed to the symmetric-operand-size instruction.
Another advantage is that as it is not necessary to zero-extend or sign-extend the narrower weights stored in memory when loading them into registers, which makes load processing simpler, and also means that the full read or write port bandwidth supported to match the register size used is available for loading the -bit weights (rather than needing to artificially limit the read or write bandwidth used for an individual load instruction to half that represented by the register size to allow for the zero-/sign-extension). Hence, support for this instruction can speed up the processing of quantized machine learning networks that use mixed precision on its inputs.
One potential challenge for widespread acceptance of an instruction like this would be overflow violations in the relatively narrow accumulators. While the matrix multiply operation in Figure 1 uses -bit accumulators to accumulate -bit products resulting from multiplication of two -bit operands, and so has bits spare to accommodate carries before any risk of overflow occurs, the asymmetric-operand-size operation in Figure 2 uses -bit accumulators instead to accumulate -bit products, so there are only bits spare for accommodating carries before there is a risk of overflow. In the worst case, only -bit products resulting from signed multiplication of - and -bit values () can be accumulated into a -bit ( to ) register before overflowing. While this would be fine for a single instance of the instruction, typical use cases reuse a stationary accumulator register over multiple instances of the instruction within a loop.

V Experiments and Results
In order to observe the amount of overflow that happens in practice while using -bit accumulators for performing matrix multiplication between -bit activations and -bit weights in our proposal, test data from the ImageNet dataset was fed to the ResNet18 architecture where activations and weights are quantized to -bit and -bit respectively. For -bit width of accumulator, almost non-existent () overflow (% of accumulation operation causing overflow while generating the output activations of each layer) is observed as shown in Figure 3 and Table I. Figure 3 shows the percentage of accumulation operations causing overflow observed while using accumulators of different bit-widths for performing high throughput matrix multiplication between 8-bit activations and 4-bit weights of the ResNet18 architecture. Table I shows the overflow observed while using a -bit accumulator for performing matrix multiplication between -bit activations and -bit weights. Table II shows the number of matrix MAC operations () performed for generating each output element of different layers of the ResNet18 architecture, where is the number of input channel values, and and are the width and height of each kernel array.
Table I and Table II show that in practice overflow only happens in the largest of neural network layers (which are falling out of favour compared to more efficient modern architectures) where over multiplication results are accumulated into each -bit accumulator result. This demonstrates that in the common case overflow for -bit accumulators is very rare.
Hence, the matrix multiplication operation between asymmetric bit-width operands proposed in this work is not expected to cause significant difficulties concerning the occurrence of overflow. If overflow detection is desired, making the overflow sticky (in that the max negative or positive value does not change once it is overflowed) can enable a simple error detection routine as well by scanning the outputs for any and results. Additionally, since machine learning workloads are tolerant to such numerical errors, in most use cases the sticky max values can just be used directly in the next stage of compute without any checking routine.

| ResNet18 Layers | Overflow (%) using |
|---|---|
| -bit accumulator | |
| Convolution layer 2 | 0.0 |
| Convolution layer 4 | 0.0 |
| Convolution layer 7 | 0.0 |
| Convolution layer 9 | 0.0 |
| Convolution layer 12 | 0.001 |
| Convolution layer 14 | 0.003 |
| Convolution layer 17 | 0.061 |
| Convolution layer 19 | 0.054 |
| ResNet18 Layers | MAC operations | ||||
|---|---|---|---|---|---|
| Convolution layer 2 | 64 | 64 | 3 | 3 | 576 |
| Convolution layer 4 | 64 | 64 | 3 | 3 | 576 |
| Convolution layer 7 | 128 | 128 | 3 | 3 | 1152 |
| Convolution layer 9 | 128 | 128 | 3 | 3 | 1152 |
| Convolution layer 12 | 256 | 256 | 3 | 3 | 2304 |
| Convolution layer 14 | 256 | 256 | 3 | 3 | 2304 |
| Convolution layer 17 | 512 | 512 | 3 | 3 | 4608 |
| Convolution layer 19 | 512 | 512 | 3 | 3 | 4608 |
VI Suitability to Hardware Accelerators for Deep Neural Networks
This section shows an example of how processing circuitry designed for performing the MAC operations in state-of-the-art DNN hardware accelerators can be adapted to support the proposed matrix multiplication instruction between asymmetric bit-width operands. A convolutional operation in DNN layers are typically implemented by lowering 2D convolution to general matrix multiply (GEMM) kernels, which are typically the runtime bottleneck when executed on CPUs, motivating hardware acceleration. Spatial architectures are a class of accelerators that can exploit high compute parallelism of GEMM kernels using direct communication between an array of relatively simple processing engines (PEs). The systolic array (SA) is a coarse-grained spatial architecture for efficiently accelerating GEMM. The SA consists of an array of MAC processing elements (PEs), which communicate operands and results using local register-to-register communication only, which makes the array very efficient and easily scalable without timing degradation. These advantages have led to their deployment in commercial products, e.g., the Google Tensor Processing Unit (TPU) [9].
The proposed matrix multiplication instruction at different vector widths (e.g., -bit vector width, etc. as shown in the examples above) will not only play a vital role in offering improvement in throughput of matrix multiplication involving -bit weights and -bit activations in future CPUs, but also will be effective to support MAC operation between - and -bit operands in state-of-the-art DNN hardware accelerators (e.g., TPU, etc.) and offer similar improvement in matrix multiply performance seamlessly without violating the various implementation constraints.
Figure 4 shows the structure of a SA widely deployed in Google TPUs. It is designed for supporting multiplications involving operands with equal element size. Each MAC operation in the SA requires two -bit operand registers. The -bit products are collected into the -bit accumulator buffers. This SA organization enables output-stationary dataflow, which keeps the larger -bit accumulators in place and instead shifts the smaller -bit operands.
Figure 5 shows how a MAC operation acting on -bit and -bit operands can be performed using a SA architecture. The -bit operand registers now can accommodate two -bit weight values and a MAC unit now can perform two MACs between -bit and -bit operands values to generate two -bit products. The -bit products in turn are accumulated into -bit accumulators, thus enabling the -bit accumulator buffer of the SA of Figure 4 to be re-purposed for collecting two -bit wide MAC output values. Thus the MAC operation between -bit and -bit operands generating -bit output values can be seamlessly integrated into the SA matrix multiplication engine to achieve improvement in MAC throughput without violating the implementation constraints around the size of operand buffers and accumulator buffers. Similarly, a SA architecture that enforces weight-stationary dataflow can easily be extended to support the proposed matrix multiplication operation involving asymmetric bit-width operands. Weight-stationary dataflow keeps the smaller -bit weights in place and shifts the larger -bit accumulator values.


VII Conclusion and Future Work
We propose a SIMD matrix multiplication operation to obtain increase in MAC throughput for asymmetric bit-width operands without requiring either additional register read and write ports in CPUs or larger operand and accumulator buffers in DNN accelerators. The matrix multiply instruction makes this possible by accumulating product values into -bit accumulators as opposed to -bit accumulators used for symmetric -bit operands. We observed negligible overflow () from - bit accumulators for the pre-trained ResNet-18 model with -bit weights and -bit activations. A natural next step is to explore the impact of this negligible overflow on the accuracy of the pre-trained ResNet-18 model. We believe this overflow from narrower -bit accumulators can be avoided via integrating the constraint on accumulator’s width into the training procedure of the ResNet-18 model with -bit weights. We leave this exploration for future work. In future, we plan to explore the impact of -bit weights and -bit accumulators on other highly optimized CNNs, especially MobileNets. In addition, it will be interesting to see how the theoretical gains reported here from asymmetric bit-width operands translate into actual energy savings and runtime speedups on DNN accelerator and CPU simulators [12].
References
- [1] R. Banner, Y. Nahshan, E. Hoffer, and D. Soudry, “Post-training 4-bit quantization of convolution networks for rapid-deployment,” in 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), 2019.
- [2] R. Gong, X. Liu, S. Jiang, T. Li, P. Hu, J. Lin, F. Yu, and J. Yan, “Differentiable soft quantization: Bridging full-precision and low-bit neural networks,” in The IEEE International Conference on Computer Vision (ICCV), October 2019.
- [3] D. Gope, J. Beu, U. Thakker, and M. Mattina, “Ternary mobilenets via per-layer hybrid filter banks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, June 2020.
- [4] D. Gope, J. G. Beu, U. Thakker, and M. Mattina, “Aggressive compression of mobilenets using hybrid ternary layers,” tinyML Summit, 2020. [Online]. Available: https://www.tinyml.org/summit/abstracts/Gope_Dibakar_poster_abstract.pdf
- [5] D. Gope, G. Dasika, and M. Mattina, “Ternary hybrid neural-tree networks for highly constrained iot applications,” in Proceedings of Machine Learning and Systems 2019, 2019, pp. 190–200.
- [6] Y. Guo, A. Yao, H. Zhao, and Y. Chen, “Network sketching: Exploiting binary structure in deep cnns,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, July 21-26, 2017, 2017, pp. 4040–4048.
- [7] S. Han, H. Mao, and W. J. Dally, “Deep compression: Compressing deep neural network with pruning, trained quantization and huffman coding,” CoRR, vol. abs/1510.00149, 2015.
- [8] M. Jaderberg, A. Vedaldi, and A. Zisserman, “Speeding up convolutional neural networks with low rank expansions,” in British Machine Vision Conference, BMVC 2014, Nottingham, UK, September 1-5, 2014, 2014.
- [9] N. P. Jouppi, C. Young, N. Patil, D. Patterson, G. Agrawal, R. Bajwa, S. Bates, S. Bhatia, N. Boden, A. Borchers, R. Boyle, P.-l. Cantin, C. Chao, C. Clark, J. Coriell, M. Daley, M. Dau, J. Dean, B. Gelb, T. V. Ghaemmaghami, R. Gottipati, W. Gulland, R. Hagmann, C. R. Ho, D. Hogberg, J. Hu, R. Hundt, D. Hurt, J. Ibarz, A. Jaffey, A. Jaworski, A. Kaplan, H. Khaitan, D. Killebrew, A. Koch, N. Kumar, S. Lacy, J. Laudon, J. Law, D. Le, C. Leary, Z. Liu, K. Lucke, A. Lundin, G. MacKean, A. Maggiore, M. Mahony, K. Miller, R. Nagarajan, R. Narayanaswami, R. Ni, K. Nix, T. Norrie, M. Omernick, N. Penukonda, A. Phelps, J. Ross, M. Ross, A. Salek, E. Samadiani, C. Severn, G. Sizikov, M. Snelham, J. Souter, D. Steinberg, A. Swing, M. Tan, G. Thorson, B. Tian, H. Toma, E. Tuttle, V. Vasudevan, R. Walter, W. Wang, E. Wilcox, and D. H. Yoon, “In-datacenter performance analysis of a tensor processing unit,” in Proceedings of the 44th Annual International Symposium on Computer Architecture, ser. ISCA ’17. New York, NY, USA: ACM, 2017, pp. 1–12.
- [10] S. Jung, C. Son, S. Lee, J. Son, J.-J. Han, Y. Kwak, S. J. Hwang, and C. Choi, “Learning to quantize deep networks by optimizing quantization intervals with task loss,” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2019.
- [11] C. Louizos, M. Reisser, T. Blankevoort, E. Gavves, and M. Welling, “Relaxed quantization for discretized neural networks,” in 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, May 6-9, 2019, 2019.
- [12] J. Lowe-Power, A. M. Ahmad, A. Akram, M. Alian, R. Amslinger, M. Andreozzi, A. Armejach, N. Asmussen, S. Bharadwaj, G. Black, G. Bloom, B. R. Bruce, D. R. Carvalho, J. Castrillón, L. Chen, N. Derumigny, S. Diestelhorst, W. Elsasser, M. Fariborz, A. F. Farahani, P. Fotouhi, R. Gambord, J. Gandhi, D. Gope, T. Grass, B. Hanindhito, A. Hansson, S. Haria, A. Harris, T. Hayes, A. Herrera, M. Horsnell, S. A. R. Jafri, R. Jagtap, H. Jang, R. Jeyapaul, T. M. Jones, M. Jung, S. Kannoth, H. Khaleghzadeh, Y. Kodama, T. Krishna, T. Marinelli, C. Menard, A. Mondelli, T. Mück, O. Naji, K. Nathella, H. Nguyen, N. Nikoleris, L. E. Olson, M. S. Orr, B. Pham, P. Prieto, T. Reddy, A. Roelke, M. Samani, A. Sandberg, J. Setoain, B. Shingarov, M. D. Sinclair, T. Ta, R. Thakur, G. Travaglini, M. Upton, N. Vaish, I. Vougioukas, Z. Wang, N. Wehn, C. Weis, D. A. Wood, H. Yoon, and É. F. Zulian, “The gem5 simulator: Version 20.0+,” CoRR, vol. abs/2007.03152, 2020. [Online]. Available: https://arxiv.org/abs/2007.03152
- [13] Q. Sun, F. Shang, K. Yang, X. Li, Y. Ren, and L. Jiao, “Multi-precision quantized neural networks via encoding decomposition of {-1, +1},” in The Thirty-Third AAAI Conference on Artificial Intelligence, AAAI 2019, The Thirty-First Innovative Applications of Artificial Intelligence Conference, IAAI 2019, The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2019, Honolulu, Hawaii, USA, January 27 - February 1, 2019., 2019, pp. 5024–5032.
- [14] U. Thakker, J. G. Beu, D. Gope, G. Dasika, and M. Mattina, “Run-time efficient RNN compression for inference on edge devices,” CoRR, vol. abs/1906.04886, 2019.
- [15] U. Thakker, J. G. Beu, D. Gope, C. Zhou, I. Fedorov, G. Dasika, and M. Mattina, “Compressing rnns for iot devices by 15-38x using kronecker products,” CoRR, vol. abs/1906.02876, 2019.
- [16] U. Thakker, I. Fedorov, J. Beu, D. Gope, C. Zhou, G. Dasika, and M. Mattina, “Pushing the limits of rnn compression,” CoRR, vol. abs/1910.02558, 2019.
- [17] M. Tschannen, A. Khanna, and A. Anandkumar, “StrassenNets: Deep learning with a multiplication budget,” in Proceedings of the 35th International Conference on Machine Learning, ser. Proceedings of Machine Learning Research, J. Dy and A. Krause, Eds., vol. 80. Stockholmsmässan, Stockholm Sweden: PMLR, 10–15 Jul 2018, pp. 4985–4994.
- [18] J. Yang, X. Shen, J. Xing, X. Tian, H. Li, B. Deng, J. Huang, and X.-s. Hua, “Quantization networks,” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2019.
- [19] D. Zhang, J. Yang, D. Ye, and G. Hua, “Lq-nets: Learned quantization for highly accurate and compact deep neural networks,” in Computer Vision - ECCV 2018 - 15th European Conference, Munich, Germany, September 8-14, 2018, Proceedings, Part VIII, 2018, pp. 373–390.
- [20] S. Zhu, X. Dong, and H. Su, “Binary ensemble neural network: More bits per network or more networks per bit?” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2019.
- [21] B. Zhuang, C. Shen, M. Tan, L. Liu, and I. Reid, “Structured binary neural networks for accurate image classification and semantic segmentation,” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2019.