High rectifying performance of heterojunctions with interface between armchair C₃N nanoribbons with and without edge H-passivation

To study the effect of nanoribbons edge configuration on the electronic structures of AC₃NNRs, the band structures of CCA, CNA and CCCNA are calculated, respectively. The detailed results are shown in Figs. 1(d-f). As is seen in Fig. 1(d), the electronic band structure of CCA along a high-symmetry path in the Brillouin zone is shown that have four bands crossing the Fermi level, so the CCA ribbon is metal. Additionally, our results also show that the CNA and CCCNA are metal, because there are two bands and three bands across the Fermi level in the band structures of CNA and CCCNA as shown in Figs. 1(e) and 1(f), respectively. So the pristine AC₃NNRs are metal, which is in good agreement with other theoretical calculations Y. Ren . Interestingly, we find that these ribbon’s edge configuration and band structures have a law with the CN-edge changes. The number of bands crossing the Fermi level gradually decreases from 4 to 2 as the number of CN-edge in ribbon increases from 0 to 2. And the H-passivated ZC₃NNRs have the same electronic band Congxin Xia . It is well known that the electronic states near the Fermi level play an important role in the electron property. To further understand why the bands across the Fermi level are decreasing, we give the spatial Bloch state distributions of AC₃NNRs at the band structure near the Fermi level.

Further, as can be seen from Fig. 1(g), the contours of Bloch states of pristine AC₃NNRs are dominated by the atoms near the edges. The color in the picture only represents the phase, and the size represents how much the electron contributes at the Fermi level Cao1 ; Y. Ren ; Q. Y. Wu . Further, we find that the electronic density of edge C atoms is much larger than that of the edge N atoms for each ribbon. This is very similar to the situation in graphene nanoribbon, in which the energy bands near $E_{F}$ are mainly contributed by the edge C atoms, and the contribution to the electron orbital is mainly due to the $p$-orbital near the Fermi level. The graphene-like AC₃NNRs here also show a very strong edge state effect. In addition, we also calculate the projected density of state (PDOS) of CCCNA as depicted in Fig. 1(h), calculated the contribution of the CC-edge and the CN-edge to the density of state (DOS) near the Fermi level. PDOS analysis for CCCNA shows that the CN-edge have little contribution to the DOS near the Fermi level. This similar phenomenon also occurs in B and N-doped zigzag graphene nanoribbons S. Dutta . It is found that electrons flow preferentially from C to B, but the transfer of charge from C to N is hindered by the existence of large Coulomb repulsion at the N position. As a result, the N atoms and the connected C atoms contribute very little to DOS near the Fermi level. So in our nanoribbon structures, it is the large Coulomb repulsion on N atoms that hinders the electron transfer from the nearest C atoms, which causes the CN-edge to contribute little to the DOS near the Fermi level, and further causes the state of the band crossing the Fermi level to be affected, thereby reducing its number.

Considering the effect of edge passivation on the nanoribbons, we tested the passivation of CCA, CNA and CCCNA ribbon edge by H atoms. As shown in Figs. 2(a-c), the three kinds of AC₃NNRs after edge terminate in Hydrogen atoms were named H-CCA, H-CNA and H-CCCNA, respectively. Through the calculated edge energy of the ribbons of bare edges and hydrogen passivation, we found that all the AC₃NNRs edges passivated by H atoms can enhance the stability of the ribbons. Not only that, but hydrogen passivation can also tune the bandgap of the ribbons. The corresponding band structures after hydrogen passivation are illustrated in Figs. 2(d-f). From the CBM and VBM at $\Gamma$ point and along the $\Gamma$-Z line shown in Fig. 2(d), we know the H-CCA is an indirect band gap semiconductor with a gap value of 0.7 eV. Interestingly, the H-CNA structure possesses the direct bandgap with a gap value of 0.35 eV in Fig. 2(e). So H-passivation achieves the indirect-direct gap transition in nanostructure of C₃N. In addition, the H-CCCNA structure is an indirect gap semiconductor with a gap value of 0.46 eV in Fig. 2(f). Therefore, for AC₃NNRs, H-passivation can cause the bands acrossing the Fermi level to disappear and thus induce the transition from metal to semiconductor. In other words, the unpassivated AC₃NNRs are metal while the H-passivated AC₃NNRs are semiconductor. The reason for the edge states vanishing and the insulating band appearing is the electrons from H-atom bonds with unpaired electrons of outermost edge atoms, and the edge state is full-filled and buried deeply in the valence band. The zigzag phosphorene nanoribbon also has the similar electronic structure Fan .

To further investigate the effect of H-passivation on the electronic property of AC₃NNRs, we select a few points on the energy band diagram and plotted its electron density. Hence states 1-4 of three passivated AC₃NNRs spatial distribution of Bloch state are shown in Fig. 2(g). Observing the respective Bloch functions, it is first observed that the edge states disappear in the H-passivated AC₃NNRs. Secondly, the contours of Bloch state indicate that both CBM and VBM are contributed by the hybridized s-p states of the C and N atoms of the AC₃NNRs. The outline of the Bloch state shows that the VBM of H-CCA (state 1) and the VBM of H-CNA (state 2) are both contributed by central atoms in the ribbons. The Bloch state of their CBM is not given in this paper because its contour is similar to the Bloch state of VBM. Furthermore, the states of electron density are distributed almost symmetrically throughout the structure. This is because of the inversion symmetry of the CCA and the mirror symmetry of the CNA ribbon. On the contrary, for H-CCCNA, the contours of the Bloch state indicate that both CBM (state 3) and VBM (state 4) are contributed by edge atoms and partial central atoms in the ribbon, and that the states are gradually localized towards the edge of the ribbon. This is caused by the asymmetry structure for the H-CCCNA ribbon. Namely, the H-CCCNA transport channels for carrier transport under a low bias are different from the other two structures.

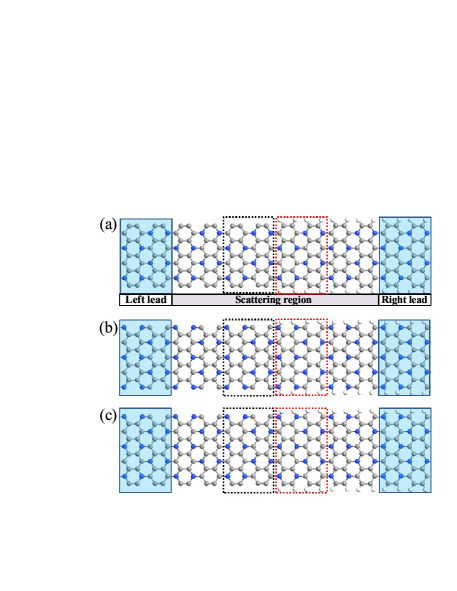
Based on the knowledge that the pristine and H-passivated AC₃NNRs are metal and semiconductor, we build the heterojunction models of Schottky junctions in Fig. 3, where the left lead and right lead are the unit cell of pristine and H-passivated AC₃NNRs, respectively. The central scattering regions are constructed by two unit cells of metallic AC₃NNRs and corresponding to two unit cells of semiconducting H-passivated AC₃NNRs. The interface is the border between the black and red dashed boxes. For the sake of the simplicity, we named M1 of the heterojunction with CCA on the left and H-CCA on the right in Fig. 3(a). Likewise, Figs. 3(b-c) show the CNA/H-CNA heterojunction (M2) and CCCNA/H-CCCNA heterojunction (M3), respectively.

The current-voltage (I-V) characteristics and rectification ratio of planar metal-semiconductor junctions are illustrated clearly in Fig. 4. Interestingly, all heterojunction models show forward-conducting and reverse-blocking rectifier diode characteristics. In other words, all currents increase rapidly under positive bias, yet they are still almost zero under negative bias. But the difference is that when the M2 junction bias is 0.4 V-0.65 V, the current decreases as the voltage increases, showing a negative differential resistance (NDR) effect. To precisely describe the rectification behaviors, we introduced the rectification ratio. It is defined as RR= I₊/I_-, where the I₊ and I_- are the currents at positive and negative bias for the same bias magnitude. The rectification ratios of three junctions under different bias are exhibited in the inset figure of Fig. 4, showing that the junction of M3 has larger rectification ratio under the 0.2 V-0.4 V bias. And it’s important to note that the RR depends on the ratio between positive and negative voltages by definition. Although the current of M2 is greater than that of M3 under positive bias voltage, the former is much smaller than the latter under negative bias voltage, so the RR of M3 is greater than that of M2 in Fig. 4.

To understand the rectification behavior, transmission spectra of M1, M2 and M3 at several representative bias voltages are shown in Figs. 5(a-c). The green dashed line represent the bias window. According to the Landauer-B$\rm\ddot{u}$ttiker formula H. M. Pastawski , the value of the current passing through the central scattering region depends on the integrated area of the transmission probability within the bias window under consideration. For the M1 junction, as shown in Fig. 5(a), when a negative bias of -0.6 V is applied, there is no transmission peak in the bias window, therefore the electrons in this system cannot be transmitted, so the current shown in the I-V curve is almost zero. When a positive bias of 0.6 V is applied, there is a transmission peak in the bias window, so the integral area of the transmission probability in the bias window is not zero, therefore, the current reflected on the I-V curve has a certain value.

The I-V curves become asymmetrical with those at positive and negative bias, indicating rectification behavior. In Figs. 5(b-c), the rectification mechanism of M2 and M3 junctions is the same as that of M1 junction. To precisely understand the mechanism of the NDR behavior appearing in M2 structure, we draw the transmission spectrum in Fig. 5(d). The red solid lines represents the bias window. It is clear that the integral area in the bias window first increased, then decreased, and increased again as the bias voltage increased, which is consistent with the I-V curve of M2 in Fig. 4. Thus, the conductivity of this junction was high at 0.3 V-0.4 V biases, whereas it is intensively suppressed at 0.5 V-0.6 V biases suggesting the NDR behavior emerged. It is well known that, the energy band structure of the material determines the property of electron transport, which will be discussed in detail in the next section.

Next, choosing M1 as the representative junction to analyze, the left and right electrodes are CCA and H-CCA, respectively. If we apply a bias to the electrodes, there will be a potential difference between them, and their band structures will move downward or upward relatively. We apply a forward bias of 0.35 V in Fig. 6(a), and an energy window (light blue shaded area) appears due to Fermi level migration. Band structures of CCA and H-CCA without applied voltage are shown in Figs. 1(d) and 2(d), respectively. Compared with Fig. 6(a), it is found that the Fermi level of the left electrode will move downward when the positive voltage is applied, while the Fermi level of the right electrode will move upward. In this energy window, only the left electrode has several bands while the right electrode has a band gap between the VBM and the energy window, so electrons cannot jump from the right electrode to the left electrode, resulting in electron transmission is prohibited. As the forward bias continues to increase, the valence band of the right electrode will enter the energy window, causing electrons can jump between the two electrodes, and the junction opens. This is why the positive cut-off bias of M1 in Fig. 4 is 0.35 V. Fundamentally speaking, the forward cut-off bias depends on the absolute value of the right electrode VBM, and the larger the value, the greater the cut-off bias. This value is about -0.18 eV for H-CNA, and about -0.22 eV for H-CCCNA, so the forward cut-off biases for their corresponding junctions are 0.18 V and 0.22 V, respectively, as shown in Fig. 4.

Further, after applying a reverse bias of -0.35 V, the band structures of the left and right electrodes are shown in Fig. 6(b). Compared with a positive voltage, applying a negative voltage causes the Fermi level of the left electrode to move up and the Fermi level of the right electrode to move down. Like the forward bias mechanism, due to the band gap between the CBM of the right electrode and the energy window, electrons cannot jump within the energy window. The difference is that when the bias voltage increases, the right electrode conduction band can enter the energy window and electrons can jump, but the reverse current in Fig. 4 is still zero. We find that this situation also exists in the M3 junction, so there is no jumping restriction caused by symmetry. In this case, we suspect that there is a potential barrier prevents electrons from being transmitted. Therefore, we calculate the projected local density of states (PLDOS) shown in Fig. 7 to examine the interface barriers under different bias voltages.

Moreover, as shown in Fig. 7(a), it is observed that the left part is metallic, while the right part is a semiconductor with a band gap of about 0.7 eV which is consistent with the analysis of Fig. 2(d). There are several forbidden bands appear on either side of the heterojunction under the near Fermi level. The energy region of forbidden bands are from 0.65 to 0.75 eV in the CCA and from -0.35 to 0.65 eV in the H-CCA. These interleaved forbidden bands account for the zero transmission in the energy regimes from -0.35 to 0.75 eV. However, the density of states exists on both sides of the heterojunction in the energy range of 0.75 to 1.2 eV, and the transmission also disappears at this time. The transmission disappeared in this energy region may be caused by other reasons. As we all know, when two materials in a metal-semiconductor junction are in contact, the carrier diffusion flow must make the Fermi energy levels on both sides of the contact surface equal to reach an equilibrium state. Therefore, as shown in Fig. 7(a), the energy band in the semiconductor will be bent downwards due to the built-in electric field after contact. In this way, an electron potential barrier is formed on the contact surface, called the Schottky barrier. The Schottky barrier height ($\Phi$_b) is 1.2 eV, as seen in Fig. 7(a). The transport forbidden in the energy region from 0.75 to 1.2 eV is explained. In Fig. 7(b), when a forward bias of 0.8 V is applied, the addition of an external electric field raises the Fermi level on the semiconductor side. So the chemical potential of the right electrode is higher than the energy of the left electrode, the electrons flow from the right to the left electrode, and current flows from the left to the right electrode. Because the Fermi level on the right side rises,the CBM and VBM near the Fermi level are flattened or bent upward W. X. Zhang .

Also, we can find that the electrons do not need to overcome any potential barriers on the interface during the flow, so the M1 junction has a larger current under high forward bias. On the contrary, after applying a reverse bias of -0.8 V, the Fermi level on the metal side rises and the Fermi level on the semiconductor side falls as shown in Fig. 7(c). So the chemical potential of the left electrode is higher in energy than the chemical potential of the right electrode, and electrons flow from the left to the right electrode. However, although the left Fermi level moves upward under the reverse bias, its energy is still lower than the energy of the CBM on the right side at the interface, so a potential barrier appears at the interface Z. X. Yang ; W. X. Zhang . In the process of flowing from the left electrode to the right electrode, electrons must overcome this potential barrier, so it generate a very low current. Therefore the M1 junction is off at reverse bias. Fundamentally, the potential barrier is still due to the semiconductor nature with the wide bandgap in the right part of heterojunction.

In order to explore the effect of channel length on transport property, as shown in Fig. 8(a), we chose CCA and H-CCA ribbon to construct lateral heterojunction devices. The central scattering region (except for electrode extension) which contains one unit cell of metallic CCA and one unit cell of semiconducting H-CCA is named M1S1. After the CCA increases to two unit cells, the structure is named as M2S1. When the H-CCA extends to two unit cells, three unit cells, and four unit cells, the structures are named as M1S2, M1S3 and M1S4, respectively. The I-V curve of five Schottky contact structures are presented in Fig. 8(b). When the applied positive bias exceeds 0.35 V, for each Schottky junction, the current increases rapidly with increasing the positive bias. This is consistent with the forward cut-off bias of 0.35 V calculated in the previous section. For M2S1, the length of the CCA ribbon in scattering region is twice that of the H-CCA ribbon, and the I-V curve nearly overlaps with that of M1S1. By expanding the length of H-CCA ribbon in scattering region, the currents of the lateral heterostructure decrease accordingly. The reason can be given as follows. The transmission spectrum near the Fermi level at zero bias can evaluate the current of junctions under low bias. From Fig. 8(d), the M1S2, M1S3 and M1S4 transmission coefficient near the Fermi level is smaller, which induces the decrease of current. Interesting, although the current value decreases under both positive and negative bias, the rectification ratio [Fig. 8(c)] can be significantly increased. In Fig. 8(c), we can see that the junctions of expanding H-CCA ribbon have larger rectification ratio under the same bias.

Furthermore, the longer the extended length, the greater the rectification ratio Fan . The rectification ratios of M1S2, M1S3 and M1S4 junctions possess largest values at 0.35 V, and the largest value of M1S4 junction arrives to the magnitude of 10⁵. Discussed above demonstrate increasing the semiconductor length of Schottky junctions based on CCA and H-CCA ribbon will block the transmission of electrons at the interface and reduce of the transmission coefficients. This is the reason why the current will decrease, but current value is also have an extreme, which will not always decrease, and this can be clearly seen from the I-V curve. But expanding the metal length of Schottky junctions causes transport property almost unchanged.