High Recovery with Fewer Injections: Practical Binary Volumetric Injection Attacks against Dynamic Searchable Encryption
Abstract
Searchable symmetric encryption enables private queries over an encrypted database, but it also yields information leakages. Adversaries can exploit these leakages to launch injection attacks (Zhang et al., USENIX’16) to recover the underlying keywords from queries. The performance of the existing injection attacks is strongly dependent on the amount of leaked information or injection. In this work, we propose two new injection attacks, namely BVA and BVMA, by leveraging a binary volumetric approach. We enable adversaries to inject fewer files than the existing volumetric attacks by using the known keywords and reveal the queries by observing the volume of the query results. Our attacks can thwart well-studied defenses (e.g., threshold countermeasure, static padding) without exploiting the distribution of target queries and client databases. We evaluate the proposed attacks empirically in real-world datasets with practical queries. The results show that our attacks can obtain a high recovery rate () in the best case and a roughly recovery even under a large-scale dataset with a small number of injections ( files).
1 Introduction
| Attack | Leakage | Type | Injection volume | Round2 | ||
| Passive | Injection | Length | Size | |||
| IKK [25] | ap | ✓ | – | – | – | |
| Count [7] | ap,rlp | ✓ | – | – | – | |
| SelVolAn, Subgraph [3] | ap,vp | ✓ | – | – | – | |
| LEAP [35] | ap | ✓ | – | – | – | |
| SAP [36] | sp,rlp | ✓ | – | – | – | |
| ZKP [52] | aip | ✓ | 1 | |||
| Multiple-round1 [39] | rlp | ✓ | ||||
| Single-round [39] | rlp | ✓ | 1 | |||
| Decoding [3] | rsp | ✓ | 1 | |||
| Search1 [3] | rsp | ✓ | ||||
| BVA | rsp | ✓ | 1 | |||
| BVMA | vp, sp3 | ✓ | 1 | |||
-
1
Unlike those schemes easily restoring multiple queries, search [3] and multiple-round [39] attacks can only recover a keyword at a time by running many attack rounds. This means that the client should make many queries, and the queries must include the target query at each attack round. The multiple-round is a strategy that depends on query replay, requiring the adversary to evoke the same query repeatedly by controlling the client. These two attacks commit more rounds and injected files (than others in the table) to recover multiple queries.
-
2
We here say that an attack round consists of (1) an active and complete injection and then (2) an observation within a specific period. We will present a formal definition in Appendix C.
-
3
BVMA mainly investigates the vp to recover the queries. Thus, the sp is an optional and non-essential leakage for the attack (see Appendix E).
Song et al. [43] proposed the notion of searchable symmetric encryption (SSE) that enables secure search over an encrypted database. Following the notion, researchers have presented various SSE schemes to balance practicability and security [9, 6, 21, 46, 27, 37]. In a standard SSE scheme, a search query is a series of interactions between a client and a server. The server can perform matching operations for the query, such as paring a search token given by the client with ciphertexts, and return the query results. Unfortunately, the statistics on the responses leak some patterns of the encrypted database. These patterns seem natural and harmless to data privacy, as they do not directly reveal the files’ contents. Adversaries can still exploit them to recover the client’s query. Leakage abuse attacks (LAA) [33, 26, 25, 7, 40, 36, 35, 31], a classic type of passive attacks on SSE, enable adversaries to observe the leakage patterns for a continuous query period and then combine prior knowledge to recover the target queries. The recovery rate significantly relies on the “sufficiently large" amount of prior knowledge [25, 36], which restricts LAA in practical use.
Unlike passive attacks, injection attacks [7, 52, 39, 3] enable adversaries to actively inject files into the encrypted database. An adversary can generate a certain number of injected files containing known keywords for the client who packs these encrypted files and sends them to the server. It can then recover the keywords with a high probability by observing the leakage patterns of the target queries. Surprisingly, many real-world applications are unable to prevent file injection [39].
Cash et al. [7] introduced a seminal active attack against property-preserving encryption [1, 4], allowing the adversary to “implant" files into the client’s database and then reconstruct partial plaintexts. Following a similar philosophy, Zhang et al. [52] proposed a concrete file injection attack (ZKP) to SSE. ZKP enables the adversary to generate and inject files by using known keywords, such that each keyword is in a unique subset of the files. After the client makes queries, the adversary must identify the exact set of the returned injected files and further reveal the queries. The adversary must also know the access injection pattern, i.e., the set of injected files matching the queries.
The SSE schemes protecting the access (injection) pattern, such as those built on ORAM [19, 15], can successfully resist ZKP [52] and other access pattern based attacks [25, 7, 35]. However, they still leak the volume pattern (vp) from the search results. We say that the vp includes (1) the number of response files, referred to as the response length pattern (rlp), and (2) the word count of returned files, referred to as the response size pattern (rsp). In this work, we will exploit these patterns in volumetric injection attacks (VIAs)111Note recent VIAs naturally leverage either the rlp or rsp..
Poddar et al. [39] proposed injection-based multiple-round and single-round attacks by only exploiting the rlp. In each round of the multiple-round attack, the adversary divides the candidate keywords into partitions and generates the same number of empty files. For a keyword in the th partition, the adversary adds the keyword to files as injection. If there are more response files to the target query than before (i.e., a previous round), the adversary can narrow the search space of the candidate keyword to the th partition. The adversary must run rounds of injections and observations to recover a query, given known keywords. The attack works properly as long as the adversary can make the client constantly repeat the same query. This restriction works in some scenarios, e.g., websites using HTTP/1.1 RFC [16]. The single-round attack selects a specific and enables the adversary to inject files for known keywords in which a keyword is in files. When observing a query with the response of files, the adversary will recover the query as . The should be much larger than the number of the client’s files containing so that is equal to and the adversary can correctly recover the query. Compared to the multiple-round technique, this attack reduces the number of interactive rounds and recovers multiple queries. But its injection amount is still large.
Blackstone et al. [3] leveraged the rsp to propose a decoding attack and a search attack for multi-query and one query recovery, respectively. For each keyword , the attack generates and injects a file with a size of . Given a query, if the difference of its response sizes before and after injection exceeds (i.e., observing more after injection), the adversary can infer that the underlying keyword is . A drawback of this attack is that the adversary consumes a considerable amount of resources in calculating offset and injections (which are linear w.r.t. the number of keywords) to perform well in query recovery. The attack, recovering one keyword at a time, uses a binary search method. The adversary can inject a file containing half of the candidate keywords at an attack round. It can determine if the injected file is associated with the target query by a follow-up observation. Using this inject-and-observe approach in the following rounds, the adversary can filter the candidate keywords by half until there is only one keyword left. The attack can only recover a single keyword via massive file injections and attack rounds.
Existing VIAs are limited by round complexity and injection amount. An interesting question thus arises:
Could we propose practical injection attacks that provide a high recovery rate with fewer injections and further circumvent popular defenses?
Our contributions.
We present an affirmative answer to the above question by proposing two new injection attacks for dynamic SSE schemes and particular defense mechanisms (e.g., ORAM and static padding).
Our attacks leverage the dynamic coding injection approach with fewer injections than prior works.
We show the comparison among the attacks in Table 1.
The main contributions are summarized as follows.
Practical binary volumetric attacks. We propose two practical injection attacks (see Section 3) that provide comparable performances to prior attacks, e.g., [3, 39].
First, we present the binary variable-parameter attack (BVA) by exploiting the rsp.
We use a dynamic injection parameter to balance a trade-off between injection size and recovery rate.
Second, we develop the binary volumetric matching attack (BVMA), which is the first injection attack combining the (small) leakage of the rlp and rsp.
For any queries, the BVMA can filter incorrect keywords, with a small amount of injection, by observing the difference in the response volume before and after injection.
We may leverage other leakage information(e.g., query frequency) to refine the recovery.
We also present a generic method that can transform current VIAs ([3, 39] and ours) to counter the threshold countermeasure (TC)222Note TC enables SSE schemes to constrain each (encrypted) file’s word-count to a small threshold in order to defend against injection attacks. [52].
Comprehensive evaluations. We compare our attacks with BKM [3], PWLP [39], and ZKP [52] in three real-world datasets (see Section 4).
We generate queries by obtaining keyword trends from Google trend [22] and the Pageviews tool [34].
Experimental results show that our attacks can provide a comparable level of recovery rate (e.g., on average in Enron and Lucene) as the single-round (with ) and decoding attacks while requiring fewer injections (e.g., saving of injection costs given the keyword universe).
Our attacks can also practically apply to a large-scale dataset such as Wikipedia, with around recovery.
We evaluate our attacks against defenses (e.g., TC, padding) and client’s active update. Under TC, our attacks require relatively “lightweight" injections (e.g., files injected by the BVMA in Enron and Lucene). In contrast, the single-round and decoding attacks require a serious number of injections to work properly, with injection sizes respectively over and the cost of the BVMA (particularly in Wikipedia). The static padding cannot effectively resist our attacks ( recovery rate on average against SEAL [15]), while the dynamic padding (ShieldDB [47]) requires an expensive overhead ( query overhead more than no padding) to restrict our attacks’ performance. We show that an optimization of our attacks can yield a high recovery rate against ShieldDB. For example, our attacks maintain recovery by injecting around files in Enron, under ShieldDB. We also demonstrate that our attacks perform well under the client’s active updates. We also demonstrate that our modified attacks from BVA perform well under client’s active updates. Even if the client commits updates with respect to the dataset, our modified attack can achieve recovery rate by increasing the injection size (e.g., ) while maintaining injection length.
2 Model Definitions
A dynamic SSE scheme (see Appendix B) should not directly leak any other information to adversaries except those that can be inferred from setup leakage , query leakage , and update leakage , throughout interactions between the client and the server. It captures the adaptive security if adversaries can choose the target queries and the corresponding operations adaptively [11].
2.1 Leakage Model
The operations of a dynamic SSE scheme naturally yield multiple leakage patterns.
We denote an adaptive semantic secure SSE scheme as , in which is the encrypted database, is the set of files matching the queries , is the set of updates containing and , and represents the state of the client after the update from .
We define two types of patterns:
the is the function family where such that for a sequence of queries , it outputs the response file identifiers .
the is similar to the , except that we need to recognize the injected file identifiers such that , where represents the injected file identifiers for the queries.
We note that most of LAA schemes [25, 7, 35] rely on the access pattern; while ZKP [52] exploits the access injection pattern for injection attack.
We also formally define the search and volume patterns used in our attacks.
the is the function family that where for a sequence of queries , it outputs a binary matrix such that if and otherwise, .
the is the function family that where, for a sequence of queries , it outputs the number of the response files .
the is the function family that
where, for a sequence of queries , it outputs the size of the response files .
2.2 Attack Model
To capture a general injection attack model, we enable the adversary to actively generate and inject files.
We regard the adversary as an honest-but-curious server who follows the protocols but can still inject files to the client database333Or one may regard the adversary as an active observer who can generate injected files for the client and observe the query response..
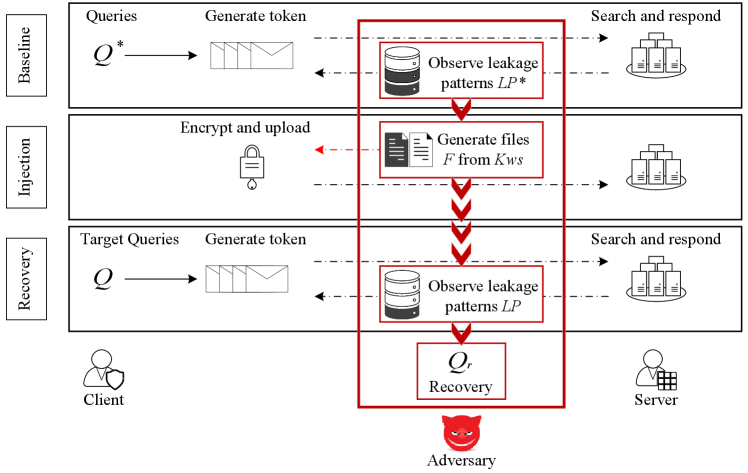
We divide the whole attack process into three stages (see Figure 1).
(1) In the baseline phase, the adversary observes the client’s query leakage as pre-knowledge (provided the client sends queries to the server).
This step is of importance for injection attacks (except for ZKP [52] and single-round attack [39]).
This is because the adversary should obtain the correlation between the keywords and response files from the baseline’s observations.
The idea is to compare the volume difference between the response results before (baseline) and after injection for query recovery.
(2) In the injection, the adversary should carefully generate files by using its known keywords and the information obtained from the baseline.
Next, the client encrypts the files and uploads them to the server.
(3) During the recovery phase, the adversary obtains the target queries’ leakages and recovers them by combining all the known information, namely , , , and .
We let denote the target query set observed by the adversary and denote the query recovery results. We refer to the recovery rate as . We denote the number of injected files as and the word count of the injected files as , where is the set of injected files. The goal of injection attacks is to obtain a high Rer and make ILen and ISize as “small” as possible by only exploiting the known keyword universe and pre-injection leakage.
3 Practical Volumetric Injection Attacks
Given the keyword universe , VIAs can recover the client’s queries on the encrypted database by observing the vp from the response results. A well-design and practical injection attack should limit the number and size of injected files. Our first attack, BVA, uses a dynamic parameter to flexibly set the size of files to adjust the recovery rate. With a slight loss of recovery rate, it can significantly reduce the size of injection. Unlike the decoding attack, it does not need to calculate fully and accurately, reducing the computational cost. To further optimize the injection size and boost the recovery rate in the worst-case scenario (i.e., ), we propose the second attack called BVMA by both the volume and search pattern. By carefully controlling the size of each injected file, the BVMA can ensure that each known keyword has a distinct injection volume. For any query, it can reveal the underlying keyword according to the difference of the response results before and after injection. We also provide a generic conversion that enables VIAs (e.g., [3, 39] and our attacks) to counter the TC.
3.1 Binary Variable-Parameter Attack
The BVA (see Algorithm 1) works as follows. In the baseline phase, the adversary observes and records the response sizes of unknown queries. During the injection phase, it generates and injects files according to the injection parameter in a way. In the last phase, the adversary observes an additional sequence of the client’s queries as the attack targets with response size . It aims to recover all the queries in .
The adversary observes the response size for a sequence of queries (line 1).
The adversary identifies the keyword universe with the set and indicates the injected files with set . First, the adversary adaptively selects the injection parameter satisfying and to ensure each file can accommodate half of the keywords (line 1). Second, each file has a size of and contains keywords whose th bit is equal to so that when is queried, the total response size of injected files is (lines 1-1).
Note an example (see Figure 12, Appendix D) shows the differences between the decoding attack and ours in terms of injection length and size.
The adversary observes again for the target queries . For a query whose response size is , it traverses (obtained from the phase) to get a , satisfying the condition: The adversary then recovers the query with (lines 1-1).
Let be the probability distribution over the keyword universe and be the probability that the client will query the keyword . We use to represent the response size of observed in the phase. We formalize the probability of incorrect recovery as follows.
Claim 1. For any query and , the probability that () outputs an incorrect is
Proof. Consider the client made a query with probability , and its response size was observed in the baseline. In the recovery phase, the adversary observed that the target query ’s response size is after injection. We then have three cases. (1) . The response size (after injection) must be (before injection). In this case, the adversary will not guess any keywords. (2) but . The adversary will not output any guess according to the recovery algorithm. (3) and . The adversary will guess an incorrect so that if ; otherwise, it will reveal the correct keyword.
We see that only the third case can cause an incorrect recovery, which implies that the recovery rate depends on the selection of . A well-selected can greatly reduce the occurrence of the third case and make the adversary achieve the same recovery rate as the decoding attack. Even in the worst case (i.e., ), the recovery rate can still maintain in Enron and Lucene. We further state that the binary injection approach can restrict the injection length to , which outperforms prior schemes [3, 39]. Note more details will be given in the experiments (see Section 4).
Claim 2. For the keyword universe and the injection parameter , the total injection size incurred by () is .
Proof. Through the binary injection, the BVA requires files in total, and the size of each file is for . Therefore, the total injection size during this phase is .
The attack can recover multiple queries with a high recovery rate (e.g., averagely in Enron) and a small injection volume by leveraging the rsp, even the file contents and co-occurrences of keywords are hidden. It does not require any knowledge of query and file distribution. The BVA is a more practical VIA compared to prior attacks.
3.2 Binary Volumetric Matching Attack
Unlike the decoding attack relying on offset, the BVA adjusts a proper for different datasets. This could affect the recovery rate and injection size. For example, setting a small can decrease the injection size (compared with decoding) but could fail to distinguish some queries. To refine the attack performance, we introduce the BVMA, which is fully independent of any offset or . The BVMA is the first injection attack that the response length and size patterns (as well as the sp). The combination can filter known candidate keywords precisely with less injection size, so that it enhances the recovery rate. See the BVMA in Algorithm 2.
This is similar to the BVA-Baseline; but we get queries’ response length , response size , and frequency from the sp after a period of observation (line 2).
We inject files in a binary manner. Different from the BVA (where the size of injected files relies on the ), we set the size of file with for containing the keywords whose th bit is 1 (lines 2-2). For the keyword , we then record its injection length as and injection size as equal to . Each keyword has a unique pair of injection size and length and thus we can distinguish different keywords with a relatively high probability.
We combine the leakage pattern , , to filter candidate keywords. For a target query , we generate a candidate set by adding all to it for (line 2). In the beginning, we exploit the rsp to remove from such that the pair does not satisfy (lines 2-2). This condition means that and are not the original response size and underlying keyword of , respectively. In the second filtering stage, we exclude those candidate keywords that dissatisfy for by exploiting the rlp (lines 2-2). If the condition does not hold, we confirm that the and are not the response length of before injection and the correct recovery keyword, respectively. We then remove the pair from the candidate set. Finally, we can use the sp to identify the closest frequency of the queries between the and phases from the remaining candidate keywords of (line 2). We note that the sp moderately improves the recovery rate. Even without using it, the BVMA can still achieve about 80% recovery, e.g., in Enron (see Appendix E).
Claim 3. For any target query , the probability that () outputs an incorrect is
Proof. Assume that the adversary observed the response size and length of a query with probability during the baseline. In the recovery phase, the adversary observed the target query , whose response length is and response size is (after injection). If it determines as the underlying keyword, that means the difference of the rsp before () and after () injection is equal to the total injection size () and the difference on rlp before and after injection is the injection length (). The adversary chooses as an incorrect recovery only when the above two conditions (for response length and size) and are satisfied. The probability is no more than as we can use other leakages (e.g., the frequency exploited by using the sp) to further eliminate those incorrect keywords.
We also provide a claim and its proof for the injection size.
Claim 4. For the keyword universe , the total size output by the () is .
Proof. Similar to the BVA, the attack requires files but with size of for . Thus, the total injection size is .
We see that the BVMA inherits the advantages of the BVA (except the usage of ) and further provides an improvement on injection size, for example, the BVMA outperforms the best case’s BVA (i.e., when , see Figure 5).
3.3 Attacks against Threshold Countermeasure
Threshold countermeasure (TC) [52] can prevent large-size files (e.g., #word > the threshold ) from being injected into the database. The could be set relatively small in practice to counter injection attacks, without seriously affecting the functionality of dynamic SSE. For example, only of the files in Enron () contain more than 500 words. If employing TC with , we could skip these of files from indexing. Under this setting, a dynamic SSE can effectively resist prior attacks (e.g., [3, 39] and ours). This is because each injected file must contain a considerably large number of words (e.g., words), in particular, the single-round [39] and decoding [3] attacks force an injected file to contain and words.
We design a generic transformation method to “protect” VIAs from TC (see Algorithm 3). The transformation takes the threshold and the set of large files as input and runs the cutting and refilling, where is the output of a concrete VIA algorithm, e.g., BVA. In Algorithm 3, we cut large files (with #word>) into smaller ones to satisfy the threshold of TC. To eliminate the impact of file cutting on recovery rate, we keep the injection length or size of each keyword consistent before and after Algorithm 3. For example, in the single-round attack [39], for any keyword , we keep its injection length unchanged (after cutting) in order to avoid bring any impact to the recovery phase. In the decoding [3] and our attacks, we keep keywords’ injection size consistent (by refilling).
During the cutting phase (lines 3-3), for each , we extract all keywords from . We then generate files for by following 1) the size (word count) of each file is ; and 2) each file contains up to distinct (non-overlapped) keywords from so that each keyword ’s injection length is 1 (note the number remains the same before and after cutting). We finally have sets of small-size files to bypass TC while maintaining the consistency of the keywords’ injection length.
In the refilling phase (lines 3-3), for each file , we generate two file sets and . is constructed by refilling files, in which each file is with size of and it contains all the keywords in . Next, we generate as few files as possible (for ) to accommodate all the keywords in , with each file having a size of . We ensure that the injection size of keywords in is still after the refilling.
Claim 5. For a large-size file set output by ) and a threshold , the injection size of each keyword output by the algorithm is the same as that of ), where ) is the injection phase of a VIA (e.g., [39, 3], BVA, BVMA).
Proof. During the phase, for a file from the set , we produce multiple small files containing different keywords with size , so the injection size of each keyword is . In the phase, we generate files, in which each file is with size and contains all the keywords in a small file . For each keyword , we generate another file with size of to include the keyword. After the above steps, the injection size of each keyword is , which is the same as the amount before the transformation.
We say that the injection length strongly relies on the word count of each file and the number of files in . Our attacks, requiring fewer injected files than others, can naturally provide a practical performance against TC. This is proved by the experiments (see Figure 7). For example, in Enron with , setting , for the BVA, and for the single-round attack, we see that the lower bounds of the injected files for our attacks are approximately and which are at least less than that of the single-round () and decoding () attacks.
4 Evaluation
We compared our attacks with the multiple-round and single-round attacks [39], the search and decoding attacks [3], and ZKP [52], under various metrics in the real-world datasets. We also evaluated our attacks against well-studied defenses (e.g., TC, padding) and client’s active update. We used Python 3.5 to implement the experiments and run the codes in Ubuntu 16.04 of 64-bit mode with 16 cores of an Intel(R) Xeon(R) Gold 5120 CPU(2.20GHz) and 64 GB RAM. The codes for the BVA and BVMA are publicly available in https://github.com/Kskfte/BVA-BVMA.
4.1 Experimental Setup
Datasets. We used three real-world datasets with different scales. The first one is the Enron email corpus [50] between 2000-2002, which contains 30,109 emails. The second one is the Lucene mailing list between 2001-2020, with about 113,201 emails from Apache Foundation [17]. The last dataset is from Wikipedia [18]. We extracted the contents of Wikipedia (in 2020) into a subset with 6,154,345 files by using an extraction algorithm in [42]. We also applied Python’s NLTK corpus [45] to obtain a list of all English words without stopwords and then selected the most frequent words to build the keywords set. We set the total extracted keyword universe for Enron, Lucene, and Wikipedia as 3,000, 5,000, and 100,000, respectively.
| Enron | Lucene | Wikipedia | |
| #Keyword | 3,000 | 5,000 | 100,000 |
| #File | 30,109 | 113,201 | 6,154,345 |
| QI | GTrend [22] | GTrend | Pageview [34] |
| Coverage | 260 weeks | 260 weeks | 75 months |
We used Google Trends [22] of 260 weeks trends between October 2016 and October 2021 to simulate the real query trends for Enron and Lucene. We applied the Pageviews, Toolforge [34] containing 75 months of page views from July 2015 to September 2021 to generate monthly query trends for Wikipedia. We assumed that the client performs 1,000 queries weekly for Enron (Lucene) and 5,000 queries monthly for Wikipedia. We regarded the queries generated by the client (within ten weeks/months) as the target in the recovery phase. We put the dataset information in Table 2, in which QI represents the source of query trends, and “coverage" is the time interval of QI.
In the experiments, we made 30 runs for each test and further output the average result. We measured the query recovery rate for the compared attacks, in which the rate represents how much percentage of the client’s queries the attacks could recover correctly.
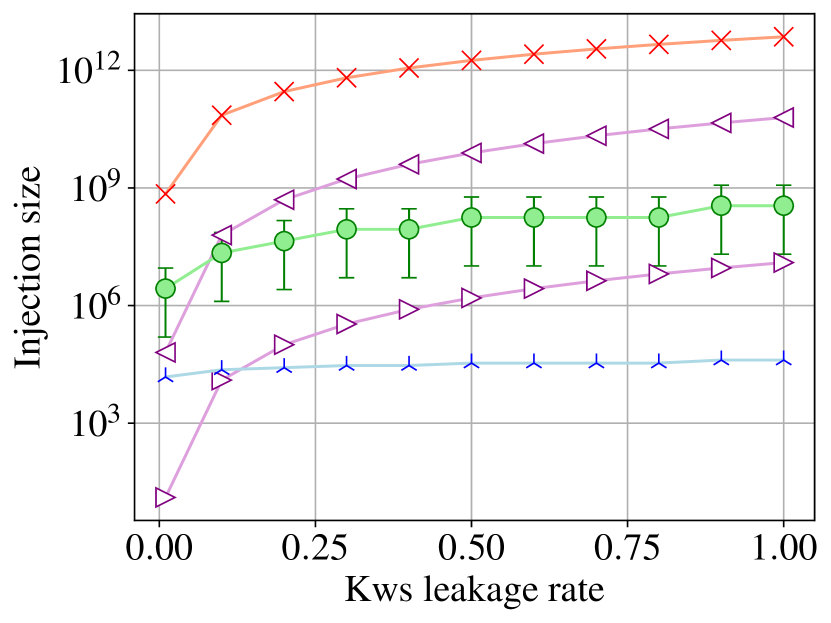
Keyword leakages. We used keywords (Kws) leakage percentage to measure the prior knowledge of the adversary. We say that the keyword universe could be easily and partially obtained for several reasons: (1) a tiny amount of files could contain a large number of keywords; (2) a public database known by the adversary, which shares similar distribution with the target database, could contain partial target keywords [12]; (3) some expired or spam emails could leak keywords. To test our statements, we present the number of known keywords with file leakage in Figure 2. We assume that Enron is the client database and Lucene (rather than Wikipedia) is the public database known by the adversary. We state that Enron and Lucene are both email datasets and thus, they have similar keyword distributions; and also, they share similar keyword universes. In Enron, leakage files can lead to the exposure of half of the keyword universe; while obtaining of the leakage files, the adversary can reveal the entire universe. Given Lucene as the similar database, the adversary easily reveals keywords from Enron.
Observation periods. Different datasets could require different observation periods. For Enron and Lucene, which contain several thousand keywords, we only used a few weeks to observe queries to obtain the statistical information of most keywords. We spent more time (dozens of months) on Wikipedia than others to collect sufficient leakage information. To help the reader to understand the relationship between the occurrence of new queries and observation period, we show some examples in Figure 3. We observed 1,000 queries per week for Enron and Lucene, and 5,000 per month for Wikipedia. The number of new queries in Figure 3 decreases dramatically with the extension of observation period under different datasets and query distributions. In particular, there are new queries per week for Enron (resp. Lucene) after the observation lasts (resp. 16) weeks. We say that 8 (resp. 16) weeks are sufficient for the adversary to observe queries leakage from these datasets. Even for Wikipedia, a 32-month observation is practical to obtain statistics information. Note we also see that the occurrence probability of new queries performs similarly under different query distributions (i.e., real-world and uniform). We set the observation period to 8 weeks, 16 weeks and 32 months respectively for Enron, Lucene and Wikipedia. We further randomly selected the start period for the observation from the coverage given in Table 2.







4.2 Comparison with Other Attacks
We compared our attacks with prior injection attacks in three real-world datasets. Note we do not consider padding strategies in this section but will test the attacks against them later. We tested the performance of the BVA and decoding attack under different parameters since they exploit the rsp with similar recovery approaches. We also performed empirically evaluations on the BVA, the BVMA and other attacks. Note that we did not put ZKP into further comparisons (except in Figure 7 against TC). The crucial difference between our attacks and ZKP is on the leakage pattern. Our attacks exploit the vp while ZKP focuses on the aip. There are both pros and cons for the attacking strategies. For example, our attacks could bypass ORAM (around against both static padding and ORAM on average, see Figure 8), while ZKP cannot; but ZKP requires less injection size than ours (see Figure 7).
Injection Parameter for BVA and Decoding. Recall that the BVA uses to flexibly control the injection volume. We evaluated the recovery rate and injection size while varies from to the offset (see Figure 4). Like the setting in the decoding attack[3], we assume that all queried keywords fall in the adversary’s known keyword universe. As the increases, the recovery rate of the BVA abruptly rises to the maximum (providing the same recovery as the decoding attack) and meanwhile, the injection size performs steady. One can observe that even in the worst case, where , the BVA can still achieve practical recovery rates ( in Enron and Lucene, in the large-scale Wikipedia). It shows decline on average in Enron and Lucene (note in Wikipedia) at the recovery in this case, as compared to the decoding attack. But its injection size is approximately five orders of magnitude less than that of the decoding attack. We also see that setting can sufficiently ensure the BVA to achieve the similar recovery rate ( gap) as the decoding attack. A further increase on could not produce significant improvement on the recovery rate. Based on the results, we confirm that a small but reasonable (e.g., ) can guarantee a practical recovery rate () with a relatively small injection size (around in Enron and Lucene, in Wikipedia) as compared to the decoding attack ( in Enron and Lucene, in Wikipedia).
Overall Comparison with Decoding and Single-round. We compared our attacks with the single-round [39] and decoding [3] attacks. We tested the recovery rate , the injection length , and the injection size under different keyword leakage ratios in the fixed observation period. We evaluated the BVA with error bars by varying . We used a constant to control the recovery rate and simulated two particular cases where and in the single-round attack. We put the running time in Table 3 and the recovery rate in Figure 5 (and Table 6-7, Figure 14-15 in Appendix G).
Table 3 shows the time cost of restoring queries (provided that the adversary knows the keyword universe). Most of the attacks take , while the BVMA is slower than others (about ). This is because it merges multiple leakages for keyword filtering, which naturally increases the time complexity.
| Decoding | Single-round | Single-round | BVA | BVMA | |
| Running time | 2.48 | 0.01 | 0.02 | (1.81, 2.46) | 19.16 |
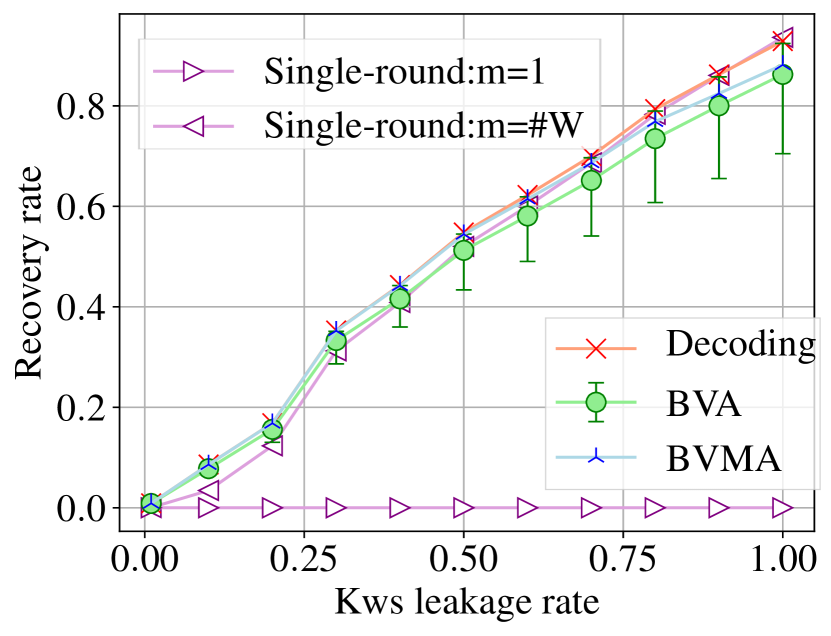


Figure 5 illustrates that as the number of leaked keywords increases, , and present an upward trend. More concretely, delivers a quasi-linear growth, while the incline of and gradually flattens. From the recovery rate, we see that the single-round attack with can only restore queries, which performs the worst. The BVA and BVMA share a small gap (e.g., on average in Enron and Lucene) with the decoding and the single-round () attacks. We also notice that the BVMA surpasses the minimum recovery rate of the BVA (see the error bar in Figure 5(a)) by almost when the keyword leakage reaches . This is reasonable as the BVMA combines different leakage patterns (e.g., rlp and rsp) to filter candidate keywords, which can bring advantage on recovery rate.
The results of (see Figure 5(b)) show that both BVA and BVMA (only injecting files) require much fewer injections (at least ) than the decoding attack. The single-round attack with takes the same injection length as the decoding attack but with a poor recovery rate (see Figure 5(a)). We note one may set to produce a practical recovery in the single-round attack. But this requires a massive amount of (> ) injected files.
As for the metric , the decoding attack gives the worst performance. This is because the attack strongly relies on offset. Table 4 illustrates that offset grows abruptly with the expansion of keyword universe. When , each injected file must contain words (where ), which is extremely impractical in reality. Similarly, the performance of the single-round attack is restricted by . To achieve a recovery, the attack (with ) requires a relatively large injection size, around in Enron.
| 30 | 300 | 1,000 | 3,000 | 100,000 | |
| offset | 157 | 6,615 | 48,447 | 207,015 |
Fortunately, the BVA and BVMA are independent of the offset (and ) and require fewer injections. For example, in Enron (resp. Lucene) with 3,000 (resp. 5,000) keywords (see Figure 5, 14), they achieve recovery rate on average by only taking nearly and injection size, respectively. The costs are multiple orders of magnitude less than those of the decoding attack () and single-round attack with (). In Wikipedia (see Figure 15) including 100,000 keywords, the injections of the BVA and BVMA are only and with approx. recovery rate. To maintain the same level of recovery, the single-round and decoding attacks must take respectively and costs.
We conclude that our attacks can provide: 1) practical recovery rate, and 2) much fewer injections (length and size) than other attacks. Our attacks (the BVA in particular) can be also applicable to the large-scale dataset (see Appendix G).
Comparison for Single Query. The multiple-round [39] and search attacks [3] only recover one query at a time. In Figure 6, we show how the average injection size (per query) varies with the increasing number of target queries. We ignored the recovery rate in the experiments, because the recovery performances of the BVA and BVMA with a single query is similar to those given in Figure 5(a) (and Figure 14(a), 15(a) in Appendix G). We note the multiple-round and search attacks can provide recovery rate by taking sufficiently large (e.g., ) injection volumes and attack rounds.
With the increase in the target queries, the multiple-round and search attacks give constant straight lines on injection size, while our attacks provide a sharp decline. The cause of the drop is that we can reuse injections on the previous queries to recover the following queries. At the beginning, when no. of queries is 10, the cost of the BVMA (e.g., slightly ) is close to that of the multiple-round and search attacks. After queries, the BVMA outperforms others. In Enron and Lucene, the BVA yields the similar results as the multiple-round and search attacks, around , when no. of queries is up to . But its cost is roughly larger than that of the BVMA. Our attacks do show a noticeable advantage on injection size with the increase of query number.
Comparison against TC. To circumvent TC, we proposed a transformation Algorithm 3 (see Section 3.3). We note there is also a variant for the ZKP [52] that can counter TC. We evaluated the number of injected files caused by the Algorithm 3 and the ZKP variant with different thresholds (see Figure 7). We limited to be no more than the total number of keywords (i.e., ) in the experiments, because 1) when reaches to , the number of injected files approaches to stable, in particular, for the ZKP and BVMA; and 2) the word count of a file (in a real-world dataset) is normally less than the total number of keywords. For example, in Enron, the file with the largest size contains roughly words, which is smaller than the size of ( keywords).






In Figure 7, increasing leads to the decline of the injection length. The ZKP variant requires the least number of injection. This is because it uses a unique approach (instead of just the volume information) to recognize the injected files. In contrast, other attacks leverage injections to increase the differences in the volume of each keyword. There is a small gap on injection between the BVMA and the ZKP variant. The injection amount of the former drops fast and ultimately approaches to that of the latter. Given a small and reasonable (e.g.,), the injection length of the BVMA is around in Enron and Lucene, which is still practical. Under a large threshold (e.g., ), the single-round and decoding attacks take > injected files in Enron and Lucene which are at least and larger than our costs, respectively. In Wikipedia (under ), they require at least and more injections than ours.
Our attacks (especially the BVMA) outperform most of existing VIAs against TC in terms of injection length. The BVMA and the ZKP variant deliver similar results under a proper (e.g., injected files in Enron with ). The former is more applicable than the latter if the adversary prefers to exploit the vp.
4.3 Attacks against Padding
Padding [47, 5, 7, 51, 15, 10, 38] can protect the volume pattern. One may apply static padding [5, 15, 10, 38] upon establishing a database, while using dynamic padding [47, 51, 2, 53] both in the setup and update stages. Efficient padding strategies use keyword clustering to balance security and padding overhead. Keyword clustering technique assigns keywords into different clusters so that the keywords in a cluster share the same or computationally indistinguishable volume after padding.
We tested our attacks against both the static and dynamic padding strategies in Enron. We used SEAL [15] as the static padding solution. This is because it requires less query bandwidth than [10, 38] and it can mitigate well-known attacks (e.g., [25, 7]). As for the dynamic padding, we chose ShieldDB [47] (which is a more practical encrypted database than [2, 53]) supporting keyword search with a dynamic countermeasure against query recovery attacks. In our experiments, we assumed that each dummy file employed dummy keywords not present in the database, utilizing the padding modules of ShieldDB and SEAL for random file padding to ensure that the file’s size is within as obfuscation, where (resp., ) is the smallest (resp., largest) file size in the original client database. Note when using the ORAM module in SEAL, we assumed that the system uses blocks with the same size for filling (instead of dummy files with random sizes). We tested the padding overhead of SEAL and ShieldDB besides the recovery rate. We defined the padding overhead as , which reflects a ratio between the increased overhead (i.e., number of files) of padding and “no padding". We calculated the storage overhead from setup and injection&fill , and the bandwidth overhead from queries-after-setup - and queries-after- -.
Static Padding by SEAL. SEAL has two core modules. One is the quantized ORAM module [44] hiding the ap and sp, and the other is the parameterized padding module concealing the vp. We assume the response is for a query , where is the encrypted database stored in the form of ORAM blocks. Note each block in ORAM shares the same size (e.g., with keywords). The number of blocks rlp for a query is , and the total response size rsp is . In this case, the rsp and rlp are somewhat “mixed", which indicates that the rlp can be derived from rsp and vice versa, so that the BVMA “degenerates" to the BVA only relying on the rsp. We thus only evaluated the BVA against SEAL (with both padding and ORAM, see Figure 8(b)).
In the ORAM module, for a file , if its size is smaller than the block size (i.e., ), the system will pad the file to size and then store the resulting file in a random block; if , the system will split and store the file in blocks. Due to ORAM, each query will obliviously access to the related blocks. In the padding module, the system can add dummy blocks with the underlying keyword of until the query’s response length is the next power of :
In the experiments, we set as the average size of files in Enron. We selected a minimum satisfying to ensure that each injected file can be exactly divided into blocks. We tested the BVA and BVMA against SEAL with only padding module (see Figure 8(a)) and also investigated the BVA applying both padding and ORAM modules (see Figure 8(b)). Note we tested SEAL’s padding overhead instead of ORAM cost, as it was hard to evaluate the ORAM’s complexity which relies on various factors (e.g., block variables, access method, bucket size). We could regard the overhead as the lower bound of SEAL’s cost. This makes sense as ORAM definitely yields extra and noticeable cost.
In Figure 8(a), the increase of (in the padding module) has little influence over the recovery rate. The recovery remains at about . But the padding cost, especially in the setup and query, increases by and (when is up to 16), which seriously affects the practicability. Figure 8(b) shows that padding and ORAM modules disturb the stability of the BVA’s performance. For example, when , the BVA achieves recovery in the best case and only in the worst case. The negative impact incurred by SEAL on the average recovery rate is still limited. Under various , the BVA can maintain recovery on average. We note that one may keep increasing , but this will make SEAL become less and less practical. The results indicate that the static padding is not the best countermeasure to our attacks.


Extend SEAL to Dynamic Padding. We notice that SEAL describes a possible extension for dynamic updates (e.g., by handling the update operation using [14]); but it is still unknown how we could properly extend SEAL to support dynamic padding. A straightforward idea444Following the SEAL’s padding (as well as settings), the idea supports the strategy during (dynamic) update. could be to fill the total rlp of the corresponding keyword into after every batch update. We designed an extra experiment (see Table 8, Appendix H) to evaluate our attacks against such a dynamic variant. We assume that after a batch injection (by our attacks), the padding module recalculates the rlp of each keyword and then fills it to the proper . The padding can appropriately resist VIAs ( recovery rate) but at the same time produce extreme overheads. More concretely, given (i.e., the minimum padding), as compared to “no padding", the query-after-injection overhead raises by nearly . Meanwhile, the number of extra files for padding expands by . The padding requires approx. extra files against injections and this number is even larger than the total files of the entire database ( files).
Dynamic Padding by ShieldDB. ShieldDB [47] uses the parameter to measure the size (i.e., number of keywords) of each cluster. In the update phase, there are two for upload according to if the keywords (of clusters) have been stored in the server.


-
•
Case 1: The server’s current database has not yet contained any keywords of a cluster. In this case, only after all the existing keywords of the cluster have been (updated and) stored in the local cache, they are filled and uploaded.
-
•
Case 2: All the keywords in the cluster have already been stored in the server’s database. There are two triggers for the uploads: 1) if the interval between the last and the current upload time slots exceeds a specific threshold (i.e. Tthreshold); 2) if the number of keyword-file (i.e. (w, id)) pairs of the cluster stored locally exceeds a concrete size (i.e. Cthreshold).
Once keywords meet the corresponding conditions, the system fills the keywords to the same volume (which is usually the largest volume, called high mode in ShieldDB) and uploads to the server. Concretely, assume the client added files is for a keyword . After padding, the update length of is: For simplicity, we considered two batch paddings in our experiments. The first padding is to cluster the keywords in the setup phase, fill them in each cluster, and upload to the server; while the second is in the injection phase, where we injected specific files containing all the keywords and further used the padding strategy to obfuscate the volume.
The adversary takes the following three steps for query recovery: (1) guess each keyword’s cluster; (2) relate the target queries to the correct clusters; and (3) use attack algorithms (BVA and BVMA) to recover the queries from the clusters.


The adversary can use the observe-inject-observe approach to guess the cluster for . First, one can inject a file containing all keywords and wait for a time period Tthreshold to ensure that the injection file has been uploaded to the server. It ensures that all keywords have been included in the server, and the follow-up uploads (and injections) follow Case 2. Then given the keyword , to guess its cluster, it first observes the volume of all queries, sends a injection file containing only to the user, waits for a time period Tthreshold, and observes the volume again. In this case, only the cluster containing will be uploaded to the server (in which none of the keywords in other clusters is updated). This cluster with the “changed" volume after injection is the one that belongs to. We can see that the above also requires injection length and attack rounds. The adversary can also properly guess the clusters by using extra prior knowledge. Recall that ShieldDB uses a training dataset to cluster keywords in the real database. The training dataset could not be completely confidential. The adversary can leverage other public datasets with similar distributions (i.e., similar data attacks) to determine the cluster. In the second step, the adversary should identify the cluster according to the response length of each query. We present the accuracy of the “identification" under various in Figure 9(a). With the growth of , the number of clusters (i.e., ) gradually decreases, which increases the probability of correctly locating queries to the clusters. For example, we can achieve around accuracy when , and nearly when . At last, we used the BVA and BVMA to recover the queries from the identified clusters.
We tested the query recovery rate and the related overhead under different parameters (see Figure 9(b)). As the increases, ShieldDB is more effective against VIAs but at the same time, it yields more overheads. When , its total overheads incurred by the setup, query, and update phases are still . But it cannot resist our attacks (with nearly recovery rate). Whilst our attacks only achieve around recovery (under ), the costs of the injection approach to about , and the query bandwidth increases by . More concretely, without padding, the server returns of data per query in Enron; after padding by ShieldDB (under ), it responds (averagely) of data (per query), which is extra bandwidth.
A traditional dynamic (encrypted) database usually leaks more information (such as the update pattern [48]) than a static one. Dynamic padding can mitigate the leakage and resist our attacks to some extent by sacrificing the bandwidth overheads (e.g., query bandwidth). It is an open problem to design a cost-effective countermeasure to VIAs.
Optimization against ShieldDB.Clustering-based padding pads the keywords in the same cluster to make them indistinguishable. Most current strategies are deterministic, which means that they fill the keywords to a fixed rlp. We can leverage this to develop an optimization on our attacks (see Appendix I). Upon injection, we can use “multi-group" coding injections and keep the keywords in the cluster to have the same rlp so as to circumvent the padding.
In Figure 10, we show the recovery rate and injection length of the optimization against ShieldDB in Enron under different parameters , where is the parameter of ShieldD and is the number of groups of keywords. The now has little influence on the recovery rate, in particular, when , the recovery can still remain . To mitigate the impact of padding, we set the number of keyword groups () to be the same as that of clusters () in ShieldDB. We also see that the injection length increases steadily, from around 20 to 200, and finally up to around 600. Figure 10(a) and 10(b) indicate that by increasing the number of injected files (i.e., enhancing the attack ability), we can still counter the dynamic padding. The results show that “more" injections can definitely lead to a “higher" recovery.
4.4 Injections with Client Active Update
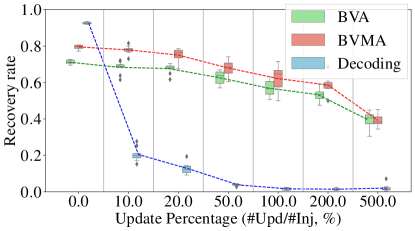
We evaluated our attacks performance under the client’s active updates in Enron. We used half of the files in Enron (about 15k) as the real database and the rest as the auxiliary database for the “add" file operations (which means that each newly added file is from this auxiliary database). We assume that the client can randomly select an operation from for each update. For an operation, the client randomly selects a file from the auxiliary database and further creates the keyword-file indexes; as for a , it deletes a file and the keyword-file pairs randomly from the real database. We present the results in Fig. 11, in which the -axis is the ratio between the number of updates and the number of (adversary) injections, and the -axis is the recovery rate.
The updates are equivalent to “adding noise" in the adversary’s view, which can “blur" the observations. We see that the decoding attack slides into the biggest drop after the client commits update, for example, its recovery rate falls sharply from to ; and after update, the recovery is below . In contrast, as the ratio increases, our recovery rates undergo a downward drift. Our attacks still remain recovery after update. Even in the worst case ( update), our performances still stand at .
We note the experiment did not include the single-round attack. This is because the attack requires an extreme amount of injected files, . More concretely, it could need 9 million injection emails, which is seriously impractical for Enron. We conclude that the client’s updates can easily depress the recovery rate of prior attacks, but they have limited impact on the BVA and BVMA.
For frequent file updates, e.g., file updates (i.e. files in the Enron dataset), when these file updates (covering almost all keywords) happen between baseline phase and recovery phase of VIAs, our attacks without optimisation ( injection length) and decoding attack ( injection length) could easily fail. The single-round attack could survive only if we set its constant to be considerably large (e.g., m the number of updated files). Recall that its injection length is . Setting a large could make the single-round attack more impractical w.r.t. injection cost. In Appendix K, we present a modified algorithm with files to deal with users’ frequent updates.
5 Conclusion
We proposed new attacks against dynamic SSE using a binary volumetric injection strategy. Unlike existing attacks which require a considerable amount of prior knowledge (e.g., LAA [25, 7]) and injections (e.g., [3, 39]), our attacks can offer a high recovery rate with fewer injections and pose a non-trivial threat to current defenses (e.g., padding). We provided empirical evidence to confirm the performance of our attacks.
References
- [1] Rakesh Agrawal, Jerry Kiernan, Ramakrishnan Srikant, and Yirong Xu. Order preserving encryption for numeric data. In Proceedings of the 2004 ACM SIGMOD international conference on Management of data, pages 563–574, 2004.
- [2] Ghous Amjad, Sarvar Patel, Giuseppe Persiano, Kevin Yeo, and Moti Yung. Dynamic volume-hiding encrypted multi-maps with applications to searchable encryption. Cryptology ePrint Archive, 2021.
- [3] Laura Blackstone, Seny Kamara, and Tarik Moataz. Revisiting leakage abuse attacks. In 27th Annual Network and Distributed System Security Symposium, 2020.
- [4] Alexandra Boldyreva, Nathan Chenette, Younho Lee, and Adam O’neill. Order-preserving symmetric encryption. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 224–241. Springer, 2009.
- [5] Raphael Bost and Pierre-Alain Fouque. Thwarting leakage abuse attacks against searchable encryption–a formal approach and applications to database padding. Cryptology ePrint Archive, 2017.
- [6] Raphaël Bost, Brice Minaud, and Olga Ohrimenko. Forward and backward private searchable encryption from constrained cryptographic primitives. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pages 1465–1482, 2017.
- [7] David Cash, Paul Grubbs, Jason Perry, and Thomas Ristenpart. Leakage-abuse attacks against searchable encryption. In Proceedings of the 22nd ACM SIGSAC conference on computer and communications security, pages 668–679, 2015.
- [8] David Cash, Stanislaw Jarecki, Charanjit Jutla, Hugo Krawczyk, Marcel-Cătălin Roşu, and Michael Steiner. Highly-scalable searchable symmetric encryption with support for boolean queries. In Annual cryptology conference, pages 353–373. Springer, 2013.
- [9] David Cash and Stefano Tessaro. The locality of searchable symmetric encryption. In Annual international conference on the theory and applications of cryptographic techniques, pages 351–368. Springer, 2014.
- [10] Guoxing Chen, Ten-Hwang Lai, Michael K Reiter, and Yinqian Zhang. Differentially private access patterns for searchable symmetric encryption. In IEEE INFOCOM 2018-IEEE Conference on Computer Communications, pages 810–818. IEEE, 2018.
- [11] Reza Curtmola, Juan Garay, Seny Kamara, and Rafail Ostrovsky. Searchable symmetric encryption: improved definitions and efficient constructions. In Proceedings of the 13th ACM conference on Computer and communications security, pages 79–88, 2006.
- [12] Marc Damie, Florian Hahn, and Andreas Peter. A highly accurate query-recovery attack against searchable encryption using non-indexed documents. In 30th USENIX Security Symposium, pages 143–160, 2021.
- [13] Emma Dauterman, Eric Feng, Ellen Luo, Raluca Ada Popa, and Ion Stoica. DORY: an encrypted search system with distributed trust. In 14th USENIX Symposium on Operating Systems Design and Implementation, pages 1101–1119, 2020.
- [14] Ioannis Demertzis, Javad Ghareh Chamani, Dimitrios Papadopoulos, and Charalampos Papamanthou. Dynamic searchable encryption with small client storage. In 27th Annual Network and Distributed System Security Symposium, 2020.
- [15] Ioannis Demertzis, Dimitrios Papadopoulos, Charalampos Papamanthou, and Saurabh Shintre. SEAL: attack mitigation for encrypted databases via adjustable leakage. In 29th USENIX Security Symposium, pages 2433–2450, 2020.
- [16] Roy Fielding and Reschke. Hypertext transfer protocol (http/1.1): Message syntax and routing. RFC 7230, 2014.
- [17] Apache Foundation. Mail archieves of lucene, 1999. https://mail-archives.apache.org/mod_mbox/#lucene.
- [18] Wikipedia Foundation. Wikipedia databases, 2020. https://www.wikipedia.org.
- [19] Sanjam Garg, Payman Mohassel, and Charalampos Papamanthou. Tworam: efficient oblivious ram in two rounds with applications to searchable encryption. In Annual International Cryptology Conference, pages 563–592. Springer, 2016.
- [20] Marilyn George, Seny Kamara, and Tarik Moataz. Structured encryption and dynamic leakage suppression. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, pages 370–396. Springer, 2021.
- [21] Javad Ghareh Chamani, Dimitrios Papadopoulos, Charalampos Papamanthou, and Rasool Jalili. New constructions for forward and backward private symmetric searchable encryption. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pages 1038–1055, 2018.
- [22] Google. Google trends, 2004. https://trends.google.com/trends/.
- [23] Peeyush Gupta, Sharad Mehrotra, Shantanu Sharma, Nalini Venkatasubramanian, and Guoxi Wang. Concealer: Sgx-based secure, volume hiding, and verifiable processing of spatial time-series datasets. In Proceedings of the 24th International Conference on Extending Database Technology, pages 277–288, 2021.
- [24] Yanyu Huang, Siyi Lv, Zheli Liu, Xiangfu Song, Jin Li, Yali Yuan, and Changyu Dong. Cetus: an efficient symmetric searchable encryption against file-injection attack with SGX. Sci. China Inf. Sci., 64(8), 2021.
- [25] Mohammad Saiful Islam, Mehmet Kuzu, and Murat Kantarcioglu. Access pattern disclosure on searchable encryption: Ramification, attack and mitigation. In 19th Annual Network and Distributed System Security Symposium, 2012.
- [26] Seny Kamara, Abdelkarim Kati, Tarik Moataz, Thomas Schneider, Amos Treiber, and Michael Yonli. Sok: Cryptanalysis of encrypted search with leaker – a framework for leakage attack evaluation on real-world data. In 2022 IEEE 7th European Symposium on Security and Privacy, pages 90–108, 2022.
- [27] Seny Kamara and Tarik Moataz. Boolean searchable symmetric encryption with worst-case sub-linear complexity. In 36th Annual International Conference on the Theory and Applications of Cryptographic Techniques, volume 10212, pages 94–124, 2017.
- [28] Seny Kamara and Tarik Moataz. Computationally volume-hiding structured encryption. In Advances in Cryptology – EUROCRYPT, pages 183–213, 2019.
- [29] Seny Kamara, Tarik Moataz, and Olga Ohrimenko. Structured encryption and leakage suppression. In 38th Annual International Cryptology Conference, volume 10991, pages 339–370, 2018.
- [30] Seny Kamara, Charalampos Papamanthou, and Tom Roeder. Dynamic searchable symmetric encryption. In Proceedings of the 2012 ACM conference on Computer and communications security, pages 965–976, 2012.
- [31] Evgenios M. Kornaropoulos, Nathaniel Moyer, Charalampos Papamanthou, and Alexandros Psomas. Leakage inversion: Towards quantifying privacy in searchable encryption. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, page 1829–1842, 2022.
- [32] Shangqi Lai, Sikhar Patranabis, Amin Sakzad, Joseph K Liu, Debdeep Mukhopadhyay, Ron Steinfeld, Shi-Feng Sun, Dongxi Liu, and Cong Zuo. Result pattern hiding searchable encryption for conjunctive queries. In Proceedings of the 2018 ACM SIGSAC conference on computer and communications security, pages 745–762, 2018.
- [33] Steven Lambregts, Huanhuan Chen, Jianting Ning, and Kaitai Liang. VAL: volume and access pattern leakage-abuse attack with leaked documents. In 27th European Symposium on Research in Computer Security, volume 13554, pages 653–676, 2022.
- [34] Marcel Ruiz Forns MusikAnimal, Kaldari. Pageviews toolforge, 2015. https://pageviews.toolforge.org/.
- [35] Jianting Ning, Xinyi Huang, Geong Sen Poh, Jiaming Yuan, Yingjiu Li, Jian Weng, and Robert H. Deng. LEAP: leakage-abuse attack on efficiently deployable, efficiently searchable encryption with partially known dataset. In 2021 ACM SIGSAC Conference on Computer and Communications Security, pages 2307–2320. ACM, 2021.
- [36] Simon Oya and Florian Kerschbaum. Hiding the access pattern is not enough: Exploiting search pattern leakage in searchable encryption. In 30th USENIX Security Symposium, pages 127–142, 2021.
- [37] Sarvar Patel, Giuseppe Persiano, and Kevin Yeo. Symmetric searchable encryption with sharing and unsharing. In 23rd European Symposium on Research in Computer Security, volume 11099, pages 207–227, 2018.
- [38] Sarvar Patel, Giuseppe Persiano, Kevin Yeo, and Moti Yung. Mitigating leakage in secure cloud-hosted data structures: Volume-hiding for multi-maps via hashing. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, pages 79–93, 2019.
- [39] Rishabh Poddar, Stephanie Wang, Jianan Lu, and Raluca Ada Popa. Practical volume-based attacks on encrypted databases. In IEEE European Symposium on Security and Privacy, pages 354–369, 2020.
- [40] David Pouliot and Charles V. Wright. The shadow nemesis: Inference attacks on efficiently deployable, efficiently searchable encryption. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pages 1341–1352, 2016.
- [41] Zhiwei Shang, Simon Oya, Andreas Peter, and Florian Kerschbaum. Obfuscated access and search patterns in searchable encryption. In 28th Annual Network and Distributed System Security Symposium, 2021.
- [42] David Shapiro. Convert wikipedia database dumps into plaintext files, 2021. https://github.com/daveshap/PlainTextWikipedia.
- [43] Dawn Xiaoding Song, D. Wagner, and A. Perrig. Practical techniques for searches on encrypted data. In Proceeding 2000 IEEE Symposium on Security and Privacy. S P 2000, pages 44–55, 2000.
- [44] Emil Stefanov, Marten van Dijk, Elaine Shi, Christopher W. Fletcher, Ling Ren, Xiangyao Yu, and Srinivas Devadas. Path ORAM: an extremely simple oblivious RAM protocol. In ACM SIGSAC Conference on Computer and Communications Security, pages 299–310. ACM, 2013.
- [45] Liling Tan Steven Bird. Nltk corpus, 2021. https://www.nltk.org/howto/corpus.html.
- [46] Shifeng Sun, Xingliang Yuan, Joseph K. Liu, Ron Steinfeld, Amin Sakzad, Viet Vo, and Surya Nepal. Practical backward-secure searchable encryption from symmetric puncturable encryption. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pages 763–780, 2018.
- [47] Viet Vo, Xingliang Yuan, Shifeng Sun, Joseph K. Liu, Surya Nepal, and Cong Wang. Shielddb: An encrypted document database with padding countermeasures. IEEE Transactions on Knowledge and Data Engineering, 2021.
- [48] Chenghong Wang, Johes Bater, Kartik Nayak, and Ashwin Machanavajjhala. Dp-sync: Hiding update patterns in secure outsourced databases with differential privacy. In SIGMOD ’21: International Conference on Management of Data, pages 1892–1905, 2021.
- [49] Jianfeng Wang, Shi-Feng Sun, Tianci Li, Saiyu Qi, and Xiaofeng Chen. Practical volume-hiding encrypted multi-maps with optimal overhead and beyond. In ACM SIGSAC Conference on Computer and Communications Security, pages 2825–2839. ACM, 2022.
- [50] CMU William W. Cohen, MLD. Enron email datasets, 2015. https://www.cs.cmu.edu/~./enron/.
- [51] Lei Xu, Anxin Zhou, Huayi Duan, Cong Wang, Qian Wang, and Xiaohua Jia. Toward full accounting for leakage exploitation and mitigation in dynamic encrypted databases. Cryptology ePrint Archive, Paper 2022/894, 2022.
- [52] Yupeng Zhang, Jonathan Katz, and Charalampos Papamanthou. All your queries are belong to us: The power of file-injection attacks on searchable encryption. In 25th USENIX Security Symposium, USENIX Security 16, pages 707–720, 2016.
- [53] Yongjun Zhao, Huaxiong Wang, and Kwok-Yan Lam. Volume-hiding dynamic searchable symmetric encryption with forward and backward privacy. IACR Cryptol. ePrint Arch., page 786, 2021.
Appendix A Summary of Notations and Concepts
We denote as the set of integers . For a set , we use to refer to its cardinality. For a file (or file set ), we use () to represent its word count, also called file . means that is the output of an algorithm . denotes natural number. We use to denote the security parameter. See the frequently used notations in Table 5.
| Notation | Description |
| An encrypted database. | |
| A keyword universe . | |
| A sequence of queries . | |
| The response to each query. | |
| A set of injected files. | |
| Total word count for a file . | |
| Injected files containing a keyword . | |
| offset | Minimum file size for decoding. |
| Basic injection size for BVA. | |
| Keyword partitions for multiple-round. | |
| Injection constant for single-round. | |
| Size threshold of each file. | |
| Leakage pattern. | |
| Response length . | |
| Response size . | |
| Query frequency . | |
| A query recovery set, . | |
| Leakage Pattern | Description |
| access pattern (ap) | identifiers of the files matching a query. |
| access injection pattern (aip) | identifiers of injected files matching a query. |
| search pattern (sp) | whether a query is repeated. |
| response length pattern (rlp) | the number of (response) returned files. |
| response size pattern (rsp) | the total word count of (response) returned files. |
| volume pattern (vp) | include rlp and rsp. |
| Injection Information | Description |
| injection length (ILen) | the number of injected files. |
| injection size (ISize) | the total word count of injected files. |
| injection volume | include ILen and ISize. |
| Attack | Description |
| passive attack | attacks only based on the observations. |
| injection attack | attacks can actively inject files. |
| volumetric injection attacks (VIAs) | injection attack relying on rlp (or rsp). |
| Defense | Description |
| ORAM | oblivious retrieval to hide ap and aip. |
| padding | index dummy files to obfuscate vp. |
| TC | limit file size to avoid large-size file injection. |
Appendix B Searchable Symmetric Encryption
A standard dynamic SSE [30] includes a polynomial-time algorithm, , executed by the client and two protocols, and , run between the client and the server.
: This probabilistic algorithm takes the security parameter as the input and outputs , where and are the secret key and state of the client, respectively; and is an empty encrypted database stored in the server.
: The update protocol carries , , , a keyword-file pair , and as input.
It outputs a new client state and an encrypted database after the “add/delete" operation.
: This protocol takes the client secret key , state , and query as input, in which the server takes the database as input.
It returns as the query’s response.
In the query protocol, the client only retrieves the response identifiers. Later, it can perform an extra interaction with the server to obtain the encrypted files with the identifiers.
Appendix C Definition for Attack Round
The multiple-round [39] and search attacks [3] recover one target query via many rounds of injections and observations. Recall that the adversary in the context of the multiple-round attack “forces" the client to replay the same query repeatedly, in which “completing a replay of the client query" is regarded as “one attack round". The search attack requires the adversary to carry out a sufficient amount of observations on the client’s queries after a successful single file injection. In this context, an attack round is referred to as “the adversary completes a single file injection". In other attacks for multiple queries, the adversary aims to reveal the queries through an immediate observation right after multiple files injection. Here, completing a batch of file injections is also seen as an attack round. We define the attack round as follows.
Definition 1
Let be a non-empty set (except the ) of continuous observation operations and denote a non-empty set containing continuous “inject" operations. We denote as all the pairwise operations for an injection attack. Then, the total number of the attack round is .
For example, in the search attack with a , the attack process is , , , , . Thus, the number of attack round is . As for other attacks against multiple queries (e.g., single-round, decoding, and our attacks) their attack process is as and thus, they only require one attack round.
Appendix D An Example: BVA Decoding
In the example (see Figure 12), we assume there exists a special case where so that the BVA and decoding attack can achieve the same recovery rate. We see that the BVA only needs three files (each with a size of ) as compared to the decoding attack injecting seven files (each with a size of ), where and . Specifically, the BVA yields injection size, while the decoding attack is of the cost of the BVA, i.e., .


Appendix E Effect of Search Pattern on BVMA
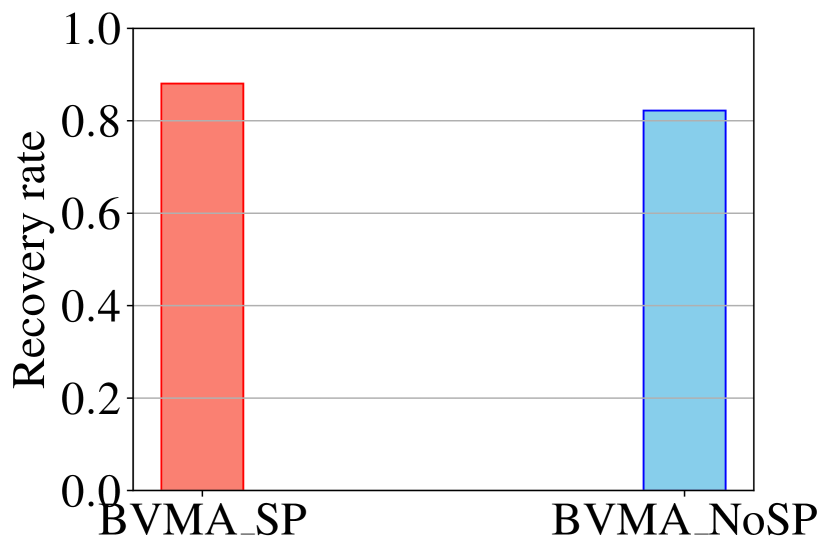
We tested the effect of the sp on the recovery rate of the BVMA (see Figure 13(a)). By exploiting the sp (i.e. “BVMA_SP"), the attack slightly improves the recovery, around (under keywords leakage); without the sp (i.e. “BVMA_NoSP"), it still provides recovery.
Appendix F Queries with Different Distributions
We used Google Trends and PageViews Toolforge to simulate the queries in the real-world distribution. Alternatively, one may use other query distributions, such as uniform query. In this section, we tested the recovery rate under two query distributions: real-world and uniform (see Figure 13(b)). We assumed that the adversary knows and has spent at least 8 weeks on observations in Enron. We set error bars for the BVA to evaluate the recovery when .
The recovery rate of the BVA varies moderately (about a gap) under the real-world query, but fluctuates (e.g., recovery in the worst case and in the best case) under the uniform distribution. This indicates that the BVA with a small (e.g., ) cannot perform stably in uniform query. The average recovery rates on the two distributions only differ approximately . The gap could nearly disappear if we set to be sufficiently large (e.g., ) to yield the max. recovery under both distributions. Recall that besides the frequency information, the BVMA relies on two types of volume patterns for query recovery. The adversary can distinguish queries and exclude the incorrect keywords by exploiting the patterns. The uniform query (hiding frequency information) only harms the recovery of the BVMA by as compared to the real-word query.
The distributions do not seriously affect our attacks’ average recovery rate (). The attacks perform slightly better on the real-world distribution than the uniform. This is because under the real-world query, the adversary can always recognize its target query of which frequency is higher than others. In contrast, the uniform distribution makes the adversary difficult to distinguish the target query, incurring the drop of the recovery rate.

Appendix G Comparison in Lucene and Wikipedia
We show the comparison among the single-round, decoding and our attacks in Lucene and Wikipedia in Table 6-7 and Figure 14-15. The single-round attack requires the least time cost () but yields the worst recovery (when ) or injection length (when ) in Lucene. The decoding attack and our attacks are at a comparable performance level in terms of recovery and running time. In Wikipedia, our attacks achieve around recovery in which the BVA and BVMA take around 3 and 15 mins respectively. For injection length, other attacks inject more files than ours. The BVMA only requires injection size in Wikipedia. To maintain a similar level of recovery (e.g., ), the decoding and single-round attacks (with ) cost at least more injection size than the BVMA. We see that the BVMA in Wikipedia (up to recovery) does not perform as well as in Enron and Lucene. If it performs on the same injection size as the BVA (but still much that of the decoding and single-round attacks), its recovery will be close to the BVA’s.
Appendix H Attacks against Extended SEAL
Extended SEAL fills the total rlp of the corresponding keyword into after every batch update. Table 8 presents our attacks against the extended SEAL. The results indicate that the extension can properly resist VIAs ( Rer) by sacrificing a huge amount of overhead. For example, when , to counter our attacks with 12 injected files, the extended SEAL should use around extra files ( of the injected files) to obfuscate the injection volume. The cost of I-Query also increases by .
Appendix I Optimization against ShieldDB
We developed an optimization (see Algorithm 4) against ShieldDB. The optimization is an extension of the BVA and BVMA. It starts with the BVA injection method (coding injection) and further optimizes the method by keyword grouping. Following the BVMA, the optimization uses the rlp to determine the keyword clustering. There are three main stages: baseline, injection, and recovery. In the baseline phase, the algorithm determines the cluster at which each keyword is located (as described previously). Here, each row represents a set containing all the keywords in cluster , and each column represents the keyword set under the same position ( of different clusters. The algorithm records the rlp referred to as and rsp as . In the injection phase, it chooses groups of keywords, in which each group contains the keywords in a column of . It selects different (from the set ) for the groups to launch the binary encoding file injection (which is similar to the BVA). Such a grouping approach ensures that the target keywords in the same cluster share the same number of injected files. In the recovery phase, given a target query , the algorithm first identifies the candidate clusters by using ’s rlp and then collects the correct keywords , from the clusters, satisfying the following: where is the rsp of , and is the injection parameter set. Since the optimization is based on both BVA and BVMA, we could predict from Figure 15 that its performance is close to that of the BVA, e.g., recovery in Wikipedia.
| Decoding | Single-round | Single-round | BVA | BVMA | |
| Running time | 3.54 | 0.01 | 0.02 | (2.53, 3.15) | 33.10 |


| Decoding | Single-round | Single-round | BVA | BVMA | |
| Running time | ( , ) |



| Extended SEAL | Overhead ( / No.) | Recovery rate | ||||
| Setup&Fill | S-Query | Inj&Fill | I-Query | BVA | BVMA | |
| no padding | / | / | / (injection) | / | ||
| / | / | / | / | |||
| / | / | / | / | |||
| / | / | / | / | |||
Appendix J Other Countermeasures
Besides the clustering-based padding strategies [7, 5, 47, 51, 15], one may consider using other defense systems. For example, some PIR (e.g., DORY [13]) and ORAM (e.g., [29, 20]) related techniques focus on protecting the ap and sp (besides the vp). These solutions could not be as simple and natural as a direct padding (on vp). Chen et al. [10] obfuscated the ap and vp by adding random false-positive and false-negative files, but this approach cannot protect the sp. Patel et al. [38] and Wang et al. [49] introduced the volume-hiding encrypted multi-maps with low server storage. Shang et al. [41] proposed to hide the sp by obfuscating the search token. As these technologies do not protect the leakage in the dynamic context, they cannot work properly against VIAs. Kamara and Moataz [28] investigated the dynamic volume-hiding system. But their approach does not support the client to make atomic update, e.g., adding and deleting a single keyword-file pair; and it also requires a high query bandwidth. [2, 53] extended KM [28] and PPYY [38] to propose fully dynamic volume-hiding encryption systems, respectively. They can resist most of the query recovery attacks with a price that the query complexity is proportional to the maximum rlp . Xu et al. [51] combined the file padding (to hide file size) and the traditional index padding (to hide response length). Through clustering and refilling files, their design ensures that files in a cluster remain the same size, which obfuscates the size of files. However, the adversary can simply counter this file padding strategy by generating a sufficient amount of injected files, in which each file is set to the same size. We say that an effective countermeasure to VIAs should be and , i.e., being able to hide both file size and response length by random (or differentially private) noisy padding.
Appendix K Attack against Frequent Updates
We optimized BVA to limit the impact of updates while maintaining the injection length. But this could increase the injection size. Please see the details below, and we’ll put the heuristic strategy in discussions on the paper.
-
•
1) Baseline: the adversary observes the queries’ result and finds the largest rsp (denoted as ). It predicts (or sets) the total size of all files that the user may update during the attack (denoted as ).
-
•
2) Injection: the adversary sets , and then injects files according to BVA’s binary injection strategy;
-
•
3) Recovery: for a target query q, the adversary observes its injected (and updated) response size (denoted as ), then it can recover query as the keyword ..
Actually, setting a small (e.g., , where is a constant and ) can achieve a practical recovery rate. We implemented the modified attack and ran experiments on the Enron dataset with the following measurements.
-
•
We tested the recovery under different (see Figure 16) and update percentage (see Figure 17, where dontes the proportion of updated files in the dataset). We investigated the recovery rate when the user update operations include: (1) all add operations (see Figure 16(a),17(a)); (2) a combination of uniform add and delete operations (see Figure 16(b),17(b)); (3) all delete operations (see Figure 16(c),17(c)).
- •






In Figure 16, the recovery enhances with the increase of . When , we achieve recovery; while increases to , the recovery rate reaches to about . We say a larger could further boost the recovery, but it would also increase the injection size. In Figure 16(c), when , our modified attack provides recovery on all reasonable (i.e. ). This is because the files in the original database and the updated files are all considered to be noise. means that the noise is completely eliminated (i.e. all files in the original database are deleted), thus allowing us to obtain a perfect recovery rate.
From Figure 17, we see that the recovery rate shows varying trends with different update operations. Figure 17(a) shows that the increase of add operations can harm the recovery. For example, when , the recovery on is about higher than that on . Figure 17(b) demonstrates that the random update barely affects the attack performance. In the last sub-figure, we prove that delete operation brings advantage to the recovery (e.g., when , the recovery on is about higher than that on ).
We present the recovery rate of BVA under different in Figure 18. As increases, the recovery drops rapidly for any and update operations. For example, a update could fail BVA. Note that when , BVA shows the advantage as its recovery is higher than that of the modified attack (e.g., when , the recovery rate of BVA is around , while that of the modified attack is ).
In Figure 19, we compare the recovery rate and injection volume of the modified attack with other VIAs. Note that we did not put single-round attack into comparison, because its injection length is extremely large (), which could be impractical. From Figure 19(a), we see that the user updates do not significantly affect the recovery rate of the modified attack (around recovery rate), but harm others (in particular when ). Figure 19(b) shows that the modified attack has an injection length of approx. , which is comparable to BVA but also better than decoding (). The injection size of the modified attack and BVA () is larger than BVMA (), but outperforms decoding (); see Figure 19(c).






Appendix L Discussions
Queries with multiple keywords. Our attacks can also apply to those dynamic SSE schemes that enable multiple keywords queries [8, 32]. We here present a heuristic solution to support our attacks for conjunctive queries with two keywords. Given , we combine any two keywords into one search query. That means a new search set is generated while a tuple is paired as a conjunctive query. For each element , we inject a file with size of ( is the parameter of BVA) containing the element. As a result, we inject files in total. It is an open problem to reduce the injection volume for the conjunctive queries.
SEAL’s Dynamic Padding. We used a straightforward approach to extend SEAL to support the dynamic padding. The extension can effectively resist VIAs, but its overhead (w.r.t. Inj&Fill) is extremely impractical, for example, the cost is even higher than simply streaming the entire database to the client. It is an open problem to design a more practical solution to balance the security and efficiency. One may consider combining clustering-based schemes (e.g., [7]) with the probabilistic padding (e.g., [38]). For example, for each batch update, one may divide keywords into several clusters and then fill each keyword in a cluster to , so that the keyword’s rlp will contain the same and probabilistic (and different) noise, where is the parameter of SEAL.
LEAKER. Kamara et al. [26] proposed an open-source attack evaluation framework LEAKER to test the recovery of passive LAA with different known file rates. LEAKER unfortunately cannot cover injection attacks [26] as it does not capture the necessary information leakage obtained and used by active adversaries. Extending this evaluation framework to test injection attacks could be an interesting problem. We note that is orthogonal to the main focus of this work.
Experiments on Multiple Datasets. In Section 4.3, 4.4 and Appendix E, G, H, we conducted the experiments in Enron. Our attacks performance will not differ significantly in Lucene and Enron as these email datasets share similar scales and keyword distributions. The Wikipedia could moderately harm the performance. For example, the recovery against static padding will be similar to that of Figure 15 (around ); whilst dynamic padding could further restrict the attacks performance. Under the clients’ active updates, the attacks could achieve similar trends and results as in Figure 11. Interested readers may use our codes to conduct extra experiments.