High-order Fusion Graph Contrastive Learning for Recommendation
Abstract.
Self-supervised learning (SSL) has recently attracted significant attention in the field of recommender systems. Contrastive learning (CL) stands out as a major SSL paradigm due to its robust ability to generate self-supervised signals. Mainstream graph contrastive learning (GCL)-based methods typically implement CL by creating contrastive views through various data augmentation techniques. Despite these methods are effective, we argue that there still exist several challenges. i) Data augmentation (e.g., discarding edges or adding noise) necessitates additional graph convolution (GCN) or modeling operations, which are highly time-consuming and potentially harm the embedding quality. ii) Existing CL-based methods use traditional CL objectives to capture self-supervised signals. However, few studies have explored obtaining CL objectives from more perspectives and have attempted to fuse the varying signals from these CL objectives to enhance recommendation performance.
To overcome these challenges, we propose a High-order Fusion Graph Contrastive Learning (HFGCL) framework for recommendation. Specifically, instead of facilitating data augmentations, we use high-order information from GCN process to create contrastive views. Additionally, to integrate self-supervised signals from various CL objectives, we propose an advanced CL objective. By ensuring that positive pairs are distanced from negative samples derived from both contrastive views, we effectively fuse self-supervised signals from distinct CL objectives, thereby enhancing the mutual information between positive pairs. Experimental results on three public datasets demonstrate the superior recommendation performance and efficiency of HFGCL compared to the state-of-the-art baselines.
1. INTRODUCTION
Self-supervised learning (SSL) (Liu et al., 2023c, a) has gained increasing recognition for its effectiveness in addressing data sparsity (Xia et al., 2023) challenges. The capability of SSL to extract self-supervised signals from large volumes of unlabeled data allows the approach to compensate for missing information, leading to widespread adoption in numerous studies (Assran et al., 2023; Chen et al., 2023; Baevski et al., 2023). Among various SSL paradigms, contrastive learning (CL) (Jing et al., 2023) stands out by acquiring self-supervised signals through maximizing mutual information between positive pairs in contrastive views. In recent years, the success of graph contrastive learning (GCL)-based methods (Wu et al., 2021; Zhang et al., 2024a) have gained significant attention in the field of recommender systems (Gao et al., 2022a).
In general, for CL to be effective, GCL-based methods require at least two distinct contrastive views. Inspired by various domains (Bayer et al., 2022; Rebuffi et al., 2021), most existing methods employ data augmentation techniques to generate these views. As illustrated in Fig. 1, data augmentation techniques can be broadly classified into two categories: graph augmentation (Wu et al., 2021) and representation augmentation (Yu et al., 2022b). Graph augmentation involves creating interaction subgraphs by randomly discarding nodes or edges on the user-item interaction graph and then generating different contrastive views through graph convolution operations. Representation augmentation generates different contrastive views by adding noise to the embeddings during the graph convolution process. With the generated contrastive views, these methods effectively mine users’ deep preferences, thereby providing more personalized recommendations.
Despite the necessity of generating contrastive views, data augmentation techniques and multiple CL objectives pose several drawbacks. On the one hand. to create diverse contrastive views, data augmentation generally requires additional graph convolution and modeling operations, which significantly increase training cost per epoch. Furthermore, techniques such as graph and representation augmentation, often implemented by discarding edges or adding noise, would potentially harm the quality of embedding between positive pairs, thus affecting the acquisition of self-supervised signals. On the other hand. existing CL-based methods construct CL objectives (Yu et al., 2022b; Yang et al., 2023b) from traditional contrastive views (e.g., user-based and item-based). While the generated self-supervised signals can improve performance to some extent, the fusion of these signals remains problematic, leading to suboptimal recommendation. However, few studies have explored contrastive views from different perspectives and attempted to fuse diverse signals from more CL objectives to further improve recommendation quality.
Based on above analysis, we present two major challenges:
-
•
How to efficiently obtain high-quality contrastive views without data augmentation?
-
•
How to better fuse self-supervised signals captured from different CL objectives?

To address these challenges, we propose a High-order Fusion Graph Contrastive Learning (HFGCL) framework for recommendation. Instead of relying on data augmentations, we derive user-item contrastive views directly from user-item interactions, and demonstrate that the graph convolution networks (GCN) encoder (He et al., 2020) enhances the similarity between user-item pairs. Through analysis in Section 3.2, we find that low-order information, having undergone minimal or no neighborhood aggregation, results in embeddings saturated with self-information. The self-information suppresses the similarity between positive pairs and complicates the maximization of mutual information. Consequently, we exclude low-order embeddings and propose high-order contrastive views. Since the negative samples provided by high-order contrastive views differ from traditional ones (e.g., user views’ negative samples are other users), we incorporate these unique negative samples into our original CL loss. Moreover, to effectively integrate self-supervised signals from different CL objectives, we present a fusion CL loss. By concurrently ensuring that positive pairs remain distant from more negative samples, we further enhance the mutual information between the positive pairs, thereby enabling the effective fusion of diverse self-supervised signals. Overall, HFGCL is a simple yet efficient recommendation framework, capable of fusing rich self-supervised signals from high-order contrastive views with a fusion CL loss, thereby significantly improving recommendation performance. The main contributions of this paper are as follows:
-
•
We reveal that most GCL-based methods are both time-consuming and potentially detrimental to embedding quality. In addition, We find that existing CL-based methods struggle to effectively fuse self-supervised signals from diverse CL objectives.
-
•
We propose High-order Fusion Graph Contrastive Learning (HFGCL) for recommendation. HFGCL directly employs high-order information to generate contrastive views and presents a fusion CL loss to integrate different self-supervised signals.
-
•
We conduct various experimental studies on three publicly datasets, and the results show that HFGCL has significant advantages in terms of recommendation performance and model training efficiency compared to existing state-of-the-art recommendation methods.
2. PRELIMINARIES
In this section, we introduce the key technologies underlying our framework’s architecture.
2.1. Graph Neural Networks for Recommendation
Given and denote the set of users and items, respectively. In recommender system (Wu et al., 2023), Graph Convolutional Networks (GCN) (Wang et al., 2019; Wu et al., 2019; He et al., 2020) are increasingly favored, which through graph convolution operations, effectively gather high-order neighborhood information to accurately capture user preference behaviors. LightGCN (He et al., 2020) as currently the most popular GCN encoder, which effectively captures high-order information through neighborhood aggregation. For efficient training, graph Laplace matrix is proposed: , where denotes graph Laplacian matrix, and denotes adjacency matrix, and denotes diagonal matrix of A. To ensure that diverse neighborhood information is integrated, final embeddings are aggregated from all layers: where denotes the number of GCN layers. The point-wise Bayesian Personalisation Ranking (BPR) loss (Rendle et al., 2009) is adopted to optimize model parameters:
| (1) |
where represents a triplet input to the model.
2.2. Contrastive Learning for Recommendation
Recent studies have demonstrated that contrastive learning (CL), through the generation of self-supervised signals, effectively addresses the challenge of data sparsity in recommender systems (Xia et al., 2023). CL-based methods create contrastive views through data augmentation and seek to optimize the mutual information between positive pairs, thereby obtaining self-supervised signals. Most of the existing methods mainly use InfoNCE (Chen et al., 2020) loss for CL:
| (2) |
where and denote samples ( user or item) in same batch , denotes the temperature coefficient. CL loss aims to maximizes the mutual information between positive pairs and , and to increase the distance between and other negative sample .
2.3. Effectiveness of Data Augmentation
Existing researches on CL underscore the critical role of data augmentations (Wu et al., 2021; Yu et al., 2022b; Yang et al., 2023b; Zhang et al., 2024b), which is attributed to CL that necessitates the creation of diverse contrastive views for effective implementation. In recommendation, there are two main types in Fig. 1: (1) graph augmentation (Wu et al., 2021) (2) representation augmentation (Yu et al., 2022b).
Graph augmentation typically involves generating two distinct subgraphs by randomly discarding edges or nodes from the original graph: where denotes the original graph, and denote the nodes and edges, respectively, denotes the augmentation subgraphs, denotes keeping rate. Representation augmentation by introducing noises into graph convolution process: where denotes embedding, denotes the added noise (, gaussian noise or uniform noise).
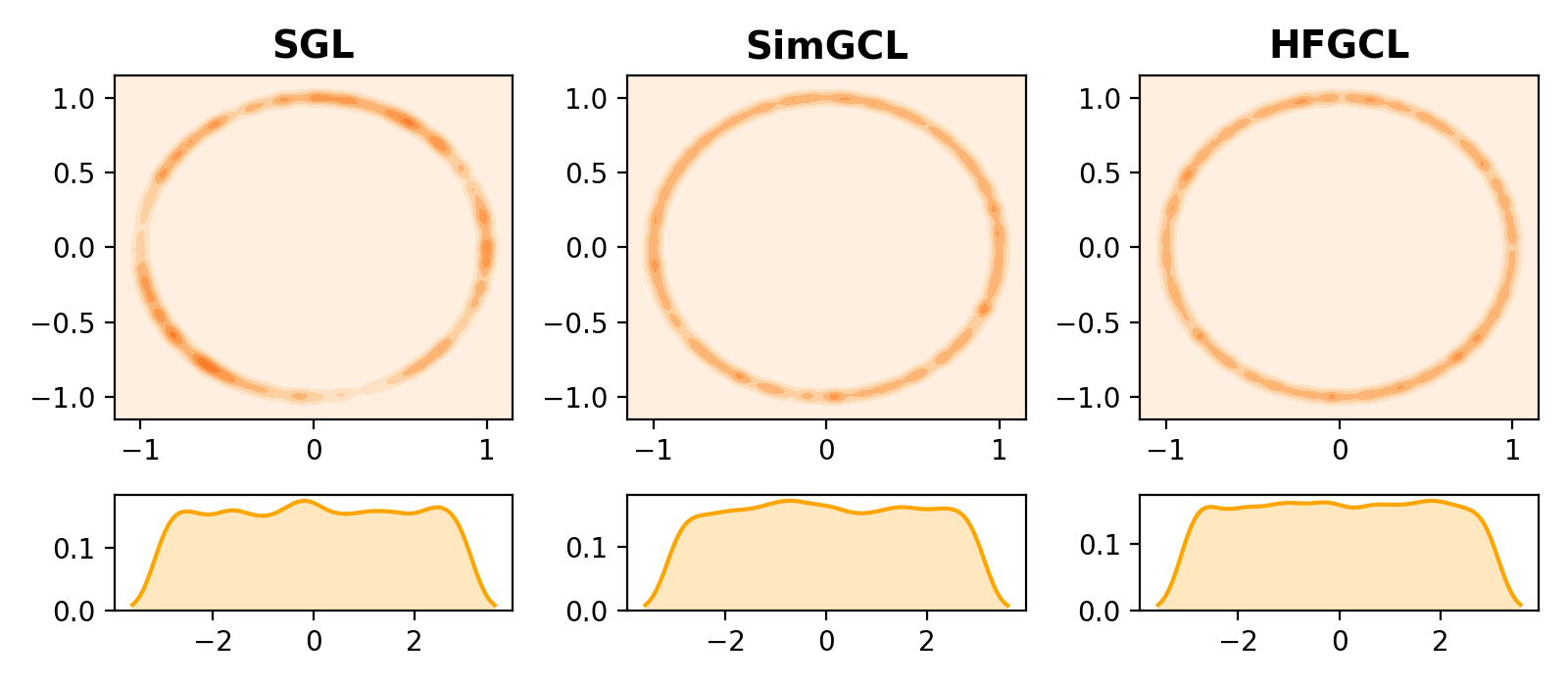
While these contrastive views are effective, data augmentations corrupt the embedding’s quality. In Fig. 2, graph augmentation methods discard edges when generating contrastive views, leading to relatively poorer embedding feature distributions and density distributions. Representation augmentation methods by adding noise to the graph convolution. Although the effect of some noise on the distribution is less pronounced than that of graph augmentation, it still results in less smooth density distribution. Additionally, data augmentations are exceptionally time-consuming. Table 1 provides the per-epoch time consumption for the GCN-based method ( LightGCN) and GCL-based methods with ( SGL and SimGCL) and without ( HFGCL) data augmentations. SGL (Wu et al., 2021), which utilizes the graph augmentation technique to generate subgraphs, is extremely time-consuming. Additionally, most GCL-based ( SimGCL and VGCL) methods require repetitive graph convolution or modeling operations to obtain the contrastive views, further contributing to the time consumption. This raises the question: Are data augmentation techniques necessary for contrastive learning in recommendation? In fact, despite the demonstrated effectiveness of data augmentations, how to efficiently generate high quality contrastive views remains a key challenge in CL.
| Method | Amazon-Book (time/epoch) | Yelp2018 (time/epoch) | Tmall (time/epoch) |
| LightGCN | 76.6 (s) | 37.7 (s) | 65.2 (s) |
| SGL | 188.1 (s) | 92.5 (s) | 154.5 (s) |
| SimGCL | 194.5 (s) | 83.5 (s) | 167.9 (s) |
| VGCL | 98.7 (s) | 51.4 (s) | 81.7 (s) |
| HFGCL | 78.6 (s) | 38.9 (s) | 66.2 (s) |
Feature
Density
Angles
Angles
Angles

Feature
Density
Angles
Angles
Angles
3. HFGCL: HIGH-ORDER FUSION GRAPH CONTRASTIVE LEARNING
In this section, we propose a High-order Fusion Graph Contrastive Learning (HFGCL) framework in Fig. 3. HFGCL generates high quality contrastive views exclusively from high-order information, and efficiently fusing the diverse self-supervised signals by aggregating information from both positive pairs and negative samples.

3.1. Different Perspectives for Contrastive Views
Following the analysis in Section 2.3, we shift our attention to the traditional recommendation task. Inspired by the natural language processing (NLP) (Gao et al., 2022b), which generates contrastive views by applying the dropout function to input sentence. We believe that the contrastive views same exist in traditional recommendation task.
Considering a different perspective, we directly treat users and items as contrasting views. Given that users and items are first-order neighbors of each other, their high-order information are essentially identical. As graph convolution progresses, users and items gradually capture neighborhood information, resulting in their embeddings becoming progressively closer. Therefore, GCN process ultimately generates a set of distinctive contrastive views.
The previous contrastive views originate from the same sample ( and from ), necessitating that a set of views can be selected as negative samples ( ) to calculate CL losses.
| (3) |
However, considering that the user-item contrastive views differs from the previous contrastive views, we utilize the item views and user views as negative samples for the user and item, respectively.
Formally, we propose the CL loss of user-item contrastive views is different from Eq. 3 as follows:
| (4) |
where and are from .
3.2. High-order Contrastive Views
Many studies use aggregation methods to combine layer-wise embeddings into the final embeddings. Though this method effectively fuses information from both the sample itself and its neighborhoods, we find that the low-order information is extremely unique. This uniqueness can seriously affect the similarity between positive pairs, thereby interfering with the mutual information of them.
To make the positive pairs more similar, we eliminate the low-order information () and aggregate high-order information () as the final embeddings.
| (5) | ||||
| (6) |
where denotes high-order information beginning at layer . Unlike various GCL-based methods, by mining the properties in the existing embedding, we find the high-order contrastive views in the graph convolution process. This idea reduces the time cost while preserving the original embedding information, thus improving the efficiency and performance of the model.
3.3. More Negative Samples to CL Loss
In recommender systems, data augmentation typically involve augmenting the original user or item embeddings with multiple GCN operations to generate different contrastive views. When calculating CL loss, different views of the same sample are regarded as positive pairs, while a set of augmented views are selected as negative samples. Among them, it is not difficult to find that the negative samples used in the previous CL loss come from a set of augmented views. In contrast, for the high-order contrastive views propose in Section 3.2, we give the corresponding CL loss in Eq. 4. It is differently from the previous negative samples sampling approach, the negative samples come from the opposing views. This difference leads to the self-supervised signals of users and items themselves are missing.
Original CL Loss. To be able to obtain this part of the self-supervised signal, we attempt to treat the samples themselves as negative samples and introduce the corresponding CL loss:
| (7) |
where and denote different users/items samples. Unlike traditional CL loss, the positive pairs ( -) of samples are identical. Subsequently, we combine the CL loss associated with the users and the items themselves:
| (8) |
After obtaining the CL objectives for both users and items themselves, we integrate these with our main CL loss:
| (9) |
Fusion CL Loss. Most studies obtain self-supervised signals through traditional CL objectives (e.g., separately obtaining signals from users and items). Although effective, we argue that differences in these self-supervised signals lead to suboptimal recommendations. Instead, in our CL objective, we propose four CL objectives to capture self-supervised signals. While proposed CL objectives capture more signals, in fact, different self-supervised signals make them extremely difficult to effectively integrate these self-supervised signals. It motivates us to further improve our CL loss to fuse these diverse self-supervised signals. Considering that, unlike the traditional CL loss, our proposed CL loss allows both users and items to serve as negative samples. One simple method involves directly concatenating the two contrastive views and using them as negative samples in CL:
| (10) |
where and denote the embeddings of and within the same batch, denotes the concatenation of and . While this approach appears to be sound, the CL loss disregard the distance between and , focusing solely on the computation of with , resulting in bias in the obtained self-supervised signals.

To enable our method to better aggregate with more negative samples , we present an advanced fusion CL loss that is specifically adapted to high-order contrastive views:
| (11) |
By separately calculating the similarity between view and view with all negative samples, we effectively fuse the self-supervised signals of different views and maximize the mutual information between positive pairs. Meanwhile, to effectively illustrate how HFGCL combines more negative samples, we show the positive pairs and selected negative samples for various contrastive methods in Fig. 4. Since our high-order contrastive views are derived from two different samples, in the selection of negative samples, unlike traditional contrastive views where only one set can be chosen as negative samples, we can simultaneously use both as negative samples for contrastive loss. Furthermore, our fusion CL loss can effectively aggregate this additional negative sample information and naturally fuse all the self-supervised signals.
Formally, we propose the evolution of HFGCL’s CL loss:
| (12) |
Through the study of relationships between positive pairs and negative samples, we have simplified the diverse contrastive objectives traditionally used to capture different self-supervised signals. By utilizing a fusion CL loss, we efficiently obtain the richer self-supervised signals, enabling personalized recommendations.
3.4. Model Optimization
For the purpose of enhancing our contrastive model’s suitability for the primary recommendation task, we implement a multi-task training strategy to optimize the model’s parameters. The overall loss function for HFGCL is defined as follows:
| (13) |
where and denote the weights for and , denotes the regularization parameter applied to the naive embedding .
3.5. Theoretical Analysis
| Layer | Amazon-book | Yelp2018 | Tmall |
| 0.231 | 0.254 | 0.249 | |
| 0.312 | 0.306 | 0.277 | |
| 0.476 | 0.490 | 0.390 |
The core motivation of this paper is to construct high-quality contrastive views and fuse self-supervised signals from different CL objectives. For the former, after proposing the user-item contrastive views, to find high-quality contrastive views, we utilize cosine similarity to measure the similarity between positive pairs ( and ) in Table 2. For the latter, to better integrate different self-supervised signals, we propose a fusion paradigm applicable to contrastive views. Specifically, the fusion CL loss simultaneously considers the distance between both positive pairs and more negative samples, further improving the alignment of positive pairs and the uniformity of the sample space (Wang et al., 2022a). To further explain, we present the gradient of user in fusion CL loss:
| (14) |
where , is the contribution provided. For the first term , the contribution of item to the gradient encourages user to move closer to item , directly strengthening the connection between the positive pair. For the second term , the contribution of item and negative sample to the gradient indicates that user must consider the relationship between positive item and negative sample , thereby improving the distancing from hard negative samples filtered by item . The above demonstrates the effectiveness of proposed fusion paradigm:
-
•
For user-item pairs, maximizing the mutual information directly reflects users’ deeper preferences.
-
•
For more negative sample pairs, effective fusion of information between positive and negative pairs makes the feature space more uniform distribution.
The same conclusion holds for the gradient of item . Furthermore, for the temperature coefficient , unlike previous work, we must assign a slightly larger to the fusion CL loss due to the inclusion of information from both positive pairs and more negative samples.
4. EXPERIMENTS
In this section, to demonstrate the effectiveness of HFGCL, we perform experimental comparisons with the state-of-the-art recommendation methods on three real datasets.
4.1. Experimental Settings
Datasets. In selecting datasets to validate the effectiveness of our HFGCL, we choose three datasets that are widely recognized and frequently used for benchmarking in numerous studies: Amazon-book (He et al., 2020), Yelp2018 (Sang et al., 2024), Tmall (Ren et al., 2023). For all datasets, we consider all ratings ‘¿3’ as presence of interactions (i.e., presence of interaction is 1 otherwise 0). We filter out users with less than 10 interactions to ensure the validity of the recommendation. Subsequently, we divide the training and test data into ‘80%’ and ‘20%’ for every users. The details of all the datasets are shown in Table 3.
| Dataset | #Users | #Items | #Interactions | Density |
| Amazon-book | 52.6k | 91.6k | 2984.1k | 0.06% |
| Yelp2018 | 31.7k | 38.0k | 1561.4k | 0.13% |
| Tmall | 47.9k | 41.4k | 2619.4k | 0.13% |
Baselines. To demonstrate the effectiveness of HFGCL, we select numerous state-of-the-art methods for comparison.
-
•
MF-based method: BPR-MF (Koren et al., 2009).
- •
- •
- •
Evaluation Indicators. To evaluate the recommendation efficacy of the HFGCL method, we choose the widely used metrics (Zhang et al., 2023; Yu et al., 2022b), Recall@K and NDCG@K (K=10, 20).
Hyperparameters. To ensure fair and consistent comparisons, all experiments run on a Linux system equipped with a GeForce RTX 2080Ti GPU. We implement HFGCL in the Pytorch environment111. The batch size for all methods are set to 4096, 2048 and 4096 for Amazon-book, Yelp2018 and Tmall datasets, respectively. Except for RecDCL, all methods use an embedding size of 64, while RecDCL uses 2048, as it primarily studies variations across different embedding sizes. Embeddings are initialized using the Xavier strategy (Glorot and Bengio, 2010). Adam is used as the optimizer by default. For methods utilizing the GCN encoder, the number of GCN layers is chosen from {1, 2, 3}. Specifically, for HFGCL, the number of GCN layers is set to 3, the high-order information is varied within {1, 2, 3}, and the parameter is selected from {0.20, 0.22, 0.24, 0.26, 0.28, 0.30}. The regularization weights is chosen from {0.1,0.5,1.0, 2.5}, and is set from {1e-3, 1e-4, 1e-5, 1e-6}.
| Method | Amazon-book | Yelp2018 | Tmall | |||||||||
| R@10 | R@20 | N@10 | N@20 | R@10 | R@20 | N@10 | N@20 | R@10 | R@20 | N@10 | N@20 | |
| BPR-MF | 0.0170 | 0.0308 | 0.0182 | 0.0239 | 0.0278 | 0.0486 | 0.0317 | 0.0394 | 0.0312 | 0.0547 | 0.0287 | 0.0400 |
| NGCF | 0.0199 | 0.0337 | 0.0200 | 0.0262 | 0.0331 | 0.0579 | 0.0368 | 0.0477 | 0.0374 | 0.0629 | 0.0351 | 0.0465 |
| LightGCN | 0.0228 | 0.0411 | 0.0241 | 0.0315 | 0.0362 | 0.0639 | 0.0414 | 0.0525 | 0.0435 | 0.0711 | 0.0406 | 0.0530 |
| CAGCN* | 0.0300 | 0.0506 | 0.0305 | 0.0400 | 0.0414 | 0.0711 | 0.0470 | 0.0590 | 0.0524 | 0.0840 | 0.0495 | 0.0726 |
| DirectAU | 0.0296 | 0.0506 | 0.0297 | 0.0401 | 0.0414 | 0.0703 | 0.0477 | 0.0583 | 0.0475 | 0.0752 | 0.0443 | 0.0576 |
| GraphAU | 0.0300 | 0.0502 | 0.0310 | 0.0400 | 0.0401 | 0.0691 | 0.0463 | 0.0574 | 0.0517 | 0.0840 | 0.0488 | 0.0625 |
| SGL | 0.0263 | 0.0478 | 0.0281 | 0.0379 | 0.0395 | 0.0675 | 0.0448 | 0.0555 | 0.0457 | 0.0738 | 0.0434 | 0.0556 |
| NCL | 0.0266 | 0.0481 | 0.0284 | 0.0373 | 0.0403 | 0.0685 | 0.0458 | 0.0577 | 0.0459 | 0.0750 | 0.0429 | 0.0553 |
| SimGCL | 0.0313 | 0.0515 | 0.0334 | 0.0414 | 0.0424 | 0.0721 | 0.0488 | 0.0601 | 0.0559 | 0.0884 | 0.0536 | 0.0674 |
| CGCL | 0.0274 | 0.0483 | 0.0284 | 0.0380 | 0.0404 | 0.0690 | 0.0452 | 0.0560 | 0.0542 | 0.0880 | 0.0510 | 0.0655 |
| VGCL | 0.0312 | 0.0515 | 0.0332 | 0.0410 | 0.0425 | 0.0715 | 0.0485 | 0.0587 | 0.0557 | 0.0880 | 0.0533 | 0.0670 |
| LightGCL | 0.0303 | 0.0506 | 0.0318 | 0.0397 | 0.0377 | 0.0657 | 0.0437 | 0.0539 | 0.0531 | 0.0832 | 0.0533 | 0.0637 |
| RecDCL | 0.0311 | 0.0525 | 0.0318 | 0.0407 | 0.0408 | 0.0690 | 0.0464 | 0.0567 | 0.0527 | 0.0853 | 0.0492 | 0.0632 |
| BIGCF | 0.0294 | 0.0500 | 0.0320 | 0.0398 | 0.0431 | 0.0730 | 0.0497 | 0.0603 | 0.0547 | 0.0876 | 0.0524 | 0.0664 |
| HFGCL | 0.0346∗ | 0.0566∗ | 0.0376∗ | 0.0458∗ | 0.0448∗ | 0.0752∗ | 0.0515∗ | 0.0624∗ | 0.0577∗ | 0.0911∗ | 0.0555∗ | 0.0697∗ |
| Improv.% | 10.54% | 7.81% | 12.57% | 10.63% | 3.94% | 3.01% | 3.62% | 3.83% | 3.22% | 3.05% | 3.54% | 3.41% |
4.2. Overall Performance Comparisons
To illustrate the superior performance of HFGCL, we compare with all baselines in Table 4. The following observations are made:
-
•
Our HFGCL achieves the most superior performance compared to all baselines on three sparse datasets. Specifically, compared to the strongest baseline, HFGCL improves NDCG@20 by 10.63%, 3.83%, and 3.41% on the Amazon-book, Yelp2018, and Tmall datasets, respectively. The experimental results are sufficient to show that HFGCL has a strong recommendation performance, enabling the provision of personalized recommendations.
-
•
Traditional MF-based method generally underperform compared to GNN-based methods, underscoring the substantial improvements that graph structures bring to recommender systems. Among these, LightGCN serves as the encoder for most GNN-based methods due to its straightforward and efficient architectural design. HFGCL uses this encoder, and by extracting the high-order information, we obtain the high-quality contrastive views thus further improving the method efficiency.
-
•
All GCL-based methods such as SimGCL, RecDCL, and BIGCF demonstrate clear superiority over traditional methods, largely due to the self-supervised signals derived from CL. Within this group, HFGCL achieves the best performance. This is mainly attributed to the high quality contrastive views and the ability to fuse different self-supervised signals with CL loss. Additionally, while RecDCL achieves sub-optimal performance Recall@20 on the Amazon-book dataset, the use of the 2048 embedding size may compromise the fairness of comparisons with other methods. In contrast, HFGCL achieves superior recommendation performance by leveraging high-order contrastive for CL, without the need for any data augmentation.
4.3. Method Variants and Ablation Study
| Method | Amazon-book | Yelp2018 | Tmall | |||
| R@20 | N@20 | R@20 | N@20 | R@20 | N@20 | |
| LightGCN | 0.0411 | 0.0315 | 0.0639 | 0.0525 | 0.0711 | 0.0530 |
| 0.0535 | 0.0430 | 0.0666 | 0.0548 | 0.0845 | 0.0644 | |
| 0.0536 | 0.0431 | 0.0718 | 0.0598 | 0.0873 | 0.0667 | |
| 0.0555 | 0.0452 | 0.0734 | 0.0612 | 0.0888 | 0.0680 | |
| w/o high | 0.0545 | 0.0432 | 0.0704 | 0.0581 | 0.0782 | 0.0590 |
| w/o GCN | 0.0539 | 0.0422 | 0.0722 | 0.0595 | 0.0870 | 0.0666 |
| w/o view | 0.0466 | 0.0373 | 0.0671 | 0.0550 | 0.0725 | 0.0540 |
| w/o CL | 0.0372 | 0.0289 | 0.0570 | 0.0457 | 0.0580 | 0.0426 |
| HFGCL | 0.0566 | 0.0458 | 0.0752 | 0.0624 | 0.0911 | 0.0697 |
| Improv.% | 37.71% | 45.40% | 17.68% | 18.86% | 28.13% | 31.51% |
To demonstrate the effectiveness of HFGCL’s components, we introduce various variants and conduct an ablation study:
From the results shown in Table 5, we draw the following conclusions. Firstly, HFGCL outperforms LightGCN across all performance metrics. For variant , which utilizes user-item contrastive views, the performance not only matches that of SGL but also significantly surpasses LightGCN. For variant , which eliminates low-order information, the CL loss effectively gets self-supervised signals from high-order information. For variant , with the addition self-sueprvies signals, there is a discernible enhancement in the method’s recommendation quality. These variants adequately address the question raised in Section 2.3 regarding the necessity of data augmentations, demonstrating that it is not essential for creating contrastive views.
Furthermore, for the fusion CL loss, we conduct a series of ablation studies to validate the effectiveness. For , the results show that low-order information hinders similarity between positive pairs. For , and , we remove the widely used GCN encoder, use the original CL loss and remove the CL loss, respectively, and the experimental results demonstrate the power of the fusion CL loss. Finally, compared to HFGCL, all ablations result in significant performance declines, which clearly demonstrate the superiority of the fusion CL loss.
4.4. Method Efficiency Study

To verify the efficiency of HFGCL, we compare the total training cost of the state-of-the-art methods. As shown in Fig. 5, our HFGCL has the shortest training cost on three datasets. This efficiency is primarily due to HFGCL quickly fuse self-supervised signals over the contrastive views, which enables it to converge exceedingly quickly. For SGL and SimGCL, both data augmentation necessitate graph convolution, a process that is notably time-consuming. For NCL and CGCL, though they also do not require data augmentations, it is again extremely time-consuming to compute all users/items from the user-item interaction as negative samples. Moreover, for most of the GCL-based methods (using data augmentations), the overall convergence speed is significantly impacted because the quality of the generated embedding information is perturbed to varying degrees. It is noteworthy that despite the absence of training cost data for RecDCL, it ranks as the most time-consuming method in the comparison, primarily because of its embedding size of 2048.
4.5. Method Sparsity Study
To show the ability of HFGCL in addressing the data sparsity issue, we categorize the users of the dataset into three groups—sparse, common, and popular—following methodologies from previous research. The experimental results are shown in Fig. 6. HFGCL maintains superior performance across different sparsity degrees, and performs exceptionally well within the sparsest user category. Additionally, on Amazon-book dataset, we observe a general decrease in performance in the normal category, possibly attributed to high levels of noise in this user segment. Even so, HFGCL maintains superior recommendation performance, demonstrating its robustness and resistance to sparsity.
NDCG@20(%)



4.6. Method Hyperparameter Study
In this section, we provide the sensitivity of HFGCL to various hyperparameters in Fig. 7 and Table 6. As depicted in Fig. 7, the method’s performance is significantly affected by the value of , which is slightly higher compared to the previous method. This increase is primarily due to the elevated number of negative samples, necessitating a larger to ensure optimal acquisition of mutual information. However, HFGCL’s performance is barely affected by . We attribute this to our CL loss’s robust adaptation to the high-order contrastive views, ensuring the method performs optimally regardless of the value. This efficacy underscores the strength of HFGCL’s CL loss. The results presented in Table 6 confirm the efficacy of high-order information, demonstrating that HFGCL significantly enhances method performance when . This also confirms that the low-order information decreases the similarity between positive pairs, leading to suboptimal recommendation.
5. RELATED WORK
GNN-based Recommendation. Graph Neural Networks (GNNs) (Wu et al., 2022) have emerged as a pivotal research direction in recommender systems due to their unique architecture, which enables the effective capture of high-order information. The pioneering work of NGCF (Wang et al., 2019) introduced the use of GNNs for aggregating high-order domain information. Building on this, SGCN (Wu et al., 2019) advanced the field by eliminating nonlinearities and consolidating multiple weight matrices. The most critical development, LightGCN (He et al., 2020), has been widely adopted for its ability to achieve high-quality encoding by retaining only the essential neighborhood aggregation component.
Furthermore, GNNs have been extensively explored in various recommendation scenarios (Wang et al., 2022b; Sharma et al., 2024). In sequential recommendation, many methods, SURGE (Chang et al., 2021) and GCE-GNN (Wang et al., 2020), leverage GNN to aggregate items within each sequence via interaction graphs, thereby enhancing the quality of item encoding. In social recommendation, numerous methods, DVGRL (Zhang et al., 2024c), GraphRec (Fan et al., 2019), and ESRF (Yu et al., 2022a), combine interaction graphs with social relationship graphs to more effectively incorporate social relationships. However, despite the effectiveness, their lack of self-supervised signals hinders their ability to accurately capture users’ preferences.
CL-based Recommendation. Recent developments in recommender systems research have predominantly emphasized contrastive learning (CL) (Yu et al., 2024; Liu et al., 2023b). The self-supervised signals generated by CL effectively address data sparsity issues. CL-based methods like NCL (Lin et al., 2022), SimGCL (Yu et al., 2022b), VGCL(Yang et al., 2023b), and BIGCF (Zhang et al., 2024b) typically employ data augmentation to create contrastive views, by facilitating CL. For example, SimGCL (Yu et al., 2022b) incorporates noise during graph convolution to generate multiple contrastive views. In contrast to traditional GCL-based methods, NCL (Lin et al., 2022) and CGCL (He et al., 2023) do not rely on data augmentation. For instance, NCL uses cross-layer and clustering methods to generate contrastive views and treats all user and item embeddings as negative samples for training. While these method have some benefits, they significantly increase the training cost. Our HFGCL, however, achieves optimal training efficiency and recommendation performance by considering high-order information as contrastive views and proposing a fusion CL loss.


| Method | Amazon-book | Yelp2018 | Tmall | |||
| R@20 | N@20 | R@20 | N@20 | R@20 | N@20 | |
| 0.0526 | 0.0419 | 0.0742 | 0.0616 | 0.0888 | 0.0680 | |
| 0.0566 | 0.0458 | 0.0752 | 0.0624 | 0.0906 | 0.0684 | |
| 0.0542 | 0.0441 | 0.0744 | 0.0616 | 0.0911 | 0.0697 | |
6. CONCLUSION
In this paper, we revealed the connection between data augmentations and contrastive learning (CL), then pointed out the challenges of each. These challenges motivated us to propose a novel recommendation method called Higher-order Fusion Graph Contrastive Learning (HFGCL), which filtered the low-order information to create high-order contrastive views. Additionally, we proposed a fusion CL loss which by more negative samples to maximize the mutual information, thus fusing diverse self-supervised signals. Our experimental results demonstrated the effectiveness of HFGCL on three public datasets.
In the future, we will focus on exploring the mechanism by which contrastive objectives generate self-supervised signals, particularly the interpretability of CL in recommender systems.
Acknowledgements.
References
- (1)
- Assran et al. (2023) Mahmoud Assran, Quentin Duval, Ishan Misra, Piotr Bojanowski, Pascal Vincent, Michael Rabbat, Yann LeCun, and Nicolas Ballas. 2023. Self-supervised Learning From Images With a Joint-Embedding Predictive Architecture. In IEEE Conference on Computer Vision and Pattern Recognition. 15619–15629.
- Baevski et al. (2023) Alexei Baevski, Arun Babu, Wei-Ning Hsu, and Michael Auli. 2023. Efficient Self-supervised Learning with Contextualized Target Representations for Vision, Speech and Language. In Proceedings of the 40th International Conference on Machine Learning, Vol. 202. 1416–1429.
- Bayer et al. (2022) Markus Bayer, Marc-André Kaufhold, and Christian Reuter. 2022. A Survey on Data Augmentation for Text Classification. Comput. Surveys 55, 7, Article 146 (dec 2022), 39 pages.
- Cai et al. (2023) Xuheng Cai, Chao Huang, Lianghao Xia, and Xubin Ren. 2023. LightGCL: Simple Yet Effective Graph Contrastive Learning for Recommendation. In The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1-5, 2023.
- Chang et al. (2021) Jianxin Chang, Chen Gao, Yu Zheng, Yiqun Hui, Yanan Niu, Yang Song, Depeng Jin, and Yong Li. 2021. Sequential Recommendation with Graph Neural Networks. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’21). 378–387.
- Chen et al. (2020) Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. 2020. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the 37th International Conference on Machine Learning, Vol. 119. 1597–1607.
- Chen et al. (2023) Weihua Chen, Xianzhe Xu, Jian Jia, Hao Luo, Yaohua Wang, Fan Wang, Rong Jin, and Xiuyu Sun. 2023. Beyond Appearance: A Semantic Controllable Self-supervised Learning Framework for Human-Centric Visual Tasks. In IEEE Conference on Computer Vision and Pattern Recognition. 15050–15061.
- Fan et al. (2019) Wenqi Fan, Yao Ma, Qing Li, Yuan He, Eric Zhao, Jiliang Tang, and Dawei Yin. 2019. Graph Neural Networks for Social Recommendation. In The World Wide Web Conference (San Francisco, CA, USA) (WWW ’19). 417–426.
- Gao et al. (2022a) Chen Gao, Xiang Wang, Xiangnan He, and Yong Li. 2022a. Graph Neural Networks for Recommender System. In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining (WSDM ’22). 1623–1625.
- Gao et al. (2022b) Tianyu Gao, Xingcheng Yao, and Danqi Chen. 2022b. SimCSE: Simple Contrastive Learning of Sentence Embeddings. arXiv:2104.08821
- Glorot and Bengio (2010) Xavier Glorot and Yoshua Bengio. 2010. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the thirteenth international conference on artificial intelligence and statistics. JMLR Workshop and Conference Proceedings, 249–256.
- He et al. (2023) Wei He, Guohao Sun, Jinhu Lu, and Xiu Susie Fang. 2023. Candidate-aware Graph Contrastive Learning for Recommendation. In Proceedings of the 46th International ACM SIGIR Conference (SIGIR ’23). 1670–1679.
- He et al. (2020) Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, YongDong Zhang, and Meng Wang. 2020. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. 639–648.
- Jing et al. (2023) Mengyuan Jing, Yanmin Zhu, Tianzi Zang, and Ke Wang. 2023. Contrastive Self-supervised Learning in Recommender Systems: A Survey. ACM Transactions on Information Systems 42, 2, Article 59 (nov 2023), 39 pages.
- Koren et al. (2009) Yehuda Koren, Robert Bell, and Chris Volinsky. 2009. Matrix Factorization Techniques for Recommender Systems. Computer 42, 8 (Aug. 2009), 30–37.
- Lin et al. (2022) Zihan Lin, Changxin Tian, Yupeng Hou, and Wayne Xin Zhao. 2022. Improving Graph Collaborative Filtering with Neighborhood-enriched Contrastive Learning. In Proceedings of the ACM Web Conference 2022 (WWW ’22). 2320–2329.
- Liu et al. (2023c) Xiao Liu, Fanjin Zhang, Zhenyu Hou, Li Mian, Zhaoyu Wang, Jing Zhang, and Jie Tang. 2023c. Self-supervised Learning: Generative or Contrastive. IEEE Transactions on Knowledge and Data Engineering 35, 1 (2023), 857–876.
- Liu et al. (2023a) Yixin Liu, Ming Jin, Shirui Pan, Chuan Zhou, Yu Zheng, Feng Xia, and Philip S. Yu. 2023a. Graph Self-supervised Learning: A Survey. IEEE Transactions on Knowledge and Data Engineering 35, 6 (2023), 5879–5900.
- Liu et al. (2023b) Yixin Liu, Ming Jin, Shirui Pan, Chuan Zhou, Yu Zheng, Feng Xia, and Philip S. Yu. 2023b. Graph Self-supervised Learning: A Survey. IEEE Transactions on Knowledge and Data Engineering 35, 6 (2023), 5879–5900.
- Rebuffi et al. (2021) Sylvestre-Alvise Rebuffi, Sven Gowal, Dan Andrei Calian, Florian Stimberg, Olivia Wiles, and Timothy A Mann. 2021. Data Augmentation Can Improve Robustness. In Advances in Neural Information Processing Systems, Vol. 34. 29935–29948.
- Ren et al. (2023) Xubin Ren, Lianghao Xia, Jiashu Zhao, Dawei Yin, and Chao Huang. 2023. Disentangled Contrastive Collaborative Filtering. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval (Taipei, Taiwan) (SIGIR ’23). 1137–1146.
- Rendle et al. (2009) Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. 2009. BPR: Bayesian Personalized Ranking from Implicit Feedback. In Proceedings of the 25th Conference on Uncertainty in AI. 452–461.
- Sang et al. (2024) Lei Sang, Yu Zhang, Yi Zhang, Honghao Li, and Yiwen Zhang. 2024. Towards Similar Alignment and Unique Uniformity in Collaborative Filtering. Expert Systems with Applications (2024).
- Sharma et al. (2024) Kartik Sharma, Yeon-Chang Lee, Sivagami Nambi, Aditya Salian, Shlok Shah, Sang-Wook Kim, and Srijan Kumar. 2024. A Survey of Graph Neural Networks for Social Recommender Systems. ACM Comput. Surv. 56, 10, Article 265 (jun 2024), 34 pages.
- Wang et al. (2022a) Chenyang Wang, Yuanqing Yu, Weizhi Ma, Min Zhang, Chong Chen, Yiqun Liu, and Shaoping Ma. 2022a. Towards Representation Alignment and Uniformity in Collaborative Filtering. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 1816–1825.
- Wang et al. (2022b) Shoujin Wang, Qi Zhang, Liang Hu, Xiuzhen Zhang, Yan Wang, and Charu Aggarwal. 2022b. Sequential/Session-based Recommendations: Challenges, Approaches, Applications and Opportunities. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval (Madrid, Spain) (SIGIR ’22). 3425–3428.
- Wang et al. (2019) Xiang Wang, Xiangnan He, Meng Wang, Fuli Feng, and Tat-Seng Chua. 2019. Neural Graph Collaborative Filtering. In Proceedings of the 42nd International ACM SIGIR Conference. 165–174.
- Wang et al. (2023) Yu Wang, Yuying Zhao, Yi Zhang, and Tyler Derr. 2023. Collaboration-Aware Graph Convolutional Network for Recommender Systems. In Proceedings of the ACM Web Conference 2023 (Austin, TX, USA) (WWW ’23). 91–101.
- Wang et al. (2020) Ziyang Wang, Wei Wei, Gao Cong, Xiao-Li Li, Xian-Ling Mao, and Minghui Qiu. 2020. Global Context Enhanced Graph Neural Networks for Session-based Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. 169–178.
- Wu et al. (2019) Felix Wu, Amauri Souza, Tianyi Zhang, Christopher Fifty, Tao Yu, and Kilian Weinberger. 2019. Simplifying Graph Convolutional Networks. In Proceedings of the 36th International Conference on Machine Learning, Vol. 97. 6861–6871.
- Wu et al. (2021) Jiancan Wu, Xiang Wang, Fuli Feng, Xiangnan He, Liang Chen, Jianxun Lian, and Xing Xie. 2021. Self-supervised Graph Learning for Recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. 726–735.
- Wu et al. (2023) Le Wu, Xiangnan He, Xiang Wang, Kun Zhang, and Meng Wang. 2023. A Survey on Accuracy-Oriented Neural Recommendation: From Collaborative Filtering to Information-Rich Recommendation. IEEE Transactions on Knowledge and Data Engineering 35, 5 (2023), 4425–4445.
- Wu et al. (2022) Shiwen Wu, Fei Sun, Wentao Zhang, Xu Xie, and Bin Cui. 2022. Graph Neural Networks in Recommender Systems: A Survey. Comput. Surveys 55, 5, Article 97 (dec 2022), 37 pages.
- Xia et al. (2023) Lianghao Xia, Chao Huang, Chunzhen Huang, Kangyi Lin, Tao Yu, and Ben Kao. 2023. Automated Self-Supervised Learning for Recommendation. In Proceedings of the ACM Web Conference 2023. 992–1002.
- Yang et al. (2023a) Liangwei Yang, Zhiwei Liu, Chen Wang, Mingdai Yang, Xiaolong Liu, Jing Ma, and Philip S. Yu. 2023a. Graph-based Alignment and Uniformity for Recommendation. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management. 4395–4399.
- Yang et al. (2023b) Yonghui Yang, Zhengwei Wu, Le Wu, Kun Zhang, Richang Hong, Zhiqiang Zhang, Jun Zhou, and Meng Wang. 2023b. Generative-Contrastive Graph Learning for Recommendation. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval. 1117–1126.
- Yu et al. (2022a) Junliang Yu, Hongzhi Yin, Jundong Li, Min Gao, Zi Huang, and Lizhen Cui. 2022a. Enhancing Social Recommendation With Adversarial Graph Convolutional Networks. IEEE Transactions on Knowledge and Data Engineering 34, 8 (2022), 3727–3739.
- Yu et al. (2022b) Junliang Yu, Hongzhi Yin, Xin Xia, Tong Chen, Lizhen Cui, and Quoc Viet Hung Nguyen. 2022b. Are Graph Augmentations Necessary?: Simple Graph Contrastive Learning for Recommendation. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. 1294–1303.
- Yu et al. (2024) Junliang Yu, Hongzhi Yin, Xin Xia, Tong Chen, Jundong Li, and Zi Huang. 2024. Self-supervised Learning for Recommender Systems: A Survey. IEEE Transactions on Knowledge and Data Engineering 36, 1 (2024), 335–355.
- Zhang et al. (2024a) Dan Zhang, Yangliao Geng, Wenwen Gong, Zhongang Qi, Zhiyu Chen, Xing Tang, Ying Shan, Yuxiao Dong, and Jie Tang. 2024a. RecDCL: Dual Contrastive Learning for Recommendation. In Proceedings of the ACM on Web Conference 2024 (Singapore, Singapore) (WWW ’24). 3655–3666.
- Zhang et al. (2024b) Yi Zhang, Lei Sang, and Yiwen Zhang. 2024b. Exploring the Individuality and Collectivity of Intents behind Interactions for Graph Collaborative Filtering. In Proceedings of the 47th International ACM SIGIR Conference on Research and Development in Information Retrieval.
- Zhang et al. (2023) Yi Zhang, Yiwen Zhang, Dengcheng Yan, Shuiguang Deng, and Yun Yang. 2023. Revisiting Graph-based Recommender Systems from the Perspective of Variational Auto-Encoder. ACM Transactions on Information Systems 41, 3 (2023), 1–28.
- Zhang et al. (2024c) Yi Zhang, Yiwen Zhang, Yuchuan Zhao, Shuiguang Deng, and Yun Yang. 2024c. Dual Variational Graph Reconstruction Learning for Social Recommendation. IEEE Transactions on Knowledge and Data Engineering (2024). https://doi.org/10.1109/TKDE.2024.3386895