High Curie temperature and high hole mobility in diluted magnetic semiconductors (B, Mn)X (X = N, P, As, Sb)

Xiang Li Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China Jia-Wen Li Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China Jing-Yang You Department of Physics, National University of Singapore, 2 Science Drive 3, Singapore 117551 Gang Su [email protected] Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China CAS Center for Excellence in Topological Quantum Computation, University of Chinese Academy of Sciences, Beijing 100190, China Physical Science Laboratory, Huairou National Comprehensive Science Center, Beijing 101400, China School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China Bo Gu [email protected] Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China CAS Center for Excellence in Topological Quantum Computation, University of Chinese Academy of Sciences, Beijing 100190, China Physical Science Laboratory, Huairou National Comprehensive Science Center, Beijing 101400, China

Abstract

Doping nonmagnetic semiconductors with magnetic impurities is a feasible way to obtain diluted magnetic semiconductors (DMSs). It is generally accepted that for the most extensively studied DMS, (Ga, Mn)As, its highest Curie temperature T ${}_{\text{C}}$ was achieved at 200 K with a Mn concentration of approximately 16% in experiments. A recent experiment reported record-breaking high electron and hole mobilities in the semiconductor BAs [Science 377, 437 (2022)]. Since BAs shares the same zinc-blende structure with GaAs, here we predict four DMSs (B, Mn)X (X = N, P, As, Sb) by density functional theory calculations. Our results indicate that a significantly higher T ${}_{\text{C}}$ in the range of 254 K to 300 K for (B, Mn)As with a Mn concentration of around 15.6%, and even higher T ${}_{\text{C}}$ values above the room temperature for (B, Mn)N and (B, Mn)P with a Mn concentration exceeding 12.5%. Furthermore, we have predicted a large hole mobility of 1561 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ at 300 K for (B, Mn)As with a Mn concentration of about 3.7%, which is three orders of magnitude larger than the hole mobility of 4 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ at 300 K observed in the experiment for (Ga, Mn)As. Our findings predict the emergence of a new family of DMS, (B, Mn)X, and are expected to stimulate both experimental and theoretical studies of the DMS with high T ${}_{\text{C}}$ and high mobilities.

I Introduction

Magnetic semiconductors, owing to their combination of electron and spin degrees of freedom, hold significant promise for spintronic applications. One effective method to introduce long-range magnetic order and realize diluted magnetic semiconductor (DMS) is doping magnetic impurities such as Cr, Mn, Fe and Co in nonmagnetic semiconductors. Several efforts have focused on doping III-V zinc-blende semiconductors. In the case of the classic DMS (Ga, Mn)As, a Curie temperature T ${}_{\text{C}}$ of 110 K was obtained with a Mn impurity concentration of 5.3% [1], and a higher T ${}_{\text{C}}$ of 200 K was attained with a Mn impurity concentration of 16% by using non-eqilibrium techniques [2]. However, further enhancing T ${}_{\text{C}}$ of (Ga, Mn)As becomes challenging due to the valance mismatch of Mn ${}^{\text{2+}}$ and Ga ${}^{\text{3+}}$ . This leads Mn impurities to occupy interstitial positions as the doping concentration increases. [3, 4, 5, 6, 7]. In experiments of some Mn-doped III-V semiconductors, T ${}_{\text{C}}$ was reported at 60 K for (Ga, Mn)P with a Mn concentration of 6% [8] and T ${}_{\text{C}}$ reached 15 K in (Ga, Mn)Sb with a Mn concentration of 3.9% [9], as shown in TABLE 1. It is noted that the carrier in DMSs (Ga, Mn)X (X = P, As, Sb) is hole, i.e. p-type. The ferromagnetism in (Ga, Mn)N remains a subject of debate, some experiments reported the room-temperature ferromagnetism [10, 11, 12] and attributed the high T ${}_{\text{C}}$ to Mn ${}_{\text{x}}$ N ${}_{\text{y}}$ clusters instead of dopants [10, 11], while other experiments observed low T ${}_{\text{C}}$ below 10 K [13, 14, 15].

Table 1: Experimental results of Curie temperature, impurity concentration and carrier types for Mn-doped magnetic semiconductors (Ga, Mn)X (X = P, As, Sb) with zinc-blende structure.

Diluted magnetic semiconductors (years)	Curie temperature T ${}_{\text{C}}$	Impurity concentration	Carrier types
(Ga, Mn)P (2005) [8]	60 K	6%	p-type
(Ga, Mn)As (2011) [2]	200 K	16%	p-type
(Ga, Mn)Sb (2014) [9]	15 K	3.9%	p-type

Some DMSs with high T ${}_{\text{C}}$ have been reported in experiments in the past decade [16]. A T ${}_{\text{C}}$ of 230 K was obtained in p-type DMS (Ba, K)(Zn, Mn) ${}_{\text{2}}$ As ${}_{\text{2}}$ with a Mn impurity concentration of 15% [17, 18]. This DMS has the advantage of decoupled charge and spin doping [19, 20]. The hole-mediated ferromagnetism in (Ba, K)(Zn, Mn) ${}_{\text{2}}$ As ${}_{\text{2}}$ has been discussed in photoemission spectroscopy experiments [21, 22] and theoretical calculations [23, 24], similar to the picture discussed in (Ga, Mn)As. The T ${}_{\text{C}}$ of 45 K in Co-doped n-type DMS Ba(Zn, Co) ${}_{\text{2}}$ As ${}_{\text{2}}$ was also reported in the experiment [25]. Experiments have reported T ${}_{\text{C}}$ of 340 K in (Ga, Fe)Sb with a Fe concentration of 25% [26] and T ${}_{\text{C}}$ of 385 K in (In, Fe)Sb with Fe concentration of 35% [27]. The valence match between dopant Fe ${}^{\text{3+}}$ and hosts Ga ${}^{\text{3+}}$ and In ${}^{\text{3+}}$ and the very high impurity concentration appear to be key factors contributing to these high T ${}_{\text{C}}$ values [28]. T ${}_{\text{C}}$ of Mn-doped Si ${}_{\text{0.25}}$ Ge ${}_{\text{0.75}}$ with a Mn concentration of 5% was reported to be 280 K [29] and honeycomb structure (Zn, Co)O monolayer with a Co concentration of 11.1% was confirmed to exhibit long-range ferromagnetism with T ${}_{\text{C}}$ above 300 K [30].

Intrinsic two-dimensional (2D) magnetic semiconductors have also been synthesized sucessfully and studied in recent years. However, T ${}_{\text{C}}$ of these 2D magnetic semiconductors in experiments, such as CrI ${}_{\text{3}}$ [31], Cr ${}_{\text{2}}$ Ge ${}_{\text{2}}$ Te ${}_{\text{6}}$ [32], CrCl ${}_{\text{3}}$ [33], CrBr ${}_{\text{3}}$ [34], Cr ${}_{\text{2}}$ S ${}_{\text{3}}$ [35, 36], CrSBr [37] and CrSiTe ${}_{\text{3}}$ [38] are far below the room temperature. In order to enhance T ${}_{\text{C}}$ of 2D magnetic semiconductors, effects of strain, electric field and heterostructure are theoretically studied, where some high T ${}_{\text{C}}$ 2D magnetic semiconductors are proposed [39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49].

For the magnetic semiconductor, high mobility is also required for semiconductor applications. For the classic DMS (Ga, Mn)As with hole carriers, the experimental hole mobility of (Ga, Mn)As is lower than 4 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ at room temperature [50, 51]. In fact, there are few magnetic semiconductors with both high T ${}_{\text{C}}$ and high hole mobility in experiments [29]. Recently, it was discovered that the semiconductor boron arsenide (BAs), isostructural to the zinc-blende GaAs, has both high electron mobility and hole mobility 1600 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ [52]. Although BAs had been synthesized several decades ago [53, 54, 55, 56], some theoretical works have reported the wide gap, high electron and hole mobilities and high thermal conductivity [57, 58, 59, 60, 61, 62, 63, 64], there have been several experiments reporting transports of the high electron mobility [65, 66, 67], the high hole mobility has not been confirmed until 2022 [52]. Inspired by the experimental high hole mobility in BAs and the similarity between semiconductors BAs and GaAs, is it possible to obtain the DMS of Mn-doped BAs with both high T ${}_{\text{C}}$ and high mobility?

In this paper, we carry out calculations on the Mn-doped zinc-blende BX (X = N, P, As, Sb) with the density functional theory (DFT). Our results show a high T ${}_{\text{C}}$ in the range of 254 K to 300 K in (B, Mn)As with a Mn concentration of 15.6%, higher than the T ${}_{\text{C}}$ of 200 K in (Ga, Mn)As with a Mn concentration of 16% in experiment, which might be attributed to the shorter length of B-B bond in BAs. Mn impurities in BAs keep it a p-type semiconductor, and a high hole mobility of 1561 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ at 300 K is found in (B, Mn)As with a Mn concentration of about 3.7%. Other DMSs (B, Mn)N, (B, Mn)P and (B, Mn)Sb are also explored, T ${}_{\text{C}}$ values above the room temperature are predicted for (B, Mn)N and (B, Mn)P with a Mn concentration of above 12.5%, while low T ${}_{\text{C}}$ is obtained in (B, Mn)Sb. We use two cases for calculations of exchange coupings and Curie temperatures, results obtained from two cases all support our findings on high T ${}_{\text{C}}$ in DMS of (B, Mn)X family.

II Computational details

First-principles calculations in this work were performed with the projector augmented wave (PAW) method [68] based on the DFT as implemented in the Vienna ab initio simulation package (VASP) [69]. The choice of the electron exchange-correlation functional was generalized gradient approximation (GGA) with the form of Perdew-Burke-Ernzerhof (PBE) realization [70]. Lattice constants and atomic positions were fully relaxed until the maximum force acting on all atoms was less than 1 $\times$ 10 ${}^{\text{-4}}$ eV and the total energy was converged to 1 $\times$ 10 ${}^{\text{-8}}$ eV with the Gaussian smearing method. Calculations of exchange coupling $J_{\text{i}}$ were performed by using the 2 $\times$ 2 $\times$ 2 conventional cubic supercell. The Monkhorst-Pack k-point mesh [71] of size 6 $\times$ 6 $\times$ 6 was used for the Brillouin zone (BZ) sampling in structure optimization and self-consistent processes of exchange coupling calculations, while for calculations of band structures and mobilities using the primitive cell, the Monkhorst-Pack k-point mesh of size 9 $\times$ 9 $\times$ 9 was used. The plane-wave cutoff energy was set to be 500 eV. The electron correlation of the 3d transition atom Mn was considered by using the DFT+U method introduced by Dudarev et al. [72]. Most of results were obtained with U = 5 eV and the effect of different values of U has been discussed.

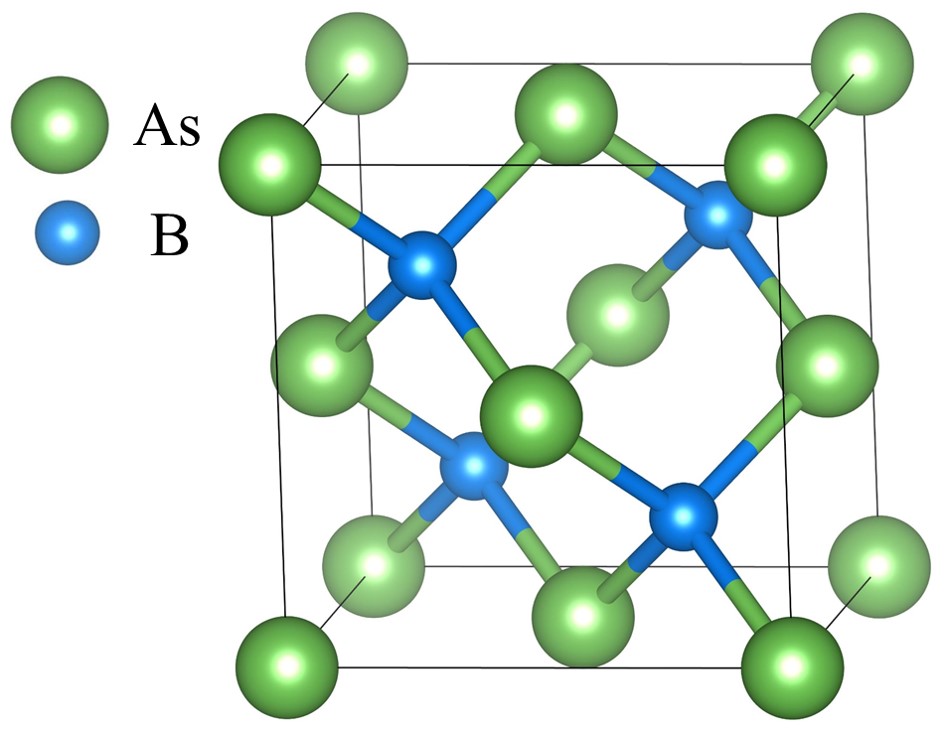
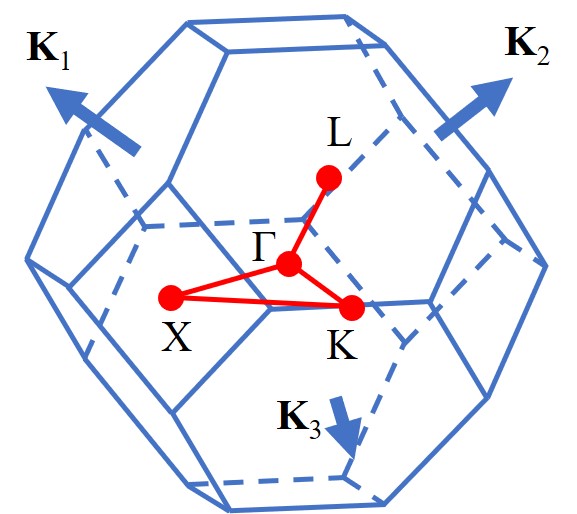
III Results

III.1 Exchange couplings of (B, Mn)As

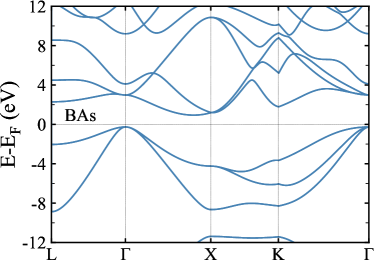
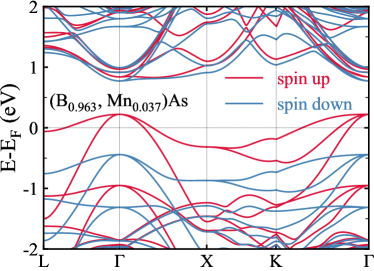
Zinc-blende BAs has the space group F $\bar{\text{4}}$ 3m (No. 216), its crystal structure and the first Brillouin zone with high symmetry paths indicated with red color are shown in FIG. 1(a) and FIG. 1(b), respectively. As shown in FIG. 1(c), BAs is a semiconductor with a calculated indirect gap of 1.20 eV, which is consistent with experimental values of 1.46 eV [53, 54, 55, 56] and other calculations [57, 58, 59, 60, 61]. The 3 $\times$ 3 $\times$ 3 primitive supercell with B ${}_{\text{26}}$ MnAs ${}_{\text{27}}$ is adopted to study the electronic structure of the Mn-doped BAs. As shown in FIG. 1(d), (B ${}_{\text{0.963}}$ , Mn ${}_{\text{0.037}}$ )As is a p-type semiconductor and the band gap shrinks to 0.55 eV and becomes direct at $\Gamma$ .

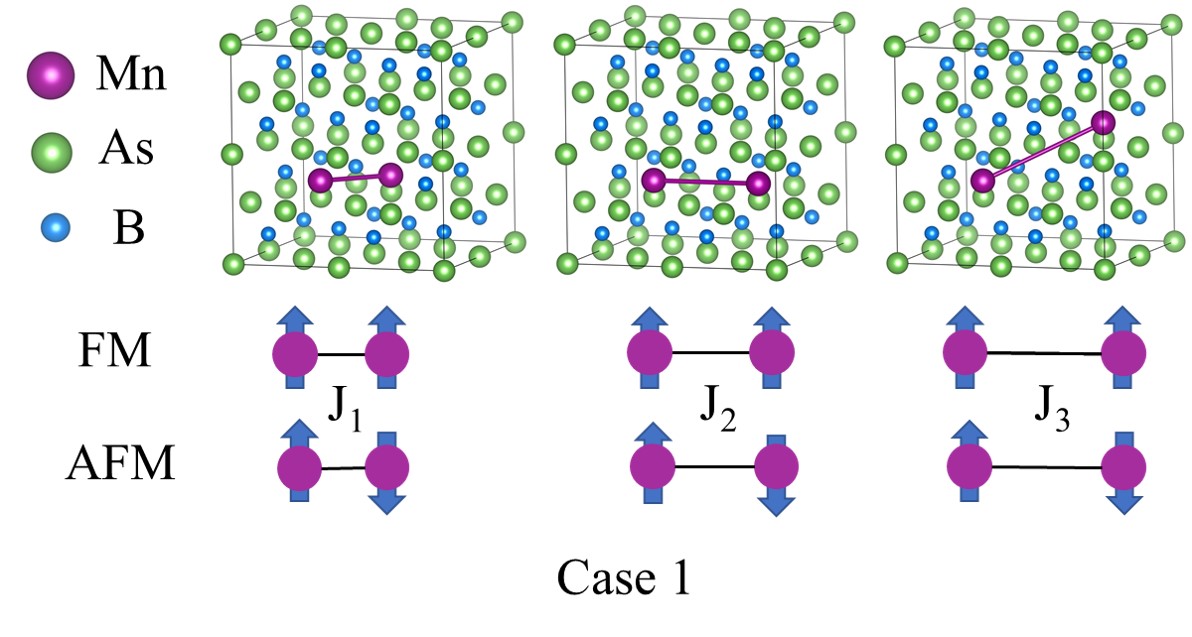
In order to estimate T ${}_{\text{C}}$ of the Mn-doped BAs, we should calculate the magnetic exchange coupling of two Mn impurities first. The disordered magnetic system is mapped to the classical Heisenberg-type Hamiltonian with $J_{\text{1}}$ , $J_{\text{2}}$ and $J_{\text{3}}$ denoting exchange couplings for the nearest neighbor, the next-nearest neighbor and the third-nearest neighbor between two impurity sites, respectively, Hamiltonian is expressed as

\displaystyle H=

\displaystyle-\sum_{i<j}J_{\text{1}}\bm{S}_{i}\cdot\bm{S}_{j}-\sum_{i<k}J_{\text{2}}\bm{S}_{i}\cdot\bm{S}_{k}-\sum_{i<l}J_{\text{3}}\bm{S}_{i}\cdot\bm{S}_{l}

(1)

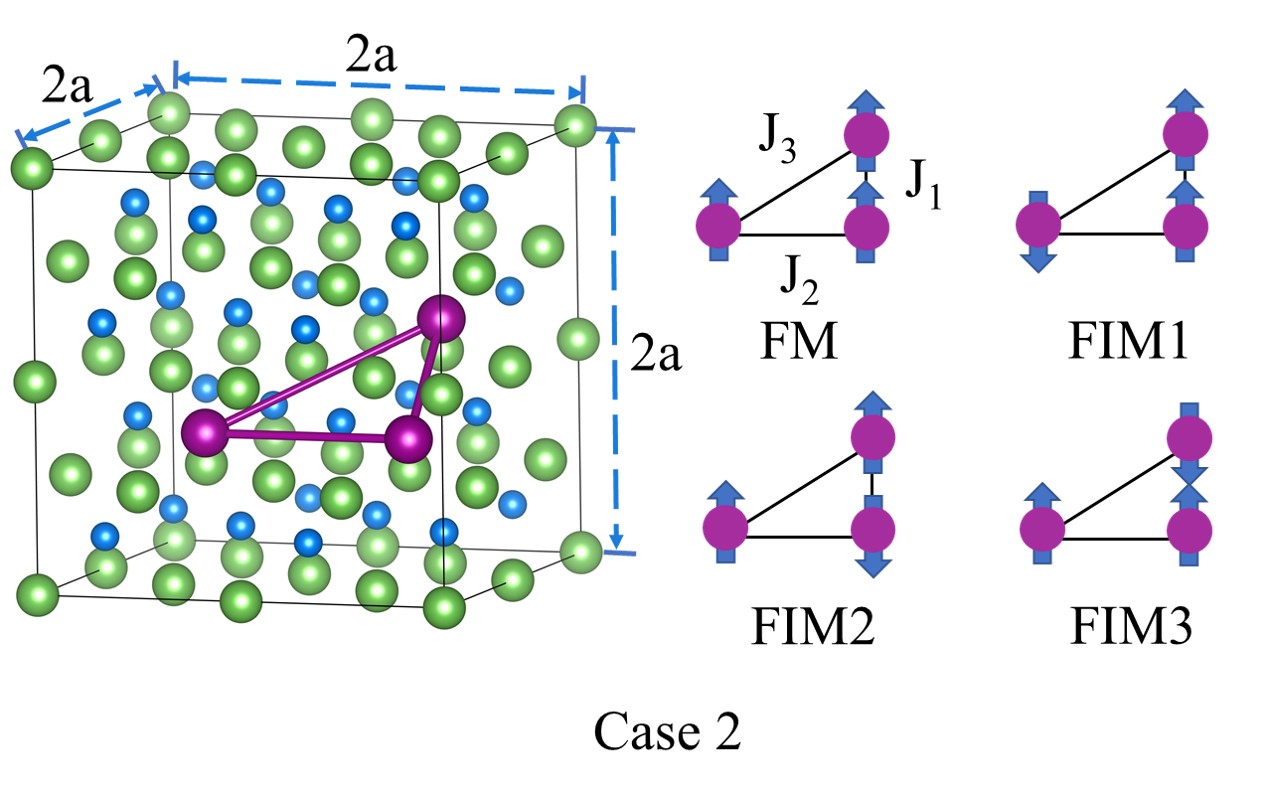
where two impurities are coupled ferromagnetically for conditions of $J_{\text{i}}$ $>$ 0 while antiferromagnetically for conditions of $J_{\text{i}}$ $<$ 0. In this work, exchange coupling parameters are calculated via two cases illustrated in FIG. 2. To avoid the influence of unphysical long-range exchange interaction from magnetic atoms in mirror neighbor cells and reduce the computation, some different 2 $\times$ 2 $\times$ 2 cubic supercells are adopted as shown in FIG. 2, where a stands for the lattice constant of BAs.

Table 2: Exchange coupling parameters

J_{\text{i}}

(meV) of two Mn impurities in (B, Mn)As and (Ga, Mn)As calculated by DFT+U with spin S = 5/2 and Hubbard correlation parameter U = 5 eV.

J_{\text{1}}

J_{\text{2}}

and

J_{\text{3}}

denote the exchange coupling for the nearest neighbor, the second-nearest neighbor and the third-nearest neighbor, respectively.

		$J_{\text{1}}$ (meV)	$J_{\text{2}}$ (meV)	$J_{\text{3}}$ (meV)
Case 1	(B, Mn)As (Ga, Mn)As	15.813 10.215	1.226 0.136	2.215 1.811
Case 2	(B, Mn)As (Ga, Mn)As	12.527 8.305	-0.884 -0.633	0.036 0.808

For Case 1, three different supercells of B ${}_{\text{30}}$ Mn ${}_{\text{2}}$ As ${}_{\text{32}}$ are used. Ferromagnetic (FM) configuration with parellel spins and antiferromagnetic (AFM) configuration with anti-parellel spins structures are considered. Case 1 is the conventional way to construct supercells in past studies of DMSs [73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86]. $J_{\text{1}}$ , $J_{\text{2}}$ and $J_{\text{3}}$ are calculated independently. For $J_{\text{1}}$ , two impurities are located at (0.375, 0.125, 0.375)2a and (0.625, 0.375, 0.375)2a illustrated in FIG. 2(a) and their energy expressions are given by

	$\displaystyle E_{\text{AFM}}=$	$\displaystyle E_{0}+J_{1}S^{2},$		(2)
	$\displaystyle E_{\text{FM}}=$	$\displaystyle E_{0}-J_{1}S^{2},$		(3)

where $E_{0}$ is the energy independent of spin configurations. The energy difference between FM and AFM configurations gives the $J_{\text{1}}$ . For $J_{\text{2}}$ , two impurities are located at (0.375, 0.125, 0.375)2a and (0.875, 0.125, 0.375)2a and their energy expressions are given by

	$\displaystyle E_{\text{AFM}}=$	$\displaystyle E_{0}+2J_{2}S^{2},$		(4)
	$\displaystyle E_{\text{FM}}=$	$\displaystyle E_{0}-2J_{2}S^{2}.$		(5)

$J_{\text{2}}$ can be calculated by Eq. (4) with DFT results of $E_{\text{AFM}}$ and $E_{\text{FM}}$ . For $J_{\text{3}}$ , two impurities are located at (0.375, 0.125, 0.375)2a and (0.875, 0.375, 0.625)2a and their energy expressions are given by

	$\displaystyle E_{\text{AFM}}=$	$\displaystyle E_{0}+2J_{3}S^{2},$		(6)
	$\displaystyle E_{\text{FM}}=$	$\displaystyle E_{0}-2J_{3}S^{2}.$		(7)

$J_{\text{3}}$ can be obtained by Eq. (6).

For Case 2, a supercell of B ${}_{\text{29}}$ Mn ${}_{\text{3}}$ As ${}_{\text{32}}$ is used, where three Mn impurities are located at (0.375, 0.125, 0.375)2a, (0.875, 0.125, 0.375)2a and (0.875, 0.375, 0.625)2a. $J_{\text{1}}$ , $J_{\text{2}}$ and $J_{\text{3}}$ are calculated conjointly. Bonds of impurity sites form a right triangle each line of which corresponds to differnt kind of exchange coupling as marked in the right panel of FIG. 2(b). Four different spin configurations including FM and three ferrimagnetic configurations (FIM1, FIM2 and FIM3) are considered and their corresponding energy formulae are expressed as

$\displaystyle E_{\text{FM}}=$	$\displaystyle E_{0}-J_{1}S^{2}-2J_{2}S^{2}-2J_{3}S^{2},$	(8)
$\displaystyle E_{\text{FIM1}}=$	$\displaystyle E_{0}-J_{1}S^{2}+2J_{2}S^{2}+2J_{3}S^{2},$	(9)
$\displaystyle E_{\text{FIM2}}=$	$\displaystyle E_{0}+J_{1}S^{2}+2J_{2}S^{2}-2J_{3}S^{2},$	(10)
$\displaystyle E_{\text{FIM3}}=$	$\displaystyle E_{0}+J_{1}S^{2}-2J_{2}S^{2}+2J_{3}S^{2}.$	(11)

$J_{\text{1}}$ , $J_{\text{2}}$ and $J_{\text{3}}$ can be calculated by Eq. (8) with DFT results of $E_{\text{FM}}$ , $E_{\text{FIM1}}$ , $E_{\text{FIM2}}$ and $E_{\text{FIM3}}$ .

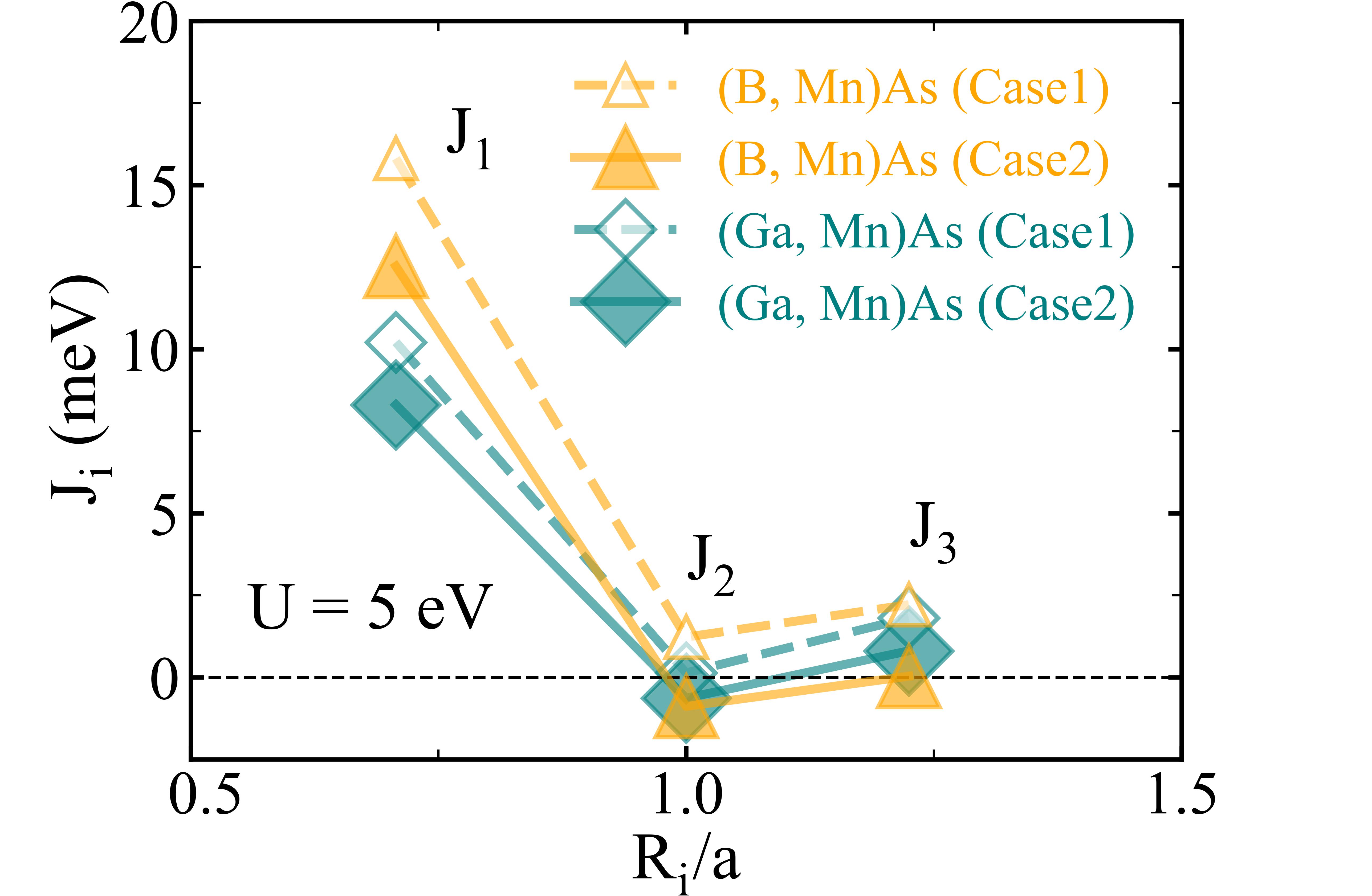
The obtained exchange coupling parameters $J_{\text{1}}$ , $J_{\text{2}}$ and $J_{\text{3}}$ for Mn-doped BAs and GaAs are shown in TABLE 2 and FIG. 3(a), where U = 5 eV. For Mn atom with five local d electrons, the spin is set to be S = 5/2. It is noted that obtained values of exchange couplings $J_{\text{1}}$ , $J_{\text{2}}$ and $J_{\text{3}}$ are independent of impurity concentrations, and the disorder effect due to impurities in DMS is included in coordination numbers in the mean-field formula of T ${}_{\text{C}}$ in Eq. (12). Exchange couplings of (B, Mn)As and (Ga, Mn)As calculated by Case 1 and Case 2 show similar behaviors as a function of distance between two impurities R ${}_{\text{i}}$ (in unit of the lattice constant a). The nearest coupling $J_{\text{1}}$ is ferromagnetic and dominants the exchange interaction. $J_{\text{i}}$ drops drastically when two impurities are placed more distant. The strength of $J_{\text{1}}$ is near ten times larger than $J_{\text{2}}$ which is weak-antiferromagnetic for Case 2 while is weak-ferromagnetic for Case 1. The third-nearest coupling $J_{\text{3}}$ rises slightly and is much smaller than the nearest coupling $J_{\text{1}}$ . Both $J_{\text{2}}$ and $J_{\text{3}}$ close to zero. $J_{\text{1}}$ of (B, Mn)As is much larger than that of (Ga, Mn)As for both cases, which might be attributed to the shorter B-B bond length in BAs and thus shorter Mn-Mn distance in (B, Mn)As.

III.2 Curie temperatures of (B, Mn)As

Curie temperature T ${}_{\text{C}}$ is estimated via Weiss mean-field formula

\displaystyle T^{\text{MFA}}_{\text{C}}=

\displaystyle\frac{2}{3k_{\text{B}}}S(S+1)\sum_{\text{i}}\sum_{\alpha}Z_{\text{i}}^{\alpha}P_{\alpha}J_{\text{i}}.

(12)

$Z_{\text{i}}^{\alpha}$ is the coordination number of one doping configuration $\alpha$ for the given doping concentration, $P_{\alpha}$ is the probability of this doping configuration. Doping configurations $\alpha$ are generated via Disorder code [88, 89]. To simulate the doped system with random distribution of magnetic impurities, different doping configurations for a given doping concentration are considered in the 2 $\times$ 2 $\times$ 2 cubic supercell with B ${}_{\text{32}}$ As ${}_{\text{32}}$ . The condition of the doping concentration 6.25% is given as an example where two B atoms in the supercell B ${}_{\text{32}}$ As ${}_{\text{32}}$ are replaced with Mn impurities, so there are three inequivalent doping configurations and their corresponding $Z_{\text{i}}^{\alpha}$ and $P_{\alpha}$ are listed in TABLE 3, see Supplemental Material for more details about this method and coordination numbers of other doping concentrations [87].

Table 3: For doping concentration 6.25%, doping configuration

\alpha

, coordination number

Z_{\text{i}}^{\alpha}

of the exchange coupling

J_{\text{i}}

, and probability

P_{\alpha}

$\alpha$	$Z_{\text{i}}^{\alpha}$ for Mn1	$Z_{\text{i}}^{\alpha}$ for Mn2	$P_{\alpha}$
1	{1, 0, 0}	{1, 0, 0}	4/9
2	{0, 2, 0}	{0, 2, 0}	1/9
3	{0, 0, 2}	{0, 0, 2}	4/9

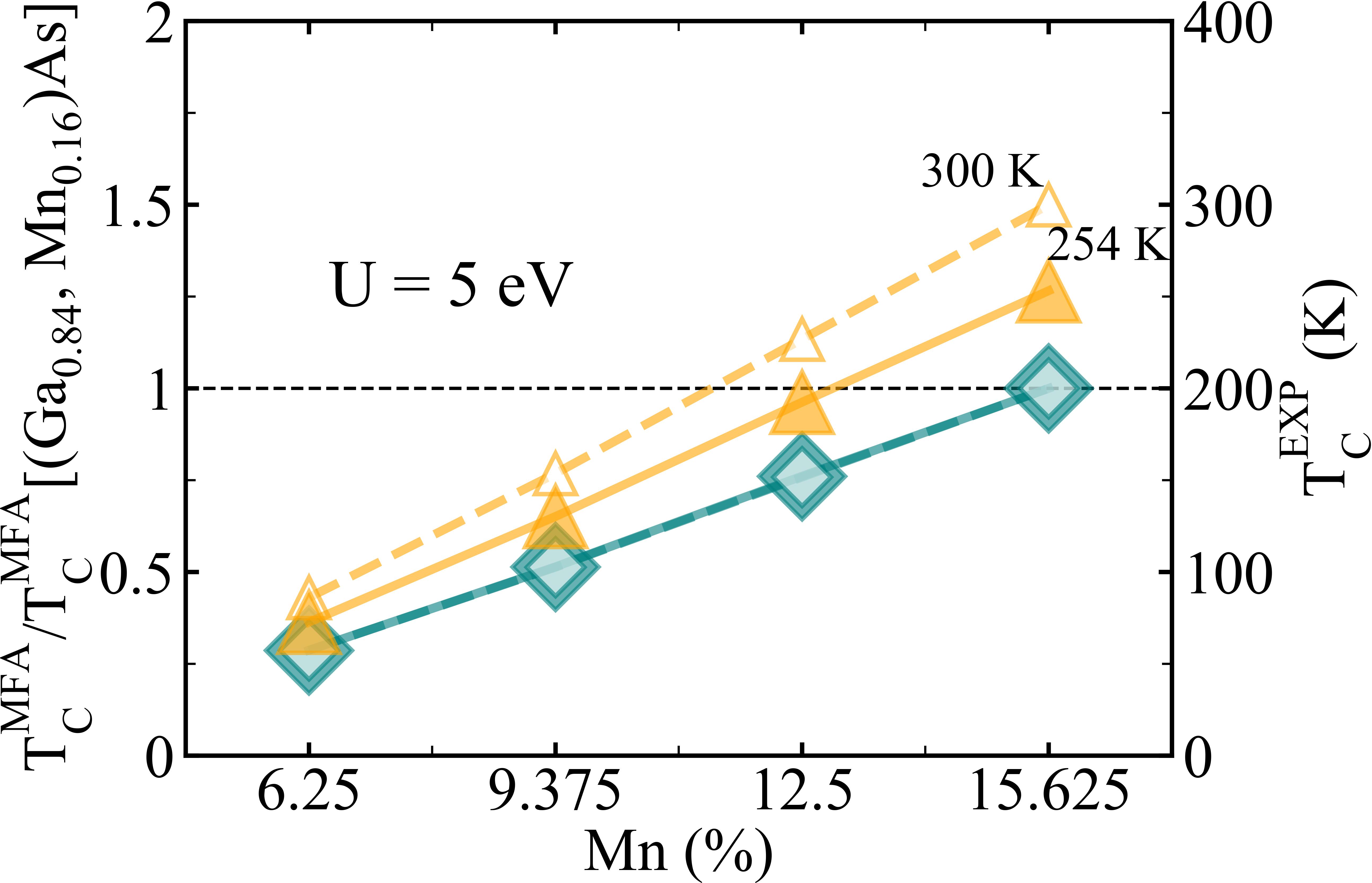
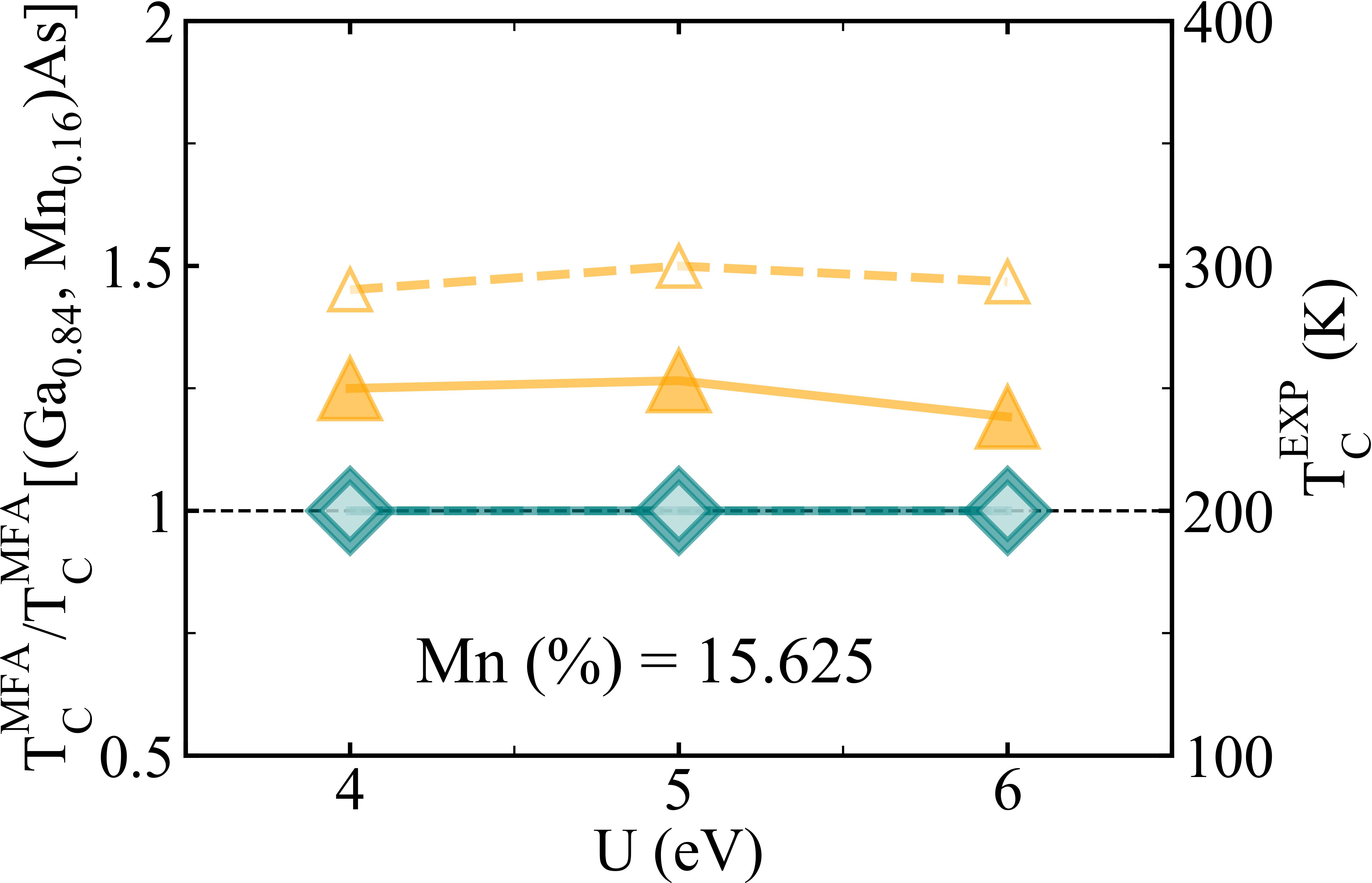
Values of T ${}_{\text{C}}^{\text{MFA}}$ , calculated by Eq. (12) with exchange couplings listed in TABLE 2, are far beyond the experimental value T ${}_{\text{C}}^{\text{EXP}}$ , because it is expected that the mean-field formula always overestimates the Curie temperature. In order to provide a more reliable estimation of Curie temperatures of (Ga, Mn)As and (B, Mn)As, we analyze our data in the following way. As shown in FIG. 3(b), the ratio of the mean-field Curie temperatures T ${}_{\text{C}}^{\text{MFA}}$ /T ${}_{\text{C}}^{\text{MFA}}$ [(Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As] as a function of Mn impurity concentration is plotted, where U = 5 eV. The T ${}_{\text{C}}^{\text{MFA}}$ of (Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As is taken as the unit one, which physically corresponds to the T ${}_{\text{C}}^{\text{EXP}}$ = 200 K of (Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As in the experiment [2]. We plot such correspondence in FIG. 3(b) by a black dashed line. In this way, it is shown that T ${}_{\text{C}}^{\text{MFA}}$ of (B, Mn)As is larger than that of (Ga, Mn)As for both Case 1 and Case 2, while the ratios T ${}_{\text{C}}^{\text{MFA}}$ /T ${}_{\text{C}}^{\text{MFA}}$ [(Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As] of (Ga, Mn)As of Case 1 and Case 2 are overlapped. T ${}_{\text{C}}^{\text{MFA}}$ /T ${}_{\text{C}}^{\text{MFA}}$ [(Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As] is 1.27 for (B, Mn)As with a Mn concentration of 15.625% for Case 2, which corresponds to T ${}_{\text{C}}^{\text{EXP}}$ = 254 K for (B, Mn)As with a Mn concentration of 15.625%. T ${}_{\text{C}}^{\text{MFA}}$ /T ${}_{\text{C}}^{\text{MFA}}$ [(Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As] is 1.50 for (B, Mn)As with 15.625% of Mn for Case 1, which corresponds to T ${}_{\text{C}}^{\text{EXP}}$ = 300 K for (B, Mn)As with 15.625% of Mn. A high Curie temperature T ${}_{\text{C}}^{\text{EXP}}$ is predicted for (B, Mn)As with a Mn concentration around 15.625%, larger than experimental value of Curie temperature T ${}_{\text{C}}^{\text{EXP}}$ of 200 K for (Ga, Mn)As with a Mn concentration of 16% [2]. For (B, Mn)As with reasonable U values of Mn impurities, T ${}_{\text{C}}^{\text{MFA}}$ /T ${}_{\text{C}}^{\text{MFA}}$ [(Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As] with a Mn concentration around 15.625% is calculated as shown in FIG. 3(c). Results of exchange couplings with U = 4 eV and U = 6 eV are listed in Supplemental Material [87]. T ${}_{\text{C}}^{\text{MFA}}$ /T ${}_{\text{C}}^{\text{MFA}}$ [(Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As] changes slightly for both Case 1 and Case 2 when varying parameter U. More results of Case 2 and U = 5 eV will be discussed in the following part.

III.3 Curie temperatures of (B, Mn)X (X = N, P, Sb)

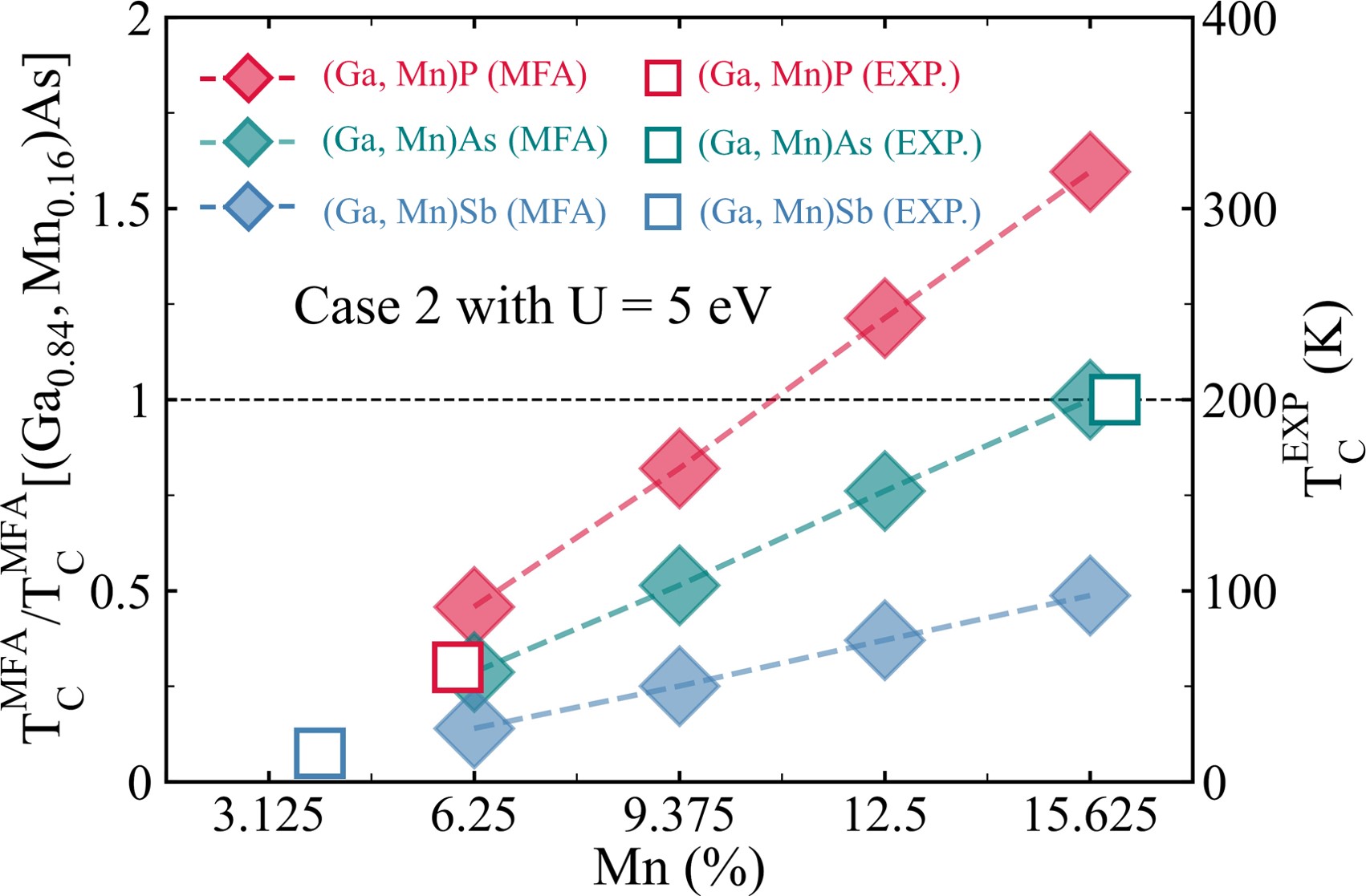
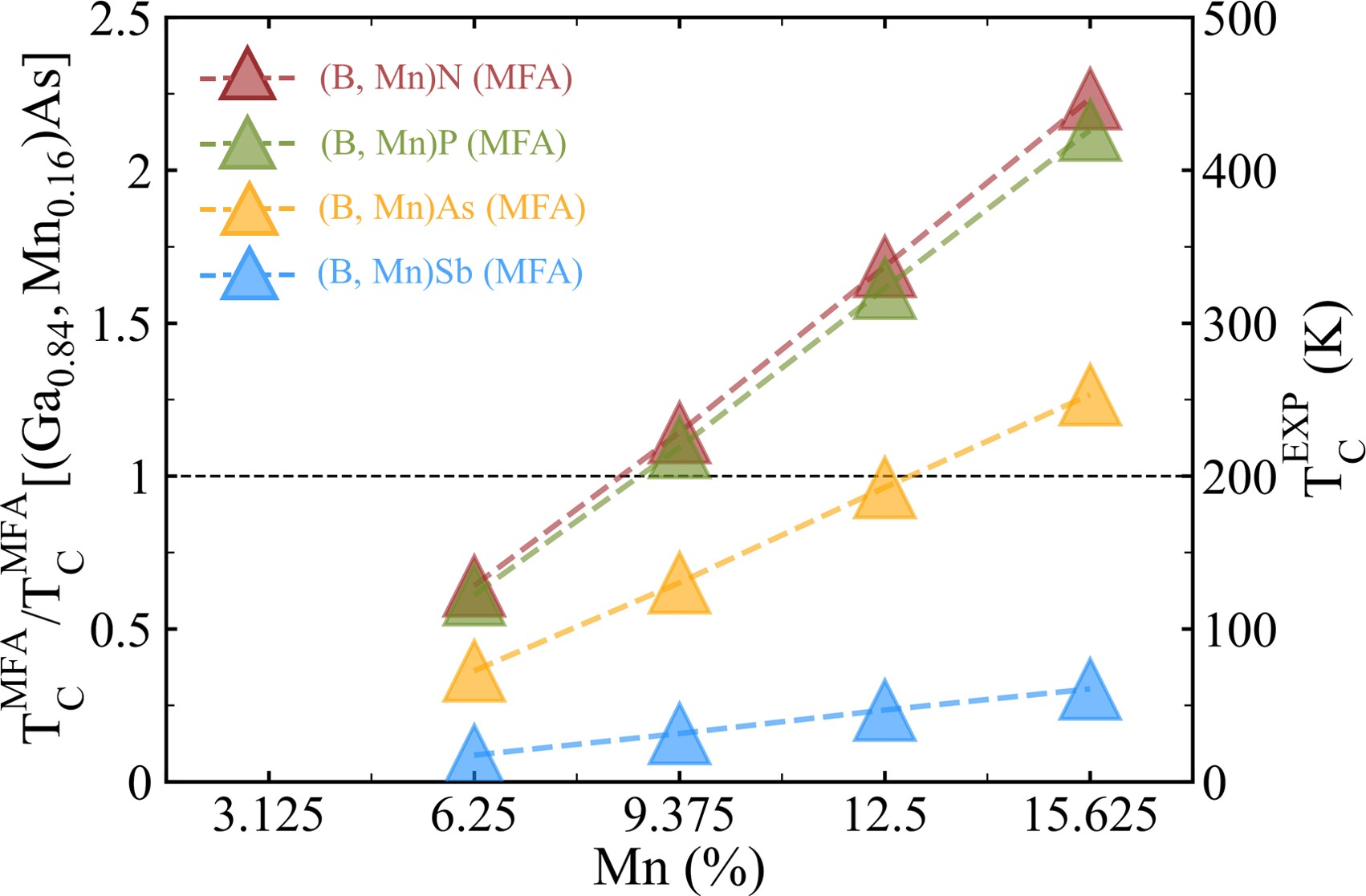
In order to verify the reliability of the above rescaling method, the ratio of the mean-field Curie temperature T ${}_{\text{C}}^{\text{MFA}}$ /T ${}_{\text{C}}^{\text{MFA}}$ [(Ga ${}_{\text{0.84}}$ , Mn ${}_{\text{0.16}})$ As] as a function of the Mn impurity concentration for (Ga, Mn)P and (Ga, Mn)Sb are calculated and shown in FIG. 4(a) with exchange coupings of Case 2. Experimental Curie temperatures of (Ga, Mn)P, (Ga, Mn)As and (Ga, Mn)Sb from TABLE 1 are labeled by hollow squares. Ultra low T ${}_{\text{C}}^{\text{EXP}}$ is found in (Ga, Mn)Sb and T ${}_{\text{C}}^{\text{EXP}}$ of 84 K is obtained for (Ga, Mn)P with a Mn concentration of 6% by our rescaling method, which are consistent with experiments [9, 8]. Curie temperatures of possible DMSs (B, Mn)X with X = N, P, Sb are also calculated in the same way. Band structures of (B, Mn)N, (B, Mn)P and (B, Mn)Sb suggest that they are all p-type semiconductors as shown in Supplemental Material [87]. FIG. 4(b) predicts high T ${}_{\text{C}}$ values above room temperature for (B, Mn)N and (B, Mn)P when the Mn concentration is above 12.5%, and low T ${}_{\text{C}}$ for (B, Mn)Sb. Similar results are obtained for Case 1 with U = 5 eV as shown in Supplemental Material [87].

III.4 Hole mobility of (B, Mn)As

We estimate the hole mobility of BAs, GaAs and (B, Mn)As by deformation potential (DP) theory. The DP theory was proposed by Bardeen and Shockley [90] in 1950s to describe the charge transport in non-polar semiconductors. The mobility formula of the three-dimensional (3D) semiconductor is derived as

\displaystyle\mu_{\text{3D}}=\frac{2\sqrt{2\pi}eC_{\text{3D}}\hbar^{4}}{3(k_{\text{B}}T)^{3/2}E^{2}{m^{*}}^{5/2}},

(13)

where $e>0$ is the charge of the electron, $\hbar$ is the reduced Planck constant, $k_{\text{B}}$ is the Boltzmann constant, $C_{\text{3D}}$ is the elastic constant or Young’s modulus for 3D system, $E$ is DP constant and $m^{*}$ is the effective mass at the band edge. Due to the isotropy of the zinc-blende BAs and (B ${}_{\text{0.963}}$ , Mn ${}_{\text{0.037}}$ )As, only transports along the $z$ -axis are calculated, this direction corrsponds to the $\Gamma$ -X path in the Brillouin zone and only transports of the heavy hole are considered.

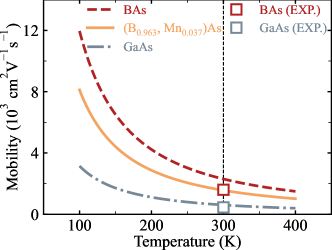
Calculated results are listed in TABLE 4 and FIG. 5 depicts the calculated mobility versus the temperature, where experimental values of BAs and GaAs at 300 K listed in TABLE 4 are added by hollow squares. It is shown that the calculated mobilities for BAs and GaAs at 300 K are consistent with experimental values. The estimated hole mobility of (B ${}_{\text{0.963}}$ , Mn ${}_{\text{0.037}}$ )As is 1561 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ at 300 K which is three orders of magnitude larger than the mobility of 4 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ at 300 K for (Ga, Mn)As.

Table 4: The calculated Young’s modulus C

{}_{\text{3D}}

(GPa), deformation potential constant

E_{\text{h}}

(eV), effective heavy hole mass

m_{\text{h}}

(

m_{0}

) where

m_{0}

is the mass of the bare electron, and heavy hole mobility

\mu_{\text{h}}

(cm

{}^{\text{2}}

{}^{\text{-1}}

{}^{\text{-1}}

) at 300 K for BAs, (B

{}_{\text{0.963}}

, Mn

{}_{\text{0.037}}

)As, and GaAs. For comparison, experimental values of

\mu_{\text{h}}

are also shown.

	C ${}_{\text{3D}}$ (GPa)	$E_{\text{h}}$ (eV)	$m_{\text{h}}$ ( $m_{0}$ )	$\mu_{\text{h}}$ (cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ )	$\mu_{\text{h}}$ (EXP.)
BAs	240.78	4.93	0.59	2301	1600 [52]
(B, Mn)As	192.74	4.78	0.64	1561
GaAs	74.71	2.81	0.98	605	450 [91]
(Ga, Mn)As					$\leq$ 4 [50, 51]

IV Conclusion

By using the density functional theory, we have studied the Mn-doped zinc-blende semiconductors (B, Mn)X (X = N, P, As, Sb). Our calculations show that Mn impurities introduce ferromagnetism in these semiconductors. By the rescaling method of the calculated Curie temperature, we predict a high T ${}_{\text{C}}$ in the range of 254 K to 300 K for (B, Mn)As with 15.6% Mn impurities, which is higher than the highest T ${}_{\text{C}}$ of 200 K for (Ga, Mn)As with 16% Mn impurities in the experiment. T ${}_{\text{C}}$ values above the room temperature are predicted for (B, Mn)N and (B, Mn)P with a Mn concentration of above 12.5%. By the deformation potential theory, (B ${}_{\text{0.963}}$ , Mn ${}_{\text{0.037}}$ )As is found to have high hole mobility 1561 cm ${}^{\text{2}}$ V ${}^{\text{-1}}$ s ${}^{\text{-1}}$ at 300 K which is three orders of magnitude larger than the hole mobility of (Ga, Mn)As in the experiment. Our results highlight the new DMS (B, Mn)As with high T ${}_{\text{C}}$ and high mobilities.

V Acknowledgements

This work is supported by National Key R&D Program of China (Grant No. 2022YFA1405100), National Natural Science Foundation of China (Grant No. 12074378), Chinese Academy of Sciences Project for Young Scientists in Basic Research (Grant No. YSBR-030), National Natural Science Foundation of China (Grant No. 11834014), Basic Research Program of the Chinese Academy of Sciences Based on Major Scientific Infrastructures (Contract No. JZHKYPT-2021-08), Beijing Municipal Science and Technology Commission (Grant No. Z191100007219013), and Strategic Priority Research Program of Chinese Academy of Sciences (Grants No. XDB28000000 and No. XDB33000000).

References

Ohno [1998] H. Ohno, Making Nonmagnetic Semiconductors Ferromagnetic, Science 281, 951 (1998).
Chen et al. [2011] L. Chen, X. Yang, F. Yang, J. Zhao, J. Misuraca, P. Xiong, and S. von Molnár, Enhancing the Curie Temperature of Ferromagnetic Semiconductor (Ga,Mn)As to 200 K via Nanostructure Engineering, Nano Lett. 11, 2584 (2011).
Jungwirth et al. [2006] T. Jungwirth, J. Sinova, J. Mašek, J. Kučera, and A. H. MacDonald, Theory of ferromagnetic (III,Mn)V semiconductors, Rev. Mod. Phys. 78, 809 (2006).
Dietl [2010] T. Dietl, A ten-year perspective on dilute magnetic semiconductors and oxides, Nat. Mater. 9, 965 (2010).
Ohno [2010] H. Ohno, A window on the future of spintronics, Nat. Mater. 9, 952 (2010).
Sato et al. [2010] K. Sato, L. Bergqvist, J. Kudrnovský, P. H. Dederichs, O. Eriksson, I. Turek, B. Sanyal, G. Bouzerar, H. Katayama-Yoshida, V. A. Dinh, T. Fukushima, H. Kizaki, and R. Zeller, First-principles theory of dilute magnetic semiconductors, Rev. Mod. Phys. 82, 1633 (2010).
Dietl and Ohno [2014] T. Dietl and H. Ohno, Dilute ferromagnetic semiconductors: Physics and spintronic structures, Rev. Mod. Phys. 86, 187 (2014).
Scarpulla et al. [2005] M. A. Scarpulla, B. L. Cardozo, R. Farshchi, W. M. H. Oo, M. D. McCluskey, K. M. Yu, and O. D. Dubon, Ferromagnetism in Ga ${}_{\text{1-x}}$ Mn ${}_{\text{x}}$ P: Evidence for Inter-Mn Exchange Mediated by Localized Holes within a Detached Impurity Band, Phys. Rev. Lett. 95, 207204 (2005).
Zhu et al. [2015] M.-Y. Zhu, J. Lu, J.-L. Ma, L.-X. Li, H.-L. Wang, D. Pan, and J.-H. Zhao, Molecular-beam epitaxy of high-quality diluted magnetic semiconductor (Ga, Mn)Sb single-crystalline films, Acta Phys. Sin. 64, 077501 (2015).
Sawicki et al. [2005] M. Sawicki, T. Dietl, C. T. Foxon, S. V. Novikov, R. P. Campion, K. W. Edmonds, K. Y. Wang, A. D. Giddings, and B. L. Gallagher, Search For Hole Mediated Ferromagnetism In Cubic (Ga,Mn)N, AIP Conf. Proc. 772, 1371 (2005).
Novikov et al. [2005] S. V. Novikov, K. W. Edmonds, L. X. Zhao, A. D. Giddings, K. Y. Wang, R. P. Campion, C. R. Staddon, M. W. Fay, Y. Han, P. D. Brown, M. Sawicki, B. L. Gallagher, and C. T. Foxon, Mn doping and p-type conductivity in zinc-blende GaMnN layers grown by molecular beam epitaxy, J. Vac. Sci. Technol. B 23, 1294 (2005).
Chitta et al. [2004] V. A. Chitta, J. A. H. Coaquira, J. R. L. Fernandez, C. A. Duarte, J. R. Leite, D. Schikora, D. J. As, K. Lischka, and E. Abramof, Room temperature ferromagnetism in cubic GaN epilayers implanted with Mn ${}^{\text{+}}$ ions, Appl. Phys. Lett. 85, 3777 (2004).
Stefanowicz et al. [2013] S. Stefanowicz, G. Kunert, C. Simserides, J. A. Majewski, W. Stefanowicz, C. Kruse, S. Figge, T. Li, R. Jakieła, K. N. Trohidou, A. Bonanni, D. Hommel, M. Sawicki, and T. Dietl, Phase diagram and critical behavior of the random ferromagnet Ga ${}_{\text{1-x}}$ Mn ${}_{\text{x}}$ N, Phys. Rev. B 88, 081201 (2013).
Freeman et al. [2007] A. A. Freeman, K. W. Edmonds, N. R. S. Farley, S. V. Novikov, R. P. Campion, C. T. Foxon, B. L. Gallagher, E. Sarigiannidou, and G. van der Laan, Depth dependence of the Mn valence and Mn-Mn coupling in (Ga,Mn)N, Phys. Rev. B 76, 081201 (2007).
Janicki et al. [2017] L. Janicki, G. Kunert, M. Sawicki, E. Piskorska-Hommel, K. Gas, R. Jakiela, D. Hommel, and R. Kudrawiec, Fermi level and bands offsets determination in insulating (Ga,Mn)N/GaN structures, Sci. Rep. 7, 41877 (2017).
Sun et al. [2023] Z. Sun, N. Tang, S. Chen, F. Zhang, H. Fan, S. Zhang, R. Wang, X. Lin, J. Liu, W. Ge, and B. Shen, Spin injection into heavily-doped n-GaN via Schottky barrier, J. Semicond. 44, 082501 (2023).
Zhao et al. [2014] K. Zhao, B. Chen, G. Zhao, Z. Yuan, Q. Liu, Z. Deng, J. Zhu, and C. Jin, Ferromagnetism at 230 K in (Ba ${}_{\text{0.7}}$ K ${}_{\text{0.3}}$ )(Zn ${}_{\text{0.85}}$ Mn ${}_{\text{0.15}}$ ) ${}_{\text{2}}$ As ${}_{\text{2}}$ diluted magnetic semiconductor, Chin. Sci. Bull. 59, 2524 (2014).
Zhao et al. [2013] K. Zhao, Z. Deng, X. C. Wang, W. Han, J. L. Zhu, X. Li, Q. Q. Liu, R. C. Yu, T. Goko, B. Frandsen, L. Liu, F. Ning, Y. J. Uemura, H. Dabkowska, G. M. Luke, H. Luetkens, E. Morenzoni, S. R. Dunsiger, A. Senyshyn, P. Böni, and C. Q. Jin, New diluted ferromagnetic semiconductor with Curie temperature up to 180 K and isostructural to the ’122’ iron-based superconductors, Nat. Commun. 4, 1442 (2013).
Dong et al. [2022] J. Dong, X. Zhao, L. Fu, Y. Gu, R. Zhang, Q. Yang, L. Xie, and F. Ning, (Ca,K)(Zn,Mn) ${}_{\text{2}}$ As ${}_{\text{2}}$ : Ferromagnetic semiconductor induced by decoupled charge and spin doping in CaZn ${}_{\text{2}}$ As ${}_{\text{2}}$ , J. Semicond. 43, 072501 (2022).
Zhao et al. [2022a] X. Zhao, J. Dong, L. Fu, Y. Gu, R. Zhang, Q. Yang, L. Xie, Y. Tang, and F. Ning, (Ba ${}_{\text{1-x}}$ Na ${}_{\text{x}}$ )F(Zn ${}_{\text{1-x}}$ Mn ${}_{\text{x}}$ )Sb: A novel fluoride-antimonide magnetic semiconductor with decoupled charge and spin doping, J. Semicond. 43, 112501 (2022a).
Suzuki et al. [2015a] H. Suzuki, K. Zhao, G. Shibata, Y. Takahashi, S. Sakamoto, K. Yoshimatsu, B. J. Chen, H. Kumigashira, F. H. Chang, H. J. Lin, D. J. Huang, C. T. Chen, B. Gu, S. Maekawa, Y. J. Uemura, C. Q. Jin, and A. Fujimori, Photoemission and X-ray absorption studies of the isostructural to Fe-based superconductors diluted magnetic semiconductor Ba ${}_{\text{1-x}}$ K ${}_{\text{x}}$ (Zn ${}_{\text{1-y}}$ Mn ${}_{\text{y}}$ ) ${}_{\text{2}}$ As ${}_{\text{2}}$ , Phys. Rev. B 91, 140401 (2015a).
Suzuki et al. [2015b] H. Suzuki, G. Q. Zhao, K. Zhao, B. J. Chen, M. Horio, K. Koshiishi, J. Xu, M. Kobayashi, M. Minohara, E. Sakai, K. Horiba, H. Kumigashira, B. Gu, S. Maekawa, Y. J. Uemura, C. Q. Jin, and A. Fujimori, Fermi surfaces and p-d hybridization in the diluted magnetic semiconductor Ba ${}_{\text{1-x}}$ K ${}_{\text{x}}$ (Zn ${}_{\text{1-y}}$ Mn ${}_{\text{y}}$ ) ${}_{\text{2}}$ As ${}_{\text{2}}$ studied by soft X-ray angle-resolved photoemission spectroscopy, Phys. Rev. B 92, 235120 (2015b).
Glasbrenner et al. [2014] J. K. Glasbrenner, I. Žutić, and I. I. Mazin, Theory of Mn-doped II-II-V semiconductors, Phys. Rev. B 90, 140403 (2014).
Gu and Maekawa [2016] B. Gu and S. Maekawa, Diluted magnetic semiconductors with narrow band gaps, Phys. Rev. B 94, 155202 (2016).
Guo et al. [2019] S. Guo, H. Man, K. Wang, C. Ding, Y. Zhao, L. Fu, Y. Gu, G. Zhi, B. A. Frandsen, S. C. Cheung, Z. Guguchia, K. Yamakawa, B. Chen, H. Wang, Z. Deng, C. Q. Jin, Y. J. Uemura, and F. Ning, Ba(Zn,Co) ${}_{\text{2}}$ As ${}_{\text{2}}$ : A diluted ferromagnetic semiconductor with n-type carriers and isostructural to 122 iron-based superconductors, Phys. Rev. B 99, 155201 (2019).
Tu et al. [2016] N. T. Tu, P. N. Hai, L. D. Anh, and M. Tanaka, High-temperature ferromagnetism in heavily Fe-doped ferromagnetic semiconductor (Ga,Fe)Sb, Appl. Phys. Lett. 108, 192401 (2016).
Tu et al. [2019] N. T. Tu, P. N. Hai, L. D. Anh, and M. Tanaka, Heavily Fe-doped ferromagnetic semiconductor (In,Fe)Sb with high Curie temperature and large magnetic anisotropy, Appl. Phys. Express 12, 103004 (2019).
You et al. [2020] J.-Y. You, B. Gu, S. Maekawa, and G. Su, Microscopic mechanism of high-temperature ferromagnetism in Fe, Mn, and Cr-doped InSb, InAs, and GaSb magnetic semiconductors, Phys. Rev. B 102, 094432 (2020).
Wang et al. [2020] H. Wang, S. Sun, J. Lu, J. Xu, X. Lv, Y. Peng, X. Zhang, Y. Wang, and G. Xiang, High Curie Temperature Ferromagnetism and High Hole Mobility in Tensile Strained Mn-Doped SiGe Thin Films, Adv. Funct. Mater. 30, 2002513 (2020).
Chen et al. [2021] R. Chen, F. Luo, Y. Liu, Y. Song, Y. Dong, S. Wu, J. Cao, F. Yang, A. N’Diaye, P. Shafer, Y. Liu, S. Lou, J. Huang, X. Chen, Z. Fang, Q. Wang, D. Jin, R. Cheng, H. Yuan, R. J. Birgeneau, and J. Yao, Tunable room-temperature ferromagnetism in Co-doped two-dimensional van der Waals ZnO, Nat. Commun. 12, 3952 (2021).
Huang et al. [2017] B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero, and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature 546, 270 (2017).
Gong et al. [2017] C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia, and X. Zhang, Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature 546, 265 (2017).
Cai et al. [2019] X. Cai, T. Song, N. P. Wilson, G. Clark, M. He, X. Zhang, T. Taniguchi, K. Watanabe, W. Yao, D. Xiao, M. A. McGuire, D. H. Cobden, and X. Xu, Atomically Thin CrCl ${}_{\text{3}}$ : An In-Plane Layered Antiferromagnetic Insulator, Nano Lett. 19, 3993 (2019).
Zhang et al. [2019] Z. Zhang, J. Shang, C. Jiang, A. Rasmita, W. Gao, and T. Yu, Direct Photoluminescence Probing of Ferromagnetism in Monolayer Two-Dimensional CrBr ${}_{\text{3}}$ , Nano Lett. 19, 3138 (2019).
Cui et al. [2020] F. Cui, X. Zhao, J. Xu, B. Tang, Q. Shang, J. Shi, Y. Huan, J. Liao, Q. Chen, Y. Hou, Q. Zhang, S. J. Pennycook, and Y. Zhang, Controlled Growth and Thickness-Dependent Conduction-Type Transition of 2D Ferrimagnetic Cr ${}_{\text{2}}$ S ${}_{\text{3}}$ Semiconductors, Adv. Mater. 32, 1905896 (2020).
Chu et al. [2019] J. Chu, Y. Zhang, Y. Wen, R. Qiao, C. Wu, P. He, L. Yin, R. Cheng, F. Wang, Z. Wang, J. Xiong, Y. Li, and J. He, Sub-millimeter-Scale Growth of One-Unit-Cell-Thick Ferrimagnetic Cr ${}_{\text{2}}$ S ${}_{\text{3}}$ Nanosheets, Nano Lett. 19, 2154 (2019).
Lee et al. [2021] K. Lee, A. H. Dismukes, E. J. Telford, R. A. Wiscons, J. Wang, X. Xu, C. Nuckolls, C. R. Dean, X. Roy, and X. Zhu, Magnetic Order and Symmetry in the 2D Semiconductor CrSBr, Nano Lett. 21, 3511 (2021).
Achinuq et al. [2022] B. Achinuq, R. Fujita, W. Xia, Y. Guo, P. Bencok, G. van der Laan, and T. Hesjedal, Covalent Mixing in the 2D Ferromagnet CrSiTe ${}_{\text{3}}$ Evidenced by Magnetic X-Ray Circular Dichroism, Phys. Status Solidi RRL 16, 2100566 (2022).
Webster and Yan [2018] L. Webster and J.-A. Yan, Strain-tunable magnetic anisotropy in monolayer CrCl ${}_{\text{3}}$ , CrBr ${}_{\text{3}}$ , and CrI ${}_{\text{3}}$ , Phys. Rev. B 98, 144411 (2018).
You et al. [2019] J.-Y. You, Z. Zhang, B. Gu, and G. Su, Two-Dimensional Room-Temperature Ferromagnetic Semiconductors with Quantum Anomalous Hall Effect, Phys. Rev. Appl. 12, 024063 (2019).
Dong et al. [2019] X.-J. Dong, J.-Y. You, B. Gu, and G. Su, Strain-Induced Room-Temperature Ferromagnetic Semiconductors with Large Anomalous Hall Conductivity in Two-Dimensional Cr ${}_{\text{2}}$ Ge ${}_{\text{2}}$ Se ${}_{\text{6}}$ , Phys. Rev. Appl. 12, 014020 (2019).
Dong et al. [2020] X.-J. Dong, J.-Y. You, Z. Zhang, B. Gu, and G. Su, Great enhancement of Curie temperature and magnetic anisotropy in two-dimensional van der Waals magnetic semiconductor heterostructures, Phys. Rev. B 102, 144443 (2020).
You et al. [2021] J.-Y. You, X.-J. Dong, B. Gu, and G. Su, Electric field induced topological phase transition and large enhancements of spin-orbit coupling and Curie temperature in two-dimensional ferromagnetic semiconductors, Phys. Rev. B 103, 104403 (2021).
Jiang et al. [2021] X. Jiang, Q. Liu, J. Xing, N. Liu, Y. Guo, Z. Liu, and J. Zhao, Recent progress on 2D magnets: Fundamental mechanism, structural design and modification, Appl. Phys. Rev. 8, 031305 (2021).
You et al. [2023] J.-Y. You, X.-J. Dong, B. Gu, and G. Su, Possible Room-Temperature Ferromagnetic Semiconductors, Chin. Phys. Lett. 40, 067502 (2023).
Li et al. [2023] J.-W. Li, Z. Zhang, J.-Y. You, B. Gu, and G. Su, Two-dimensional Heisenberg model with material-dependent superexchange interactions, Phys. Rev. B 107, 224411 (2023).
Wei [2023] D. Wei, The room temperature ferromagnetism in highly strained two-dimensional magnetic semiconductors Semiconductors, J. Semicond. 44, 040401 (2023).
You et al. [2022] J.-Y. You, B. Gu, and G. Su, The p-orbital magnetic topological states on a square lattice, Natl. Sci. Rev. 9, nwab114 (2022).
Zhao et al. [2022b] D. Zhao, C. Zhang, C. Zhang, W. Ji, S. Li, and P. Wang, Magnetic tuning in a novel half-metallic Ir ${}_{\text{2}}$ TeI ${}_{\text{2}}$ monolayer, J. Semicond. 43, 052001 (2022b).
Limmer et al. [2002] W. Limmer, M. Glunk, S. Mascheck, A. Koeder, D. Klarer, W. Schoch, K. Thonke, R. Sauer, and A. Waag, Coupled plasmon-LO-phonon modes in Ga ${}_{\text{1-x}}$ Mn ${}_{\text{x}}$ As, Phys. Rev. B 66, 205209 (2002).
Limmer et al. [2005] W. Limmer, A. Koeder, S. Frank, V. Avrutin, W. Schoch, R. Sauer, K. Zuern, J. Eisenmenger, P. Ziemann, E. Peiner, and A. Waag, Effect of annealing on the depth profile of hole concentration in (Ga,Mn)As, Phys. Rev. B 71, 205213 (2005).
Shin et al. [2022] J. Shin, G. A. Gamage, Z. Ding, K. Chen, F. Tian, X. Qian, J. Zhou, H. Lee, J. Zhou, L. Shi, T. Nguyen, F. Han, M. Li, D. Broido, A. Schmidt, Z. Ren, and G. Chen, High ambipolar mobility in cubic boron arsenide, Science 377, 437 (2022).
Perri et al. [1958] J. A. Perri, S. La Placa, and B. Post, New group III-group V compounds: BP and BAs, Acta Cryst. 11, 310 (1958).
Ku [1966] S. M. Ku, Preparation and Properties of Boron Arsenides and Boron Arsenide-Gallium Arsenide Mixed Crystals, J. Electrochem. Soc. 113, 813 (1966).
Chu and Hyslop [1974] T. L. Chu and A. E. Hyslop, Preparation and Properties of Boron Arsenide Films, J. Electrochem. Soc. 121, 412 (1974).
Wang et al. [2012] S. Wang, S. F. Swingle, H. Ye, F.-R. F. Fan, A. H. Cowley, and A. J. Bard, Synthesis and Characterization of a p-Type Boron Arsenide Photoelectrode, J. Am. Chem. Soc. 134, 11056 (2012).
Nwigboji et al. [2016] I. H. Nwigboji, Y. Malozovsky, L. Franklin, and D. Bagayoko, Calculated electronic, transport, and related properties of zinc blende boron arsenide (zb-BAs), J. Appl. Phys. 120, 145701 (2016).
Surh et al. [1991] M. P. Surh, S. G. Louie, and M. L. Cohen, Quasiparticle energies for cubic BN, BP, and BAs, Phys. Rev. B 43, 9126 (1991).
Broido et al. [2013] D. A. Broido, L. Lindsay, and T. L. Reinecke, Ab initio study of the unusual thermal transport properties of boron arsenide and related materials, Phys. Rev. B 88, 214303 (2013).
Chae et al. [2018] S. Chae, K. Mengle, J. T. Heron, and E. Kioupakis, Point defects and dopants of boron arsenide from first-principles calculations: Donor compensation and doping asymmetry, Appl. Phys. Lett. 113, 212101 (2018).
Bushick et al. [2019] K. Bushick, K. Mengle, N. Sanders, and E. Kioupakis, Band structure and carrier effective masses of boron arsenide: Effects of quasiparticle and spin-orbit coupling corrections, Appl. Phys. Lett. 114, 022101 (2019).
Liu et al. [2018] T.-H. Liu, B. Song, L. Meroueh, Z. Ding, Q. Song, J. Zhou, M. Li, and G. Chen, Simultaneously high electron and hole mobilities in cubic boron-V compounds: BP, BAs, and BSb, Phys. Rev. B 98, 081203 (2018).
Lindsay et al. [2013] L. Lindsay, D. A. Broido, and T. L. Reinecke, First-Principles Determination of Ultrahigh Thermal Conductivity of Boron Arsenide: A Competitor for Diamond?, Phys. Rev. Lett. 111, 025901 (2013).
Feng et al. [2017] T. Feng, L. Lindsay, and X. Ruan, Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids, Phys. Rev. B 96, 161201 (2017).
Kang et al. [2018] J. S. Kang, M. Li, H. Wu, H. Nguyen, and Y. Hu, Experimental observation of high thermal conductivity in boron arsenide, Science 361, 575 (2018).
Tian et al. [2018] F. Tian, B. Song, X. Chen, N. K. Ravichandran, Y. Lv, K. Chen, S. Sullivan, J. Kim, Y. Zhou, T.-H. Liu, M. Goni, Z. Ding, J. Sun, G. A. G. Udalamatta Gamage, H. Sun, H. Ziyaee, S. Huyan, L. Deng, J. Zhou, A. J. Schmidt, S. Chen, C.-W. Chu, P. Y. Huang, D. Broido, L. Shi, G. Chen, and Z. Ren, Unusual high thermal conductivity in boron arsenide bulk crystals, Science 361, 582 (2018).
Li et al. [2018] S. Li, Q. Zheng, Y. Lv, X. Liu, X. Wang, P. Y. Huang, D. G. Cahill, and B. Lv, High thermal conductivity in cubic boron arsenide crystals, Science 361, 579 (2018).
Blöchl [1994] P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B 50, 17953 (1994).
Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77, 3865 (1996).
Monkhorst and Pack [1976] H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B 13, 5188 (1976).
Dudarev et al. [1998] S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys, and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B 57, 1505 (1998).
Mahadevan and Zunger [2004] P. Mahadevan and A. Zunger, First-principles investigation of the assumptions underlying model-Hamiltonian approaches to ferromagnetism of 3d impurities in III-V semiconductors, Phys. Rev. B 69, 115211 (2004).
Mahadevan et al. [2004] P. Mahadevan, A. Zunger, and D. D. Sarma, Unusual Directional Dependence of Exchange Energies in GaAs Diluted with Mn: Is the RKKY Description Relevant?, Phys. Rev. Lett. 93, 177201 (2004).
Kulatov et al. [2002] E. Kulatov, H. Nakayama, H. Mariette, H. Ohta, and Y. A. Uspenskii, Electronic structure, magnetic ordering, and optical properties of GaN and GaAs doped with Mn, Phys. Rev. B 66, 045203 (2002).
Sanvito et al. [2001] S. Sanvito, P. Ordejón, and N. A. Hill, First-principles study of the origin and nature of ferromagnetism in Ga ${}_{\text{1-x}}$ Mn ${}_{\text{x}}$ As, Phys. Rev. B 63, 165206 (2001).
Jain et al. [2001] M. Jain, L. Kronik, J. R. Chelikowsky, and V. V. Godlevsky, Electronic structure and spin polarization of Mn-containing dilute magnetic III-V semiconductors, Phys. Rev. B 64, 245205 (2001).
Máca and Mašek [2002] F. Máca and J. Mašek, Electronic states in Ga ${}_{\text{1-x}}$ Mn ${}_{\text{x}}$ As: Substitutional versus interstitial position of Mn, Phys. Rev. B 65, 235209 (2002).
Schilfgaarde and Mryasov [2001] M. v. Schilfgaarde and O. N. Mryasov, Anomalous exchange interactions in III-V dilute magnetic semiconductors, Phys. Rev. B 63, 233205 (2001).
Cheng et al. [2013] Y. C. Cheng, Z. Y. Zhu, W. B. Mi, Z. B. Guo, and U. Schwingenschlögl, Prediction of two-dimensional diluted magnetic semiconductors: Doped monolayer MoS ${}_{\text{2}}$ systems, Phys. Rev. B 87, 100401 (2013).
Ramasubramaniam and Naveh [2013] A. Ramasubramaniam and D. Naveh, Mn-doped monolayer MoS ${}_{\text{2}}$ : An atomically thin dilute magnetic semiconductor, Phys. Rev. B 87, 195201 (2013).
Mishra et al. [2013] R. Mishra, W. Zhou, S. J. Pennycook, S. T. Pantelides, and J.-C. Idrobo, Long-range ferromagnetic ordering in manganese-doped two-dimensional dichalcogenides, Phys. Rev. B 88, 144409 (2013).
Seixas et al. [2015] L. Seixas, A. Carvalho, and A. H. Castro Neto, Atomically thin dilute magnetism in Co-doped phosphorene, Phys. Rev. B 91, 155138 (2015).
Sun et al. [2016] L. Sun, W. Zhou, Y. Liang, L. Liu, and P. Wu, Magnetic properties in Fe-doped SnS ${}_{\text{2}}$ : Density functional calculations, Comput. Mater. Sci. 117, 489 (2016).
Li et al. [2017] B. Li, T. Xing, M. Zhong, L. Huang, N. Lei, J. Zhang, J. Li, and Z. Wei, A two-dimensional Fe-doped SnS ${}_{\text{2}}$ magnetic semiconductor, Nat. Commun. 8, 1958 (2017).
Huang et al. [2022] M. Huang, Z. Zheng, Z. Dai, X. Guo, S. Wang, L. Jiang, J. Wei, and S. Chen, DASP: Defect and Dopant ab-initio Simulation Package, J. Semicond. 43, 042101 (2022).
[87] See Supplemental Material at [URL will be inserted by publisher] for additional calculations results., .
Lian et al. [2020] J.-C. Lian, H.-Y. Wu, W.-Q. Huang, W. Hu, and G.-F. Huang, Algorithm for generating irreducible site-occupancy configurations, Phys. Rev. B 102, 134209 (2020).
Lian et al. [2022] J.-C. Lian, Y. Si, T. Huang, W.-Q. Huang, W. Hu, and G.-F. Huang, Highly efficient tree search algorithm for irreducible site-occupancy configurations, Phys. Rev. B 105, 014201 (2022).
Bardeen and Shockley [1950] J. Bardeen and W. Shockley, Deformation Potentials and Mobilities in Non-Polar Crystals, Phys. Rev. 80, 72 (1950).
Sotoodeh et al. [2000] M. Sotoodeh, A. H. Khalid, and A. A. Rezazadeh, Empirical low-field mobility model for III-V compounds applicable in device simulation codes, J. Appl. Phys. 87, 2890 (2000).