Heuristic Search for Multi-Objective Probabilistic Planning

In the context of MOSSPs, given a policy $\pi$, we denote by ${\vec{V}}^{\pi}:S\to{\mathbb{R}}_{\geq 0}^{n}$ the vector value function for $\pi$. The function ${\vec{V}}^{\pi}$ is computed by replacing $V$ and $C$ by ${\vec{V}}$ and ${\vec{C}}$ in (1), respectively. In order to define the solution of an MOSSP, we need to first define how to compare two different vectors: a cost vector $\vec{v}$ dominates $\vec{u}$, denoted as $\vec{v}\preceq\vec{u}$, if $\vec{v}_{i}\leq\vec{u}_{i}$ for $i=1,\ldots,n$. A coverage set for a set of vectors ${\mathbf{V}}$, denoted as $\mathrm{CS}({\mathbf{V}})$, is any set satisfying $\forall\vec{v}\in\mathrm{CS}({\mathbf{V}}),\nexists\vec{u}\in\mathrm{CS}({\mathbf{V}})$ s.t. $\vec{u}\preceq\vec{v}$ and $\vec{u}\not=\vec{v}$.¹¹1We will denote sets of vectors or functions which map to sets of vectors with bold face, e.g. ${\mathbf{V}}$, and single vectors or functions which map to single vectors with vector notation, e.g. $\vec{V}$. An example of a coverage set is the Pareto coverage set ($\mathrm{PCS}$) which is the largest possible coverage set. For the remainder of the paper we focus on the convex coverage set ($\mathrm{CCS}$) (Barrett and Narayanan 2008; Roijers and Whiteson 2017) which is defined as the convex hull of the $\mathrm{PCS}$. Details for computing the $\mathrm{CCS}$ of a set ${\mathbf{V}}$ with a linear program (LP) can be found in (Roijers and Whiteson 2017, Sec. 4.1.3). We say that a set of vectors ${\mathbf{U}}$ dominates another set of vectors ${\mathbf{V}}$, denoted by ${\mathbf{U}}\preceq{\mathbf{V}}$, if for all $\vec{v}\in{\mathbf{V}}$ there exists $\vec{u}\in{\mathbf{U}}$ such that $\vec{u}\preceq\vec{v}$.

Given an MOSSP define the optimal value function ${\mathbf{V}}^{*}$ by ${\mathbf{V}}^{*}(s)=\mathrm{CCS}(\{{\vec{V}}^{\pi}(s)\mid\text{$\pi$ is a proper policy}\})$. Then we define a solution to the MOSSP to be any set of proper policies $\Pi$ such that the function $\varphi:\Pi\to{\mathbf{V}}^{*}(s_{0})$ with $\varphi(\pi)=\vec{V}^{\pi}(s_{0})$ is a bijection. By choosing $\mathrm{CCS}$ as our coverage set operator, we may focus our attention to only non-dominated deterministic policies, where non-dominated stochastic policies are implicitly given by the points on the surface of the polyhedron drawn out by the $\mathrm{CCS}$. In this way, we avoid having to explicitly compute infinitely many non-dominated stochastic policies.

To illustrate this statement, consider the MOSSP in Fig. 1 with actions $a_{1}$ and $a_{2}$ where $P(s_{0}|s_{0},a_{1})=P(g_{1}|s_{0},a_{1})=P(s_{0}|s_{0},a_{2})=P(g_{2}|s_{0},a_{2})=0.5$ and $\vec{C}(a_{1})=[1,0]$ and $\vec{C}(a_{2})=[0,1]$. One solution consists of only two deterministic policies $\pi_{1}(s_{0})=a_{1}$ and $\pi_{2}(s_{0})=a_{2}$ with corresponding expected costs ${[2,0]}$ and ${[0,2]}$. Notice that there are uncountably many stochastic policies obtained by the convex combinations of $\pi_{1}$ and $\pi_{2}$, i.e., $\pi_{t}(a_{1}|s_{0})=1-t,\pi_{t}(a_{2}|s_{0})=t$ for $t\in[0,1]$. The expected cost of each $\pi_{t}$ is $[2-2t,2t]$ and these stochastic policies do not dominate each other. Therefore, if the $\mathrm{PCS}$ is used instead of the $\mathrm{CCS}$ in the definition of optimal value function, then ${\mathbf{V}}^{*}(s_{0})$ would be $\left\{[2-2t,2t]\mid t\in[0,1]\right\}$ and the corresponding solution would be $\{\pi_{t}\mid t\in[0,1]\}$. The $\mathrm{CCS}$ allows us to compactly represent the potentially infinite $\mathrm{PCS}$ by storing only the deterministic policies: in this example, the actual solution is $\{\pi_{1},\pi_{2}\}$ and the optimal value function is ${\mathbf{V}}^{*}(s_{0})=\left\{[2,0],[0,2]\right\}$.

We finish this section by reviewing how to compute the optimal value function ${V}^{*}$ for SSPs and extend these results to MOSSPs in the next section. The optimal (scalar) value function ${V}^{*}$ for an SSP can be computed using the Value Iteration (VI) algorithm (Bertsekas and Tsitsiklis 1996): given an initial value function ${V}^{0}$ it computes the sequence ${V}^{1},\ldots,{V}^{k}$ where ${V}^{t+1}$ is obtained by applying a Bellman backup, that is ${V}^{t+1}(g)=0$ if $g\in G$ and, for $s\in S\setminus G$,

VI guarantees that ${V}^{k}$ converges to ${V}^{*}$ as $k\to\infty$ under the following conditions: (i) for all $s\in S$, there exists a proper policy w.r.t. $s$; and (ii) all improper policies have infinite cost for at least one state. The former condition is known as the reachability assumption and it is equivalent to requiring that no dead ends exist, while the latter condition can be seen as preventing cycles with 0 cost. Notice that finite-horizon Markov Decision Processes (MDPs) and infinite-horizon discounted MDPs are special cases of SSPs in which all policies are guaranteed to be proper (Bertsekas and Tsitsiklis 1996).

Similarly to the SO version of VI, MOVI requires that the reachability assumption holds; however, the assumption that improper policies have infinite cost needs to be generalised to the MO case. One option is to require that all improper policies cost $\vec{\infty}$ which we call the strong improper policy assumption and, if it holds with the reachability assumption, then MOVI (Alg. 1) is sound and complete for MOSSPs. The strong assumption is very restrictive because it implies that any cycle in an MOSSP must have a cost greater than zero in all dimensions; however, it is common for MOSSPs to have zero-cost cycles in one or more dimensions. For instance, in navigation domains where some actions such as wait, load and unload do not consume fuel and can be used to generate zero-fuel-cost loops.

Another possible generalisation for the cost of improper policies is that they cost infinity in at least one dimension. This requirement is not enough as illustrated by the (deterministic) MOSSP in Fig. 2. The only deterministic proper policy is $\pi(s_{0})=a_{g}$ with cost $[0,1]$, and the other deterministic policy is $\pi^{\prime}(s_{0})=a_{1},\pi^{\prime}(s_{1})=a_{2}$ which is improper and costs $[\infty,0]$. Since neither $[0,1]$ or $[\infty,0]$ dominate each other, two issues arise: MOVI tries to converge to infinity and thus never terminates; and even if it did, the cost of an improper policy would be wrongly added to the CCS.

These issues stem from VI and its generalisations not explicitly pruning improper policies. Instead they rely on the assumption that improper policies have infinite cost to implicitly prune them. This approach is enough in the SO case because any proper policy dominates all improper policies since domination is reduced to the ‘$\leq$’ operator; however, as shown in this example, the implicit pruning approach for improper policies is not correct for the MO case.

We address these issues by providing a version of MOVI that explicitly prunes improper policies and to do so we need a new assumption:

The weak assumption allows improper policies to have finite cost in some but not all dimensions at the expense of knowing an upper bound $\vec{b}$ on the cost of all proper policies. This upper bound $\vec{b}$ lets us infer that a policy $\pi$ is improper whenever $\vec{V}^{\pi}(s)\not\preceq\vec{b}$, i.e., that $\vec{V}^{\pi}(s)$ is greater than $\vec{b}$ in at least one dimension.

Alg. 2 outlines the new MOVI where the differences can be found in lines 2 and 2. In line 2, we use a modified Bellman backup which detects vectors associated to improper policies and assigns them the upper bound $\vec{b}$ given by the weak improper policy assumption. The modified backup is given by

where $\oplus_{B}$ is a modified set addition operator defined on pairwise vectors $\vec{u}$ and $\vec{v}$ by

and similarly for the generalised version ${{\bigoplus}}_{B}$. Also define $\mathrm{CS}_{B}$ to be the modified coverage set operator which does not prune away $\vec{b}$ if it is in the input set. The modified backup (7) enforces a cap on value functions (i.e., ${\mathbf{V}}^{t}(s)\preceq\{\vec{b}\}$) through the operator $\oplus_{B}$ (9). This guarantees that a finite fixed point exists for all $\vec{V}^{\pi}(s)$ and, as a result, that Alg. 2 terminates. Once the algorithm converges, we need to explicitly prune the expected cost of improper policies which is done in line 2. By Assumption 1, we have that no proper policy costs $\vec{b}$ thus we can safely remove $\vec{b}$ from the solution. Note that the overhead in applying this modified backup and post-processing pruning is negligible. Theorem 3.1 shows that MOVI converges to the correct solution.

Note that the original proof for MOMDPs by Barrett and Narayanan (2008) does not directly work for MOSSPs as some of the scalarised SSPs have a solution of infinite expected cost such that VI never converges. The upper bound $\vec{b}$ we introduce solves this issue as achieving this bound is the same as detecting improper policies. The proof remains correct in the original setting applied to discounted MOMDPs in which there are no improper policies.

The reachability assumption can also be relaxed by transforming an MOSSP with dead ends into a new MOSSP without dead ends. Formally, given an MOSSP $(S,s_{0},G,A,P,{\vec{C}})$ with dead ends, let $A^{\prime}=A\cup\{\text{give-up}\}$; $P(s_{g}|\text{give-up},s)=1$ for all $s\in S$ and any $s_{g}\in G$; ${\vec{C}}^{\prime}(a)=[{\vec{C}}(a):0]$ for all $a\in A$; and ${\vec{C}}^{\prime}(\text{give-up})=[\vec{0}:1]$.

Then the MOSSP $(S,s_{0},G,A^{\prime},P,{\vec{C}}^{\prime})$ does not have dead ends (i.e., the reachability assumption holds) since the give-up action is applicable in all states $s\in S$. This transformation is similar to the finite-penalty transformation for SSPs (Trevizan, Teichteil-Königsbuch, and Thiébaux 2017); however it does not require a large penalty constant. Instead, the MOSSP transformation uses an extra cost dimension to encode the cost of giving up and the value of the $n\!+\!1$-th dimension of ${\vec{C}}^{\prime}(\text{give-up})$ is irrelevant as long as it is greater than 0. Since the give-up action can only be applied once, defining the cost of give-up as 1 let us interpret the $n\!+\!1$-th dimension of any $\vec{V}^{\pi}(s)$ as the probability of giving up when following $\pi$ from $s$.

For the remainder of the paper, we will call a set of vectors a value. Thus, a heuristic value for a state is a set of vectors ${\mathbf{H}}(s)\subset{\mathbb{R}}_{\geq 0}^{n}$. We implicitly assume that any heuristic value ${\mathbf{H}}(s)$ has already been pruned with some coverage set operator. The definition of an admissible heuristic for MOSSPs should be at most as strong as the definition for deterministic MO search (Mandow and Pérez-de-la-Cruz 2010).

For example, if for some MOSSP we have ${\mathbf{V}}^{*}(s)=\left\{[0,2]\right\}$ for a state $s$, then ${\mathbf{H}}(s)=\left\{[0,1],[3,0]\right\}$ and ${\mathbf{H}}(s^{\prime})=\{\vec{0}\}$ for all other $s^{\prime}$ is an admissible heuristic. As in the single-objective case, admissible heuristics ensure that the algorithms below converge to near optimal value functions for $\varepsilon>0$ with finitely many iterations and to optimal value functions with possibly infinitely many iterations when $\varepsilon=0$.

The definition of consistent heuristic is derived and generalised from the definition of consistent heuristics for deterministic search: $h(s)\leq c(s,a,s^{\prime})+h(s^{\prime})$. The main idea is that assuming non-negative costs, state costs increase monotonically which results in no re-expansions of nodes in A^∗ search. Similarly, we desire monotonically increasing value functions for faster convergence.

We now turn to the question of constructing domain-independent heuristics satisfying these properties from the encoding of a planning domain. This question has only recently been addressed in the deterministic multi-objective planning setting (Geißer et al. 2022): with the exception of this latter work, MO heuristic search algorithms have been evaluated using “ideal-point” heuristics, which apply a single-objective heuristic $h_{i}$ to each objective in isolation, resulting in a single vector ${\mathbf{H}}_{\textit{ideal}}(s)=\{[h_{1}(s),\ldots h_{n}(s)]\}$. Moreover, informative domain-independent heuristics for single objective SSPs are also relatively new (Trevizan, Thiébaux, and Haslum 2017; Klößner and Hoffmann 2021): a common practice was to resort to classical planning heuristics obtained after determinisation of the SSP (Jimenez, Coles, and Smith 2006).

We consider a spectrum of options when constructing domain-independent heuristics for MOSSPs, which we instantiate using the most promising families of heuristics identified in (Geißer et al. 2022) for the deterministic case: critical paths and abstraction heuristics. All heuristics are consistent and admissible unless otherwise mentioned.

• •

  The baseline option is to ignore both the MO and stochastic aspects of the problem, and resort to an ideal-point heuristic constructed from the determinised problem. In our experiments below, we apply the classical $h^{\mathsf{max}}$ heuristic (Bonet and Geffner 2001) to each objective and call this ${\mathbf{H}}_{\textit{ideal}}^{\textit{max}}$.

• •

  A more elaborate option is to consider only the stochastic aspects of the problem, resulting in an ideal-point SSP heuristic. In our experiments, we apply the recent SSP canonical PDB abstraction heuristic by Klößner and Hoffmann (2021) to each objective which we call ${\mathbf{H}}_{\textit{ideal}}^{\textit{pdb2}}$ and ${\mathbf{H}}_{\textit{ideal}}^{\textit{pdb3}}$ for patterns of size 2 and 3, respectively.

• •

  Alternatively, one might consider only the multi-objective aspects, by applying some of the MO deterministic heuristics (Geißer et al. 2022) to the determinised SSP. The heuristics we consider in our experiments are the MO extension of $h^{\mathsf{max}}$ and canonical PDBs: ${\mathbf{H}}_{\textit{mo}}^{\textit{comax}}$, ${\mathbf{H}}_{\textit{mo}}^{\textit{pdb2}}$, and ${\mathbf{H}}_{\textit{mo}}^{\textit{pdb3}}$. These extend classical planning heuristics by using MO deterministic search to solve subproblems and combining solutions by taking the maximum of two sets of vectors with the admissibility preserving operator $\operatorname{comax}$ (Geißer et al. 2022).

• •

  The best option is to combine the power of SSP and MO heuristics. We do so with a novel heuristic ${\mathbf{H}}_{\textit{mossp}}^{\textit{pdb}}$ which extends the SSP PDB abstraction heuristic (Klößner and Hoffmann 2021) to the MO case by using an MO extension of topological VI (TVI) (Dai et al. 2014) to solve each projection and the $\operatorname{comax}$ operator to combine the results. Our experiments use ${\mathbf{H}}_{\textit{mossp}}^{\textit{pdb2}}$ and ${\mathbf{H}}_{\textit{mossp}}^{\textit{pdb3}}$.

Readers familiar with the LAO^∗ heuristic search algorithm and the multi-objective backup can convince themselves that an extension of LAO^∗ to the multi-objective case can be obtained by replacing the backup operator with the multi-objective version. This idea was first outlined by Bryce, Cushing, and Kambhampati (2007) for finite-horizon MDPs which is a special case of SSPs without improper policies. In the same vein as (Hansen and Zilberstein 2001), we provide MOLAO^∗ alongside an ‘improved’ version, iMOLAO^∗, in Alg. 3 and 4 respectively.

MOLAO^∗ begins in line 1 by lazily assigning an initial value function ${\mathbf{V}}$ to each state with the heuristic function, as opposed to explicitly initialising all initial values at once. $\Pi$ is a dictionary representing our partial solution which maps states to sets of optimal actions corresponding to their current value function. The main while loop of the algorithm terminates once there are no nongoal states on the frontier as described in line 3, at which point we have achieved a set of closed policies.

The loop begins with lines 3-5 by removing a nongoal state $s$ from the frontier representing a state on the boundary of the partial solution graph, and adding it to the interior set $I$. The nodes of the partial solution graph are partial solution states, and the edges are the probabilistic transitions under all partial solution actions. Next in line 6 we add the set of yet unexplored successors of $s$ to the frontier: any state $s^{\prime}\in S\setminus I$ such that $\exists a\in A,P(s^{\prime}|s,a)>0$. Then we extract the set $Z$ of all ancestor states of $s$ in the partial solution $\Pi$ using graph search in line 7. We run MOVI to $\varepsilon$-consistency on the MOSSP problem restricted to the set of states $Z$ and update the value functions for the corresponding states in line 8. The partial solution is updated in line 9 by extracting the actions corresponding to the value function with

This function can be seen as a generalisation of $\operatorname*{arg\,min}$ to the MO case where here we select the actions whose ${\mathbf{Q}}$ value at $s$ contribute to the current value ${\mathbf{V}}(s)$. Next, we extract the set of states $N$ corresponding to all states reachable from $s_{0}$ by the partial solution $\Pi$ in line 10.

The completeness and correctness of MOLAO^∗ follows from the same reasoning as LAO^∗ extended to the MO case. Specifically, we have that given an admissible heuristic the algorithm achieves $\varepsilon$-consistency upon termination.

One potential issue with MOLAO^∗ is that we may waste a lot of backups while running MOVI to convergence several times on partial solution graphs which do not end up contributing to the final solution. The original authors of LAO^∗ proposed the iLAO^∗ algorithm to deal with this. We provide the MO extension, namely iMOLAO^∗. The main idea with iMOLAO^∗ is that we only run one set of backups every time we (re-)expand a state instead of running VI to convergence in the loop in lines 5 to 9. Backups are also performed asynchronously using DFS postorder traversal of the states in the partial solution graph computed in line 4, allowing for faster convergence times.

To summarise, the two main changes required to extend (i)LAO^∗ to the MO case are (1) replacing the backup operator with the MO version, and (2) storing possibly more than one greedy action at each state corresponding to incomparable vector ${\mathbf{Q}}$-values, resulting in a larger set of successors associated to each state. These ideas can be applied to other asynchronous VI methods such as Prioritised VI (Wingate and Seppi 2005) and Topological VI (Dai et al. 2014).

LRTDP (Bonet and Geffner 2003) is another heuristic search algorithm for solving SSPs. The idea of LRTDP is to perform random trials using greedy actions based on the current value function or heuristic for performing backups, and labelling states as solved when the consistency threshold has been reached in order to gradually narrow down the search space and achieve a convergence criterion. A multi-objective extension of LRTDP is not as straightforward as extending the backup operator given that each state has possibly more than one greedy action to account for. The two main changes from the original LRTDP are (1) the sampling of a random greedy action before sampling successor states in the main loop, and (2) defining the descendants of a state by considering successors of all greedy actions (as opposed to just one in LRDTP). Alg. 5 outlines the MO extension of LRTDP.

MOLRTDP consists of repeatedly trialing paths through the state space and performing backups until the initial state is marked as solved. Trials are run by randomly sampling a greedy action $a$ from $\mathrm{getActions}(s,{\mathbf{V}})$ at each state $s$ followed by a next state sampled from the probability distribution of $a$ until a goal state is reached as in the first inner loop from lines 5 to 10. The second inner loop from lines 11 to 13 calls the $\mathrm{checkSolved}$ routine in the reverse trial order to label states as solved by checking whether the residual of all its descendant states under greedy actions are less than the convergence criterion.

The $\mathrm{checkSolved}$ routine begins with inserting $s$ into the open set if it has not been solved, and returns true otherwise due to line 2. The main loop in lines 3 to 10 collects the descendent states under all greedy actions (lines 8-10) and checks whether the residual of all the descendent states are small (lines 5-7). If true, all descendents are labelled as solved as in line 11. Otherwise, backups are performed in the reverse order of explored states as in lines 12 to 15.

The completeness and correctness of MOLRTDP follows similarly from its single objective ancestor. We note specifically that the labelling feature works similarly in the sense that whenever a state is marked as solved, it is known for certain that all its descendents’ values are $\varepsilon$-consistent and remain unchanged when backups are performed elsewhere.

We implemented the MO versions of the VI, TVI, (i)LAO^∗ and LRTDP algorithms and the MO version of the PDB abstraction heuristics (${\mathbf{H}}_{\textit{mossp}}^{\textit{pdb}}$) in C++.²²2Code at https://github.com/DillonZChen/cpp-mossp-planner PDB heuristics are computed using TVI, $\varepsilon=0.001$ and $\vec{b}=\vec{100}$. We include in our experiments the following heuristics for deterministic MO planning from (Geißer et al. 2022): the ideal-point version of $h^{\mathsf{max}}$ (${\mathbf{H}}_{\textit{ideal}}^{\textit{max}}$); the MO extension of $h^{\mathsf{max}}$ (${\mathbf{H}}_{\textit{mo}}^{\textit{comax}}$); and the MO canonical PDBs of size 2 and 3 (${\mathbf{H}}_{\textit{mo}}^{\textit{pdb2}}$ and ${\mathbf{H}}_{\textit{mo}}^{\textit{pdb3}}$). The SO PDB heuristics for SSPs from (Klößner and Hoffmann 2021) of size 2 and 3 (${\mathbf{H}}_{\textit{ideal}}^{\textit{pdb2}}$ and ${\mathbf{H}}_{\textit{ideal}}^{\textit{pdb3}}$) are also included in our experiments. All problem configurations are run with a timeout of 1800 seconds, memory limit of 4GB, and a single CPU core. The experiments are run on a cluster with Intel Xeon 3.2 GHz CPUs. We used CPLEX version 22.1 as the LP solver for computing CCS. The consistency threshold is set to $\varepsilon=0.001$ and we set $\vec{b}=\vec{100}$. Each experimental configuration is run 6 times and averages are taken to reduce variance in the data.

We also modify the inequality constraint in Alg. 4.3 from Roijers and Whiteson 2017 for computing CCS to ${\vec{w}}\cdot(\vec{v}-\vec{v}^{\prime})+x\leq-\lambda,\forall\vec{v}^{\prime}\in{\mathbf{V}}$ with $\lambda=0.01$ to deal with inevitable numerical precision errors when solving the LP. If the $\lambda$ term is not added, the function may fail to prune unnecessary points such as those corresponding to stochastic policies in the CCS, resulting in slower convergence. However, an overly large $\lambda$ may return incorrect results by discarding important points in the CCS. One may alternatively consider the term as an MO parameter for trading off solution accuracy and search time, similarly to the $\varepsilon$ parameter.

Fig. 3 shows the distribution of CCS sizes for different domains. Recall that the CCS implicitly represents a potentially infinite set of stochastic policies and their value functions. As a result, a small CCS is sufficient to dominate a large number of solutions, for instance, in Triangle Tireworld, a CCS of size 3 to 4 is enough to dominate all other policies even though the number of deterministic policies for this domain is double exponential in its parameter $n$.

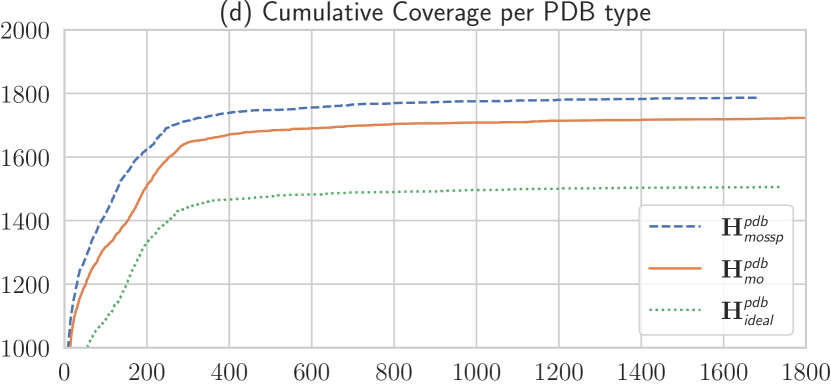
Fig. 4 summarises our results by showing the cumulative coverage of different planners and heuristics across all considered problems. The following is a summary of our findings (we omit the MO in the planner names for simplicity):