Heterogeneity and Low-Frequency Vibrations in Bidisperse Sphere Packings

Introduction.— Soft matters composed of dense macroscopic particles, such as foams, emulsions, and granular materials, commonly undergo the jamming transition into disordered solid states [1, 2]. This transition has attracted much attention in fundamental physics as it is an unusual critical phenomenon in non-thermal systems [1, 2, 3], and it also gives a fresh insight into thermal, structural glasses [4, 5]. Additionally, dense and active biological systems, such as cell tisues [6] and cytoplasm [7, 8], have been studied concerning the jamming transition.

Recent dramatic advances in jamming studies have benefitted from the simplest model, composed of nearly monodisperse, frictionless spheres. It is now established that mean-field theories can describe the jamming transition. At the transition point, a majority ($\sim 95\%$) of particles in the system get frozen simultaneously, and the system becomes isostatic; the contact number per particle becomes $Z=2d$ where $d$ is the spatial dimension [1]. In the jammed phase, vibrational properties are affected by the criticality of transition. Spatially disordered vibrations become abundant, which can not be described by the classical Debye theory based on phonon vibrations. The vibrational density of states (vDOS) shows a plateau in the frequency range down to the characteristic frequency $\omega_{\ast}$ [9]. At lower frequencies $\omega<\omega_{\ast}$, the vDOS follows the scaling law $D(\omega)\sim(\omega/\omega_{\ast})^{2}$, which is called the non-Debye scaling [10, 11]. These vibrational properties are explained by a replica theory for spherical particles [3, 12] and an effective medium theory for spring networks [13, 14, 15]. These theories are mean-field, ignoring a possible spatial heterogeneity: The former is constructed for the infinite-dimensional limit, where any spatial correlation does not exist [3], while the latter disregards a heterogeneity in the distribution of local contact numbers [15]. Therefore, the success of these theories implies that spatial heterogeneity in structure is irrelevant to the jamming transition. Instead, an unusual homogeneity, the hyperuniformity, in the density field [16, 17] and the contact number distribution [18, 19] has been debated.

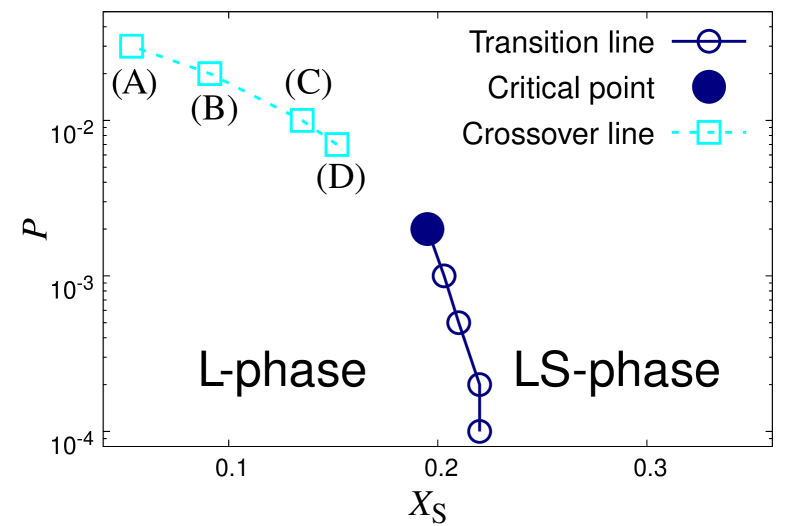
In this Letter, we demonstrate that this situation drastically changes if the size dispersity of particles is large enough: Large-scale structural heterogeneity emerges, altering the low-frequency vibrations significantly. We study a binary mixture composed of large and small particles with a large size ratio. Previous studies [21, 22, 20, 23, 24] have established the phase diagram of such systems, as shown in Fig. 1. There are two distinct jammed phases: The “L-phase” where only large particles are jammed, and the “LS-phase” where both small and large particles are jammed. These phases are separated by the first-order transition line which terminates at the critical point. Crossing the transition line, most small particles get jammed simultaneously such that the fraction of jammed small particles changes discontinuously, whereas above the critical point, it changes continuously.

In this work, we first show that the packing structure becomes highly heterogeneous in approaching the critical point. The small particles tend to form clusters, and a system-spanning cluster emerges at the critical point. We next show that the vDOS at low-frequency regime follows a linear scaling law $D(\omega)\sim\omega/\omega_{\ast}$ near the critical point; the low-frequency vibrations are significantly intensified. Finally, we numerically and theoretically demonstrate that these two properties, large-scale heterogeneity in structure and abundance of low-frequency vibrations, are closely related. The present work realizes heterogeneously jammed states, which have markedly different properties from homogeneously jammed states.

Model.— We consider $N_{\rm S}$ small and $N_{\rm L}$ large spherical particles in a three-dimensional ($d=3$) box of linear dimension $L$. We set the size ratio to be $\sigma_{\rm L}/\sigma_{\rm S}=6$, where $\sigma_{\rm S}$ and $\sigma_{\rm L}$ are diameters of small and large particles, respectively. Particles interact via the harmonic potential $v_{ij}(r_{ij})=\frac{\epsilon}{2}(\sigma_{ij}-r_{ij})^{2}\Theta(\sigma_{ij}-r_{ij})$, where $r_{ij}$ is distance between particles $i$ and $j$, $\sigma_{ij}=(\sigma_{i}+\sigma_{j})/2$, and $\Theta(r)$ is Heaviside step function. Length, time, and energy are measured in units of $\sigma_{\rm S}$, $\sqrt{m_{\rm S}\sigma_{\rm S}^{2}/\epsilon}$, and $\epsilon$, respectively ($m_{\rm S}$ is the mass of small particles).

The macroscopic state of the system is specified by two state-variables $(P,X_{\rm S})$: Pressure $P=L^{-3}\sum_{\expectationvalue{ij}}f_{ij}r_{ij}$ with contact force $f_{ij}=v_{ij}^{\prime}(r_{ij})$ ($\prime$ denotes derivative), and fraction of small particles $X_{\rm S}=N_{\rm S}/(N_{\rm S}+6^{3}N_{\rm L})$. We fix $N_{\rm S}=8000$ and tune $N_{\rm L}$ to control $X_{\rm S}$. To obtain mechanically stable packings at a given $(P,X_{\rm S})$, we quenched random configurations by using FIRE algorithm [25], and tuned the system size $L$ by an iterative compression/decompression algorithm to realize the target $P$ [20]. We prepared $200$ samples at each $(P,X_{\rm S})$ and calculated the sample average for various quantities, which is denoted by $\expectationvalue{\cdot}$.

The jammed particles are identified as particles making at least $d+1$ contacts, as usually employed [1]. The fraction of the jammed small particles,

is an order parameter to determine the phase behavior, where ${\rm S}$ denotes a set of small particles, and $S_{i}=1$ for the jammed state while $S_{i}=0$ otherwise. To systematically approach the critical point, we focus on four state points as indicated in Fig. 1: (A) $(P,X_{\rm S})=(3\times 10^{-2},0.0536)$, (B) $(2\times 10^{-2},0.0910)$, (C) $(10^{-2},0.135)$, and (D) $(7\times 10^{-3},0.152)$. These states are located on the crossover line where half of the small particles are jammed while the other half are unjammed, i.e., $\expectationvalue{R_{S}}=0.5$.

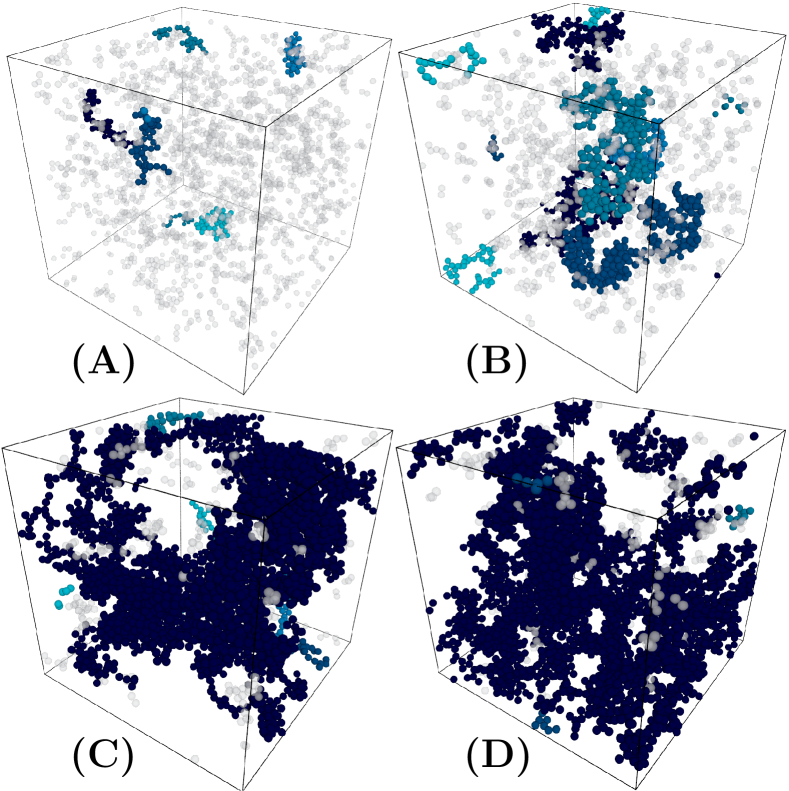
Structure.— Since the phase behavior is controlled by the jammed small particles, we first focus on their spatial structures. We define a cluster as a group of particles that are connected via contacts between the jammed small particles only. We numerically identified such clusters using Hoshen-Kopelman algorithm [26]. In Fig. 2, we show snapshots of representative packings, where the five largest clusters are in blue while the other smaller clusters are in gray. Far from the critical point (state A), small clusters are scattered throughout the system. In approaching the critical point (state D), the size of clusters grows so that the largest cluster spans the entire system. To quantify this percolation behavior, we calculated the number of particles in the largest cluster, $\expectationvalue{S_{\text{max}}}$, and showed an increasing (most likely diverging) behavior of $\expectationvalue{S_{\text{max}}}$ [see the Supplemental Material (SM)].

Figure 2 shows that the jammed small particles are distributed heterogeneously near the critical point. To discuss this heterogeneity more quantitatively, we introduce two types of radial distribution functions:

where $\vec{r}_{i}$ is the position vector of particle $i$, $\vec{r}_{ij}=\vec{r}_{i}-\vec{r}_{j}$, and $r=|\vec{r}|$. $G(r)$ is a distribution function for all the small particles including unjammed ones, while $G_{\rm S}(r)$ is for the jammed small particles only. As shown in Fig. 3, $G(r)$ is almost identical at the states A and D, meaning that the spatial distribution of all the small particles is insensitive to the criticality. In contrast, $G_{\rm S}(r)$ varies near the critical point. Far from the critical point (state A), $G_{\rm S}(r)$ becomes larger than $G(r)$ at $r\lesssim 6$, whereas $G_{\rm S}(r)\approx G(r)$ at $r\gtrsim 6$. Notice that the length $6$ is the diameter of the large particle, which should be in the same order as the size of pores formed by the jammed large particles. In approaching the critical point (state D), $G_{\rm S}(r)$ becomes substantially larger than $G(r)$, and finite spatial correlation persists even at $r\gtrsim 6$. These results indicate that the jamming of small particles takes place cooperatively in the entire system near the critical point, whereas far from the critical point the cooperativity persists only within each pore. Thus, large-scale heterogeneity emerges in the spatial distribution of the jammed small particles near the critical point. We emphasize that such heterogeneity is totally absent in the monodisperse packings.

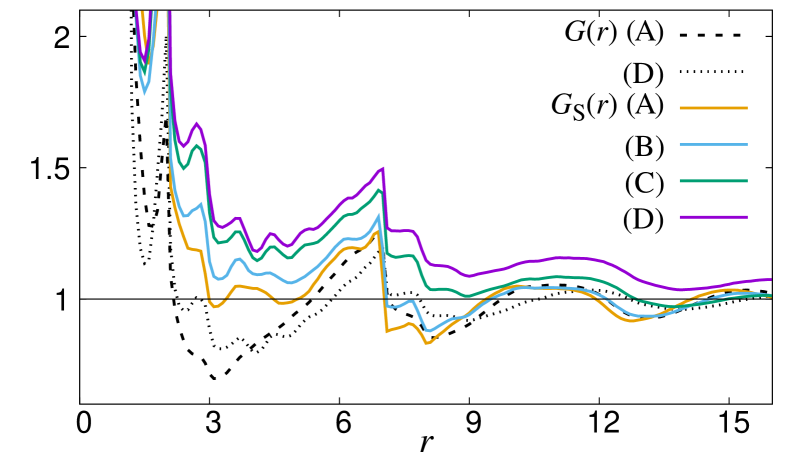
Vibrations.— We next study the low-frequency vibrations in bidisperse packings using a standard vibrational-mode analysis [27]. Vibrational modes are obtained as eigenvectors of the dynamical matrix $\mathcal{M}$. Off-diagonal elements of $\mathcal{M}$ from different particles $i\neq j$ are

where $I$ denotes unit tensor, and $k_{ij}=v_{ij}^{\prime\prime}(r_{ij})$. Diagonal elements from same particle $i=j$ are $\mathcal{M}_{ii}=-\sum_{j\in\partial_{i}}\mathcal{M}_{ij}$, where $\partial_{i}$ indicates a set of particles contacting with the particle $i$. The vDOS is then calculated as $D(\omega)=\frac{1}{3N}\langle\sum_{k}\delta(\omega-\omega_{k})\rangle$, where $\omega_{k}$ the $k$-th eigenfrequency.

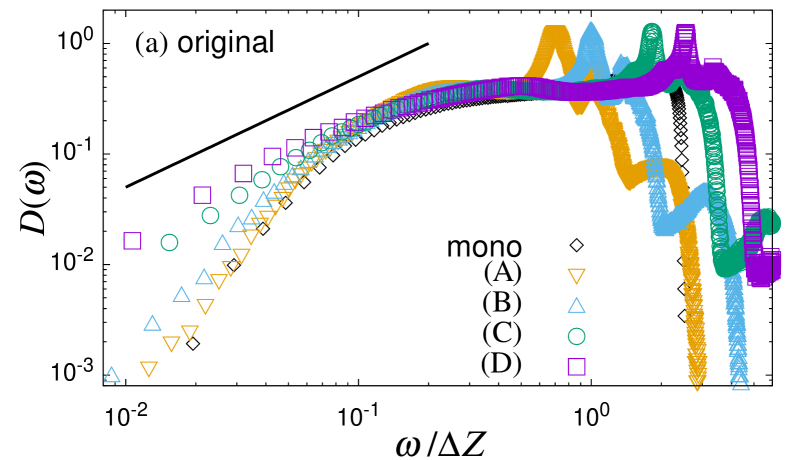
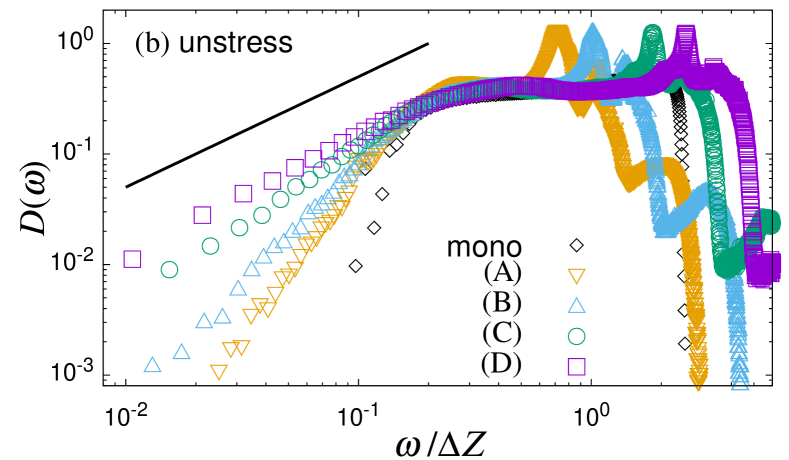
Figure 4 (a) shows the vDOSs of the bidisperse packings, compared to that of the monodisperse packing. The frequency $\omega$ is scaled by the excess contact number $\Delta Z=Z-2d$ since the characteristic frequency follows $\omega_{\ast}\propto\Delta Z$ in the monodisperse packings [9]. In the high-frequency regime $\omega/\Delta Z\gtrsim 10^{-1}$, the vDOSs of all cases collapse well and show a plateau. This result indicates that the critical point in the bidisperse packings does not affect anomalous vibrational modes in the plateau regime at $\omega>\omega_{\ast}$. In contrast, in the low-frequency regime $\omega/\Delta Z\lesssim 10^{-1}$, $D(\omega)$ strongly depends on the state; $D(\omega)$ gets larger in approaching the critical point, and near the critical point, it shows the linear dependence on $\omega$ as $D(\omega)\sim\omega/\omega_{\ast}$. This linear dependence is in sharp contrast to the monodisperse packings which show the non-Debye scaling law for the boson peak, $D(\omega)\sim(\omega/\omega_{\ast})^{2}$, and the quartic law for the quasi-localized vibrational modes, $D(\omega)\sim(\omega/\omega_{\ast})^{4}$ [28]. We also calculated the “concentration” on small particles $M^{S}_{k}$ for these modes (see the SM). A remarkable feature is that in the regime of $D(\omega)\sim\omega/\omega_{\ast}$, vibrational modes concentrate on small particles only, while the contribution from large particles is negligible. Our results establish that the low-frequency vibrations in near-critical bidisperse packings are significantly intensified compared to monodisperse packings, which are dominated by small particles.

In the monodisperse packings, the non-Debye scaling $D(\omega)\sim(\omega/\omega_{\ast})^{2}$ is a consequence of the marginal stability [12, 15]. This can be numerically confirmed by analyzing the unstressed version of the system [13]. In this analysis, the contact force $f_{ij}$ in Eq. (4) is artificially set to be zero, and we diagonalize the resulting dynamical matrix. Since the contact forces always destabilize the system, this artificial operation improves the stability of the packings. As a result, the low-frequency vibrations (except for phonon vibrations) at $\omega\lesssim\omega_{\ast}$ disappear in the unstressed system [13, 29, 28, 30].

Here, we analyze the unstressed version of the bidisperse packings and the monodisperse packing, and show their vDOSs in Fig. 4 (b). In the monodisperse packing, $D(\omega)$ at $\omega\lesssim\omega_{\ast}$ sharply drops as expected. On the contrary, such a drop does not appear for the bidisperse packings, and the vDOS near the critical point still follows the linear law $D(\omega)\sim\omega/\omega_{\ast}$. This observation indicates that the origin of the low-frequency vibrations in bidisperse packings differs fundamentally from monodisperse packings: The low-frequency vibrations in bidisperse packings do not originate from the instability due to the contact forces. Instead, as shown below, they are explained by the heterogeneities in the structures. In the SM, we also show that the participation ratio $P_{k}$ of each mode $k$ is unchanged between original and unstressed systems, which further validates the above discussion.

Link between structure and vibrations.— Now, we will demonstrate that the abundance of low-frequency vibrations is linked to structural heterogeneity.

We start with numerical evidence that spatial distributions of local contact numbers and low-frequency vibrations are correlated. We define the “concentration” of the low-frequency vibrations on the jammed small particle $i$,

where $\vec{e}_{i,k}$ is the $i$-th particle displacement in the $k$-th vibrational mode. We next define the local contact number as follows. In general, a contact between two particles constrains their relative motion. However, if one of the particles is immobile, the contact virtually constrains the motion of the other one only. In the present bidisperse packings, the low-frequency vibrations are concentrated on the jammed small particles, meaning that the large particles virtually act as such immobile obstacles. To take this into account, we introduce an effective contact number for the jammed small particle $i$,

where $Z^{SS}_{i}$ and $Z^{SL}_{i}$ are the number of contacts with small and large particles, respectively. Since the large particles are immobile, the isostatic condition is that the average of this effective contact number is equal to $2d$.

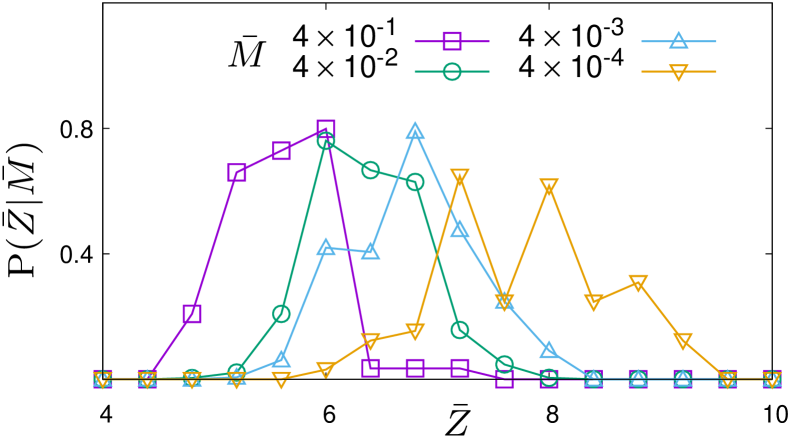
We computed above $M_{i}$ and $Z_{i}$, which are then coarse-grained as $\bar{Z}_{i}=\frac{Z_{i}+\sum_{j\in\partial i}Z_{j}}{1+N_{\partial i}}$ and $\bar{M}_{i}=\frac{M_{i}+\sum_{j\in\partial i}M_{j}}{1+N_{\partial i}}$ where $N_{\partial i}$ is the number of neibouring particles for the particle $i$. To look at correlations between $\bar{Z}_{i}$ and $\bar{M}_{i}$, we calculated a conditional distribution function, $\text{P}(\bar{Z}|\bar{M})=\langle\sum_{i\in{\rm S}}\delta(\bar{M}_{i}-\bar{M})\delta(\bar{Z}_{i}-\bar{Z})\rangle/\langle\sum_{i\in{\rm S}}\delta(\bar{M}_{i}-\bar{M})\rangle$. Figure 5 shows $\text{P}(\bar{Z}|\bar{M})$ near the critical point (state D). The distribution shifts to the left with increasing $\bar{M}$: The more a particle participates in the low-frequency vibrations, the smaller its local contact number is. For the largest $\bar{M}$, the distribution peaks at $\bar{Z}\approx 5$ which is even smaller than $2d~{}(=6)$. This result clearly demonstrates that particles with fewer contact numbers contribute more to low-frequency vibrations.

The above numerical evidence motivates us to explain the linear law $D(\omega)\sim\omega/\omega_{\ast}$ by considering the local contact-number fluctuations. Here we generalize the “cutting argument” [13], which was originally proposed to explain the plateau in the vDOS for monodisperse packings. We consider a system with the excess contact number $\Delta Z$ and linear dimension $L$, and divide it into $(L/\ell)^{3}$ subsystems of linear dimension $\ell$. In the subsystem $n$ ($n=1,2,...,(L/\ell)^{3}$) with the excess contact number $\delta z_{n}$, we estimate the number of the soft modes as $\mathcal{N}_{{\rm soft},n}(\ell)=-\delta z_{n}\ell^{3}+\ell^{2}$ for $\delta z_{n}<1/\ell$ while $\mathcal{N}_{{\rm soft},n}(\ell)=0$ otherwise, where unimportant $\mathcal{O}(1)$ coefficients are omitted. Since a soft mode in each subsystem can be used to generate a trial mode in the original system with the frequency $\omega\sim 1/\ell$, the cumulative vDOS is bounded as $C(\omega)\gtrsim L^{-3}\sum_{n}\mathcal{N}_{{\rm soft},n}(\ell\sim 1/\omega)$, thus we obtain

where $\text{P}_{\ell}(\delta z)$ is probability distribution to find subsystems with $\delta z$. Eq. (7) is a generalization of the original cutting argument, which is embedded by variation in $\delta z$ among the subsystems. Note that in the original argument for monodisperse packings [13], we suppose the delta function for $\text{P}_{\ell}(\delta z)=\delta(\delta z-\Delta Z)$, which provides $D(\omega)=dC/d\omega\gtrsim\omega^{0}$ for $\omega>\Delta Z$.

Now we assume that spatial fluctuations in $\delta z$ are sufficiently large; their standard deviation is in the same order as the average $\Delta Z$, so a certain fraction of subsystems with $\delta z\sim 0$ exists. In such the case, $\text{P}_{\ell}(\delta z)$ can be virtually treated as a constant for $\omega~{}(\sim 1/\ell)<\omega_{\ast}=\Delta Z$, and the delta function $\delta(\delta z-\Delta Z)$ for $\omega\gg\omega_{\ast}=\Delta Z$ (see the SM for a specific example with the Gaussian distribution). We thus obtain $D(\omega)\gtrsim\omega/\omega_{\ast}$ for $\omega<\omega_{\ast}$ and $D(\omega)\gtrsim\omega^{0}$ for $\omega\gg\omega_{\ast}$. Assuming that the inequality is saturated as in the original argument, we obtain $D(\omega)\sim\omega/\omega_{\ast}$ for $\omega<\omega_{\ast}$ and $D(\omega)\sim\omega^{0}$ for $\omega\gg\omega_{\ast}$, which totally agree with our numerical results in Fig. 4.

Concluding remark.— In this Letter, we investigated the structural and vibrational properties of bidisperse packings with a large size ratio. In approaching the critical point, the jamming of small particles takes place cooperatively, leading to the emergence of large-scale structural heterogeneity. Concomitantly, the low-frequency vibrations are significantly intensified near the critical point, and the vDOS follows the linear law, $D(\omega)\sim\omega/\omega_{\ast}$, at $\omega<\omega_{\ast}\propto\Delta Z$. We numerically and theoretically demonstrated that these two phenomena of spatial heterogeneity and intensified low-frequency vibrations are ultimately connected. In particular, we generalized the cutting argument to the heterogeneous packings, and successfully explained the linear law of the vDOS in terms of spatial fluctuations in the local contact numbers.

In this work, we also found that contact forces on small particles are significantly small, and interestingly, their distribution follows a power law with a negative exponent (see the SM), which is marked contrast to a positive exponent in monodisperse packings [31]. It is an interesting future work to theoretically explain this behavior by extending the stability analysis [32] or the microscopic replica theory [3].

Finally, our results suggest that the particle-size dispersity can cause a large-scale heterogeneity, exerting a strong impact on the vibrational properties of the packings. Since low-frequency vibrations play important roles in plasticy [33], it is interesting to study the non-linear mechanical properties to elucidate impacts from the low-frequency vibrations found in this work. More broadly, as many soft jammed solids, ranging from granular materials to biophysical systems, quite usually have continuous polydispersities with wide-range distributions [34, 35, 36, 37], it should be very interesting to study such systems along the line of this work.