Hereditary Effects and New Optical Properties of Nonlinear Gravitational Waves

We only focus on the second-order perturbation, since the analysis of higher-order ones shares the same method and leads to similar conclusions. Through the calculation of perturbation of any second-order metric gravity theory, we have the following most general second-order perturbation equation in the flat spacetime background:

$$\partial_{\lambda}\partial^{\lambda}h_{(2)\mu\nu}=\varepsilon_{\mu\nu}^{\ \ \ \rho\sigma\alpha\beta\gamma\delta}\partial_{\rho}h_{(1)\alpha\beta}\partial_{\sigma}h_{(1)\gamma\delta}+F_{\mu\nu},$$

(1)

where $\varepsilon_{\mu\nu}^{\ \ \ \rho\sigma\alpha\beta\gamma\delta}$ is a product of flat metric factors, the second term on the right hand side comes from the coupling of the gravitational field with extra fields in modified gravity theories and contain no higher than first-order perturbation of metric and second-order perturbation of extra fields. This formula shows that the right hand side of the equation can be regarded as the source of the second-order metric perturbation. Which means that the second-order perturbation is generated by the first-order perturbation in the wave zone. From the perspective of quantum field theory, this is a typical nonlinear feature that gravitons can exchange their own charge.

Next, we estimate how the nonlinear gravitational waves decay with distance. Most of the sources we are interested in are very far from us, hence we can treat gravitational waves as plane waves in the wave zone. We assume that there is a continuous monochromatic plane gravitational wave in wave zone. Then, Eq. (1) tells us that every part of this wave has the same effective energy-momentum tensor, and can radiate secondary gravitational waves. So, for an inertial observer at a given moment, these sources distributed in the spacetime can influence the observer’s observation through the retarded solution of gravitational waves. The retarded solution can be written as

$$h_{(2)\mu\nu}(x^{\lambda})=\int\frac{1}{|x^{i}-x^{\prime i}|}T_{\mu\nu}(t-|x^{i}-x^{\prime i}|,x^{\prime i})d^{3}x^{\prime},$$

(2)

where $T_{\mu\nu}$ represents all the energy momentum terms in the right hand side of Eq. (1)

$$T_{\mu\nu}(t-|x^{i}-x^{\prime i}|,x^{\prime i})=\varepsilon_{\mu\nu}^{\ \ \ \rho\sigma\alpha\beta\gamma\delta}\partial_{\rho}h_{(1)\alpha\beta}\partial_{\sigma}h_{(1)\gamma\delta}+F_{\mu\nu}.$$

(3)

Let us consider the schematic plotted in FIG. 1, where we have a monochromatic plane gravitational wave propagating continuously from left to right, we define this propagation direction as $+z$. Planes $S$ and $S^{\prime}$ represent two different wavefronts, and $o$ is the location of the observer.

Now, we analyze the effect of the second-order gravitational waves radiated by the two wavefronts. As shown in FIG. 1, the gravitational wave in the infinitesimal region $\delta S$ is responsible for this effect of the gravitational waves propagating along $+z$ at $o$. Since the decay with distance of gravitational wave energy follows the inverse square law, and the area of $\delta S$ increases proportionally with the square of the distance. Therefore, the gravitational waves generated by any two different wavefronts (e.g. $\delta S$ and $\delta S^{\prime}$) have the same effect on the observer.

Therefore, the second-order gravitational waves observed by the observer depend nonlocally on all historical retarded solutions. From Eq. (1), it can be seen that the second-order perturbation contains at most the square term of the first-order perturbation, its amplitude and its distance from the wave source satisfy the following relationship

$$h_{(2)}\propto\frac{1}{r^{2}}.$$

(4)

Then, after considering the hereditary effect of amplitude,

$$\begin{split}h_{(2)\mu\nu}(x^{\lambda})&=\int\frac{1}{|x^{i}-x^{\prime i}|}\mathscr{T}_{\mu\nu}(t-|x^{i}-x^{\prime i}|,x^{\prime i})d^{3}x^{\prime},\\ &=\int\mathscr{T}_{\mu\nu}(t-|z-z^{\prime}|,z^{\prime})d^{3}z^{\prime}\end{split}$$

(5)

where the second equal sign means that because each wavefront has the same contribution to the observer, after completing the integration in the $x-y$ plane, the integration in the $z$ direction is the superposition of all wavefronts with the same contribution. This means the intensity of the secondary gravitational waves at the observer’s location is the sum of the contributions of the secondary gravitational waves emitted by all sources at $x^{\prime}$.

Therefore, after taking into account the hereditary effect of amplitude, the asymptotic behavior of the second-order gravitational waves at a distance is

$$h_{(2)|\text{hereditary}}\propto\frac{1}{r}.$$

(6)

It is worth noting that the asymptotic behavior of $h_{(2)|\text{hereditary}}$ is the same as the linear-order one for continue plane waves.

But if we want to link the above results with actual observations, we need to treat the spherical waves. Since most of the sources we are interested in are far away from us, we can always treat gravitational waves as plane waves near the observer. For example, if we can treat the gravitational waves as plane waves when the distance between the gravitational wave and the observer is less than $\frac{r}{10^{3}}$. Thus, the asymptotic behavior of $h_{(2)|\text{hereditary}}$ far away from the source is still

$$h_{(2)|\text{hereditary}}\propto\frac{r}{10^{3}}\times\frac{1}{r^{2}}\propto\frac{1}{r}.$$

(7)

This will make it possible to directly observe nonlinear gravitational waves in more precise gravitational wave detection in the future, allowing further insights into the nature of gravity.

It is well known that the gravitational radiation is emitted in all directions, hence the secondary radiation from the regions outside the neighboring regions $\delta S$ in FIG. 1 can also affect the observer at point $o$. We find that gravitational waves propagating from different directions to the observer can produce special interference phenomena.

Although we demonstrated in the previous section that the secondary gravitational waves generated by $\delta S$ and $\delta S^{\prime}$ in FIG. 1 contribute the same amplitude to the ob- server, $\delta S$ and $\delta S^{\prime}$ in different propagation directions usually have different phases. This is because the distances between $\delta S$ and $\delta S^{\prime}$ are different in different directions, so the superposition of these waves will multiply or cancel each other. After simple calculation, the angular distribution of the amplitude of gravitational waves can be obtained as

$$I=\left|\cos\big{(}2\pi(\sec\theta-1)\big{)}\right|$$

(8)

Figure 2 is a schematic diagram of this interference intensity. The vertical direction in the figure represents the $z$-direction, and the distance from any point on the two-dimensional surface to the origin represents the relative amplitude of gravitational waves in the corresponding direction. That is, $h_{(2)|\text{hereditary}}$ has interference effects at different directions, which is fundamentally different from linear gravitational waves.

Now, we have analyzed the asymptotic behavior and new optical properties of nonlinear gravitational waves. The asymptotic behavior ensures the secondary gravitational waves could be observable. So, the next step is to analysis the observation properties of these optical effects and how these properties feed back into the theoretical research on gravity.

Firstly, the interference intensity distribution in FIG. 2 is not the intensity distribution of the nonlinear gravitational waves that we truly detected. It is also necessary to consider the angular dependence of the radiation intensity of gravitational waves. In other words, the amplitudes of gravitational waves in different direction emitted from the same wave source are generally different. In order to obtain the spatial angular distribution of gravitational radiation with different polarization modes, we need to consider the density of gravitational radiation energy flow:

$$F=\frac{1}{32\pi}\omega^{2}\langle h_{\mu\nu}h^{\mu\nu}\rangle.$$

(9)

The density of gravitational radiation energy flow can be calculated by substituting the amplitude of gravitational waves calculated in the previous subsection into the above equation. The angular distributions of the amplitude of tensor mode and breathing mode are shown in FIG. 3. It can be seen that for transverse gravitational waves, the radiation energy is highest along the $z$-axis direction and lowest perpendicular to the $z$-axis direction. And the angular distributions of different polarization modes are generally not the same.

Therefore, by combining the angular distribution of interference effect in FIG. 2 and the angular distribution of radiation intensity of wave source in FIG. 3, the angular distribution of the intensity of the non-linear gravitational wave can be obtained at the observer.

In addition, we can detect secondary gravitational waves in multiple directions, as shows in FIG. 2. Therefore if we can distinguish these gravitational waves in different directions, we can obtain the direction of the wave source.

Secondly, the waveform of a nonlinear gravitational wave is also different from that of a linear one. This is mainly because the nonlinear perturbation of gravity depends nonlocally on the energy distribution of gravitational waves in whole spacetime, which is exactly a typical hereditary effect.

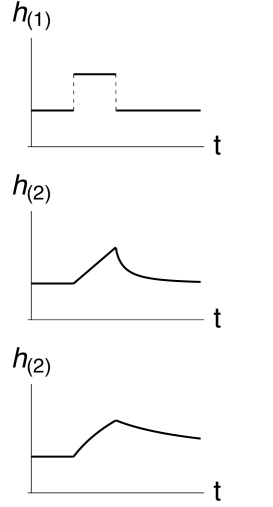
Here we take a simple example to show this difference. In FIG. 4, the amplitude of a linear harmonic gravitational wave suddenly increases at a certain moment and then recovers after a period of time $\Delta t$. The second and third figures in FIG. 4 show the waveforms of the second- order harmonic gravitational waves observed at different distances from the wave source. To calculate the amplitude values at each moment, we need to accumulate all secondary gravitational waves that can affect the observer at this moment. That is, the amplitude of each point in the waveform of $h_{(2)|\text{hereditary}}$ needs to be integrated throughout the entire historical spacetime.

It is worth noting that, as shown in FIG. 4, the amplitude of the nonlinear gravitational wave also has a tail effect. And its waveform depends on the distance between the wave source and the observer, as shown in the second and third figures in FIG. 4. In other words, the waveform of nonlinear gravitational waves contains distance information. The final stage of the $h_{(2)|\text{hereditary}}$ is a slow decay stage, because the current nonlinear gravitational wave also depends on the linear gravitational wave at any time in the past.

Therefore, due to the nonlocal dependence of the entire history of nonlinear gravitational waves, nonlinear gravitational waves will provide us with more information about polarization modes, wave source direction, and distance.