HC-SpMM: Accelerating Sparse Matrix-Matrix Multiplication for Graphs with Hybrid GPU Cores
Abstract
Sparse Matrix-Matrix Multiplication (SpMM) is a fundamental operation in graph computing and analytics. However, the irregularity of real-world graphs poses significant challenges to achieving efficient SpMM operation for graph data on GPUs. Recently, significant advancements in GPU computing power and the introduction of new efficient computing cores within GPUs offer new opportunities for acceleration.
In this paper, we present HC-SpMM, a pioneering algorithm that leverages hybrid GPU cores (Tensor cores and CUDA cores) to accelerate SpMM for graphs. To adapt to the computing characteristics of different GPU cores, we investigate the impact of sparse graph features on the performance of different cores, develop a data partitioning technique for the graph adjacency matrix, and devise a novel strategy for intelligently selecting the most efficient cores for processing each submatrix. Additionally, we optimize it by considering memory access and thread utilization, to utilize the computational resources to their fullest potential. To support complex graph computing workloads, we integrate HC-SpMM into the GNN training pipeline. Furthermore, we propose a kernel fusion strategy to enhance data reuse, as well as a cost-effective graph layout reorganization method to mitigate the irregular and sparse issues of real-world graphs, better fitting the computational models of hybrid GPU cores. Extensive experiments on 14 real-world graph datasets demonstrate that HC-SpMM achieves an average speedup of 1.33 and 1.23 over state-of-the-art SpMM kernels and GNN frameworks.
Index Terms:
GPU cores, SpMM, Graph ComputingI Introduction
Sparse Matrix-Matrix Multiplication (SpMM) is a fundamental operation that multiplies a sparse matrix and a dense matrix, which has been widely used in various graph computing tasks such as Graph Neural Networks (GNNs) training & inference [zhang2023ducati, li2024daha, gunduz2022scalable], PageRank [hou2021massively, luo2019efficient, shi2019realtime] and graph clustering [zhang2022effective, chang2017mathsf, xu2012model]. Recent studies employ matrix multiplication operations on GPUs to accelerate commonly used graph algorithms such as triangle counting and shortest path computing, with SpMM emerging as one of the core operations and becoming the efficiency bottleneck [sundaram2015graphmat, yang2022graphblast]. SpMM is also a fundamental operation in GNNs, accounting for more than 80% of the GNN training time [wang2023tc]. However, characterized by irregular memory access patterns and low computational intensity, the real-world graphs pose significant challenges for achieving efficient SpMM on GPU [wang2023tc]. Especially for GNNs, as the scale of graph data proceeds to grow and the complexity of GNN architectures escalates with an increasing number of layers, the efficiency issue becomes more serious, constraining the large-scale applicability111Training a GNN-based recommendation system over a dataset comprising 7.5 billion items consumes approximately 3 days on a 16-GPU cluster [duan2022comprehensive]., even though it achieves state-of-the-art performance on a myriad of problems such as node classification [song2022towards, zhang2022mul, wen2021meta], link prediction [gu2022hybridgnn, zou2023embedx, zhang2023disconnected, ran2023differentially], recommendation [zhang2021group, xia2021multi, wu2022graphnew] and beyond [fangshu, sun2023graph, li2023graph].
To enhance the efficiency of SpMM, some efforts have been made to employ CUDA cores in GPU for acceleration [refcusparse, hong2019adaptive, gale2020sparse, huang2020ge]. As the performance ceil is constrained by the hardware structure of CUDA cores, recent attempts have turned to explore harnessing the Tensor cores, which are specialized for efficient matrix multiplication, to accelerate SpMM [zachariadis2020accelerating, chen2021efficient, li2022efficient]. However, despite significantly improving the efficiency of dense matrix multiplication [li2022efficient], the irregularity and sparsity of real-world graphs impeding Tensor cores from achieving satisfactory performance [zachariadis2020accelerating, wang2023tc, fan2024dtc]. Various preprocessing techniques have been investigated to enhance the density of sparse matrices, yet significant sparse portions persist, hindering performance improvement222For instance, the average sparsity of the matrices output by the preprocessing method proposed in TC-GNN [wang2023tc] is still 90.9% on 10 tested datasets. .


Figure 1 illustrates the time overhead incurred by CUDA cores and Tensor cores across matrices with varying sparsity and the number of non-zero columns, which highlights their distinct applicabilities333An in-depth analyzation is provided in § LABEL:adaptivecoreselection.. CUDA cores demonstrate superior performance when handling sparser matrices with a higher number of non-zero columns, whereas Tensor cores exhibit greater efficacy in denser matrices characterized by fewer non-zero columns. Thereafter, relying solely on CUDA cores or Tensor cores for SpMM acceleration fails to fully exploit their respective computational strengths, primarily due to the irregularity of real-world graphs, which typically comprise a mixture of dense and sparse regions [yan2014blogel].
In this paper, we aim to devise a graph-friendly SpMM kernel using hybrid CUDA cores and Tensor cores, tailored to the varying computational demands of different graph regions, to support high-performance graph computing workloads. Furthermore, as a DB technique for AI acceleration, we integrate the hybrid SpMM kernel into the GNN training pipeline to enhance the training efficiency and demonstrate its effectiveness in complex graph computing scenarios.
However, crafting a hybrid SpMM kernel using CUDA cores and Tensor cores based on the characteristics of graph data and systematically integrating it into the GNN training pipeline encounters non-trivial challenges.
Challenges of designing hybrid SpMM kernel. (1) Effectively partitioning the adjacency matrix into sub-regions with distinct sparsity characteristics to leverage the different cores for collaborative computation presents a considerable challenge. (2) The computational characteristics of CUDA and Tensor cores vary significantly, which is also influenced by the graph features, making the selection of the optimal core for matrices with different sparsity levels crucial for enhancing efficiency. (3) Accurately modeling the computational performance of CUDA and Tensor cores for SpMM to facilitate precise core selection is another major difficulty. (4) Last but not least, inefficiencies inherent in the SpMM kernel, such as suboptimal memory access patterns and underutilized threads, limit the overall performance. To address these issues, we firstly propose a fine-grained partition strategy, which divides the adjacency matrix into equal-sized submatrices along the horizontal axis, allocating each submatrix to the appropriate GPU cores for efficient computation (§ IV-A). This allows CUDA and Tensor cores to perform calculations independently, eliminating the need to merge results between cores. Secondly, comprehensive quantitative experiments reveal that CUDA cores are memory-efficient while Tensor cores are computing-efficient (§ IV-B). These experiments identify two pivotal factors for submatrix characterization: sparsity and the number of non-zero columns, which dominate the most expensive parts for CUDA and Tensor cores, computation and memory access, respectively. Thirdly, leveraging these factors, we develop an algorithm tailored for the selection of appropriate GPU cores for submatrices, optimizing computational capability (§ IV-B). Finally, we conduct in-depth optimizations of the SpMM kernel, considering thread collaboration mode (§ LABEL:bottleneckofccu) and memory access patterns (§ LABEL:bootleneckTCU).
Challenges of integrating the SpMM kernel into GNN. When integrating our proposed hybrid SpMM kernel into the GNN training pipeline, there arise new challenges. (1) The isolation among GPU kernels within a GNN layer in prevalent GNN training frameworks [wang2019deep, wang2023tc] impedes data reuse, leads to additional memory access overhead, and introduces significant kernel launch overhead. (2) Tensor cores incur significantly higher throughput than CUDA cores, potentially offering substantial efficiency gain. However, real-world graph layouts inherently exhibit irregularity and sparsity, resulting in a majority of segments partitioned from the adjacency matrix being sparse and less amenable to processing via Tensor cores. Consequently, the performance gains achievable with Tensor cores are often negligible [wang2023tc]. To tackle the first problem, we discover opportunities to reuse data in the shared memory of GPU and present a kernel fusion strategy to mitigate kernel launch costs and global memory access (§ LABEL:subsec:kernelfusion). To address the second problem, we first introduce a metric termed computating intensity to estimate the calculation workload of the submatrices multiplication (§ LABEL:subsec:layout), which is calculated by the quotient of the number of non-zero elements and the number of non-zero columns. Higher computational intensity is achieved with more non-zero elements and fewer non-zero columns. Subsequently, we propose an efficient algorithm to reconstruct submatrices, adjusting the graph layouts to obtain more dense segments suitable for processing by Tensor cores, gaining significant efficiency with Tensor cores (§ LABEL:subsec:layout). This adjustment has a relatively small cost compared with GNN training but renders the graph data more compatible with hybrid GPU cores, unlocking the full computational potential of Tensor cores and thereby significantly enhancing the efficiency of GNN training (§ LABEL:eva:layout).
Contributions. In this work, we propose HC-SpMM, a novel approach for accelerating SpMM using hybrid GPU cores. Our key contributions are summarized as follows:
-
•
We quantify the difference between CUDA and Tensor cores in SpMM, and propose a hybrid SpMM kernel, which partitions the graph adjacency matrix and intelligently selects appropriate GPU cores for the computation of each submatrix based on its characteristics. We further optimize the SpMM kernel considering thread collaboration mode and memory access patterns (§ IV).
-
•
We propose a kernel fusion strategy for integrating HC-SpMM into the GNN training pipeline, eliminating kernel launch time and enabling efficient data reuse, and present a lightweight graph layout optimization algorithm to enhance irregular graph layouts and better align with the characteristics of both GPU cores (§ LABEL:sec:spmmintegration).
-
•
We conduct comprehensive evaluations demonstrating that HC-SpMM outperforms existing methods, achieving 1.33 speedup in SpMM and 1.23 speedup in GNN training on average (§ LABEL:sec:evaluation).
The rest of this paper is organized as follows. Section II reviews the related work. Section III gives the preliminaries. Section IV presents the design of the hybrid SpMM kernel. Section LABEL:sec:spmmintegration describes the optimization of integrating the SpMM kernel into GNNs. Section LABEL:sec:evaluation exhibits the experimental results. We conclude the paper in Section LABEL:sec:conclusion.
II Related Work
SpMM Using CUDA Cores. Optimization of SpMM has been a subject of extensive study [buluc2008challenges, zhang2020sparch, hong2019adaptive, yang2018design, xia2023flash]. In recent years, Yang et al. [yang2018design] leveraged merge-based load balancing and row-major coalesced memory access strategies to accelerate SpMM. Hong et al. [hong2019adaptive] designed an adaptive tiling strategy to enhance the performance of SpMM. cuSPARSE [refcusparse] offers high-performance SpMM kernels and has been integrated into numerous GNN training frameworks such as DGL [wang2019deep]. Gale et al. point out that cuSPARSE is efficient only for matrices with sparsity exceeding 98%. Consequently, they proposed Sputnik [gale2020sparse] to accelerate the unstructured SpMM in deep neural networks and achieve state-of-the-art performance. Dai et al. [dai2022heuristic] introduced an approach capable of heuristically selecting suitable kernels based on input matrices. However, it demonstrates superior performance only when the matrix dimension is less than 32. Furthermore, Fan et al. [fan2023fast] proposed an SpMM kernel employing a unified hybrid parallel strategy of mixing nodes and edges, achieving efficient performance. To the best of our knowledge, there are few SpMM kernels specifically designed for graph computing workloads. Huang et al. [huang2020ge] introduced a GNN-specified SpMM kernel, utilizing coalesced row caching and coarse-grained warp merging to optimize memory access. However, it did not fully consider the characteristics of the graph adjacency matrix. Despite highly optimized algorithms, the computational capabilities of CUDA cores are inherently restricted by the hardware structures and are less efficient than Tensor cores, hindering the efficiency improvement in dense matrix multiplication.
SpMM Using Tensor Cores. Numerous recent works have been shifted to accelerate SpMM with the assistance of Tensor cores [chen2021efficient, li2022efficient, wang2022qgtc, wang2023tc, fan2024dtc]. However, most of them require structured input matrices, which is often impractical for adjacency matrices of real-world graphs. Alternatively, other works focus on unstructured SpMM and employ preprocessing methods to reduce the number of tiles needing traversal and to avoid unnecessary computation [zachariadis2020accelerating, wang2023tc, fan2024dtc]. For example, TC-GNN [wang2023tc] compresses all zero columns within a row window and DTC-SpMM [fan2024dtc] transforms the matrix into memory-efficient format named ME-TCF. Although TC-GNN implements a CUDA and Tensor cores collaboration design, it just employs CUDA cores for data loading, not for computing. Different from it, our proposed HC-SpMM employs both cores for computing according to their characteristics. Besides, Xue et al. [xue2023releasing] propose an unstructured SpMM kernel using Tensor cores, introducing a format named Tile-CSR to reduce the zero elements in submatrices traversed by Tensor cores. However, this kernel only supports half precision. As mentioned, Tensor cores are not natively suitable for unstructured SpMM. While preprocessing can densify submatrices, they still involve some computational waste and lead to suboptimal performance.
GNN Training Frameworks. Motivated by the remarkable performance but inefficient training of GNN, plenty of GNN training frameworks have been proposed, focusing on the graph locality [wang2021gnnadvisor, zhang2023ducati], the GPU memory utilization [li2024daha], etc. Besides, various frameworks for distributed GNN training have emerged recently [wang2022neutronstar, peng2022sancus, zhang2023lotan, wan2023scalable, gunduz2022scalable, tang2024xgnn, min2021large, zhu2019aligraph], which represent an orthogonal research direction. Our work focuses on optimizing SpMM and employing hybrid GPU cores for accelerating basic matrix multiplication, which can be seamlessly integrated into any aforementioned frameworks. This integration allows the Aggregation phase to directly call the optimized SpMM kernel, significantly reducing the execution time of Aggregation. Works addressing similar problems include GE-SpMM [huang2020ge] and TC-GNN [wang2023tc] mentioned above, both of which have integrated the kernels into GNN training frameworks. However, they solely employ CUDA or Tensor cores to perform SpMM operations in GNNs, failing to fully exploit the respective computational strengths of GPU cores.
Heterogeneous processing in data computing. Some efforts are dedicated to employing heterogeneous systems for queries in databases [bogh2017template, chrysogelos2019hetexchange, rosenfeld2022query], general computing tasks [hsu2023simultaneous] and deep learning [kwon2021heterogeneous, zheng2020flextensor]. Other research employs heterogeneous processing elements for SpMM [gerogiannis2024hottiles] and employs CUDA & Tensor cores for general matrix multiplication [ho2022improving]. Our work focuses on accelerating SpMM by heterogeneous GPU cores, a topic that has barely been explored.
III Preliminaries
In this section, we provide a concise description of GPU architecture, including the characteristics of CUDA and Tensor cores, followed by an overview of GNNs.
III-A GPU Architecture
GPU is a highly parallel hardware comprising tens of Streaming Multiprocessors (SMs). Each SM features dedicated local memory, registers, and processing cores. These SMs individually schedule the execution of threads in warps, each consisting of 32 threads. Threads in a warp run simultaneously in a Single Instruction Multiple Threads (SIMT) fashion. A block consisting of multiple warps is allocated to an SM.
The GPU’s memory hierarchy includes global memory, shared memory, and registers. Global memory, shared by all SMs, offers the largest capacity but lower I/O bandwidth. Each SM contains fast but limited shared memory, typically ranging from 16 KB to 64 KB. Additionally, each SM includes registers, which serve as the fastest storage structure.
Access to global memory within a warp is granular at 128 bytes when the L1 cache is enabled or 32 bytes otherwise. Consequently, when 32 threads within a warp request consecutive data within 128 bytes, only one memory access transaction is necessary, resulting in coalesced memory access. Shared memory is partitioned into multiple independent storage areas known as banks. Each bank can independently serve a thread in a single clock cycle. Concurrent access by multiple threads to the same bank results in a conflict, diminishing memory access efficiency. In shared memory, data is allocated across 32 consecutive banks, with each bank having a granularity of 4 bytes. For instance, when storing 64 numbers of float type in shared memory, the first 32 numbers and the last 32 numbers will be mapped to the 32 banks respectively. The 1st and 33rd numbers are assigned to the same bank, with the remaining numbers following a similar pattern.
III-B Computing Cores in GPU

CUDA Cores. CUDA cores are the primary computing cores used in GPUs. Each thread is assigned to a CUDA core for performing various calculations. Furthermore, CUDA cores can execute only one operation per clock cycle. Multiplying two 4×4 matrices involves 64 multiplications and 48 additions.
Tensor Cores. Tensor cores, specifically designed for deep learning computation, have been integrated into advanced GPUs since 2017. Unlike CUDA cores, Tensor cores operate at the warp level, where threads within a warp collaboratively multiply two fixed-size matrices (e.g. 4 4) in a single clock cycle. In addition to utilizing the matrix multiplication APIs provided by cuBLAS [refcublas], Tensor cores can also be leveraged through the Warp Matrix Multiply-Accumulate (WMMA) API for more flexible programming. The WMMA API requires a fixed-size input matrix, with the required size varying depending on the data type. In this paper, we use TF-32 as the input data type of Tensor cores, following previous work [wang2023tc], which requires 16 8 16 as the input size. Although more efficient than CUDA cores in matrix multiplication, the fix-sized input requirement restricts the flexibility to avoid computing numerous zero elements in sparse adjacency matrices of graphs, limiting its efficiency in performing SpMM.
Figure 2 illustrates the disparity between CUDA and Tensor cores during SpMM. represents the -th warp and represents the -th thread. As depicted in Figure 2(a), each thread computes a single element in the result matrix, i.e., in Equation 1. CUDA cores possess the flexibility to efficiently skip zero elements in the sparse matrix and perform multiplication operations based on the CSR format. Conversely, Tensor cores conduct computations at the warp level as shown in Figure 2(b). Each warp retrieves a submatrix from both the sparse matrix and the dense matrix , subsequently computing the multiplication products. Despite the presence of numerous zeros in the sparse matrix, Tensor cores are unable to skip them, resulting in the waste of computational resources.
Based on the characteristics outlined above, we can observe that while Tensor cores offer high efficiency in matrix multiplication, they lack flexibility compared to CUDA cores, particularly in handling sparse matrices. Tensor cores process all elements indiscriminately due to their strict input criteria. Therefore, determining which cores are more efficient in the context of SpMM is challenging. This paper aims to devise a strategy for dynamically selecting the appropriate cores for submatrices within a sparse matrix for enhanced performance.
III-C Graph Neural Networks

In a graph , where and represent the node set and edge set, respectively, the adjacency matrix of is denoted by . Each node has an embedding, which is a continuous vector representation with dimension . The embedding encodes various properties of a node according to the downstream tasks. In GNNs, node embeddings are represented as matrix . Typically, a GNN layer consists of two fundamental operations: Aggregation and Update. An example of GNN is depicted in Figure 3.
In the Aggregation operation, each node aggregates its feature vector and those of its neighbors from to form the new one. This process at layer can be formalized as a matrix multiplication operation, as depicted in Equation 1, where is calculated from , and is the aggregated result. The matrix is always sparse, making the Aggregation operation analogous to an SpMM-like operation.
| (1) |
Equation 2 formalizes the Update operation, where denotes the network parameters at layer and is the updated feature matrix. This operation can be efficiently executed using the gemm kernel in cuBLAS.
| (2) |
Suppose the gradient is . Backward propagation also involves Aggregation and Update. The Update phase in layer is formalized as Equation 3, containing two gemm operations.
| (3) |
The Aggregation operation can be abstracted as an SpMM operation as Equation 4.
| (4) |
IV Hybrid SpMM Kernel
In this section, we justify our selection of row window as the fundamental hybrid unit, contrasting it with the straightforward choice of submatrices. Additionally, we delve into the essential characteristics that influence the efficiency of GPU cores, serving as the driving force behind our subsequent designs.
IV-A Combination Strategy
Initially, we need to consider how to combine the two GPU cores in a sparse matrix computation, i.e., the partitioning of the sparse matrix into submatrices and the processing strategy of each submatrix using different GPU cores. A straightforward strategy is illustrated in Figure 4(a). Due to the fixed-size input requirement of the WMMA API, it divides the input matrix into submatrices sized , named row windows. Within each row window, columns are rearranged based on the count of non-zero elements. Intuitively, the first few columns within a row window tend to be denser, while subsequent ones are sparser. It further splits each row window into submatrices and traverses the matrix in units of which is the minimum granularity required by WMMA API for input. Each submatrix is assigned to appropriate GPU cores based on our identified characteristics (§ LABEL:adaptivecoreselection).
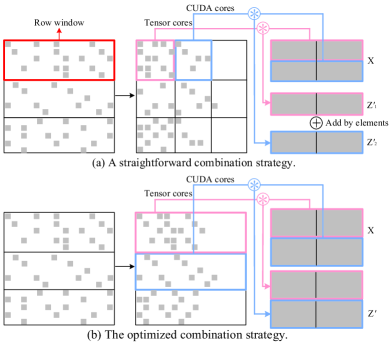
While the straightforward strategy offers fine-grained traversal, upon closer examination, it reveals several limitations. (1) Merging the results from CUDA and Tensor cores introduces extra overhead. Results computed by Tensor cores are initially buffered in registers before being transferred to shared or global memory, while those computed by CUDA cores are directly stored in shared or global memory. Within each row window, the merging of results from Tensor and CUDA cores necessitates additional I/O and adds to the overhead of addition operations444The overhead is up to 31%, which is unacceptable.. (2) Hybrid computation within a row window necessitates the separate storage of edges for Tensor cores and CUDA cores, resulting in increased preprocessing overhead and poor access locality. (3) The execution time in the granularity of matrix multiplication complicates accurate measurement555Execution time remains in microseconds in this granularity, whose tendency regarding sparsity is not easily visible.. Furthermore, sparsity is the only characteristic that can be leveraged for core selection in submatrices. These constraints hinder a comprehensive analysis of the relationship between GPU cores and matrix characteristics.
To tackle the aforementioned issues while maintaining fine granularity, instead of using a submatrix, we adopt the row window as the minimum hybrid unit. Following a strategy similar to TC-GNN [wang2023tc], we position non-zero columns at the forefront of row windows, thereby density the submatrices, i.e., the row windows. As depicted in Figure 4(b), within each row window, Tensor cores execute across all 168 submatrices, while CUDA cores compute directly using the CSR format. This approach eliminates the need for merging the results from CUDA and Tensor cores, reducing the extra computation overhead. Edges within each row window can be stored consecutively in this granularity, which ensures the access locality of edges. The sufficient duration of execution in the scale of row windows aids in the analysis of appropriate GPU core selection. Another pivotal characteristic in this granularity, the number of non-zero columns, stands out as a reference for better core allocation (§ LABEL:adaptivecoreselection).
IV-B Computing Characteristics of GPU Cores
In this subsection, we identify key features of row windows that impact the GPU cores’ performance and quantify the difference in computing characteristics between different cores.