Hawking-Page phase transition, Page curve and islands in black holes

In 1975, Hawking Hawking1975 presented that a black hole radiates as a black body with a temperature. This discovery solves the contradiction of the temperature in the thermodynamics of black holes and implies the internal relation among gravity, thermodynamics and quantum mechanics. However, this produced the black hole information paradox. The discovery of the AdS/CFT correspondence means that the question of whether information can come out of a black hole is answered by Maldacena Maldacena:1997re . By the AdS/CFT correspondence, Ryu-Takayanagi PhysRevLett.96.181602 proposed a holographic description of the entanglement entropy. It was subsequently generalized and applied to the black hole information problem by researchers. While the Page curve as a function of time Page:1993wv ; Page:2013dx which expected the entanglement entropy between the outgoing radiation and the quantum state associated to the remaining black hole, if black hole evaporation is a unitary process. To reproduce the Page Curve in solving the black hole information paradox is a key. Recently, Researchers reproduced the Page curve for the Hawking radiation’s entanglement entropy through to develop from the action of islands Almheiri:2019hni ; Penington:2019npb ; Almheiri:2019psf ; Almheiri:2020cfm . Accordingly, including the island contributions, the fine-grained entropy of Hawking radiation is Almheiri:2019hni

$$S(R)=\text{min}\{\text{ext}[\frac{\text{Area}(\partial I)}{4G_{N}}+S_{\text{matter}}(R\cup I)]\},$$

(1)

where $R$ and $I$ are regions for radiation and island respectively, the area here refers to the area of boundary of island. The island formula can be derived from replica technique in gravitational backgrounds and the replica wormholes as these new saddles of gravitational path integral are known, eventually lead to island formula Almheiri:2019qdq ; Penington:2019kki .

The paper PhysRevLett.110.091602 addressed a relation between the entanglement entropy of an excited state and its energy, which is analogous to the first law of thermodynamics like relation for a sufficiently small subsystem. The papers Blanco:2013joa ; Wong:2013gua shown that under a change in the quantum state, the entanglement entropy satisfies the first law of thermodynamics like relation

$$\delta S_{EE}=\delta\langle H_{A}\rangle,$$

(2)

where $S_{EE}$ is the entanglement entropy and $H_{A}$ is known as modular Hamiltonian. More recently, some authors PhysRevD.95.106007 ; PhysRevD.100.106008 generalize the entanglement temperature using the first law of black hole thermodynamics. The entropy of a thermodynamical system is related to the internal energy of the concerned system via the first law of thermodynamics.

On the other hand, the entanglement entropy is a good measure of quantum information for a pure state. Now, the holographic entanglement entropy is also related to the internal energy of the concerned system via the first law of thermodynamics like relation. This shows that the energy of the black hole connects the quantum information to the thermodynamic information of the black hole. When the Hawking-Page phase transition takes place, the energy of black holes suffers a sudden change accompanied. Therefore, it may pose a question whether there is an effect of the Hawking-Page phase transition on the black hole information.

The Hawking-Page phase transition began with the paper of Hawking and Page Hawking1983 who demonstrated the existence of a certain phase transition between a thermal radiation phase and a stable black hole phase in an AdS spacetime. Since then the black hole phase transition and critical phenomena have been extended to a variety of more complicated backgrounds HENNEAUX1984415 ; 1126-6708-1999-04-024 ; Witten:1998zw . One of the ideas is that the cosmological constant $\Lambda$ HENNEAUX1984415 ; TEITELBOIM1985293 in an asymptotically AdS black hole space time can be interpreted as a pressure 0264-9381-26-19-195011 $P=-\frac{\Lambda}{8\pi G_{N}}$ in a thermodynamic sense.

In this paper, we explore the relation between the Hawking-Page phase transition, the Page curve and the black hole information for the BTZ black hole coupled to two thermal baths and with the inclusion of island. We also study the holographic entanglement entropy at the Hawking-Page transition point for the BTZ black hole in the gauge/gravity setup and derive a first law of entanglement thermodynamics in the boundary field theory and bulk. Furthermore, the effect of the first-order phase transition of black hole on the Page curve is also studied.

The paper is organized as follows. In Section II, we review the Page curve for the BTZ black hole. In Section III, we study the effect of the Hawking-Page phase transition on the Page Curve. Section IV, we study the first law of entanglement when the Hawking-Page transition happens. Furthermore, to explore the effect of the first-order phase transition of black hole on the Page curve. Section V is reserved for conclusions and discussions. We set $\hbar=k_{B}=1$ in this paper.

In this section, we calculate the Page Curve where the Hawking-Page phase transition takes place for the BTZ black hole coupled to two auxiliary flat spacetime (the thermal baths system Rocha:2008fe ; Almheiri:2013hfa ; VanRaamsdonk:2013sza ). This is equivalent to introducing absorbing boundary conditions for the Hawking radiation. For the BTZ black hole, the metric can be written as

$\displaystyle ds^{2}$

$\displaystyle=-f(r)dt^{2}+\frac{dr^{2}}{f(r)}+r^{2}d\phi^{2},$

(3)

where

$\displaystyle f(r)$

$\displaystyle=-8G_{N}M+\frac{r^{2}}{l^{2}}=\frac{r^{2}-r_{+}^{2}}{l^{2}},$

(4)

and the cosmological constant $\Lambda=-\frac{1}{l^{2}}$. The parameter $r_{+}=\sqrt{8G_{N}M}l$ is horizon of the black hole. The relevant thermodynamic quantities are given by:

	$\displaystyle T_{BH}=\frac{f^{{}^{\prime}}(r_{+})}{4\pi}=\frac{r_{+}}{2\pi l^{2}},$		(5)
	$\displaystyle M=\frac{r_{+}^{2}}{8G_{N}l^{2}},$
	$\displaystyle S_{BH}=\frac{\pi r_{+}}{2G_{N}}$
	$\displaystyle P=\frac{1}{8\pi G_{N}l^{2}}$
	$\displaystyle V=\pi r_{+}^{2}.$

The Kruskal coordinate of the maximum extension of the BTZ spacetime is

	$\displaystyle\text{Right Wedge}:U=-e^{-\kappa(t-r_{\ast})},\ \ \ V=e^{\kappa(t+r_{\ast})},$		(6)
	$\displaystyle\text{Left Wedge}:U=e^{-\kappa(t-r_{\ast})},\ \ \ V=-e^{\kappa(t+r_{\ast})},$

where $\kappa=\frac{2\pi}{\beta}$ is the surface gravity, and $r_{\ast}$ denotes the tortoise coordinate and is

$\displaystyle r_{\ast}=\int f^{-1}(r)dr=\frac{l^{2}}{2r_{+}}\text{log}\left(\frac{\lvert r-r_{+}\rvert}{r+r_{+}}\right).$

(7)

We now couple two auxiliary non-gravitational flat spacetime on both sides of the BTZ black hole Rocha:2008fe ; Yu:2021rfg ; Anand:2022mla and let them in thermal equilibrium. The corresponding Penrose diagram is shown in Figure  1.

In terms of Kruskal coordinate, the whole spacetime metric as follows

$\displaystyle ds^{2}$

$\displaystyle=-\Omega^{-2}dUdV,$

(8)

where the conformal factor $\Omega=\frac{r_{+}}{l(r+r_{+})}$. Assuming that the whole system is a pure state and filled with conformal field matter of central charge $c$. Then the matter field theory approximate to the effective $2d$ CFT. When the island does not appear, the entanglement entropy of quantum matter on $R=R_{+}\cup R_{-}$ and we can see $S_{\text{gen}}(R)=S(R)=S_{\text{matter}}(R)$ from the eq.(1). The generalized entanglement entropy of the finite quantum matter is given as

$\displaystyle S_{\text{gen}}(R)=\frac{c}{3}\text{log}[d(b_{+},b_{-})],$

(9)

where $d(b_{+},b_{-})=\sqrt{\frac{[U(b_{-})-U(b_{+})][V(b_{+})-V(b_{-})]}{\Omega(b_{+})\Omega(b_{-})}}$, the exact result of the distances between the points $b{+}$ and $b_{-}$ is already obtained in Saha:2021ohr .

The result of eq.(9) is given as

$\displaystyle S_{\text{gen}}(R)=\frac{c}{3}\text{log}[(\frac{1}{T_{BH}\pi l})\sqrt{b^{2}-r_{+}^{2}}\text{cosh}(2T_{BH}\pi t_{b})],$

(10)

here $T_{BH}$ is the temperature of the black hole and $c$ is the central charge.

Now, we set the order of $b$ is same as that of $r_{+}$ and at late times, $t_{b}\gg\kappa$ then $\text{cosh}(2T_{BH}\pi t_{b})\approx\text{exp}(2T_{BH}\pi t_{b})$. The eq.(10) is approximately

$\displaystyle S_{\text{gen}}(R)\approx\frac{2c\pi T_{BH}}{3}t_{b}.$

(11)

From eq.(11), we can see that the entanglement entropy of the Hawking radiation much greater than the thermodynamic entropy of the black hole at late times. In order to resolve this paradox, we need to taken into account the contribution of the island. Using the formula of the entanglement entropy in two disconnected intervals Calabrese:2009ez ; Casini:2009sr .

$\displaystyle S_{\text{matter}}(R\cup I)=\frac{c}{3}\text{log}[\frac{d(a_{+},a_{-})d(b_{+},b_{-})d(a_{+},b_{+})d(a_{-},b_{-})}{d(a_{+},b_{-})d(a_{-},b_{+})}],$

(12)

where $a_{\pm}=(\pm t_{a},a)$ and $b_{\pm}=(\pm t_{b},b)$. Since the very large distances between the left and the right wedges, so it have

$\displaystyle d(a_{+},a_{-})\simeq d(b_{+},b_{-})\simeq d(a_{\pm},b_{\mp})\gg d(a_{\pm},b_{\pm}).$

(13)

So, after the Page time, the expression of the generalized entropy is

$\displaystyle S_{\text{gen}}(R)\approx\frac{\pi a}{G_{N}}+\frac{c}{3}\text{log}[d(a_{+},b_{+})].$

(14)

The extremization condition $\frac{\partial S_{\text{gen}}}{\partial t_{a}}=0$ yields $t_{a}=t_{b}$, then the extremization condition $\frac{\partial S_{\text{gen}}}{\partial a}=0$ gets

$\displaystyle a\approx r_{+}.$

(15)

Substitution of these extremized values in $S_{\text{gen}}$ yields

$\displaystyle S_{\text{gen}}(R)\approx 2S_{BH}.$

(16)

The entanglement entropy of Hawking radiation is going down because of the contribution of the island at late time. Thus, it is consistent with the Page curve. From eq.(11) and (16), we can get the Page time

$\displaystyle t_{\text{Page}}\approx(\frac{3}{c\pi T_{BH}})S_{BH}=\frac{3\pi l^{2}}{cG_{N}}.$

(17)

The scrambling time Hayden:2007cs which is the shortest time for information recovery from the Hawking radiation. It also corresponds to the time for the information to enter the surface of the island.

$\displaystyle t_{\text{scr}}\equiv r_{\ast}(b)-r_{\ast}(a)\approx\frac{1}{2\pi T_{BH}}\text{log}(S_{BH}).$

(18)

In the above the evaporation of the BTZ black hole process, we shall now explore to consider the Hawking-Page phase transition happens. The paper Dolan:2010ha shows that the Hawking-Page phase transition happens between a thermal radiation phase and a stable black hole phase in an AdS spacetime when the temperature of black hole $T_{BH}=T_{HP}=\frac{1}{2\pi l}$ and $M=\frac{1}{8G_{N}}$.

The relation between the thermodynamic temperature and mass of the black hole is given as

$$T_{BH}=\frac{\sqrt{8G_{N}M}}{2\pi l}.$$

(19)

This means that the thermodynamic temperature decreases as the mass of the black hole decreases by emitting the Hawking radiation, and the thermal capacity $C_{p}>0$, there is no local instability. Thus, the Hawking-Page phase transition may happen by emitting the Hawking radiation. When the temperature of the black hole reaches the critical temperature $T_{HP}$ and mass $M_{HP}=\frac{1}{8G_{N}}$, then the Hawking-Page phase transition happens.

Now, let us consider the effect of the Hawking-Page phase transition on the Page curve. If the Hawking-Page phase transition does not happen, it is well known that the Page curve is illustrated in Fig. 2.

The entanglement entropy of the Hawking radiation is a monotonically increasing linearly with time before the Page time. If the Hawking-Page phase transition happens in this time, from eq.(11), we can get the time of the Hawking-Page phase transition

$\displaystyle t_{\text{HP}}\approx\frac{3S(R)l}{c}.$

(20)

Corresponding to the Page curve is described in Fig. 3, which show that the Hawking-Page phase transition happens at the time $t_{\text{HP}}$.

If the Hawking-Page phase transition happens after the Page time or at the Page time, the entanglement entropy of the Hawking radiation is limited by the black hole entropy and becomes a decreasing function of time. In this time, the quantum extremal surface is at

$\displaystyle a\approx r_{+}=l.$

(21)

After the Page time, corresponding to the Page curve is described in Fig. 4, which shows that the Hawking-Page phase transition happens at the time $t_{HP}$. And if the Hawking-Page phase transition happens at the Page time, corresponding to the Page curve is the same as in Fig. 3, and that Page time $t_{\text{Page}}=t_{HP}$. Corresponding to the thermal entropy of the black hole

$\displaystyle S^{(HP)}_{BH}=\frac{\pi l}{2G_{N}}.$

(22)

In this section, we first calculate the change of the holographic entanglement entropy when the Hawking-Page phase transition happens for a spherical region in this geometry by the AdS/CFT correspondence.

The function $f(r)$ of (4) contains the information about the excitation properties of the boundary CFT. For a pure AdS spacetime the three-dimensional function $f(r)$ is

$$f(r)=1+\frac{r^{2}}{l^{2}}$$

(23)

This expression corresponds to the ground state in the two-dimensional boundary CFT. In the boundary, we divide the total system into $A$ and $B$. The entanglement entropy $S_{A}$ for a subsystem $A$ is defined by $S_{A}=-\text{Tr}\rho_{A}\log\rho_{A}$, where $\rho_{A}=\text{Tr}_{B}\rho_{\text{total}}$ is the reduced density matrix of the subsystem $A$ and defined by tracing out with respect to $B$ from the total density matrix of the system. In the gravity dual, the formula for the holographic entanglement entropy is given by PhysRevLett.96.181602

$$S_{A}=\frac{\text{Area}(\gamma_{A})}{4G_{N}}$$

(24)

where $\gamma_{A}$ is a minimal area surface extending into the bulk.

We assume the system is on a fixed time slice and then we choose the entangling surface of subsystem $A$ as $\theta=\theta_{c}$ and $0<\theta_{c}<\frac{\pi}{2}$. The entangling surface in the bulk can be written as $r(\theta)$ and we have the minimum radius at $\theta=0$ and $r\to\infty$ at $\theta=\theta_{c}$. Therefore its area is computed as

$$\text{Area}=2\pi\int_{0}^{\theta_{c}}d\theta\sqrt{r^{2}(\theta)+\frac{r^{\prime 2}(\theta)}{f(r_{(\theta)})}}.$$

(25)

This leads to subsystem size $\theta=\theta_{c}$ for the pure AdS spacetime, the solution to this variational problem is

$$r^{2}(\theta)=\frac{l^{2}\cos^{2}\theta_{c}}{\sin^{2}\theta_{c}-\sin^{2}\theta},$$

(26)

and the holographic entanglement entropy $S^{(0)}_{A}$ is Calabrese_2004 ; Hubeny:2013gta

$$S^{(0)}_{A}=\frac{c}{3}\log(\frac{2l}{\varepsilon}\sin\theta_{c}),$$

(27)

where $\varepsilon$ is a short distance cut-off in the boundary, $c=\frac{3l}{2G_{N}}$ is the central charge of the two-dimensional boundary CFT. For the BTZ black hole background, the holographic entanglement entropy is Hubeny:2012wa ; Hubeny:2013gta

$$S_{A}=\frac{c}{3}\log\left(\frac{\sinh(2\pi T_{BH}l\theta_{c})}{\varepsilon\pi T_{BH}}\right).$$

(28)

Now, we consider that the Hawking-Page phase transition happens for the BTZ black hole, and then the holographic entanglement entropy is written as

$$S^{(c)}_{A}=\frac{c}{3}\log(\frac{2l}{\varepsilon}\sinh\theta_{c}),$$

(29)

The reduced amount of holographic entanglement entropy from the exited state to the ground state of CFT in the subsystem $A$ is given by

$$\delta S^{(c)}_{A}=\frac{c}{3}\log\left(\frac{\sinh\theta_{c}}{\sin\theta_{c}}\right).$$

(30)

The Hawking-Page phase transition takes place and the reduced amount of energy in the subsystem $A$ can be written as

$$\delta E^{c}_{A}=\frac{\theta_{c}}{8\pi G_{N}}.$$

(31)

The first law of thermodynamics like relation for a sufficiently small subsystem is as follows

$$\delta E^{c}_{A}=T_{ent}\delta S^{(c)}_{A},$$

(32)

where the entanglement temperature is given by

$$T_{ent}=k\cdot\theta_{c}^{-1},$$

(33)

where $k$ is an order one constant, and the result of (33) agrees with PhysRevLett.110.091602 . From the above results, we can see that when the Hawking-Page phase transition happens, the system of the boundary CFT undergoes a transition from the excited state to the ground state. Therefore, there is a change of energy $\Delta E^{c}_{A}$ related to the amount of the entanglement entropy accompanied. It is well known that the BTZ black hole is dual to a thermofield doublet state in $2d$ conformal field theory, and the matter field theory may approximatively reduces to the effective $2d$ CFT in bulk. Thus, we can also use the the first law of entanglement (2) in bulk.

When the Hawing-Page phase transition happens, a stable black hole phase becomes a thermal radiation phase in the bulk. Then clearly there is a jump in the thermodynamics entropy of the black hole

$$\delta S^{(c)}_{BH}=\frac{\pi l}{2G_{N}},$$

(34)

and the latent heat is

$$\delta E^{c}=T_{HP}\delta S^{(c)}_{BH}=\frac{1}{4G_{N}}.$$

(35)

From the above results, we can see that when the Hawing-Page phase transition happens, there is a change of energy of latent heat $\delta E^{c}$. Clearly there is a jump in the thermodynamics entropy of the black hole. From (16) we can see that the thermodynamics entropy of the black hole is approximatively entanglement entropy of the black hole at late times or page time. Thus, corresponds to a jump in entanglement entropy when the Hawing-Page phase transition happens at late times or page time. Namely,

$$\delta E^{c}\approx T_{ent}\delta S_{\text{gen}}(R).$$

(36)

this energy $\delta E^{c}$ connects the quantum information of the black hole. In this time, the entanglement temperature $T_{ent}$ is approximatively equal to thermodynamics temperature $T_{HP}$ i.e.,$T_{ent}\approx T_{HP}$. If the Hawking-Page phase transition happens before the Page time, the entanglement temperature of the black hole approximatively is

$$T_{ent}\approx\frac{3l}{2cG_{N}t_{b}}.$$

(37)

These results mean that the black hole information does not have to escape by the radiation, and the Hawking-Page phase transition of the black hole can also cause information to escape.

According to the model of the paper Sun:2018muq , the thermodynamical phase transition of black holes can be interpreted as a transition of the quantized black hole. If we interpret Hawking-Page phase transition as a jump between the two levels, we can compute the black hole entropy jump between the excited state level $n$ and the ground state level $0$ is

$$S^{(c)}_{BH,n\to 0}=S^{(c)}_{BH,n}-S^{(c)}_{BH,0}.$$

(38)

Then, we may think that the information of black holes can also escape by the transition.

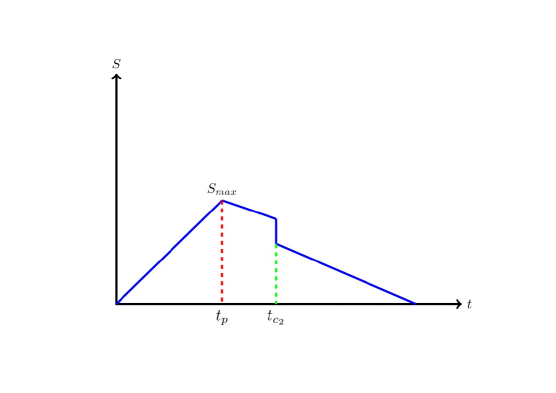
From the above results, we can infer that if there are the first-order phase transition of black holes to happen, the effect of the first-order phase transition of black holes on the Page curve will be universal. Namely, it also applies to higher dimensional and different kinds of black holes. For example, for a charged AdS black hole, the paper kubizvnak2012p shows that small-large black hole thermodynamic phase transitions which is identified with liquid-gas phase transitions of the van der Waals fluid. The Fig 5 conjectures that the first-order phase transition takes place for a charged AdS black hole at the time $t_{c_{2}}$ which is after Page time $t_{p}$ then the page curve is described by this picture. The Fig. 6 conjectures that the first order phase transition takes place for a charged AdS black hole at the time $t_{c_{1}}$ which is before Page time $t_{p}$ then the Page curve is described by this picture. The Page curve may be more complex for the first-order phase transition of a charged AdS black hole, here we only conjecture one possible situation. It is an interesting future problem to study the effect of the first-order phase transition of black holes on the Page curve.

According to the paper Sun:2018muq , a charged AdS black hole, the latent heat $L$ of each black hole molecule transiting from one phase to another phase can be calculated as Sun:2018muq

$$\L=\frac{T\Delta S}{N}=\frac{T\gamma l_{p}^{3}}{3}\sqrt{\frac{\alpha}{4\pi}}(\sqrt{n_{LBH}}-\sqrt{n_{SBH}})\frac{dP}{dT},$$

(39)

the latent heat of thermodynamical phase transition of black holes be interpreted as a transition between the number of quanta of area of LBH and the number of quanta of area of SBH. In the same way, we can think that the information of black holes can also escape by the transition when the first-order phase transition takes place.

The effect of the Hawking-Page phase transition on the Page Curve for the BTZ black hole coupled to two thermal baths and with the inclusion of island has been studied. The Page Curve has been shown by us when the Hawking-Page phase transition happens. The results show that the Hawking-Page phase transition may happen before the Page time, at the Page time and after the Page time under certain conditions. The holographic entanglement entropy when the Hawking-Page phase transition happens for the BTZ black hole in the gauge/gravity setup has also been studied. And a first law of entanglement in the boundary and bulk is derived by us. If a first law of entanglement thermodynamics is universally true, then we can conjecture that all the information of the black hole will come out at the critical temperature when the Hawking-Page phase transition happens. Furthermore, We further speculate that the effect of the first-order phase transition of black holes on the black hole information is universal. These results mean that black holes information does not have to escape by the radiation, and the first-order phase transition of black holes can also cause information to escape. The information of black holes can escape by the transition when the first-order phase transition takes place.

We would like to thank the National Natural Science Foundation of China (Grant No.41030001) for supporting us on this work.