This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Hadron-quark phase transition in neutron star by combining the relativistic Brueckner-Hartree-Fock theory and Dyson-Schwinger equation approach

Pianpian Qin Department of Physics and Chongqing Key Laboratory for Strongly Coupled Physics, Chongqing University, Chongqing 401331, China    Zhan Bai Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, China    Sibo Wang Department of Physics and Chongqing Key Laboratory for Strongly Coupled Physics, Chongqing University, Chongqing 401331, China    Chencan Wang School of Physics and Astronomy, Sun Yat-Sen University, Zhuhai 519082, China    Si-xue Qin [email protected] Department of Physics and Chongqing Key Laboratory for Strongly Coupled Physics, Chongqing University, Chongqing 401331, China
Abstract

Starting from the relativistic Brueckner-Hartree-Fock theory for nuclear matter and the Dyson-Schwinger equation approach for quark matter, the possible hadron-quark phase transition in the interior of a neutron star is explored. The first-order phase transition and crossover are studied by performing the Maxwell construction and three-window construction respectively. The mass-radius relation and the tidal deformability of the hybrid star are calculated and compared to the joint mass-radius observation of a neutron star and the constraints from gravitational wave detection. For the Maxwell construction, no stable quark core is found in the interior of a neutron star. For the three-window construction, the parameters of the smooth interpolation function are chosen in such a way to keep the thermodynamic stability and lead to a moderate crossover density region. To support a two-solar-mass neutron star under the three-window construction, the effective width of medium screening effects in quark matter should be around 0.350.35 GeV.

I Introduction

At sufficiently high temperature or density, the quarks are likely to “escape” from nucleons and become basic degrees of freedom. Such transition is known as the hadron-quark phase transition. Unlike the transition at high temperature, which is reachable in heavy ion collisions, the transition at large density is far beyond the scope of terrestrial experiments. The corresponding density can only be found in astronomical compact objects, such as neutron stars. The neutron star is the remnant of a supernova explosion, and the density inside a neutron star could reach about 5∼10​ρsat5\sim 10\rho_{\text{sat}}, where ρsat=0.16​fm−3\rho_{\text{sat}}=0.16~{}\text{fm}^{-3} is the nuclear saturation density Lattimer (2004, 2021). At such a density, it is very likely that the hadron-quark phase transition will take place and deconfined quark matter appears Annala et al. (2020); Bauswein et al. (2019). Therefore, it is possible to use an astronomical observation of neutron stars to constrain the theories about the dense matter and phase transition.

Currently, it is difficult to unitedly describe the hadron matter, quark matter and hadron-quark phase transition within a single theoretical framework. To study the hadron-quark phase transition inside the hybrid star, it is common to describe the hadron and quark matter separately with corresponding approaches, and then use different construction schemes to combine them and get a complete equation of state (EOS).

For the hadron matter, there have already been many nuclear many-body methods, among which the nonrelativistic Rikovska Stone et al. (2003); Fattoyev et al. (2013) and relativistic Fattoyev et al. (2018); Li et al. (2020); Fu et al. (2022); Sun et al. (2008); Tong et al. (2020) density functional theories (DFTs) are very important. They are based on effective nucleon-nucleon (N​N)(NN) interactions, where the parameters are determined by fitting the ground state properties of finite nuclei and infinite nuclear matter at saturation. The predictions of the neutron star properties with different DFTs are rather divergent due to the loose constraints of the effective N​NNN interactions at higher densities. In comparison, one can start from realistic N​NNN interactions where the parameters are constrained with the N​NNN scattering data in free space, and utilize the many-body methods to deal with the realistic N​NNN interactions, such as the relativistic Brueckner-Hartree-Fock (RBHF) theory Shen et al. (2019) as well as its nonrelativistic counterpart BHF theory Baldo and Maieron (2007). In particular, the RBHF theory is rooted in the relativistic framework, which contains significant three-body force effects self-consistently Sammarruca et al. (2012) and naturally avoids the problem of superluminance in nonrelativistic methods Li et al. (1992). The RBHF theory has been successfully applied to study the neutron star with pure hadron matter Krastev and Sammarruca (2006); Wang et al. (2020a); Tong et al. (2022).

In the description of quark matter, phenomenological models are widely used (see, e.g., Refs. Hatsuda and Kunihiro (1994); Buballa and Oertel (1999); Fukushima (2004); Benvenuto and Lugones (1995); Torres and Menezes (2013); Chodos et al. (1974); Zacchi et al. (2015)). In spite of these successful models, a study that is directly based on quantum chromodynamics (QCD) is still needed. The most important first-principle method, the lattice QCD Montvay and Münster (1997); Ding and et al. (2019), is powerful at zero chemical potential but encounters the notorious “sign problem” at large density. The perturbative QCD Kurkela et al. (2010); Kurkela and Vuorinen (2016) also loses its power in the phase transition region. Therefore, a nonperturbative, continuum approach is required to study the phase transition of cold-dense matter. In particular, the Dyson-Schwinger equation (DSE) approach Roberts and Schmidt (2000); Fischer (2019) is a typical functional method based on QCD. It can deal with the confinement and dynamical chiral symmetry breaking simultaneously, and can be naturally used at finite temperature and chemical potential. In recent years, there have already been studies of neutron stars by using the DSE method  Chen et al. (2011, 2012, 2015); Yasutake et al. (2016); Bai et al. (2018); Bai and Liu (2021). However, the relevant study is still in its early stages, and more efforts must be paid to make this method mature.

As for the construction of phase transition, the most widely used method is the Maxwell construction Endo et al. (2006); Hempel et al. (2009); Yasutake et al. (2009). It assumes that the phase transition is of first order Glendenning (1992); Bhattacharyya et al. (2010) and a stable quark core is formed inside the neutron star. It has also been argued that with the increase of density, the boundaries of hadrons will gradually disappear and the transition from hadron matter to quark matter will be a smooth crossover Baym et al. (2018). Under this assumption, the three-window construction Masuda et al. (2013a, b) was proposed. In this paper, both of these schemes will be used.

Apart from those theoretical approaches, on the experimental side, the study of hadron-quark phase transition relies closely on the astronomical observations of neutron stars. Several massive neutron stars have already been detected with high-precision mass measurements Demorest et al. (2010); Fonseca and et al. (2016); Antoniadis and et al. (2013); Cromartie and et al. (2020); Fonseca and et al. (2021). These observations provide the lower limit for the stiffness of the neutron star EOS. The joint mass-radius observation of the neutron star from the Neutron Star Interior Composition Explorer (NICER) mission provides additional requirements Riley and et al. (2019); Miller and et al. (2019); Riley and et al. (2021); Miller and et al. (2021). The detection of gravitational wave (GW) signals from a binary neutron star merger Abbott and et al. (2017, 2018) has also provided an important constraint for the neutron star properties.

In previous works, numerious methods for nuclear matter and quark matter have been implemented to study the hadron-quark phase transition in the hybrid star Schertler et al. (1999); Agrawal (2010); Logoteta et al. (2013); Orsaria et al. (2013); Wu and Shen (2017); Miao et al. (2020); Ju et al. (2021); Contrera et al. (2022); Huang et al. (2022); Burgio et al. (2002); Klähn et al. (2007); Agrawal (2010); Li et al. (2015); Baym et al. (2019); Nicotra et al. (2006); Bai et al. (2018); Bai and Liu (2021). In Refs. Chen et al. (2011, 2012, 2015); Yasutake et al. (2016), the BHF theory and the DSE approach have been combined. Nevertheless, this prescription is inconsistent with respect to the relativity, as the BHF theory is nonrelativistic while the DSE approach is relativistic. This paper utilizes the RBHF theory for nuclear matter and the DSE approach for quark matter, which are both in the relativistic framework. To construct the EOS of the hybrid star, the Maxwell construction and three-window construction are employed to describe the first-order phase transition and crossover, respectively. The mass-radius relation and tidal deformability of the hybrid star are calculated and are compared with the astronomical observations.

This paper is organized as follows. In Sec. II, the RBHF theory for nuclear matter, the DSE approach for quark matter, and the construction schemes for hadron-quark phase transition are briefly introduced. The results and discussions are presented in Sec. III. Finally, a summary is given in Sec. IV.

II Nuclear matter, quark matter, and hadron-quark phase transition

II.1 Nuclear matter

In the RBHF theory, the nuclear matter is described with the nucleons as the basic degrees of freedom. The single-particle motion of a nucleon in nuclear medium is described by the Dirac equation

(𝜶⋅𝒑+β​Mτ+β​U^τ)​uτ​(𝒑,s)=E𝒑,τ​uτ​(𝒑,s),(\bm{\alpha}\cdot\bm{p}+\beta M_{\tau}+\beta\hat{U}_{\tau})u_{\tau}(\bm{p},s)=E_{\bm{p},\tau}u_{\tau}(\bm{p},s)\,, (1)

where the subscript τ=n,p\tau=n,p indicates neutron or proton. MτM_{\tau} is the mass of a free nucleon. uτ​(𝒑,s)u_{\tau}(\bm{p},s) is the Dirac spinor of a nucleon with momentum 𝒑\bm{p}, spin ss, and single-particle energy E𝒑,τE_{\bm{p},\tau}. The single-particle potential operator U^τ\hat{U}_{\tau} is generally divided into scalar and vector components

U^τ​(𝒑)=US,τ​(p)+γ0​U0,τ​(p)+𝜸⋅𝒑^​UV,τ​(p).\hat{U}_{\tau}(\bm{p})=U_{S,\tau}(p)+\gamma^{0}U_{0,\tau}(p)+\bm{\gamma}\cdot\hat{\bm{p}}U_{V,\tau}(p)\,. (2)

Here 𝒑^=𝒑/p\hat{\bm{p}}=\bm{p}/p is the unit vector parallel to the momentum 𝒑\bm{p}. The quantities US,τ​(p)U_{S,\tau}(p), U0,τ​(p)U_{0,\tau}(p), and UV,τ​(p)U_{V,\tau}(p) are the scalar potential, the timelike part, and the spacelike part of the vector potential. The momentum dependent potentials can be determined uniquely by considering the positive- and negative-energy states simultaneously, i.e., the RBHF theory in the full Dirac space Wang et al. (2021). However, this method is now limited up to the density ρ=0.57​fm−3\rho=0.57\ \text{fm}^{-3} Wang et al. (2022), which is not high enough to study the hadron-quark phase transition in neutron stars. This density limitation is absent if the momentum-independence approximation Brockmann and Machleidt (1990) is utilized, where US,τU_{S,\tau} and U0,τU_{0,\tau} are approximated to be constants and UV,τU_{V,\tau} is neglected. Within this approximation, the single-particle potential operator U^τ\hat{U}_{\tau} is written as

U^τ=US,τ+γ0​U0,τ.\hat{U}_{\tau}=U_{S,\tau}+\gamma^{0}U_{0,\tau}\,. (3)

By defining the effective nucleon mass Mτ∗M^{*}_{\tau} and effective energy E𝒑,τ∗E^{*}_{\bm{p},\tau}

Mτ∗=Mτ+US,τ,E𝒑,τ∗=E𝒑,τ−U0,τ,M^{*}_{\tau}=M_{\tau}+U_{S,\tau}\,,\qquad E^{*}_{\bm{p},\tau}=E_{\bm{p},\tau}-U_{0,\tau}\,, (4)

the Dirac equation (1) in nuclear medium can be rewritten as

(𝜶⋅𝒑+β​Mτ∗)​uτ​(𝒑,s)=E𝒑,τ∗​uτ​(𝒑,s).(\bm{\alpha}\cdot\bm{p}+\beta M^{*}_{\tau})u_{\tau}(\bm{p},s)=E^{*}_{\bm{p},\tau}u_{\tau}(\bm{p},s). (5)

From the Dirac equation (5), the dispersion relation E𝒑,τ∗=𝒑2+Mτ∗2E^{*}_{\bm{p},\tau}=\sqrt{\bm{p}^{2}+M^{*2}_{\tau}} is obtained and the Dirac spinor can be solved exactly as

uτ​(𝒑,s)=E𝒑,τ∗+Mτ∗2​Mτ∗​(1𝝈⋅𝒑E𝒑,τ∗+Mτ∗)​χs​χτ,u_{\tau}(\bm{p},s)=\sqrt{\frac{E^{*}_{\bm{p},\tau}+M^{*}_{\tau}}{2M^{*}_{\tau}}}\begin{pmatrix}1\\ \frac{\bm{\sigma}\cdot\bm{p}}{E^{*}_{\bm{p},\tau}+M^{*}_{\tau}}\end{pmatrix}\chi_{s}\chi_{\tau}\,, (6)

where χs\chi_{s} and χτ\chi_{\tau} are the spin and isospin wave function respectively. The normalization condition is u¯τ​(𝒑,s)​uτ​(𝒑,s)=1\bar{u}_{\tau}(\bm{p},s)u_{\tau}(\bm{p},s)=1.

In the RBHF theory, the single-particle potentials US,τU_{S,\tau} and U0,τU_{0,\tau} are self-consistently determined with the effective N​NNN interaction, GG matrix, which can be obtained by solving the Thompson equation Thompson (1970); Brockmann and Machleidt (1990)

Gτ​τ′​(𝒒′,𝒒|𝑷)=Vτ​τ′​(𝒒′,𝒒)+∫d3​k(2​π)3​Vτ​τ′​(𝒒′,𝒌)​Qτ​τ′​(𝒌,𝑷)Wτ​τ′−Eτ​τ′∗​Gτ​τ′​(𝒌,𝒒|𝑷),G_{\tau\tau^{\prime}}(\bm{q^{\prime}},\bm{q}|\bm{P})=V_{\tau\tau^{\prime}}(\bm{q^{\prime}},\bm{q})+\int\frac{d^{3}k}{(2\pi)^{3}}V_{\tau\tau^{\prime}}(\bm{q^{\prime}},\bm{k})\frac{Q_{\tau\tau^{\prime}}(\bm{k},\bm{P})}{W_{\tau\tau^{\prime}}-E^{*}_{\tau\tau^{\prime}}}G_{\tau\tau^{\prime}}(\bm{k},\bm{q}|\bm{P})\,, (7)

where τ​τ′=\tau\tau^{\prime}= n​nnn, p​ppp, or n​pnp. In Eq. (7), 𝑷=(𝒌1+𝒌2)/2\bm{P}=(\bm{k}_{1}+\bm{k}_{2})/2 is the center-of-mass momentum, and 𝒌=(𝒌1−𝒌2)/2\bm{k}=(\bm{k}_{1}-\bm{k}_{2})/2 is the relative momentum of two interacting nucleons with momenta 𝒌1\bm{k}_{1} and 𝒌2\bm{k}_{2} in the rest frame of nuclear matter. The quantities 𝒒\bm{q}, 𝒒′\bm{q^{\prime}}, and 𝒌\bm{k} are the initial, final, and intermediate relative momenta of the two nucleons scattering in nuclear matter, respectively. Wτ​τ′=E𝑷+𝒒,τ∗+E𝑷−𝒒,τ′∗W_{\tau\tau^{\prime}}=E^{*}_{\bm{P}+\bm{q},\tau}+E^{*}_{\bm{P}-\bm{q},\tau^{\prime}} is the starting energy, and Eτ​τ′∗=E𝑷+𝒌,τ∗+E𝑷−𝒌,τ′∗E^{*}_{\tau\tau^{\prime}}=E^{*}_{\bm{P}+\bm{k},\tau}+E^{*}_{\bm{P}-\bm{k},\tau^{\prime}} is the total single-particle energy of intermediate two-nucleon states. The Pauli operator Qτ​τ′Q_{\tau\tau^{\prime}} avoids the N​NNN scattering to occupied states in the Fermi sea and is defined as

Qτ​τ′(𝒌,𝑷)={1if|𝑷+𝒌|>kFτand|𝑷−𝒌|>kFτ′,0otherwise,Q_{\tau\tau^{\prime}}(\bm{k},\bm{P})=\left\{\begin{aligned} &1&\qquad&\text{if}\quad|\bm{P}+\bm{k}|>k_{F}^{\tau}\quad\text{and}\quad|\bm{P}-\bm{k}|>k_{F}^{\tau^{\prime}}\,,\\ &0&\qquad&\text{otherwise}\,,\end{aligned}\right. (8)

where kFτk_{F}^{\tau} represents the Fermi momentum for nucleon τ\tau. For nuclear matter with total nucleon density ρ=ρn+ρp\rho=\rho_{n}+\rho_{p} and isospin asymmetry δ=(ρn−ρp)/(ρn+ρp)\delta=(\rho_{n}-\rho_{p})/(\rho_{n}+\rho_{p}), the Fermi momentum is calculated as kFτ=[3​π2​(1±δ)​ρ/2]1/3k_{F}^{\tau}=\left[3\pi^{2}(1\pm\delta)\rho/2\right]^{1/3}.

With the GG matrix, one can calculate the single-particle potential energy

Uτ​(p)=∑s′,τ′∫0kFτ′d3​p′(2​π)3​Mτ′∗E𝒑′,τ′∗​⟨u¯τ​(𝒑,1/2)​u¯τ′​(𝒑′,s′)|G¯​(W)|uτ​(𝒑,1/2)​uτ′​(𝒑′,s′)⟩,U_{\tau}(p)=\sum_{s^{\prime},\tau^{\prime}}\int_{0}^{k^{\tau^{\prime}}_{F}}\frac{d^{3}p^{\prime}}{(2\pi)^{3}}\frac{M^{*}_{\tau^{\prime}}}{E^{*}_{\bm{p}^{\prime},\tau^{\prime}}}\langle\bar{u}_{\tau}(\bm{p},1/2)\bar{u}_{\tau^{\prime}}(\bm{p}^{\prime},s^{\prime})|\bar{G}(W)|u_{\tau}(\bm{p},1/2)u_{\tau^{\prime}}(\bm{p}^{\prime},s^{\prime})\rangle\,, (9)

where G¯\bar{G} is the antisymmetried GG matrix and the factor Mτ′∗/E𝒑′,τ′∗M^{*}_{\tau^{\prime}}/E^{*}_{\bm{p}^{\prime},\tau^{\prime}} comes from the normalization condition above. Alternatively, the single-particle potential energy can be obtained by sandwiching the single-particle potential operator between the Dirac spinors

Uτ​(p)=Mτ∗E𝒑,τ∗​⟨u¯τ​(𝒑,1/2)|U^τ|uτ​(𝒑,1/2)⟩=Mτ∗E𝒑,τ∗​US,τ+U0,τ.U_{\tau}(p)=\frac{M^{*}_{\tau}}{E^{*}_{\bm{p},\tau}}\langle\bar{u}_{\tau}(\bm{p},1/2)|\hat{U}_{\tau}|u_{\tau}(\bm{p},1/2)\rangle=\frac{M^{*}_{\tau}}{E^{*}_{\bm{p},\tau}}U_{S,\tau}+U_{0,\tau}\,. (10)

By combining Eqs. (9) and (10), one can extract the two constants US,τU_{S,\tau} and U0,τU_{0,\tau} with two momenta, e.g., 0.5​kFτ0.5k^{\tau}_{F} and kFτk^{\tau}_{F}.

Equations (1), (7), (9), and (10) constitute a coupled set of equations that needs to be solved self-consistently. Starting from initial values of US,τ(0),U0,τ(0)U^{(0)}_{S,\tau},U^{(0)}_{0,\tau} in vacuum, the Dirac spinors are obtained by solving the Dirac equation (1). Then one solves the Thompson equation (7) to get the GG matrix and obtain the single-particle potential energy by using the integrals in Eq. (9). From Eq. (10) a new set of values for US,τ(1),U0,τ(1)U^{(1)}_{S,\tau},U^{(1)}_{0,\tau} are found, which are to be used in the next iteration. This iterative procedure is repeated until the satisfactory convergence is reached.

Once the solution is converged, the binding energy per nucleon in nuclear matter can be calculated as

EA=1ρ​∑s,τ∫0kFτd3​p(2​π)3​Mτ∗E𝒑,τ∗​⟨u¯τ​(𝒑,s)|γ⋅𝒑+Mτ|uτ​(𝒑,s)⟩−1−δ2​Mp−1+δ2​Mn+12​ρ​∑s,s′,τ,τ′∫0kFτd3​p(2​π)3​∫0kFτ′d3​p′(2​π)3​Mτ∗E𝒑,τ∗​Mτ′∗E𝒑′,τ′∗×⟨u¯τ​(𝒑,s)​u¯τ′​(𝒑′,s′)|G¯​(W)|uτ​(𝒑,s)​uτ′​(𝒑′,s′)⟩.\begin{split}\frac{E}{A}=&\frac{1}{\rho}\sum_{s,\tau}\int_{0}^{k^{\tau}_{F}}\frac{d^{3}p}{(2\pi)^{3}}\frac{M^{*}_{\tau}}{E^{*}_{\bm{p},\tau}}\langle\bar{u}_{\tau}(\bm{p},s)|\gamma\cdot\bm{p}+M_{\tau}|u_{\tau}(\bm{p},s)\rangle\\ &\ -\frac{1-\delta}{2}M_{p}-\frac{1+\delta}{2}M_{n}+\frac{1}{2\rho}\sum_{s,s^{\prime},\tau,\tau^{\prime}}\int_{0}^{k^{\tau}_{F}}\frac{d^{3}p}{(2\pi)^{3}}\int_{0}^{k^{\tau^{\prime}}_{F}}\frac{d^{3}p^{\prime}}{(2\pi)^{3}}\frac{M^{*}_{\tau}}{E^{*}_{\bm{p},\tau}}\frac{M^{*}_{\tau^{\prime}}}{E^{*}_{\bm{p}^{\prime},\tau^{\prime}}}\\ &\ \times\langle\bar{u}_{\tau}(\bm{p},s)\bar{u}_{\tau^{\prime}}(\bm{p^{\prime}},s^{\prime})|\bar{G}(W)|u_{\tau}(\bm{p},s)u_{\tau^{\prime}}(\bm{p^{\prime}},s^{\prime})\rangle\,.\end{split} (11)

The neutron star matter is regarded as the beta-equilibrium nuclear matter consisting of protons, neutrons, electrons, and muons. The energy density εH\varepsilon_{H} of the neutron star matter or pure hadron star is calculated as εH=ρ​etot\varepsilon_{H}=\rho e_{\text{tot}}, where the total energy etote_{\text{tot}} is defined as

etot​(ρ,Yn,Yp,Ye,Yμ)=E/A​(ρ,Yp)+Yp​Mp+Yn​Mn+Ee/A+Eμ/A.e_{\text{tot}}(\rho,Y_{n},Y_{p},Y_{e},Y_{\mu})=E/A(\rho,Y_{p})+Y_{p}M_{p}+Y_{n}M_{n}+E_{e}/A+E_{\mu}/A. (12)

The quantities Ee/AE_{e}/A and Eμ/AE_{\mu}/A are the contributions from electrons and muons, which are treated as gas of relativistic noninteracting fermions. The equilibrium particle concentrations Yi=ρi/ρ​(i=n,p,e,μ)Y_{i}=\rho_{i}/\rho\ (i=n,p,e,\mu) can be calculated via the β\beta-stability condition and charge neutrality condition

μn−μp=\displaystyle\mu_{n}-\mu_{p}= μe,\displaystyle\ \mu_{e}, (13a)
μn−μp=\displaystyle\mu_{n}-\mu_{p}= μμ,\displaystyle\ \mu_{\mu}, (13b)
ρe+ρμ=\displaystyle\rho_{e}+\rho_{\mu}= ρp,\displaystyle\ \rho_{p}, (13c)

where μi​(i=n,p,e,μ)\mu_{i}\ (i=n,p,e,\mu) is the chemical potential for particle ii. For electrons and muons, the chemical potential is obtained via

μi=∂etot∂Yi.\mu_{i}=\frac{\partial e_{\text{tot}}}{\partial Y_{i}}. (14)

For protons and neutrons, the chemical potential is calculated as the single-particle energy at the Fermi surface. Once the total energy etote_{\text{tot}} is calculated, the pressure of the neutron star matter can be obtained as

PH=ρ2​∂etot∂ρ.P_{H}=\rho^{2}\frac{\partial e_{\text{tot}}}{\partial\rho}. (15)

Owing to the cluster effects in nuclear matter with density ρ<0.08​fm−3\rho<0.08\ \text{fm}^{-3}, the RBHF theory is not applicable and the EOS introduced with the Baym-Bethe-Pethick Baym et al. (1971) and Baym-Pethick-Sutherland models Baym et al. (1971) is used. It should also be noticed that the results of the RBHF calculation are not so smooth that numerical derivatives can be performed. Parametrization or regression strategies Krastev and Sammarruca (2006); Katayama and Saito (2013) are often employed to the neutron star EOS. In this work, Gaussian process regression Huang et al. (2022) is implemented to process our RBHF results.

II.2 Quark matter

The DSEs are the equations of motion for fields. They can be derived by differentiating the action of QCD and contain all the information of QCD Lagrangian. In this paper, the DSE of the quark propagator is concerned, the quark-gluon vertex is truncated by a symmetry preserving scheme, and the gluon propagator is approximated by the interaction model. Therefore, the complicated DSE set can be reduced to a solvable gap equation. The Feynman diagram for the gap equation is shown in Fig. 1.

Refer to caption
Figure 1: The Feynman diagram for the gap equation. The solid (wavy) line with black thick dot is for the dressed quark (gluon) propagator, the thick gray dot represents the dressed quark-gluon interaction vertex, and the thin black dot represents the bare quark-gluon interaction vertex.

At zero temperature and finite chemical potential, the gap equation for the quark propagator S​(p;μ)S(p;\mu) reads as

S−1​(p;μ)=Z2​(i​𝜸⋅𝒑+i​γ4​p~4+mq)+Σ​(p;μ),S^{-1}(p;\mu)=Z_{2}(i\bm{\gamma}\cdot\bm{p}+i\gamma_{4}\tilde{p}_{4}+m_{q})+\Sigma(p;\mu)\,, (16)

where p=(𝒑,p4)p=(\bm{p},p_{4}) is the four-momentum and p~4=p4+i​μ\tilde{p}_{4}=p_{4}+i\mu with μ\mu is the quark chemical potential. In Eq. (16), the Euclidean metric is used, which is different from the Minkowski metric used in Eq. (3). mqm_{q} is the current mass of the quark qq with q=u,d,sq=u,d,s. In this paper, the current-quark masses mu/d=0m_{u/d}=0 are chosen for simplicity, while ms=115​MeVm_{s}=115~{}\text{MeV} is obtained by fitting the KK meson mass in vacuum Alkofer et al. (2002). Σ​(p;μ)\Sigma(p;\mu) is the renormalized self-energy of the quark

Σ​(p;μ)=Z1​∫d4​q(2​π)4​g2​(μ)​Dρ​σ​(k;μ)​λa2​γρ​S​(q,μ)​λa2​Γσ​(q,p;μ),\Sigma(p;\mu)=Z_{1}\int\frac{d^{4}q}{(2\pi)^{4}}g^{2}(\mu)D_{\rho\sigma}(k;\mu)\frac{\lambda^{a}}{2}\gamma_{\rho}S(q,\mu)\frac{\lambda^{a}}{2}\Gamma_{\sigma}(q,p;\mu)\,, (17)

where Z1Z_{1}, Z2Z_{2} are the renormalization constants. λa/2\lambda^{a}/2 is the fundamental representation of S​U​(3)SU(3) color symmetry. Dρ​σ​(k;μ)D_{\rho\sigma}(k;\mu) with k=p−qk=p-q is the renormalized dressed gluon propagator, and Γσ​(q,p;μ)\Gamma_{\sigma}(q,p;\mu) is the renormalized dressed quark-gluon vertex. g​(μ)g(\mu) is the density-dependent coupling constant.

To solve the gap equation (16), we have to know the quark-gluon vertex Γσ​(q,p;μ)\Gamma_{\sigma}(q,p;\mu) and gluon propagator Dρ​σ​(k;μ)D_{\rho\sigma}(k;\mu). In this paper, the dressed quark-gluon vertex Γσ​(q,p;μ)\Gamma_{\sigma}(q,p;\mu) is truncated by using the rainbow approximation Maris and Roberts (1997), and the nonperturbative dressing effect of the dressed gluon propagator Dρ​σ​(k;μ)D_{\rho\sigma}(k;\mu) can be absorbed in the effective interaction function 𝒢​(k2;μ)\mathcal{G}(k^{2};\mu) Alkofer et al. (2002). Therefore, the interaction kernel can be expressed as

Z1​g2​(μ)​Dρ​σ​(k;μ)​Γσ​(q,p;μ)=𝒢​(k2;μ)​Dρ​σfree​(k)​γσ,Z_{1}g^{2}(\mu)D_{\rho\sigma}(k;\mu)\Gamma_{\sigma}(q,p;\mu)=\mathcal{G}(k^{2};\mu)D_{\rho\sigma}^{\text{free}}(k)\gamma_{\sigma}\,, (18)

where Dρ​σfree​(k)=1k2​(δρ​σ−kρ​kσ/k2)D_{\rho\sigma}^{\text{free}}(k)=\frac{1}{k^{2}}\left(\delta_{\rho\sigma}-k_{\rho}k_{\sigma}/k^{2}\right) is the free gluon propagator in the Landau gauge. The interaction function 𝒢​(k2;μ)\mathcal{G}(k^{2};\mu) is usually divided into two parts: the infrared part and ultraviolet perturbative part. At zero temperature, the quark properties are mainly determined by its infrared behavior, so we omit the ultraviolet part as in Ref. Chen et al. (2011) for better numerical behavior. The gluon interaction function we applied is Chen et al. (2011)

𝒢​(k2;μ)k2=4​π2​Dω6​k2​e−k2/ω2​e−μ2/ωeff2.\frac{\mathcal{G}(k^{2};\mu)}{k^{2}}=\frac{4\pi^{2}D}{\omega^{6}}k^{2}e^{-k^{2}/\omega^{2}}e^{-\mu^{2}/\omega_{\text{eff}}^{2}}\,. (19)

Hence, the integration is finite at the ultraviolet limit, and the renormalization procedure can be omitted by simply setting all the renormalization factors to unit. The parameters DD and ω\omega control the strength and width of the interaction in vacuum respectively. It is found that the observables of vector and pseudoscalar mesons are insensitive to variations of ω∈[0.4,0.6]\omega\in[0.4,0.6] as long as D​ω=constantD\omega=\text{constant} Maris and Tandy (1999); Qin et al. (2011). As in Refs. Chen et al. (2011); Bai et al. (2018), we choose ω=0.5\omega=0.5 GeV and D=1.0​GeV2D=1.0~{}\text{GeV}^{2}.

In the interaction model Eq. (19), the factor e−μ2/ωeff2e^{-\mu^{2}/\omega_{\text{eff}}^{2}} depicts the effects of the medium screening on the interaction at finite chemical potential μ\mu, where ωeff\omega_{\text{eff}} is the effective width of medium screening effects. The larger the ωeff\omega_{\text{eff}}, the weaker the medium screening effects and the stronger the gluon interaction. In Refs. Chen et al. (2011, 2016); Bai et al. (2018); Bai and Liu (2021), the effective width of medium screening effects is primarily adopted as ωeff≲0.5\omega_{\text{eff}}\lesssim 0.5 GeV to study the hadron-quark phase transition. In this paper, we will also study the dependence of our results on the effective width ωeff\omega_{\text{eff}}.

With the interaction model in Eqs. (18) and (19), the self-energy in Eq. (17) can be reduced as

Σ​(p;μ)=∫d4​q(2​π)4​4​π2​Dω6​k2​e−k2/ω2​e−μ2/ωeff2​(δρ​σ−kρ​kσ/k2)​λa2​γρ​S​(q,μ)​λa2​γσ.\Sigma(p;\mu)=\int\frac{d^{4}q}{(2\pi)^{4}}\frac{4\pi^{2}D}{\omega^{6}}k^{2}e^{-k^{2}/\omega^{2}}e^{-\mu^{2}/\omega_{\text{eff}}^{2}}\left(\delta_{\rho\sigma}-k_{\rho}k_{\sigma}/k^{2}\right)\frac{\lambda^{a}}{2}\gamma_{\rho}S(q,\mu)\frac{\lambda^{a}}{2}\gamma_{\sigma}\,. (20)

Therefore, the gap equation (16) is simplified as an solvable equation in terms of the quark propagator S​(q,μ)S(q,\mu), which can be decomposed according to the Lorentz structure

S​(p;μ)−1=i​𝜸⋅𝒑​A​(|𝒑|2,p~42)+B​(|𝒑|2,p~42)+i​γ4​p~4​C​(|𝒑|2,p~42).S(p;\mu)^{-1}=i\bm{\gamma}\cdot\bm{p}A(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2})+B(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2})+i\gamma_{4}\tilde{p}_{4}C(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2})\,. (21)

The scalar functions A​(|𝒑|2,p~42)A(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2}), B​(|𝒑|2,p~42)B(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2}), and C​(|𝒑|2,p~42)C(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2}) can then be solved with the gap equation. It is known that the gap equation has multiple solutions. In vacuum, massless quarks may have the solution B​(p)≡0B(p)\equiv 0 or B​(p)≠0B(p)\neq 0, which are called the Wigner solution and Nambu solution, respectively. The Wigner solution corresponds to the dynamical chiral symmetry (DCS) phase, where the quarks are bare and have no dynamical mass. The Nambu solution corresponds to the dynamical chiral symmetry breaking (DCSB) phase, where the massless quarks are dressed and the mass functions M​(p)=B​(p)/A​(p)M(p)=B(p)/A(p) acquire nonzero values. Although there are arguments that there might exist quarkyonic matter that is DCS but still confined, it is usually believed that DCSB and confinement appear simultaneously. Therefore, the Wigner solution corresponds to the deconfined quark phase, and the Nambu solution corresponds to the confined hadron phase. To describe the quark core in the interior of a neutron star at high density, we only consider the Wigner solution in this paper. In the left and right panel in Fig. 2, the Wigner solution of the quark propagator for the massless quark is shown as the functions of momentum and chemical potential, respectively. At zero chemical potential, the functions AA and CC are identical as the Lorentz O​(4)O(4) symmetry is satisfied. At zero momentum, the function AA shows different chemical potential dependence in comparison to the function CC at intermediate chemical potential, while both functions AA and CC approach unit as the quark propagator approaches asymptotic freedom at high chemical potential.

Refer to caption
Figure 2: The Wigner solution of the quark propagator for massless quark with varying momentum (left) or varying chemical potential (right).

With the Wigner solution, the distribution function f1​(𝒑;μ)f_{1}(\bm{p};\mu) can be obtained from the quark propagator

f1​(𝒑;μ)=14​π​∫−∞∞𝑑p4​trD​[−γ4​S​(p;μ)]f_{1}(\bm{p};\mu)=\frac{1}{4\pi}\int_{-\infty}^{\infty}dp_{4}\ \text{tr}_{D}[-\gamma_{4}S(p;\mu)] (22)

where the trace is for the spinor indices. With the quark propagator, the integration in f1​(𝒑;μ)f_{1}(\bm{p};\mu) can be converted to a contour integral on the complex plane of p4~\tilde{p_{4}},

f1​(𝒑;μ)=1π​∫−∞∞𝑑p4​i​(p4+i​μ)​C​(|𝒑|2,(p4+i​μ)2)ℳ,f_{1}(\bm{p};\mu)=\frac{1}{\pi}\int_{-\infty}^{\infty}dp_{4}\ \frac{i(p_{4}+i\mu)C\left(\left|\bm{p}\right|^{2},(p_{4}+i\mu)^{2}\right)}{\mathcal{M}}, (23)

where

ℳ=𝒑2​A2​(|𝒑|2,p~42)+p~42​C2​(|𝒑|2,p~42)+B​(|𝒑|2,p~42).\mathcal{M}=\bm{p}^{2}A^{2}(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2})+\tilde{p}_{4}^{2}C^{2}(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2})+B(\left|\bm{p}\right|^{2},\tilde{p}_{4}^{2}). (24)

Then the number density nqn_{q} with quark flavor q=u,d,sq=u,d,s can be obtained as a function of chemical potential Chen et al. (2008)

nq​(μ)=2​Nc​Nf​∫d3​p(2​π)3​f1​(𝒑;μ),n_{q}(\mu)=2N_{c}N_{f}\int\frac{d^{3}p}{(2\pi)^{3}}f_{1}(\bm{p};\mu)\,, (25)

where Nf=3N_{f}=3 and Nc=3N_{c}=3 denote the number of flavor and color, respectively.

The quark star matter is composed of quarks and leptons under the β\beta equilibrium and electric charge neutral condition,

μd=\displaystyle\mu_{d}= μu+μe=μs,\displaystyle\ \mu_{u}+\mu_{e}=\mu_{s}\,, (26a)
μd=\displaystyle\mu_{d}= μu+μμ,\displaystyle\ \mu_{u}+\mu_{\mu}\,, (26b)
2​nu−nd−ns3=\displaystyle\frac{2n_{u}-n_{d}-n_{s}}{3}= ne+nμ,\displaystyle\ n_{e}+n_{\mu}\,, (26c)

where the chemical potential for quark is denoted by μq\mu_{q} with q=u,d,sq=u,d,s. In Eq. (26c), the number density of lepton nln_{l} with l=e,μl=e,\mu is calculated as nl=kF​l3/3​π2n_{l}=k^{3}_{Fl}/3\pi^{2} where the Fermi momentum kF​lk_{Fl} is related to the chemical potential μl\mu_{l} by kF​l2=μl2−ml2k^{2}_{Fl}=\mu^{2}_{l}-m^{2}_{l}. In the description of the pure quark star, we take me=0.511​MeVm_{e}=0.511~{}\text{MeV} and mμ=105​MeVm_{\mu}=105~{}\text{MeV}. In practice, for given μn\mu_{n} with

μn=μu+2​μd,\mu_{n}=\mu_{u}+2\mu_{d}, (27)

one can obtain the chemical potential μi\mu_{i} with i=u,d,s,e,μi=u,d,s,e,\mu by solving Eqs. (26) and (27).

Once the quark chemical potential μq\mu_{q} is obtained, the number density nq​(μq)n_{q}(\mu_{q}) can be calculated with Eq. (25) and the baryon number density ρ\rho is found as ρ=13​(nu+nd+ns)\rho=\frac{1}{3}(n_{u}+n_{d}+n_{s}). Furthermore, one can calculate the pressure by integrating the number density

Pq​(μq)=Pq​(μq,0)+∫μq,0μq𝑑μ​nq​(μ).P_{q}(\mu_{q})=P_{q}(\mu_{q,0})+\int_{\mu_{q,0}}^{\mu_{q}}d\mu\ n_{q}(\mu)\,. (28)

Theoretically, the starting point of the integral μq,0\mu_{q,0} can be any value. In this paper we take μu,0=μd,0=0\mu_{u,0}=\mu_{d,0}=0 and choose μs,0\mu_{s,0} as the value of the starting point of the Wigner phase. Similar to Ref. Chen et al. (2011), we take the vacuum pressure Pu​(μu,0)=Pd​(μd,0)=−45​MeV⋅fm−3P_{u}(\mu_{u,0})=P_{d}(\mu_{d,0})=-45~{}\text{MeV}\cdot\text{fm}^{-3} and Ps​(μs,0)=0P_{s}(\mu_{s,0})=0. Since the leptons are treated as free Fermi gas, their pressure is

Pl=124​π2​[kF​l​μl​(2​kF​l2−3​ml2)+3​ml4​ln⁡(|kF​l+μlml|)],l=e,μ.P_{l}=\frac{1}{24\pi^{2}}\left[k_{Fl}\mu_{l}\left(2k_{Fl}^{2}-3m_{l}^{2}\right)+3m_{l}^{4}\ln\left(\left|\frac{k_{Fl}+\mu_{l}}{m_{l}}\right|\right)\right]\,,\quad l=e,\mu\,. (29)

Finally, with the chemical potential μi\mu_{i} and number density nin_{i} with i=u,d,s,e,μi=u,d,s,e,\mu, the total pressure and total energy density of the pure quark star can be obtained as

PQ=\displaystyle P_{Q}= ∑i=u,d,s,e,μPi​(μi),\displaystyle\sum_{i=u,d,s,e,\mu}P_{i}(\mu_{i})\,, (30a)
εQ=\displaystyle\varepsilon_{Q}= ∑i=u,d,s,e,μμi​ni−PQ.\displaystyle\sum_{i=u,d,s,e,\mu}\mu_{i}n_{i}-P_{Q}\,. (30b)

II.3 Hadron-quark phase transition

In this paper, we will study the hadron-quark phase transition as a first-order transition as well as a crossover. The first-order phase transition is described with the Maxwell construction, and the crossover is described with the three-window construction. For the Maxwell construction, the phase transition occurs when the baryon chemical potential and pressure of the two phases are equal

PH​(μn,c)=PQ​(μn,c),P_{H}(\mu_{n,c})=P_{Q}(\mu_{n,c})\,, (31)

where μn,c\mu_{n,c} is the critical baryon chemical potential of the first-order phase transition. Therefore, the pressure of the hybrid star under the Maxwell construction is

P(μn)={PH,ifμn≤μn,c,PQ,ifμn>μn,c.P(\mu_{n})=\left\{\begin{aligned} P_{H}\,,\qquad\text{if}\quad\mu_{n}\leq\mu_{n,c}\,,\\ P_{Q}\,,\qquad\text{if}\quad\mu_{n}>\mu_{n,c}\,.\end{aligned}\right. (32)

Correspondingly, the energy density of the hybrid star under the Maxwell construction is

ε(μn)={εH,ifμn≤μn,c,εQ,ifμn>μn,c.\varepsilon(\mu_{n})=\left\{\begin{aligned} \varepsilon_{H}\,,\qquad\text{if}\quad\mu_{n}\leq\mu_{n,c}\,,\\ \varepsilon_{Q}\,,\qquad\text{if}\quad\mu_{n}>\mu_{n,c}\,.\end{aligned}\right. (33)

For the three-window construction, a smooth interpolation of the energy density between the hadron and quark phases is performed

ε​(ρ)=f−​(ρ)​εH​(ρ)+f+​(ρ)​εQ​(ρ).\varepsilon(\rho)=f_{-}(\rho)\varepsilon_{H}(\rho)+f_{+}(\rho)\varepsilon_{Q}(\rho)\,. (34)

The interpolation function f±f_{\pm} is chosen as Masuda et al. (2013a, b)

f±=12​(1±tanh⁡(ρ−ρ¯Γ)),f_{\pm}=\frac{1}{2}\left(1\pm\tanh\left(\frac{\rho-\bar{\rho}}{\Gamma}\right)\right)\,, (35)

where the parameters ρ¯\bar{\rho} and Γ\Gamma describe the center density and the width of the transition region.

Taking parameters (ρ¯,Γ\bar{\rho},\Gamma)=(3.5,1.53.5,1.5) as an example, the variation behavior of the function f±f_{\pm} in terms of the baryon density is shown in Fig. 3. Once the energy density of the hybrid star has been obtained, the pressure can be determined with the thermodynamic relation,

P​(ρ)=ρ2​∂(ε/ρ)∂ρ.\displaystyle P(\rho)=\rho^{2}\frac{\partial(\varepsilon/\rho)}{\partial\rho}. (36)
Refer to caption
Figure 3: The interpolation functions f±f_{\pm} with respect to the baryon density ρ/ρsat\rho/\rho_{\text{sat}}. The center density and the width of the transition region are (ρ¯,Γ(\bar{\rho},\Gamma)=(3.5,1.53.5,1.5). The shaded region denotes the crossover region ρ¯−Γ≤ρ≤ρ¯+Γ\bar{\rho}-\Gamma\leq\rho\leq\bar{\rho}+\Gamma.

With the EOS of the neutron star matter, the mass-radius relation of the neutron star can be obtained by solving the Tolman–Oppenheimer–Volkov equation Oppenheimer and Volkoff (1939); Tolman (1939), and the tidal deformability can be calculated as in Ref. Hinderer et al. (2010).

III Results and discussion

Refer to caption
Figure 4: Left panel: energy density and pressure as functions of density for the pure hadron star described by the RBHF theory with potentials pvCD-Bonn A, B, and C. Right panel: similar to the left panel, but for the pure quark star described by the DSE approach with different effective width ωeff\omega_{\text{eff}} of medium screening in the interaction model (19).

In the left panel of Fig. 4, the energy density ε\varepsilon and pressure PP of the pure hadron star are calculated by the RBHF theory with N​NNN interactions pvCD-Bonn A, B, and C Wang et al. (2019). It is clear that the difference of the results from pvCD-Bonn A, B, and C is negligible. This is reasonable since the main difference between the three parametrizations is in the tensor force strength, which is mostly reflected in the (T=0T=0) S13{}^{3}S_{1}-D13{}^{3}D_{1} states with TT the total isospin. This partial wave does not contribute to the (T=1T=1) neutron-neutron state Krastev and Sammarruca (2006), which is dominant in the neutron star. In the following discussion, the potential pvCD-Bonn A is used, since the empirical nuclear saturation properties can be described satisfactorily by the RBHF theory with pvCD-Bonn A Wang et al. (2020b). In the right panel, the energy density ε\varepsilon and pressure PP of the pure quark star are calculated by the DSE approach with different effective width ωeff\omega_{\text{eff}} of medium screening in the interaction model (19). It is found that with the effective width ωeff\omega_{\text{eff}} increasing, i.e., the increasing of the gluon interaction, the energy density and pressure become larger. Besides, the differences of the energy density and pressure become more evident at higher density.

Refer to caption
Figure 5: The P​-​μnP\mbox{-}\mu_{n} relation (left) and P​-​ρP\mbox{-}\rho relation (right) of the hybrid star under Maxwell construction with nuclear matter described by the RBHF theory with potential pvCD-Bonn A and quark matter described by the DSE approach with different effective width ωeff\omega_{\text{eff}} of medium screening in the interaction model (19). In comparison, the results of the hadron star described by the RBHF theory with potential pvCD-Bonn A and the P​-​μP\mbox{-}\mu relation obtained by the BHF theory with potential Bonn B from Ref. Chen et al. (2011) are also given.
Table 1: Critical chemical potential μn,c\mu_{n,c}, critical pressure P​(μn,c)P(\mu_{n,c}), and the phase transition density region [ρH,ρQ][\rho_{H},\rho_{Q}] obtained with the RBHF theory and DSE approach under the Maxwell construction. The results obtained with the BHF theory and DSE approach from Ref. Chen et al. (2011) are also shown.
Model μn,c\mu_{n,c} P​(μn,c)P(\mu_{n,c}) ρH\rho_{H} ρQ\rho_{Q}
[GeV] [GeV⋅fm−3\cdot\text{fm}^{-3}] [ρsat\rho_{\text{sat}}] [ρsat\rho_{\text{sat}}]
A-0.5 1.995 0.916 8.105 16.689
A-0.35 1.640 0.471 6.078 10.940
A-0.25 1.366 0.225 4.379 7.189
BHF-0.35 1.416 0.193 3.556 5.744

Figure 5 shows the P​-​μnP\mbox{-}\mu_{n} relation and P​-​ρP\mbox{-}\rho relation of the hybrid star under Maxwell construction. The legend A-ωeff\omega_{\text{eff}} denotes that the nuclear matter is described by the RBHF theory with potential pvCD-Bonn A and the quark matter is described by the DSE approach with effective width ωeff\omega_{\text{eff}} of medium screening. For comparison, the results of the pure hadron star described by the RBHF theory are also given. In the left panel, the intersection points of the EOSs in P​-​μnP\mbox{-}\mu_{n} plane are the critical points of the first-order phase transition in Eq. (31). In the right panel, the pressure is constant at the critical point of the first-order phase transition, while the density jumps from ρH\rho_{H} to ρQ\rho_{Q}. The values of μn,c\mu_{n,c}, P​(μn,c)P(\mu_{n,c}), ρH\rho_{H}, and ρQ\rho_{Q} are listed in Table 1. It is found that for a larger ωeff\omega_{\text{eff}}, the critical baryon chemical potential μn,c\mu_{n,c} and density region [ρH,ρQ][\rho_{H},\rho_{Q}] are higher, and the corresponding pressure P​(μn,c)P(\mu_{n,c}) is larger. For ωeff=0.5\omega_{\text{eff}}=0.5 GeV, the corresponding density of the critical point is about 8.1​ρsat8.1~{}\rho_{\text{sat}}. Considering that the nucleon degrees of freedom becomes less available at higher density, the parameter ωeff\omega_{\text{eff}} should be smaller than 0.50.5 GeV to obtain a reasonable EOS of the hybrid star. For comparison, in the left panel of Fig. 5, we also show the P​-​μP\mbox{-}\mu relation calculated by the BHF theory with the potential Bonn B and corresponding three-body forces from Ref. Chen et al. (2011). The critical properties obtained with the Maxwell construction are also shown in the last row in Table 1. It is found that the nonrelativistic calculations lead to a softer EOS and the first-order phase transition happens much earlier than the relativistic ones.

Refer to caption
Figure 6: The mass-radius relation of the hybrid star under Maxwell construction with nuclear matter described by the RBHF theory with potential pvCD-Bonn A and quark matter described by the DSE approach with different effective width ωeff\omega_{\text{eff}} of medium screening in the interaction model (19). In comparison, the results of the pure hadron star described by the RBHF theory are also given.

The mass-radius relation of the hybrid star under the Maxwell construction are plotted in Fig. 6. It can be found that, once the first-order transition happens, the mass and radius decrease simultaneously. It is known that, if the mass decreases with respect to the increase of central density, the neutron star is unstable against oscillation. Therefore, this sharpness reflects that the appearance of quark matter leads to an unstable hybrid star. In other words, under the Maxwell construction with the present models, there is no such a quark core in the interior of a neutron star. We note that similar results are also found by combining the BHF theory with the DSE approach in Ref. Chen et al. (2011).

Refer to caption
Figure 7: The pressure of the hybrid star as a function of density under the three-window construction with four representative parameter sets (ρ¯,Γ)(\bar{\rho},\Gamma). The results for the pure hadron star are also shown. The effective width ωeff=0.35\omega_{\text{eff}}=0.35 GeV is fixed for the description of quark matter with the DSE approach.

Under the three-window construction, a phenomenological interpolation of the energy density between the hadron and quark phases is performed, where the interpolation function is given in Eq. (35). The parameters ρ¯\bar{\rho} and Γ\Gamma characterize the center and effective width of the crossover region in baryon density. Inspired by and basing them on Ref. Masuda et al. (2013a), we consider two constraints on the choice of the two parameters: (1) the system is always thermodynamically stable, i.e., d​P/d​ρ>0dP/d\rho>0, and (2) the crossover density region should be moderate to avoid the failure of the nuclear matter method and quark matter method, i.e., ρ¯−Γ>ρsat\bar{\rho}-\Gamma>\rho_{\text{sat}} and ρ¯+Γ<6​ρsat\bar{\rho}+\Gamma<6\rho_{\text{sat}}. In addition, a stiffer EOS is favored to satisfy the observation of massive neutron stars.

Figure 7 depicts the P​-​ρP\mbox{-}\rho relation of the hybrid star under the three-window construction. The quark matter effective width ωeff=0.35\omega_{\text{eff}}=0.35 GeV is chosen as an example and four representative parameter sets (ρ¯,Γ\bar{\rho},\Gamma) are shown. The parameter sets (3.5,1.0)(3.5,1.0) and (4.0,1.5)(4.0,1.5) lead to nonmonotonic pressure and should be discarded. The maximum density of the parameter set (4.0,2.0)(4.0,2.0) is 6​ρsat6\rho_{\text{sat}}, which is somehow too large for the RBHF theory. The parameter set (3.5,1.53.5,1.5) satisfies the conditions (1) and (2) and is chosen in the following calculations.

Refer to caption
Figure 8: The ε​-​ρ\varepsilon\mbox{-}\rho relation (left) and P​-​ρP\mbox{-}\rho relation (right) of the hybrid star under the three-window construction with nuclear matter described by the RBHF theory with potential pvCD-Bonn A and quark matter described by the DSE approach with different effective width ωeff\omega_{\text{eff}} of medium screening in the interaction model (19). In comparison, the results of the hadron star described by the RBHF theory are also given.

In Fig. 8, the ε​-​ρ\varepsilon\mbox{-}\rho relation and P​-​ρP\mbox{-}\rho relation of the hybrid star under the three-window construction are shown. In the left panel, the ε​-​ρ\varepsilon\mbox{-}\rho relations are interpolated in the crossover region. Outside the crossover region, pure nuclear matter or pure quark matter dominates. In the right panel, the pressure in the crossover region increases monotonically with an increasing baryon density for the effective width ωeff\omega_{\text{eff}} of different quarks. From Fig. 8, it is clear that with a lager ωeff\omega_{\text{eff}}, the energy density ε\varepsilon and pressure PP are larger in the crossover region.

Refer to caption
Figure 9: The mass-radius relation of the hybrid star under the three-window construction with nuclear matter described by the RBHF theory with potential pvCD-Bonn A and quark matter described by the DSE approach with different effective width ωeff\omega_{\text{eff}} of medium screening in the interaction model (19). In comparison, the results of the hadron star described by the RBHF theory are also given.
Table 2: The maximum mass MmaxM_{\text{max}} of the neutron star, the corresponding radius RMmaxR_{M_{\text{max}}}, and the radius for 1.4​M⊙1.4M_{\odot} neutron star R1.4​M⊙R_{1.4M_{\odot}} under the three-window construction with different effective width ωeff\omega_{\text{eff}}.
Model MmaxM_{\text{max}} RMmaxR_{M_{\text{max}}} R1.4​M⊙R_{1.4M_{\odot}}
[M⊙M_{\odot}] [km] [km]
pvCD-Bonn A 2.198 11.15 12.47
A-0.5 2.530 13.54 13.93
A-0.35 2.102 12.91 13.20
A-0.25 1.539 12.39 12.57

The mass-radius relation of the hybrid star under the three-window construction is plotted in Fig. 9. The maximum mass with different models, the corresponding radius, and the radius for 1.4​M⊙1.4M_{\odot} neutron star are listed in Table 2. For ωeff=0.25\omega_{\text{eff}}=0.25 GeV, the maximum mass of the hybrid star is about 1.5​M⊙1.5~{}M_{\odot}, which cannot support the astrophysical observation of massive neutron stars. For ωeff=0.5\omega_{\text{eff}}=0.5 GeV, the maximum mass of the hybrid star is 2.53​M⊙2.53~{}M_{\odot}. This is in contradiction to the results from binary neutron star mergers, which require that the EOS cannot be too stiff, and provide an upper bound for the maximum mass Annala et al. (2018). For ωeff=0.35\omega_{\text{eff}}=0.35 GeV, the maximum mass of the hybrid star is 2.1​M⊙2.1~{}M_{\odot}, which is consistent with the current constraints from astrophysical observation. Therefore, to obtain a hybrid star supporting 2​M⊙2~{}M_{\odot} with three-window construction, the effective width ωeff\omega_{\text{eff}} of medium screening effects should be close to 0.350.35 GeV.

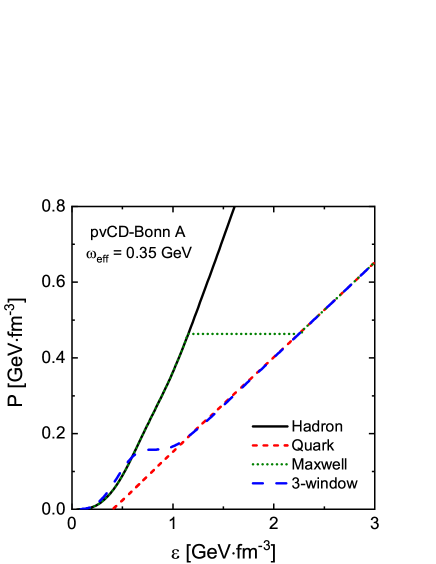
Refer to caption
Figure 10: The P​-​εP\mbox{-}\varepsilon relation of the pure hadron star, the pure quark star and the hybrid star under the Maxwell construction and three-window construction. Nuclear matter is described by the RBHF theory with potential pvCD-Bonn A and quark matter is described by the DSE approach with effective width ωeff=0.35\omega_{\text{eff}}=0.35 GeV.

In Fig. 10, the EOSs of the pure hadron star, the pure quark star, and the hybrid star under the Maxwell construction and three-window construction are compared. For the Maxwell construction, there is a clear plateau of pressure as a function of energy density. This corresponds to the latent heat of the first-order phase transition. For the three-window construction, the central density of the phase transition region is ρ¯=3.5​ρsat\bar{\rho}=3.5\rho_{\text{sat}} with an effective width Γ=1.5​ρsat\Gamma=1.5\rho_{\text{sat}}. Outside the crossover region, the EOS of the hybrid star asymptotically approaches that of the pure hadron star or the pure quark star. We also find the crossover region is lower than the first-order phase transition region in terms of energy density.

Refer to caption
Figure 11: The mass-radius relation of the pure hadron star, the pure quark star, and the hybrid star under the Maxwell construction and three-window construction. Nuclear matter is described by the RBHF theory with potential pvCD-Bonn A and quark matter is described by the DSE approach with the effective width ωeff=0.35\omega_{\text{eff}}=0.35 GeV. The dark (light) green and purple regions indicate the 68%​(95%)68\%(95\%) confidence intervals constrained by the NICER analysis of PSR J0030+0451 Miller and et al. (2019) and PSR J0740+6620 Miller and et al. (2021).

In Fig. 11, the mass-radius relation of the pure hadron star, the pure quark star, and the hybrid star under the Maxwell construction and three-window construction is depicted. Except for the pure quark star modeled by the DSE approach, both the pure hadron star and the hybrid star can support 2​M⊙2M_{\odot}. In comparison, the joint constraints of the mass and radius of neutron stars are also shown. The 68%68\% and 95%95\% contours of the joint probability density distribution of the mass and radius of PSR J0030+0451 Miller and et al. (2019) and PSR J0740+6620 Miller and et al. (2021) from the NICER analysis are also shown. It can be found that the mass radius of the pure hadron star, the hybrid stars with the Maxwell, and three-window constructions are all consistent with the recent constraints by NICER. The radii of a 1.4​M⊙1.4M_{\odot} hybrid star R1.4​M⊙R_{1.4M_{\odot}} under the Maxwell construction and three-window construction are 12.4712.47 km and 13.2013.20 km, respectively.

Refer to caption
Figure 12: Tidal deformability of the pure hadron star, the pure quark star, and the hybrid star under the Maxwell construction and three-window construction. Nuclear matter is described by the RBHF theory with potential pvCD-Bonn A and quark matter is described by the DSE approach with the effective width ωeff=0.35\omega_{\text{eff}}=0.35 GeV. The constraints from GW170817 Λ1.4​M⊙=190−120+390\Lambda_{1.4M_{\odot}}=190^{+390}_{-120} Abbott and et al. (2018) are also shown.

The tidal deformability of the pure hadron star, the pure quark star, and the hybrid star under the Maxwell construction and three-window construction are shown in Fig. 12. The tidal deformability of the pure hadron star and that of the hybrid star under the Maxwell construction share the same value, 473473, which is consistent with the constraints Λ1.4​M⊙=190−120+390\Lambda_{1.4M_{\odot}}=190^{+390}_{-120} from GW170817 Abbott and et al. (2018). The tidal deformability of the hybrid star under the three-window construction is 715715, which is slightly higher than that from the astronomical observation. We notice that the RBHF theory used in the present work can be improved by considering the negative-energy states in the full Dirac space Wang et al. (2021); Tong et al. (2022), where the tidal deformability can be reduced to a value which is much closer to the center value from GW170817. Therefore, the three-window construction with the nuclear matter described by the RBHF theory in the full Dirac space might lead to a tidal deformability which is consistent with the GW constraints.

IV Summary and prospects

The possible hadron-quark phase transition is explored by combining the RBHF theory for nuclear matter and the DSE approach for quark matter. The Maxwell construction and three-window construction are implemented to study the first-order phase transition and crossover, respectively. For the Maxwell construction, the phase transition occurs where the baryon chemical potential and pressure of the two phases are equal. With the RBHF theory and DSE approach, there is no stable quark core in the interior of a neutron star, which confirms previous studies with nonrelativistic Brueckner-Hartree-Fock theory and the DSE approach. For the three-window construction, a smooth interpolation of the energy density between the hadron and quark phases is performed, where the parameters in the interpolation function are chosen in such a way as to keep the thermodynamic stability and lead to a moderate crossover density region. To support a two-solar-mass neutron star under the three-window construction, the effective width of medium screening effects in quark matter should be around ωeff=0.35\omega_{\text{eff}}=0.35 GeV. The mass-radius relation of the hybrid star is consistent with the joint mass-radius observation, while the tidal deformability of a 1.41.4 solar mass is found slightly higher than the constraints from gravitational wave detection.

In the future, this work can be extended by improving the theoretical methods for hadron matter, quark matter, and construction schemes. The RBHF theory can be improved by considering the negative energy states in the full Dirac space. For the DSE framework, the parameters cannot be changed arbitrarily as they are determined by the hadron properties as well as the phase transition at finite temperature. To obtain a stiffer EOS for the quark matter, it is necessary to improve the vertex and gluon truncation in the DSE approach, for example, by using the Ball-Chiu or Chang-Liu-Roberts vertex Ball and Chiu (1980); Qin et al. (2013) and including more interaction channels Eichmann et al. (2016) as well as higher order corrections Gao et al. (2021). As for the construction schemes, considering the studies by combing BHF and DSE approaches Chen et al. (2011), the Gibbs construction is likely to support a stable quark core. After the corrections and improvements are realized, it is hopeful to achieve a better understanding of the hadron-quark phase transition in neutron stars.

Acknowledgements.
This work was partly supported by the China Postdoctoral Science Foundation under Grants No. 2021M700610 and No. 2022M723230; the CAS Project for Young Scientists in Basice Research (YSBR060); the National Natural Science Foundation of China under Grants No. 12147102, No. 12005060, No. 12205353, and No. 12205030; and the Fundamental Research Funds for the Central Universities under Grants No. 2020CDJQY-Z003 and No. 2021CDJZYJH-003.

References