LABEL:sub@\par
Guided Cooperation in Hierarchical Reinforcement Learning via Model-based Rollout
Abstract
Goal-conditioned hierarchical reinforcement learning (HRL) presents a promising approach for enabling effective exploration in complex, long-horizon reinforcement learning (RL) tasks \chreplacedthroughvia temporal abstraction. \chreplacedEmpirically,In essence, for \chreplacedheightenedincreased inter-level communication and coordination can induce more stable and robust policy improvement in hierarchical systems. Yet, most existing goal-conditioned HRL algorithms \chaddedhave primarily focused on the subgoal discovery, \chreplacedneglectingregardless of \chreplacedinter-level cooperation.inter-level coupling. Here, we propose a goal-conditioned HRL framework named Guided Cooperation via Model-based Rollout (GCMR)111Code is available at https://github.com/HaoranWang-TJ/GCMR_ACLG_official , \chreplacedaiming to bridge inter-layer information synchronization and cooperation by exploiting forward dynamics.which estimates forward dynamics to promote inter-level cooperation. \chaddedFirstly, \chreplacedtThe GCMR \chreplacedmitigatesalleviates the state-transition error within off-policy correction \chreplacedviathrough a model-based rollout, \chreplacedthereby enhancingfurther improving the sample efficiency. \chreplacedSecondlyMeanwhile, \chreplacedto prevent disruption byto avoid being disrupted by \chdeletedthese corrected \chreplacedthebut possibly unseen\chdeleted or faraway subgoals and states, lower-level Q-function gradients are constrained using a gradient penalty with a model-inferred upper bound, leading to a more stable behavioral policy \chaddedconducive to effective exploration. \chreplacedThirdlyBesides, we propose a one-step rollout-based planning\chdeleted to further facilitate inter-level cooperation, \chreplacedusingwherein the higher-level \chreplacedcriticsQ-function \chreplacedto guideis used to guide the lower-level policy\chreplaced. Specifically, we estimate by estimating the value of future states \chaddedof the lower-level policy \chaddedusing the higher-level \chreplacedcritic Q-function, thereby transmitting \chdeletedso that global task information\chdeleted is transmitted downwards to avoid local pitfalls. \chaddedThese three critical components in GCMR are expected to facilitate inter-level cooperation significantly. Experimental results demonstrate that incorporating the proposed GCMR framework with a disentangled variant of HIGL, namely ACLG, yields more stable and robust policy improvement \chreplacedcompared tothan various baselines and \chreplacedsignificantlysubstantially outperforms previous state-of-the-art \chdeleted(SOTA) HRL algorithms\chdeleted in both hard-exploration problems and robotic control.
1 Introduction
Hierarchical reinforcement learning (HRL) has made significant contributions toward solving complex and long-horizon tasks with sparse rewards. Among HRL frameworks, goal-conditioned HRL is an especially promising paradigm for goal-directed learning in a divide-and-conquer manner\chdeleted[dayan1992feudal][51]. In goal-conditioned HRL, multiple goal-conditioned policies are stacked hierarchically, where the higher-level policy assigns a directional subgoal to the lower-level policy, and the lower strives toward it. Recently, related advances [60, 50, 31, 28, 18, 19, 9, 58] have made significant progress in improving exploration efficiency via reachable subgoal generation with adjacency constraint [60, 50]\chadded, long-term decision-making with state-temporal compression [18], and graph-based planning [48, 19, 9, 58]. \chaddedFurthermore, the challenges posed by local optima and transient traps [16] can also be mitigated by boosting exploration through auxiliary rewards[5, 42, 22]. Yet, integrating these strategies with an off-policy learning method still struggles with being sample efficient. Previous research handles this issue by relabeling experiences with more faithful goals [38, 30, 61], in which the relabeling aims to explore how to match the higher-level intent and the actual outcome of the lower-level subroutine. The HER-style approaches [1, 30, 61] overwrite the former with the latter, while the HIRO [38] modifies the past instruction to adapt to the current behavioral policy, thereby improving the data-efficiency. \chaddedAnother effective approach for enhancing data efficiency is to leverage model-based transition dynamics in planning. Recent advancements in dynamics generalization [27, 44] have demonstrated that unseen latent dynamics empower agents with robust generalization capabilities, effectively adapting to unseen scenarios. Related research in autonomous navigation systems [21, 14] has indicated that learning dynamics can ensure the robustness of long-term planning against unpredictable changes and perturbations in open environments. However, there has been limited literature [59, 37, 40, 61] studying the model exploitation in the goal-conditioned RL. Several studies have attempted to deploy model-based hierarchical reinforcement learning on various real-world control tasks, such as autonomous aerial vehicles[59] and physical humanoids[37]. These studies employed model predictive control (MPC) for high-level motion planning and model-free RL for motion primitive learning[52, 37]. However, to our knowledge, there is no prior work studying inter-level model-based cooperation in goal-conditioned HRL.
Within a hierarchical architecture, promoting inter-level cooperation is a notably more effective approach to accelerating reinforcement learning[45, 13, 46]. \chreplacedTo achieveIt can be seen that, empirically, an inter-level association and communication mechanism bridging the gap between the intent and outcome is essential for robust policy improvement. For achieving inter-level cooperation and communication, addressing the following questions is essential: 1) how does the lower level comprehend and synchronize with the higher level? 2) how does the lower level \chreplacedmaintain robustness in the face ofhandle errors from the higher level? 3) how does the lower level directly understand the overall task without relying on higher-level proxies? \chaddedEmpirically, a learned dynamics model can function as the inter-level communication mechanism to bridge the gap between the \chaddedhigh-level intent and \chaddedfinal (low-level) outcome, leading to robust policy improvement.
In this paper, we propose a novel goal-conditioned HRL framework to systematically \chdeletedaddress these questionsfacilitate inter-level cooperation, which mainly consists of three crucial components: 1) the goal-relabelling for synchronizing, 2) the gradient penalty for enhancing robustness against high-level errors, and 3) the one-step rollout-based planning for \chreplacedtransmitting global tasks downwardscollectively working towards achieving a global task. The key insight in the proposed framework is to modularly integrate a forward dynamics prediction model into HRL framework for improving the data efficiency and enhancing learning efficiency. Specifically, our framework, named Guided Cooperation via Model-based Rollout (GCMR), brings together three crucial ingredients:
-
•
\chreplaced
We propose a novel model-based rollout-basedA novel off-policy correction\chdeleted based on weighted model-based rollout\chadded, which was deployed to mitigate the cumulative state-transition error in HIRO [38]. Additionally, we \chreplacedalso propose \chreplaceda trick, two tricks, the exponential weighting and soft goal-relabeling, to \chdeletedsuppress the cumulative error in long-horizon rollouts and make the correction more robust to outliers employed exponential weighting to suppress the cumulative error in long-horizon rollouts, assigning higher weights to the initial transitions. We also propose a convenient trick, soft goal-relabeling, to make correction robust to outliers. All of these contribute to further improving the data efficiency.
-
•
We propose a gradient penalty to suppress sharp lower-level Q-function gradients, which clamps the Q-function gradient by means of an inferred upper bound. \chreplacedThe gradient penalty implicitly constrained the behavioral policy to change steadily, enhancing the stability of the optimizationConsequently, the behavioral policy is implicitly constrained to change steadily, yielding conservative action. This, in turn, enhances the stability of the hierarchical optimization.
-
•
Meanwhile, we designed a one-step rollout-based planning method to prevent the lower-level policy from getting stuck in local optima\chreplaced, wherein the values of future transitions of lower-level agents were evaluated using the higher-level critics. Such foresight helps the lower-level policy cooperate better with the goal planner.. Specifically, we use the learned dynamics to simulate one-step rollouts and evaluate task-specific values of future transitions through the higher-level Q-function. Such foresight and planning help the lower-level policy cooperate better with the goal planner.
To justify the superiority of the proposed \chreplacedGCMRmethod\chdeleted and achieve a remarkable SOTA, we integrate \chreplaceditthe GCMR with a strong baseline: ACLG, a disentangled variant of HIGL [23]. Experimental results show that incorporating the proposed framework \chreplacedachievedimproves the \chreplacedstate-of-the-art performanceperformance of state-of-the-art HRL algorithms in complex and sparse reward environments. \chaddedThe contributions of this article are summarized as follows:
-
1)
\chadded
This article proposes GCMR, a novel method designed to facilitate inter-level cooperation in HRL, thereby accelerating learning.
-
2)
\chadded
We benchmark our method on various long-horizon control and planning tasks, which are commonly used in the HRL literature[11, 38, 39, 60, 23, 28, 54, 50, 57]. Extensive experiments demonstrate the superior performance of our proposed method. Moreover, we conduct sufficient ablation studies to validate the contribution of different components in GCMR.
-
3)
\chadded
Our study emphasizes the importance of inter-level cooperation, contributing to new insights in hierarchical RL.
The rest of this article is structured as follows. Section 2 introduces the preliminaries on HRL, adjacency constraint, landmark-based planning, and our proposed disentangled variant of HIGL. Section 3 provides a review of related works, focusing on transition relabeling and model exploitation in goal-conditioned HRL. Section 4 offers a detailed implementation of the proposed GCMR method. In Section 5, we outline our experimental environments, explore the impact of different parameters in ACLG and GCMR, and present our main experimental results along with ablation analyses. Section 6 discusses the principal findings, highlights several limitations of this study, and outlines potential directions for future research. Section 7 presents our conclusions.
2 Preliminaries
Consider a finite-horizon, goal-conditioned Markov decision process (MDP) represented by a tuple , where , , and denote the state space, goal space, and action space, respectively. The transition function defines the transition dynamics of environment, and the is the reward function. Specifically, the environment will transition from to a new state while yielding a reward once it takes an action , where and is conditioned on a final goal . In most real-world scenarios, complex tasks can often be decomposed into a sequence of simpler movements and interactions. Therefore, we formulate a hierarchical reinforcement learning framework, which typically has two \chreplacedlayershierarchies: higher- and lower-level policies, to deal with these challenging tasks. The higher-level policy observes the state of environment and produces a high-level action , i.e., a subgoal indicating a desired change of state or absolute location to reach every time steps. The lower-level policy attempts to reach these assigned subgoals within a time interval. Suppose that the higher-level policy and lower-level policy are parameterized by neural networks with parameters and , respectively. The above procedure of the higher-level controller can be formulated: when (mod ). The lower-level policy observes the state as well as subgoal and then yields a low-level atomic action to interact directly with the environment: . Notably, for the relative subgoal scheme, subgoals evolve following a pre-defined subgoal transition process when (mod ), where is a known mapping function that transforms a state into the goal space. The pre-defined transition makes the lower-level agent seem completely self-contained and like an autonomous dynamical system.
2.1 Parameterized Rewards
During interaction with the environment, the higher-level agent makes a plan using subgoals and receives entire feedback by accumulating all external rewards within the planning horizon:
| (1) |
The lower-level agent is intrinsically motivated in the form of internal reward that evaluates subgoal-reaching performance:
| (2) |
Where denotes a Boolean hyper-parameter whose value is 0/1 for the relative/absolute subgoal scheme.
2.2 Experience Replay for Off-Policy Learning
Experience replay has been the fundamental component for off-policy RL algorithms, which greatly improves the sample efficiency by reusing previously collected experiences. Here, there is no dispute that the lower-level agent can collect the experience by using the behavioral policy to directly interact with the environment. The higher-level agent interacts indirectly with it through the lower-level proxy and then stores a series of state-action transitions as well as a cumulative reward, i.e., , into the high-level replay buffer. The lower- and higher-level policies can be trained by sampling transitions stored in these experience replay buffers , . The aim of optimization is to maximize the expected discounted reward , where is the discount factor. In practice, we instantiate lower- and higher-level agents based on the TD3 algorithm [12], each having a pair of online critic networks with parameters and , along with a pair of target critic networks with parameters and . Additionally, TD3 has a single online actor parameterized by and a target actor parameterized by . All target networks are updated using a soft update approach. Then, the Q-network can be updated by minimizing the mean squared temporal-difference (TD) error over all sampled transitions. To simplify notation, we adopt unified symbols and to indicate the observation and performed action, where for lower-level while for higher-level. Hence, the Q-learning loss can be written as follows:
| (3) |
Where , i.e., or , is dependent on or correspondingly because target policies map states to the "optimal" actions in an almost deterministic manner:
| (4) | ||||
Where is the s.d. of the Gaussian noise, defines the range of the auxiliary noise, and refers to the next obtained observation after taking an action. It is noteworthy that with respect to the higher-level while for the lower-level. Drawing support from Q-network, the policy can be optimized by minimizing the following loss:
| (5) |
As mentioned above, we outline the common actor-critic approach with the deterministic policy algorithms [32, 12]. For more details, please refer to [12].
2.3 Adjacency Constraint
For the high-level subgoal generation, reachability within steps is a sufficient condition for facilitating reasonable exploration. Zhang et al. [60, 50] mined the adjacency information from trajectories gathered by the changing behavioral policy over time\chdeleted during the training procedure. In that study, a -step adjacency matrix was constructed to memorize -step adjacent state-pairs appearing in these trajectories. To ensure this procedure is differentiable and can be generalized to newly-visited states, the adjacency information stored in such matrix was further distilled into an adjacency network parameterized by . Specifically, the adjacency network approximates a mapping from a goal space into an adjacency space. Subsequently, the resulting embeddings can be utilized to measure whether two states are -step adjacent using the Euclidean distance. For example, the -step adjacent estimation (or shortest transition distance) of two states and can be calculated as: , where is a scaling factor and the function maps states into the goal space. Such an adjacency network can be learned by minimizing the following contrastive-like loss: , where is a hyper-parameter indicating a margin between embeddings and is the label indicating whether and are \chreplaced-step adjacent.
2.4 Landmark-based Planning
Graph-based navigation has become a popular technique for solving complex and sparse reward tasks by providing a long-term horizon. The relevant frameworks [43, 19, 9, 8, 53, 23, 58, 28, 24] commonly contain two components: (a) a graph built by sampling landmarks and (b) a graph planner to select waypoints. In a graph, each node corresponds to an observation state, while edges between nodes are weighted using a distance estimation. Specifically, a set of observations randomly subsampling from the replay buffer are organized as nodes, where high-dimensional samples (e.g., images) may be embedded into low-dimensional representations [43, 9, 33, 53, 58]. However, operations over the direct subsampling of the replay buffer will be costly. The state aggregation [8] and landmark sampling based on farthest point sampling (FPS) were proposed for further sparsification [19, 23, 28, 24]. Our study follows prior works of Kim et al. [23, 24], in which FPS was employed to select a collection of landmarks, i.e., coverage-based landmarks , from the replay buffer. In addition to this, HIGL [23] used random network distillation [5] to explicitly sample novel landmarks, i.e., novelty-based landmarks , a set of states rarely visited in the past. Hence, the final collection of landmarks was . Once landmarks are added to the graph, the edge weight between any two vertices can be estimated by a lower-level value function [19, 9, 23, 28, 24] or the (Euclidean-based or contrastive-loss-based) distance between low-dimensional embeddings of states [43, 53, 33, 60]. Following prior works [19, 23, 24], in this study, we estimated the edge weight via the lower-level value function, i.e., . After that, unreachable edges were clipped by a preset threshold [19]. In the end, the shortest path planning algorithm was run to plan the next subgoal, the very first landmark in the shortest path from the current state to the goal :
| (6) |
2.5 \chaddedDisentangled Variant of HIGL [23]: Adjacency Constraint and Landmark-\chreplacedGuided pbased Planning (ACLG)

In HIGL, after finding a landmark through landmark-based planning (see Equation 6), the raw selected landmark was shifted towards the current state for reachability: , where denotes the shift magnitude. Then, the higher-level policy was guided to generate subgoals adjacent to the planned landmarks and the landmark loss of HIGL was formulated as:
| (7) |
Here, Kim et al.\chadded[23] employed the adjacency constraint to encourage the generated subgoals to be in the -step adjacent region to the planned landmark. However, the entanglement between the adjacency constraint and landmark-based planning limited the performance of HIGL.
Inspired by PIG [24], we proposed a disentangled variant of HIGL. We only made minor modifications to the landmark loss (see Equation 7) of HIGL:
| (8) | ||||
The former term is the adjacency constraint and the latter is the landmark-guided loss, so the proposed method was called ACLG. The hyper-parameters and were introduced to better balance the adjacency constraint and landmark-based planning. \chaddedThe illustrations (see Fig. 1) visually demonstrate the differences between HIGL and ACLG.
3 Related work
3.1 Transition Relabeling
Training a hierarchy using an off-policy algorithm remains a prominent challenge due to the non-stationary state transitions [38, 30, 61]. Specifically, the higher-level policy takes the same action under the same state but could receive markedly different outcomes because of the low-level policy changing, so the previously collected transition tuple is no longer valid. To address the issues, HIRO [38] deployed an off-policy correction to maintain the validity of past experiences, which relabeled collected transitions with appropriate high-level actions chosen to maximize the probability of the past lower-level actions. Alternative approaches, HAC [1, 30], replaced the original high-level action with the achieved state (projected to the goal space) in the form of hindsight. However, HAC-style relabeled subgoals are \chdeletedonly compatible with the past low-level policy rather than the current one, deteriorating the non-stationarity issue.
Our work is related to HIRO [38], and the majority of modification is that we roll out the off-policy correction using learned transition dynamics to suppress the accumulative error. The closest work is the MapGo [61], a model-based HAC-style framework in which the original goal was replaced with a foresight goal by reasoning using an ensemble transition model. Our work differs in that we screen out a faithful subgoal that induces rollout-based action sequence similar to the past transitions, while the MapGo overwrites the subgoal with a foresight goal based on the model-based rollout. Meanwhile, our framework proposes a gradient penalty with model-inferred upper bound to prohibit the disturbance caused by relabeling to the behavioral policy.
3.2 Model Exploitation in Goal-conditioned HRL
The promises of model-based RL (MBRL) have been extensively discussed in past research [36]. The well-known model-based RL algorithm, Dyna [49], leveraged a dynamics model to generate one-step transitions and then update the value function using these imagined data, thus accelerating the learning. Recently, instantiating environment dynamics\chdeletedmodel using an ensemble of probabilistic networks has become quite popular because of its ability to model both aleatory uncertainty and epistemic uncertainty [7]. Hence, a handful of Dyna-style methods proposed to simulate multi-step rollouts by using ensemble models, such as SLBO [35] and MBPO [20]. Alternatively, the model-based value expansion methods performed multi-step simulation and estimated the future transitions using the Q-function, which helped to reduce the value estimation error. The representative \chdeletedvalue estimation algorithms include MVE [10] and STEVE [4]. Besides, in fact, the estimated value of states can directly provide gradients to the policy when the learned dynamic models are differentiable, like Guided Policy Search [29] and Imagined Value Gradients [6]. Our work differs from these works since we use the higher-level Q-function to estimate the value of future lower-level transitions. As stated in a recent survey [34], there have been only a few works [40, 61] involving the model exploitation in the goal-conditioned RL. To our knowledge, there is no prior work studying such inter-level planning.
4 Methods
This section explains how our framework with Guided Cooperation via Model-based Rollout (GCMR) promotes inter-level cooperation. The GCMR involves three critical components: 1) the off-policy correction via model-based rollouts, 2) gradient penalty with a model-inferred upper bound, and 3) one-step rollout-based planning. Below, we \chdeletedfirst introduce a strong baseline, ACLG, and then detail the architecture of the dynamics model and such three critical components.
4.1 Forward Dynamics Modeling
A bootstrapped ensemble of dynamics models is constructed to approximate the true transition dynamics of environment: , which has been demonstrated in several studies [7, 26, 20, 47, 55, 56]. We denote the dynamics approximators as , where is the ensemble size and denotes the parameters of models. Each model of the ensemble projects the state conditioned on the action to a Gaussian distribution of the next state, i.e., , with . In usage, a model is picked out uniformly at random to predict the next state. Note that, here, we do not learn the reward function because the compounding error from multi-step rollouts makes it infeasible for higher-level to infer the future cumulative rewards. As for the lower-level agent, the reward can be computed through the intrinsic reward function (see Equation 2) on the fly. Finally, such dynamics models are trained via maximum likelihood and are incorporated to encourage inter-level cooperation and stabilize the policy optimization process.
4.2 Off-Policy Correction via Model-based Rollouts
With well-trained dynamics models, we expand the vanilla off-policy correction in HIRO [38] by using the model-generated state transitions to bridge the gap between the past and current behavioral policies. Recall a stored high-level transition in the replay buffer, which is converted into a state-action-reward transition: during training. Relabeling either the cumulative rewards or the final state via -step rollouts, resembling the FGI in MapGo [61], substantially suffers from the high variance of long-horizon prediction. In essence, both the final state and the reward sequence are explicitly affected by the action sequence . Hence, relabeling the , instead of the or , with an action sequence-based maximum likelihood is a promising way to improve sample efficiency. Following prior work [38], we consider the maximum likelihood-based action relabeling:
| (9) |
Where indicates the candidate subgoals sampled randomly from a Gaussian centered at . Meanwhile, the original goal and the achieved state (in goal space) are also taken into consideration. Specifically, according to Equation 9, the current low-level policy performed -step rollouts conditioned on these candidate subgoals. These sub-goals maximizing the similarity between original and rollout-based action sequences will be selected as optimal. Yet, we find that the current behavioral policy cannot produce the same action as in the past, so the \chreplaced may not be revisited. will not be reached at all.Therefore, the vanilla off-policy correction still suffers from the cumulative error due to the gap between the and the unknown transitions . In view of this fact, we roll out these transitions using the learned dynamics models to mitigate the issue. Besides, we employ an exponential weighting function along the time axis to highlight shorter rollouts and \chreplacedslowly shift the original states to the rollout-based ones.eliminate the effect of cumulative error. Then Equation 9 is rewritten as:
| (10) | ||||
Where and . . is a hyper-parameter indicating the base of the exponential function, where in practice, we set to 0.95.
Soft-Relabeling: Inspired by the pseudo-landmark shift of HIGL [23], instead of an immediate overwrite, we use a soft mechanism to smoothly update subgoals:
| (11) |
Where represents the shift magnitude\chreplaced from the original subgoals updated at the constant speed . The soft update is expected to be robust to outliers\chdeleted and protect the Q-learning, which is highly sensitive to noise.
4.3 Gradient Penalty with a Model-Inferred Upper Bound
Apparently, from the perspective of the lower-level policy, the subgoal relabeling implicitly brings in a distributional shift of observation. Specifically, these relabeled subgoals are sampled from the goal space but are not executed in practice. The behavioral policy is prone to produce unreliable actions under such an unseen or faraway goal, resulting in ineffective exploration. Motivated by \chreplaced[2, 25, 15][25, 15], we pose the Lipschitz constraint on the Q-function gradients to stabilize the Q-learning of behavioral policy. To understand the effect of the gradient penalty, we highlight the \chreplacedLipschitzLlipschitz property of the learned Q-function.
Proposition 1.
Let and be the policy and the reward function in an MDP. Suppose there are the upper bounds of Frobenius norm of the policy and reward gradients w.r.t. input actions, i.e., and . Then the gradient of the learned Q-function w.r.t. action can be upper-bounded as:
| (12) |
Where denotes the dimension of the action and is the discount factor.
Proof.
Remark 1.
Proposition 1 proposes a tight upper bound. A more conservative upper bound can be obtained by employing the inequality pertaining to :
| (13) |
Hence, a core challenge in the applications is how to estimate the upper bound of reward gradients w.r.t. input actions.
Now, we propose an approximate upper-bound approach grounded on the learned dynamics . Fortunately, the lower-level reward function is specified in the form of L2 distance and is immune to environment stochasticity. Naturally, the upper bound of reward gradients w.r.t. input actions can be estimated as:
| (14) | ||||
In practice, we approximate the upper bound using a mini-batch of lower-level observations independently sampled from the replay buffer , yielding a tighter upper bound and, in turn, more forcefully penalizing the gradient:
| (15) | ||||
Then, following prior works [15], we plug the gradient penalty term into the lower-level Q-learning loss (see Equation 3), which can be formulated as:
| (16) | ||||
Where is a hyper-parameter controlling the effect of the gradient penalty term. Because the gradient penalty enforces the Lipschitz constraint on the critic, limiting its update, we had to increase the number of critic training iterations to 5, a recommended value in WGAN-GP [17], per actor iteration. Considering the computational efficiency, we apply the gradient penalty every 5 training steps.
4.4 One-Step Rollout-based Planning

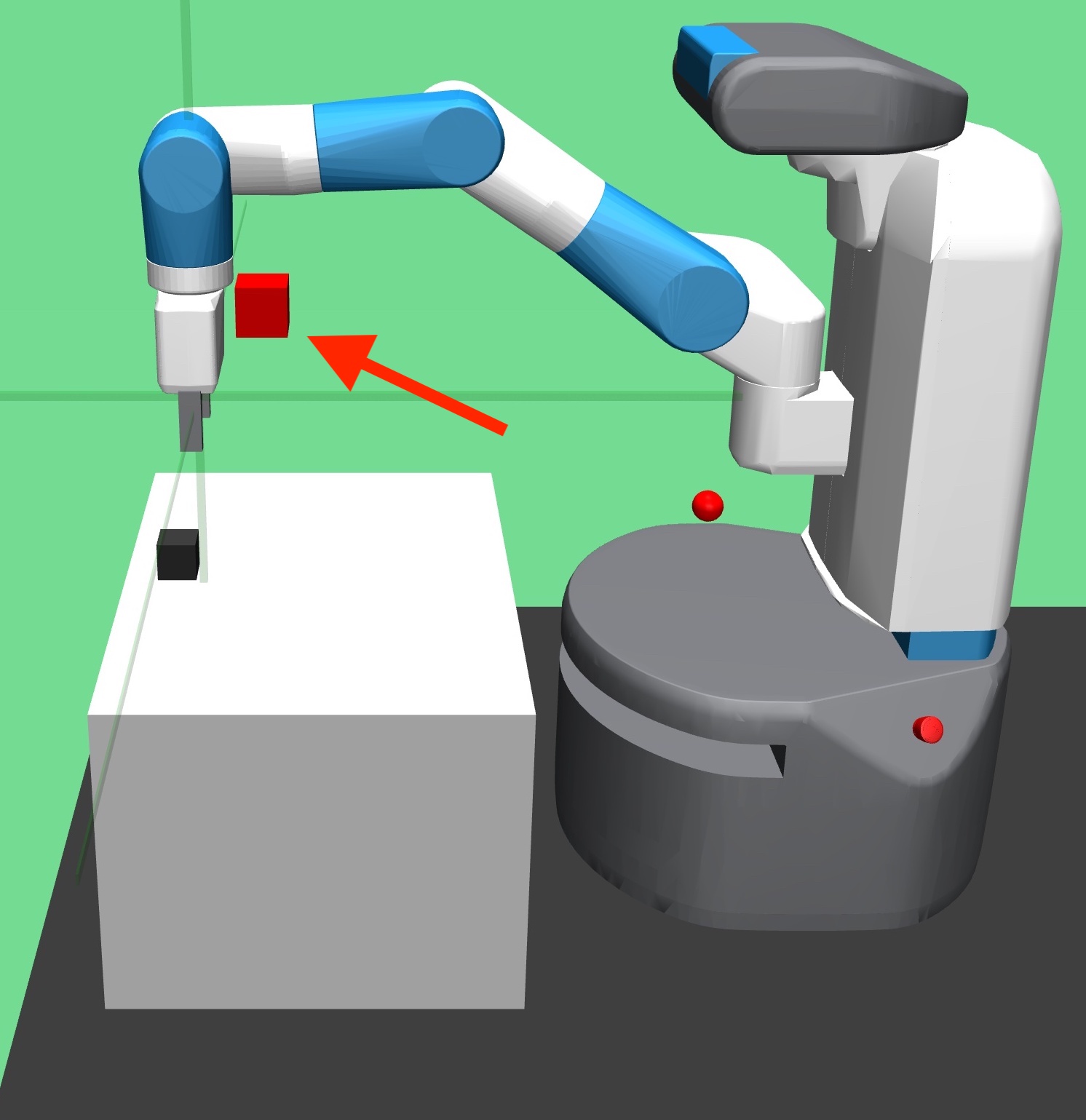
In a flat model-based RL framework, model-based value expansion-style methods [10, 4] use dynamics models to simulate short rollouts and evaluate future transitions using the Q-function. Here\chadded, as shown in Fig. 2, we steer the behavioral policy towards globally valuable states, i.e., having a higher higher-level Q-value. Specifically, we perform a one-step rollout and evaluate the next transition using the higher-level critics. The objective is to minimize the following loss:
| (17) | ||||
Where is a hyper-parameter to weigh the planning loss. Note that the is not determined by higher-level policy solely. Meanwhile, considering that the higher-level policy is also \chdeletedconstantly changing over time, the is sampled randomly from a Gaussian distribution centered at . In practice, a pool of and is sampled from the buffer , and then they are repeated ten times with shuffling the . Next, these samples are duplicated again to accommodate the variance of . On the other hand, the next step’s subgoal is also produced by the fixed goal transition function or by the higher-level policy conditioning on the observation. But, from the perspective of lower-level policy, the probability of such two events is equal because of the property of Markov decision process, i.e.,
| (18) |
Hence, the Equation 17 is instantiated:
| (19) | ||||
Obviously, the second term is too dependent on current higher-level policy. The TD3 [12] seeks to smoothen the value estimate by bootstrapping off of nearby state-action pairs. Similarly, we add clipped noise to keep the value estimate robust. This makes our modified term :
| (20) | ||||
Where the hyper-parameters and are common in the TD3 algorithm (see Equation 4). In the end, is incorporated into lower-level actor loss (see Equation 5) to guide the lower-level policy towards valuable highlands with respect to the overall task. Here, in the same way, we employ the one-step rollout-based planning every 10 training steps.
5 Experiments
We evaluated the proposed GCMR on challenging continuous control tasks, as shown in Fig. 3. Specifically, the following simulated robotics environments are considered:
-
•
Point Maze [23]: In this environment, a simulated ball starts at the bottom left corner and navigates to the top left corner in a ’’-shaped corridor.
-
•
Ant Maze (W-shape) [23]: In a ’’-shaped corridor, a simulated ant starts from a random position and must navigate to the target location at the middle left corner.
-
•
Ant Maze (U-shape) [38, 23], Stochastic Ant Maze (U-shape) [60, 50], and Large Ant Maze (U-shape): A simulated ant starts at the bottom left corner in a ’’-shaped corridor and seeks to reach the top left corner. As for the randomized variation, Stochastic Ant Maze (U-shape) introduces environmental stochasticity by replacing the agent’s action at each step with a random action (with a probability of 0.25).
-
•
Ant Maze-Bottleneck [28]: The environment is almost the same as the Ant Maze (U-shape). Yet, in the middle of the maze, there is a very narrow bottleneck so that the ant can barely pass through it.
-
•
Pusher [23]: A 7-DOF robotic arm is manipulated into pushing a (puck-shaped) object on a plane to a target position.
-
•
Reacher [23]: \chreplacedA 7-DOF robotic arm is manipulated to make the end-effector reach a spherical object that is randomly placed in mid-air.A 7-DOF robotic arm is manipulated to make the end-effector reach a target position.


(W-shape)

(U-shape)

Bottleneck



These general ’’-shaped mazes have the same size of while is for the ’’-shaped maze. Besides, the size of the Large Ant Maze (U-shape) is twice as large as that of the general Ant Maze (U-shape), i.e., 24 × 24.
- •
- •
Further environment details are available in the "Supplementary Materials".
5.1 Hyper-parameters in ACLG
First, we conduct experiments on Ant Maze (U-shape) to explore the effect of hyper-parameters in ACLG: (1) the number of landmarks and (2) the balancing coefficient .


Landmark Number Selection
Since the number of landmarks plays an important role in the graph-related method, we explored the effects of different numbers of landmarks on performance. Here, we sample the same number of landmarks for each criterion, i.e., the same number for novelty-based and novelty-based landmarks . As shown in Fig. LABEL:sub@landmark_num, overall, the ACLG significantly outperforms the HIGL since the disentanglement between the adjacency constraint and landmark-based planning further highlights the advantages of landmarks. Finally, the setting was adopted for further analysis.
Balancing Coefficient
In Fig. LABEL:sub@landmark_param, we investigate the effectiveness of the balancing coefficient , which determines the effect of the landmark-based planning term in ACLG on performance. We find that ACLG with outperforms others. Moreover, ACLG with outperforms that with , which shows a large value of helps unleash the guiding role of landmarks.
5.2 \chaddedHyper-parameters in GCMR
Next, we highlight the impact of the hyper-parameters in GCMR: the shift magnitude in soft-relabeling, the penalty coefficient , and the coefficient for the rollout-based planning. We deploy ACLG+GCMR in multiple environments.
\chaddedShift Magnitude for Soft-Relabeling
In Fig. 5, we conduct experiments to examine the impact of . Fig. LABEL:sub@org_goals illustrates the original subgoals sampled from the experience replay buffer of Large Ant Maze (U-shape) at 0.6M steps. Fig. LABEL:sub@no_shift-LABEL:sub@shift_40 depict the relabeled subgoals without or with varying shift magnitude. By comparing Fig. LABEL:sub@org_goals and Fig. LABEL:sub@no_shift, it is evident that relabeling introduces out-of-distribution (OOD) subgoals, which in turn lead to instability. The OOD issue can be addressed using the soft-relabeling method, which involves shifting the original subgoals towards the relabeled ones by a certain magnitude, as shown in Fig. LABEL:sub@shift_10-LABEL:sub@shift_40. However, it should be noted that small shift magnitudes will weaken the corrective effect. As shown in Fig. LABEL:sub@success_shift, we observe that too large or little value of harms the performance. Therefore, the shift magnitude needs to be carefully tuned to strike a balance between suppressing the OOD issue and maintaining corrective effectiveness. In our experiments, is set to 20 for the small maze and 30 for the large maze.







\chaddedPenalty Coefficient
In Fig. 6, we explore the impact of the penalty coefficient on the performance of ACLG+GCMR. Overall, when , applying the gradient penalty leads to improved asymptotic performance. Furthermore, across most environments, we consistently find that the value emerges as optimal. For highly intricate environments, the gradient penalty should be strengthened, as in the case of the Ant Maze-Bottleneck (see Fig. LABEL:sub@mgp_lambda2).




\chaddedBalancing Coefficient for One-Step Rollout-based Planning
In Fig. 7, we investigate the impact of , which determines the effect of the proposed one-step rollout-based planning term, (see Equation 17), on the proposed framework. The results show that utilizing one-step rollout-based planning achieved a more stable asymptotic performance in the Ant Maze (U-shape) and Point Maze. In fact, a slightly larger could powerfully and aggressively force the lower-level policy to follow the one-step rollout-based planning, leading to accelerated learning. However, if is too large, it may restrict the exploration capability of the behavioral policy itself. The recommended range for the parameter is between and .
5.3 Comparative Experiments
To validate the effectiveness of the GCMR, we plugged it into the ACLG, the disentangled variant of HIGL, and then compared the performance of the integrated framework with that of ACLG, HIGL [23], HRAC [60], DHRL [28], as well as the PIG [24]. Note that the numbers of landmarks used in these methods are different. In most tasks, HIGL employed 40 landmarks, ACLG used \chreplaced60120 landmarks, DHRL utilized 300 landmarks, and PIG employed 400 landmarks (see Table 3 in the "Supplementary Materials" for details). This is in line with prior works. Also, consistent with prior research, our experiments were performed on the above-mentioned environments with sparse reward settings, where the agent will obtain no reward until it reaches the target area.

But we also present a discussion about dense experiments based on AntMaze (U-shape), as shown in Fig. 8. Note that the comparison on dense reward setting did not involve DHRL and PIG due to the scope and limitations of their applicability. In the implementation, we did not use the learned dynamics model until we had sufficient transitions for sampling, which would avoid a catastrophic performance drop arising from inaccurate planning. It means that our method was enabled only if the step number of interactions was over a pre-set value. Here, the time step limit was set to for maze-related tasks and for robotic arm manipulation. After that, the dynamics model was trained at a frequency of steps. In the end, we evaluate their performance over 5 random seeds \chadded(the seed number is set from 0 to 5 for all tasks), conducting 10 test episodes every time step. All of the experiments were carried out on a computer with the configuration of Intel(R) Xeon(R) Gold 5220 CPU @ 2.20GHz, 8-core, 64 GB RAM. And each experiment was processed using a single GPU (Tesla V100 SXM2 32 GB). We provide more detailed experimental configurations in the "Supplementary Materials".
\chaddedSubgoals generated by different HRL algorithms
We visualize the subgoals generated by the high-level policies of different HRL algorithms. As depicted in Fig. 9, due to the introduction of adjacency constraints, HRAC[60], HIGL[23], ACLG, and ACLG+GCMR generated subgoals with better reachability (fewer outliers), compared to HIRO[38]. Moreover, HIGL[23], ACLG, and ACLG+GCMR displayed a preference for exploration, attributed to the use of landmark-based planning. However, the subgoals of HIGL exhibited a greater goal-reaching distance, farther from the current state. Conversely, ACLG and ACLG+GCMR achieved a better balance between reachability and planning. Fig. LABEL:sub@reachability_comp provides statistical evidence supporting these findings, with the goal-reaching distance quantified using the lower-level Q functions[19, 23, 24]. The results show that ACLG and ACLG+GCMR had smaller average goal-reaching distances.






Comparison results
As shown in Fig. 10, GCMR contributes to achieving better performance and shows resistance to performance degradation. By integrating the GCMR with ACLG, we find that the proposed method outperforms the prior SOTA methods in almost all tasks. Especially in complicated tasks requiring meticulous operation (e.g., Ant Maze-Bottleneck, Stochastic Ant Maze, and Large Ant Maze), our method steadily improved the policy without getting stuck in local optima. \chreplacedIn most tasksIn all Ant Maze tasks, as shown in Fig. LABEL:sub@maze_u, LABEL:sub@maze_u_stoch, LABEL:sub@maze_u_large, LABEL:sub@maze_w, LABEL:sub@maze_u_bot, \chdeletedand 10f, \chaddedLABEL:sub@pusher_comp, and LABEL:sub@fetch_pp_comp, our method achieved a faster asymptotic convergence rate than others. There was no catastrophic failure. \chreplacedOAlthough our method slightly trailed behind the PIG\chreplaced in the Reacher (see Fig. LABEL:sub@reacher_comp) and FetchPush (see Fig. LABEL:sub@fetch_push_comp) tasks and DHRL on Reacher (see Fig. 10g) and Pusher (see Fig. 10h) tasks, respectively, it still achieved the second-best performance. Moreover, in Fig. 8, we investigated the performance of the proposed method in the Dense-reward environment, i.e., Ant Maze (Dense, U-shape). The results demonstrate the GCMR is also effective and significantly improves the performance of ACLG. To verify whether GCMR can be solely applied to goal-reaching tasks, we conducted experiments in the Point Maze and Ant Maze (U-shape) tasks. From the experimental results depicted in Fig. 1 in the "Supplementary Materials", it can be observed that the GCMR can be used independently and achieve similar results to HIGL.



(U-shape)








Comparison to existing goal-relabeling
To justify the superiority of \chreplacedthe proposed \chaddedmodel-based off-policy correction the proposed goal-relabeling approachover the others. We compared it with various goal-relabeling technologies: (a) vanilla off-policy correction\chdeleted(OPC) in HIRO [38], (b) hindsight-based goal-relabeling in HAC [30], and (c) foresight goal inference\chdeleted(FGI) in MapGo [61], which is a model-based variant of vanilla hindsight-based goal-relabeling. \chaddedThe average success rate illustrated in Fig. 11 highlights the significance of (both HIRO-style and HAC-style) relabeling for enhancing data efficiency, leading to accelerated learning compared to the case not using relabeling. Moreover, Fig. 11 also illustrates that HIRO-style relabeling outperforms HAC-style ones. Among them, the proposed relabeling with the soft-relabeling exhibits a slight advantage over the vanilla off-policy correction. However, the final performance of the proposed relabeling method is sensitive to the value of the shift magnitude , as shown in Fig. 5. When soft-relabeling is not applied, the proposed relabeling exhibits inferior performance compared to the vanilla off-policy correction during the early stages of training. \chdeletedBefore making the comparison, we would like to first recognize the effectiveness of two tricks: the exponential weighting and soft-relabeling. [20] has been systematically explained that inaccuracies in learned models make long rollouts unreliable due to the compounding error. The gap between true returns and learned model returns cannot be eliminated, hence cumulative errors will be huge for too long rollouts. To address this, we employed an exponential weighting function along the horizontal axis to highlight shorter rollouts. Fig. LABEL:exp_weight illustrates the significance of the exponential weighting in suppressing cumulative errors. On the other hand, \chdeletedsoft relabeling was utilized to enhance the robustness of goal relabeling against outliers\chdeleted, ensuring that the relabelled subgoals remain in close proximity to the original ones. Fig. 11 provides insights into the impact of soft-relabeling on different goal-relabelling technologies. It can be observed that the soft-relabeling enhanced the robustness of different goal-relabelling technologies. \chdeletedIn the end, we investigated the impact of the model-based gradient penalty on different goal-relabelling technologies. As shown in Fig. 11, all goal-relabelling technologies had a faster asymptotic convergence rate under gradient penalty. The result highlights the role of the gradient penalty in enhancing robustness against high-level errors, such as an unreachable or faraway goal.

5.4 Ablation study
We also investigate the effectiveness of different crucial components in our method.
\chaddedIncreased Critic Training Iterations in Lower-level
In this section, we investigate the effectiveness of two crucial factors in our algorithm: the gradient penalty term and the one-step planning term. Considering that the number of lower-level critic training iterations was increased to alleviate the impact of the gradient penalty, we additionally provide a comprehensive analysis concerning the effects of increased iterations on various alternative methods. As depicted in Fig. 12, increasing the number of critic training iterations led to improved performance when compared to the original approach. Moreover, even without increasing the training iterations, ACLG+GCMR consistently outperformed other methods and overtook the ACLG with increased training iterations after several timesteps. The results demonstrate that the \chreplacedgradient penaltyGCMR can enhance the robustness of HRL frameworks and prevent falling into local pitfalls.

\chaddedAblation Study on Gradient Penalty term
In Fig. 13 and Fig. 14, we investigate the effectiveness of the gradient penalty term on enhancing the generalization of the low-level policy and the impact on the final performance, respectively. Fig. 13 LABEL:sub@weights_wo_mgp and LABEL:sub@weights_w_mgp depict the weight distribution of the final layer in the low-level actor over training steps (100K, 300K, and 500K). Intriguingly, we observe that in the constrained network with the gradient penalty, the weights fewer centred at zero compared to those in the unconstrained network. The uncertainty in the weights of the network has been evidenced to potentially enhance generalization performance[3]. Meanwhile, in Fig. LABEL:sub@state_q, the result of the value estimation indicates that even in unseen scenarios, similar state-action pairs still yield higher value estimations when applying the gradient penalty, thereby demonstrating robust generalization. Here, we shift the state distribution to simulate the unseen scenarios. Moreover, the learning curves in Fig. 14 demonstrate that the application of gradient penalty contributes to achieving better asymptotic performance compared to not using it.





\chaddedAblation Study on One-Step Rollout-based Planning term
In Fig. 16 and Fig. 15, we clarify the role of the one-step rollout-based planning term and highlight its importance. As anticipated, in Fig. 16, under the guidance of the one-step rollout-based planning, the agent consistently discovers smoother trajectories towards the final goal. These paths swiftly traverse the contours of higher-level Q-value, ultimately advancing towards positions of the highest higher-level Q-value. Comparing the first and second rows of Fig. 16, we can observe that this effect is more pronounced in the Point Maze because its maximum distance within a single step exceeds that in the Ant Maze (U-shape). Also, in Fig. 15, we observe that applying the one-step rollout-based planning term can significantly enhance the final performance across various control tasks, demonstrating the effectiveness of the introduced planning term.








6 Discussion
6.1 \chaddedAccelerating reinforcement learning from the perspective of inter-level cooperation, with emphasis on the lower level.
In prior works, there has been a strong emphasis on optimizing the higher-level policy, as global planning is determined by the higher-level policy. The lower-level policy is overlooked, merely seen as an "unintelligent" subordinate to the higher level. Yet, in fact, the behavior of lower-level policy significantly influences the effectiveness of exploration and the stability of the hierarchical system because the lower-level policy interacts directly with the environment. Reinforcing the robustness of the lower-level policy can prevent catastrophic failures, such as collisions or tipping over, thereby accelerating reinforcement learning. This study reemphasizes the importance of the lower-level policy from the perspective of inter-level cooperation, drawing attention to related research on optimizing lower-level policies.
6.2 \chaddedEffectiveness of the gradient penalty and one-step rollout-based planning is significant, while model-based relabeling is weak.
For facilitating inter-level cooperation and communication, we propose a novel goal-conditioned HRL framework, which mainly consists of three crucial components: the model-based off-policy correction for the data efficiency, the gradient penalty on the lower-level policy for the robustness, and one-step rollout-based planning for the cooperation. The experimental results indicate that the gradient penalty and one-step rollout-based planning achieved the expected effects, significantly enhancing the performance of the HRL framework. However, the model-based off-policy correction did not yield significant effects. The reason might be that these predicted states in correction could potentially suffer from compounding errors in long-horizon rollouts. Although soft-relabeling can mitigate this error, it is unstable due to the introduction of sensitive hyper-parameter (see Fig. 5).
6.3 \chaddedLimitations and future research
This study has certain limitations. First, our experiments show that the GCMR achieved significant performance improvement, and such improvement came at the expense of more computational cost (see Table 4 in the "Supplementary Materials" for a quantitative analysis of computational cost). However, the time-consuming issue only occurs during the training stage and will not affect the execution response time in the applications. Second, we need to clarify that the scope of applicability is off-policy goal-conditioned HRL. The effectiveness in general RL tasks or online tasks \chreplacedstill needs to be validated in future workhad not been validated. Third, the experimental environments used in this study have 7 or 30 dimensions. Our network architecture of transition dynamics models is relatively simple, leading to limited regression capability. Applications in complex environments that closely resemble real-world scenarios with high-dimensional observation, like the large-scale point cloud environments encountered in autonomous driving, might face limitations. This issue will be investigated in our future work. \chaddedBesides, related research on cooperative multi-robot HRL has successfully coped with extremely complex environments by enabling multiple robots to learn through the collective exchange of environmental data[45, 13, 46]. Integrating the proposed algorithm into multi-robot HRL systems is expected to enhance the performance in complex environments further, and this will be investigated in future work. Finally, we can observe that the effect of one-step rollout-based planning is more pronounced in an environment with a higher maximum distance within a single step. This observation inspires us to delve into multi-step rollout-based planning in the future to broaden its application.
7 Conclusion
This study proposes a new goal-conditioned HRL framework with Guided Cooperation via Model-based Rollout (GCMR), which uses the learned dynamics as a bridge for inter-level cooperation. Experimentally we instantiated several cooperation and communication mechanisms to improve the stability of hierarchy, achieving both data efficiency and learning efficiency. To our knowledge, very few prior works have discussed the model exploitation problem in goal-conditioned HRL. This research not only provides a SOTA HRL algorithm but also demonstrates the potential of integrating the learned dynamics model into goal-conditioned HRL, which is expected to draw the attention of researchers to such a direction.
References
- Andrychowicz et al. [2017] Marcin Andrychowicz, Filip Wolski, Alex Ray, Jonas Schneider, Rachel Fong, Peter Welinder, Bob McGrew, Josh Tobin, Abbeel Pieter, and Wojciech Zaremba. Hindsight experience replay. In Proc. Adv. Neural Inf. Process. Syst., volume 30, pages 5049–5059, 2017.
- Blondé et al. [2022] Lionel Blondé, Pablo Strasser, and Alexandros Kalousis. Lipschitzness is all you need to tame off-policy generative adversarial imitation learning. Mach. Learn., 111(4):1431–1521, 2022.
- Blundell et al. [2015] Charles Blundell, Julien Cornebise, Koray Kavukcuoglu, and Daan Wierstra. Weight uncertainty in neural network. In Proc. 32th Int. Conf. Mach. Learn., volume 2, pages 1613–1622, 2015.
- Buckman et al. [2018] Jacob Buckman, Danijar Hafner, George Tucker, Eugene Brevdo, and Honglak Lee. Sample-efficient reinforcement learning with stochastic ensemble value expansion. In Proc. Adv. Neural Inf. Process. Syst., volume 31, pages 8224–8234, 2018.
- Burda et al. [2019] Yuri Burda, Harrison Edwards, Amos Storkey, and Oleg Klimov. Exploration by random network distillation. In Proc. Int. Conf. Learn. Represent., pages 1–17, 2019.
- Byravan et al. [2020] Arunkumar Byravan, Jost Tobias Springenberg, Abbas Abdolmaleki, Roland Hafner, Michael Neunert, Thomas Lampe, Noah Siegel, Nicolas Heess, and Martin Riedmiller. Imagined value gradients: Model-based policy optimization with tranferable latent dynamics models. In Proc. Mach. Learn. Res., pages 566–589, 2020.
- Chua et al. [2018] Kurtland Chua, Roberto Calandra, Rowan McAllister, and Sergey Levine. Deep reinforcement learning in a handful of trials using probabilistic dynamics models. Proc. Adv. Neural Inf. Process. Syst., 31:4754–4765, 2018.
- Emmons et al. [2020] Scott Emmons, Ajay Jain, Misha Laskin, Thanard Kurutach, Pieter Abbeel, and Deepak Pathak. Sparse graphical memory for robust planning. Proc. Adv. Neural Inf. Process. Syst., 33:5251–5262, 2020.
- Eysenbach et al. [2019] Ben Eysenbach, Russ R Salakhutdinov, and Sergey Levine. Search on the replay buffer: Bridging planning and reinforcement learning. In Proc. Adv. Neural Inf. Process. Syst., volume 32, pages 15246–15267, 2019.
- Feinberg et al. [2018] Vladimir Feinberg, Alvin Wan, Ion Stoica, Michael I Jordan, Joseph E Gonzalez, and Sergey Levine. Model-based value expansion for efficient model-free reinforcement learning. In Proc. 35th Int. Conf. Mach. Learn., 2018.
- Florensa et al. [2017] Carlos Florensa, Yan Duan, and Pieter Abbeel. Stochastic neural networks for hierarchical reinforcement learning. In Proc. Int. Conf. Learn. Represent., 2017.
- Fujimoto et al. [2018] Scott Fujimoto, Herke Hoof, and David Meger. Addressing function approximation error in actor-critic methods. In Proc. 35th Int. Conf. Mach. Learn., pages 1587–1596, 2018.
- G. E. Setyawan, P. Hartono, and H. Sawada [2022] G. E. Setyawan, P. Hartono, and H. Sawada. An in-depth analysis of cooperative multi-robot hierarchical reinforcement learning. In ACM Int. Conf. Proc. Ser., pages 119–126, 2022.
- G. Kahn, P. Abbeel, and S. Levine [2021] G. Kahn, P. Abbeel, and S. Levine. Land: Learning to navigate from disengagements. IEEE Robot. Autom. Lett., 6(2):1872–1879, 2021.
- Gao et al. [2022] Chengqian Gao, Ke Xu, Liu Liu, Deheng Ye, Peilin Zhao, and Zhiqiang Xu. Robust offline reinforcement learning with gradient penalty and constraint relaxation. CoRR, abs/2210.10469, 2022. doi: 10.48550/arXiv.2210.10469. URL https://doi.org/10.48550/arXiv.2210.10469.
- Gao et al. [2023] Haichuan Gao, Zhile Yang, Tian Tan, Tianren Zhang, Jinsheng Ren, Pengfei Sun, Shangqi Guo, and Feng Chen. Partial consistency for stabilizing undiscounted reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst., 34(12):10359–10373, 2023.
- Gulrajani et al. [2017] Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron C Courville. Improved training of wasserstein gans. In Proc. Adv. Neural Inf. Process. Syst., volume 30, pages 5768–5778, 2017.
- Guo et al. [2021] Shangqi Guo, Qi Yan, Xin Su, Xiaolin Hu, and Feng Chen. State-temporal compression in reinforcement learning with the reward-restricted geodesic metric. IEEE Trans. Pattern Anal. Mach. Intell., 44(9):5572–5589, 2021.
- Huang et al. [2019] Zhiao Huang, Fangchen Liu, and Hao Su. Mapping state space using landmarks for universal goal reaching. In Proc. Adv. Neural Inf. Process. Syst., volume 32, pages 1942–1952, 2019.
- Janner et al. [2019] Michael Janner, Justin Fu, Marvin Zhang, and Sergey Levine. When to trust your model: Model-based policy optimization. Proc. Adv. Neural Inf. Process. Syst., 32, 2019.
- Kahn et al. [2021] Gregory Kahn, Pieter Abbeel, and Sergey Levine. Badgr: An autonomous self-supervised learning-based navigation system. IEEE Robot. Autom. Lett., 6(2):1312–1319, 2021.
- Kim et al. [2024] Dongyoung Kim, Jinwoo Shin, Pieter Abbeel, and Younggyo Seo. Accelerating reinforcement learning with value-conditional state entropy exploration. In Proc. Adv. Neural Inf. Process. Syst., volume 36, 2024.
- Kim et al. [2021] Junsu Kim, Younggyo Seo, and Jinwoo Shin. Landmark-guided subgoal generation in hierarchical reinforcement learning. Proc. Adv. Neural Inf. Process. Syst., 34:28336–28349, 2021.
- Kim et al. [2023] Junsu Kim, Younggyo Seo, Sungsoo Ahn, Kyunghwan Son, and Jinwoo Shin. Imitating graph-based planning with goal-conditioned policies. In Proc. Int. Conf. Learn. Represent., 2023.
- Kumar et al. [2019] Aviral Kumar, Justin Fu, Matthew Soh, George Tucker, and Sergey Levine. Stabilizing off-policy q-learning via bootstrapping error reduction. In Proc. Adv. Neural Inf. Process. Syst., volume 32, 2019.
- Kurutach et al. [2018] Thanard Kurutach, Ignasi Clavera, Yan Duan, Aviv Tamar, and Pieter Abbeel. Model-ensemble trust-region policy optimization. In Proc. Int. Conf. Learn. Represent., 2018.
- Lee et al. [2020] Kimin Lee, Younggyo Seo, Seunghyun Lee, Honglak Lee, and Jinwoo Shin. Context-aware dynamics model for generalization in model-based reinforcement learning. In Proc. 37th Int. Conf. Mach. Learn., pages 5713–5722, 2020.
- Lee et al. [2022] Seungjae Lee, Jigang Kim, Inkyu Jang, and H Jin Kim. Dhrl: A graph-based approach for long-horizon and sparse hierarchical reinforcement learning. In Proc. Adv. Neural Inf. Process. Syst., 2022.
- Levine and Koltun [2013] Sergey Levine and Vladlen Koltun. Guided policy search. In Proc. 30th Int. Conf. Mach. Learn., pages 1–9, 2013.
- Levy et al. [2019] Andrew Levy, George Konidaris, Robert Platt, and Kate Saenko. Learning multi-level hierarchies with hindsight. In Proc. Int. Conf. Learn. Represent., pages 1–15, 2019.
- Li et al. [2021] Siyuan Li, Lulu Zheng, Jianhao Wang, and Chongjie Zhang. Learning subgoal representations with slow dynamics. In Proc. Int. Conf. Learn. Represent., pages 1–18, 2021.
- Lillicrap et al. [2016] Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. In Proc. Int. Conf. Learn. Represent., 2016.
- Liu et al. [2020] Kara Liu, Thanard Kurutach, Christine Tung, Pieter Abbeel, and Aviv Tamar. Hallucinative topological memory for zero-shot visual planning. In Proc. 37th Int. Conf. Mach. Learn., pages 6215–6226, 2020.
- Luo et al. [2024] Fan-Ming Luo, Tian Xu, Hang Lai, Xiong-Hui Chen, Weinan Zhang, and Yang Yu. A survey on model-based reinforcement learning. Sci. China Inf. Sci., 67(2), 2024.
- Luo et al. [2019] Yuping Luo, Huazhe Xu, Yuanzhi Li, Yuandong Tian, Trevor Darrell, and Tengyu Ma. Algorithmic framework for model-based deep reinforcement learning with theoretical guarantees. In Proc. Int. Conf. Learn. Represent., 2019.
- Moerland et al. [2023] Thomas M Moerland, Joost Broekens, Aske Plaat, Catholijn M Jonker, et al. Model-based reinforcement learning: A survey. Found. Trends Mach. Learn., 16(1):1–118, 2023.
- Mordatch et al. [2016] Igor Mordatch, Nikhil Mishra, Clemens Eppner, and Pieter Abbeel. Combining model-based policy search with online model learning for control of physical humanoids. In Proc. IEEE Int. Conf. Robot. Autom., pages 242–248, 2016.
- Nachum et al. [2018] Ofir Nachum, Shixiang Shane Gu, Honglak Lee, and Sergey Levine. Data-efficient hierarchical reinforcement learning. In Proc. Adv. Neural Inf. Process. Syst., volume 31, pages 3303–3313, 2018.
- Nachum et al. [2019] Ofir Nachum, Shixiang Gu, Honglak Lee, and Sergey Levine. Near-optimal representation learning for hierarchical reinforcement learning. In Proc. Int. Conf. Learn. Represent., 2019.
- Nair and Finn [2020] Suraj Nair and Chelsea Finn. Hierarchical foresight: Self-supervised learning of long-horizon tasks via visual subgoal generation. In Proc. Int. Conf. Learn. Represent., 2020.
- Ramachandran et al. [2018] Prajit Ramachandran, Barret Zoph, and Quoc V. Le. Searching for activation functions. In International Conference on Learning Representations, 2018. URL https://openreview.net/forum?id=SkBYYyZRZ.
- Ren et al. [2021] Jinsheng Ren, Shangqi Guo, and Feng Chen. Orientation-preserving rewards’ balancing in reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst., 33(11):6458–6472, 2021.
- Savinov et al. [2018] Nikolay Savinov, Alexey Dosovitskiy, and Vladlen Koltun. Semi-parametric topological memory for navigation. In Proc. Int. Conf. Learn. Represent., 2018.
- Seo et al. [2020] Younggyo Seo, Kimin Lee, Ignasi Clavera Gilaberte, Thanard Kurutach, Jinwoo Shin, and Pieter Abbeel. Trajectory-wise multiple choice learning for dynamics generalization in reinforcement learning. In Proc. Adv. Neural Inf. Process. Syst., volume 33, pages 12968–12979, 2020.
- Setyawan et al. [2022a] Gembong Edhi Setyawan, Pitoyo Hartono, and Hideyuki Sawada. Cooperative multi-robot hierarchical reinforcement learning. Int. J. Adv. Comput. Sci. Appl., 13:35–44, 2022a.
- Setyawan et al. [2022b] Gembong Edhi Setyawan, Hideyuki Sawada, and Pitoyo Hartono. Combinations of micro-macro states and subgoals discovery in hierarchical reinforcement learning for path finding. Int. J. Innov. Comput. Inf. Control, 18(2):447–462, 2022b.
- Shen et al. [2020] Jian Shen, Han Zhao, Weinan Zhang, and Yong Yu. Model-based policy optimization with unsupervised model adaptation. Proc. Adv. Neural Inf. Process. Syst., 33:2823–2834, 2020.
- Simsek et al. [2005] Ozgür Simsek, Alicia P Wolfe, and Andrew G Barto. Identifying useful subgoals in reinforcement learning by local graph partitioning. In Proc. 22th Int. Conf. Mach. Learn., pages 817–824, 2005.
- Sutton [1991] Richard S Sutton. Dyna, an integrated architecture for learning, planning, and reacting. ACM Sigart Bulletin, 2(4):160–163, 1991.
- T. Zhang, S. Guo, T. Tan, X. Hu, and F. Chen [2022] T. Zhang, S. Guo, T. Tan, X. Hu, and F. Chen. Adjacency constraint for efficient hierarchical reinforcement learning. IEEE Trans. Pattern Anal. Mach. Intell., 45(4):4152–4166, 2022.
- Vezhnevets et al. [2017] Alexander Sasha Vezhnevets, Simon Osindero, Tom Schaul, Nicolas Heess, Max Jaderberg, David Silver, and Koray Kavukcuoglu. Feudal networks for hierarchical reinforcement learning. In Proc. 34th Int. Conf. Mach. Learn., pages 3540–3549, 2017.
- Xie et al. [2016] Chris Xie, Sachin Patil, Teodor Moldovan, Sergey Levine, and Pieter Abbeel. Model-based reinforcement learning with parametrized physical models and optimism-driven exploration. In Proc. IEEE Int. Conf. Robot. Autom., pages 504–511. IEEE, 2016.
- Yang et al. [2020] Ge Yang, Amy Zhang, Ari Morcos, Joelle Pineau, Pieter Abbeel, and Roberto Calandra. Plan2vec: Unsupervised representation learning by latent plans. In Proc. Mach. Learn. Res., pages 935–946, 2020.
- Yang et al. [2022] Xintong Yang, Ze Ji, Jing Wu, Yu-Kun Lai, Changyun Wei, Guoliang Liu, and Rossitza Setchi. Hierarchical reinforcement learning with universal policies for multistep robotic manipulation. IEEE Trans. Neural Netw. Learn. Syst., 33(9):4727–4741, 2022.
- Yu et al. [2020] Tianhe Yu, Garrett Thomas, Lantao Yu, Stefano Ermon, James Y Zou, Sergey Levine, Chelsea Finn, and Tengyu Ma. Mopo: Model-based offline policy optimization. In Proc. Adv. Neural Inf. Process. Syst., volume 33, pages 14129–14142, 2020.
- Yu et al. [2021] Tianhe Yu, Aviral Kumar, Rafael Rafailov, Aravind Rajeswaran, Sergey Levine, and Chelsea Finn. Combo: Conservative offline model-based policy optimization. In Proc. Adv. Neural Inf. Process. Syst., volume 34, pages 28954–28967, 2021.
- Zeng et al. [2023] Hongliang Zeng, Ping Zhang, Fang Li, Chubin Lin, and Junkang Zhou. Ahegc: Adaptive hindsight experience replay with goal-amended curiosity module for robot control. IEEE Trans. Neural Netw. Learn. Syst., pages 1–14, 2023.
- Zhang et al. [2021] Lunjun Zhang, Ge Yang, and Bradly C Stadie. World model as a graph: Learning latent landmarks for planning. In Proc. 38th Int. Conf. Mach. Learn., pages 12611–12620, 2021.
- Zhang et al. [2016] Tianhao Zhang, Gregory Kahn, Sergey Levine, and Pieter Abbeel. Learning deep control policies for autonomous aerial vehicles with mpc-guided policy search. In Proc. IEEE Int. Conf. Robot. Autom., pages 528–535, 2016.
- Zhang et al. [2020] Tianren Zhang, Shangqi Guo, Tian Tan, Xiaolin Hu, and Feng Chen. Generating adjacency-constrained subgoals in hierarchical reinforcement learning. In Proc. Adv. Neural Inf. Process. Syst., volume 33, pages 21579–21590, 2020.
- Zhu et al. [2021] Menghui Zhu, Minghuan Liu, Jian Shen, Zhicheng Zhang, Sheng Chen, Weinan Zhang, Deheng Ye, Yong Yu, Qiang Fu, and Wei Yang. Mapgo: Model-assisted policy optimization for goal-oriented tasks. In Proc. Int. Joint Conf. Artif. Intell., pages 3484–3491, 2021.
Appendix A Lipschitz Property of the Q-function w.r.t. action
In this appendix, we provide a brief proof for Proposition 1. More detailed proof can be found in \chreplaced[2, 15][15]. We start out with a lemma that helps with subsequent derivation.
Lemma 1.
Assume policy gradients w.r.t. input actions in an MDP admit a bound at any time : . Then the following holds for any non-negative integer and :
| (21) | ||||
Proof.
| (22) | ||||
∎
Remark 2.
Lemma 21 gives the discrepancy of reward gradients starting from adjacent states. We can apply this lemma sequentially and infer the upper bound of reward gradients:
| (23) | ||||
Proposition 2.
Let and be the policy and the reward function in an MDP. Suppose there are the upper bounds of Frobenius norm of the policy and reward gradients w.r.t. input actions, i.e., and . Then the gradient of the learned Q-function w.r.t. action can be upper-bounded as:
| (24) |
Where denotes the dimension of the action and is the discount factor.
Appendix B Algorithm table
We provide the pseudo code below for this algorithm. Python-based implementation is available at https://github.com/HaoranWang-TJ/GCMR_ACLG_official.
-
•
Key hyper-parameters: the number of candidate goals , gradient penalty loss coefficient , one-step planning term coefficient, soft update rate of the shift magnitude within relabeling .
-
•
General hyper-parameters: the subgoal scheme (set to 0/1 for the relative/absolute scheme), training batch number , higher-level update frequency , learning frequency of dynamics models , initial steps without using dynamics models , usage frequencies of gradient penalty and planning term , .
Appendix C Environment Details
Most experiments were conducted under the same environments as that in [23], including Point Maze, Ant Maze (W-shape), Ant Maze (U-shape), Pusher, and Reacher. Further detail is available in public repositories 111Our code is available at https://github.com/HaoranWang-TJ/GCMR_ACLG_official 222https://github.com/junsu-kim97/HIGL.git. Besides, we introduced a more challenging locomotion environment, i.e., Ant Maze-Bottleneck, to validate the stability and robustness of the proposed GCMR in long-horizon and complicated tasks requiring delicate controls.
Ant Maze-Bottleneck
The Ant Maze-Bottleneck environment was first introduced in [28], which provided implementation details in public repositories in 1 333https://github.com/jayLEE0301/dhrl_official.git. In this study, we resized it to be the same as the other mazes. Specifically, the size of the environment is . At training time, a goal point was selected randomly from a two-dimensional planar where both - and -axes range from -2 to 10. At evaluation time, the goal was placed at (0, 8) (i.e., the top left corner). A minimum threshold of competence was set to an L2 distance of 2.5 from the goal. Each episode would be terminated after 600 steps.
Appendix D Experimental Configurations
D.1 Network Structure
For a fair comparison, we adopted the same architecture as [60, 23]. In detail, all actor and critic networks had two hidden layers composed of a fully connected layer with 300 units and a ReLU nonlinearity function. The output layer in actor networks had the same number of cells as the dimension of the action space and normalized the output to using the function. After that, the output was rescaled to the range of action space.
For the dynamics model, the ensemble size was set to 5, a recommended value in [7]. Each of the ensembles was instantiated with three layers, similar to the above actor network. Yet, each hidden layer had 256 units and was followed by the Swish activation [41]. Note that units of the output layer were twice as much as the actor because the action distribution was represented with the mean and covariance of a Gaussian.
The Adam optimizer was utilized for all networks.
D.2 Hyper-Parameter Settings
In Table 1, we list common hyper-parameters used across all environments. Hyper-parameters that differ across the environments are presented in Table 2. These hyper-parameters involving HIGL remained the same as proposed by [23]. Besides, the update speed of the shift magnitude of goals was set at 0.01.
| Hyper-parameters | Value | |
| Higher-level | Lower-level | |
| Actor learning rate | 0.0001 | 0.0001 |
| Critic learning rate | 0.001 | 0.001 |
| Soft update rate | 0.005 | 0.005 |
| 0.99 | 0.95 | |
| Reward scaling | 0.1 | 1.0 |
| Training frequency | 10 | 1 |
| Batch size | 128 | 128 |
| Candidates’ number | 10 | |
| 1.0 | ||
| Shift Magnitude | 2030a | |
| 1.010b | ||
| 0.0005 0.00005c | ||
| usage frequencies | 5 | |
| usage frequencies | 10 | |
| Dynamics model | ||
| Ensemble number | 5 | |
| Learning rate | 0.005 | |
| Batch size | 256 | |
| Training epochs | 20 50 | |
-
a
is set to 20 for small mazes, such as Ant Maze (U-shape, W-shape), and 30 for larger mazes, such as the Large Ant Maze (U-shape).
-
b
Only for the Ant Maze-Bottleneck, while are set to 1.0 for others.
-
c
Only for the FetchPush and FetchPickAndPlace, while are set to 0.0005 for others.
| Hyper-parameters | Maze-baseda | Arm-basedb |
| Higher-level | ||
| High-level action frequency | 10 | 5 |
| Exploration strategy | Gaussian () | Gaussian () |
| Lower-level | ||
| Exploration strategy | Gaussian () | Gaussian () |
| 20.0 | 0 | |
| Dynamics model | ||
| Training frequency | 2000 | 500 |
| Initial steps w/o model | 20000 | 10000 |
-
a
Maze-based environments include the Point Maze, Ant Maze (U/W-shape), and Ant Maze-Bottleneck.
-
b
Arm-based environments are the Pusher, Reacher, FetchPush, and FetchPickAndPlace.
| Environments | GCMRACLG* | ACLG* | HIGL* | DHRL | PIG |
| Ant Maze (U-shape) | 6060 | 2020 | 300 | 400 | |
| Ant Maze (W-shape) | 6060 | 6060 | 300 | 400 | |
| Point Maze | 6060 | 2020 | 300 | 200 | |
| Pusher and Reacher | 2020 | 2020 | 300 | 80 | |
| FetchPush and FetchPickAndPlace | 6060 | 2020 | 300 | 80 | |
-
*
Where connects the numbers of coverage-based landmarks and novelty-based landmarks.
Appendix E Additional Experiments
E.1 GCMR Solely Employed for Goal-Reaching Tasks
In our experiments, the proposed GCMR was used as an additional plugin. Of course, GCMR can be solely applicable to goal-reaching tasks. We conducted experiments in the Point Maze and Ant Maze (U-shape) tasks. As shown in Figure 17, the results indicate that GCMR can be used independently and achieve similar results to HIGL. Meanwhile, in Figure 18, we investigate how the gradient penalty term and the one-step planning term impact the final performance when solely using the GCMR method in Ant Maze (U-shape). Figure 18 illustrates similar conclusions as those of Figure 2 in the "Main Paper".





E.2 Quantification of Extra Computational Cost
The extra computational cost is primarily composed of three aspects:
-
•
(1) dynamic model training,
-
•
(2) model-based gradient penalty and one-step rollout planning in low-level policy training,
-
•
(3) goal-relabeling in high-level policy training.
Therefore, we ran both methods ACLG+GCMR and ACLG on Ant Maze (U-shape) for steps to compare their runtime in these aspects.
| Training time (s) | Total | Dynamic model | Low-level policy | High-level policy |
| ACLG+GCMR | 5065.18 | 16.51 | 3603.01 | 854.64 |
| ACLG | 1845.63 | 0 | 632.97 | 614.01 |
