Guesswork of a quantum ensemble
Abstract
The guesswork of a quantum ensemble quantifies the minimum number of guesses needed in average to correctly guess the state of the ensemble, when only one state can be queried at a time. Here, we derive analytical solutions of the guesswork problem subject to a finite set of conditions, including the analytical solution for any qubit ensemble with uniform probability distribution. As explicit examples, we compute the guesswork for any qubit regular polygonal and polyhedral ensemble.
I Introduction
We consider a communication scenario involving two parties, Alice and Bob. An ensemble of quantum states with labels in a set is given and known to both parties. At each round, Alice picks a label with probability and hands state over to Bob. Bob aims at correctly guessing label being allowed to query one element of at a time, until his query is correct, at which point the round is over. The cost function incurred by Bob is the average number of guesses, or guesswork, until he correctly guesses . Bob’s most general strategy consists of performing a quantum measurement outputing an element from the set of numberings of and querying the elements of in the order specified by . Hence, the guesswork is given by the occurence of label in numbering , averaged over all numberings. Using the formalism [1] of quantum circuits, the setup is as follows:
| (3) |
The guesswork has been extensively studied for classical ensembles [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12], but only very recently tackled for quantum ensembles [13, 14, 15]. While previous works focused on the derivation of entropic bounds, our aim is instead the derivation of analytical solutions. Our main result, Theorem 1, provides an analytical solution subject to a finite set of conditions. In particular, Corollary 1 provides the analytical solution for any qubit ensemble with uniform probability distribution, thus disproving the conjecture [13] that analytical solutions exist only for binary and symmetric ensembles. As explicit examples, in Corollaries 2 and 3 we explicitly compute the minimum guesswork of any qubit regular polygonal and polyhedral ensebles, respectively. This proves a conjecture [14] on the guesswork of the square qubit ensemble.
II Formalization
In this section we define the guesswork problem. We use standard results from quantum information theory [1].
First, we introduce the sets of ensembles and numbering-valued measurements that appear in the setup of Eq. (3). For any finite dimensional Hilbert space , we denote with the cone of positive semi-definite operators on . For any finite set , we denote with the set of numberings given by
We denote with the set of ensembles given by
and with the set of numbering-valued measurements given by
Next, we introduce the probability distributions that describe the setup in Eq. (3). For any ensemble and any numbering-valued measurement , we denote with the joint probability distribution that the outcome of is numbering and that the -th guess is correct, that is . In formula:
for any and any . We denote with the probability distribution that the -th guess is correct, obtained marginalizing the joint probability distribution . In formula:
for any and any .
Finally, we are in a position to introduce the guesswork. The guesswork is a function mapping any pair of ensemble and numbering-valued measurement into the expectation value of the number of guesses, averaged with the probability distribution of correctness of the -th guess. In formula:
The minimum guesswork is a function mapping any ensemble into the minimum over numbering-valued measurements of the guesswork . In formula:
III Main results
In this section we derive the analytical solution of the guesswork problem subject to a finite set of conditions, including any qubit ensemble with uniform probability distribution.
In order to state our main result, we need the following definitions. For any finite dimensional Hilbert space , we denote with the space of Hermitian operators on . For any finite set and any ensemble , we denote with the map given by
for any . For any numbering , we denote with the reversed numbering. In formula:
for any . We denote with and the projectors on the negative and null parts of , respectively. We denote with the family of numbering-valued measurements given by
for any . It follows from Lemma 1 that the corresponding guesswork is given by
| (4) |
for any .
Upon denoting with the absolute value of operator , the following theorem provides analytical solutions of the minimum guesswork problem subject to a finite set of conditions.
Theorem 1.
For any finite set , any finite dimensional Hilbert space , and any ensemble , if there exists numbering such that
| (5) |
for any , then numbering-valued measurement minimizes the guesswork, that is
We remark that, while the minimum guesswork problem is by definition an optimization over a continuous set, the conditions given by Eq. (5) are finite in number and hence can be checked by exhaustive search. If they hold, Eq. (4) provides the analytical solution of the minimum guesswork problem.
Proof.
The following corollary provides the analytical solution of the minimum guesswork problem for any qubit ensemble with uniform probability distribution.
Corollary 1.
For any finite set , any two dimensional Hilbert space , and any ensemble such that the prior probability distribution is uniform, there exists numbering such that measurement minimizes the guesswork, that is
We remark that Corollary 1 recasts the minimum guesswork problem, by definition an optimization problem over a continuous set, as an optimization problem over a finite set, that can be therefore performed by exhaustive search.
Proof.
Since by hypothesis , one has
for any . Hence, since by hypothesis is two-dimensional, one has
for any . Hence, the range is totally ordered. Hence, there exists such that
for any . Hence the statement follows from Theorem 1. ∎
IV Explicit Examples
In this section we provide the minimum guesswork of any qubit regular polygonal or polyhedral ensemble by explicitly solving the optimization over a finite set given by Corollary 1.
Corollary 2 (Regular polygonal ensembles).
For any discrete set , any two-dimensional Hilbert space , and any bijective ensemble whose range is proportional to a regular polygon in the Bloch circle, one has
Proof.
Due to Corollary 1, there exists numbering such that . Due to Lemma 4, is not increasing. One way of representing is as follows. Without loss of generality take and , where . Then one has
Numbering is illustrated in Fig. 1 for . By summing finite trigonometric series, for even one has
and for odd one has
By explicit computation one has
Hence the statement follows from Eq. (4). ∎
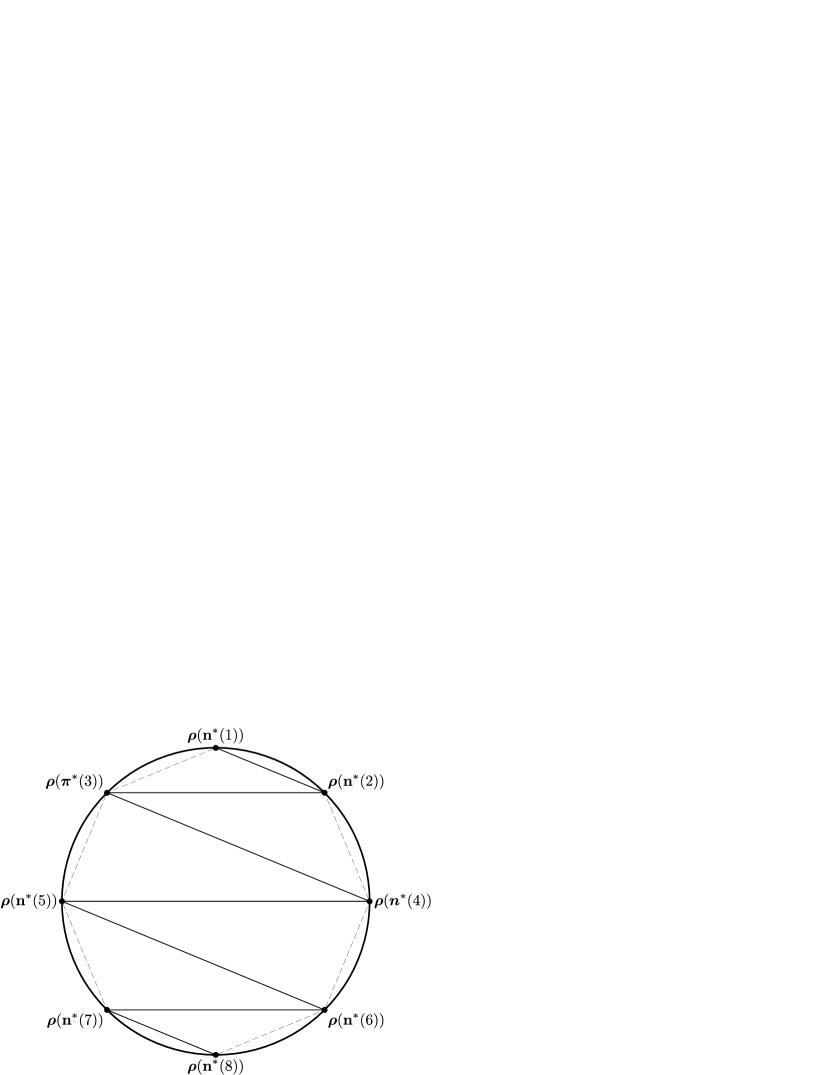
Corollary 3 (Regular polyhedral ensembles).
For any discrete set , any two-dimensional Hilbert space , and any bijective ensemble whose range is proportional to a regular polyhedron in the Bloch sphere, one has
Proof.
Due to Corollary 1, there exists numbering such that . For any is such that , hence the result for follows. Let us consider the case . Due to Lemma 4, is not increasing. Since the range is centrally symmetric, that is
any with not increasing satisfies
Since fixing the value of also fixes the value of , numbering can be found in steps. Also, since regular polyhedra are vertex transitive, the choice of is irrelevant, hence can be found in steps. The exhaustive search is practical even for the dodecahedron for which and hence . Numbering is illustrated in Fig. 2 for . Hence the results for follow. Further details can be found in Ref. [15], where algorithms for the classical computation of the quantum guesswork in analytical closed form based on the present results are provided and analyzed. ∎

Appendix
In this appendix we derive technical results needed for the derivation of our main results.
Lemma 1.
For any finite set , any finite dimensional Hilbert space , any ensemble , and any numbering-valued measurement , the guesswork is given by
Proof.
By definition of map one has , where
Using the identity one has
Hence the statement follows. ∎
For any finite dimensional Hilbert space and any operator , let be a dephasing map given by , where is a complete set of eigenvectors of .
Lemma 2.
For any finite dimensional Hilbert space and any , if one has that .
Proof.
Since is linear, positive, and unital, by the hypothesis it follows that . Since , the statement follows. ∎
Lemma 3.
For any finite dimensional Hilbert space and any , if one has that .
Proof.
Since is linear and positive and , by the hypothesis it follows that . Since and by the hypothesis it follows that , one has . Since is trace preserving, by tracing both sides the statement follows. ∎
The following lemma provides a necessary condition for any measurement to attain the minimum guesswork.
Lemma 4.
For any discrete set , any finite dimensional Hilbert space , and any ensemble , a measurement minimizes the guesswork, that is , only if is not increasing for any .
Proof.
We show that for any measurement there exists a measurement such that is not increasing for any and , with equality if and only if for any . Let be a family of permutations such that is not increasing for any . Let be given by
for any . Let be the coarse graining of given by
for any , where denotes the counter-image of with respect to . By explicit computation one has
for any . Hence by construction
for any , with equality if and only if for any . Hence the statement follows by definition of guesswork. ∎
V Conclusion
The guesswork of a quantum ensemble quantifies the minimum number of guesses needed in average to correctly guess the state of the ensemble, when only one state can be queried at a time. Here, we derived analytical solutions subject to a finite set of conditions, including analytical solutions for any qubit ensemble with uniform probability distribution, thus disproving the conjecture [13] that analytical solutions only exist for binary and symmetric ensembles. As explicit examples, we computed the guesswork for any qubit regular polygonal and polyhedral ensemble, thus proving a conjecture [14] on the guesswork of the square qubit ensemble.
VI Acknowledgments
M. D. is grateful to Eric Hanson and Nilanjana Datta for insightful discussions during a visit to the University of Cambridge. M. D. acknowledges support from MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) Grant No. JPMXS0118067285, JSPS KAKENHI Grant Number JP20K03774, and the International Research Unit of Quantum Information, Kyoto University. F. B. acknowledges support from MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) Grant No. JPMXS0120319794; from MEXT-JSPS Grant-in-Aid for Transformative Research Areas (A) “Extreme Universe”, No. 21H05183; from JSPS KAKENHI Grants No. 19H04066 and 20K03746. T. K. acknowledges support from MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) Grant No. JPMXS0118067285 and No. JPMXS0120319794 and JSPS KAKENHI Grant Number 16H01705, 17H01695, 19K22849 and 21H04879.
References
- [1] M. M. Wilde, Quantum Information Theory, (Cambridge University Press, 2017).
- [2] J. Massey, Guessing and entropy, Proceedings of 1994 IEEE International Symposium on Information Theory, 204 (1994).
- [3] E. Arikan, An inequality on guessing and its application to sequential decoding, IEEE Trans. Inform. Theory 42, 99 (1996).
- [4] E. Arikan and N. Merhav, Guessing subject to distortion, IEEE Trans. Inform. Theory 44, 1041 (1998).
- [5] E. Arikan and N. Merhav, Joint source-channel coding and guessing with application to sequential decoding, IEEE Trans. Inform. Theory 44, 1756 (1998).
- [6] J. Pliam, The Disparity between Work and Entropy in Cryptology, Cryptology ePrint Archive 1998/024 (1998).
- [7] D. Malone and W. Sullivan, Guesswork and Entropy, IEEE Trans. Inform. Theory 50, 525 (2004).
- [8] R. Sundaresan, Guessing Under Source Uncertainty, IEEE Trans. Inform. Theory 53, 269 (2007).
- [9] M. K. Hanawal and R. Sundaresan, Guessing Revisited: A Large Deviations Approach, IEEE Trans. Inform. Theory 57, 70 (2011).
- [10] M. M. Christiansen and K. R. Duffy, Guesswork, Large Deviations, and Shannon Entropy, IEEE Trans. Inform. Theory 59, 796 (2013).
- [11] I. Sason and S. Verdú, Improved Bounds on Lossless Source Coding and Guessing Moments via Rényi Measures, IEEE Trans. Inform. Theory 64, 4323 (2018).
- [12] I. Sason, Tight Bounds on the Rényi Entropy via Majorization with Applications to Guessing and Compression, Entropy 20, 896 (2018).
- [13] W. Chen, Y. Cao, H. Wang, Y. Feng, Minimum guesswork discrimination between quantum states, Quantum Information & Computation 15, 0737 (2015).
- [14] E. P. Hanson, V. Katariya, N. Datta, and M. M. Wilde, Guesswork with Quantum Side Information, IEEE Trans. Inform. Theory 68, 322 (2022).
- [15] M. Dall’Arno, F. Buscemi, and T. Koshiba, Classical computation of quantum guesswork, arXiv:2112.01666.
Michele Dall’Arno received his PhD in theoretical physics from the University of Pavia, Italy, in 2012. He held post-doc positions in ICFO (Barcelona), Nagoya University (Japan), and the National University of Singapore. Since 2020, he is assistant professor in quantum information in Kyoto University, and visiting researcher in Waseda University, Tokyo.
Francesco Buscemi received his PhD in theoretical physics from the University of Pavia, Italy, in 2006. After post-doc positions in Tokyo, Japan, and Cambridge, UK, he joined Nagoya University in 2009, where he is a professor in the department of mathematical informatics. In 2018 he was awarded the Birkhoff-von Neumann Prize by the International Quantum Structures Association.
Takeshi Koshiba received his PhD degree from the Tokyo Institute of Technology. He is a full professor at the Department of Mathematics, Faculty of Education and Integrated Arts and Sciences, Waseda University, Japan. His interests include theoretical and applied cryptography, randomness in algorithms, and quantum computing, cryptography and information.