Gromov-Hausdorff distances from simply connected geodesic spaces to the circle.
Abstract
We prove that the Gromov-Hausdorff distance from the circle with its geodesic metric to any simply connected geodesic space is never smaller than . We also prove that this bound is tight through the construction of a simply connected geodesic space which attains the lower bound . We deduce the first statement from a general result that we also establish which gives conditions on how small the Gromov-Hausdorff distance between two geodesic metric spaces and has to be in order for and to be isomorphic.
1 Introduction
In the following, for we give the unit sphere its intrinsic metric . That is, for any two points seen as vectors in , is the angle between and .
The Gromov-Hausdorff (GH) distance provides a quantitative measure of how far two metric spaces are from being isometric. Since being introduced by Edwards ([Ed], 1975) and Gromov ([Gr1, Gr2], 1981), it has proved useful in the study of, for example, shapes formed by point cloud data [MS, BBK], convergence results for sequences of Riemannian manifolds [CC, PW, C1, C2], differentiability results in metric measure spaces [Ke, Ch] or the stability of topological invariants of metric spaces under small deformations (see [Pe] and the present article).
However, it is hard to find the exact value of the GH distance between two given metric spaces. There have been recent efforts to determine the precise value of the GH distance between spheres. In [LMS, Theorem B] it is proved that for all which implies that
| (1) |
for all . Via these lower bounds and matching upper bounds, the authors find the precise value of the GH distance for the pairs , , and . Similarly, in [Ka, Lemma 2.3] it was proved that for any interval we have (see also [LMS, Prop. B.1]; in [JT, Theorem 6.8] the exact GH distances from to intervals of any length are computed). In [ABC] the authors identify lower bounds for that are often tighter than the ones from [LMS].
Via considerations related to persistent homology and the filling radius, in [LMO, Remark 9.19] it was deduced that for any compact geodesic metric space one has and, as a generalization of Equation (1), the following conjecture was formulated:
Conjecture 1.1 ([LMO, Conjecture 4]).
For any compact, simply connected geodesic space we have .
In 1.1, the condition that is geodesic is necessary to relate the metric of to the fact that it is simply connected; if not, we could consider the space , with its metric inherited from . Then is simply connected, but we clearly have . The present article gives a complete answer to 1.1; we state the main results after recalling some standard notation.
Let be a metric space, and let be nonempty and let . The distance from to is defined as , and the Hausdorff distance between and is given by
Given two nonempty metric spaces and , we write , or just when the metrics are clear, whenever and are isometric. The Gromov-Hausdorff (GH) distance between and is defined as the value in given by
Recall that a metric space is a length space when for all , the distance is the infimum of lengths of paths with and (cf. [BBI, Chapter 2]). If in addition we have that for all there is a path from to with length , we say that is geodesic.
Theorem 1.2.
There exists a simply connected geodesic space E with .
Theorem 1.3.
Let be length spaces. Suppose there is a constant such that and all loops of diameter are nulhomotopic in and . Then and are isomorphic.
Corollary 1.4.
Any simply connected length space X satisfies .
To prove 1.4 from Theorem 1.3 note that every loop with diameter is nulhomotopic. So if there was a simply connected space with , then we could choose the constant from Theorem 1.3 to be just below , which would give a contradiction as .
Section 2 is almost entirely devoted to the proof of Theorem 1.3. At the end of the section we also give a lower bound for the distances from simply connected length spaces to with the metric inherited from .
Remark 1.5.
As was well pointed out to me by F. Mémoli, the arguments used in Section 2 are similar to those in Petersen’s article [Pe]. The Theorem in [Pe, Section 4] claims that, under adequate conditions, if the GH distance between two metric spaces is small enough, then they are homotopy equivalent; in our case, as we are comparing simply connected spaces with , it will be enough to give conditions on such that . This allows us to give better bounds for for our purposes; for example, in the Main Lemma of [Pe, Section 2], if one sets and if is a length space instead of a LGC space, then one can improve Petersen’s conclusion (with ) to the sharper condition .
Section 3 is devoted to the construction of a simply connected geodesic space E with . This, in conjunction with 1.4, proves Theorem 1.2. In Section 3 we will not use the definition of Gromov-Hausdorff distance given above; we now recall (cf. §7.3 in [BBI]) an equivalent definition based on correspondences between sets, which will be more convenient for our purposes.
Given two sets and , we say a relation is a correspondence between and if and , where and are the coordinate projections. If and are metric spaces, we define the distortion of a nonempty relation as
| (2) |
In [BBI, Theorem 7.3.25] it is proved that, if are nonempty metric spaces, then
| (3) |
In Section 4 we adress the question of whether the space we construct to prove Theorem 1.2, which is a compact -tree, is the unique space satisfying Theorem 1.2. It turns out that it is not hard to use E to construct a big family of spaces that satisfy Theorem 1.2 (see 4.2), and that there are -trees which satisfy Theorem 1.2 and are not isometric to E (see Note 4.6).
However, in 4.5 we prove a minimality result for our space E: it is, up to isometry, the only complete -tree of length at most which satisfies Theorem 1.2.
Acknowledgements. Special thanks to Facundo Mémoli for introducing the author to the topic of Gromov-Hausdorff distances and providing guidance while writing this article. The author gratefully acknowledges support from the grants BSF 2020124 and NSF CCF AF 2310412.
2 Proof of Theorem 1.3
Lemma 2.1.
Let be a length space such that, for some constant , all loops of diameter are contractible in , and let . Then any two loops based at satisfying for all are path-homotopic.
Proof.
Let be such that for all .
Let be big enough that for all , the paths and have diameter . Note that and . Also, for each let be a path with and with length , as in Figure 1.
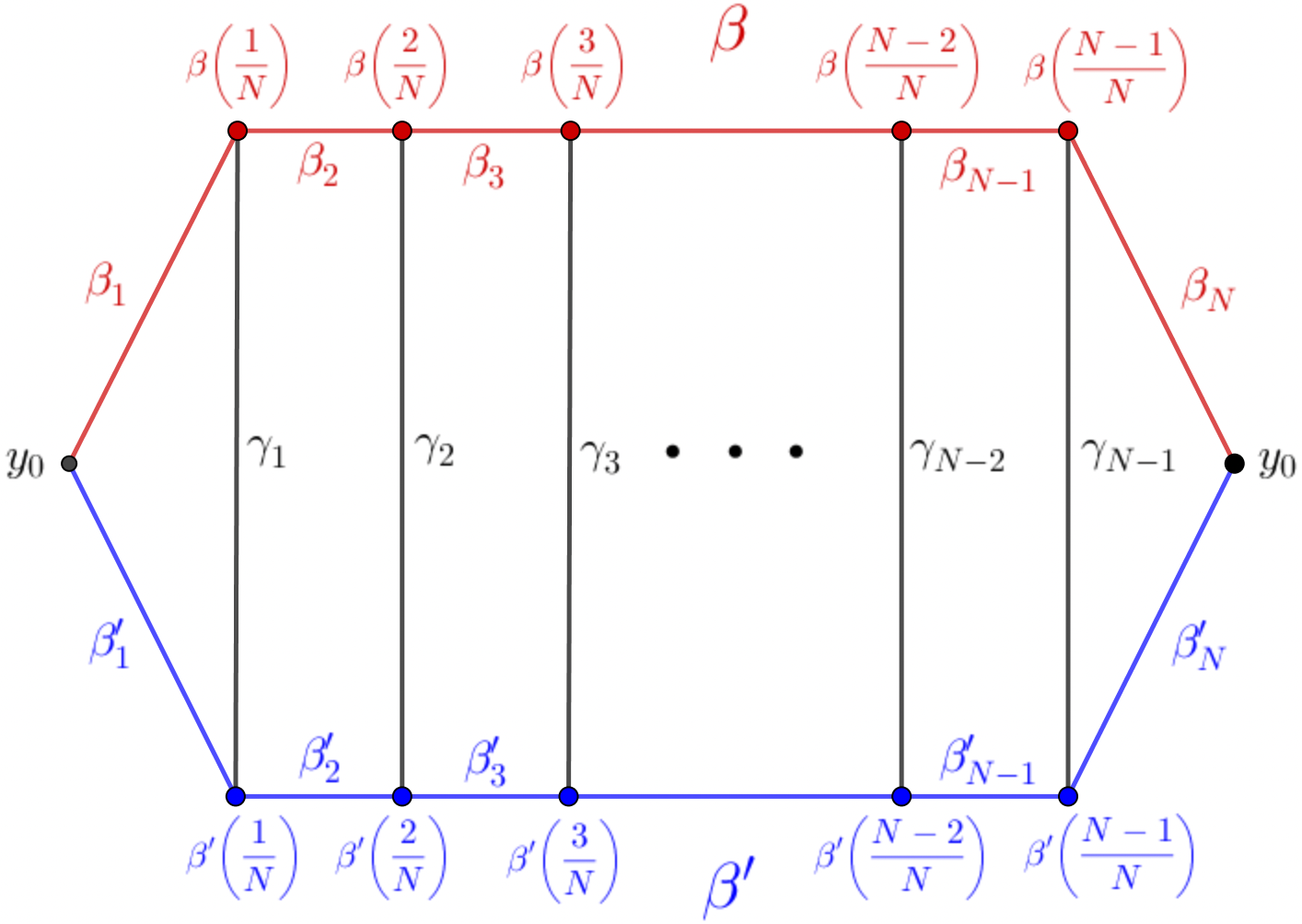
Now consider the sequence of loops , where for we have . Then for all , is homotopic to . Indeed, for (the cases are easier) we have
and the loop is null because it has diameter (this follows from the facts that have diameter and have length ). We conclude then that and are homotopic, as we wanted. ∎
Theorem 2.2.
Let be length spaces and let . Suppose and are embedded isometrically into a metric space with . Let with . Then for any loop based at there is a loop based at such that for all .
Moreover, if all loops (not necessarily based at ) of diameter in are contractible in , then the function defined above gives a well defined, surjective111If is not a length space, then Theorem 2.2 still holds with the same proof, except that the map need not be surjective. map .
Proof.
Let be such that . Let be big enough that diam for all , and for each define to be a point of such that (one can choose ). By the triangular inequality, , thus we can define to be a path from to of length .
Note that all points in are at distance of either or . Moreover, and are both at distance from all points in . Thus, all points in are at distance from all points in , and in particular for all , as we wanted. This concludes the proof of the first part of the theorem.
Suppose now that all loops of diameter are contractible in . Suppose that are path-homotopic loops (the path-homotopy being inside ) based at , and let be loops based at such that and for all . We want to prove that are homotopic.
To do it, let be such that and such that and for all . Let be a path-homotopy in from to . By uniform continuity of the homotopy, we can choose big enough such that for all and for all we have . Now by the first part of the theorem, we can let be a loop in based at such that for all (with and ). By the triangular inequality we have for all and that , thus by Lemma 2.1, and are path-homotopic. We conclude then that and are path-homotopic. This proves that the map is well defined.
To check that is surjective note that, by the first part of the theorem, for any loop based at we can find a loop based at such that for all , so . ∎
Proof of Theorem 1.3.
Let contain isometrically and choose basepoints in respectively with . Define maps and as in Theorem 2.2. Then the composition is the identity (similarly with ): indeed, for any loop based at , will be for some loop based at such that for all . But then we also have , so . ∎
Note 2.3.
One can use the ideas from this section to find lower bounds for the distance from any simply connected length space to with the Euclidean metric inherited from . In , the conclusion of Lemma 2.1 holds for , that is, any two loops with for all are path-homotopic, with a homotopy between them defined by, for each , letting be the shortest geodesic from to . Also note that for any and any two points with , the points in the shortest path from to will not be at distance from the set . That and the proof of Theorem 2.2 imply that, if we have a length space at Hausdorff distance from inside some bigger metric space , then for each loop we can find a loop such that for all , . If , as in Theorem 2.2 we obtain a well defined surjective map , so cannot be simply connected.
This proves that the GH distance from to a simply connected length space cannot satisfy . Thus we obtain a lower bound for of approximately . We could not construct an optimal example similar to the one in Section 3 and we currently see no reason why this lower bound should be optimal, which naturally leads to the following question:
Question 2.4.
What is the infimal distance from a simply connected geodesic space to ?
3 A simply connected geodesic space with
d
Figure 2 shows two metric graphs (see [BBI, Definition 3.2.9.] for a definition of metric graph) which we will call E and for obvious reasons, with all edges having length . The graph E has five edges, and . We have also labelled the eight edges of with the letters .
We define a function which sends each of the edges of isometrically to one of the segments of E as indicated by the labels and orientations in the figure. This specification of gives two possible values to ; for definiteness we choose . Note that is locally -Lipschitz except at , where there is a jump of length from to .
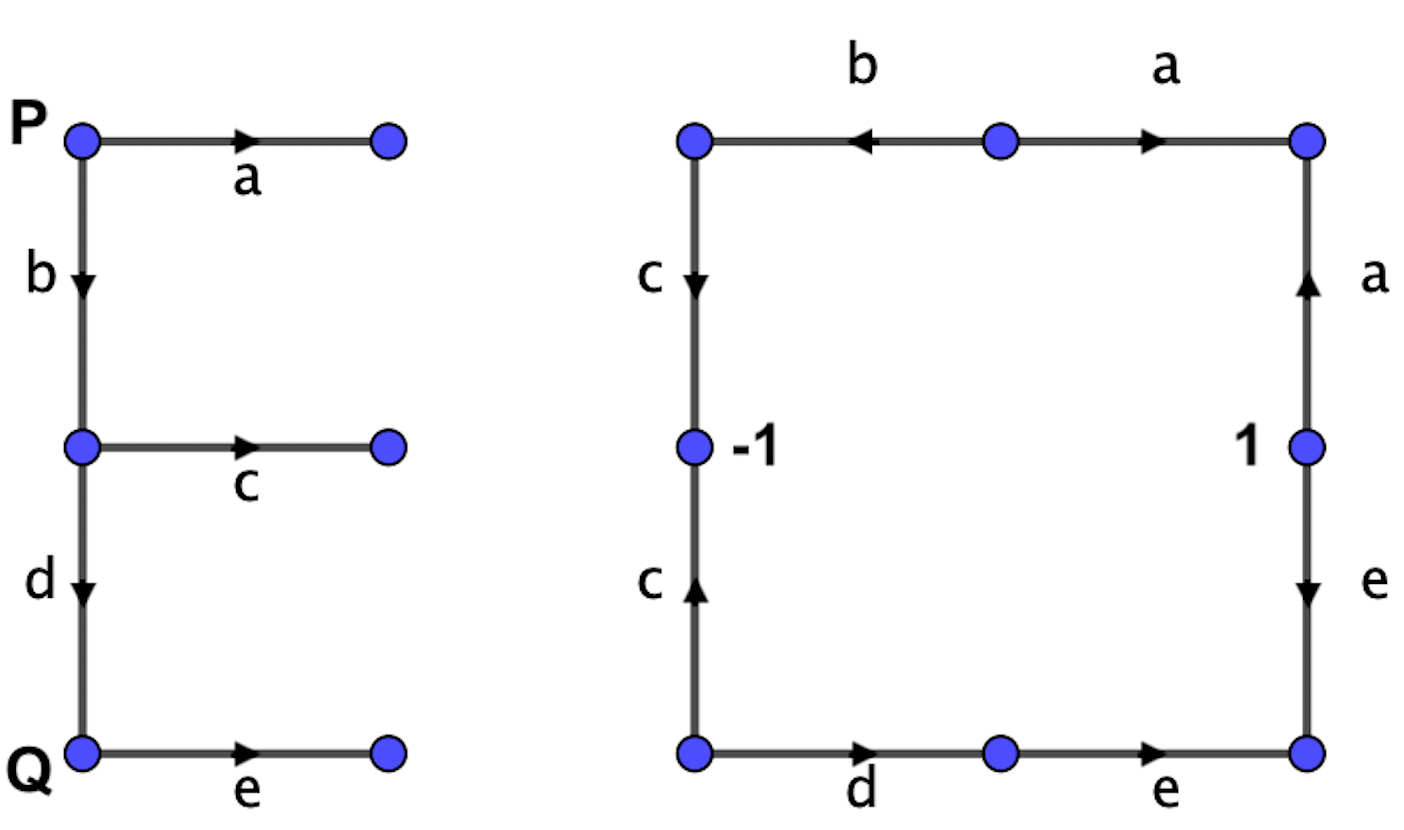
Claim 3.1.
The graph of , , is a correspondence between and E with .
Note that, by Equation 3, the claim above implies that . Since E is a simply connected geodesic space, by 1.4 we obtain , which is the goal of this section.
Proof of 3.1.
First note that is surjective, so is indeed a correspondence between and . It remains to prove that for all we have
First we prove the inequality . To do this, we may assume and consider the geodesic segment , given by a unit speed curve with , and . Then the curve either is -Lipschitz, in which case , or it has a jump of length at some point . In this case, is still -Lipschitz in and , so we have the inequality we wanted:
Now we prove the remaining inequality, . When are antipodal, we have equality: . This can be checked using the definition of in the eight edges of .
For general points , note that cannot be in both of the geodesic segments and , because they are antipodal segments of length . Suppose without loss of generality that is not in , so that, if is the unit speed geodesic with , and , then the path is -Lipschitz. Now consider the function
Then is increasing, because and the map is -Lipschitz. Thus, as we wanted,
∎
4 A uniqueness result for the space
It is natural to ask whether is, up to isometry, the only geodesic simply connected space with GH distance to . We now use to obtain a big family of simply connected geodesic spaces which are exactly at GH distance from .
Proposition 4.1.
Let , and be nonempty metric spaces, and suppose . Then the space , with the metric
satisfies .
Proof.
For any correspondence , which by Equation 3 satisfies dis, we can define the correspondence
We will be done by Equation 3 if we prove that . Indeed, letting , we have
Corollary 4.2.
Let be a nonempty simply connected geodesic space with . Give the metric
Then is a simply connected geodesic space and .
Proof.
Note 4.3.
More generally, the proof of 4.2 shows that any geodesic, simply connected subspace such that the coordinate projection is surjective will also be at distance from .
So E is not the only geodesic, simply connected space at distance from . However, we prove below that E is the only complete tree with minimal length at distance from ; to formalize this statement we will need to introduce some concepts and notation:
Definition 4.4 ([Be, Defs. 2.1, 2.2.]).
An arc in a metric space is a subspace of homeomorphic to the interval . A metric space is an -tree if for every there is a unique arc with endpoints and this arc is a geodesic segment (i.e., isometric to an interval of ). We denote by the geodesic segment from to . We will define the length of the -tree to be the supremum of all sums of lengths of disjoint arcs contained in .
Note that all -trees are geodesic by definition, and the distance between any two points of an -tree is the length of the arc . Moreover, any -tree is contractible: indeed, for any we can define a homotopy , , from a constant map to IdX by letting be the point in at distance from . Thus, by 1.4, any -tree satisfies .
Proposition 4.5.
Let be a complete -tree with length and such that . Then is isometric to E.
Note 4.6.
4.5 does not hold for finite simplicial graphs instead of -trees: for example, the metric space has length and is at GH distance from (the identity map gives an optimal correspondence).
The condition of having length is also necessary to prove uniqueness of E in 4.5, that is, there are -trees not isometric to E and such that 222This fact doesn’t seem to follow from Note 4.3, so we give a separate construction.. Indeed, consider a metric tree E’ obtained from E by increasing the length of the edge (see Figure 2) from to . We can consider E as a subspace of E’, with being a segment of length . Letting be the correspondence from 3.1, we can define a correspondence
and it is not hard to check that .
Note 4.7.
Note that the condition ‘’ can be equivalently expressed in the following way333To check that both statements are equivalent, one needs to use that -trees of finite length are compact, see 4.8.: there exist isometric copies of and inside a bigger metric space such that the two following conditions are satisfied:
-
1.
for all .
-
2.
for all .
Thus, 4.5 may be informally expressed as ‘besides , no other complete -tree of length can satisfy conditions 1 and 2 simultaneously’. If we remove condition 2, it is clear that many complete -trees of length can satisfy condition 1 (e.g. the -tree formed by a single point). So we certainly need to use condition 2 in order to prove our theorem. However, one may at first think that condition 1 is not necessary to prove our uniqueness theorem, that is, that any -tree of length satisfying condition 2 is isometric to . That is, ‘if an -tree is smaller than , then we cannot place and in such a way that all points of are at distance of ’. This is, however, not true. Indeed, consider the -tree shown below, which has four edges of length and four extreme points . Then has length , but if we divide into four intervals of length , one can give the disjoint union a metric in which, for each , all the points of are at distance from .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/8516d804-d5c0-4c7e-a8ea-f88a53cf81ed/X.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/8516d804-d5c0-4c7e-a8ea-f88a53cf81ed/Circ4.png)
The proof of 4.5 comprises the rest of this section. Fix a complete -tree of length at most satisfying .
Claim 4.8.
is compact.
Proof.
It is enough to prove that is totally bounded. If not, there is some and points with if . So the balls are pairwise disjoint, and each contains a segment of length , contradicting the fact that has finite length. ∎
As and are compact and , it is proved in [CM, Proposition 1.1.] that there is a correspondence achieving the minimal distortion , and such that is a closed subspace of .
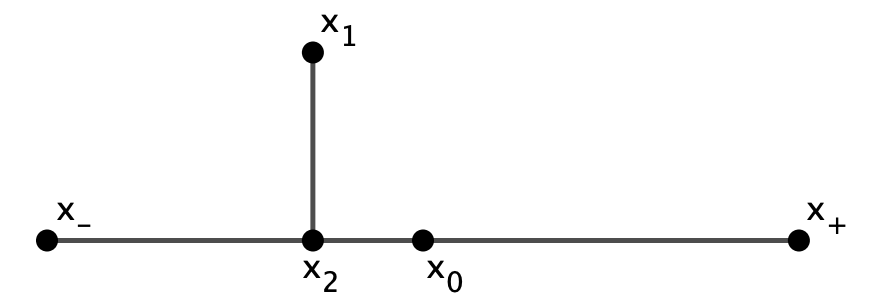
So from now on, we fix a closed correspondence with distortion . For any we let , and for any we let and we denote by the antipodal of . We will fix two points with and let be the midpoint of . Finally, we define the ‘projection’ map
by the equation . Note that if two points have , then the union of and is the geodesic arc from to (see figure Figure 3), so we have
| (4) |

We will repeatedly use Equation 4 to compute distances in .
Definition 4.9.
A tripod is an -tree with three points (the extreme points of ) such that .
Claim 4.10.
We have , and the space is a tripod with extreme points , and a point with .
Proof.
We first deduce that . To do it, note that any point is at distance from : if not, depending on whether or we would have or , a contradiction. Now let and let . Using that , we obtain
We will now deduce the rest of the theorem. First note that for all we have ; indeed, as has length , we have
And if for some , then all the inequalities above are equalities, so and , so the tree must be the union and we would be done proving 4.10. We can therefore suppose for all , and we will obtain a contradiction.
For each choose a point . Note that we have for all . Moreover, for all , because
| (5) |
So, if we order the segment by iff , then for any we have either or .
Now, let be a geodesic segment of length in , so that . We can suppose w.l.o.g. that . Thus, .
Let . Suppose that (the case is similar). Then by definition of , there has to be some sequence in convergent to and such that for all . By taking a subsequence, we can assume that converge when to some points respectively, so that and, as is closed, we have and .
So we have points and with and . Thus, we cannot have that both and are strictly smaller than both and or viceversa. Equivalently, there are points such that and for some we have and (this in turn implies that : we cannot have equality by Equation 5). But then, we have a contradiction: as ,
Now, let be the segment of length we append to to obtain , with . We necessarily have (as ), and we may assume without loss of generality that . Thus we already have a very concrete description of , illustrated in Figure 4. Note that is determined up to isometry by , so we will be done if we prove that , in which case the space is isometric to E.
For each , we will denote by the open interval centered at with radius . Also, we divide the tree into two parts: and .
Claim 4.11.
Let . Then , and exactly one of the following cases happens:
-
Case 1.
. Then no point of can be related to any point of .
-
Case 2.
. Then no point of can be related to a point of .
Proof.
There has to be some point in , because is a correspondence. As has distortion and , we have , which implies (and may only happen if ).
If , then for any and we have:
But no point can satisfy both of these inequalities at the same time, thus, as we wanted, no point of can be related to any point of . The cases and are similar. Also note that if , or cannot be in , because they are at distance from and . ∎
Claim 4.12.
We have for some with and such that , .
Proof.
We first prove that there are points in Case 1. and Case 2. of 4.11 respectively. Suppose for contradiction that all the points of are in Case 2. (the same argument works for Case 1.), so that all points in are not related to points of . Note that any point with satisfies . So as , for any its antipodal must be related to some point of . Thus . Letting approach , and using that is closed, we obtain that there is some point of outside , a contradiction.
So let satisfy Case 1. and Case 2. of 4.11 respectively. Then we necessarily have ; if not, would be nonempty, and its points could not be related to either or . Now, as , has to be contained in the geodesic segment , and all points in have to be at distance from either or for the same reasoning we just stated. So , as we wanted. ∎
We now conclude the proof of 4.5. Let be as in 4.12 and let be at the same distance from , as in the figure below.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/8516d804-d5c0-4c7e-a8ea-f88a53cf81ed/LastPartProofUnique.png)
Note that, as is closed in and all points of are related to some point of , has to be related to some point . Similarly, is related to some point . Note that , so using that , we have
Thus the inequalities above are equalities, and .
Meaning that is the midpoint of and is either the midpoint of or some point in . Now, let . As and , we have . Now we divide in cases:
-
•
is the midpoint of . Then there are no points in at distance from both and , unless and , proving 4.5.
-
•
is in . If , then again is the midpoint of the segment , so we are back to the previous case. If , then by the proof of 4.11. In this case we also have : if not, the inequalities would imply that is at distance from , which contradicts the facts that and .
References
- [ABC] H. Adams et al. Gromov-Hausdorff distances, Borsuk-Ulam theorems, and Vietoris-Rips complexes. arXiv preprint arXiv:2301.00246v1, 2022.
- [Be] M. Bestvina. Handbook of Geometric Topology, Chapter 2: -Trees in Topology, Geometry, and Group Theory. North-Holland, 2001.
- [BBI] D. Burago, Y. Burago, S. Ivanov. A Course in Metric Geometry. American Mathematical Society, 2001.
- [BBK] Efficient computation of isometry-invariant distances between surfaces. SIAM J. Scientific Computing 28, no. 5, pp. 1812–1836, 2006.
- [CC] J. Cheeger, T. H. Colding. On the structure of spaces with Ricci curvature bounded below. I. J. Differential Geom. 46(3) pp. 406-480, 1997.
- [Ch] J. Cheeger. Differentiability of Lipschitz Functions on metric measure spaces. GAFA, Geom. funct. anal. Vol. 9, pp. 428–517, 1999.
- [CM] S. Chowdhury, F. Mémoli. Explicit geodesics in Gromov-Hausdorff space. Electronic Research Announcements in Mathematical Sciences, Vol. 25, pp. 48-59, 2018.
- [C1] T. H. Colding. Shape of manifolds with positive Ricci curvature. Invent. math. 124, pp. 175–191, 1996.
- [C2] T. H. Colding. Large manifolds with positive Ricci curvature. Invent. math. 124, pp. 193–214, 1996.
- [Ed] D. A. Edwards. The Structure of Superspace. Studies in Topology, Academic Press, 1975.
- [Gr1] M. Gromov. Metric structures for Riemannian and non-Riemannian spaces. Birkhaüser, 2007.
- [Gr2] M. Gromov. Groups of Polynomial growth and Expanding Maps. Publications mathematiques I.H.E.S., 53, 1981.
- [JT] Y. Ji and A. Tuzhilin. Gromov-Hausdorff Distance Between Interval and Circle. Topology and its Applications Volume 307, 2022.
- [Ka] M. Katz. Torus cannot collapse to a segment. Journal of Geometry, vol. 111 pp. 1–8, 2020.
- [Ke] S. Keith. Modulus and the Poincaré inequality on metric measure spaces. Math. Z. 245, pp. 255–292, 2003.
- [Kı] M. Kılıç and Ş. Koçak. On Products of Uniquely Geodesic Spaces. The American Mathematical Monthly, vol. 122, no. 10, pp. 990–94, 2015.
- [LMO] S. Lim, F. Mémoli, O. Okutan. Vietoris-Rips Persistent Homology, Injective Metric Spaces, and The Filling Radius. To appear in Algebraic and Geometric Topology. arXiv preprint arXiv:2001.07588v6, 2023.
- [LMS] S. Lim, F. Mémoli, Z. Smith. The Gromov-Hausdorff distances between spheres. Geometry & Topology 27 pp. 3733–3800, 2023.
- [MS] F. Mémoli and G. Sapiro. A theoretical and computational framework for isometry invariant recognition of point cloud data. Foundations of Computational Mathematics, vol. 5 pp. 313–347, 2005.
- [Pe] P. Petersen. A finiteness theorem for metric spaces. J. Differential Geometry 31 pp. 387-395, 1990.
- [PW] C. Plaut, J. Wilkins. Discrete homotopies and the fundamental group. Advances in Mathematics 232 pp. 271–294, 2013.