GridPull: Towards Scalability in Learning Implicit Representations from 3D Point Clouds
Abstract
Learning implicit representations has been a widely used solution for surface reconstruction from 3D point clouds. The latest methods infer a distance or occupancy field by overfitting a neural network on a single point cloud. However, these methods suffer from a slow inference due to the slow convergence of neural networks and the extensive calculation of distances to surface points, which limits them to small scale points. To resolve the scalability issue in surface reconstruction, we propose GridPull to improve the efficiency of learning implicit representations from large scale point clouds. Our novelty lies in the fast inference of a discrete distance field defined on grids without using any neural components. To remedy the lack of continuousness brought by neural networks, we introduce a loss function to encourage continuous distances and consistent gradients in the field during pulling queries onto the surface in grids near to the surface. We use uniform grids for a fast grid search to localize sampled queries, and organize surface points in a tree structure to speed up the calculation of distances to the surface. We do not rely on learning priors or normal supervision during optimization, and achieve superiority over the latest methods in terms of complexity and accuracy. We evaluate our method on shape and scene benchmarks, and report numerical and visual comparisons with the latest methods to justify our effectiveness and superiority. The code is available at https://github.com/chenchao15/GridPull.
1 Introduction
It is vital to reconstruct surfaces from 3D point clouds for downstream applications. A widely used strategy is to learn implicit representations [59, 62, 26, 10, 91, 77, 54, 68, 88] from 3D point clouds in a data-driven manner. With the learned implicit representations, we can reconstruct surfaces in meshes by running the marching cubes algorithm [48]. By learning priors from large scale datasets during training, previous methods [57, 21, 31, 46, 78, 73, 17] generalize the learned priors to either global implicit functions [89, 80, 8, 32, 6, 50] or local ones for unseen point clouds. However, the generalization ability limits their performances on large structure or geometry variations of training samples.
More recent methods [23, 12, 2, 100, 3, 95, 4, 49, 14, 65, 35] achieved better generalization by directly overfitting neural networks on single unseen point clouds. They rely on extensive calculations of distances between queries and surface points to probe the space, which supervises neural networks to converge to a distance or occupancy field [49, 23, 2, 100, 3, 11, 52, 83, 40]. However, this inference procedure is time consuming due to the extensive distance calculations and the slow convergence of neural networks. This demerit makes these methods hard to scale up to large scale point clouds for surface reconstruction.
To address the scalability challenge, we propose GridPull to speed up the learning of implicit function from large scale point clouds. GridPull does not require learned priors or point normal, and directly infers a distance field from a point cloud without using any neural components. We infer the distance field on grids near the surface, which reduces the number of grids we need to infer. Moreover, we organize surface points in a tree structure to speed up the nearest neighbor search for the calculation of distances to the surface. Specifically, we infer the discrete distance field by pulling queries onto the surface in grids of interests. Our loss function encourages continuous distances and consistent gradients in the field, which makes up the lack of continuousness brought by neural networks. We justify our effectiveness and highlight our superiority by numerical and visual comparisons with the latest methods on the widely used benchmarks. Our contributions are listed below.
-
i)
We propose GridPull to reconstruct surfaces from large scale point clouds without using neural networks. GridPull speeds up the learning of implicit function, which addresses the scalability challenge in surface reconstruction.
-
ii)
We introduce a loss function to directly infer a discrete distance field defined on grids but achieving continuous distances and consistent gradients in the field.
-
iii)
Our method outperforms state-of-the-art methods in surface reconstruction in terms of speed and accuracy on the widely used benchmarks.
2 Related Work
Neural implicit representations have made a huge progress in various tasks [59, 62, 26, 10, 101, 91, 77, 54, 68, 53, 39, 36, 60, 28, 7, 41, 76]. We can use different supervision including 3D supervision [58, 64, 63, 56, 13, 92, 87], multi-view [72, 45, 34, 99, 44, 90, 61, 42, 94, 93, 19, 84, 98, 86, 81, 82, 25, 22, 29, 69, 74, 33, 55], and point clouds [89, 43, 57, 21] to learn neural implicit representations. In the following, we focus on reviewing works on surface reconstruction by learning implicit representations point clouds below.
Learning with Priors. With neural networks, one intuitive strategy is to use neural networks to learn priors from a training set and then generalize the learned priors to unseen samples. We can learn either global priors to map a shape level point cloud into a global implicit function [57, 21, 31, 46, 78, 73, 17] or local priors for local implicit functions to represent parts or patches [89, 80, 8, 32, 6, 50] which are further used to approximate a global implicit function.
These methods require large scale datasets to learn priors. However, the learned priors may not generalize well to unseen point clouds that have large geometric variations compared to training samples. Our method does not require priors, and falls into the following category.
Learning with Overfitting. To improve the generalization, we can learn implicit functions by overfitting neural networks on single point clouds. Methods using this strategy introduce novel constraints [23, 2, 100, 3, 95, 4], ways of leveraging gradients [49, 14], differentiable poisson solver [65] or specially designed priors [50, 51] to learn signed [49, 23, 2, 100, 3, 11] or unsigned distance functions [14, 102, 47].
These methods rely on neural networks to infer implicit functions without learning priors. However, the slow convergence of neural networks is a big limit for them to scale up to large scale point clouds. Our method addresses the scalability challenge by directly inferring a discrete distance field without using neural networks. Our novel loss leads to less complexity and higher accuracy than the overfitting based methods.
Learning with Grids. Learning implicit functions with grids has been used in prior-based methods [77, 54, 66, 79, 46, 34, 85]. Using neural networks, these methods learn features at vertices of grids and further map the interpolated features into a distance or occupancy field. Some methods [70, 75, 96, 38] inferred a discrete radiance field defined on grids to speed up the learning of a radiance field, while they cared more about the quality of synthesized views than the underlying geometry. Without using neural components, some methods [67, 65] directly infer discrete implicit functions on grids. To make up the continuousness of neural networks, they employed different constraints, such as Possion equations or Viscosity priors, to pursue a continuous field from a single point cloud. However, these methods are slowly converged, which makes them hard to scale up to large scale point clouds. Although we also use grids to speed up the inference, we introduce a more efficient training strategy to decrease optimization space and more effective losses to increase inference efficiency.
3 Method
Overview. GridPull aims to achieve a fast inference of a distance field, such as a signed distance field, from a 3D point cloud without using any neural components. As shown in Fig. 1 (b), we represent the distance field by a signed distance function (SDF) defined on a set of discrete grids with a resolution of , where the vertices shared among these grids hold learnable signed distances . For an arbitrary location in Fig. 1 (e), such as a randomly sampled query or a surface point, we use trilinear interpolation to approximate the signed distance from the eight nearest grid vertices below,
| (1) |
Our goal is to conduct direct optimization in Fig. 1 (c) to infer the signed distances on grid vertices by minimizing our loss function on queries below,
| (2) |
With the learned function , we run the marching cubes algorithm [48] to reconstruct a mesh as the surface as shown in Fig. 1 (d).

Discrete Grids. We split the space occupied by the point cloud into discrete grids with a resolution of in Fig. 1 (b). GridPull can work with high resolutions, such as , because of our efficient and effective loss function and training strategy. Within each grid, we interpolate the signed distance of query using the trilinear interpolation in Eq. 1. We organize surface points in a tree structure to speed up the search of the nearest surface point for queries . Since we need to extensively conduct trilinear interpolation on signed distances for queries , we use uniform grids for fast nearest grid search for queries. We did not use an Octree to organize grids, due to its inefficient and inaccurate grid search for queries.
Geometric Initialization. We initialize the signed distances on grid vertices which represent a sphere in the field. The initialization can speed up the convergence during optimization. Our preliminary results show that a small sphere with a radius of one or two grids works well. Since enlarging a small sphere to the target shape can calculate the continuous distance loss over smaller regions than shrinking a large sphere.
Signed Distance Inference. For a query , we infer its signed distance through pulling it onto its nearest surface point in the point cloud . As shown in Fig. 1 (e), we first obtain as the interpolation of the signed distances on the nearest eight vertices of . We implement the trilinear interpolation by solving in a linear regression system on the eight vertices below,
| (3) |
where is the coordinate of and the eight constraints are .
With the predicted signed distance and the gradient , we pull a query onto the surface and obtain a pulled query by in Fig. 1 (f).
Our goal is to minimize the distance between the pulled query and the nearest surface point of query below,
| (4) |
We adopt this pulling loss from [49]. Instead, we do not rely on neural network in the pulling procedure. We use the trilinear interpolation on signed distances on grid vertices to obtain signed distances and gradients according to Eq. 3.
We sample queries around surface points in each epoch. For each randomly sampled surface point, we sample queries using a gaussian distribution with the surface point as the center and a two-grid length variance. We build a KD-tree on surface points so that we can speed up the searching of the nearest neighbor from a large number of surface points for each query.
To speed up the optimization, we only calculate the pulling loss on grids near the surface. We regard the grids containing surface points as the base and find the union of their nearest neighboring grids. These grids form a -bandwidth near the surface in Fig. 1 (c).
Continuous Distance Fields. Although the pulling loss can infer correct signed distances at grid vertices, it fails to learn continuous signed distances across the field, especially near the surface. Fig. 2 (a) shows severe artifacts on the surface and gradients near the surface are messy and inconsistent, which are caused by the discontinuous signed distances across neighboring regions.
Neural network based methods [49, 51] do not have this issue, since the continuous character of neural networks makes the sudden change of signs on the same shape side hard. While our method uses signed distances on grid vertices to represent a discrete field, this makes that one can change separately without considering the change of neighboring , which leads to a poor continuousness in the field.
To resolve this issue, we impose a total variation (TV) loss as a continuous constraint on our signed distances on grid vertices. Our key idea is to make the change of one affect the change of its neighboring , which smoothes the local distance field and propagates local updates to the rest grids. Hence, as shown in a 2D case in Fig. 1 (g), we approximate one to each one of its six neighbors by minimizing the difference between each two below,
| (5) |
where is the difference between and the signed distance along the axis, i.e., axis. Fig. 2 (b) shows that the continuous constraints can significantly improve the signed distance field in terms of continuousness and gradients.
One remaining issue is its computational complexity. Since we are targeting grids at a high resolution, such as , it is very time consuming to impose this constraint on all across the field.
To resolve this issue, we focus on grids near the surface. Similar to imposing the pulling loss on grids in the -bandwidth near the surface, we impose our continuous constraints on the grids in the -bandwidth near the surface, which significantly reduces the number of learnable parameters to optimize.
Signed Distance Supervision. For signed distances, one supervision we can directly use is the input point cloud . It is a discrete surface indicating the zero level-set of the signed distance function. Hence, as introduced in Fig. 1 (h), we can constrain the signed distances at the points on the surface below,
| (6) |
Although Fig. 2 (c) indicates that slightly improves the signed distance field and leads to a little bit more continuous surface, it is helpful to determine the zero level set with other losses. For noises on , our continuous constraint can relieve the impact of noises on this supervision. We will show this in experiments.
Consistent Gradients. Fig. 2 (a) indicates that the pulling loss produces gradients that are messy and non-orthogonal to the surface. This leads to inaccurate signed distance inference during the pulling procedure.
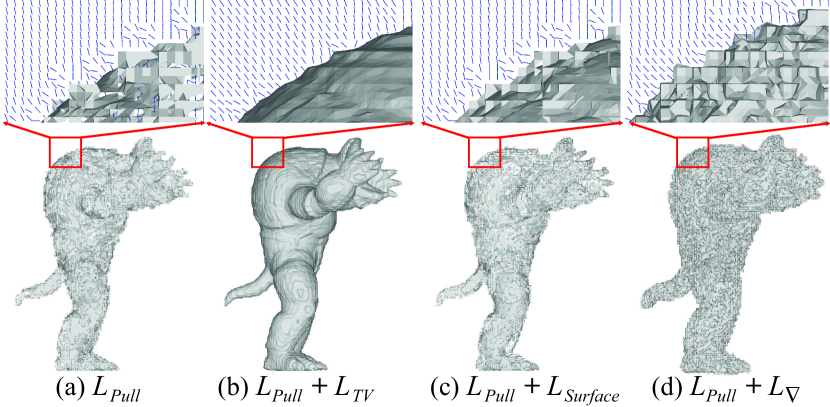
We additionally introduce a constraint on gradients to improve the field near the surface. As shown in Fig. 1 (i), we aim to encourage the gradient at a query to point to the same direction of the gradient at its nearest surface point . We use a cosine distance below to achieve more consistent gradients,
| (7) |
constrains the gradients in the field and corrects inaccurate gradients. Fig. 2 (d) shows that more consistent gradients can improve the surface to be more continuous using small planes on the surface which however the surface not smooth at all.
Loss Function. We learn signed distances on grid vertices by minimizing the loss function below,
| (8) |
where , , and are balance weights to make each term contribute equally. Fig. 3 shows the signed distance field on a slide of during optimization. Our optimization starts from an initial sphere and only optimizes variables in the bandwidth. We skip the grids that are not optimized after the initialization during the marching cubes for surface reconstruction. Please watch our video for more details.

4 Experiments and Analysis
We evaluate GridPull by numerical and visual comparisons with the latest methods on synthetic and real datasets in surface reconstruction.
Datasets and Metrics. We use benchmarks for shapes and scenes in evaluations. For shapes, we conduct evaluations on five datasets including a subset of ShapeNet [1], FAMOUS [17], Thingi10k [103], Surface Reconstruction Benchmark (SRB) [89] and D-FAUST [5]. For scenes, we also report comparisons on five datasets including 3DScene [104], SceneNet [27], 3DFRONT [18], Matterport [9] and KITTI [20].
We use L2 Chamfer distance (), and Hausdorff distance(HD) to measure the error between the reconstructed surface and the ground truth. Moreover, we use normal consistency (NC) and F-score to evaluate the accuracy of normal on the reconstructed surface. We also report our time and storage complexity to highlight our advantage towards scalability. We also use the intersection over union (IoU) to measure the reconstruction for fair comparison with the latest methods.
Details. We use to infer a distance field. We calculate the pulling loss on grids in a bandwidth with . We impose the continuous constraint on grids in a bandwidth with for shapes and for scenes, since scenes contain open surfaces with larger empty spaces. We run the marching cubes for surface reconstruction at a resolution of 256.
We use the Adam optimizer with an initial learning rate of 1.0. We decrease the learning rate with a decay rate of 0.3 every 400 iterations. We use queries in each iteration, and run 1600 iterations for each point cloud during optimization. We set the balance weights , , and for equal contribution from the three terms.

4.1 Surface Reconstruction for Shapes
ShapeNet. Following predictive context prior (PCP) [51] and NeuralPull (NP) [49], we report our results on a subset in ShapeNet in terms of in Tab. 1, Normal Consistency (NC) in Tab. 2, and F-Score with thresholds of and in Tab. 3 and Tab. 4, which show our superiority over PCP and NP in numerical comparisons over all classes, even though PCP employs a local shape prior learned from a large scale dataset. The visual comparison in Fig. 4 shows that we can reveal more accurate and detailed geometry.
| Class | NP [49] | PCP [51] | Ours |
|---|---|---|---|
| Display | 0.039 | 0.0087 | 0.0082 |
| Lamp | 0.080 | 0.0380 | 0.0347 |
| Airplane | 0.008 | 0.0065 | 0.0007 |
| Cabinet | 0.026 | 0.0153 | 0.0112 |
| Vessel | 0.022 | 0.0079 | 0.0033 |
| Table | 0.060 | 0.0131 | 0.0052 |
| Chair | 0.054 | 0.0110 | 0.0043 |
| Sofa | 0.012 | 0.0086 | 0.0015 |
| Mean | 0.038 | 0.0136 | 0.0086 |
| Class | NP [49] | PCP [51] | Ours |
|---|---|---|---|
| Display | 0.964 | 0.9775 | 0.9847 |
| Lamp | 0.930 | 0.9450 | 0.9693 |
| Airplane | 0.947 | 0.9490 | 0.9614 |
| Cabinet | 0.930 | 0.9600 | 0.9689 |
| Vessel | 0.941 | 0.9546 | 0.9667 |
| Table | 0.908 | 0.9595 | 0.9755 |
| Chair | 0.937 | 0.9580 | 0.9733 |
| Sofa | 0.951 | 0.9680 | 0.9792 |
| Mean | 0.939 | 0.9590 | 0.9723 |
| Class | NP [49] | PCP [51] | Ours |
|---|---|---|---|
| Display | 0.989 | 0.9939 | 0.9963 |
| Lamp | 0.891 | 0.9382 | 0.9455 |
| Airplane | 0.996 | 0.9942 | 0.9976 |
| Cabinet | 0.980 | 0.9888 | 0.9901 |
| Vessel | 0.985 | 0.9935 | 0.9956 |
| Table | 0.922 | 0.9969 | 0.9977 |
| Chair | 0.954 | 0.9970 | 0.9979 |
| Sofa | 0.968 | 0.9943 | 0.9974 |
| Mean | 0.961 | 0.9871 | 0.9896 |
| Class | NP [49] | PCP [51] | Ours |
|---|---|---|---|
| Display | 0.991 | 0.9958 | 0.9963 |
| Lamp | 0.924 | 0.9402 | 0.9538 |
| Airplane | 0.997 | 0.9972 | 0.9989 |
| Cabinet | 0.989 | 0.9939 | 0.9946 |
| Vessel | 0.990 | 0.9958 | 0.9972 |
| Table | 0.973 | 0.9985 | 0.9990 |
| Chair | 0.969 | 0.9991 | 0.9990 |
| Sofa | 0.974 | 0.9987 | 0.9992 |
| Mean | 0.976 | 0.9899 | 0.9923 |

FAMOUS. We follow the experimental setting in PCP [51] and NP [49] to evaluate GridPull on FAMOUS. We compare GridPull with the latest methods with priors including PCP, GenSDF, FGC and no priors including NP and IGR. GridPull outperforms these methods in terms of and running time. Although FGC is fast, it does not reconstruct a watertight mesh but just a polygon soup with no normal, which contains almost no geometry details. Worse than that, it fails to reconstruct some point clouds in more than eight hours, hence we remove these shapes from its results. We highlight our superiority in visual comparison in Fig. 5. We can reveal details like hair and expressions more clearly.
| Method | Min time | Mean time | |
|---|---|---|---|
| IGR [24] | 1.650 | 402s | 407s |
| GenSDF [15] | 0.668 | 230s | 232s |
| NP [49] | 0.220 | 593s | 605s |
| FGC [97] | 0.055 | 10s | Timeout |
| PCP [51] | 0.044 | 3416s | 3534s |
| Ours | 0.040 | 198s | 201s |

SRB. We follow the experimental setting in VisCo [67] to evaluate GridPull on real scans in SRB. We report the comparison with the latest overfitting based methods in terms of in Tab. 6. Meanwhile, we also report their one-sided distances between the reconstructed mesh and the input noisy point cloud. The numerical comparison shows that our method significantly outperforms the latest. Moreover, we also report our results of learning unsigned distances in Tab. 7. We replace our pulling loss with the pulling loss introduced for unsigned distances in CAP-UDF [102], and remove the gradient loss due to the nondifferentiable character of UDF on surface. Visual comparison in Fig. 6 shows that our method can reconstruct surfaces that are more compact than the methods learning SDF like SIREN or more smooth than the methods learning UDF like CAP-UDF.
| Poisson [37] | IGR [24] | SIREN [71] | VisCo [67] | SAP [65] | Ours | ||
|---|---|---|---|---|---|---|---|
| Anchor | 0.60 | 0.22 | 0.32 | 0.21 | 0.12 | 0.093 | |
| 14.89 | 4.71 | 8.19 | 3.00 | 2.38 | 1.804 | ||
| 0.60 | 0.12 | 0.10 | 0.15 | 0.08 | 0.066 | ||
| 14.89 | 1.32 | 2.43 | 1.07 | 0.83 | 0.460 | ||
| Daratech | 0.44 | 0.25 | 0.21 | 0.26 | 0.07 | 0.062 | |
| 7.24 | 4.01 | 4.30 | 4.06 | 0.87 | 0.648 | ||
| 0.44 | 0.08 | 0.09 | 0.14 | 0.04 | 0.039 | ||
| 7.24 | 1.59 | 1.77 | 1.76 | 0.41 | 0.293 | ||
| DC | 0.27 | 0.17 | 0.15 | 0.15 | 0.07 | 0.066 | |
| 3.10 | 2.22 | 2.18 | 2.22 | 1.17 | 1.103 | ||
| 0.27 | 0.09 | 0.06 | 0.09 | 0.04 | 0.036 | ||
| 3.10 | 2.61 | 2.76 | 2.76 | 0.53 | 0.539 | ||
| Gargoyle | 0.26 | 0.16 | 0.17 | 0.17 | 0.07 | 0.063 | |
| 6.80 | 3.52 | 4.64 | 4.40 | 1.49 | 1.129 | ||
| 0.26 | 0.06 | 0.08 | 0.11 | 0.05 | 0.045 | ||
| 6.80 | 0.81 | 0.91 | 0.96 | 0.78 | 0.700 | ||
| Lord Quas | 0.20 | 0.12 | 0.17 | 0.12 | 0.05 | 0.047 | |
| 4.61 | 1.17 | 0.82 | 1.06 | 0.98 | 0.569 | ||
| 0.20 | 0.07 | 0.12 | 0.07 | 0.04 | 0.031 | ||
| 4.61 | 0.98 | 0.76 | 0.64 | 0.51 | 0.370 |

Thingi10K. We follow the experimental setting in SAP [65] to evaluate GridPull in Thingi10K. Tab. 8 indicates our superiority over the overfitting based methods in the numerical comparison. Visual comparisons in Fig. 7 show our more accurate surfaces with complex details.
| IGR [24] | SAP [65] | Ours | ||
|---|---|---|---|---|
| Thing10k | 0.440 | 0.054 | 0.051 | |
| F-Score | 0.505 | 0.940 | 0.948 | |
| NC | 0.692 | 0.947 | 0.965 | |
| DFAUST | 0.235 | 0.043 | 0.015 | |
| F-Score | 0.805 | 0.966 | 0.975 | |
| NC | 0.911 | 0.959 | 0.978 |
D-FAUST. We also follow the experimental setting in SAP [65] to evaluate GridPull in D-FAUST. Tab. 8 shows that we outperform the overfitting based methods with more surface details. As shown in Fig. 7, we recover more accurate human bodies and more detailed expressions on faces.

4.2 Surface Reconstruction for Scenes
3DScene. We follow PCP [51] to report , and Normal Consistency(NC) for evaluation. We report the comparisons with the latest methods in Tab. 9. We outperform both kinds of methods with learned priors such as ConvOcc [73] and PCP [51] and overfitting based NP [49] in all scenes. The visual comparisons 8 shows that our method can work well with real scans on scenes and reveal more geometry details on surfaces.
| ConvOcc [73] | NP [49] | PCP[51] | Ours | ||
|---|---|---|---|---|---|
| Burghers | 26.69 | 1.76 | 0.267 | 0.246 | |
| 0.077 | 0.010 | 0.008 | 0.008 | ||
| NC | 0.865 | 0.883 | 0.914 | 0.926 | |
| Lounge | 8.68 | 39.71 | 0.061 | 0.055 | |
| 0.042 | 0.059 | 0.006 | 0.005 | ||
| NC | 0.857 | 0.857 | 0.928 | 0.922 | |
| Copyroom | 10.99 | 0.51 | 0.076 | 0.069 | |
| 0.045 | 0.011 | 0.007 | 0.006 | ||
| NC | 0.848 | 0.884 | 0.918 | 0.929 | |
| Stonewall | 19.12 | 0.063 | 0.061 | 0.058 | |
| 0.066 | 0.007 | 0.0065 | 0.006 | ||
| NC | 0.866 | 0.868 | 0.888 | 0.893 | |
| Totepole | 1.16 | 0.19 | 0.10 | 0.093 | |
| 0.016 | 0.010 | 0.008 | 0.007 | ||
| NC | 0.925 | 0.765 | 0.784 | 0.847 |

SceneNet. Following the experimental setting in PCP [51], we report our , NC, and F-score in Tab. 10. The comparison indicates that we outperform these methods by producing more accurate and smooth surfaces. This is also verified by our visual comparison in Fig. 9, where the latest methods reveal either no or inaccurate indoor geometry.
| NP [49] | PCP [51] | Ours | ||
| Livingroom | 0.088 | 0.017 | 0.015 | |
| 0.881 | 0.933 | 0.922 | ||
| FScore | 0.801 | 0.966 | 0.953 | |
| Bathroom | 0.036 | 0.016 | 0.013 | |
| 0.912 | 0.945 | 0.952 | ||
| FScore | 0.860 | 0.977 | 0.974 | |
| Bedroom | 0.034 | 0.014 | 0.014 | |
| 0.905 | 0.948 | 0.951 | ||
| FScore | 0.876 | 0.980 | 0.986 | |
| Kitchen | 0.049 | 0.015 | 0.014 | |
| 0.900 | 0.945 | 0.952 | ||
| FScore | 0.825 | 0.976 | 0.984 | |
| Office | 0.062 | 0.024 | 0.022 | |
| 0.879 | 0.919 | 0.931 | ||
| FScore | 0.729 | 925 | 0.940 | |
| Mean | 0.054 | 0.017 | 0.0156 | |
| 0.895 | 0.938 | 0.9416 | ||
| FScore | 0.818 | 965 | 0.9674 |

3D-FRONT. We follow the experimental setting in NeuralPoisson [16] to report , IoU and L2 distance over the voxelization of meshes. IoU and L2 distances are calculated as the error between the reconstructed surfaces and the ground truth over the voxelization at a resolution of 128. The comparison in Tab. 11 shows that our results are more accurate than the latest method. Our visual comparison with SIREN in Fig. 10 shows that GridPull can infer an accurate zero level set which leads to very sharp corners.
| Method | CD | IOU | L2 |
|---|---|---|---|
| SIREN [71] | 0.0183 | 0.524 | 2.373 |
| NeuralPoisson [16] | 0.0161 | 0.545 | 2.073 |
| Ours | 0.0141 | 0.562 | 1.984 |

Matterport. We follow the experimental setting in NGS [30], and report the comparison in terms of , NC, and F-score in Tab. 12. We achieve the best performance in terms of accuracy. NGS [30] has a pretty fast inference but it costs about four to five days to learn priors from the training set in Matterport. Visual comparison in Fig. 11 shows that we can reconstruct more accurate surfaces while NGS is poorly generalized to unseen scenes.

4.3 Ablation Studies
We conduct ablation studies on FAMOUS [17] to justify the effectiveness of modules in GridPull.
Loss. We justify the effectiveness of our loss in terms of in Tab. 13. For the pulling loss, it is able to estimate a coarse shape but with discontinuous meshes and artifacts. The gradient loss can improve the continuousness on the surface. Using the TV loss, we obtained a more continuous field, which removes most of artifacts and significantly improve the accuracy. The surface loss encourages a more accurate zero level-set, which also improves the accuracy.
| Loss | |
|---|---|
| 0.184 | |
| 0.126 | |
| 0.056 | |
| 0.040 |

Resolution . We compare the effect of resolution on the reconstructed surfaces. We try several candidates to learn the discrete distance field. We use the same bandwidth for the calculation of the pulling loss and the TV loss, and reconstruct meshes by running the marching cubes at the same resolution. The numerical and visual comparisons show that higher resolutions can infer more geometry details but also cost more inference time.
| 32 | 64 | 128 | 256 | 512 | |
|---|---|---|---|---|---|
| 0.186 | 0.097 | 0.048 | 0.040 | 0.035 | |
| Time | 50s | 67s | 84s | 201s | 645s |
Point Number. We compare our performance on different numbers of points. We use the same set of shapes but with different numbers of points including . The numerical comparison in Tab. 15 shows that our method can estimate a discrete distance field from different numbers of points well, which leads to more accurate reconstructed surfaces than the latest overfitting based methods. In addition, our time complexity is not affected by the number of points a lot, while the latest methods require more time to converge on more points.
| Number | Method | Time | Memory | |
|---|---|---|---|---|
| 10K | NP | 0.351 | 548s | 4.5G |
| SAP | 0.275 | 147s | 3.5G | |
| Ours | 0.122 | 82s | 3.3G | |
| 100K | NP | 0.224 | 615s | 4.6G |
| SAP | 0.076 | 354s | 3.6G | |
| Ours | 0.040 | 84s | 3.3G | |
| 1000K | NP | 0.175 | 1304s | 4.8G |
| SAP | 0.063 | 841s | 3.7G | |
| Ours | 0.039 | 90s | 3.4G |
Initialization. We highlight our geometric initialization of distances on grid vertices by comparing it with random initialization. The comparison in Tab. 16 shows that random initialization makes the optimization converge hard, and cannot work well with the TV loss, especially with a bandwidth, which produces lots of artifacts in empty spaces. Moreover, we try an Eikonal constraint on gradients based on the geometric initialization, but did not get improvement.
| Random | Geometric | ||
|---|---|---|---|
| 0.155 | 0.040 | 0.054 |
Bandwidth. We report the effect of bandwidth and in the pulling loss and the TV loss in Tab. 17. For both losses, the bandwidth controls the scope of query sampling and continuous constraints. A larger bandwidth would cover more parameters which require more time and make the optimization converge slowly. For instance, if we sample queries and impose the pulling in all grids, the speed is even slower than NeuralPull which uses neural network for the pulling, since neural networks can generalize signed distances nearby and do not need to infer in all grids. Although a small bandwidth would save time, a too small bandwidth would cover too few grids around the surface, which leads to discontinuousness and artifacts. While if the bandwidth is large enough, we may not see surface improvement but just cost more time. Moreover, even with the same loss, NeuralPull does not produce better results than ours. Comparing with methods using neural networks, our discrete SDF can have faster convergence, as indicated by the angular error of gradients in Fig. 14.
| Bandwidth | Time | |
|---|---|---|
| () | 0.040 | 84s |
| (All Grids) | 0.043 | 628s |
| () | 0.079 | 83s |
| () | 0.040 | 84s |
| () | 0.041 | 89s |
| () | 0.040 | 96s |
| (All Grids) | 0.040 | 101s |
| NeuralPull | 0.220 | 552s |
| NeuralPull++ | 0.203 | 554s |

Noises. We report our performance on point clouds with noise. We follow the experimental setting in PCP, and report our results with middle and large level noise in Tab. 18. To handle noise, we weight more on the continuous constraint using a larger to decrease the impact of noise. The comparison shows that our method can handle noise better than the neural network based methods. Since the continuousness of neural networks make gradients near the surface over smooth to overfit all noise, this makes it hard to infer accurate zero level-set.
Normals. We report our performance on point clouds with normals. If GT normal is available, we could add a supervision on normals at points on the surface. What we do is to supervise the gradients at points on the surface using their ground truth normals. The comparisons in Tab. 19 show that the normal supervision improves the performance a little. This indicates that our method can infer pretty accurate gradients on the surface or near the surface, where gradients on the surface can be highly accurate to the normal ground truth on surfaces.
| Class | Ours | Ours(Normals) |
|---|---|---|
| 0.0401 | 0.0403 |
5 Conclusion
We introduce GridPull for the fast inference of distance fields from large scale point clouds without using neural components. We infer a distance field using learnable parameters defined on discrete grids, which we can directly optimize in a more efficient way than neural networks. Besides the complexity advantage, our loss function manages to achieve more continuous distance fields with more consistent gradients, which leads to higher accuracy in surface reconstruction. We evaluate GridPull and justify its effectiveness on benchmarks. Numerical and visual comparisons show that GridPull outperforms the latest methods in terms of accuracy and complexity, even without using priors, normal, and neural networks.
References
- [1] ShapeNet. https://www.shapenet.org/.
- [2] Matan Atzmon and Yaron Lipman. SAL: Sign agnostic learning of shapes from raw data. In IEEE Conference on Computer Vision and Pattern Recognition, 2020.
- [3] Matan Atzmon and yaron Lipman. SALD: sign agnostic learning with derivatives. In International Conference on Learning Representations, 2021.
- [4] Yizhak Ben-Shabat, Chamin Hewa Koneputugodage, and Stephen Gould. DiGS : Divergence guided shape implicit neural representation for unoriented point clouds. CoRR, abs/2106.10811, 2021.
- [5] Federica Bogo, Javier Romero, Gerard Pons-Moll, and Michael J. Black. Dynamic FAUST: Registering human bodies in motion. In IEEE Computer Vision and Pattern Recognition, 2017.
- [6] Alexandre Boulch and Renaud Marlet. POCO: Point convolution for surface reconstruction. In IEEE Conference on Computer Vision and Pattern Recognition, pages 6302–6314, 2022.
- [7] Tim Brooks, Aleksander Holynski, and Alexei A. Efros. Instructpix2pix: Learning to follow image editing instructions. In CVPR, 2023.
- [8] Rohan Chabra, Jan Eric Lenssen, Eddy Ilg, Tanner Schmidt, Julian Straub, Steven Lovegrove, and Richard A. Newcombe. Deep local shapes: Learning local SDF priors for detailed 3D reconstruction. In European Conference on Computer Vision, volume 12374, pages 608–625, 2020.
- [9] Angel Chang, Angela Dai, Thomas Funkhouser, Maciej Halber, Matthias Niessner, Manolis Savva, Shuran Song, Andy Zeng, and Yinda Zhang. Matterport3d: Learning from rgb-d data in indoor environments. International Conference on 3D Vision (3DV), 2017.
- [10] Chao Chen, Zhizhong Han, Yu-Shen Liu, and Matthias Zwicker. Unsupervised learning of fine structure generation for 3D point clouds by 2D projections matching. In IEEE International Conference on Computer Vision, 2021.
- [11] Chao Chen, Yu-Shen Liu, and Zhizhong Han. Latent partition implicit with surface codes for 3d representation. In European Conference on Computer Vision, 2022.
- [12] Chao Chen, Yu-Shen Liu, and Zhizhong Han. Unsupervised inference of signed distance functions from single sparse point clouds without learning priors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 17712–17723, 2023.
- [13] Zhiqin Chen and Hao Zhang. Learning implicit fields for generative shape modeling. IEEE Conference on Computer Vision and Pattern Recognition, 2019.
- [14] Julian Chibane, Aymen Mir, and Gerard Pons-Moll. Neural unsigned distance fields for implicit function learning. arXiv, 2010.13938, 2020.
- [15] Gene Chou, Ilya Chugunov, and Felix Heide. GenSDF: Two-stage learning of generalizable signed distance functions. In Proc. of Neural Information Processing Systems (NeurIPS), 2022.
- [16] Angela Dai and Matthias Nießner. Neural Poisson: Indicator functions for neural fields. arXiv preprint arXiv:2211.14249, 2022.
- [17] Philipp Erler, Paul Guerrero, Stefan Ohrhallinger, Niloy J. Mitra, and Michael Wimmer. Points2Surf: Learning implicit surfaces from point clouds. In European Conference on Computer Vision, 2020.
- [18] Huan Fu, Bowen Cai, Lin Gao, Lingxiao Zhang, Cao Li, Zengqi Xun, Chengyue Sun, Yiyun Fei, Yu Zheng, Ying Li, Yi Liu, Peng Liu, Lin Ma, Le Weng, Xiaohang Hu, Xin Ma, Qian Qian, Rongfei Jia, Binqiang Zhao, and Hao Zhang. 3d-front: 3d furnished rooms with layouts and semantics. CoRR, abs/2011.09127, 2020.
- [19] Qiancheng Fu, Qingshan Xu, Yew-Soon Ong, and Wenbing Tao. Geo-Neus: Geometry-consistent neural implicit surfaces learning for multi-view reconstruction. 2022.
- [20] Andreas Geiger, Philip Lenz, and Raquel Urtasun. Are we ready for autonomous driving? the kitti vision benchmark suite. In Computer Vision and Pattern Recognition, 2012.
- [21] Kyle Genova, Forrester Cole, Daniel Vlasic, Aaron Sarna, William T. Freeman, and Thomas Funkhouser. Learning shape templates with structured implicit functions. In International Conference on Computer Vision, 2019.
- [22] Lily Goli, Daniel Rebain, Sara Sabour, Animesh Garg, and Andrea Tagliasacchi. nerf2nerf: Pairwise registration of neural radiance fields. In 2023 IEEE International Conference on Robotics and Automation (ICRA), pages 9354–9361. IEEE, 2023.
- [23] Amos Gropp, Lior Yariv, Niv Haim, Matan Atzmon, and Yaron Lipman. Implicit geometric regularization for learning shapes. In International Conference on Machine Learning, volume 119 of Proceedings of Machine Learning Research, pages 3789–3799, 2020.
- [24] Amos Gropp, Lior Yariv, Niv Haim, Matan Atzmon, and Yaron Lipman. Implicit geometric regularization for learning shapes. arXiv, 2002.10099, 2020.
- [25] Zhizhong Han, Chao Chen, Yu-Shen Liu, and Matthias Zwicker. ShapeCaptioner: Generative caption network for 3D shapes by learning a mapping from parts detected in multiple views to sentences. ArXiv, abs/1908.00120, 2019.
- [26] Zhizhong Han, Chao Chen, Yu-Shen Liu, and Matthias Zwicker. DRWR: A differentiable renderer without rendering for unsupervised 3D structure learning from silhouette images. In International Conference on Machine Learning, 2020.
- [27] A. Handa, V. Patraucean, V. Badrinarayanan, S. Stent, and R. Cipolla. Understanding realworld indoor scenes with synthetic data. In IEEE Conference on Computer Vision and Pattern Recognition, pages 4077–4085, 2016.
- [28] Ayaan Haque, Matthew Tancik, Alexei Efros, Aleksander Holynski, and Angjoo Kanazawa. Instruct-nerf2nerf: Editing 3d scenes with instructions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
- [29] Amir Hertz, Ron Mokady, Jay Tenenbaum, Kfir Aberman, Yael Pritch, and Daniel Cohen-Or. Prompt-to-prompt image editing with cross attention control. arXiv preprint arXiv:2208.01626, 2022.
- [30] Jiahui Huang, Hao-Xiang Chen, and Shi-Min Hu. A neural galerkin solver for accurate surface reconstruction. ACM Trans. Graph., 41(6), 2022.
- [31] Meng Jia and Matthew Kyan. Learning occupancy function from point clouds for surface reconstruction. arXiv, 2010.11378, 2020.
- [32] Chiyu Jiang, Avneesh Sud, Ameesh Makadia, Jingwei Huang, Matthias Nießner, and Thomas Funkhouser. Local implicit grid representations for 3D scenes. In IEEE Conference on Computer Vision and Pattern Recognition, 2020.
- [33] Sijia Jiang, Jing Hua, and Zhizhong Han. Coordinate quantized neural lmplicit representations for multi-view reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
- [34] Yue Jiang, Dantong Ji, Zhizhong Han, and Matthias Zwicker. SDFDiff: Differentiable rendering of signed distance fields for 3D shape optimization. In IEEE Conference on Computer Vision and Pattern Recognition, 2020.
- [35] Chuan Jin, Tieru Wu, and Junsheng Zhou. Multi-grid representation with field regularization for self-supervised surface reconstruction from point clouds. Computers & Graphics, 2023.
- [36] Heewoo Jun and Alex Nichol. Shap-e: Generating conditional 3d implicit functions. arXiv preprint arXiv:2305.02463, 2023.
- [37] Michael M. Kazhdan and Hugues Hoppe. Screened poisson surface reconstruction. ACM Transactions Graphics, 32(3):29:1–29:13, 2013.
- [38] Hai Li, Xingrui Yang, Hongjia Zhai, Yuqian Liu, Hujun Bao, and Guofeng Zhang. Vox-Surf: Voxel-based implicit surface representation. CoRR, abs/2208.10925, 2022.
- [39] Shujuan Li, Junsheng Zhou, Baorui Ma, Yu-Shen Liu, and Zhizhong Han. Neaf: Learning neural angle fields for point normal estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, 2023.
- [40] Tianyang Li, Xin Wen, Yu-Shen Liu, Hua Su, and Zhizhong Han. Learning deep implicit functions for 3D shapes with dynamic code clouds. In IEEE Conference on Computer Vision and Pattern Recognition, pages 12830–12840, 2022.
- [41] Zhaoshuo Li, Thomas Müller, Alex Evans, Russell H Taylor, Mathias Unberath, Ming-Yu Liu, and Chen-Hsuan Lin. Neuralangelo: High-fidelity neural surface reconstruction. In IEEE Conference on Computer Vision and Pattern Recognition, 2023.
- [42] Chen-Hsuan Lin, Chaoyang Wang, and Simon Lucey. SDF-SRN: Learning signed distance 3D object reconstruction from static images. In Advances in Neural Information Processing Systems, 2020.
- [43] Minghua Liu, Xiaoshuai Zhang, and Hao Su. Meshing point clouds with predicted intrinsic-extrinsic ratio guidance. In European Conference on Computer vision, 2020.
- [44] Shichen Liu, Shunsuke Saito, Weikai Chen, and Hao Li. Learning to infer implicit surfaces without 3D supervision. In Advances in Neural Information Processing Systems, 2019.
- [45] Shaohui Liu, Yinda Zhang, Songyou Peng, Boxin Shi, Marc Pollefeys, and Zhaopeng Cui. DIST: Rendering deep implicit signed distance function with differentiable sphere tracing. In IEEE Conference on Computer Vision and Pattern Recognition, 2020.
- [46] Shi-Lin Liu, Hao-Xiang Guo, Hao Pan, Pengshuai Wang, Xin Tong, and Yang Liu. Deep implicit moving least-squares functions for 3D reconstruction. In IEEE Conference on Computer Vision and Pattern Recognition, 2021.
- [47] Yu-Tao Liu, Li Wang, Jie Yang, Weikai Chen, Xiaoxu Meng, Bo Yang, and Lin Gao. NeUDF: Leaning neural unsigned distance fields with volume rendering. In Computer Vision and Pattern Recognition (CVPR), 2023.
- [48] William E. Lorensen and Harvey E. Cline. Marching cubes: A high resolution 3D surface construction algorithm. Computer Graphics, 21(4):163–169, 1987.
- [49] Baorui Ma, Zhizhong Han, Yu-Shen Liu, and Matthias Zwicker. Neural-Pull: Learning signed distance functions from point clouds by learning to pull space onto surfaces. In International Conference on Machine Learning, 2021.
- [50] Baorui Ma, Yu-Shen Liu, and Zhizhong Han. Reconstructing surfaces for sparse point clouds with on-surface priors. In IEEE Conference on Computer Vision and Pattern Recognition, pages 6305–6315, 2022.
- [51] Baorui Ma, Yu-Shen Liu, Matthias Zwicker, and Zhizhong Han. Surface reconstruction from point clouds by learning predictive context priors. In IEEE Conference on Computer Vision and Pattern Recognition, pages 6316–6327, 2022.
- [52] Baorui Ma, Yu-Shen Liu, and Zhizhong Han. Learning signed distance functions from noisy 3d point clouds via noise to noise mapping. In Advances in Neural Information Processing Systems (NeurIPS), 2023.
- [53] Baorui Ma, Junsheng Zhou, Yu-Shen Liu, and Zhizhong Han. Towards better gradient consistency for neural signed distance functions via level set alignment. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 17724–17734, 2023.
- [54] Julien N. P. Martel, David B. Lindell, Connor Z. Lin, Eric R. Chan, Marco Monteiro, and Gordon Wetzstein. ACORN: adaptive coordinate networks for neural scene representation. CoRR, abs/2105.02788, 2021.
- [55] Xiaoxu Meng, Weikai Chen, and Bo Yang. NeAT: Learning neural implicit surfaces with arbitrary topologies from multi-view images. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, June 2023.
- [56] Lars Mescheder, Michael Oechsle, Michael Niemeyer, Sebastian Nowozin, and Andreas Geiger. Occupancy networks: Learning 3D reconstruction in function space. In IEEE Conference on Computer Vision and Pattern Recognition, 2019.
- [57] Zhenxing Mi, Yiming Luo, and Wenbing Tao. SSRNet: Scalable 3D surface reconstruction network. In IEEE Conference on Computer Vision and Pattern Recognition, 2020.
- [58] Mateusz Michalkiewicz, Jhony K. Pontes, Dominic Jack, Mahsa Baktashmotlagh, and Anders P. Eriksson. Deep level sets: Implicit surface representations for 3D shape inference. CoRR, abs/1901.06802, 2019.
- [59] Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. NeRF: Representing scenes as neural radiance fields for view synthesis. In European Conference on Computer Vision, 2020.
- [60] Thomas Müller, Alex Evans, Christoph Schied, and Alexander Keller. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph., 41(4):102:1–102:15, July 2022.
- [61] Michael Niemeyer, Lars Mescheder, Michael Oechsle, and Andreas Geiger. Differentiable volumetric rendering: Learning implicit 3D representations without 3D supervision. In IEEE Conference on Computer Vision and Pattern Recognition, 2020.
- [62] Michael Oechsle, Songyou Peng, and Andreas Geiger. UNISURF: Unifying neural implicit surfaces and radiance fields for multi-view reconstruction. In International Conference on Computer Vision, 2021.
- [63] Amine Ouasfi and Adnane Boukhayma. Few ‘zero level set’-shot learning of shape signed distance functions in feature space. In European Conference on Computer Vision, 2022.
- [64] Jeong Joon Park, Peter Florence, Julian Straub, Richard Newcombe, and Steven Lovegrove. DeepSDF: Learning continuous signed distance functions for shape representation. In IEEE Conference on Computer Vision and Pattern Recognition, 2019.
- [65] Songyou Peng, Chiyu “Max” Jiang, Yiyi Liao, Michael Niemeyer, Marc Pollefeys, and Andreas Geiger. Shape as points: A differentiable poisson solver. In Advances in Neural Information Processing Systems, 2021.
- [66] Songyou Peng, Michael Niemeyer, Lars M. Mescheder, Marc Pollefeys, and Andreas Geiger. Convolutional occupancy networks. In European Conference on Computer Vision, volume 12348, pages 523–540, 2020.
- [67] Albert Pumarola, Artsiom Sanakoyeu, Lior Yariv, Ali Thabet, and Yaron Lipman. Visco grids: Surface reconstruction with viscosity and coarea grids. In Advances in Neural Information Processing Systems, 2022.
- [68] Konstantinos Rematas, Ricardo Martin-Brualla, and Vittorio Ferrari. Sharf: Shape-conditioned radiance fields from a single view. In International Conference on Machine Learning, 2021.
- [69] Radu Alexandru Rosu and Sven Behnke. Permutosdf: Fast multi-view reconstruction with implicit surfaces using permutohedral lattices. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2023.
- [70] Sara Fridovich-Keil and Alex Yu, Matthew Tancik, Qinhong Chen, Benjamin Recht, and Angjoo Kanazawa. Plenoxels: Radiance fields without neural networks. In IEEE Conference on Computer Vision and Pattern Recognition, 2022.
- [71] Vincent Sitzmann, Julien N.P. Martel, Alexander W. Bergman, David B. Lindell, and Gordon Wetzstein. Implicit neural representations with periodic activation functions. In Advances in Neural Information Processing Systems, 2020.
- [72] Vincent Sitzmann, Michael Zollhöfer, and Gordon Wetzstein. Scene representation networks: Continuous 3D-structure-aware neural scene representations. In Advances in Neural Information Processing Systems, 2019.
- [73] Lars Mescheder Marc Pollefeys Andreas Geiger Songyou Peng, Michael Niemeyer. Convolutional occupancy networks. In European Conference on Computer Vision, 2020.
- [74] Cheng Sun, Min Sun, and Hwann-Tzong Chen. Direct voxel grid optimization: Super-fast convergence for radiance fields reconstruction. CoRR, abs/2111.11215, 2021.
- [75] Cheng Sun, Min Sun, and Hwann-Tzong Chen. Direct voxel grid optimization: Super-fast convergence for radiance fields reconstruction. In IEEE Conference on Computer Vision and Pattern Recognition, 2022.
- [76] Cheng Sun, Min Sun, and Hwann-Tzong Chen. Improved direct voxel grid optimization for radiance fields reconstruction. arXiv preprint arXiv:2206.05085, 2022.
- [77] Towaki Takikawa, Joey Litalien, Kangxue Yin, Karsten Kreis, Charles Loop, Derek Nowrouzezahrai, Alec Jacobson, Morgan McGuire, and Sanja Fidler. Neural geometric level of detail: Real-time rendering with implicit 3D shapes. In IEEE Conference on Computer Vision and Pattern Recognition, 2021.
- [78] Jiapeng Tang, Jiabao Lei, Dan Xu, Feiying Ma, Kui Jia, and Lei Zhang. SA-ConvONet: Sign-agnostic optimization of convolutional occupancy networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021.
- [79] Jia-Heng Tang, Weikai Chen, Jie Yang, Bo Wang, Songrun Liu, Bo Yang, and Lin Gao. Octfield: Hierarchical implicit functions for 3d modeling. In The Annual Conference on Neural Information Processing Systems, 2021.
- [80] Edgar Tretschk, Ayush Tewari, Vladislav Golyanik, Michael Zollhöfer, Carsten Stoll, and Christian Theobalt. PatchNets: Patch-Based Generalizable Deep Implicit 3D Shape Representations. European Conference on Computer Vision, 2020.
- [81] Delio Vicini, Sébastien Speierer, and Wenzel Jakob. Differentiable signed distance function rendering. ACM Transactions on Graphics, 41(4):125:1–125:18, 2022.
- [82] Jiepeng Wang, Peng Wang, Xiaoxiao Long, Christian Theobalt, Taku Komura, Lingjie Liu, and Wenping Wang. NeuRIS: Neural reconstruction of indoor scenes using normal priors. In European Conference on Computer Vision, 2022.
- [83] Meng Wang, Yu-Shen Liu, Yue Gao, Kanle Shi, Yi Fang, and Zhizhong Han. Lp-dif: Learning local pattern-specific deep implicit function for 3d objects and scenes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 21856–21865, June 2023.
- [84] Peng Wang, Lingjie Liu, Yuan Liu, Christian Theobalt, Taku Komura, and Wenping Wang. NeuS: Learning neural implicit surfaces by volume rendering for multi-view reconstruction. In Advances in Neural Information Processing Systems, pages 27171–27183, 2021.
- [85] Peng-Shuai Wang, Yang Liu, and Xin Tong. Dual octree graph networks for learning adaptive volumetric shape representations. ACM Transactions on Graphics, 41(4):1–15, 2022.
- [86] Yiqun Wang, Ivan Skorokhodov, and Peter Wonka. HF-NeuS: Improved surface reconstruction using high-frequency details. In Advances in Neural Information Processing Systems, 2022.
- [87] Xin Wen, Peng Xiang, Zhizhong Han, Yan-Pei Cao, Pengfei Wan, Wen Zheng, and Yu-Shen Liu. Pmp-net++: Point cloud completion by transformer-enhanced multi-step point moving paths. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45(1):852–867, 2022.
- [88] Xin Wen, Junsheng Zhou, Yu-Shen Liu, Hua Su, Zhen Dong, and Zhizhong Han. 3d shape reconstruction from 2d images with disentangled attribute flow. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 3803–3813, 2022.
- [89] Francis Williams, Teseo Schneider, Claudio Silva, Denis Zorin, Joan Bruna, and Daniele Panozzo. Deep geometric prior for surface reconstruction. In IEEE Conference on Computer Vision and Pattern Recognition, 2019.
- [90] Yunjie Wu and Zhengxing Sun. DFR: differentiable function rendering for learning 3D generation from images. Computer Graphics Forum, 39(5):241–252, 2020.
- [91] Peng Xiang, Xin Wen, Yu-Shen Liu, Yan-Pei Cao, Pengfei Wan, Wen Zheng, and Zhizhong Han. SnowflakeNet: Point cloud completion by snowflake point deconvolution with skip-transformer. In IEEE International Conference on Computer Vision, 2021.
- [92] Peng Xiang, Xin Wen, Yu-Shen Liu, Yan-Pei Cao, Pengfei Wan, Wen Zheng, and Zhizhong Han. Snowflake point deconvolution for point cloud completion and generation with skip-transformer. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45(5):6320–6338, 2022.
- [93] Lior Yariv, Jiatao Gu, Yoni Kasten, and Yaron Lipman. Volume rendering of neural implicit surfaces. In Advances in Neural Information Processing Systems, 2021.
- [94] Lior Yariv, Yoni Kasten, Dror Moran, Meirav Galun, Matan Atzmon, Basri Ronen, and Yaron Lipman. Multiview neural surface reconstruction by disentangling geometry and appearance. Advances in Neural Information Processing Systems, 33, 2020.
- [95] Wang Yifan, Shihao Wu, Cengiz Oztireli, and Olga Sorkine-Hornung. Iso-Points: Optimizing neural implicit surfaces with hybrid representations. CoRR, abs/2012.06434, 2020.
- [96] Alex Yu, Ruilong Li, Matthew Tancik, Hao Li, Ren Ng, and Angjoo Kanazawa. PlenOctrees for real-time rendering of neural radiance fields. In IEEE International Conference on Computer Vision, 2021.
- [97] Mulin Yu and Florent Lafarge. Finding good configurations of planar primitives in unorganized point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 6367–6376, June 2022.
- [98] Zehao Yu, Songyou Peng, Michael Niemeyer, Torsten Sattler, and Andreas Geiger. MonoSDF: Exploring monocular geometric cues for neural implicit surface reconstruction. ArXiv, abs/2022.00665, 2022.
- [99] Sergey Zakharov, Wadim Kehl, Arjun Bhargava, and Adrien Gaidon. Autolabeling 3D objects with differentiable rendering of sdf shape priors. In IEEE Conference on Computer Vision and Pattern Recognition, 2020.
- [100] Wenbin Zhao, Jiabao Lei, Yuxin Wen, Jianguo Zhang, and Kui Jia. Sign-agnostic implicit learning of surface self-similarities for shape modeling and reconstruction from raw point clouds. CoRR, abs/2012.07498, 2020.
- [101] Junsheng Zhou, Baorui Ma, Shujuan Li, Yu-Shen Liu, and Zhizhong Han. Learning a more continuous zero level set in unsigned distance fields through level set projection. In Proceedings of the IEEE/CVF international conference on computer vision, 2023.
- [102] Junsheng Zhou, Baorui Ma, Yu-Shen Liu, Yi Fang, and Zhizhong Han. Learning consistency-aware unsigned distance functions progressively from raw point clouds. Advances in Neural Information Processing Systems, 35:16481–16494, 2022.
- [103] Qingnan Zhou and Alec Jacobson. Thingi10k: A dataset of 10, 000 3d-printing models. CoRR, abs/1605.04797, 2016.
- [104] Qian-Yi Zhou and Vladlen Koltun. Dense scene reconstruction with points of interest. ACM Transactions on Graphics, 32(4):112:1–112:8, 2013.