Green’s Function Zeros in Fermi Surface Symmetric Mass Generation

As a specific example of Fermi surface SMG, we consider a bilayer square lattice [104, 105, 106] model of spin-1/2 fermions, as illustrated in Fig. 1(a). Let $c_{il\sigma}$ be the fermion annihilation operator on site-$i$ layer-$l$ ($l=1,2$) and spin-$\sigma$ ($\sigma=\uparrow,\downarrow$). The model is described by the following Hamiltonian

where ${\bm{S}}_{il}:=\tfrac{1}{2}c_{il\sigma}^{\dagger}{\bm{\sigma}}_{\sigma\sigma^{\prime}}c_{il\sigma^{\prime}}$ denotes the spin operator with ${\bm{\sigma}}:=(\sigma^{1},\sigma^{2},\sigma^{3})$ being the Pauli matrices. The Hamiltonian $H$ contains a nearest-neighbor hopping $t$ of the fermions within each layer and an inter-layer Heisenberg spin-spin interaction with antiferromagnetic coupling $J>0$. The Heisenberg interaction should be understood as a four-fermion interaction, that there is no explicitly formed local moment degrees of freedom. Unlike the standard $t$-$J$ model [107], we do not impose any on-site single-occupancy constraint [108] here. We assume that the fermions are half-filled in each layer.

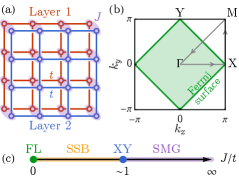
In the non-interacting limit ($J/t\to 0$), the ground state of the tight-binding Hamiltonian in Eq. (3) is a Fermi liquid with a four-fold degenerated (two layers and two spins) square-shaped Fermi surface in the Brillouin zone, as shown in Fig. 1(b). The fermion system is gapless in this limit. However, given that the fermion carries one unit charge under the $\mathrm{U}(1)$ symmetry, the Fermi surface anomaly vanishes due to [87, 76]

where $a$ indexes the four-fold degenerated Fermi surface with $q_{a}=1$ being the $\mathrm{U}(1)$ charge carried by the fermion and $\nu_{a}=1/2$ being the filling fraction. This implies there must be a way to gap out the Fermi surface into a trivial insulator while preserving both the translation and the $\mathrm{U}(1)$ charge conservation symmetries. Nevertheless, these symmetry requirements are restrictive enough to rule out all possible fermion bilinear gapping mechanisms, leaving Fermi surface SMG the only available option.

One possible SMG gapping interaction is the interlayer Heisenberg spin-spin interaction $J$ in Eq. (3). In the strong interaction limit ($J/t\to\infty$), the system has a unique ground state, given by

which is a direct product of the inter-layer spin-singlet state on every site. $|\text{vac}\rangle$ stands for the vacuum state of fermions (i.e. $c_{il\sigma}|\text{vac}\rangle=0$). The SMG ground state $|0\rangle$ does not break any symmetry and does not have topological order. All excitations are gapped by an energy of the order $J$ from the ground state. Any local perturbation far below the energy scale $J$ can not close this excitation gap, so the SMG phase is expected to be stable in a large parameter regime as long as $J\gg t$.

Given the distinct ground states in the two limits of $J/t$, we anticipate at least one quantum phase transition separating the Fermi liquid and the SMG insulator. However, due to the perfect nesting of the Fermi surface, the Fermi liquid state is unstable towards spontaneous symmetry breaking (SSB) upon infinitesimal interaction, so a more plausible phase diagram should look like Fig. 1(c), where an intermediate SSB phase sets in. A mean-field analysis based on the Fermi liquid fixed point shows that there are two degenerated leading instabilities: (i) the inter-layer exciton condensation (EC) and (ii) the inter-layer superconductivity (SC). They are respectively described by the following order parameters

Here, $(-)^{i}$ denotes the stagger sign on the square lattice of lattice momentum $(\pi,\pi)$. $(-)^{\sigma}=+1$ for $\sigma=\uparrow$ and $-1$ for $\sigma=\downarrow$. $\bar{\sigma}$ stands for the opposite spin of $\sigma$.

The energetic degeneracy of these two SSB orders can be explained by the fact that their order parameters $\phi_{\text{EC}}$ and $\phi_{\text{SC}}$ are related by a particle-hole transformation $c_{i2\sigma}\to(-)^{i}(-)^{\sigma}c_{i2\bar{\sigma}}^{\dagger}$ in the second layer only, which is a symmetry of the model Hamiltonian in Eq. (3). The EC $\langle\phi_{\text{EC}}\rangle\neq 0$ spontaneously breaks the translation and interlayer $\mathrm{U}(1)$ symmetry, and the SC $\langle\phi_{\text{SC}}\rangle\neq 0$ spontaneously breaks the total $\mathrm{U}(1)$ symmetry. Both of them gap out the Fermi surfaces fully, leading to an SSB insulator (or superconductor). The SSB and SMG phases are likely separated by an XY transition, at which the symmetry gets restored. We will leave the numerical verification of the proposed phase diagram Fig. 1(c) for future study, as the main focus of this research is to investigate the structure of fermion Green’s function in the SMG insulating phase.

We note that the model Eq. (3) was also introduced as the “coupled ancilla qubit” model to describe the pseudo-gap physics in the recent literature [70, 72, 73]. Its honeycomb lattice version has been investigated in recent numerical simulations [109], where a direct quantum phase transition between semimetal and insulator phases was observed.

The Luttinger theorem [110, 100] asserts that in a fermion many-body system with lattice translation and charge $\mathrm{U}(1)$ symmetries, the ground state charge density $\langle N\rangle/V$ (i.e., the $\mathrm{U}(1)$ charge per unit cell) is tied to the momentum space volume in which the real part of the zero-frequency fermion Green’s function is positive $\operatorname{Re}G(0,{{\bm{k}}})>0$. This can be formally expressed as

Here, the $\mathrm{U}(1)$ symmetry generator $N=\sum_{i,l,\sigma}c_{il\sigma}^{\dagger}c_{il\sigma}$ measures the total charge, and the volume $V=\sum_{i}1$ is defined as the number of unit cells in the lattice system. $N_{f}=4$ counts the fermion flavor number (or the Fermi surface degeneracy), including two layers and two spins. The Green’s function $G(\omega,{{\bm{k}}})$ in Eq. (7) is defined by the fermion two-point correlation as

The correlation function is proportional to an identity matrix in the flavor (layer-spin) space because of the layer $\mathrm{U}(1):c_{l\sigma}\to\mathrm{e}^{(-)^{l}\mathrm{i}\theta}c_{l\sigma}$, the layer interchange $\mathbb{Z}_{2}:c_{1\sigma}\leftrightarrow c_{2\sigma}$, and the spin $\mathrm{SU}(2):c_{l\sigma}\to(\mathrm{e}^{\mathrm{i}{\bm{\theta}}\cdot{\bm{\sigma}}/2})_{\sigma\sigma^{\prime}}c_{l\sigma^{\prime}}$ symmetries.

The Luttinger theorem applies to the Fermi liquid and SMG states in the bilayer square lattice model Eq. (3), as both states preserve the translation and charge $\mathrm{U}(1)$ symmetries. Given that the fermions are half-filled ($\nu=1/2$) in the system, the Fermi volume should be

The Fermi volume is enclosed by the Fermi surface, across which $\operatorname{Re}G(0,{{\bm{k}}})$ changes sign. The sign change can be achieved either by poles or zeros in the Green’s function.

In the Fermi liquid state, the required Fermi volume is satisfied via Green’s function poles along the Fermi surface, as pictured in Fig. 1(b). However, the SMG insulator is a fully gapped state of fermions that has no low-energy quasi-particles (below the energy scale $J$). Consequently, the Green’s function $G(\omega,{{\bm{k}}})$ cannot develop poles at $\omega=0$, meaning the required Fermi volume can only be satisfied by Green’s function zeros. Therefore, the Lutinger theorem implies that there must be robust Green’s function zeros at low energy in the SMG phase, and the zero Fermi surface must enclose half of the Brillouin zone volume in place of the original pole Fermi surface.

It is known that the Luttinger theorem can be violated in the presence of topological order [111, 112, 113, 114, 115, 86, 102, 116, 88, 117]. However, this concern does not affect our discussion in the SMG phase, because the SMG insulator is a trivial insulator without topological order.

The Luttinger theorem only constrains the Fermi volume but does not impose requirements on the shape of the Fermi surface. However, in this particular example of the bilayer square lattice model Eq. (3), the system has sufficient symmetries to determine even the shape of the Fermi surface.

The key symmetry here is a particle-hole symmetry $\mathbb{Z}_{2}^{C}$, which acts as

The Hamiltonian $H$ in Eq. (3) is invariant under this transformation. Since the Green’s function is an identity matrix in the flavor space Eq. (8) which is invariant under any flavor basis transformation, we can omit the flavor indices and focus on the frequency-momentum dependence of the Green’s function, written as

Given Eq. (10), the fermion field $c(t,{\bm{x}})$ transforms under the $\mathbb{Z}_{2}^{C}$ symmetry as

where ${\bm{Q}}=(\pi,\pi)$ is the momentum associated with the stagger sign factor $(-)^{i}$ on the square lattice. As a consequence, the Green’s function transforms as

Furthermore, there are also two diagonal reflection symmetries on the square lattice, which maps ${{\bm{k}}}=(k_{x},k_{y})$ to $(k_{y},k_{x})$ or $(-k_{y},-k_{x})$ in the momentum space.

Both the Fermi liquid and the SMG states preserve the particle-hole symmetry $\mathbb{Z}_{2}^{C}$ and the lattice reflection symmetry, which requires the Green’s function to be invariant under the combined symmetry transformations. So the zero-frequency Green’s function must satisfy

meaning that the sign change of $G(0,{{\bm{k}}})$ should happen along $k_{x}\pm k_{y}=\pi\mod 2\pi$, which precisely describes the shape of the Fermi surface. The Fermi surface is pole-like in the Fermi liquid state and becomes zero-like in the SMG state, but its shape and volume remain the same.

However, it should be noted that the precise overlap of the zero Fermi surface in the SMG insulator and the pole Fermi surface in the Fermi liquid is a fine-tuned feature of the bilayer square lattice model Eq. (3). In more general cases, such as including further neighbor hopping in the model, the particle-hole symmetry would cease to exist, thus the invariance in the shape of the Fermi surface is no longer guaranteed. Nevertheless, the Luttinger theorem can still ensure the invariance in the Fermi volume, thereby providing the SMG insulator with robust Green’s function zeros.

To verify this proposition, we will analyze the behavior of the Green’s function in the SMG phase from both strong and weak coupling perspectives in Sec. III. Our calculations suggest that, for this specific model, the SMG state indeed possesses a Fermi surface (of Green’s function zeros) that is identical in shape to that in the Fermi liquid state.

We will first focus on the strong interaction limit $(J/t\to\infty)$, where the system is deep in the SMG phase and the exact ground state is known (see Eq. (5)). We start from this limit and turn on the hopping term as a perturbation. We employ exact diagonalization and cluster perturbation theory (CPT) [94, 118] to compute the Green’s function in the SMG phase. The details of our method are described in Appendix A. It is valid to use a small cluster to reconstruct the Green’s function in the SMG phase since the ground state is close to a product state that does not have long-range correlation or long-range quantum entanglement. This is quite different from the Hubbard model, where the Fermi surface anomaly is non-vanishing, and the infrared phase must be either SSB order or topological order [111, 114, 115, 86]. In either case, the ground state wave functions cannot be reconstructed from the small clusters due to the long-range correlation/entanglement. This argument has been noted in the original paper on the CPT method [94].

To be specific, we first partition the square lattice (including both layers) into $2\times 2$ square clusters as shown in Fig. 2. Let us first ignore the inter-cluster hopping. Within each cluster, we represent the Hamiltonian in the many-body Hilbert space and use the Lanczos method to obtain the lowest $\sim 2000$ eigenvalues and eigenvectors. The Green’s function in the cluster can then be obtained by the Källén–Lehmann representation

where $|m\rangle$ is the $m$th excited state with energy $E_{m}$, and $|0\rangle$ is the ground state with energy $E_{0}$, whose wave function was previously given in Eq. (5). Since the four fermion flavors (two spins and two layers) are identical under the internal flavor symmetry, we can drop the flavor index in the Green’s function and only focus on one particular flavor with the site indices $i,j$, where $i,j=1,2,3,4$ as indicated in Fig. 2. The convergence of the Green’s function can be verified by including more eigenstates from the Lanczos method. We checked that increasing the number of eigenpairs to $\sim 8000$ will not change the result significantly, indicating that the result with $\sim 2000$ eigenpairs has already converged.

Now we restore the inter-cluster hoping to extend the Green’s function from small clusters to the infinite lattice. The Green’s function of super-lattice momentum ${{\bm{k}}}$ can be obtained from the random phase approximation (RPA) approach [94],

where the $T({{\bm{k}}})$ matrix

describes the inter-cluster fermion hopping. The resulting Green’s function $G(\omega,{{\bm{k}}})_{ij}$ is defined in the folded Brillouin zone ${{\bm{k}}}\in(-\pi/2,\pi/2]^{\times 2}$ with sub-lattice indices $i,j$. To unfold the Green’s function to the original Brillouin zone ${{\bm{k}}}\in(-\pi,\pi]^{\times 2}$, we perform the following (partial) Fourier transform

We numerically calculated the unfolded Green’s function $G(\omega,{{\bm{k}}})$ using the above-mentioned cluster perturbation method. We take a large interaction strength $J/t=8$ deep in the SMG phase and present the resulting Green’s function in Fig. 3. From Fig. 3(a), the poles of the Green’s function form two dispersing bands around $\omega=\pm J$, which resembles the upper and lower Hubbard bands in the Hubbard model. This indicates the quasi-particles are fully gapped in the SMG phase. Meanwhile, from Fig. 3(b,c), the zeros of the Green’s function appear around $\omega=-\alpha\epsilon_{{\bm{k}}}/J^{2}$ with some non-universal but positive coefficient $\alpha>0$. We find that the “dispersion” of zeros is reversed compared to the original band dispersion $\epsilon_{{\bm{k}}}$. In Fig. 4, we also numerically confirmed that the “bandwidth” $w_{\text{zero}}$ of zeros is suppressed by the interaction $J$ as $w_{\text{zero}}\sim J^{-2}$ as $J\to\infty$.

Building upon the above observation of the poles and zeros of the Green’s function, we put forth the following empirical formula:

as an approximate description of our numerical result Eq. (18). An important aspect of this formula is the positioning of the Green’s function zeros precisely around the initial Fermi surface (where $\epsilon_{{\bm{k}}}=0$) at $\omega=0$. This is indicated by the small arrows in Fig. 3(c).

Assuming $\operatorname{Re}G_{\text{SMG}}(0,{{\bm{k}}})=0$ as the definition of the zero Fermi surface in the SMG phase, it would encompass the same Fermi volume as the pole Fermi surface in the Fermi liquid phase. As both translation and charge conservation symmetries remain unbroken in the SMG phase, the Luttinger theorem mandates the preservation of the Fermi volume. Given that the SMG state is a fully gapped trivial insulator, there is no pole (no quasi-particle) at low energy, thus the Green’s function can only rely on zeros to fulfill the Fermi volume required by the Luttinger theorem, which is explicitly demonstrated by Eq. (19).

Nevertheless, SMG is not the sole mechanism for gapping out the Fermi surface. SSB might also open a full gap on the Fermi surface, which corresponds to the Higgs mechanism for fermion mass generation. Specifically, in the bilayer square lattice model Eq. (3), due to the perfect nesting of the Fermi surface, the Fermi liquid exhibits strong instability toward SSB orders. Without loss of generality, we will focus on the inter-layer exciton condensation in the weak coupling limit. The corresponding order parameter $\phi_{\text{EC}}$ was introduced in Eq. (6), which carries momentum ${\bm{Q}}=(\pi,\pi)$. The exciton condensation leads to an SSB insulating phase, as noted in the phase diagram Fig. 1(c). However, there are significant differences between the SMG insulator and the SSB insulator, especially in terms of the structure of Green’s function zeros.

In the SSB insulator phase, the Brillouin zone folds by the nesting vector ${\bm{Q}}=(\pi,\pi)$. The fermion Green’s function can be written in the $(c_{{{\bm{k}}}},c_{{{\bm{k}}}+{\bm{Q}}})^{\intercal}$ basis (omitting layers and spins freedom) as

where $\Delta=J\langle\phi_{\text{EC}}\rangle$ denotes the exciton gap induced by the exciton condensation $\langle\phi_{\text{EC}}\rangle\neq 0$. The properties of $G_{\text{SSB}}$ are illustrated in Fig. 5. The spectral function in Fig. 5(a) depicts the quasi-particle peak along the band dispersion, reflecting a gapped (insulating) band structure.

Since $G_{\text{SSB}}$ is a matrix, its zero structure should be defined by its determinant being zero, i.e., $\det G_{\text{SSB}}(\omega,{{\bm{k}}})=0$, which is the only way to define the zero structure in a basis independent manner. Fig. 5(b) indicates the determinant of $G_{\text{SSB}}$ remains the same sign within the band gap induced by the exciton condensation. Since $G_{\text{SSB}}$ does not preserve the translation symmetry (as $\Delta\to-\Delta$ is translation-odd), and $\Delta$ is non-zero, $\det G_{\text{SSB}}$ does not have zeros crossing $\omega=0$ at the original Fermi surface. These two observations are linked: the absence of translation symmetry makes the Luttinger theorem ineffective, hence there is no expectation for the zero Fermi surface in the SSB insulator.

As the interaction $J$ intensifies, the SSB insulator ultimately transitions into the SMG insulator, as depicted in the phase diagram Fig. 1(c). During this transition, the broken symmetry is restored, yet the fermion excitation gap remains intact, similar to the pseudo-gap phenomenon seen in correlated materials [119, 120]. In the context of modeling fermion spectral functions, the pseudo-gap phenomenon can be interpreted as a consequence of the phase (or orientation) fluctuations of fermion bilinear order parameters [121, 122, 123, 124, 125, 126, 127, 128]. In this picture, the order parameter $\Delta=\Delta_{0}\mathrm{e}^{\mathrm{i}\theta}$ maintains a finite amplitude $\Delta_{0}$ as we enter the SMG phase from the adjacent SSB phase, but its phase $\theta$ is disordered by long-wavelength random fluctuations. Consequently, on the large scale, $\Delta$ cannot condense to form long-range order; but on a smaller scale, $\Delta_{0}$ still provides a local excitation gap everywhere for fermions.

Based on this picture of the SMG state, the simplest treatment is to focus on the long wavelength fluctuation of $\Delta$ and estimate its self-energy correction for the fermion by

$$\Sigma(\omega,{{\bm{k}}})=\raisebox{-3.0pt}{\includegraphics[scale={0.65}]{diag_Sigma}}=\mathop{\mathbb{E}}_{\Delta}\hat{\Delta}^{\dagger}G_{0}(\omega,{{\bm{k}}})\hat{\Delta}=\frac{\Delta_{0}^{2}}{\omega\sigma^{0}+\epsilon_{{\bm{k}}}\sigma^{3}},$$

(21)

where the vertex operator is $\hat{\Delta}:=\operatorname{Re}\Delta\sigma^{1}+\operatorname{Im}\Delta\sigma^{2}$ and the bare Green’s function is $G_{0}(\omega,{{\bm{k}}})=(\omega\sigma^{0}-\epsilon_{{\bm{k}}}\sigma^{3})^{-1}$. Here we have assumed that the correlation length $\xi$ of the bosonic field $\Delta$ is long enough that its momentum is negligible for fermions. This assumption is valid near the transition to the SSB phase, as the correlation length diverges ($\xi\to\infty$) at the transition.

Using this self-energy to correct the bare Green’s function, we obtain

Since the translation symmetry has been restored in the SMG phase, we can unfold the Green’s function back to the original Brillouin zone (by taking the $G(\omega,{{\bm{k}}})_{11}$ component), which leads to a weak coupling description of the Green’s function in the shallow SMG phase near the transition to the SSB phase

A more rigorous treatment of a similar problem can be found in Ref. 95, which includes finite momentum fluctuations of $\Delta$. The major effect of these fluctuations is to introduce a spectral broadening for the fermion Green’s function as if replacing $\omega\to\omega+\mathrm{i}\delta$ in Eq. (23). It was also found that the broadening $\delta\sim\xi^{-1}$ scales inversely with the correlation length $\xi$ of the order parameter, which justifies our simple treatment in the large-$\xi$ regime. Similar Green’s functions as Eq. (23) was previously constructed to describe non-Fermi liquid [98] statisfying the Luttinger theorem. However, its physical meaning is now clarified as Green’s function in the SMG phase.

The features of $G^{\prime}_{\text{SMG}}$ in Eq. (23) are presented in Fig. 6. When comparing Fig. 6(a) and Fig. 5(a), we can observe that the pole structure of $G^{\prime}_{\text{SMG}}$ is identical to that of $G_{\text{SSB}}$ (in the diagonal component), both showcasing a gapped spectrum. However, they significantly differ in their zero structures, as seen by comparing Fig. 6(b) and Fig. 5(b). Due to the restoration of symmetry, the low-energy zeros reemerge in the Green’s function in the SMG phase. Additionally, its zero Fermi surface perfectly aligns with the original pole Fermi surface, fulfilling the Luttinger theorem’s requirement for the Fermi volume.

Comparing the Green’s function in the SMG phase derived from the strong coupling analysis Eq. (19) and the weak coupling analysis Eq. (23) (see also Fig. 3 and Fig. 6), we find that despite the apparent difference in high-energy spectral features, the zero Fermi surface defined by $G(0,{{\bm{k}}})=0$ remains a resilient low-energy feature. The persistent zero Fermi surface in the SMG phase is a consequence of the Luttinger theorem.

Nonetheless, besides the low-energy zero structure, it is also intriguing to understand how the high-energy spectral feature deforms from the weak coupling case to the strong coupling case. However, this problem requires non-perturbative numerical simulations. Fortunately, the bilayer square lattice model Eq. (3) admits a sign-problem-free [129] quantum Monte Carlo [130, 131, 132, 133, 134] simulation. We will leave this interesting direction for future research.