Great Truths are Always Simple: A Rather Simple Knowledge Encoder for Enhancing the Commonsense Reasoning Capacity of Pre-Trained Models
Abstract
Commonsense reasoning in natural language is a desired ability of artificial intelligent systems. For solving complex commonsense reasoning tasks, a typical solution is to enhance pre-trained language models (PTMs) with a knowledge-aware graph neural network (GNN) encoder that models a commonsense knowledge graph (CSKG). Despite the effectiveness, these approaches are built on heavy architectures, and can’t clearly explain how external knowledge resources improve the reasoning capacity of PTMs. Considering this issue, we conduct a deep empirical analysis, and find that it is indeed relation features from CSKGs (but not node features) that mainly contribute to the performance improvement of PTMs. Based on this finding, we design a simple MLP-based knowledge encoder that utilizes statistical relation paths as features. Extensive experiments conducted on five benchmarks demonstrate the effectiveness of our approach, which also largely reduces the parameters for encoding CSKGs. Our codes and data are publicly available at https://github.com/RUCAIBox/SAFE.
1 Introduction
In the era of artificial intelligence, it is desirable that intelligent systems can be empowered by the capacity of commonsense reasoning in natural language. For this purpose, a surge of commonsense reasoning tasks and datasets are proposed to evaluate and improve such an ability of NLP models, e.g., CommonsenseQA Talmor et al. (2019) and SocialIQA Sap et al. (2019b). Although large-scale pre-trained models (PTMs) Devlin et al. (2019); Liu et al. (2019) have surpassed human performance in a number of NLP benchmarks, it is still hard for PTMs to accurately capture and understand commonsense knowledge for accomplishing complex reasoning tasks Talmor et al. (2021).
In order to enhance the reasoning capacity, commonsense knowledge graphs (CSKGs) (e.g., ConceptNet (Speer et al., 2017) and ATOMIC (Sap et al., 2019a)) have been adopted for injecting external commonsense knowledge into PTMs. By conducting entity linking to CSKGs, existing methods Yasunaga et al. (2021); Feng et al. (2020a) aim to capture the structured knowledge semantics via knowledge graph (KG) encoders (e.g., graph neural network (GNN) Velickovic et al. (2018); Kipf and Welling (2017)), and then integrate the KG encoders for improving the commonsense reasoning capacity of PTMs Yasunaga et al. (2021).
Despite the effectiveness, these approaches are built on highly complicated network architectures (involving both PTMs and GNNs). Thus, it is difficult to explain how and why external commonsense knowledge improves the commonsense reasoning capacity of PTMs. Besides, existing CSKGs Mehrabi et al. (2021); Nguyen et al. (2021) are mostly crowdsourced from massive selected resources (e.g., books, encyclopedias, and scraped web corpus), containing a wide variety of content. Without a clear understanding of how these external resources should be utilized, it is likely to incorporate irrelevant concepts or even knowledge biases Mehrabi et al. (2021); Nguyen et al. (2021) into PTMs, which might hurt the reasoning performance. Indeed, some researchers have noted this issue and questioned whether existing GNN-based modules are over-complicated for commonsense reasoning Wang et al. (2021a). Furthermore, they find that even a simple graph neural counter can outperform existing GNN modules on CommonsenseQA and OpenBookQA benchmarks.
However, existing studies can’t well answer the fundamental questions about knowledge utilization for commonsense reasoning: How do external knowledge resources enhance the commonsense reasoning capacity of PTMs? What is necessarily required from external knowledge resources for PTMs? Since the simplified knowledge-aware GNN has already yielded performance improvement on the CommonsenseQA Wang et al. (2021a), we speculate that there might be a simpler solution if we could identify the essential knowledge for commonsense reasoning.
Focusing on this issue, we think about designing the solution by further simplifying the KG encoder. Based on our empirical analysis, we observe a surprising result that it is indeed relation features from CSKGs, but not node features, that are the key to the task of commonsense reasoning (See more details in Section 3). According to this finding, we propose a rather simple approach to leveraging external knowledge resources for enhancing the commonsense reasoning capacity of PTMs. Instead of using a heavy GNN architecture, we design a lightweight KG encoder fully based on the multi-layer perceptron (MLP), which utilizes Statistical relation pAth from CSKGs as FEatures, namely SAFE. We find that semantic relation paths can provide useful knowledge evidences for PTMs, which is the key information for helping commonsense reasoning. By conducting extensive experiments on five benchmark datasets, our approach achieves superior or competitive performance compared with state-of-the-art methods, especially when training data is limited. Besides the performance improvement, our approach largely reduces the parameters for encoding CSKGs (fewer than 1% trainable parameters compared to GNN-based KG encoders (Yasunaga et al., 2021)).
Our main contributions can be summarized as follows: (1) We empirically find that relation features from CSKGs are the key to the task of commonsense reasoning; (2) We design a simple MLP-based architecture with relation paths as features for enhancing the commonsense reasoning capacity of PTMs; (3) Extensive experiments conducted on five benchmark datasets demonstrate the effectiveness of our proposed approach, which also largely reduces the parameters of the KG encoder.
2 Task Description
According to pioneer works (Talmor et al., 2019; Mihaylov et al., 2018), the commonsense reasoning task can be generally described as a multi-choice question answering problem: given a natural language question and a set of choices as the answer candidates, the goal is to select the most proper choice from these candidates to answer the question based on necessary commonsense knowledge.
To explicitly capture commonsense knowledge, external commonsense knowledge graphs (CSKGs) have often been utilized in this task, e.g., ConceptNet (Speer et al., 2017). A CSKG can be formally described as a multi-relational graph , where is the set of all concept (or entity) nodes (e.g., hair and water), is the set of relation types (e.g., relatedto and atlocation), and is the set of relational links that connect two concept nodes in .
Following prior studies Lin et al. (2019), we solve the commonsense reasoning task in a knowledge-aware setting, where a CSKG is available as input. We first link the mentioned concepts from the question and the answer candidates to the CSKG, so that we can leverage the rich semantic knowledge from the CSKG for commonsense reasoning. Based on the linked concepts in the question and each answer candidate, we further extract their neighbouring nodes from and the relational links that connect them, to compose a subgraph for characterizing the commonsense knowledge about the question and the answer candidate .
3 Empirical Analysis on the Commonsense KG Encoder
In this section, we conduct an empirical study to investigate how the external KG encoder helps PTMs with commonsense reasoning.
3.1 Analysis Setup
To conduct the analysis experiments, we select QA-GNN (Yasunaga et al., 2021), a representative approach that integrates PTM with GNN for the commonsense QA task, as the studied model. We adopt the CommonsenseQA (Talmor et al., 2019) and OpenBookQA Mihaylov et al. (2018), two of the most widely used commonsense reasoning benchmarks, for evaluation, with the same data split setting in Lin et al. (2019).
We perform two analysis experiments: one examines the effect of the commonsense KG encoder, and the other one examines the effect of different features in the commonsense KG encoder. To be specific, the two experiments focus on two key questions about commonsense reasoning: (1) what is the effect of the commonsense KG encoder on PTMs? (2) what is the key information within the commonsense KG encoder?
3.2 Results and Findings
Next, we conduct the experiments and present our findings of commonsense reasoning.
Effect of Commonsense KG Encoder. Since existing studies have widely utilized a GNN module to encode the commonsense knowledge, we examine its contribution to the improvement of reasoning performance. We consider comparing three variants of QA-GNN: (A) PTM-Only that directly removes the GNN module and degenerates into a pure PTM, (B) PTM-Pred that trains the PTM and GNN simultaneously but only makes the prediction with the PTM module, and (C) GNN-Pred that trains the PTM and GNN simultaneously but only makes the prediction with the GNN module.
The comparison results are shown in Figure 1. As we can see, using the predictions solely based on the GNN module (i.e., GNN-Pred) can only answer a relatively minor proportion of the questions (no more than 60% in CommonsenseQA). As a comparison, when trained independently (i.e., PTM-Only) or jointly with the GNN module (i.e., PTM-Pred), the PTM module can answer a large proportion of the questions (at least 70% in CommonsenseQA). Furthermore, the incorporation of the GNN encoder is useful to improve the performance of PTMs (PTM-Only v.s. QAGNN). These results show that:
In the joint PTM-GNN approach, PTM contributes the most to the commonsense reasoning task, which is the key to the reasoning performance.
Commonsense KG encoder is incapable of performing effective reasoning independently, but can enhance PTM as the auxiliary role.




Effect of Node/Relation Features from KG. The major aim of the KG encoder is to characterize the commonsense knowledge and provide necessary knowledge evidence for enhancing the reasoning capacity of PTMs. Generally, a CSKG consists of concept nodes and relational links. To identify the key knowledge information that is necessarily needed, we now examine the effect of node and relation features from CSKG. To eliminate the effect of PTM module, we remove it and compare the performance of only KG encoder under two experiment settings: (A) reducing the dimension of node embeddings to (PCA (Jolliffe, 1986) is applied to select most informative dimensions), and (B) randomly removing percent of relational links in the KG subgraph for a question-candidate pair.
As shown in Figure 2, we surprisingly find that even after reducing the dimension of node embeddings to 1, the performance of the GNN encoder can be still improved. These results show that node features are not the key information utilized by the GNN encoder. In contrast, removing a considerable proportion of links significantly reduces the performance. From these observations, we can conclude that: The relation features from the CSKG are indeed the key knowledge information that is actually needed by the KG encoder.
4 Approach
The former sections show that the role of the KG encoder on CSKGs is to mainly complement PTMs in the task of commonsense reasoning. Instead of node features, relations features are the key to the KG encoder for improving PTMs. Based on these findings, we develop a simple commonsense KG encoder based on the statistical relation features from CSKGs, namely SAFE. Figure 3 presents the overview of our model.
4.1 Capturing High-Order Relation Semantics
Since relation features are shown useful to improve the performance of commonsense reasoning, we consider extracting relation features for better capturing the knowledge semantics from the CSKG. Inspired by KG reasoning studies Lin et al. (2018); Feng et al. (2020b), we construct multi-hop relation paths that connect question nodes with answer candidate nodes on the CSKG to capture the higher-order semantic relatedness among them.
Formally, given the commonsense subgraph for the question and the answer candidate , we first extract a set of relation paths within hops that connect a question concept node and an answer concept node , denoted as . Specifically, a path can be represented as a sequence of nodes and relations as . Based on the empirical findings in Section 3, we consider a simplified representation for relation paths that removes node IDs but only keeps the relations on a path. To keep the role of each node, we replace a node ID by a three-valued type, indicating this node belongs to a question node (0), answer node (1) or others (2). In this way, a path can be represented by , where is the role type of node . Since we remove explicit node IDs, our model can concentrate on more essential relation features.
Based on the above method, for a question and an answer candidate , we extract all the simplified relation paths and count their frequencies among all the paths. We use to denote all the paths for the question and the answer candidate , where each entry consists of the -th path and its frequency . Unlike prior approaches (e.g., QA-GNN), we use such very simple features of relation paths from CSKGs to improve the reasoning capacity of PTMs.

4.2 A MLP-based KG encoder
Our KG encoder is built on a full MLP architecture based on simplified relation path features, consisting of a path encoder and a feature aggregator.
Path Encoder. The path encoder is a two-layer MLP that encodes a relation path into a scalar feature value. As shown in Section 4.1, we can obtain the path feature set for the question and the answer candidate . Different from general KGs, CSKGs usually contain much fewer types of relations (e.g., 36 relations in ConceptNet), we adopt one-hot representations of these types to represent these relations. For node type (from question, candidate or others), we also adopt the similar representations. Then, we concatenate these one-hot vectors to compose the sparse representation of a relation path in order, denoted as . Subsequently, the sparse path representation is encoded by a two-layer MLP (i.e., the path encoder) to produce the corresponding scalar feature value :
| (1) |
where reflects the importance of such a relation path for commonsense reasoning.
Feature Aggregator. Based on the above path encoder, we can generate the scalar feature values for all the relation paths in the feature set . The feature aggregator aims to aggregate these feature values to produce the confidence score of the answer candidate w.r.t. the question, from the KG perspective. Concretely, we sum the different feature values of relation paths weighted by their frequencies as follows:
| (2) |
where is the mapping feature value of path and is the frequency of path . Here, aims to capture the overall confidence score based on the subgraph given the question and the answer candidate. However, since the weighted sum is likely to cause extreme values (i.e., too large or too small), we add an extra two-layer MLP for scaling:
| (3) |
where is the prediction score indicating the confidence level that candidate is the right answer to question from the perspective of KG.
4.3 Integrating KG Encoder with PTM
In this part, we integrate the above KG encoder with the PTM for commonsense reasoning.
The PTM Encoder. Following existing works Yasunaga et al. (2021), we utilize a PTM as the backbone of commonsense reasoning. Given a question and an answer candidate , we concatenate their text to compose the input of the PTM. After encoding by the multiple Transformer layers, we select the output of the [CLS] token in the last layer as the contextual representation of the question-candidate pair, denoted by . Then, we feed into a MLP layer to produce a scalar output ,
| (4) | ||||
| (5) |
which is the plausibility score of the answer candidate from the perspective of PTM.
Combining the Prediction Scores. We then derive the prediction score of each answer candidate for a question by leveraging both the PTM and KG encoder based on either textual or structured semantics. For each question-candidate pair , we combine the prediction scores of the two modules as:
| (6) |
where (Eq. 5) and (Eq. 3) are the prediction scores of PTM and KG encoder, respectively. Given a set of answer candidates , we further normalize into a conditional probability via the softmax operation over the candidates.
During the training stage, we optimize the parameters of the whole model (including both the PTM and KG encoder) with the cross entropy loss between the predictions and the ground-truth answer (based on the probability distribution ). During inference, we first compute the probability score for each answer candidate, and then select the highest one as the predicted answer.
| RGCN | MHGRN | QAGNN | SAFE | |
| Node emb. | ||||
| Relation | ||||
| GNN | ||||
| MLP-based | ||||
| # Params | 365K | 547K | 2845K | 4.7k |
4.4 Comparison with Existing KG Encoders
For the task of commonsense reasoning, it has become a common approach by integrating PTM with an external KG encoder based on CSKGs. The major difference among these methods (including our approach) lies in the design of the KG encoder. Next, we compare these variants for the KG encoder.
We summarize the comparison between our KG encoder and representative KG encoders in Table 1. We can see that, our approach no longer lies in the node embeddings and the structure of GNNs. Instead, we mainly utilize relation paths as the features of the KG encoder, which is built on a simple MLP-based architecture. Therefore, the number of the model parameters involved in our KG encoder is much smaller than those of existing KG encoders. As will be shown in Section 5, our KG encoder yields better or at least comparable performance compared with existing GNN-based encoders, based on the same configuration for PTMs.
Specifically, our approach can largely reduce the computational costs for encoding the CSKG. For our approach, we need to extract the relation paths from question nodes to all the answer candidate nodes on the CSKG, and it can be efficiently fulfilled via a -hop constrained Depth-First Search Tarjan (1972), which can be pre-computed in offline processing. When the relation paths have been extracted, it is efficient to encode these paths with our MLP architecture. Such a process can be easily paralleled or accelerated by optimized matrix multiplication. In contrast, existing GNN-based encoders rely on iterative propagation and aggregation on the entire subgraph, which takes a much larger computational time cost.
5 Experiment
5.1 Experimental Setup
In this part, we introduce the experimental setup.
Evaluation Tasks. We conduct experiments on five commonsense reasoning tasks, shown in Table 2.
CommonsenseQA (Talmor et al., 2019) is a 5-way multiple-choice QA dataset. It is created based on ConceptNet (Speer et al., 2017).
OpenBookQA (Mihaylov et al., 2018) is a 4-way multiple-choice QA dataset about elementary science questions to evaluate the science commonsense knowledge.
SocialIQA (Sap et al., 2019b) is a 3-way multiple-choice QA dataset to evaluate the understanding of social commonsense knowledge.
PIQA (Bisk et al., 2020) is a binary-choice QA dataset about physical commonsense.
CoPA (Roemmele et al., 2011) is a commonsense inference dataset, to select the most plausible alternative with the causal relation to the premise.
| Task | Train | Dev | Test |
| CommonsenQA | 9,741 | 1,221 | 1,140 |
| OpenBookQA | 4,957 | 500 | 500 |
| SocialIQA | 33,410 | 1,954 | - |
| PIQA | 16,113 | 1,838 | - |
| CoPA | - | 500 | 500 |
Data Preprocessing. For CommonsenseQA and OpenBookQA, we use their original train/dev/test split settings. Since the test set of CommonsenseQA is not available, we follow previous work Lin et al. (2019) that extracts 1,241 examples from the original training set as the test set. Besides, the test sets of SocialIQA and PIQA are not available. Therefore, we report the experimental results on their development sets for a fair comparison Shwartz et al. (2020). For CoPA that only provides development and test sets, we follow Niu et al. (2021) to train models on the development set and evaluate the performance on the test set. For commonsense KG, we adopt ConceptNet Speer et al. (2017), a general-domain and task-agnostic CSKG, as our external knowledge source for all the above models and tasks. For each question-candidate pair , we follow previous works Lin et al. (2019); Feng et al. (2020a) to retrieve and construct the subgraph from the CSKG .
Baseline Methods. We compare our model with the following six baseline methods, including a fine-tuned PTM and five PTM+GNN models:
Fine-tuned PTM directly fine-tunes a PTM without using any CSKG. We use RoBERTa-large Liu et al. (2019) for all tasks. Additionally, we also use BERT-large (Devlin et al., 2019) and AristoRoBERTa (Clark et al., 2020a) for OpenBookQA to evaluate the generality of our KG-encoder.
PTM+GNN models integrate PTM with additional GNN-based KG encoders. Based on the same PTM (the above baseline), we consider five variants with different KG encoders: (1) Relation Network (RN) (Santoro et al., 2017) using a relational reasoning structure over the CSKG; (2) GcoAttn (Lin et al., 2019) using a graph concept attention model to aggregate entity information from the CSKG; (3) RGCN (Schlichtkrull et al., 2018) extending the GCN with relation-specific weights; (4) MHGRN (Feng et al., 2020a) using a GNN architecture reasoning over the CSKG that unifies both GNNs and path-based models; (5) QA-GNN (Yasunaga et al., 2021) using a GAT to perform jointly reasoning over the CSKG.
For all these methods, we adopt the same architecture and configuration for the PTM, so that we can examine the effect of different KG encoders.
| Methods | CommonsenseQA | OpenBookQA | ||||||||||
| 5% | 10% | 20% | 50% | 80% | 100% | 5% | 10% | 20% | 50% | 80% | 100% | |
| RoBERTa-large | 29.66 | 42.84 | 58.47 | 66.13 | 68.47 | 68.69† | 37.00 | 39.4 | 41.47 | 53.07 | 57.93 | 64.8† |
| + RGCN | 24.41 | 43.75 | 59.44 | 66.07 | 68.33 | 68.41† | 38.67 | 37.53 | 43.67 | 56.33 | 63.73 | 62.45† |
| + GconAttn | 21.92 | 49.83 | 60.09 | 66.93 | 69.14 | 68.59† | 38.60 | 36.13 | 43.93 | 50.87 | 57.87 | 64.75† |
| + RN | 23.77 | 34.09 | 59.90 | 65.62 | 67.37 | 69.08† | 33.73 | 35.93 | 41.40 | 49.47 | 59.00 | 65.20† |
| + MHGRN | 29.01 | 32.02 | 50.23 | 68.09 | 70.83 | 71.11† | 38.00 | 36.47 | 39.73 | 55.73 | 55.00 | 66.85† |
| + QA-GNN | 32.95 | 37.77 | 50.15 | 69.33 | 70.99 | 73.41† | 33.53 | 35.07 | 42.40 | 54.53 | 52.47 | 67.80⋆ |
| + SAFE(Ours) | 36.45 | 56.51 | 65.16 | 70.72 | 73.22 | 74.03 | 38.80 | 41.20 | 44.93 | 58.33 | 65.60 | 69.20 |
| Methods | SocialIQA | PIQA | CoPA |
| RoBERTa-large | 78.25 | 77.53 | 67.60 |
| + GcoAttn | 78.86 | 78.24 | 70.00 |
| + RN | 78.45 | 76.88 | 70.20 |
| + MHGRN | 78.11 | 77.15 | 71.60 |
| + QAGNN | 78.10 | 78.24 | 68.40 |
| + SAFE (Ours) | 78.86 | 79.43 | 71.60 |
5.2 Implementation Details
We implement all PTMs based on HuggingFace Transformers Wolf et al. (2020). For all the baselines, we keep the common hyper-parameters as identical as possible and set their special hyper-parameters following the suggestions from the original papers. In our approach, we extract the relation paths with no more than 2 hops between the concept nodes from the question and the answer candidate. We tune the hidden dimension of MLPs from the path encoder in {32, 64, 100}, and the batch size in {32, 48, 60, 120}. The parameters of the model are optimized by RAdam (Liu et al., 2020), and the learning rate of the PTM and the KG encoder is also tuned in {1-4, 1-5, 2-5} and {1-3, 1-2}, respectively. To accelerate the training process, we don’t incorporate Dropout regularization in our model. All the above hyper-parameters are tuned on the development set.
5.3 Results Analysis
Following previous works Yasunaga et al. (2021); Wang et al. (2021a), we take the results on CommonsenseQA and OpenBookQA as the main experiments to compare different methods. In order to test their robustness to data sparsity, we examine the performance under five different proportions of training data, i.e., .
CommonsenseQA and OpenBookQA. The results of different methods on CommonsenseQA and OpenBookQA are presented in Table 3.
Comparing the results under the full-data setting (i.e., 100% training data), we can see that all the PTM+GNN methods perform better than vanilla PTM (i.e., RoBERTa-large). It indicates that the KG encoder on the CSKG is able to incorporate useful knowledge information to improve PTMs on commonsense reasoning tasks. Additionally, among all the PTM+GNN baselines, QA-GNN performs the best. The major reason is that QA-GNN uses the PTM to estimate the importance of KG nodes and connects the QA context and the CSKG to form a joint graph, which is helpful to improve the reasoning ability on the CSKG. Finally, our method consistently outperforms all the baselines. Our approach incorporates a lightweight MLP architecture as the KG encoder with relation paths as features. It reduces the parameter redundancy of the KG encoder and focuses on the most essential features for reasoning, i.e., semantic relation paths. Such an approach is effective to enhance the commonsense reasoning capacity of PTMs.
Comparing the results under different sparsity ratios of training data, we can see that the performance substantially drops when the size of training data is reduced. While, our method performs consistently better than all baselines. It is because that our KG encoder consists of significantly fewer parameters than those of the baselines, which reduces the risk of overfitting and endows our approach with better robustness in data scarcity scenarios.
| Methods | BERT-large | AristoRoBERTa |
| Fine-tuned PTMs | 59.00 | 78.40† |
| + RGCN | 45.40 | 74.60† |
| + GconAttn | 48.20 | 71.80† |
| + RN | 48.60 | 75.35† |
| + MHGRN | 46.20 | 80.60† |
| + QA-GNN | 58.47 | 82.77† |
| + SAFE (Ours) | 59.20 | 87.13 |
Other Commonsense Reasoning Datasets. To further verify the effectiveness of our method, we also compare the results of different methods on other commonsense reasoning datasets. These datasets are from different domains or different tasks. These results are shown in Table 4. Similarly, our approach also achieves the best performance in most cases. It indicates that our approach is generally effective for various commonsense reasoning datasets or tasks, by outperforming competitive but complicated baselines. Among all the datasets, our approach improves the performance of the PTM on CoPA dataset by a large margin. The reason is that CoPA is a small dataset with only 500 training examples. Baselines with heavy architectures are easy to overfit on it. In contrast, our KG encoder is lightweight, which is more capable of resisting the overfitting issue.
5.4 Evaluation with Other PTMs
The major contribution of our approach lies in the lightweight KG encoder, which can be also used to enhance the commonsense reasoning capacity of various PTMs. To validate it, we examine the performance of our KG encoder when integrated with two other PTMs, i.e., BERT-large and AristoRoBERTa, on OpenBookQA dataset.
As shown in Table 5, the BERT-large and AristoRoBERTa enhanced by our KG encoder perform better than original PTMs. Especially, our KG encoder can improve the performance of AristoRoBERTa by a large margin (with 8.73% improvement). These results show that our KG encoder is a general method to improve PTMs for commonsense reasoning. In contrast, when adapting other KG encoders to these two PTMs, the performance decreases in most cases. It is mainly because these KG encoders have complicated architectures, which may not be easily adapted to other PTMs.
5.5 Hyper-parameters Analysis
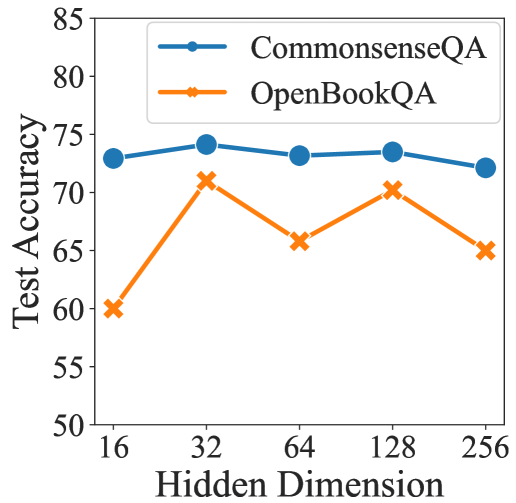
For hyper-parameter analysis, we study the hidden dimension size of the MLP in the path encoder. Concretely, we evaluate our model with varying values of the hidden dimension size on CommonsenseQA and OpenBookQA datasets using RoBERTa-large model. The results are shown in Figure 4. We can see that with the increase of the hidden dimension size, the performance improves at first and then drops to some extent. The possible reason lies in two aspects. On the one hand, a too small hidden dimension size makes the path encoder hard to represent sufficient information from relation paths for commonsense reasoning. On the other hand, a larger hidden dimension size enlarges the parameter number of our KG encoder, which increases the risk of overfitting that may cause performance degradation.
5.6 Case Study

We propose a rather simple KG encoder to effectively utilize the relation features from the CSKG, which first computes the feature values of the relation paths and then aggregates these values as the confidence score of the question and choice from the perspective of KG. In this way, we can generate a table in advance that maps each type of relation path into its feature value that reflects its contribution to the confidence score. Based on this table, it is convenient to directly judge the importance of the relation path and quickly assess the confidence about if the choice is the answer to the question from the perspective of KG. Figure 5 shows some path-value examples on CommonsenseQA dataset. As we can see, the path with a higher value indeed provide more persuasive evidence (e.g., causes and capableof) that indicates the choice is more likely to be the answer to the question. In contrast, the path with a lower value usually represents an ambiguous relationship (e.g., relatedto), which contributes less to the judge of whether the choice is the answer.
6 Related Work
We review the related studies in two aspects, i.e., commonsense reasoning and KG-enhanced pretrained models.
Commonsense Reasoning. Commonsense reasoning tasks aim to evaluate the understanding of commonsense knowledge Davis and Marcus (2015), e.g., physical commonsense (Zellers et al., 2019), which are mostly formulated as a multi-choice QA problem. Early studies either rely on explicit text features (Clark et al., 2016) to capture the relations between the question and answer candidates, or adopt neural networks (e.g., DNN or LSTM) (Yu et al., 2014; Chen et al., 2017) to model the implicit correlation features. Recently, pre-trained models (PTM) (Devlin et al., 2019; Liu et al., 2019) have achieved remarkable performance on commonsense reasoning tasks. Furthermore, a surge of works incorporate external knowledge resources to further improve the reasoning performance. Among them, CSKG (e.g., ConceptNet (Speer et al., 2017)) has been widely studied, and existing works mainly adopt graph neural networks to learn useful commonsense knowledge from the CSKG to enhance PTMs. Based on these works, we systemically study what is necessarily needed from CSKGs for improving PTMs. Our analysis leads to an important finding that relation features mainly contribute to the performance improvement, and we design a lightweight MLP architecture to simplify the KG encoder.
KG-Enhanced Pre-trained Models. Recently, a series of works focus on enhancing PTMs with external KGs to improve the performance on factual knowledge understanding Sun et al. (2020); Wang et al. (2021b) and knowledge reasoning tasks Talmor et al. (2019); Zhang et al. (2019); He et al. (2020). These works inject the structured knowledge from the external KG into PTMs in either pre-training or fine-tuning stage. The first class of works mainly focus on devising knowledge-aware pre-training tasks Wang et al. (2021b); Zhang et al. (2019) to improve the understanding of entities or triples from the KG, e.g., knowledge completion Wang et al. (2021b) and denoising entity auto-encoder Zhang et al. (2019). Another class of works adopt task-specific KG encoders to enhance PTMs during fine-tuning, e.g., path-based relation network Feng et al. (2020a) and GNN Yasunaga et al. (2021). Different from them, we aim to directly enhance PTMs with a KG encoder on the downstream commonsense reasoning tasks, and design a rather simple yet effective KG encoder.
7 Conclusion
In this work, we study how the external commonsense knowledge graphs (CSKGs) are utilized to improve the reasoning capacity of pre-trained models (PTMs). Our work makes an important contribution to understanding and enhancing the commonsense reasoning capacity of PTMs. Our results show that relation paths from the CSKG are the key to performance improvement. Based on this finding, we design a rather simple MLP-based KG encoder with relation paths from the CSKG as features, which can be generally integrated with various PTMs for commonsense reasoning tasks. Such a lightweight KG encoder has significantly fewer than 1% trainable parameters compared to previous GNN-based KG encoders. Experimental results on five commonsense reasoning datasets demonstrate the effectiveness of our approach.
In future work, we will study how to effectively leverage the commonsense knowledge from large-scale unstructured data to improve PTMs. We will also try to apply our approach to other knowledge-intensive tasks, e.g., knowledge graph completion and knowledge graph based question answering Lan et al. (2021).
8 Ethical Consideration
This work primarily investigates how external commonsense knowledge graphs (CSKGs) enhance the commonsense reasoning capacity of pre-trained models (PTMs) and proposes a simple but effective KG encoder on CSKGs to enhance PTMs. A potential problem derives from using PTMs and CSKGs in our approach. PTMs have been shown to capture certain biases from the data that have been pre-trained on Bender et al. (2021). And existing works Mehrabi et al. (2021) have found that CSKGs are likely to contain biased concepts derived from human annotations. However, a comprehensive analysis of such biases is outside of the scope of this work. It is a compelling direction to investigate to what extent the combination of CSKGs and PTMs can help mitigate such biases. An alternative consideration is to consider filtering biased concepts in the process of subgraph extraction from the CSKG. By devising proper rules, it is promising to reduce the influence of biased concepts on our approach.
9 Acknowledgments
This work was partially supported by Beijing Natural Science Foundation under Grant No. 4222027, and National Natural Science Foundation of China under Grant No. 61872369, Beijing Outstanding Young Scientist Program under Grant No. BJJWZYJH012019100020098. This work is also supported by Beijing Academy of Artificial Intelligence (BAAI). Xin Zhao is the corresponding author.
References
- Bender et al. (2021) Emily M Bender, Timnit Gebru, Angelina McMillan-Major, and Shmargaret Shmitchell. 2021. On the dangers of stochastic parrots: Can language models be too big? In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, pages 610–623.
- Bisk et al. (2020) Yonatan Bisk, Rowan Zellers, Ronan LeBras, Jianfeng Gao, and Yejin Choi. 2020. PIQA: reasoning about physical commonsense in natural language. In The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, February 7-12, 2020, pages 7432–7439.
- Chen et al. (2017) Qian Chen, Xiaodan Zhu, Zhen-Hua Ling, Si Wei, Hui Jiang, and Diana Inkpen. 2017. Enhanced LSTM for natural language inference. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, ACL 2017, Vancouver, Canada, July 30 - August 4, Volume 1: Long Papers, pages 1657–1668.
- Clark et al. (2020a) Peter Clark, Oren Etzioni, Tushar Khot, Daniel Khashabi, Bhavana Dalvi Mishra, Kyle Richardson, Ashish Sabharwal, Carissa Schoenick, Oyvind Tafjord, Niket Tandon, Sumithra Bhakthavatsalam, Dirk Groeneveld, Michal Guerquin, and Michael Schmitz. 2020a. From ’f’ to ’a’ on the N.Y. regents science exams: An overview of the aristo project. AI Mag., pages 39–53.
- Clark et al. (2020b) Peter Clark, Oren Etzioni, Tushar Khot, Daniel Khashabi, Bhavana Dalvi Mishra, Kyle Richardson, Ashish Sabharwal, Carissa Schoenick, Oyvind Tafjord, Niket Tandon, Sumithra Bhakthavatsalam, Dirk Groeneveld, Michal Guerquin, and Michael Schmitz. 2020b. From ’f’ to ’a’ on the N.Y. regents science exams: An overview of the aristo project. AI Mag., 41(4):39–53.
- Clark et al. (2016) Peter Clark, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Oyvind Tafjord, Peter D. Turney, and Daniel Khashabi. 2016. Combining retrieval, statistics, and inference to answer elementary science questions. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, February 12-17, 2016, Phoenix, Arizona, USA, pages 2580–2586.
- Davis and Marcus (2015) Ernest Davis and Gary Marcus. 2015. Commonsense reasoning and commonsense knowledge in artificial intelligence. Communications of the ACM, 58(9):92–103.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 4171–4186.
- Feng et al. (2020a) Yanlin Feng, Xinyue Chen, Bill Yuchen Lin, Peifeng Wang, Jun Yan, and Xiang Ren. 2020a. Scalable multi-hop relational reasoning for knowledge-aware question answering. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing, EMNLP 2020, Online, November 16-20, 2020, pages 1295–1309.
- Feng et al. (2020b) Yanlin Feng, Xinyue Chen, Bill Yuchen Lin, Peifeng Wang, Jun Yan, and Xiang Ren. 2020b. Scalable multi-hop relational reasoning for knowledge-aware question answering. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 1295–1309.
- He et al. (2020) Gaole He, Junyi Li, Wayne Xin Zhao, Peiju Liu, and Ji-Rong Wen. 2020. Mining implicit entity preference from user-item interaction data for knowledge graph completion via adversarial learning. In WWW ’20: The Web Conference 2020, Taipei, Taiwan, April 20-24, 2020, pages 740–751. ACM / IW3C2.
- Jolliffe (1986) Ian T. Jolliffe. 1986. Principal Component Analysis. Springer Series in Statistics.
- Kipf and Welling (2017) Thomas N. Kipf and Max Welling. 2017. Semi-supervised classification with graph convolutional networks. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings.
- Lan et al. (2021) Yunshi Lan, Gaole He, Jinhao Jiang, Jing Jiang, Wayne Xin Zhao, and Ji-Rong Wen. 2021. A survey on complex knowledge base question answering: Methods, challenges and solutions. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI 2021, Virtual Event / Montreal, Canada, 19-27 August 2021, pages 4483–4491. ijcai.org.
- Lin et al. (2019) Bill Yuchen Lin, Xinyue Chen, Jamin Chen, and Xiang Ren. 2019. Kagnet: Knowledge-aware graph networks for commonsense reasoning. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, EMNLP-IJCNLP 2019, Hong Kong, China, November 3-7, 2019, pages 2829–2839.
- Lin et al. (2018) Xi Victoria Lin, Richard Socher, and Caiming Xiong. 2018. Multi-hop knowledge graph reasoning with reward shaping. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 3243–3253.
- Liu et al. (2020) Liyuan Liu, Haoming Jiang, Pengcheng He, Weizhu Chen, Xiaodong Liu, Jianfeng Gao, and Jiawei Han. 2020. On the variance of the adaptive learning rate and beyond. In 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, April 26-30, 2020.
- Liu et al. (2019) Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. 2019. Roberta: A robustly optimized BERT pretraining approach. CoRR, abs/1907.11692.
- Mehrabi et al. (2021) Ninareh Mehrabi, Pei Zhou, Fred Morstatter, Jay Pujara, Xiang Ren, and Aram Galstyan. 2021. Lawyers are dishonest? quantifying representational harms in commonsense knowledge resources. arXiv preprint arXiv:2103.11320.
- Mihaylov et al. (2018) Todor Mihaylov, Peter Clark, Tushar Khot, and Ashish Sabharwal. 2018. Can a suit of armor conduct electricity? A new dataset for open book question answering. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, October 31 - November 4, 2018, pages 2381–2391.
- Nguyen et al. (2021) Tuan-Phong Nguyen, Simon Razniewski, Julien Romero, and Gerhard Weikum. 2021. Refined commonsense knowledge from large-scale web contents. arXiv preprint arXiv:2112.04596.
- Niu et al. (2021) Yilin Niu, Fei Huang, Jiaming Liang, Wenkai Chen, Xiaoyan Zhu, and Minlie Huang. 2021. A semantic-based method for unsupervised commonsense question answering. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, ACL/IJCNLP 2021, (Volume 1: Long Papers), Virtual Event, August 1-6, 2021, pages 3037–3049.
- Roemmele et al. (2011) Melissa Roemmele, Cosmin Adrian Bejan, and Andrew S. Gordon. 2011. Choice of plausible alternatives: An evaluation of commonsense causal reasoning. In Logical Formalizations of Commonsense Reasoning, Papers from the 2011 AAAI Spring Symposium, Technical Report SS-11-06, Stanford, California, USA, March 21-23, 2011.
- Santoro et al. (2017) Adam Santoro, David Raposo, David G. T. Barrett, Mateusz Malinowski, Razvan Pascanu, Peter W. Battaglia, and Tim Lillicrap. 2017. A simple neural network module for relational reasoning. In Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 4967–4976.
- Sap et al. (2019a) Maarten Sap, Ronan Le Bras, Emily Allaway, Chandra Bhagavatula, Nicholas Lourie, Hannah Rashkin, Brendan Roof, Noah A. Smith, and Yejin Choi. 2019a. ATOMIC: an atlas of machine commonsense for if-then reasoning. In The Thirty-Third AAAI Conference on Artificial Intelligence, AAAI 2019, The Thirty-First Innovative Applications of Artificial Intelligence Conference, IAAI 2019, The Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2019, Honolulu, Hawaii, USA, January 27 - February 1, 2019, pages 3027–3035.
- Sap et al. (2019b) Maarten Sap, Hannah Rashkin, Derek Chen, Ronan Le Bras, and Yejin Choi. 2019b. Social iqa: Commonsense reasoning about social interactions. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, EMNLP-IJCNLP 2019, Hong Kong, China, November 3-7, 2019, pages 4462–4472.
- Schlichtkrull et al. (2018) Michael Sejr Schlichtkrull, Thomas N. Kipf, Peter Bloem, Rianne van den Berg, Ivan Titov, and Max Welling. 2018. Modeling relational data with graph convolutional networks. In The Semantic Web - 15th International Conference, ESWC 2018, Heraklion, Crete, Greece, June 3-7, 2018, Proceedings, volume 10843, pages 593–607.
- Shwartz et al. (2020) Vered Shwartz, Peter West, Ronan Le Bras, Chandra Bhagavatula, and Yejin Choi. 2020. Unsupervised commonsense question answering with self-talk. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pages 4615–4629.
- Speer et al. (2017) Robyn Speer, Joshua Chin, and Catherine Havasi. 2017. Conceptnet 5.5: An open multilingual graph of general knowledge. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, February 4-9, 2017, San Francisco, California, USA, pages 4444–4451.
- Sun et al. (2020) Tianxiang Sun, Yunfan Shao, Xipeng Qiu, Qipeng Guo, Yaru Hu, Xuanjing Huang, and Zheng Zhang. 2020. Colake: Contextualized language and knowledge embedding. In Proceedings of the 28th International Conference on Computational Linguistics, COLING 2020, Barcelona, Spain (Online), December 8-13, 2020, pages 3660–3670.
- Talmor et al. (2019) Alon Talmor, Jonathan Herzig, Nicholas Lourie, and Jonathan Berant. 2019. Commonsenseqa: A question answering challenge targeting commonsense knowledge. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 4149–4158.
- Talmor et al. (2021) Alon Talmor, Ori Yoran, Ronan Le Bras, Chandrasekhar Bhagavatula, Yoav Goldberg, Yejin Choi, and Jonathan Berant. 2021. Commonsenseqa 2.0: Exposing the limits of ai through gamification.
- Tarjan (1972) Robert Endre Tarjan. 1972. Depth-first search and linear graph algorithms. SIAM J. Comput., pages 146–160.
- Velickovic et al. (2018) Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. 2018. Graph attention networks. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings.
- Wang et al. (2021a) Kuan Wang, Yuyu Zhang, Diyi Yang, Le Song, and Tao Qin. 2021a. GNN is a counter? revisiting GNN for question answering. CoRR, abs/2110.03192.
- Wang et al. (2021b) Xiaozhi Wang, Tianyu Gao, Zhaocheng Zhu, Zhengyan Zhang, Zhiyuan Liu, Juanzi Li, and Jian Tang. 2021b. Kepler: A unified model for knowledge embedding and pre-trained language representation. Transactions of the Association for Computational Linguistics, 9:176–194.
- Wolf et al. (2020) Thomas Wolf, Lysandre Debut, Victor Sanh, Julien Chaumond, Clement Delangue, Anthony Moi, Pierric Cistac, Tim Rault, Remi Louf, Morgan Funtowicz, Joe Davison, Sam Shleifer, Patrick von Platen, Clara Ma, Yacine Jernite, Julien Plu, Canwen Xu, Teven Le Scao, Sylvain Gugger, Mariama Drame, Quentin Lhoest, and Alexander Rush. 2020. Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations.
- Yasunaga et al. (2021) Michihiro Yasunaga, Hongyu Ren, Antoine Bosselut, Percy Liang, and Jure Leskovec. 2021. QA-GNN: reasoning with language models and knowledge graphs for question answering. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2021, Online, June 6-11, 2021, pages 535–546.
- Yu et al. (2014) Lei Yu, Karl Moritz Hermann, Phil Blunsom, and Stephen Pulman. 2014. Deep learning for answer sentence selection. CoRR, abs/1412.1632.
- Zellers et al. (2019) Rowan Zellers, Ari Holtzman, Yonatan Bisk, Ali Farhadi, and Yejin Choi. 2019. Hellaswag: Can a machine really finish your sentence? In Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, July 28- August 2, 2019, Volume 1: Long Papers, pages 4791–4800.
- Zhang et al. (2019) Zhengyan Zhang, Xu Han, Zhiyuan Liu, Xin Jiang, Maosong Sun, and Qun Liu. 2019. Ernie: Enhanced language representation with informative entities. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 1441–1451.