Gray-body factor and absorption of the Dirac field in ESTGB gravity

In the decades after Einstein’s general theory of relativity predicted the existence of black holes, the research on the related properties of black holes has gradually become a frontier hot issue in astrophysics. An important feature of black holes is that no information can escape from its event horizon. As a result, the existence of black holes can only be detected by a lot of the indirect methods in the previous decades. Nevertheless, with the development of technology, the Event Horizon Telescope Cooperation Organization has successfully captured the first image of a black hole in the center of the M87 galaxy 1 . This picture directly proves the existence of black holes in the universe. However, a lot of phenomenons cannot be explained by the basic general relativity. These phenomenons include but are not limited to the acceleration expansion stage of the universe Riess1998 , the combination of gravity and the laws of quantum physics Fradkin1985 , and the flatness of the spiral curve for a spiral galaxy Capozziello2007 . Accordingly, this presents a wide room for altering and interpreting theories of gravity, such as the so called extended scalar-tensor-Gauss-Bonnet(ESTGB) Doneva2018 , which is a theory in four dimensions. Specifically, the scalar field is coupled with Gauss-Bonnet invariant in ESTGB to avoid the Ostrogradsky instability Woodard02210 . The black hole solutions have been presented by solving the complex field equation in ESTGB gravity without matter field in four dimensions. In addition, these numerical solutions are also given in the context of different matter fields, for instance, massive scalar Doneva2019 , charged case Doneva2018 , Dilatonic Kanti1996 , multi-scalarscalariz_Doneva , and a particular form of nonlinear electrodynamics Canate2020 .

Black hole that is not an isolated system will interact with the surrounding environment. Interactions present more interesting phenomena, such as radiation, absorption, and scattering. Therefore, we can study how black holes interact with the surrounding environment to obtain interrelated information about special objects. In addition, the experiments to explore black holes rely largely on GW astronomy, shadow images and X-ray spectroscopy. In a way, all three aspects depend on the effect of black holes on the environment. As we all know, the accretion plays a non-negligible role in the phenomenology of active galactic nuclei Macedo2014 . Accretion of fundamental field, i.e., scalar field, electromagnetic field and Dirac field etc., is usually associated with the research of absorption cross section. So it is necessary to research the absorption of waves and particles by black hole. Since the 1960s, theorists have begun to study the problems related to scattering. Moreover, the gray-body factor can help us understand the absorption and scattering of particles, and it is also an important factor to solve Hawking radiation. Hawking radiation Hawking1976 proposed by Hawking in 1976, which depends on the gray-body factor and black hole temperature, is of crucial importance when studying the black hole information paradox. It may be the most difficult obstacle to a thorough understanding of quantum gravity. The gray-body factor is defined as the possibility that the incident particle with frequency $\omega$ is absorbed by the black hole, which encodes valuable information about the near-horizon structure and correlative physics of the black hole. And it is used to measure the deviation from the radiation of the ideal and perfect black-body Kanti2002 . Many authors Songbai2010 ; Ama-Tul-Mughani2021 ; Sharif2020 ; Qanitah Ama-Tul-Mughani2020 ; Konoplya2021 have also studied the gray-body of various black holes with the different methods.

A plethora of methods have been proposed to calculate the gray-body factor with different accuracy, including the new cancellation between contributions to the wave function for the different spin particles Cvetic1998 , the exact numerical method Zhang2018 , the rigorous bounds for the gray-body factor Miao2017 , the WKB methodKonoplya2011 , etc. The WKB approximation stands out among the above-mentioned various calculation methods because of its versatility and flexibility. Blome, Hans-Joachim and Mashhoon Blome1984 proposed the first simple semi-analytic formula to calculate the quasinormal frequency by matching the effective potential with the inverse P$\rm\ddot{o}$schl-Teller potential. However, this formula fails to improve the accuracy for the lower multi-pole numbers. A year later, Schutz and Will Schutz1985 calculated the quasinormal modes using the WKB approximation based on Mashhoon’s formula. The method is to match the WKB solution with the Taylor expansion that passes two turning points. Subsequently, Iyer, Sai and Will Iyer1987 introduced the third-order formula of the WKB method, which improved the accuracy up to one percent on the basis of Schutz and Will. Moreover, Konoplya Konoplya2003 and Matyjasek et al. Matyjasek2017 proposed higher WKB order terms. The WKB approximation can calculate not only the gray-body factor, but also the quasinormal mode. The quasinormal modes Wongjun2020 ; Cai2020 ; Hu2020 ; Liang2018 ; Saleh2018 ; Liang20018 ; Aragon2021 ; Li2017 ; Wang2021 ; Jawad2020 ; Sharif2021 ; Guo2013 containing complex frequencies represent the response of black holes to external perturbations such as massless scalar fields, neutrino fields, gravitational fields, electromagnetic fields, Dirac fields, etc.

In the 1970s, Hawking discovered that the evaporation rate of a black hole is directly proportional to its absorption cross section Futterman . Subsequently, a wealth of important researches on the absorption and scattering of plane waves acting on black holes were established in the 1970s and 1980s. For instance, Sanchez Sanchez1978 indicated that the absorption cross section of a Schwarzschild black hole for the massless scalar field is oscillatory with respect to the geometry-optical limit $(27/4)\pi r_{s}^{2}$, and Unruh Unruh1976 studied the absorption in the massive scalar. Besides, Crispino Crispino2007 presented the absorption of electromagnetic waves in the Schwarzschild spacetime for arbitrary frequencies, and Jung Jung2004 studied the absorption of massive scalar field for the Reissner-Nordstr$\rm\ddot{o}$m spacetime. Next, the result of absorption of electromagnetic waves was obtained in Ref. Crispino2008 . In addition, the absorption of massless scalar by kerr spacetime was investigated in Ref. Macedo2013 , and the absorption of electromagnetic waves was analyzed in Ref. Leite2017 . Liao Hao, Songbai Chen et al. Songbai Chen2014 analyzed the absorption and Hawking radiation of electromagnetic waves with Weyl correction in 4D black hole spacetime. A lots of authors Huang2019 ; Huang2015 ; 2018 ; Anacleto2020 ; Magalhaes2020 ; Junior2020 ; Benone2018 have also studied the absorption and scattering cross sections of various black holes. In this paper we will study the gray-body factor and absorption cross section of the black hole in ESTGB gravity with an unusual form of nonlinear electrodynamics in four dimensions.

This paper is organized as follows. The second section outlines the basic information of the four-dimensional (4D) extended scalar-tensor-Gauss-Bonnet theory (ESTGB) coupled with a special form of nonlinear electrodynamics, and the settings of related parameters are also given. In the third section, the massless Dirac equation is reduced to master wave equations and the effective potential is analyzed. Next, the gray-body factor is calculated using the WKB method in the fourth section. The fifth section presents the expression of the absorption cross section of the Dirac field and the corresponding results are also given. Summary and conclusions are presented in the last section.

Without loss of generality, we adopt natural units in this paper, namely c = G = $\hbar$ = 1. The $4D$ extended scalar-tensor-Gauss-Bonnet theory coupled with a particular form of nonlinear electrodynamics (ESTGB-NLED) Canate2020 is defined as follows,

$\displaystyle S=\int d^{4}x\sqrt{-g}\left\{\frac{1}{16\pi}\left(R-\frac{1}{2}\partial_{\mu}\phi\partial^{\mu}\phi+\bm{f}(\phi)R_{{}_{GB}}^{2}-2\cal U(\phi)\right)-\frac{1}{4\pi}\mathcal{L}_{\rm matter}\right\}.$

(1)

where $R$ is the Ricci scalar, $\phi$ is the scalar field, $\bm{f}(\phi)$ is a coupling function that depends only on $\phi$, $R_{{}_{GB}}^{2}$ is the Gauss-Bonnet term and $\cal U(\phi)$ means the scalar field potential. The first term is the Einstein-Hilbert Lagrangian density. The Lagrangian density $\mathcal{L}_{\rm matter}$ represents any matter field. Assuming that the metric is static, then we have the following spherically symmetric form,

$\displaystyle\text{d}s^{2}=-f(r)\text{d}t^{2}+f^{-1}(r)\text{d}r^{2}+r^{2}\text{d}\Omega^{2},$

(2)

with

$\displaystyle f(r)=1-\frac{2m}{r}-\frac{q^{3}}{r^{3}},$

(3)

where $m$ represents the ADM mass and $q$ indicates the magnetic charge. Supposing that both the effective energy-momentum tensor and the corresponding NLED energy-momentum tensor satisfy the weak energy condition, we can obtain that $m>0$ and $q<0$. The metric is similar to those used in the Reissner-Nordstr$\rm\ddot{o}$m black hole that retains two horizons, one horizon, or none. Moreover, the Schwarzschild black hole is recovered when $q$ is set to $0$. Without loss of generality, we consider the black hole is non-extreme Canate2020 satisfying the value of $0>q/m>-2^{(\frac{5}{3})}/3$. If we set the ADM mass $m=1$ and then the magnetic charge $-2^{(\frac{5}{3})}/3<q<0$.

For later comparisons, it is beneficial to explicitly mention the Reissner-Nordstr$\rm\ddot{o}$m black hole solution. The metric of Reissner-Nordstr$\rm\ddot{o}$m black hole is given by

$\displaystyle\text{d}s^{2}=-(1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}})\text{d}t^{2}+(1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}})^{-1}\text{d}r^{2}+r^{2}\text{d}\Omega^{2},$

(4)

where $Q$ is the electric charge of the black hole and $M$ is the mass of black hole.

In this section, we reduce the massless Dirac equation in the black hole spacetime to a series of Schr$\rm\ddot{o}$dinger-like radial equations, and analyze the properties of the effective potential. The massless Dirac equation in black hole spacetime has the following form according to Ref. Brill1957 ,

$$\gamma^{\alpha}\ e_{\alpha}^{\mu}\left(\partial_{\mu}+\Gamma_{\mu}\right)\Psi=~{}0,$$

(5)

where $\gamma^{\alpha}$ mean the Dirac matrices, defined as follows,

$$\gamma^{0}=\left(\begin{array}[]{c c}-i&0\\ 0&i\end{array}\right),~{}~{}\gamma^{i}=\left(\begin{array}[]{c c}0&-i\sigma^{i}\\ i\sigma^{i}&0\end{array}\right),$$

(6)

with $\sigma_{i}$ representing the pauli matrix, for any $i\in\{1,2,3\}$, respectively. Moreover, $e_{\alpha}^{\mu}$ is the inverse of the tetrad $e_{\mu}^{\alpha}$, of which the particular form is defined by the metric $g_{\mu\nu}$,

$$g_{\mu\nu}=\eta_{ab}e_{\mu}^{a}e^{b}_{\nu},$$

(7)

where $\eta_{ab}$ is the Minkowski metric, and $\eta_{ab}=\text{diag}(-1,1,1,1)$. Additionally, $\Gamma_{\mu}$ is the spin connection defined by

$$\Gamma_{\mu}=\frac{1}{8}[\gamma^{a},\gamma^{b}]e_{a}^{\nu}e_{b\nu;\mu},$$

(8)

with $e_{b\nu;\mu}=\partial_{\mu}e_{b\nu}-\Gamma_{\mu\nu}^{\alpha}e_{b\alpha}$ being the covariant derivative of $e_{b\nu}$, where $\Gamma_{\mu\nu}^{\alpha}$ is the Christoffel symbol. In the spacetime of a static and spherical black hole, $e_{\mu}^{a}$ can be expressed as

$$e_{\mu}^{a}=\text{diag}(\sqrt{f},\frac{1}{\sqrt{f}},r,r\sin\theta).$$

(9)

Hence, the components of $\Gamma_{\mu}$ can be obtained by substituting equation (9) into equation (8) as follows,

$$\Gamma_{0}=\frac{1}{4}f^{{}^{\prime}}\gamma^{1}\gamma^{0},\Gamma_{1}=0,\Gamma_{2}=\frac{1}{2}\sqrt{f}\gamma^{1}\gamma^{2},\Gamma_{3}=\frac{1}{2}(\sin\theta\sqrt{f}\gamma^{1}\gamma^{3}+\cos\theta\gamma^{2}\gamma^{3}).$$

(10)

Further substituting the above expressions into the Dirac equation (5), the Dirac equation becomes

$$\frac{\gamma^{0}}{\sqrt{f}}\frac{\partial{\Psi}}{\partial{t}}+\sqrt{f}\gamma^{1}(\frac{\partial}{\partial{r}}+\frac{1}{r}+\frac{1}{4f}\frac{df}{dr})\Psi+\frac{\gamma^{2}}{r}(\frac{\partial}{\partial\theta}+\frac{1}{2}\cot\theta)\Psi+\frac{\gamma^{3}}{r\sin\theta}\frac{\partial{\Psi}}{\partial{\psi}}=~{}0.$$

(11)

Furthermore, we can transform equation (11) into the following equation

$$\frac{\gamma^{0}}{\sqrt{f}}\frac{\partial{\Phi}}{\partial{t}}+\sqrt{f}\gamma^{1}(\frac{\partial}{\partial{r}}+\frac{1}{r})\Phi+\frac{\gamma^{2}}{r}(\frac{\partial}{\partial\theta}+\frac{1}{2}\cot\theta)\Phi+\frac{\gamma^{3}}{r\sin\theta}\frac{\partial{\Phi}}{\partial{\phi}}=~{}0,$$

(12)

by defining a tortoise coordinate change as

$\displaystyle r_{\star}=\int\frac{dr}{f},$

(13)

introducing the ansatz as

$\displaystyle\Phi=\left(\begin{array}[]{c}\frac{iG^{\pm}(r)}{r}\phi_{jm}^{\pm}(\theta,\varphi)\\ \frac{F^{\pm}(r)}{r}\phi_{jm}^{\mp}(\theta,\varphi)\end{array}\right)e^{-iwt},$

(16)

and defining spinor angular harmonics as

$\displaystyle\phi_{jm}^{+}=\left(\begin{array}[]{c}\sqrt{\frac{l+\frac{1}{2}+m}{2l+1}}Y_{l}^{m-\frac{1}{2}}\\ \sqrt{\frac{l+\frac{1}{2}-m}{2l+1}}Y_{l}^{m+\frac{1}{2}}\end{array}\right),(j=l+\frac{1}{2}),$

(19)

$\displaystyle\phi_{jm}^{-}=\left(\begin{array}[]{c}\sqrt{\frac{l+\frac{1}{2}-m}{2l-1}}Y_{l}^{m-\frac{1}{2}}\\ -\sqrt{\frac{l+\frac{1}{2}+m}{2l-1}}Y_{l}^{m+\frac{1}{2}}\end{array}\right),(j=l-\frac{1}{2}).$

(22)

As a result, equation (11) can be rewritten as

$\displaystyle\left(\begin{array}[]{cc}0&-\omega\\ \omega&0\end{array}\right)\left(\begin{array}[]{c}F^{\pm}\\ G^{\pm}\end{array}\right)-\frac{\partial}{\partial{r_{\star}}}\left(\begin{array}[]{c}F^{\pm}\\ G^{\pm}\end{array}\right)+\sqrt{f}\left(\begin{array}[]{cc}\frac{k_{\pm}}{r}&0\\ 0&-\frac{k_{\pm}}{r}\end{array}\right)\left(\begin{array}[]{c}F^{\pm}\\ G^{\pm}\end{array}\right)=~{}0,$

(33)

where the different cases for $(+)$ and $(-)$ in the function $F^{\pm}$ and $G^{\pm}$ are given by Cho2005

	$\displaystyle\frac{d^{2}{F}}{d{r_{\star}^{2}}}+(\omega^{2}-V_{1})F=~{}0,$		(34)
	$\displaystyle\frac{d^{2}{G}}{d{r_{\star}^{2}}}+(\omega^{2}-V_{2})G=~{}0,$		(35)

with

	$\displaystyle V_{1}=\frac{\sqrt{f}\left|\kappa\right|}{r^{2}}(\left|\kappa\right|\sqrt{f}+\frac{r}{2}\frac{df}{dr}-f),(for~{}\kappa=j+\frac{1}{2},~{}~{}~{}~{}~{}and~{}j=l+\frac{1}{2}),$		(36)
	$\displaystyle V_{2}=\frac{\sqrt{f}\left|\kappa\right|}{r^{2}}(\left|\kappa\right|\sqrt{f}-\frac{r}{2}\frac{df}{dr}+f),(for~{}\kappa=-(j+\frac{1}{2}),~{}and~{}j=l-\frac{1}{2}).$		(37)

It is worth noting that the potentials $V_{1}$ and $V_{2}$ are super-symmetric partners Cooper1995 , and they are derived from the same super-potential. It is well established that the potentials $V_{1}$ and $V_{2}$ related in this way have the same spectra. Therefore, we only need to consider the effective potential $V_{1}$ in calculating the gray-body factor and the absorption cross section for the massless Dirac field by the WKB approximation. As a result, the equation (34) can be written as

$\displaystyle\frac{d^{2}{\psi}}{dr_{\star}^{2}}+(\omega^{2}-V_{eff})\psi=0.$

(38)

Note that Eq.(38) is a Schr$\rm\ddot{o}$dinger-like equation with an effective potential $V_{eff}$. The effective potential is depicted in Fig.1 when we consider $\kappa$ as a variable with the fixed $q=-0.8$. We can observe from Fig.1 that the height of the effective potential barrier becomes larger if $\kappa$ is increased. Furthermore, the location of the peak point moves towards the right with increasing $\kappa$. In addition, we compare the effective potential $V_{eff}$ in Fig.2(a) with $\kappa$ = 5 under four scenarios, i.e., $q=-0.4$, $q=-0.8$, $q=-1.0$ and $q=-2^{5/3}/3$ respectively. It can be seen that, when the absolute value of the magnetic charge is increased, the height of the effective potential barrier increases and then the value diminishes and converges to almost the same value as $r$ increasing. Because this metric is similar to the Reissner-Nordstr$\rm\ddot{o}$m spacetime, we compare the change of the effective potential for the two black hole when $\kappa$ is set to 5. It is obvious in Fig.2(b) that the maximum value of the effective potential of Reissner-Nordstr$\rm\ddot{o}$m spacetime increases faster with electric charge than that of ESTGB-NLED spacetime increases with magnetic charge. This means that the effective potential is more sensitive to the electric charge. Finally, it is worth noting that the effective potential has the form of a single-peak positive definite potential barrier, because it inclines to zero as $r\rightarrow\infty$. In other words, it vanishes at the event horizon $r_{+}$.

In this section, we are going to discuss the grey-body factor for the Dirac field in 4D ESTGB gravity with a nonlinear electrodynamics, i.e., we calculate the reflection probability and transmission probability. The discussion bases on the six-order WKB method for the different value of the magnetic charge. Hawking Hawking1975 predicted that when the temperature of the black hole is proportional to its surface gravity, the black hole will emit particles, which behaves almost like a black body. So black holes are the thermal systems that has an associated temperature and entropy. Therefore black holes produce radiation when thermodynamic laws is satisfied and take into account the quantum effects Hawking19761 . Hawking proposed the expression that the evaporation rate of a black hole in a mode with frequency $\omega$ at the event horizon,

$$\Gamma(\omega)=\frac{1}{e^{\beta\omega}\pm 1}\frac{d^{3}k}{(2\pi)^{3}},$$

(39)

where $\beta$ is the inverse of the black hole temperature, i.e., $\frac{1}{T_{BH}}$, and the plus as well as minus sign are the emission of the fermions and bosons. However the emission rate, which is measured by the spectator located far away, could be affected by the geometry situated on the outside of the event horizon. That is to say, the geometry situated on the outside of the event horizon is going to serve as a potential barrier for the radiation that emits from a black hole. The strong gravitational potential near the event horizon of the black hole will scatter part of the radiation particles back to the black hole, that is, part of the radiation is reflected back to the black hole. Another part of the particles will pass through the gravitational potential due to the quantum tunneling effect, fly to infinity, and be measured by the remote observer. And the radiation, which reaches the remote observer through the potential barrier, will no longer appear as the form of a black body. Hence we can rewrite the expression of the emission rate recorded by the remote observer with the frequency $\omega$ as,

$$\Gamma(\omega)=\frac{\gamma(\omega)}{e^{\beta\omega}\pm 1}\frac{d^{3}k}{(2\pi)^{3}},$$

(40)

$\gamma(\omega)$ is the gray-body factor related to frequency in the action.

The gray-body factor is defined as,

$$\gamma(\omega)=\left|\mathcal{T}_{\omega l}\right|^{2}.$$

(41)

The solution of the second-order differential equation (34), with the postulation of purely outgoing waves at infinity and purely incoming waves at the event horizon, has the following boundary conditions:

$\displaystyle\psi(r_{\star})\sim\left\{\begin{aligned} \mathcal{I}_{\omega l}e^{-i\omega r_{\star}}+\mathcal{R}_{\omega l}e^{i\omega r_{\star}},~{}r_{\star}~{}\rightarrow+\infty,\\ \mathcal{T}_{\omega l}e^{-i\omega r_{\star}},~{}r_{\star}\rightarrow-\infty.\end{aligned}\right.$

(42)

Where $\mathcal{R}_{\omega l}$ and $\mathcal{T}_{\omega l}$ are the reflection coefficient and transmission coefficient, respectively. Due to the conservation of flux, $\mathcal{R}_{\omega l}$ and $\mathcal{T}_{\omega l}$ satisfy the following relationship

$\displaystyle\left|\mathcal{R}_{\omega l}\right|^{2}+\left|\mathcal{T}_{\omega l}\right|^{2}=\left|\mathcal{I}_{\omega l}\right|^{2}.$

(43)

The phase shift $\delta_{l}$ can be expressed by

$\displaystyle e^{-2i\delta_{l}}=(-1)^{l+1}\mathcal{R}_{\omega l}/\mathcal{I}_{\omega l}.$

(44)

Now, we discuss the use of WKB method to determine the gray-body factor Konoplya2011 . The gray-body factor relies on the special relation between $\omega$ and $V_{m}$, which $V_{m}$ is the peak value of the effective potential $V(r)$. There are three cases with $\omega^{2}\gg V_{m}$, $\omega^{2}\approx V_{m}$ and $\omega^{2}\ll V_{m}$ to consider: when $\omega^{2}\gg V_{m}$, i.e., the wave will not be reflected back to the black hole by the barrier when the wave with a frequency $\omega$ is higher than the height of the potential barrier. So the transmission probability $\mathcal{T}_{\omega l}$ is almost equal to one. And the reflection probability $\mathcal{R}_{\omega l}$ is close to zero. Almost all of the radiation pass the potential and fly to infinity under this condition. When $\omega^{2}\ll V_{m}$, the transmission probability $\mathcal{T}_{\omega l}$ is almost equal to zero as well as the reflection probability $\mathcal{R}_{\omega l}$ is close to one. This means that almost all of the radiation is reflected back to the black hole by the potential. When $\omega^{2}\approx V_{m}$, we compute the gray-body in the limit since the highest precision value is obtained in the WKB approximation.

Under the WKB approximation, when incident probability $\mathcal{I}_{\omega l}$ is equal to one the reflection coefficient can be expressed by

$\displaystyle\mathcal{R}_{\omega l}=(1+e^{-2\pi i\alpha})^{-\frac{1}{2}},$

(45)

$\displaystyle\mathcal{T}_{\omega l}=\sqrt{1-\left|(1+e^{-2\pi i\alpha})^{-\frac{1}{2}}\right|^{2}}.$

(46)

Where $\alpha$ is defined by

$\displaystyle\alpha=\frac{i(\omega^{2}-V_{0})}{\sqrt{-2V_{0}^{(2)}}}-\Lambda_{2}-\Lambda_{3}-\Lambda_{4}-\Lambda_{5}-\Lambda_{6}.$

(47)

Where $V_{0}$ is the peak value of the effective potential $V(r)$ at $r=r_{0}$. Then,

$\displaystyle\begin{aligned} &\Lambda_{2}=\frac{1}{\sqrt{-2V^{(2)}_{0}}}[\frac{1}{8}(\frac{V^{(4)}_{0}}{V^{(2)}_{0}})(b^{2}+\frac{1}{4})-\frac{1}{288}(\frac{V^{(3)}_{0}}{V^{(2)}_{0}})^{2}(7+60b^{2})]\\ &\Lambda_{3}=\frac{n+\frac{1}{2}}{-2V^{(2)}_{0}}[\frac{5}{6912}(\frac{V^{(3)}_{0}}{V^{(2)}_{0}})^{4}(77+188b^{2})-\frac{1}{384}(\frac{(V^{(3)}_{0})^{2}V^{(4)}_{0}}{(V^{(2)}_{0})^{3}})(51+100b^{2})\\ &+\frac{1}{2304}(\frac{V^{(4)}_{0}}{V^{(2)}_{0}})^{2}(67+68b^{2})-\frac{1}{288}(\frac{V^{(6)}_{0}}{V^{(2)}_{0}})(5+4b^{2})+\frac{1}{288}(\frac{V^{(3)}_{0}V^{(5)}_{0}}{(V^{(2)}_{0})^{2}})(19+28b^{2})].\end{aligned}$

(48)

In Eqs. (47) and (48), the superscript (2,3,4,5,6) denotes the differentiation with respect to the tortoise coordinate $r_{\star}$ and $b=n+\frac{1}{2}$. Considering that the expression of $\Lambda_{4}$, $\Lambda_{5}$ and $\Lambda_{6}$ found by Konoplya2003 is overly cumbersome, we do not describe it in detail here.

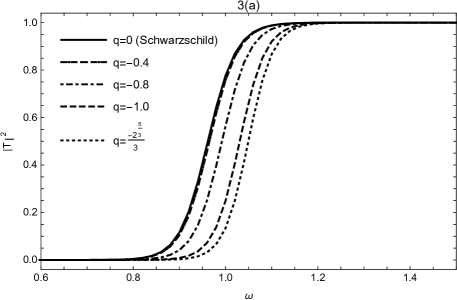
In order to understand the nature of the transmission and reflection coefficients, we shall plot them with the frequency $\omega$ for different values of the magnetic charge. The results for transmission probability are represented in Fig.3(a), where the different values of magnetic charge have been chosen. It can be observed that, for all values of magnetic charge $q$, the transmission coefficient starts from $0$ and reaches $1$ when $\omega$ is increased. Besides, one can see that the transmission coefficient diminishes as the absolute value of the magnetic charge $q$ increases. In other words, the magnetic charge has the behaviour of obstructing the wave from passing through the black hole. The reason may be that the magnetic charge increases the peak value of the effective potential. Fig.3(b) shows the comparison of transmission coefficient for Reissner-Nordstr$\rm\ddot{o}$m and ESTGB-NLED black hole. The transmission coefficient of ESTGB-NLED black hole presents the smaller change than that of Reissner-Nordstr$\rm\ddot{o}$m black hole when we view the magnetic (electric) charge as the variable parameter. We also exhibit the reflection coefficient with $\kappa=5$ in Fig.3(c) and compare it with Reissner-Nordstr$\rm\ddot{o}$m black hole in Fig.3(d). On the contrary, the reflection coefficient starts from $1$ and reaches $0$ with the increase of $\omega$. Furthermore, as shown in Fig.4, we present the results of the transmission and reflection coefficients in the case where $q=-0.8$ and $\kappa$ varies from $1$ to $4$. When $\kappa$ is increasing, the reflection coefficient becomes larger and the transmission coefficient becomes smaller. The reason for this behavior is that the peak value of the effective potential increases with the increase of $\kappa$.

In this section, we calculate the absorption cross section for the Dirac field, which is defined as the ratio of the number of particles absorbed by the black hole to the incident particle flux. Benone Benone104053 proposed the partial wave method to get total absorption cross section as follows,

$$\sigma_{abs}=\sum_{l=0}^{\infty}\sigma_{abs}^{l},$$

(49)

and the partial absorption cross section is given by

$$\sigma_{abs}^{l}=\frac{\pi}{\omega^{2}}(2l+1)(1-\left|e^{-2i\delta_{l}}\right|^{2}),$$

(50)

we substitute the phase shift $e^{-2i\delta_{l}}$ of different $l$ subwaves into the Eq.(33), then we can get another expression,

$$\sigma_{abs}=\frac{\pi}{\omega^{2}}\sum_{l=0}^{\infty}(2l+1)(1-{\left|\mathcal{R}_{\omega l}\right|^{2}}).$$

(51)

Considering the effects of the Dirac field, the results of the partial absorption cross section are shown in Fig.5 and Fig.6. One can see from Fig.5 that the peak value of the partial absorption cross section decreases and the location of the maximum moves to the right when $\kappa$ is increased. By observing the curves in Fig.6(a) for different magnetic charge $q$, one can obtain that the partial absorption cross section tends to almost the same value on the low and high frequencies, and the peak value moves slightly to the right when the absolute value of $q$ is increased. In Fig.6(b), we compare the partial absorption cross section of Reissner-Nordstr$\rm\ddot{o}$m and ESTGB-NLED black holes. We note that the partial absorption cross section of the two types black hole also goes to almost the same value on the low- and high-frequency regions due to the effective potential has the form of a single-peak positive. The effective potential is more sensitive to the electric charge. Specifically, the electric charge can hinder the passage of the wave more. So in the mid-frequency the curve change of the partial absorption cross section of the ESTGB-NLED black hole is not as obvious as that of the Reissner-Nordstr$\rm\ddot{o}$m black hole when we take the magnetic (electric) charge as the variable. As shown in Fig.7(a), we draw the results of the total absorption cross section from $\kappa=1$ to $\kappa=10$ with the magnetic charge $q=-0.4,q=-0.8,q=-1.0$ and $q=-2^{5/3}/3$ respectively. We can see that the total absorption cross section increases and then tends to a stable value when we increase the frequency $\omega$. We also obtain that, as we increase the absolute value of the magnetic charge, the total absorption cross section gradually diminishes. That is to say that, the magnetic charge weakens the absorption for the Dirac field. This is in agreement with the results presented in Ref. Huang2015 . Additionally, we plot the total absorption cross section for the Reissner-Nordstr$\rm\ddot{o}$m black hole in Fig.7(b), for comparison purposes. Compared with the effective potential of Reissner-Nordstr$\rm\ddot{o}$m black hole, we find that the effective potential of the ESTGB-NLED black hole changes slower. We can say that the magnetic charge has a smaller effect on the total absorption cross-section of the Dirac field than the electric charge. Therefore, the variation of total absorption cross section of the ESTGB-NLED black hole with the magnetic charge is not as pronounced as for the Reissner-Nordstr$\rm\ddot{o}$m black hole black hole with the charge.

In the preceding sections, we have studied the gray-body factor and the absorption cross section for the massless Dirac field of the black hole, which is the solution of the 4D ESTGB gravity in the context of the nonlinear electrodynamics. Due to the fact that the solution is characterized by the ADM mass $m$ and the magnetic charge $q$, the black holes will have different structure according to the different choices of these parameters. Therefore, in order to consider the generality, we have studied the case that the black hole is non-extreme where $m=1$ and $-2^{(\frac{5}{3})}/3<q<0$, which is similar to the Reissner-Nordstr$\rm\ddot{o}$m spacetime. Specifically, we have plotted the effective potentials in Fig.1 and Fig.2 for two cases. We have found that the effective potential of the Dirac field is more sensitive for the electric charge owing to that the variation of the effective potential of Reissner-Nordstr$\rm\ddot{o}$m spacetime is more obvious than that of ESTGB-NLED spacetime. Besides, we have carried out numerical calculations to get the gray-body factors using the sixth-order WKB approximations. We have shown the changes of the transmission and reflection coefficients with respect to the magnetic charge in Fig.3, respectively. We have observed that due to the magnetic charge the reflection coefficient is increasing and the transmission coefficient is decreasing comparing the Schwarzschild spacetime. In other words, we have obtained that the magnetic charge impedes the wave from passing the black hole. Moreover, when $\kappa$ is increasing, the reflection coefficient becomes larger and the transmission coefficient becomes smaller. It has been discovered in Fig.7(a) that the total absorption cross section of the Dirac field decreases when we augment the absolute value of the magnetic charge, but increases with the increasing of frequency. Finally, in Fig.7(b), we have compared the total absorption cross section for the Reissner-Nordstr$\rm\ddot{o}$m and ESTGB-NLED black hole. It has been found that the absorption cross section of the Dirac field is more sensitive to electric charge than magnetic charge in these two types of black hole.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported partly by the National Natural Science Foundation of China (Grants No. 12065012, No. 12065013), Yunnan High-level Talent Training Support Plan Young & Elite Talents Project (YNWR-QNBJ-2018-360) and the Fund for Reserve Talents of Young and Middle-aged Academic and Technical Leaders of Yunnan Province (Grant No. 2018HB006).