Gravitational Wave Signatures of Gauged Baryon and Lepton Number

As mentioned in Section I, we consider extending the usual single-scalar symmetry breaking sector to possibly include two scalars per each symmetry breaking. Each of the fields breaking the ${\rm U}(1)_{L}$ symmetry comes in the representation

$\displaystyle\Phi_{Li}=(1,1,0,0,2)\ ,$

(2)

while each of the scalars breaking ${\rm U}(1)_{B}$ is

$\displaystyle\Phi_{Bi}=(1,1,0,3,3)\ .$

(3)

Within this framework, there are four possible cases:

• $(a)$

  $\Phi_{B}$ breaks ${\rm U(1)}_{B}$ and $\Phi_{L}$ breaks ${\rm U(1)}_{L}$,

• $(b)$

  $\Phi_{B1}$, $\Phi_{B2}$ break ${\rm U(1)}_{B}$ and $\Phi_{L}$ breaks ${\rm U(1)}_{L}$,

• $(c)$

  $\Phi_{B}$ breaks ${\rm U(1)}_{B}$ and $\Phi_{L1}$, $\Phi_{L2}$ break ${\rm U(1)}_{L}$,

• $(d)$

  $\Phi_{B1}$, $\Phi_{B2}$ break ${\rm U(1)}_{B}$ and $\Phi_{L1}$, $\Phi_{L2}$ break ${\rm U(1)}_{L}$.

We assume that the mixed terms involving scalars breaking different ${\rm U}(1)$ gauge groups have negligible coefficients. This implies that for a given ${\rm U}(1)$, if only one scalar breaks the symmetry, the scalar potential is

$\displaystyle V(\Phi)$

$\displaystyle=$

$\displaystyle-m^{2}|\Phi|^{2}+\lambda|\Phi|^{4}\ ,$

(4)

whereas if two scalars participate in symmetry breaking,

	$\displaystyle V(\Phi_{1},\Phi_{2})$	$\displaystyle=$	$\displaystyle-\,m_{1}^{2}|\Phi_{1}|^{2}+\lambda_{1}|\Phi_{1}|^{4}-m_{2}^{2}|\Phi_{2}|^{2}+\lambda_{2}|\Phi_{2}|^{4}$		(5)
		$\displaystyle+$	$\displaystyle\left[(\lambda_{4}|\Phi_{1}|^{2}\!+\!\lambda_{5}|\Phi_{2}|^{2}\!+\!\lambda_{6}\Phi_{1}^{*}\Phi_{2})\Phi_{1}^{*}\Phi_{2}+{\rm h.c.}\right]$
		$\displaystyle-$	$\displaystyle(m_{12}^{2}\Phi_{1}^{*}\Phi_{2}+{\rm h.c.})+\lambda_{3}|\Phi_{1}|^{2}|\Phi_{2}|^{2}\ .$

The scalars develop the following vacuum expectation values,

$\displaystyle\langle\Phi_{i}\rangle=\frac{v_{i}}{\sqrt{2}}\ .$

(6)

Whenever two scalars take part in the symmetry breaking, we define $v\equiv\sqrt{v_{1}^{2}+v_{2}^{2}}\ .$ This way one can collectively describe the ${\rm U}(1)_{B}$ breaking scale as $v=v_{B}$, and the ${\rm U}(1)_{L}$ breaking scale as $v=v_{L}$, independent of whether the vacuum expectation value comes from a single scalar or two scalars.

If lepton number is broken at a higher scale than baryon number, the symmetry breaking pattern is:

$$\begin{array}[]{c}{\rm SU}(3)_{c}\times{\rm SU}(2)_{L}\times{\rm U}(1)_{Y}\times{\rm U}(1)_{B}\times{\rm U}(1)_{L}\\[3.0pt] \hskip 31.86707pt\bigg{\downarrow}\hskip 8.53581pt{\scriptstyle\langle\Phi_{Li}\rangle\ \neq\ 0}\\[12.0pt] {\rm SU}(3)_{c}\times{\rm SU}(2)_{L}\times{\rm U}(1)_{Y}\times{\rm U}(1)_{B}\\[3.0pt] \hskip 31.86707pt\bigg{\downarrow}\hskip 8.53581pt{\scriptstyle\langle\Phi_{Bi}\rangle\ \neq\ 0}\\[12.0pt] {\rm SU}(3)_{c}\times{\rm SU}(2)_{L}\times{\rm U}(1)_{Y}\ ,\\[7.0pt] \end{array}$$

followed by the usual electroweak symmetry breaking by the Standard Model Higgs. We note that the order of ${\rm U}(1)_{B}$ and ${\rm U}(1)_{L}$ breaking may be reversed.

To provide a concrete quantitative example, we consider the model with gauged ${\rm U}(1)_{B}$ and ${\rm U}(1)_{L}$ proposed in Fileviez Perez et al. (2014), which involves the minimal fermionic particle content for a theory with such a gauge group. It is straightforward to check that all gauge anomalies are cancelled if the Standard Model quark fields $Q_{L}^{j}$, $u_{R}^{j}$, $d_{R}^{j}$ and lepton fields $l_{L}^{j}$, $e_{R}^{j}$ are augmented by

	$\displaystyle\nu_{R}^{j}$	$\displaystyle=$	$\displaystyle(1,1,0,0,1)\ ,$
	$\displaystyle\Psi_{L}$	$\displaystyle=$	$\displaystyle\begin{pmatrix}\psi_{L}^{+}\\[2.0pt] \psi_{L}^{0}\end{pmatrix}=\left(1,2,\tfrac{1}{2},\tfrac{3}{2},\tfrac{3}{2}\right)\ ,$
	$\displaystyle\Psi_{R}$	$\displaystyle=$	$\displaystyle\begin{pmatrix}\psi_{R}^{0}\\ \psi_{R}^{-}\end{pmatrix}=\left(1,2,\tfrac{1}{2},-\tfrac{3}{2},-\tfrac{3}{2}\right)\ ,$
	$\displaystyle\Sigma_{L}$	$\displaystyle=$	$\displaystyle\tfrac{1}{2}\begin{pmatrix}\sigma^{0}&\sqrt{2}\,\sigma^{+}\\[2.0pt] \sqrt{2}\,\sigma^{-}&-\sigma^{0}\end{pmatrix}=\left(1,3,0,-\tfrac{3}{2},-\tfrac{3}{2}\right)\ ,$
	$\displaystyle\chi_{L}$	$\displaystyle=$	$\displaystyle\left(1,1,0,-\tfrac{3}{2},-\tfrac{3}{2}\right)\ ,$		(7)

where $j$ is the family index. Among the fields above, $\nu_{R}^{j}$ are the right-handed neutrinos, whereas $\chi_{L}$ is a Majorana dark matter candidate discussed in Section III.

The scalars $\Phi_{Bi}$ and $\Phi_{Li}$ generate masses for the new fermions through the following Lagrangian terms,

	$\displaystyle-\mathcal{L}$	$\displaystyle\supset$	$\displaystyle\sum_{i}\!\left(Y_{\Psi}^{i}\overline{\Psi}_{R}\Psi_{L}\Phi_{Bi}^{*}\!+\!Y_{\Sigma}^{i}{\rm Tr}(\Sigma_{L}^{2})\Phi_{Bi}\!+\!Y_{\chi}^{i}\chi_{L}\chi_{L}\Phi_{Bi}\right)$		(8)
		$\displaystyle+$	$\displaystyle y_{\nu}^{j}\,\bar{l}_{L}^{j}H\nu_{R}^{j}+\sum_{i}Y_{\nu}^{ij}\nu_{R}^{j}\nu_{R}^{j}\Phi_{Li}+{\rm h.c.}\ ,\ \ \ \$

which provide vector-like masses to the new fermions, as well as introduce a type I seesaw mechanism for the neutrinos. For example, assuming that the Yukawa couplings are $y_{\nu}^{j}\sim 1$ and $Y_{\nu}^{j}\sim 10^{-2}$, the measured neutrino mass splittings are reproduced if $v_{L}\sim 10^{5}\ {\rm PeV}$. The mass matrices for the new fermions are provided in Fileviez Perez et al. (2014).

The spontaneous breaking of ${\rm U}(1)_{L}$ and ${\rm U}(1)_{B}$ leads to the appearance of vector gauge bosons $Z_{L}$ and $Z_{B}$. Given the charges of the scalars breaking the two symmetries, the corresponding masses are

$\displaystyle m_{Z_{L}}=2g_{L}v_{L}\ ,\ \ \ \ \ \ \ \ m_{Z_{B}}=3g_{B}v_{B}\ ,$

(9)

where $g_{L}$ and $g_{B}$ are the ${\rm U}(1)_{L}$ and ${\rm U}(1)_{B}$ gauge couplings, respectively, whose values are free parameters.

After ${\rm U}(1)_{B}$ breaking, there remains a residual discrete ${Z}_{2}$ symmetry under which the new fermions transform as

	$\displaystyle\Psi_{L}$	$\displaystyle\to$	$\displaystyle-\Psi_{L}\ ,\ \ \ \ \overline{\Psi}_{R}\to-\overline{\Psi}_{R}\ ,$
	$\displaystyle\Sigma$	$\displaystyle\to$	$\displaystyle-\Sigma\ ,\ \ \ \ \ \ \ \chi_{L}\to-\chi_{L}\ .$		(10)

If $\chi_{L}$ is the lightest of the new fermions, there is no decay channel available for it, thus it becomes a good candidate for particle dark matter.

It was argued in Duerr and Fileviez Perez (2015); Fileviez Perez et al. (2019) that in models with gauged baryon and lepton number consistency with the dark matter relic abundance of $h^{2}\Omega_{\rm DM}\approx 0.12$ Aghanim et al. (2020) imposes an upper bound on the ${\rm U(1)}_{B}$ breaking scale. In particular, if the dark matter annihilation happens via the resonant $s$-channel process

$\displaystyle\chi_{L}\,\chi_{L}\to Z_{B}^{*}\to\bar{q}\,q\ ,$

(11)

a dependence between the parameters $v_{B}$, $Y_{\chi}$, and $g_{B}$ arises, and the perturbativity requirement leads to $g_{B}v_{B}\lesssim 20\ {\rm TeV}$. This was the reason why in Fornal and Shams Es Haghi (2020), where the gravitational wave signal from a model with gauged baryon and lepton number was considered, a low scale of ${\rm U}(1)_{B}$ was imposed.

However, as was demonstrated in Ohmer and Patel (2015), in the model we are considering other dark matter annihilation channels remain unsuppressed, including the nonresonant $t$-channel process

$\displaystyle\chi_{L}\,\chi_{L}\to\Phi_{B}\,\Phi_{B}\ ,$

(12)

whose cross section can be sufficiently large to explain the dark matter relic density. Therefore, the arguments in Duerr and Fileviez Perez (2015); Fileviez Perez et al. (2019) do not apply in our case, and the scale of ${\rm U}(1)_{B}$ breaking can be high. Alternatively, the aforementioned bound on the ${\rm U}(1)_{B}$ breaking scale can always be avoided by assuming nonthermal dark matter production.

There cannot exist any primordial baryon or lepton number asymmetry above the scales of ${\rm U}(1)_{B}$ and ${\rm U}(1)_{L}$ breaking. An excess of matter over antimatter can only arise once one of those two symmetries is broken. A natural setting to achieve this below the scale of ${\rm U}(1)_{L}$ breaking is offered by high-scale leptogenesis (see Davidson et al. (2008) and references therein), in which a lepton number asymmetry is generated through the out-of-equilibrium decays of the lightest right-handed neutrino,

$\displaystyle N_{1}\to H\,l_{L}\ .$

(13)

The $CP$ asymmetry is introduced through the standard interference between the tree-level diagram for the process in Eq. (13) and the one-loop diagrams involving $H$, $l_{L}$, and the two heavier right-handed neutrinos $N_{2}$, $N_{3}$ in the loop.

The generated lepton asymmetry is calculated by solving the Boltzmann equations for the evolution of the lightest right-handed neutrino abundance $Y_{N_{1}}=n_{N_{1}}/s$ (where $n_{N_{1}}$ is the $N_{1}$ particle density and $s$ is the co-moving entropy density) and the $B\!-\!L$ asymmetry $Y_{B-L}$ Buchmuller et al. (2005),

	$\displaystyle\frac{dY_{N_{1}}}{dz}$	$\displaystyle=$	$\displaystyle-(D+S)(Y_{N_{1}}-Y_{N_{1}}^{\rm eq})\ ,$
	$\displaystyle\frac{dY_{B-L}}{dz}$	$\displaystyle=$	$\displaystyle-\epsilon_{1}D(Y_{N_{1}}-Y_{N_{1}}^{\rm eq})-WY_{B-L}\ ,$		(14)

where $z=m_{N_{1}}/T$, the term $D$ accounts for decays and inverse decays, $S$ represents $\Delta L=1$ scatterings, $W$ describes the washout effects, and $\epsilon_{1}$ is the $CP$ asymmetry parameter. In our case, the Boltzmann equations are slightly different than in the standard leptogenesis scenario, since the right-handed neutrinos have an extra interaction with the $Z_{L}$ gauge boson. Those equations were solved in Fileviez Perez et al. (2021), and the amount of the generated lepton asymmetry $\Delta L$ was determined for various values of model parameters.

The produced lepton asymmetry is then partially converted into a baryon asymmetry through the electroweak sphalerons. Above the scale of ${\rm U}(1)_{B}$ breaking the sphaleron-induced interactions have the form

$\displaystyle(QQQL)^{3}\overline{\Psi}_{R}\Psi_{L}\Sigma_{L}^{4}\ ,$

(15)

and it was shown in Duerr and Fileviez Perez (2015) that if the breaking of ${\rm U}(1)_{B}$ occurs close to the electroweak scale, then the final baryon asymmetry predicted by the model is given by

$\displaystyle|\Delta B|=\frac{32}{99}|\Delta L|\ .$

(16)

This can explain the observed baryon-to-photon ratio Workman et al. (2022)

$\displaystyle\eta\approx 6\times 10^{-10}$

(17)

if the scale of ${\rm U}(1)_{L}$ breaking satisfies the relation

$\displaystyle v_{L}\gtrsim 4000\ {\rm PeV}\ .$

(18)

The requirement for such a high ${\rm U}(1)_{L}$ symmetry breaking scale provides the desired setting accommodating the type I seesaw mechanism for the neutrinos.

There are two main processes governing the behavior of a cosmic string network: formation of string loops and stretching due to the expansion of the Universe. The first of those contributions, creation of string loops, happens when long strings intersect and intercommute. The newly created string loops oscillate and emit gravitational radiation, mainly from cusps and kinks propagating through the string loop, and from kink-kink collisions Olum and Blanco-Pillado (2000); Moore et al. (2002).

A competition between these two effects leads to the so-called scaling regime, in which there is a large number of string loops and a small number of Hubble-size strings Kibble (1985); Bennett and Bouchet (1988, 1989); Albrecht and Turok (1989); Allen and Shellard (1990). There is a continuous flow of energy from long strings to string loops, and then to gravitational radiation through their decays. This gravitational radiation makes up a fixed fraction of the energy density of the Universe Hindmarsh and Kibble (1995).

To describe this process quantitatively, we follow the steps outlined in Cui et al. (2019); Gouttenoire et al. (2020b). We consider a string loop created at time $t_{0}$ with initial length $l(t_{0})=\alpha\,t_{0}$, where $\alpha$ is a constant loop size parameter. The loop oscillates emitting gravitational waves with frequencies

$\displaystyle\tilde{f}=\frac{2k}{l}\ ,$

(21)

where $k$ is a positive integer. Rescaling this result by the scale factor $a(t)$, one obtains the currently observed frequency,

$\displaystyle f=\frac{a(t_{e})}{a(T)}\,\tilde{f}\ ,$

(22)

where $t_{e}$ is the time of the emission and $T$ is the time today. The spectrum of the emitted gravitational waves from a single oscillating string loop is given by Blanco-Pillado et al. (2014); Blanco-Pillado and Olum (2017)

$\displaystyle P_{(k,n)}=\frac{\Gamma G\mu^{2}}{k^{n}}\bigg{(}\sum_{p=1}^{\infty}\frac{1}{p^{n}}\!\bigg{)}^{-1},$

(23)

where for the contribution from cusps $n=4/3$, from kinks $n=5/3$, and from kink-kink collisions $n=2$, while the overall factor $\Gamma\simeq 50$ Vachaspati and Vilenkin (1985b). Due to the constant emission of gravitational radiation, the string loop shrinks and its length at the time of the gravitational wave emission is

$\displaystyle l(t_{e})=\alpha\,t_{0}-\Gamma G\mu\,(t_{e}-t_{0})\ ,$

(24)

causing the loop to vanish after the time ${\alpha\,t_{0}}/{(\Gamma G\mu)}$.

The only model-dependent quantity describing the cosmic string network is the loop distribution function $F(l,t_{0})$ for the created loops. Adopting the well-established model developed in Martins and Shellard (1996a, b, 2002), describing the string network just by the mean string velocity and the correlation length, leads in the scaling regime to the following formula,

$\displaystyle F(l,t_{0})=\frac{\sqrt{2}\,{C}_{\rm eff}}{\alpha\,t_{0}^{4}}\,\delta(l-\alpha\,t_{0})\ ,$

(25)

where the constant ${C}_{\rm eff}$ depends on the era in the evolution of the Universe (for radiation $C_{\rm eff}=5.4$, whereas for the matter dominated era $C_{\rm eff}=0.39$ Cui et al. (2019)).

The stochastic gravitational wave background generated by the dynamics of the cosmic string network is Cui et al. (2019); Gouttenoire et al. (2020b)

	$\displaystyle h^{2}\Omega_{\rm CS}(f)$	$\displaystyle=$	$\displaystyle\frac{2h^{2}\mathcal{F}_{\alpha}}{\rho_{c}\alpha^{2}f}\,\sum_{k,n}\,{k\,P_{(k,n)}}\int_{t_{F}}^{T}\!dt_{e}\ \frac{C_{\text{eff}}(t_{0k})}{t_{0k}^{\,4}}\ \ \ \$		(26)
		$\displaystyle\times$	$\displaystyle\left(\frac{a(t_{e})}{a(T)}\right)^{\!5}\left(\frac{a(t_{0k})}{a(t_{e})}\right)^{\!3}\theta(t_{0k}-t_{F})\ ,$

where

$\displaystyle t_{0k}=\frac{1}{\alpha}\left(\frac{2k}{f}\frac{a(t_{e})}{a(T)}+\Gamma G\mu\,t_{e}\right)\ .$

(27)

In Eqs. (26) and (27) the parameters are the following: $\mathcal{F}_{\alpha}$ is the fraction of the loops contributing to the gravitational wave signal, estimated to be $\mathcal{F}_{\alpha}\approx 0.1$ Blanco-Pillado et al. (2014) since the majority of the energy is lost by long strings going into highly boosted smaller loops which provide only a subdominant contribution; $\rho_{c}$ is the critical density of the Universe; the loop size parameter $\alpha=0.1$ provides an accurate estimate of the loop size distribution Blanco-Pillado et al. (2014); Blanco-Pillado and Olum (2017); $t_{F}$ is the time at which the cosmic string network was formed, related to the density of the Universe at that time via $\sqrt{\rho(t_{F})}=\mu$ Gouttenoire et al. (2020b), $t_{0k}$ is the instance when the loop was produced, and $\theta(x)$ is the Heaviside step function. We also note that, as argued in Cui et al. (2019); Gouttenoire et al. (2020b), the largest contribution to the gravitational wave signal comes from the cusps.

The resulting stochastic gravitational wave background is presented in Fig. 1 for four values of the symmetry breaking scale, in the range of frequencies relevant for the upcoming gravitational wave experiments, whose sensitivities are denoted by the colored regions. If $v\gtrsim 10^{4}\ {\rm PeV}$, the signal can be seen by all the detectors: LISA Amaro-Seoane et al. (2017), DECIGO Kawamura et al. (2011), Big Bang Observer Crowder and Cornish (2005), Einstein Telescope Punturo et al. (2010), and Cosmic Explorer Reitze et al. (2019). This is illustrated in more detail in Fig. 2, which shows the reach of each experiment in terms of the symmetry breaking scale leading to a cosmic string signal. The lower bound is detector-specific, whereas the upper bound reflects the cosmic microwave background constraint in Eq. (20).

The cosmic string network will be produced if either ${\rm U}(1)_{B}$ or ${\rm U}(1)_{L}$ is spontaneously broken by a single scalar. Therefore, among the cases enumerated in Section II, the gravitational wave signals discussed here are relevant in case $(a)$ for both baryon and lepton number breaking, in case $(b)$ only for lepton number breaking, and in case $(c)$ only for baryon number breaking.

The profile of the domain wall configuration $\vec{\phi}_{dw}(z)$ is the solution to the equation Chen et al. (2020)

$\displaystyle\frac{d^{2}\vec{\phi}_{dw}(z)}{dz^{2}}-\vec{\nabla}_{\!\phi}V_{\rm eff}\big{[}\vec{\phi}_{dw}(z)\big{]}=0\ ,$

(28)

where the $z$-axis was chosen to be perpendicular to the domain wall, and the boundary conditions are,

$\displaystyle\vec{\phi}_{dw}(-\infty)=\vec{\phi}_{\rm vac1}\ ,\ \ \ \ \ \vec{\phi}_{dw}(\infty)=\vec{\phi}_{\rm vac2}.$

(29)

As mentioned earlier, there are only two parameters which describe the gravitational wave spectrum from domain walls. The first of them is the domain wall tension $\sigma$ given by

$\displaystyle\sigma=\int_{-\infty}^{\infty}dz\!\left[\frac{1}{2}\bigg{(}\frac{d\vec{\phi}_{dw}(z)}{dz}\bigg{)}^{2}+V_{\rm eff}\big{[}\vec{\phi}_{dw}(z)\big{]}\right].$

(30)

In the model we are considering, to a good approximation

$\displaystyle\sigma\,\sim\,v^{3}\ .$

(31)

The other parameter is the potential bias $\Delta\rho$, i.e., the energy density difference between the vacua, in our case equal to

$\displaystyle\Delta\rho=\big{(}m_{12}^{2}+\tfrac{1}{2}\lambda_{4}v_{1}^{2}+\tfrac{1}{2}\lambda_{5}v_{2}^{2}\big{)}\,v_{1}v_{2}\ .$

(32)

The created domain walls are unstable and undergo annihilation, emitting gravitational radiation, provided that Saikawa (2017)

$\displaystyle\Delta\rho\gtrsim\left(\frac{\sigma}{M_{Pl}}\right)^{2}\ .$

(33)

If in Eq. (32) the term involving $m_{12}^{2}$ is the dominant one, then Eq. (33) takes the form $m_{12}\gtrsim{v^{2}}/{M_{Pl}}$. For example, if the symmetry breaking scale is $v\sim 10^{3}\ \rm PeV$, this implies $m_{12}\gtrsim 100\ {\rm MeV}$. An independent constraint arises from the necessity of domain wall annihilation happening before Big Bang nucleosynthesis, so the ratios of the produced elements are not altered, but the bound in Eq. (33) remains stronger.

Domain wall annihilation leads to a stochastic gravitational wave background given by Kadota et al. (2015); Saikawa (2017),

	$\displaystyle h^{2}\Omega_{\rm DW}(f)$	$\displaystyle\approx$	$\displaystyle 7.1\times 10^{-33}\left(\frac{\sigma}{\rm PeV^{3}}\right)^{4}\left(\frac{\rm TeV^{4}}{\Delta\rho}\right)^{2}\left(\frac{100}{g_{*}}\right)^{\frac{1}{3}}$		(34)
		$\displaystyle\times$	$\displaystyle\!\!\bigg{[}\!\left(\frac{f}{f_{d}}\right)^{3}\!\theta(f_{d}-f)+\left(\frac{f_{d}}{f}\right)\theta(f-f_{d})\bigg{]},\ \ \ \ \ \ \$

where for the area parameter we used $\mathcal{A}=0.8$ and for the efficiency parameter we adopted the value $\tilde{\epsilon}_{\rm gw}=0.7$ Hiramatsu et al. (2014),$\theta$ denotes the step function, and the peak frequency $f_{d}$ is

$\displaystyle f_{d}\approx(0.14\ {\rm Hz})\,\sqrt{\frac{\rm PeV^{3}}{\sigma}\frac{\Delta\rho}{\rm TeV^{4}}}\ .$

(35)

The slope of the signal falls $\sim f^{3}$ to the left of the peak when moving toward lower frequencies, and falls like $f^{-1}$ to the right of the peak when moving toward higher frequencies. The cosmic microwave background constraint on the strength of the signal at the peak is $h^{2}\Omega(f)<2.9\times 10^{-7}$ Clarke et al. (2020), which translates to the following condition on the parameters,

$\displaystyle\frac{\sigma}{\sqrt{\Delta\rho}}\lesssim 2.5\times 10^{12}\ \rm PeV\ ,$

(36)

stronger than the bound imposed by Eq. (33).

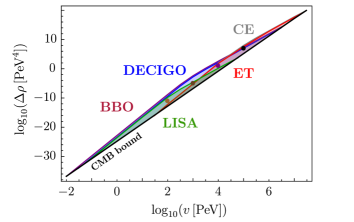
Several examples of gravitational wave spectra from domain wall annihilation, plotted using Eq. (34), are shown in Fig. 3 for representative values of the parameters $v$ and $\Delta\rho$. The reach of the upcoming gravitational wave detectors is also shown, including LISA, Big Bang Observer, DECIGO, Einstein Telescope, and Cosmic Explorer. A more detailed look at their sensitivity is provided by Fig. 4, which shows the full parameter space that can be probed by those experiments. The lower bound on the domain wall parameter $\Delta\rho$ is a reflection of the cosmic microwave background constraint from Eq. (36). The parameter $\Delta\rho$ depends in general on all three fundamental Lagrangian parameters $m_{12}$, $\lambda_{4}$, and $\lambda_{5}$ through the relation in Eq. (32). Under the assumption that the term involving $m_{12}$ is dominant, the experimental sensitivity plot in the plane $(v,m_{12})$ would be the same as in figure 4 of Fornal et al. (2023).

The effective potential for the background field $\phi$ consists of the tree-level part, the one-loop Coleman-Weinberg zero temperature correction, and the finite temperature contribution. Upon imposing the condition that the minimum of the zero temperature potential and the mass of $\phi$ remain at their tree-level values (i.e., the cutoff regularization scheme), the effective potential is given by

	$\displaystyle V_{\rm eff}(\phi,T)=-\frac{1}{2}\lambda v^{2}\phi^{2}+\frac{1}{4}\lambda\phi^{4}$
	$\displaystyle+\sum_{i}\frac{n_{i}m_{i}^{2}(\phi)}{64\pi^{2}}\bigg{\{}\!m_{i}^{2}(\phi)\!\left[\log\!\left(\frac{m_{i}^{2}(\phi)}{m_{i}^{2}(v)}\right)\!-\!\frac{3}{2}\right]\!+\!2m_{i}^{2}(v)\!\bigg{\}}$
	$\displaystyle+\ \frac{T^{4}}{2\pi^{2}}\sum_{i}n_{i}\int_{0}^{\infty}dx\,x^{2}\log\left(1\mp e^{-\sqrt{{m_{i}^{2}(\phi)}/{T^{2}}+x^{2}}}\right)$
	$\displaystyle+\ \frac{T}{12\pi}\sum_{j}n^{\prime}_{j}\left\{m_{j}^{3}(\phi)-\left[m_{j}^{2}(\phi)+\Pi_{j}(T)\right]^{\frac{3}{2}}\right\}\ .$		(37)

In the expression above the sums are over all particles charged under the ${\rm U}(1)$ including the Goldstone bosons $\chi_{\rm GB}$, $m_{i}(\phi)$ are the field-dependent masses, $n_{i}$ is the number of degrees of freedom for a given particle ($n_{Z^{\prime}}=3$, $n_{\phi}=1$, $n_{\chi_{\rm GB}}=1$), $n_{j}^{\prime}$ is similar but includes only scalars and longitudinal components of vector bosons ($n^{\prime}_{Z^{\prime}}=1$, $n^{\prime}_{\phi}=1$, $n^{\prime}_{\chi_{\rm GB}}=1$), and for the Goldstones one needs to replace $m_{\chi_{\rm GB}}(v)\to m_{\phi}(v)$. We will assume that all new Yukawa couplings are small, so that the only relevant field-dependent masses are

	$\displaystyle m_{Z^{\prime}}(\phi)=xg\phi\ ,\ \ \ \ m_{\phi}(\phi)=\sqrt{\lambda(3\phi^{2}-v^{2})}\ ,$
	$\displaystyle m_{\chi_{\rm GB}}(\phi)=\sqrt{\lambda(\phi^{2}-v^{2})}\ .$		(38)

In the limit $\lambda\ll g$, the thermal masses are

	$\displaystyle\Pi_{Z^{\prime}}(T)$	$\displaystyle=$	$\displaystyle\frac{1}{3}\left(x^{2}+\frac{9}{2}\right)g^{2}T^{2}\ ,$
	$\displaystyle\Pi_{\phi}(T)$	$\displaystyle=$	$\displaystyle\Pi_{\chi_{\rm GB}}(T)=\frac{1}{4}x^{2}g^{2}T^{2}\ ,$		(39)

where for gauged baryon number $g=g_{B}$ and $x=3$, while for gauged lepton number $g=g_{L}$ and $x=2$.

For a range of $\lambda$ and $g$ values the effective potential develops a vacuum at $\phi\neq 0$ (true vacuum) with a lower energy density than the high temperature vacuum at $\phi=0$ (false vacuum), separated by a potential bump, which are precisely the conditions needed for a first order phase transition to take place. The changing shape of the effective potential is shown in Fig. 5 for a particular choice of parameters, in the case of gauged baryon number.

A first order phase transition from the false vacuum to the true vacuum of a given patch of the Universe corresponds to the nucleation of a bubble which then starts expanding. This process is initiated at the nucleation temperature $T_{*}$, which is determined from the condition that the bubble nucleation rate Linde (1983) becomes comparable with the Hubble expansion,

$\displaystyle\bigg{(}\frac{S(T_{*})}{2\pi T_{*}}\bigg{)}^{3/2}T_{*}^{4}\,e^{-{S(T_{*})}/{T_{*}}}\approx H(T_{*})^{4}\ ,$

(40)

where $S(T)$ is the Euclidean action given by

$\displaystyle S(T)=\int d^{3}r\left[\frac{1}{2}\left(\frac{d\phi_{b}}{dr}\right)^{2}+V_{\rm eff}(\phi_{b},T)\right],$

(41)

with $\phi_{b}$ being the solution of the bubble equation,

$\displaystyle\frac{d^{2}\phi}{dr^{2}}+\frac{2}{r}\frac{d\phi}{dr}-\frac{dV_{\rm eff}(\phi,T)}{d\phi}=0\ ,$

(42)

subject to the boundary conditions

$\displaystyle\frac{d\phi}{dr}\bigg{|}_{r=0}=0\ ,\ \ \ \ \ \phi(\infty)=\phi_{\rm false}\ .$

(43)

Since $H(T)\approx(T^{2}/M_{Pl})\sqrt{4\pi^{3}g_{*}/45}$, Eq. (40) becomes

$\displaystyle\frac{S(T_{*})}{T_{*}}\approx 4\log\!\left(\frac{M_{Pl}}{T_{*}}\right)\!-\!\log\left[\left(\frac{4\pi^{3}g_{*}}{45}\right)^{\!\!2}\!\left(\frac{2\pi\,T_{*}}{S(T_{*})}\right)^{\!\!\frac{3}{2}}\right]\!.\ \$

(44)

The phase transition parameters relevant for determining the gravitational wave signal are: the bubble wall velocity $v_{w}$, the nucleation temperature $T_{*}$, the phase transition strength $\alpha$, and its duration $1/\tilde{\beta}$. In our analysis we assume $v_{w}=c$, but other choices are also possible Espinosa et al. (2010); Caprini et al. (2016). The other three parameters, $T_{*}$, $\alpha$, and $\tilde{\beta}$, are determined from the behavior of the effective potential with changing temperature. As such, those parameters encode information about the details of the particle physics model considered.

The phase transition strength is calculated as the ratio of the energy density difference between the false and true vacuum, and that of radiation, both taken at nucleation temperature,

$\displaystyle\alpha=\frac{\rho_{\rm vac}(T_{*})}{\rho_{\rm rad}(T_{*})}\ .$

(45)

Those two quantities are obtained from the relations

	$\displaystyle\rho_{\rm vac}(T)$	$\displaystyle=$	$\displaystyle V_{\rm eff}(\phi_{\rm false},T)-V_{\rm eff}(\phi_{\rm true},T)$
		$\displaystyle-$	$\displaystyle T\frac{\partial}{\partial T}{\left[V_{\rm eff}(\phi_{\rm false},T)-V_{\rm eff}(\phi_{\rm true},T)\right]}\ ,$
	$\displaystyle\rho_{\rm rad}(T)$	$\displaystyle=$	$\displaystyle\frac{\pi^{2}}{30}g_{*}T^{4}\ ,$		(46)

where $g_{*}$ is the number of degrees of freedom active when the bubbles are nucleated. The parameter $\tilde{\beta}$, related to the time scale of the phase transition, is determined via

$\displaystyle\tilde{\beta}=T_{*}\frac{d}{dT}\bigg{(}\frac{S(T)}{T}\bigg{)}\bigg{|}_{T=T_{*}}\ .$

(47)

The dynamics of the nucleated bubbles generates gravitational waves through sound shock waves in the early Universe plasma, bubble collisions, and magnetohydrodynamic turbulence. The expected contribution of each of those processes to the stochastic gravitational wave background was determined through numerical simulations, and the corresponding empirical formulas were derived. The resulting gravitational wave signal is the sum of the three contributions,

$\displaystyle h^{2}\Omega_{\rm PT}(f)=h^{2}\Omega_{s}(f)+h^{2}\Omega_{c}(f)+h^{2}\Omega_{t}(f)\ .$

(48)

The expected signal from sound waves is Hindmarsh et al. (2014); Caprini et al. (2016)

	$\displaystyle h^{2}\Omega_{s}(f)\,$	$\displaystyle\approx$	$\displaystyle\,\frac{1.9\times 10^{-5}}{\tilde{\beta}}\left(\frac{\kappa_{s}\,\alpha}{\alpha+1}\right)^{2}\left(\frac{100}{g_{*}}\right)^{\frac{1}{3}}\Upsilon$		(49)
		$\displaystyle\times$	$\displaystyle\frac{(f/f_{s})^{3}}{\big{[}1+0.75(f/f_{s})^{2}\big{]}^{7/2}}\ ,$

where $f_{s}$ is the peak frequency, $\kappa_{s}$ is the fraction of the latent heat transformed into the bulk motion of the plasma Espinosa et al. (2010), and $\Upsilon$ is the suppression factor Ellis et al. (2020b); Guo et al. (2021),

	$\displaystyle f_{s}$	$\displaystyle=$	$\displaystyle(0.19\ {\rm Hz})\left(\frac{T_{*}}{1\ {\rm PeV}}\right)\left(\frac{g_{*}}{100}\right)^{\frac{1}{6}}\tilde{\beta}\ ,$
	$\displaystyle\kappa_{s}$	$\displaystyle=$	$\displaystyle\frac{\alpha}{0.73+0.083\sqrt{\alpha}+\alpha}\ ,$
	$\displaystyle\Upsilon\,$	$\displaystyle=$	$\displaystyle 1-\frac{1}{\Big{[}1+\frac{8\pi^{\frac{1}{3}}}{\tilde{\beta}}\big{(}\frac{{\alpha+1}}{3\kappa_{s}\alpha}\big{)}^{\frac{1}{2}}\Big{]}^{\frac{1}{2}}}\ .$		(50)

The signal from bubble wall collisions is Kosowsky et al. (1992); Huber and Konstandin (2008); Caprini et al. (2016) (see Lewicki and Vaskonen (2021) for recent updates)

	$\displaystyle h^{2}\Omega_{c}(f)\,$	$\displaystyle\approx$	$\displaystyle\,\frac{4.9\times 10^{-6}}{\tilde{\beta}^{2}}\left(\frac{\kappa_{c}\,\alpha}{\alpha+1}\right)^{2}\left(\frac{100}{g_{*}}\right)^{\frac{1}{3}}$		(51)
		$\displaystyle\times$	$\displaystyle\frac{(f/f_{c})^{2.8}}{1+2.8(f/f_{c})^{3.8}}\ ,\ \ \ \ \ \$

where now $f_{c}$ is the peak frequency and $\kappa_{c}$ is the fraction of the latent heat deposited into the bubble front Kamionkowski et al. (1994),

	$\displaystyle f_{c}$	$\displaystyle=$	$\displaystyle(0.037\ {\rm Hz})\left(\frac{T_{*}}{1\ {\rm PeV}}\right)\left(\frac{g_{*}}{100}\right)^{\frac{1}{6}}\tilde{\beta}\ ,$
	$\displaystyle\kappa_{c}$	$\displaystyle=$	$\displaystyle\frac{\frac{4}{27}\sqrt{\frac{3}{2}\alpha}+0.72\,\alpha}{1+0.72\,\alpha}\ .$		(52)

The final contribution is provided by turbulence Caprini and Durrer (2006); Caprini et al. (2009),

	$\displaystyle h^{2}\Omega_{t}(f)\,$	$\displaystyle\approx$	$\displaystyle\,\frac{3.4\times 10^{-4}}{\tilde{\beta}}\left(\frac{\epsilon\,\kappa_{s}\,\alpha}{\alpha+1}\right)^{\frac{3}{2}}\left(\frac{100}{g_{*}}\right)^{\frac{1}{3}}$		(53)
		$\displaystyle\times$	$\displaystyle\frac{({f}/{f_{t}})^{3}}{\big{(}1+{8\pi f}/{f_{*}}\big{)}\big{(}1+{f}/{f_{t}}\big{)}^{{11}/{3}}}\ ,$

where $\epsilon=0.05$ Caprini et al. (2016), while the peak frequency $f_{t}$ and the parameter $f_{*}$ are

	$\displaystyle f_{t}$	$\displaystyle=$	$\displaystyle(0.27\ {\rm Hz})\left(\frac{g_{*}}{100}\right)^{\frac{1}{6}}\left(\frac{T_{*}}{1\ {\rm PeV}}\right)\tilde{\beta}\ ,$
	$\displaystyle f_{*}$	$\displaystyle=$	$\displaystyle(0.17\ {\rm Hz})\left(\frac{g_{*}}{100}\right)^{\frac{1}{6}}\left(\frac{T_{*}}{1\ {\rm PeV}}\right)\ .$		(54)

The resulting gravitational wave signals from the first order phase transition triggered by ${\rm U}(1)_{B}$ breaking are shown in Fig. 6 for several symmetry breaking scales: $10\ {\rm TeV}$ (light brown curve), $100\ {\rm TeV}$ (brown curve), $1\ {\rm PeV}$ (purple curve), and $10\ {\rm PeV}$ (black curve). The gauge coupling was assumed to be $g_{B}=0.25$, and the quartic coupling was chosen to be $\lambda_{B}=0.006$. Spectra with peaks at larger frequencies correspond to higher symmetry breaking scales.

The effect of the suppression factor $\Upsilon$ reducing the sound wave contribution in Eq. (49) is that the bubble collision and turbulence components become distinguishable in the spectrum. Although the main peak is still due to sound waves, the slope at lower frequencies is dominated by bubble collisions, whereas for higher frequencies the turbulence contribution visibly changes the slope of the curve. Without the suppression factor, the spectrum would be determined, to a good approximation, just by the sound wave component in the region relevant for future detectors.

Depending on the Lagrangian parameters, the signal may be detectable in upcoming gravitational wave experiments: LISA, DECIGO, Big Bang Observer, Einstein Telescope, and Cosmic Explorer. To study this more quantitatively, in Fig. 7 we show part of the $(g_{B},\lambda_{B})$ parameter space for which the signal can be detected in each experiment when $v_{B}=1\ {\rm PeV}$. Specifically, the upper boundary for each detector corresponds to a signal-to-noise ratio of five upon a single year of data taking, while the lower boundary arises when either $S(T)/T$ is too large to satisfy Eq. (44) or the new vacuum has an energy density larger than that of the high temperature vacuum.

As mentioned earlier, our analysis of the first order phase transition signal from ${\rm U}(1)_{B}$ breaking differs from the one in Fornal and Shams Es Haghi (2020) in several aspects. The fermionic particle content in Eq. (II) is different, and we chose the corresponding Yukawa couplings to be small, which is a more minimal scenario than $Y=0.6$ in Fornal and Shams Es Haghi (2020). Our analysis is also applicable to ${\rm U}(1)_{L}$ breaking, since we calculate the thermal masses in the general case – this result will be used in Section VII. Finally, when determining the gravitational wave signal we included the effect of bubble collisions, which was not considered in Fornal and Shams Es Haghi (2020), but which increases the reach of upcoming detectors due to the enhancement of the signal in the lower frequency region.

A new gravitational wave signature arises when each of the two ${\rm U}(1)$ symmetries is broken by two scalars, leading to the production of domain walls at two different energy scales during the evolution of the Universe. The signal consists of two sharp domain wall peaks. The slope on the left side of each peak depends on the frequency like $\sim f^{3}$, whereas the slope on the right side of the peak falls like $\sim 1/f$. There is a nontrivial structure created between the two peaks, which can be used to distinguish this type of signal from others. If the two symmetry breaking scales are high, this signature can be searched for in all the upcoming gravitational wave experiments we considered: LISA, DECIGO, Big Bang Observer, Einstein Telescope, and Cosmic Explorer. A realization of this scenario in our model is shown in Fig. 8, where the parameters for the ${\rm U(1)}_{B}$ breaking were chosen to be $v_{B}=10^{3}\ {\rm PeV}$ and $\Delta\rho=10^{-5}\ {\rm PeV^{4}}$, whereas for the ${\rm U(1)}_{L}$ breaking they are $v_{L}=5\times 10^{4}\ {\rm PeV}$ and $\Delta\rho=1.6\times 10^{5}\ {\rm PeV^{4}}$.

Another gravitational wave signature, not considered in the literature before, is realized when one of the ${\rm U}(1)$ symmetries is broken by one scalar, leading to cosmic string production, whereas the other ${\rm U}(1)$ is broken by two scalars, resulting in domain wall creation. If the two symmetry breaking scales are high, their contributions may overlap and produce a very unusual domain wall peak over the cosmic string background. An example is shown in Fig. 9, where the symmetry breaking scale for ${\rm U}(1)_{L}$ was chosen to be $v_{L}=10^{6}\ {\rm PeV}$, whereas the parameters for ${\rm U}(1)_{B}$ breaking are $v_{B}=8\times 10^{3}\ {\rm PeV}$ and $\Delta\rho=2\ {\rm PeV^{4}}$. For this particular selection of parameters, Big Bang Observer and DECIGO can probe the peak area, but for lower ${\rm U}(1)_{B}$ breaking scales this structure is accessible to LISA, whereas higher symmetry breaking scales would make it detectable by Einstein Telescope and Cosmic Explorer.