Gravitational wave signatures of first-order phase transition in two-component dark matter model

Seyed Yaser Ayazi [email protected] Department of Physics, Semnan University, P.O. Box 35131-19111, Semnan, Iran 0000-0002-5994-3316 Mojtaba Hosseini [email protected] Department of Physics, Semnan University, P.O. Box 35131-19111, Semnan, Iran Rouzbeh Rouzbehi [email protected] Department of Physics, Semnan University, P.O. Box 35131-19111, Semnan, Iran 0009-0005-7139-5841

Abstract

Here, we consider a classically scale-invariant extension of the Standard Model (SM) with two-component dark matter (DM) candidates, including a Dirac spinor and a scalar DM. We probe the parameter space of the model, constrained by relic density and direct detection, and investigate the generation of gravitational waves (GWs) produced by an electroweak first-order phase transition. The analysis demonstrates that there are points in the parameter space, leading to a detectable GW spectrum arising from the first-order phase transition, which is also consistent with the DM relic abundance and direct detection bounds. These GWs could be observed by forthcoming space-based interferometers such as the Big Bang Observer, Decihertz Interferometer Gravitational-wave Observatory, and Ultimate-Decihertz Interferometer Gravitational-wave Observatory.

1 Introduction

Impressive progress has been made in the Standard Model (SM) after the discovery of the Higgs boson in 2012 by the ATLAS and CMS experiments [1, 2], providing us with a deep insight into the building blocks of the Universe. However, there are still unanswered questions, including the matter-antimatter asymmetry, the hierarchy problem, and the nature of dark matter (DM). There is substantial evidence from various cosmological and astrophysical observations indicating the existence of DM [3], which accounts for $\sim$ 27% of the energy content of the Universe. Weakly interacting massive particles following the freeze-out scenario have been the most popular DM candidates for decades [4]. Given that, no trace of DM has been found in direct detection experiments so far, and considering the strong bounds on these experiments in one-component DM models, multicomponent DM may present a more promising avenue for future research [5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61]. Neither the electroweak phase transition [62, 63] nor the QCD phase transition [64, 65] within the SM are strongly first order, therefore, they do not generate the gravitational wave (GW) signal. However, first-order phase transitions can be caused by various extensions of the SM and the DM candidates, leading to the generation of GWs [66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132].

In 2015, the LIGO and Virgo collaboration made the first direct detection of GWs caused by binary black hole mergers [133]. While GWs sourced by strong astrophysical objects can be probed by ground-based GW detectors, upcoming space-based GW interferometers, such as the Laser Interferometer Space Antenna [134], Big Bang Observer (BBO) [135], Decihertz Interferometer Gravitational-wave Observatory (DECIGO) [136], and Ultimate-DECIGO (UDECIGO) [137], will be able to probe these waves in the millihertz to decihertz range. Detecting such stochastic GWs resulting from cosmological phase transitions in the early Universe could supplement ground experiments like the LHC, thereby opening a unique observational window to explore new physics beyond the SM.

As it is known, the hierarchy problem in particle physics refers to the large discrepancy between the weak force scale ( $100~{}\rm GeV$ ) and the Planck scale ( $10^{19}~{}\rm GeV$ ). Resolving these issues is a major motivation for theories beyond SM. In the SM, the Higgs mechanism introduces a scalar field that acquires a nonzero vacuum expectation value, breaking the electroweak symmetry and giving mass to gauge bosons and fermions. However, this requires fine-tuning the Higgs mass parameter to be much smaller than the Planck scale. A scale-invariant solution to this problem proposes that both the Planck and weak scales should emerge as quantum effects rather than fundamental scales in the theory[138]. In the paper, we present a classically scale-invariant extension of the SM where all the particle masses are generated using the Coleman-Weinberg mechanism[139]. We use the freeze-out mechanism to produce dark matter. The model includes three new fields, two scalars, and one fermion. We probe the parameter space of the model according to constraints from relic density and direct detection. DM relic density is reported by Planck collaboration[140] and DM-nucleon cross section is constrained by XENONnT experiment results[141]. We study the possibility of the electroweak phase transition with respect to the bounded parameter space, where we use the effects of the effective potential of the finite temperature. We probe the parameter space of the model which is consistent with these constraints and leads to a strong first-order electroweak phase transition. Also, the GW signal resulting from this phase transition has been studied in the BBO, DECIGO, and UDECIGO detectors.

The paper is organized as follows. The two-component DM model is developed in Sec. 2. Then the thermal relic density via freeze-out mechanism is calculated in Sec. 3. DM-nucleon cross section is discussed in Sec. 4. Electroweak phase transition and gravitational wave signals are studied in Sec. 5. In Sec. 6, we present the results. Finally, our conclusion comes in Sec. 7.

2 The Model

In this paper, we review the model presented in [32]. We consider a scale-invariant extension of SM where the Higgs mass term is absent. Before electroweak symmetry breaking all fields in the scale-invariant sector of potential are massless but as a result of breaking the symmetry of the scale, these fields gain mass from Coleman-Weinberg mechanism[139]. We add three new fields, two scalars, and one spinor in the model and all fields are singlets under SM gauge transformation. Two of these new fields, the scalar $S$ and the spinor $\chi$ are assumed to be odd under a $Z_{2}$ symmetry. Under $Z_{2}$ symmetry new fields transform as follows:

\phi\to\phi,S\to-S,\chi\to-\chi.

(2.1)

The other scalar ﬁeld, $\phi$ , and all SM particles are even under $Z_{2}$ . $Z_{2}$ symmetry guarantees the stability of the lightest odd particles.

The scalar part of the Lagrangian including the new ﬁelds is

{\cal{L}}_{scalar}=\frac{1}{2}\partial_{\mu}\phi\partial^{\mu}\phi+\frac{1}{2}\partial_{\mu}S\partial^{\mu}S+D_{\mu}H^{\dagger}D^{\mu}H-V(H,\phi,S)

(2.2)

where the most general scale-invariant potential $V(H,\phi,S)$ , which is renormalizable and invariant under gauge and $Z_{2}$ symmetry, is

V(H,\phi,S)=\frac{1}{6}\lambda_{H}(H^{\dagger}H)^{2}+\frac{1}{4!}\lambda_{\phi}\phi^{4}+\frac{1}{4!}\lambda_{s}S^{4}+\lambda_{\phi H}\phi^{2}H^{\dagger}H+\lambda_{SH}S^{2}H^{\dagger}H+\lambda_{\phi s}\phi^{2}S^{2}

(2.3)

where $H$ , $\phi$ , and $S$ are the doublet Higgs, the scalon, and DM scalars, respectively. The scale-invariant Lagrangian of the new spinor field and its Yukawa interaction are given by

{\cal{L}}_{spinor}=\bar{\chi}(i\gamma^{\mu}\partial_{\mu}-g\phi)\chi

(2.4)

In unitary gauge

H=\frac{1}{\sqrt{2}}\begin{pmatrix}0\\ h_{1}\end{pmatrix}

(2.5)

and potential (2.3) becomes

V(h_{1},\phi,S)=\frac{1}{4!}\lambda_{H}h_{1}^{4}+\frac{1}{4!}\lambda_{\phi}\phi^{4}+\frac{1}{4!}\lambda_{s}S^{4}+\frac{1}{2}\lambda_{\phi H}\phi^{2}h_{1}^{2}+\frac{1}{2}\lambda_{SH}S^{2}h_{1}^{2}+\lambda_{\phi s}\phi^{2}S^{2}.

(2.6)

The Higgs field after spontaneous symmetry breaking is given by

H=\frac{1}{\sqrt{2}}\begin{pmatrix}0\\ \nu_{1}+h_{1}\end{pmatrix},

(2.7)

where $\nu_{1}=246~{}\rm GeV$ . The vacuum expectation value of the field $\phi$ is given by

\phi=\nu_{2}+h_{2}.

(2.8)

Notice that $h_{1}$ and $h_{2}$ mix with each other and can be rewritten by the mass eigenstates $H_{1}$ and $H_{2}$ as

\begin{pmatrix}H_{1}\\ H_{2}\end{pmatrix}=\begin{pmatrix}cos\alpha~{}~{}~{}-sin\alpha\\ sin\alpha~{}~{}~{}~{}~{}cos\alpha\end{pmatrix}\begin{pmatrix}h_{1}\\ h_{2}\end{pmatrix},

(2.9)

where $H_{2}$ is along the flat direction, thus $M_{H_{2}}=0$ , and $H_{1}$ is perpendicular to the flat direction which we identify as the SM-like Higgs observed at the LHC with $M_{H_{1}}=125$ GeV. Along the flat direction, the one-loop effective potential has the general form [142]

V_{T=0}^{1-loop}=aH_{2}^{4}+bH_{2}^{4}\,\log\frac{H_{2}^{2}}{\Lambda^{2}},

(2.10)

where $a$ and $b$ are the dimensionless constants that given by

	$\displaystyle a=\frac{1}{64\pi^{2}\nu^{4}}\left(\sum_{bosons}n_{j}M^{4}_{j}(\log\frac{M^{2}_{j}}{\nu^{2}}-\frac{3}{2})-\sum_{fermions}n_{j}M^{4}_{j}(\log\frac{M^{2}_{j}}{\nu^{2}}-\frac{3}{2})\right),$
	$\displaystyle b=\frac{1}{64\pi^{2}\nu^{4}}\left(\sum_{bosons}n_{j}M^{4}_{j}-\sum_{fermions}n_{j}M^{4}_{j}\right),$		(2.11)

and $\Lambda$ is the renormalization group scale. In (2.11), $M_{j}$ and $n_{j}$ are, the tree-level mass and the internal degrees of freedom of the particle $j$ . By minimizing the relation (2.10) and rewriting in terms of the one-loop vacuum expectation value $\nu$ , we have

V_{T=0}^{1-loop}=bH_{2}^{4}\,\left(\log\frac{H_{2}^{2}}{\nu^{2}}-\frac{1}{2}\right),

(2.12)

where $\nu^{2}=\nu_{1}^{2}+\nu_{2}^{2}$ . Since in tree level, $M_{H_{2}}=0$ , and the elastic scattering cross section of DM off nuclei becomes severely large, the model is immediately excluded by direct detection experiments. However, at the one-loop level, radiation corrections give a mass to the massless eigenstate $H_{2}$ [142, 143]:

M_{H_{2}}^{2}=\frac{d^{2}V_{T=0}^{1-loop}}{dH_{2}^{2}}\bigg{\rvert}_{\nu}=-\frac{\lambda_{\phi H}}{16\pi^{2}M_{H_{1}}^{2}}(M_{H_{1}}^{4}+M_{S}^{4}+6M_{W}^{4}+3M_{Z}^{4}-4M_{\chi}^{4}-12M_{t}^{4}).

(2.13)

After the symmetry breaking, we have the following constraints:

$\displaystyle\nu_{2}=\frac{M_{\chi}}{g},$	$\displaystyle sin\alpha=\frac{\frac{\nu_{1}}{\nu_{2}}}{\sqrt{1+(\frac{\nu_{1}}{\nu_{2}})^{2}}},$
$\displaystyle M_{H_{2}}=0,$	$\displaystyle\lambda_{H}=\frac{3M_{H_{1}}^{2}}{\nu_{1}^{2}}cos^{2}\alpha,$
$\displaystyle\lambda_{\phi}=\frac{3M_{H_{1}}^{2}}{\nu_{2}^{2}}sin^{2}\alpha,$	$\displaystyle\lambda_{\phi H}=-\frac{M_{H_{1}}^{2}}{2\nu_{1}\nu_{2}}sin\alpha cos\alpha,$
$\displaystyle\lambda_{SH}=\frac{M_{S}^{2}-2\lambda_{\phi s}\nu_{2}^{2}}{v_{1}^{2}}$		(2.14)

where $M_{S}$ and $M_{\chi}$ are the masses of scalar and spinor DM after symmetry breaking, respectively.

According to Eq. (2.14), the model introduces only ﬁve free parameters, $\lambda_{s},\lambda_{\phi s},M_{S},M_{\chi},g$ . In addition, the quartic coupling $\lambda_{s}$ is irrelevant to the DM relic density. Therefore, the remaining free parameters are $\lambda_{\phi s},M_{S},M_{\chi},g$ .

3 Relic density

The evolution of the number density of DM particles with time is governed by the Boltzmann equation. The coupled Boltzmann equations for fermion ${\chi}$ and scalar $S$ DM are given by

\frac{dn_{\chi}}{dt}+3Hn_{\chi}=-\sum_{j}\langle\sigma_{\chi\chi\rightarrow jj}\upsilon\rangle(n_{\chi}^{2}-n_{\chi,eq}^{2})-\langle\sigma_{\chi\chi\rightarrow{S}{S}}\upsilon\rangle(n_{\chi}^{2}-n_{\chi,eq}^{2}\frac{n_{S}^{2}}{n_{{S},eq}^{2}}),

(3.1)

\frac{dn_{S}}{dt}+3Hn_{S}=-\sum_{j}\langle\sigma_{{S}{S}\rightarrow jj}\upsilon\rangle(n_{S}^{2}-n_{{S},eq}^{2})-\langle\sigma_{{S}{S}\rightarrow\chi\chi}\upsilon\rangle(n_{S}^{2}-n_{{S},eq}^{2}\frac{n_{\chi}^{2}}{n_{\chi,eq}^{2}}),

(3.2)

where $j$ runs over SM massive particles, $H_{1}$ and $H_{2}$ . In $\langle\sigma_{ab\rightarrow cd}\upsilon\rangle$ all annihilations are taken into account except $\langle\sigma_{\chi S}\rightarrow_{\chi S}\upsilon\rangle$ , which does not affect the number density. By using $x=M/T$ and $Y=n/s$ , where $T$ and $s$ are the photon temperature and the entropy density, respectively, one can rewrite the Boltzmann equations in terms of $Y=n/s$ :

\frac{dY_{\chi}}{dx}=-\sqrt{\frac{45}{\pi}}M_{pl}g_{*}^{1/2}\frac{M}{x^{2}}[\sum_{j}\langle\sigma_{\chi\chi\rightarrow jj}\upsilon\rangle(Y_{\chi}^{2}-Y_{\chi,eq}^{2})+\langle\sigma_{\chi\chi\rightarrow{S}{S}}\upsilon\rangle(Y_{\chi}^{2}-Y_{\chi,eq}^{2}\frac{Y_{S}^{2}}{Y_{{S},eq}^{2}})],

(3.3)

\frac{dY_{S}}{dx}=-\sqrt{\frac{45}{\pi}}M_{pl}g_{*}^{1/2}\frac{M}{x^{2}}[\sum_{j}\langle\sigma_{{S}{S}\rightarrow jj}\upsilon\rangle(Y_{S}^{2}-Y_{{S},eq}^{2})+\langle\sigma_{{S}{S}\rightarrow\chi\chi}\upsilon\rangle(Y_{S}^{2}-Y_{{S},eq}^{2}\frac{Y_{\chi}^{2}}{Y_{\chi,eq}^{2}})],

(3.4)

where $M_{pl}$ is the Planck mass and $g_{*}^{1/2}$ is the effective numbers parameter. As can be seen from the above equations, there are new terms in the Boltzmann equations that describe the conversion of two DM particles into each other. These two cross sections are also described by the same matrix element, so we expect $\langle\sigma_{\chi\chi\rightarrow{S}{S}}\upsilon\rangle$ and $\langle\sigma_{{S}{S}\rightarrow\chi\chi}\upsilon\rangle$ are not independent and their relation is

Y_{\chi,eq}^{2}\langle\sigma_{\chi\chi\rightarrow{S}{S}}\upsilon\rangle=Y_{{S},eq}^{2}\langle\sigma_{{S}{S}\rightarrow\chi\chi}\upsilon\rangle.

(3.5)

We know that the conversion of the heavier particle into the lighter one is relevant, thus the contribution of $\chi$ in the relic density is dominant. The relic density for any DM candidate associated with the $Y$ at the present temperature is given by the following relation:

\Omega_{{\chi},S}h^{2}=2.755\times 10^{8}\frac{M_{{\chi},S}}{\rm GeV}Y_{{\chi},S}(T_{0})

(3.6)

where $h$ is the Hubble expansion rate at present time in units of 100 (km/s)/Mpc. We implemented the model in the micrOMEGAs package[144] to numerically solve the coupled Boltzmann differential equations. According to the data from the Planck collaboration[140], the DM constraint in this model reads

\Omega_{DM}h^{2}=\Omega_{\chi}h^{2}+\Omega_{{S}}h^{2}=0.120\pm 0.001.

(3.7)

We also define the fraction of the DM density of each component by

\xi_{\chi}=\frac{\Omega_{\chi}}{\Omega_{DM}},~{}~{}~{}~{}~{}\xi_{S}=\frac{\Omega_{{S}}}{\Omega_{DM}},~{}~{}~{}\xi_{\chi}+\xi_{S}=1.

(3.8)

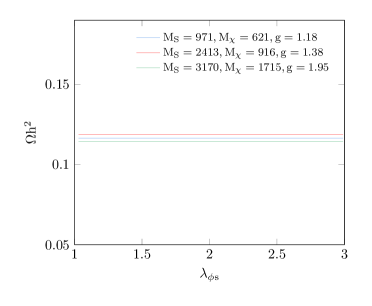
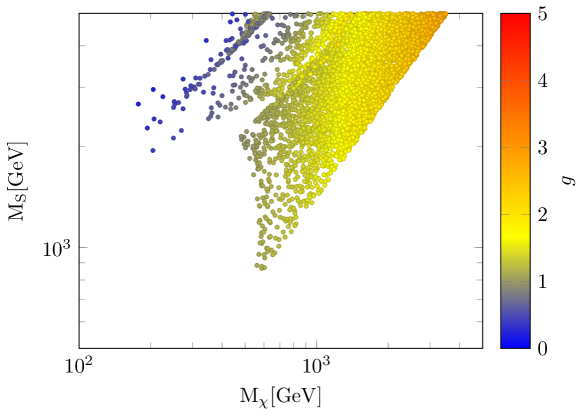
Refer to caption — Figure 1: The dependency of $\lambda_{\phi s}$ with the total DM relic density.

In Fig. 2, the parameter space consistent with DM relic density is obtained. Contrary to the review done in [32], we have extended the model and investigated more parameter space. As can be seen, there is an agreement with the relic density observed for $100<M_{\chi}<3800$ GeV, $900<M_{S}<5000$ GeV and $0<g<5$ . It is necessary to mention two important points here:
(1) As can be seen from Fig. 1 and it has been investigated in[32], $\lambda_{\phi s}$ has no effect on the relic density, and for this reason, it has been investigated in Fig. 2 with three quantities of the parameter space. Therefore, we have set $\lambda_{\phi s}$ to be 0.5 throughout the paper.
(2) The mass of the scalar is always greater than that of the fermion, and for this reason(due to conversion $SS\rightarrow\chi\chi$ ), the fermion( $\chi$ ) occupies a larger share of the observed relic density.

4 Direct detection

In this section, we investigate constraints on the parameters space of the model which are imposed by searching for scattering of DM nuclei. The spin-independent direct detection cross sections of $\chi$ and ${S}$ are determined by $H_{1}$ and $H_{2}$ exchanged diagrams[32]:

	$\displaystyle\sigma_{DM-N}^{S}=\xi_{S}\frac{\mu_{S}^{2}}{4\pi M_{H_{1}}^{4}M_{H_{2}}^{4}M_{S}^{2}}[\frac{M_{S}^{2}-2\lambda_{\phi s}M_{\chi}^{2}/g^{2}}{\nu_{1}}(\frac{M_{H_{2}}^{2}}{1+(\nu_{1}g/M_{\chi})^{2}}+\frac{M_{H_{1}}^{2}g^{2}\nu_{1}^{2}}{g^{2}\nu_{1}^{2}+M_{\chi}^{2}})$
	$\displaystyle+\frac{2\nu_{1}\lambda_{\phi s}}{1+(\nu_{1}g/M_{\chi})^{2}}(M_{H_{1}}^{2}-M_{H_{2}}^{2})]^{2}f_{N}^{2},$		(4.1)

\sigma_{DM-N}^{\chi}=\xi_{\chi}\frac{g^{3}\nu_{1}}{\pi M_{\chi}(1+(\nu_{1}g/M_{\chi})^{2})}\mu_{\chi}^{2}(\frac{1}{M_{H_{1}}^{2}}-\frac{1}{M_{H_{2}}^{2}})^{2}f_{N}^{2},

(4.2)

where

\mu_{S}=M_{N}M_{S}/(M_{N}+M_{S}),~{}~{}~{}~{}~{}\mu_{\chi}=M_{N}M_{\chi}/(M_{N}+M_{\chi}).

(4.3)

$M_{N}$ is the nucleon mass and $f_{N}\simeq 0.3$ parametrizes the Higgs-nucleon coupling.

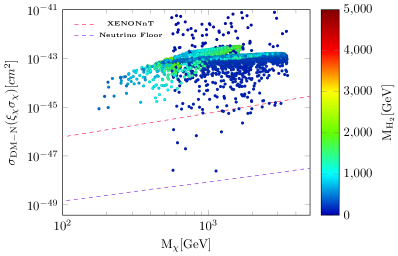
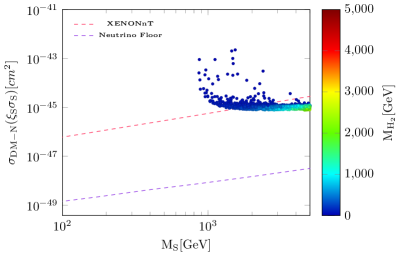
We use the XENONnT[141] experiment results to constrain the parameter space of the model. We have also used the neutrino floor as the irreducible background coming from scattering of SM neutrinos on nucleons[145]. In Fig. 3, rescaled DM-nucleon cross sections( $\xi_{S}\sigma_{S}$ and $\xi_{\chi}\sigma_{\chi}$ ) are depicted for the parameters that are in agreement with the relic density. What is clear is that, for large masses, practical parameter space is available for both dark matter candidates.

5 Electroweak phase transition and gravitational wave signal

5.1 Finite temperature one-loop potential

In addition, to consider the one-loop effective potential at zero temperature, we must compute the one-loop effective potential at finite temperature to discuss electroweak phase transition and gravitational wave. The thermal corrections for finite temperature one-loop potential are given by [146]¹¹1For a review, see [147, 148, 149].

V^{1-loop}_{T\neq 0}(H_{2},T)=\frac{T^{4}}{2\pi^{2}}\left(\sum_{bosons}n_{j}J_{B}(\frac{M^{2}_{j}(H_{2})}{T^{2}})-\sum_{fermions}n_{j}J_{F}(\frac{M^{2}_{j}(H_{2})}{T^{2}})\right),

(5.1)

with thermal functions

J_{B,F}(x)=\int_{0}^{\infty}dyy^{2}ln\Bigl{(}1\mp e^{-\sqrt{y^{2}+x^{2}}}\Bigl{)}.

(5.2)

These thermal functions can be expanded in terms of modified Bessel functions of the second kind [78]

	$\displaystyle J_{B}(x)\simeq-\sum_{k=1}^{3}\frac{1}{k^{2}}x^{2}K_{2}(kx),$
	$\displaystyle J_{F}(x)\simeq-\sum_{k=1}^{2}\frac{(-1)^{k}}{k^{2}}x^{2}K_{2}(kx).$		(5.3)

We included the daisy diagrams to improve the validity of perturbation theory [74], where $V_{daisy}$ ²²2For theoretical uncertainties exhibits in effective potential including daisy resummation, see [150, 151, 152, 153, 154] is as follows [155, 156]

V_{daisy}=\frac{T}{12\pi}\sum_{bosons}n_{j}\left(M^{3}_{j}(H_{2})-(M^{2}_{j}+\Pi_{j}(T))^{\frac{3}{2}}\right)

(5.4)

The thermal masses, $\Pi_{j}(T)$ are given by [77]

	$\displaystyle\Pi_{W}=\frac{11}{6}g_{SM}^{2}T^{2},~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}\Pi_{z}/\gamma=\frac{11}{6}\begin{pmatrix}g^{2}_{SM}&0\\ 0&g^{\prime 2}_{SM}\end{pmatrix}T^{2},$
	$\displaystyle\Pi_{S}=\frac{1}{24}(\lambda_{SH}+6\lambda_{S}+\lambda_{\phi S})T^{2},$
	$\displaystyle\Pi_{h/\phi}=\frac{1}{24}\begin{pmatrix}(\frac{9}{2}g^{2}_{SM}+\frac{3}{2}g^{\prime 2}_{SM})+6\lambda^{2}_{t}+\lambda_{\phi H}+\lambda_{HS}+6\lambda_{H}&0\\ 0&6g^{2}+\lambda_{\phi H}+6\lambda_{\phi}+\lambda_{\phi S}\end{pmatrix}T^{2}.$		(5.5)

Finally, the full effective one-loop potential containing (2.12), (5.1), and (5.4) is given by

V_{\rm eff}(H_{2},T)=V^{1-loop}_{T=0}(H_{2})+V^{1-loop}_{T\neq 0}(H_{2},T)+V_{daisy}(H_{2},T).

(5.6)

In order to get $V_{\rm eff}(0,T)=0$ at all temperatures, we make the following substitution:

V_{\rm eff}(H_{2},T)\rightarrow V_{\rm eff}(H_{2},T)-V_{\rm eff}(0,T).

(5.7)

By having the potential (5.6) now we are ready to study the phase transition and GWs associated with that.

5.2 First-order phase transition and gravitational waves

Due to the recent advancements in cosmological instruments, the imprints of GWs associated with the first-order phase transitions in the early universe could be detected in the near future. A primary example that encompasses a broad class of phase transitions is electroweak symmetry breaking, which is related to the spontaneous breaking of the gauge symmetry. Electroweak symmetry breaking is a well-studied topic within the context of the SM and can also shed light on the baryon asymmetry of the Universe. Furthermore, the spontaneous breaking of gauge symmetry in the dark sector during the early Universe could result from a first-order phase transition. In this regard, many beyond the SM models predict and study such first-order phase transition and their associated GW signals, including those arising from the dark sector. In the following, we will examine the dynamics of first-order phase transition and identify which parameter points of our model are responsible for such transitions.

The existence of a barrier between the symmetric and broken phases is the first-order phase transition property. When the temperature of the Universe drops below the critical temperature ( $T_{C}$ ) the electroweak phase transitions can happen. At this temperature, the effective potential 5.6 has two degenerate minima separated by a high barrier, one in $H_{2}=0$ and the other in $H_{2}=\nu_{C}\neq 0$ :

	$\displaystyle V_{\rm eff}(0,T_{C})=V_{\rm eff}(\nu_{C},T_{C}),$
	$\displaystyle\left.\frac{dV_{\rm eff}(H_{2},T_{C})}{dH_{2}}\right\|_{H_{2}=\nu_{C}}=0.$		(5.8)

One can obtain $\nu_{C}$ and $T_{C}$ by solving the above equations. In the model, all independent parameters contribute to the effective potential. However, we find the daisy term is negligible compared to other terms. Therefore $\lambda_{\phi S}$ and $\lambda_{S}$ are irrelevant and dynamic of the phase transition only depends on $M_{S}$ , $M_{\chi}$ , and $g$ [77].

At very high temperatures symmetry remains unbroken, and $H_{2}=0$ represents the true vacuum. As the Universe cools down and the temperature drops below the critical one, an additional vacuum begins to appear. The phase transition from the false vacuum $H_{2}=0$ to the true vacuum $H_{2}\neq 0$ occurs via thermal tunneling at ﬁnite temperature. However, if the barrier is sufficiently high, the tunneling rate may remain very small even at temperatures significantly below the critical temperature. Consequently, it is conventional to deﬁne the nucleation temperature $T_{N}$ , where the corresponding Euclidean action is $S_{E}=S_{3}(T_{N})/T_{N}\sim 140$ ³³3It is necessary to treat this condition more carefully at the vacuum-dominated period (see [157]). [158]. The theory of such transitions and bubble nucleation was ﬁrst addressed in [159, 160]. The function $S_{3}(T)$ is the three-dimensional Euclidean action for a spherical symmetric bubble given by

S_{3}(T)=4\pi\int_{0}^{\infty}drr^{2}\Biggl{(}\frac{1}{2}\Bigl{(}\frac{dH_{2}}{dr}\Bigl{)}^{2}+V_{\rm eff}(H_{2},T)\Biggl{)},

(5.9)

where $H_{2}$ satisﬁes the differential equation that minimizes $S_{3}$ :

\frac{d^{2}H_{2}}{dr^{2}}+\frac{2}{r}\frac{dH_{2}}{dr}=\frac{dV_{\rm eff}(H_{2},T)}{dH_{2}},

(5.10)

with the boundary conditions:

\left.\frac{dH_{2}}{dr}\right|_{r=0}=0,~{}~{}~{}~{}and~{}~{}~{}~{}H_{2}(r\rightarrow\infty)=0.

(5.11)

We use the publicly available ANYBUBBLE package [161] to solve the Eq. (5.10) and ﬁnd the Euclidean action (5.9).

The stochastic GWs associated with the strong first-order phase transition come from three results:
(1) Collisions of bubble walls and the resulting shocks in the plasma.
(2) Generation of sound waves contributing to the stochastic background after bubble collisions but before the expansion dissipates the kinetic energy in the plasma.
(3) Formation of turbulence in the plasma following bubble collisions.

These three processes may coexist, and each one contributes to the stochastic GW background:

\Omega_{GW}h^{2}\simeq\Omega_{coll}h^{2}+\Omega_{sw}h^{2}+\Omega_{turb}h^{2}.

(5.12)

To describe the GW spectrum, we need to define three parameters $\alpha,\beta$ , and $\upsilon_{\omega}$ in addition to the nucleation temperature, $T_{N}$ that have contributed and controlled the (5.12). $\alpha$ is the ratio of the free energy density difference between the true and false vacuum and the total energy density given by

\alpha=\frac{\Delta\Bigl{(}V_{\rm eff}-T\frac{\partial V_{\rm eff}}{\partial T}\Bigl{)}\bigg{|}_{T_{N}}}{\rho_{\ast}},

(5.13)

where $\rho_{\ast}$ is

\rho_{\ast}=\frac{\pi^{2}g_{\ast}}{30}T_{N}^{4}.

(5.14)

$\beta$ is the inverse time duration of the phase transition given by

\frac{\beta}{H_{\ast}}=T_{N}\frac{d}{dT}\Bigl{(}\frac{S_{3}(T)}{T}\Bigl{)}\bigg{|}_{T_{N}}.

(5.15)

Finally, $\upsilon_{\omega}$ is the velocity of the bubble wall, anticipated to be close to 1 for the strong transitions[162].

GWs are not generated by isolated spherical bubbles, instead, they arise from collisions between nucleated bubbles. The production of GWs from bubble collisions is given by [163]

\Omega_{coll}(f)h^{2}=1.67\times 10^{-5}\Bigl{(}\frac{\beta}{H_{\ast}}\Bigl{)}^{-2}\Bigl{(}\frac{\kappa\alpha}{1+\alpha}\Bigl{)}^{2}\Bigl{(}\frac{g_{\ast}}{100}\Bigl{)}^{-\frac{1}{3}}\Bigl{(}\frac{0.11\upsilon_{\omega}^{3}}{0.42+\upsilon_{\omega}^{2}}\Bigl{)}S_{coll},

(5.16)

where $S_{coll}$ parametrizes the spectral shape is given by

S_{coll}=\frac{3.8(f/f_{coll})^{2.8}}{2.8(f/f_{coll})^{3.8}+1},

(5.17)

with

f_{coll}=1.65\times 10^{-5}\Bigl{(}\frac{0.62}{\upsilon_{\omega}^{2}-0.1\upsilon_{\omega}+1.8}\Bigl{)}\Bigl{(}\frac{\beta}{H_{\ast}}\Bigl{)}\Bigl{(}\frac{T_{N}}{100}\Bigl{)}\Bigl{(}\frac{g_{\ast}}{100}\Bigl{)}^{1/6}Hz.

(5.18)

The dominant contribution to the GW spectrum is sound waves formed by bubble collisions, given by [164]

\Omega_{sw}(f)h^{2}=2.65\times 10^{-6}\Bigl{(}\frac{\beta}{H_{\ast}}\Bigl{)}^{-1}\Bigl{(}\frac{\kappa_{\upsilon}\alpha}{1+\alpha}\Bigl{)}^{2}\Bigl{(}\frac{g_{\ast}}{100}\Bigl{)}^{-\frac{1}{3}}\upsilon_{\omega}S_{sw}.

(5.19)

The spectral shape of $S_{sw}$ is

S_{sw}=(f/f_{sw})^{3}\Bigl{(}\frac{7}{3(f/f_{sw})^{2}+4}\Bigl{)}^{3.5},

(5.20)

where

f_{sw}=1.9\times 10^{-5}\frac{1}{\upsilon_{\omega}}\Bigl{(}\frac{\beta}{H_{\ast}}\Bigl{)}\Bigl{(}\frac{T_{N}}{100}\Bigl{)}\Bigl{(}\frac{g_{\ast}}{100}\Bigl{)}^{1/6}Hz.

(5.21)

Ultimately, turbulence motion in the plasma resulting from bubble collisions can indeed serve as a source of GWs [165]. The GW arising from the turbulence is given by [166]

\Omega_{turb}(f)h^{2}=3.35\times 10^{-4}\Bigl{(}\frac{\beta}{H_{\ast}}\Bigl{)}^{-1}\Bigl{(}\frac{\kappa_{turb}\alpha}{1+\alpha}\Bigl{)}^{3/2}\Bigl{(}\frac{g_{\ast}}{100}\Bigl{)}^{-\frac{1}{3}}\upsilon_{\omega}S_{turb},

(5.22)

where

S_{turb}=\frac{(f/f_{turb})^{3}}{(1+8\pi f/h_{\ast})(1+f/f_{turb})^{11/3}}

(5.23)

and

f_{turb}=2.27\times 10^{-5}\frac{1}{\upsilon_{\omega}}\Bigl{(}\frac{\beta}{H_{\ast}}\Bigl{)}\Bigl{(}\frac{T_{N}}{100}\Bigl{)}\Bigl{(}\frac{g_{\ast}}{100}\Bigl{)}^{1/6}Hz.

(5.24)

The parameter $h_{\ast}$ in Eq. (5.23) is the value of the inverse Hubble time at GW production and accounts for the redshift of the frequency to today,

h_{\ast}=1.65\times 10^{-5}\Bigl{(}\frac{T_{N}}{100}\Bigl{)}\Bigl{(}\frac{g_{\ast}}{100}\Bigl{)}^{1/6}.

(5.25)

We choose the following values in computing the GW spectrum based on the suggestion from numerical simulations [167, 168],

	$\displaystyle\kappa=\frac{1}{1+0.715\alpha}(0.715\alpha+\frac{4}{27}\sqrt{\frac{3\alpha}{2}}),$
	$\displaystyle\kappa_{\upsilon}=\frac{\alpha}{0.73+0.083\sqrt{\alpha}+\alpha},~{}~{}~{}~{}\kappa_{turb}=0.05\kappa_{\upsilon},$		(5.26)

where the parameters $\kappa$ , $\kappa_{\upsilon}$ , and $\kappa_{turb}$ denote the fraction of latent heat that is transformed into gradient energy of the Higgs-like field, bulk motion of the fluid, and MHD turbulence, respectively.

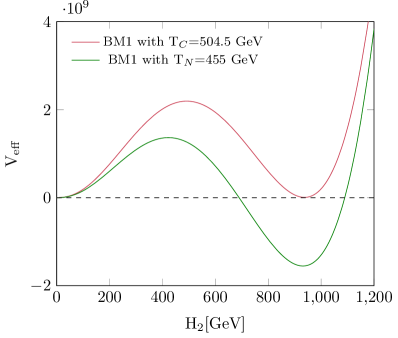
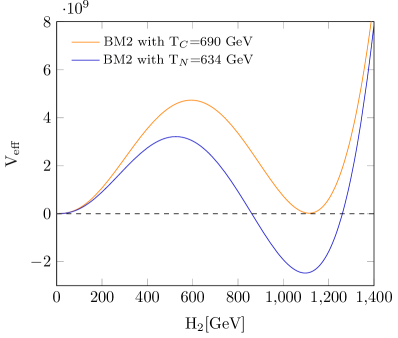
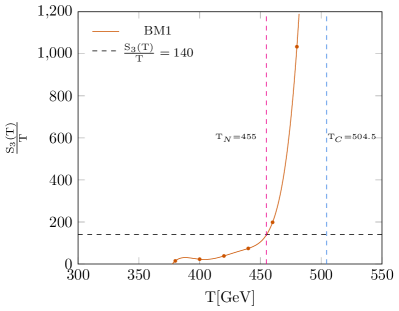
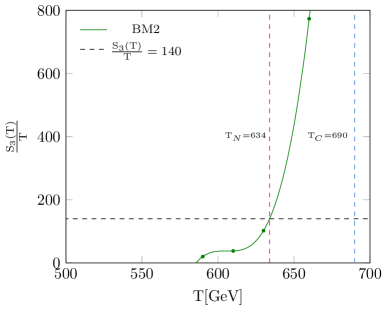
6 Results

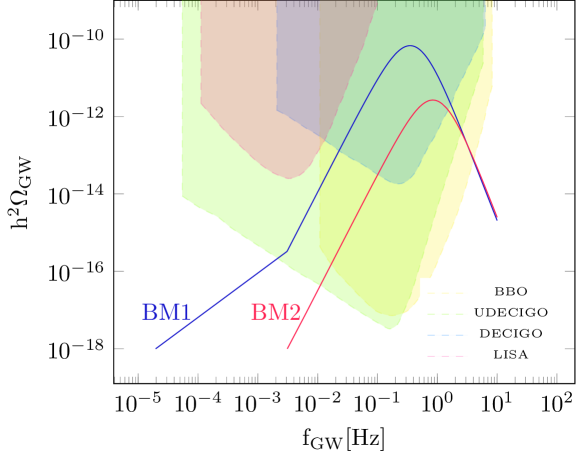
To investigate the GWs arising from a first-order electroweak phase transition, we conducted a comprehensive scan of the model’s parameter space and selected two benchmark points that satisfy both the relic abundance and direct detection constraints. For the parameter points in Table 1, we have compared freeze-out temperature with nucleation temperature and find out $T_{F}<T_{N}$ where $T_{F}\sim\rm max(M_{S},M_{\chi})/20$ . Therefore, this issue does not affect our result and the DM properties would not be modified between $T_{F}$ and the present day. For each of the selected benchmark points, we computed the parameters $\alpha$ , $\frac{\beta}{H_{*}}$ at the nucleation temperature. The values obtained for these parameters are presented in Table 1. To provide a clear understanding of the phase transition behavior, Fig. 4 illustrates the effective potential for the chosen benchmark points at both the critical and nucleation temperatures. Additionally, the figure shows the variation of $\frac{S_{3}}{T}$ in terms of temperature. The primary results of our study, depicted in Fig. 5, show the predicted GW signals for the selected benchmark points. These signals are within the sensitivity range of upcoming space-based GW detectors such as BBO, DECIGO, and UDECIGO. This indicates that the model’s predictions could be tested with the next generation of GW observatories, providing a potential avenue for detecting signatures of new physics related to the electroweak phase transition.

$\#$	$M_{S}(\rm GeV)$	$M_{\chi}(\rm GeV)$	$g$	$M_{H_{2}}(\rm GeV)$
1	2062	1380	1.748	128.9
2	2215	1501	1.854	129.4
$\#$	$\Omega_{S}h^{2}$	$\Omega_{{\chi}}h^{2}$	$\Omega_{DM}h^{2}$	$\xi_{S}\sigma_{S}(\rm cm^{2})$	$\xi_{{\chi}}\sigma_{{\chi}}(\rm cm^{2})$
1	$3.258\times 10^{-6}$	$1.186\times 10^{-1}$	$1.186\times 10^{-1}$	$1.169\times 10^{-45}$	$5.563\times 10^{-46}$
2	$2.834\times 10^{-6}$	$1.116\times 10^{-1}$	$1.116\times 10^{-1}$	$1.246\times 10^{-45}$	$7.374\times 10^{-46}$
$\#$	$T_{C}(\rm GeV)$	$T_{N}(\rm GeV)$	$\alpha$	$\beta/H_{\ast}$	$(\Omega_{GW}h^{2})_{\rm max}$
1	504.5	455	1.19	4060.06	$1.13\times 10^{-11}$
2	690	634	0.36	6976.03	$9.07\times 10^{-12}$

Table 1: Two benchmark points with DM and phase transition parameters.

7 Conclusion

We have considered an extension of the SM with three new fields: a fermion and two scalars. One of the scalars( $S$ ) together with fermion( $\chi$ ) constitute our dark matter candidates, and the other scalar( $\phi$ ) is considered to be the intermediary between the SM and dark parts. The model is scale invariant and particles are massed through scale symmetry breaking. Therefore, the model can provide a potential solution for the hierarchy problem. The parameter space of the model has been extended to large masses(5 TeV) and a large number of points that agree with the constraints of the relic density and direct detection have been obtained.

We focused our attention on the phase transition dynamics after presenting the model and exploring DM phenomenology. The full finite-temperature effective potential of the model at the one-loop level was obtained to investigate the nature of the electroweak phase transition. It was demonstrated that the finite-temperature effects induce the first-order conditions of the transition and thereby give rise to a phase transition, which can generate GWs.

After studying the phase transition, we investigated the resulting GWs. We have demonstrated that the model can survive DM relic density and direct detection constraints, while also producing GWs during the first-order electroweak phase transition. We showed GWs for the two benchmark points. These waves can be placed within the observation window of BBO, DECIGO, and UDECIGO. These waves and their investigation in the future can be a hope for new physics.

References

[1] G. Aad, T. Abajyan, B. Abbott, J. Abdallah, S. Abdel Khalek, A. Abdelalim et al., Observation of a new particle in the search for the standard model higgs boson with the atlas detector at the lhc, Physics Letters B 716 (2012) 1.
[2] S. Chatrchyan, V. Khachatryan, A. Sirunyan, A. Tumasyan, W. Adam, E. Aguilo et al., Observation of a new boson at a mass of 125 gev with the cms experiment at the lhc, Physics Letters B 716 (2012) 30.
[3] G. Bertone and D. Hooper, History of dark matter, Rev. Mod. Phys. 90 (2018) 045002.
[4] J. L. Feng, The WIMP paradigm: Theme and variations, SciPost Phys. Lect. Notes (2023) 71.
[5] K. M. Zurek, Multi-Component Dark Matter, Phys. Rev. D 79 (2009) 115002 [0811.4429].
[6] S. Profumo, K. Sigurdson and L. Ubaldi, Can we discover multi-component WIMP dark matter?, JCAP 12 (2009) 016 [0907.4374].
[7] M. Aoki, M. Duerr, J. Kubo and H. Takano, Multicomponent dark matter systems and their observation prospects, Phys. Rev. D 86 (2012) 076015.
[8] A. Biswas, D. Majumdar, A. Sil and P. Bhattacharjee, Two Component Dark Matter : A Possible Explanation of 130 GeV $\gamma-$ Ray Line from the Galactic Centre, JCAP 12 (2013) 049 [1301.3668].
[9] P.-H. Gu, Multi-component dark matter with magnetic moments for Fermi-LAT gamma-ray line, Phys. Dark Univ. 2 (2013) 35 [1301.4368].
[10] M. Aoki, J. Kubo and H. Takano, Two-loop radiative seesaw mechanism with multicomponent dark matter explaining the possible $\gamma$ excess in the higgs boson decay and at the fermi lat, Phys. Rev. D 87 (2013) 116001.
[11] Y. Kajiyama, H. Okada and T. Toma, Multicomponent dark matter particles in a two-loop neutrino model, Phys. Rev. D 88 (2013) 015029.
[12] L. Bian, R. Ding and B. Zhu, Two Component Higgs-Portal Dark Matter, Phys. Lett. B 728 (2014) 105 [1308.3851].
[13] S. Bhattacharya, A. Drozd, B. Grzadkowski and J. Wudka, Two-Component Dark Matter, JHEP 10 (2013) 158 [1309.2986].
[14] C.-Q. Geng, D. Huang and L.-H. Tsai, Imprint of multicomponent dark matter on ams-02, Phys. Rev. D 89 (2014) 055021.
[15] S. Esch, M. Klasen and C. E. Yaguna, A minimal model for two-component dark matter, JHEP 09 (2014) 108 [1406.0617].
[16] K. R. Dienes, J. Kumar, B. Thomas and D. Yaylali, Dark-matter decay as a complementary probe of multicomponent dark sectors, Phys. Rev. Lett. 114 (2015) 051301.
[17] L. Bian, T. Li, J. Shu and X.-C. Wang, Two component dark matter with multi-Higgs portals, JHEP 03 (2015) 126 [1412.5443].
[18] C.-Q. Geng, D. Huang and C. Lai, Revisiting multicomponent dark matter with new ams-02 data, Phys. Rev. D 91 (2015) 095006.
[19] A. DiFranzo and G. Mohlabeng, Multi-component Dark Matter through a Radiative Higgs Portal, JHEP 01 (2017) 080 [1610.07606].
[20] M. Aoki and T. Toma, Implications of Two-component Dark Matter Induced by Forbidden Channels and Thermal Freeze-out, JCAP 01 (2017) 042 [1611.06746].
[21] A. Dutta Banik, M. Pandey, D. Majumdar and A. Biswas, Two component WIMP–FImP dark matter model with singlet fermion, scalar and pseudo scalar, Eur. Phys. J. C 77 (2017) 657 [1612.08621].
[22] M. Pandey, D. Majumdar and K. P. Modak, Two Component Feebly Interacting Massive Particle (FIMP) Dark Matter, JCAP 06 (2018) 023 [1709.05955].
[23] D. Borah, A. Dasgupta, U. K. Dey, S. Patra and G. Tomar, Multi-component fermionic dark matter and icecube pev scale neutrinos in left-right model with gauge unification, Journal of High Energy Physics 2017 (2017) 5.
[24] J. Herrero-Garcia, A. Scaffidi, M. White and A. G. Williams, On the direct detection of multi-component dark matter: sensitivity studies and parameter estimation, JCAP 11 (2017) 021 [1709.01945].
[25] A. Ahmed, M. Duch, B. Grzadkowski and M. Iglicki, Multi-Component Dark Matter: the vector and fermion case, Eur. Phys. J. C 78 (2018) 905 [1710.01853].
[26] S. Peyman Zakeri, S. Mohammad Moosavi Nejad, M. Zakeri and S. Yaser Ayazi, A Minimal Model For Two-Component FIMP Dark Matter: A Basic Search, Chin. Phys. C 42 (2018) 073101 [1801.09115].
[27] M. Aoki and T. Toma, Boosted Self-interacting Dark Matter in a Multi-component Dark Matter Model, JCAP 10 (2018) 020 [1806.09154].
[28] S. Chakraborti and P. Poulose, Interplay of Scalar and Fermionic Components in a Multi-component Dark Matter Scenario, Eur. Phys. J. C 79 (2019) 420 [1808.01979].
[29] N. Bernal, D. Restrepo, C. E. Yaguna and O. Zapata, Two-component dark matter and a massless neutrino in a new $b-l$ model, Phys. Rev. D 99 (2019) 015038.
[30] A. Poulin and S. Godfrey, Multicomponent dark matter from a hidden gauged su(3), Phys. Rev. D 99 (2019) 076008.
[31] J. Herrero-Garcia, A. Scaffidi, M. White and A. G. Williams, On the direct detection of multi-component dark matter: implications of the relic abundance, JCAP 01 (2019) 008 [1809.06881].
[32] S. Yaser Ayazi and A. Mohamadnejad, Scale-Invariant Two Component Dark Matter, Eur. Phys. J. C 79 (2019) 140 [1808.08706].
[33] F. Elahi and S. Khatibi, Multi-component dark matter in a non-abelian dark sector, Phys. Rev. D 100 (2019) 015019.
[34] D. Borah, A. Dasgupta and S. K. Kang, Two-component dark matter with cogenesis of the baryon asymmetry of the universe, Phys. Rev. D 100 (2019) 103502.
[35] A. Biswas, D. Borah and D. Nanda, Type III seesaw for neutrino masses in U(1)_B-L model with multi-component dark matter, JHEP 12 (2019) 109 [1908.04308].
[36] D. Nanda and D. Borah, Connecting Light Dirac Neutrinos to a Multi-component Dark Matter Scenario in Gauged $B-L$ Model, Eur. Phys. J. C 80 (2020) 557 [1911.04703].
[37] S. Bhattacharya, P. Ghosh, A. K. Saha and A. Sil, Two component dark matter with inert Higgs doublet: neutrino mass, high scale validity and collider searches, JHEP 03 (2020) 090 [1905.12583].
[38] C. E. Yaguna and O. Zapata, Multi-component scalar dark matter from a $Z_{N}$ symmetry: a systematic analysis, JHEP 03 (2020) 109 [1911.05515].
[39] G. Bélanger, A. Pukhov, C. E. Yaguna and O. Zapata, The Z₅ model of two-component dark matter, JHEP 09 (2020) 030 [2006.14922].
[40] P. Van Dong, C. H. Nam and D. Van Loi, Canonical seesaw implication for two-component dark matter, Phys. Rev. D 103 (2021) 095016.
[41] S. Khalil, S. Moretti, D. Rojas-Ciofalo and H. Waltari, Multicomponent dark matter in a simplified ${\mathrm{e}}_{6}\mathrm{SSM}$ , Phys. Rev. D 102 (2020) 075039.
[42] A. D. Banik, R. Roshan and A. Sil, Two component singlet-triplet scalar dark matter and electroweak vacuum stability, Phys. Rev. D 103 (2021) 075001.
[43] J. Hernandez-Sanchez, V. Keus, S. Moretti, D. Rojas-Ciofalo and D. Sokolowska, Complementary Probes of Two-component Dark Matter, 2012.11621.
[44] N. Chakrabarty, R. Roshan and A. Sil, Two-component doublet-triplet scalar dark matter stabilizing the electroweak vacuum, Phys. Rev. D 105 (2022) 115010.
[45] C. E. Yaguna and O. Zapata, Two-component scalar dark matter in Z_2n scenarios, JHEP 10 (2021) 185 [2106.11889].
[46] B. Díaz Sáez, P. Escalona, S. Norero and A. R. Zerwekh, Fermion singlet dark matter in a pseudoscalar dark matter portal, JHEP 10 (2021) 233 [2105.04255].
[47] Y. G. Kim, K. Y. Lee and S.-h. Nam, Phenomenology of a two-component dark matter model, Phys. Lett. B 834 (2022) 137412 [2201.11485].
[48] S.-Y. Ho, P. Ko and C.-T. Lu, Scalar and fermion two-component SIMP dark matter with an accidental $\mathbb{Z}_{4}$ symmetry, JHEP 03 (2022) 005 [2201.06856].
[49] S. Bhattacharya, P. Ghosh, J. Lahiri and B. Mukhopadhyaya, Mono-X signal and two component dark matter: New distinction criteria, Phys. Rev. D 108 (2023) L111703 [2211.10749].
[50] S. Bhattacharya, P. Ghosh, J. Lahiri and B. Mukhopadhyaya, Distinguishing two dark matter component particles at e⁺e^- colliders, JHEP 12 (2022) 049 [2202.12097].
[51] S. Bhattacharya, P. Ghosh and N. Sahu, Multipartite Dark Matter with Scalars, Fermions and signatures at LHC, JHEP 02 (2019) 059 [1809.07474].
[52] S. Bhattacharya, P. Poulose and P. Ghosh, Multipartite Interacting Scalar Dark Matter in the light of updated LUX data, JCAP 04 (2017) 043 [1607.08461].
[53] R. Wiley Deal, K. Sankharva, K. Sinha and S. Watson, Multi-component Dark Matter and small scale structure formation, JHEP 02 (2024) 085 [2308.16242].
[54] A. Bas i Beneito, J. Herrero-García and D. Vatsyayan, Multi-component dark sectors: symmetries, asymmetries and conversions, JHEP 10 (2022) 075 [2207.02874].
[55] S. Khalil, S. Moretti, D. Rojas-Ciofalo and H. Waltari, Multicomponent dark matter in a simplified E₆SSM, Phys. Rev. D 102 (2020) 075039 [2007.10966].
[56] F. Costa, S. Khan and J. Kim, A two-component vector WIMP — fermion FIMP dark matter model with an extended seesaw mechanism, JHEP 12 (2022) 165 [2209.13653].
[57] PandaX collaboration, A search for two-component Majorana dark matter in a simplified model using the full exposure data of PandaX-II experiment, Phys. Lett. B 832 (2022) 137254 [2205.08066].
[58] A. Das, S. Gola, S. Mandal and N. Sinha, Two-component scalar and fermionic dark matter candidates in a generic U(1)X model, Phys. Lett. B 829 (2022) 137117 [2202.01443].
[59] C. E. Yaguna and O. Zapata, Fermion and scalar two-component dark matter from a Z4 symmetry, Phys. Rev. D 105 (2022) 095026 [2112.07020].
[60] G. P. Berman, V. N. Gorshkov, V. I. Tsifrinovich, M. Merkli and V. V. Tereshchuk, Two-Component Axionic Dark Matter Halos, Mod. Phys. Lett. A 35 (2020) 2050227 [2001.10584].
[61] M. Becker and W.-C. Huang, Two-component asymmetric dark matter via bound states and freeze-in decay, 1911.06788.
[62] K. Kajantie, M. Laine, K. Rummukainen and M. E. Shaposhnikov, The Electroweak phase transition: A Nonperturbative analysis, Nucl. Phys. B 466 (1996) 189 [hep-lat/9510020].
[63] K. Kajantie, M. Laine, K. Rummukainen and M. E. Shaposhnikov, Is there a hot electroweak phase transition at $m_{H}\gtrsim m_{W}$ ?, Phys. Rev. Lett. 77 (1996) 2887 [hep-ph/9605288].
[64] Y. Aoki, G. Endrodi, Z. Fodor, S. D. Katz and K. K. Szabo, The Order of the quantum chromodynamics transition predicted by the standard model of particle physics, Nature 443 (2006) 675 [hep-lat/0611014].
[65] T. Bhattacharya et al., QCD Phase Transition with Chiral Quarks and Physical Quark Masses, Phys. Rev. Lett. 113 (2014) 082001 [1402.5175].
[66] N. Okada and O. Seto, Probing the seesaw scale with gravitational waves, Phys. Rev. D 98 (2018) 063532 [1807.00336].
[67] D. Croon, V. Sanz and G. White, Model Discrimination in Gravitational Wave spectra from Dark Phase Transitions, JHEP 08 (2018) 203 [1806.02332].
[68] E. Madge and P. Schwaller, Leptophilic dark matter from gauged lepton number: Phenomenology and gravitational wave signatures, JHEP 02 (2019) 048 [1809.09110].
[69] T. Hasegawa, N. Okada and O. Seto, Gravitational waves from the minimal gauged $U(1)_{B-L}$ model, Phys. Rev. D 99 (2019) 095039 [1904.03020].
[70] D. Gonçalves, A. Kaladharan and Y. Wu, Gravitational waves, bubble profile, and baryon asymmetry in the complex 2HDM, Phys. Rev. D 108 (2023) 075010 [2307.03224].
[71] T. Abe, K. S. Babu and A. Kaladharan, Gravitational wave signatures of a chiral fermion dark matter model, JCAP 07 (2024) 048 [2312.17203].
[72] J. M. Cline and P.-A. Lemieux, Electroweak phase transition in two Higgs doublet models, Phys. Rev. D 55 (1997) 3873 [hep-ph/9609240].
[73] F. Costa, S. Khan and J. Kim, A two-component dark matter model and its associated gravitational waves, JHEP 06 (2022) 026 [2202.13126].
[74] V. V. Khoze and D. L. Milne, Gravitational waves and dark matter from classical scale invariance, Phys. Rev. D 107 (2023) 095012 [2212.04784].
[75] M. Hosseini, S. Yaser Ayazi and A. Mohamadnejad, Gravitational wave effects and phenomenology of a two-component dark matter model, Eur. Phys. J. C 84 (2024) 485 [2308.00395].
[76] M. Hosseini, S. Y. Ayazi and A. Mohamadnejad, Gravitational wave in a filtered vector dark matter model, 2405.10662.
[77] A. Mohamadnejad, Electroweak phase transition and gravitational waves in a two-component dark matter model, JHEP 03 (2022) 188 [2111.04342].
[78] A. Mohamadnejad, Gravitational waves from scale-invariant vector dark matter model: Probing below the neutrino-floor, Eur. Phys. J. C 80 (2020) 197 [1907.08899].
[79] S. Yaser Ayazi and A. Mohamadnejad, Conformal vector dark matter and strongly first-order electroweak phase transition, JHEP 03 (2019) 181 [1901.04168].
[80] P. Asadi, E. D. Kramer, E. Kuflik, G. W. Ridgway, T. R. Slatyer and J. Smirnov, Thermal squeezeout of dark matter, Phys. Rev. D 104 (2021) 095013 [2103.09827].
[81] A. Soni and Y. Zhang, Gravitational Waves From SU(N) Glueball Dark Matter, Phys. Lett. B 771 (2017) 379 [1610.06931].
[82] R. Flauger and S. Weinberg, Gravitational Waves in Cold Dark Matter, Phys. Rev. D 97 (2018) 123506 [1801.00386].
[83] W. Chao, H.-K. Guo and J. Shu, Gravitational Wave Signals of Electroweak Phase Transition Triggered by Dark Matter, JCAP 09 (2017) 009 [1702.02698].
[84] A. Beniwal, M. Lewicki, J. D. Wells, M. White and A. G. Williams, Gravitational wave, collider and dark matter signals from a scalar singlet electroweak baryogenesis, JHEP 08 (2017) 108 [1702.06124].
[85] F. P. Huang and C. S. Li, Probing the baryogenesis and dark matter relaxed in phase transition by gravitational waves and colliders, Phys. Rev. D 96 (2017) 095028 [1709.09691].
[86] L. Bian and X. Liu, Two-step strongly first-order electroweak phase transition modified FIMP dark matter, gravitational wave signals, and the neutrino mass, Phys. Rev. D 99 (2019) 055003 [1811.03279].
[87] V. R. Shajiee and A. Tofighi, Electroweak Phase Transition, Gravitational Waves and Dark Matter in Two Scalar Singlet Extension of The Standard Model, Eur. Phys. J. C 79 (2019) 360 [1811.09807].
[88] K. Kannike, K. Loos and M. Raidal, Gravitational wave signals of pseudo-goldstone dark matter in the ${\mathbb{z}}_{3}$ complex singlet model, Phys. Rev. D 101 (2020) 035001.
[89] B. Barman, A. Dutta Banik and A. Paul, Singlet-doublet fermionic dark matter and gravitational waves in a two-higgs-doublet extension of the standard model, Phys. Rev. D 101 (2020) 055028.
[90] T. Alanne, N. Benincasa, M. Heikinheimo, K. Kannike, V. Keus, N. Koivunen et al., Pseudo-Goldstone dark matter: gravitational waves and direct-detection blind spots, JHEP 10 (2020) 080 [2008.09605].
[91] X.-F. Han, L. Wang and Y. Zhang, Dark matter, electroweak phase transition, and gravitational waves in the type ii two-higgs-doublet model with a singlet scalar field, Phys. Rev. D 103 (2021) 035012.
[92] Y. Wang, C. S. Li and F. P. Huang, Complementary probe of dark matter blind spots by lepton colliders and gravitational waves, Phys. Rev. D 104 (2021) 053004.
[93] W. Chao, X.-F. Li and L. Wang, Filtered pseudo-scalar dark matter and gravitational waves from first order phase transition, JCAP 06 (2021) 038 [2012.15113].
[94] K. Hashino, M. Kakizaki, S. Kanemura, P. Ko and T. Matsui, Gravitational waves from first order electroweak phase transition in models with the U(1)_X gauge symmetry, JHEP 06 (2018) 088 [1802.02947].
[95] I. Baldes and G. Servant, High scale electroweak phase transition: baryogenesis \& symmetry non-restoration, JHEP 10 (2018) 053 [1807.08770].
[96] K. Fujikura, K. Kamada, Y. Nakai and M. Yamaguchi, Phase Transitions in Twin Higgs Models, JHEP 12 (2018) 018 [1810.00574].
[97] P. Athron, C. Balazs, A. Fowlie, G. Pozzo, G. White and Y. Zhang, Strong first-order phase transitions in the NMSSM — a comprehensive survey, JHEP 11 (2019) 151 [1908.11847].
[98] A. Alves, D. Gonçalves, T. Ghosh, H.-K. Guo and K. Sinha, Di-Higgs Production in the $4b$ Channel and Gravitational Wave Complementarity, JHEP 03 (2020) 053 [1909.05268].
[99] D. Gonçalves, A. Kaladharan and Y. Wu, Resonant top pair searches at the LHC: A window to the electroweak phase transition, Phys. Rev. D 107 (2023) 075040 [2206.08381].
[100] J. Ellis, M. Lewicki and J. M. No, On the Maximal Strength of a First-Order Electroweak Phase Transition and its Gravitational Wave Signal, JCAP 04 (2019) 003 [1809.08242].
[101] T. Alanne, T. Hugle, M. Platscher and K. Schmitz, A fresh look at the gravitational-wave signal from cosmological phase transitions, JHEP 03 (2020) 004 [1909.11356].
[102] A. Paul, B. Banerjee and D. Majumdar, Gravitational wave signatures from an extended inert doublet dark matter model, JCAP 10 (2019) 062 [1908.00829].
[103] G. Arcadi, N. Benincasa, A. Djouadi and K. Kannike, Two-higgs-doublet-plus-pseudoscalar model: Collider, dark matter, and gravitational wave signals, Phys. Rev. D 108 (2023) 055010.
[104] A. Addazi, A. Marcianò, A. P. Morais, R. Pasechnik, R. Srivastava and J. W. F. Valle, Gravitational footprints of massive neutrinos and lepton number breaking, Phys. Lett. B 807 (2020) 135577 [1909.09740].
[105] K. Kannike and M. Raidal, Phase Transitions and Gravitational Wave Tests of Pseudo-Goldstone Dark Matter in the Softly Broken U(1) Scalar Singlet Model, Phys. Rev. D 99 (2019) 115010 [1901.03333].
[106] F. Ertas, F. Kahlhoefer and C. Tasillo, Turn up the volume: listening to phase transitions in hot dark sectors, JCAP 02 (2022) 014 [2109.06208].
[107] W. Wang, W.-L. Xu and J. M. Yang, A hidden self-interacting dark matter sector with first-order cosmological phase transition and gravitational wave, Eur. Phys. J. Plus 138 (2023) 781 [2209.11408].
[108] G. Arcadi, G. C. Dorsch, J. P. Neto, F. S. Queiroz and Y. M. Oviedo-Torres, Probing a dark sector with collider physics, direct detection, and gravitational waves, Phys. Lett. B 848 (2024) 138382 [2307.06376].
[109] S. Kanemura and S.-P. Li, Dark phase transition from WIMP: complementary tests from gravitational waves and colliders, JCAP 03 (2024) 005 [2308.16390].
[110] L. Bian, W. Cheng, H.-K. Guo and Y. Zhang, Cosmological implications of a B $-$ L charged hidden scalar: leptogenesis and gravitational waves, Chin. Phys. C 45 (2021) 113104 [1907.13589].
[111] T. Abe and K. Hashino, Gravitational Waves from First-Order Phase Transition in an Electroweakly Interacting Vector Dark Matter Model, PTEP 2024 (2024) 063B02 [2302.13510].
[112] I. Baldes and C. Garcia-Cely, Strong gravitational radiation from a simple dark matter model, JHEP 05 (2019) 190 [1809.01198].
[113] M. Fairbairn, E. Hardy and A. Wickens, Hearing without seeing: gravitational waves from hot and cold hidden sectors, JHEP 07 (2019) 044 [1901.11038].
[114] T. Ghosh, H.-K. Guo, T. Han and H. Liu, Electroweak phase transition with an SU(2) dark sector, JHEP 07 (2021) 045 [2012.09758].
[115] A. J. Helmboldt, J. Kubo and S. van der Woude, Observational prospects for gravitational waves from hidden or dark chiral phase transitions, Phys. Rev. D 100 (2019) 055025.
[116] D. Dunsky, L. J. Hall and K. Harigaya, Dark Matter, Dark Radiation and Gravitational Waves from Mirror Higgs Parity, JHEP 02 (2020) 078 [1908.02756].
[117] J. B. Dent, B. Dutta, S. Ghosh, J. Kumar and J. Runburg, Sensitivity to dark sector scales from gravitational wave signatures, JHEP 08 (2022) 300 [2203.11736].
[118] M. Dichtl, J. Nava, S. Pascoli and F. Sala, Baryogenesis and leptogenesis from supercooled confinement, JHEP 02 (2024) 059 [2312.09282].
[119] M. Ahmadvand, Filtered asymmetric dark matter during the Peccei-Quinn phase transition, JHEP 10 (2021) 109 [2108.00958].
[120] A. Ghoshal, D. Paul and S. Pal, Primordial Gravitational Waves as Probe of Dark Matter in Interferometer Missions: Fisher Forecast and MCMC, 2405.06741.
[121] S. Bhattacharya, N. Mondal, R. Roshan and D. Vatsyayan, Leptogenesis, dark matter and gravitational waves from discrete symmetry breaking, JCAP 06 (2024) 029 [2312.15053].
[122] N. Benincasa, A. Hryczuk, K. Kannike and M. Laletin, Phase transitions and gravitational waves in a model of $\mathbb{Z}_{3}$ scalar dark matter, JHEP 02 (2024) 207 [2312.04627].
[123] Y. Gu, L. Su, L. Wu, Y. Wu and B. Zhu, Gravitational wave as a probe of light feebly interacting dark matter, Phys. Rev. D 110 (2024) 015022 [2312.03349].
[124] T. Bringmann, T. E. Gonzalo, F. Kahlhoefer, J. Matuszak and C. Tasillo, Hunting WIMPs with LISA: correlating dark matter and gravitational wave signals, JCAP 05 (2024) 065 [2311.06346].
[125] C. Han, K.-P. Xie, J. M. Yang and M. Zhang, Self-interacting dark matter implied by nano-Hertz gravitational waves, Phys. Rev. D 109 (2024) 115025 [2306.16966].
[126] M. J. Baker, J. Kopp and A. J. Long, Filtered Dark Matter at a First Order Phase Transition, Phys. Rev. Lett. 125 (2020) 151102 [1912.02830].
[127] M. Breitbach, J. Kopp, E. Madge, T. Opferkuch and P. Schwaller, Dark, Cold, and Noisy: Constraining Secluded Hidden Sectors with Gravitational Waves, JCAP 07 (2019) 007 [1811.11175].
[128] M. J. Baker, M. Breitbach, J. Kopp and L. Mittnacht, Dynamic Freeze-In: Impact of Thermal Masses and Cosmological Phase Transitions on Dark Matter Production, JHEP 03 (2018) 114 [1712.03962].
[129] E. Morgante, N. Ramberg and P. Schwaller, Gravitational waves from dark SU(3) Yang-Mills theory, Phys. Rev. D 107 (2023) 036010 [2210.11821].
[130] P. Schwaller, Gravitational Waves from a Dark Phase Transition, Phys. Rev. Lett. 115 (2015) 181101 [1504.07263].
[131] F. Gao, J. Harz, C. Hati, Y. Lu, I. M. Oldengott and G. White, Sphaleron freeze-in baryogenesis with gravitational waves from the QCD transition, 2309.00672.
[132] R. Pasechnik, M. Reichert, F. Sannino and Z.-W. Wang, Gravitational waves from composite dark sectors, JHEP 02 (2024) 159 [2309.16755].
[133] LIGO Scientific Collaboration and Virgo Collaboration collaboration, Observation of gravitational waves from a binary black hole merger, Phys. Rev. Lett. 116 (2016) 061102.
[134] LISA collaboration, Laser Interferometer Space Antenna, 1702.00786.
[135] J. Crowder and N. J. Cornish, Beyond lisa: Exploring future gravitational wave missions, Phys. Rev. D 72 (2005) 083005.
[136] H. Kudoh, A. Taruya, T. Hiramatsu and Y. Himemoto, Detecting a gravitational-wave background with next-generation space interferometers, Phys. Rev. D 73 (2006) 064006.
[137] K. Yagi and N. Seto, Detector configuration of decigo/bbo and identification of cosmological neutron-star binaries, Phys. Rev. D 83 (2011) 044011.
[138] R. Foot, A. Kobakhidze, K. L. McDonald and R. R. Volkas, A Solution to the hierarchy problem from an almost decoupled hidden sector within a classically scale invariant theory, Phys. Rev. D 77 (2008) 035006 [0709.2750].
[139] S. R. Coleman and E. J. Weinberg, Radiative Corrections as the Origin of Spontaneous Symmetry Breaking, Phys. Rev. D 7 (1973) 1888.
[140] Planck collaboration, Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641 (2020) A6 [1807.06209].
[141] XENON collaboration, First Dark Matter Search with Nuclear Recoils from the XENONnT Experiment, Phys. Rev. Lett. 131 (2023) 041003 [2303.14729].
[142] E. Gildener and S. Weinberg, Symmetry Breaking and Scalar Bosons, Phys. Rev. D 13 (1976) 3333.
[143] K. Ghorbani and H. Ghorbani, Scalar Dark Matter in Scale Invariant Standard Model, JHEP 04 (2016) 024 [1511.08432].
[144] G. Bélanger, F. Boudjema, A. Pukhov and A. Semenov, micrOMEGAs4.1: two dark matter candidates, Comput. Phys. Commun. 192 (2015) 322 [1407.6129].
[145] J. Billard, L. Strigari and E. Figueroa-Feliciano, Implication of neutrino backgrounds on the reach of next generation dark matter direct detection experiments, Phys. Rev. D 89 (2014) 023524 [1307.5458].
[146] L. Dolan and R. Jackiw, Symmetry Behavior at Finite Temperature, Phys. Rev. D 9 (1974) 3320.
[147] M. Laine and A. Vuorinen, Basics of Thermal Field Theory, vol. 925. Springer, 2016, [1701.01554].
[148] D. Croon, TASI lectures on Phase Transitions, Baryogenesis, and Gravitational Waves, PoS TASI2022 (2024) 003 [2307.00068].
[149] P. Athron, C. Balázs, A. Fowlie, L. Morris and L. Wu, Cosmological phase transitions: From perturbative particle physics to gravitational waves, Prog. Part. Nucl. Phys. 135 (2024) 104094 [2305.02357].
[150] O. Gould, J. Kozaczuk, L. Niemi, M. J. Ramsey-Musolf, T. V. I. Tenkanen and D. J. Weir, Nonperturbative analysis of the gravitational waves from a first-order electroweak phase transition, Phys. Rev. D 100 (2019) 115024 [1903.11604].
[151] D. Croon, O. Gould, P. Schicho, T. V. I. Tenkanen and G. White, Theoretical uncertainties for cosmological first-order phase transitions, JHEP 04 (2021) 055 [2009.10080].
[152] O. Gould and T. V. I. Tenkanen, On the perturbative expansion at high temperature and implications for cosmological phase transitions, JHEP 06 (2021) 069 [2104.04399].
[153] L. Niemi, P. Schicho and T. V. I. Tenkanen, Singlet-assisted electroweak phase transition at two loops, Phys. Rev. D 103 (2021) 115035 [2103.07467].
[154] P. M. Schicho, T. V. I. Tenkanen and J. Österman, Robust approach to thermal resummation: Standard Model meets a singlet, JHEP 06 (2021) 130 [2102.11145].
[155] M. E. Carrington, The Effective potential at finite temperature in the Standard Model, Phys. Rev. D 45 (1992) 2933.
[156] P. B. Arnold and O. Espinosa, The Effective potential and first order phase transitions: Beyond leading-order, Phys. Rev. D 47 (1993) 3546 [hep-ph/9212235].
[157] Z. Kang and J. Zhu, Scale-genesis by Dark Matter and Its Gravitational Wave Signal, Phys. Rev. D 102 (2020) 053011 [2003.02465].
[158] R. Apreda, M. Maggiore, A. Nicolis and A. Riotto, Gravitational waves from electroweak phase transitions, Nuclear Physics B 631 (2002) 342.
[159] S. Coleman, Erratum: Fate of the false vacuum: semiclassical theory, Phys. Rev. D 16 (1977) 1248.
[160] C. G. Callan and S. Coleman, Fate of the false vacuum. ii. first quantum corrections, Phys. Rev. D 16 (1977) 1762.
[161] A. Masoumi, K. D. Olum and J. M. Wachter, Approximating tunneling rates in multi-dimensional field spaces, JCAP 10 (2017) 022 [1702.00356].
[162] D. Bodeker and G. D. Moore, Can electroweak bubble walls run away?, JCAP 05 (2009) 009 [0903.4099].
[163] S. J. Huber and T. Konstandin, Gravitational Wave Production by Collisions: More Bubbles, JCAP 09 (2008) 022 [0806.1828].
[164] M. Hindmarsh, S. J. Huber, K. Rummukainen and D. J. Weir, Numerical simulations of acoustically generated gravitational waves at a first order phase transition, Phys. Rev. D 92 (2015) 123009 [1504.03291].
[165] E. Witten, Cosmic separation of phases, Phys. Rev. D 30 (1984) 272.
[166] C. Caprini, R. Durrer and G. Servant, The stochastic gravitational wave background from turbulence and magnetic fields generated by a first-order phase transition, JCAP 12 (2009) 024 [0909.0622].
[167] C. Caprini et al., Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions, JCAP 04 (2016) 001 [1512.06239].
[168] M. Kamionkowski, A. Kosowsky and M. S. Turner, Gravitational radiation from first order phase transitions, Phys. Rev. D 49 (1994) 2837 [astro-ph/9310044].