Graph Topic Modeling for Documents with Spatial or Covariate Dependencies
Abstract
We address the challenge of incorporating document-level metadata into topic modeling to improve topic mixture estimation. To overcome the computational complexity and lack of theoretical guarantees in existing Bayesian methods, we extend probabilistic latent semantic indexing (pLSI), a frequentist framework for topic modeling, by incorporating document-level covariates or known similarities between documents through a graph formalism. Modeling documents as nodes and edges denoting similarities, we propose a new estimator based on a fast graph-regularized iterative singular value decomposition (SVD) that encourages similar documents to share similar topic mixture proportions. We characterize the estimation error of our proposed method by deriving high-probability bounds and develop a specialized cross-validation method to optimize our regularization parameters. We validate our model through comprehensive experiments on synthetic datasets and three real-world corpora, demonstrating improved performance and faster inference compared to existing Bayesian methods.
Keywords: graph cross validation, graph regularization, latent dirichlet allocation, total variation penalty
1 Introduction
Consider a corpus of documents, each composed of words (or more generally, terms) from a vocabulary of size . This corpus can be represented by a document-term matrix , where each entry denotes the number of times term appears in document . The objective of topic modeling is to retrieve low-dimensional representations of the data by representing each document as a mixture of latent topics, defined as distributions over term frequencies.
In this setting, each document is usually assumed to be sampled from a multinomial distribution with an associated probability vector that can be decomposed as a mixture of topics. In other words, letting denote the length of document :
| (1) |
In the previous equation, corresponds to the proportion of topic in document , and the vector provides a low-dimensional representation of document in terms of its topic composition. Each entry of the vector corresponds to the expected frequency of word in topic . Since document lengths are usually treated as nuisance variables, most topic modeling approaches work in fact directly with the word frequency matrix , which can be written in a “signal + noise” form as:
| (2) |
Here, is the true signal whose entry denotes the expected frequency of word in document , while denotes some centered multinomial noise. The objective of topic modeling is thus to estimate and from .
Originally developed to reduce document representations to low-dimensional latent semantic spaces, topic modeling has been successfully deployed for the analysis of count data in a number of applications, ranging from image processing (Tu et al. 2016, Zheng et al. 2015) and image annotation(Feng & Lapata 2010, Shao et al. 2009), to biochemistry (Reder et al. 2021), genetics (Dey et al. 2017, Kho et al. 2017, Liu et al. 2016, Yang et al. 2019), and microbiome studies (Sankaran & Holmes 2019, Symul et al. 2023).
A notable extension of topic modeling occurs when additional document-level data is available. Although original topic modeling approaches rely solely on the analysis of the empirical frequency matrix , this additional information has the potential to significantly improve the estimation of the word-topic matrix and the document-topic mixture matrix , particularly in difficult inference settings, such as when the number of words per document is small. Examples include:
-
1.
Analyzing tumor microenvironments: In this context, slices of tumor samples are partitioned into smaller regions known as tumor microenvironments, where the frequency of specific immune cell types is recorded (Chen et al. 2020). Here, documents correspond to microenvironments, and words to cell types. The objective is to identify communities of co-abundant cells (topics), taken here as proxies for tumor-immune cell interactions and potential predictors of patient outcomes. In this setting, we assume that neighboring microenvironments share similar topic proportions. Since these microenvironments are inherently small, leveraging the spatial smoothness of the mixture matrix can significantly improve inference (Chen et al. 2020). We develop this example in further detail in Section 4.1.
-
2.
Microbiome studies: Topic models have also been proven to be extremely useful in microbiome analysis (Sankaran & Holmes 2019, Symul et al. 2023). In this setting, the data consists of a microbiome count matrix recording the amount of different types of bacteria found in each sample. In this case, microbiome samples are identified to documents, with bacteria playing the roles of the vocabulary, and the goal becomes to identify communities of co-abundant bacteria (Sankaran & Holmes 2019). When additional covariate information is available (such as age, gender, and other demographic details), we can expect similar samples (documents) to exhibit similar community compositions (topic proportions).
-
3.
The analysis of short documents, such as a collection of scientific abstracts or recipes: In this case, while recipes might be short, information on the origin of the recipe can help determine the topics and mixture matrix more accurately by leveraging the assumption that recipes of neighboring countries will typically share similar topic proportions. We elaborate on this example in greater detail in Section 4.3.
Prior works. Previous attempts to incorporate metadata in topic estimation have focused on the Bayesian extensions of latent Dirichlet allocation (LDA) model of Blei et al. (2001). By and large, these methods typically incorporate the metadata—often in the form of a covariate matrix—within a prior distribution (Blei & Lafferty 2006a, b, Roberts et al. 2014, Mcauliffe & Blei 2007). However, these models (a) are difficult to adapt to different types of covariates or information encoded as a graph, and (b) typically lack theoretical guarantees. Recent work by Chen et al. (2020) proposes extending LDA to analyze documents with known similarities by smoothing the topic proportion hyperparameters along the edges of the graph. However, this method does not empirically yield spatially smooth structures (see Sections 3.4 and 4), and significantly increases the algorithm’s running time.
In the frequentist realm, probabilistic latent semantic indexing (pLSI) has gained renewed interest over the past five years. Similar to LDA, it effectively models documents as bags of words but differs by treating matrices and as fixed parameters. In particular, new work by Ke & Wang (2017) and Klopp et al. (2021) suggest procedures to reliably estimate the topic matrix and mixture matrix , characterizing consistency and efficiency through high-probability error bounds Although recent work has begun investigating the use of structures in pLSI-based topic models, most approaches have limited this to considering various versions of sparsity (Bing et al. 2020, Wu et al. 2023) or weak sparsity (Tran et al. 2023) for the topic matrix . To the best of our knowledge, no pLSI approach has yet been proposed that effectively leverages similarities between documents nor characterizes the consistency of these estimators.
Contributions
In this paper, we propose the first pLSI method that can be made amenable to the inclusion of additional information on the similarity between documents, as encoded by a known graph. More specifically:
-
a.
We propose a scalable algorithm based on a graph-aligned singular decomposition of the empirical frequency matrix to provide estimates of and (Section 2). Additionally, we develop a new cross-validation procedure for our graph-based penalty that allows us to choose the optimal regularization parameter adaptively (Section A of the Appendix).
- b.
-
c.
Finally, we showcase the advantage of our method over LDA-based methods and non-structured pLSI techniques on three real-world datasets: two spatial transcriptomics examples and a recipe dataset in Section 4.
Notations
Throughout this paper, we use the following notations. For any , denotes the set . For any , we write and . We use to denote the vector with all entries equal to 1 and to denote the vector with element set to 1 and 0 otherwise. For any vector , its , and norms are defined respectively as , , and . Let denote the identity matrix. For any matrix , denote the -entry of , and denote the row and column of respectively. Throughout this paper, stands for the largest singular value of the matrix with , . We also denote as and the left and right singular matrix from the rank- SVD of . The Frobenius, entry-wise norm and the operator norms of are denoted as , , and , respectively. The norm is denoted as . For any positive semi-definite matrix , denotes its principal square root that is positive semi-definite and satisfies . The trace inner product of two matrices is denoted by . denotes the pseudo-inverse of the matrix and denotes the projection matrix onto the subspace spanned by columns of .
2 Graph-Aligned pLSI
In this section, we introduce graph-aligned pLSI (GpLSI), an extension of the standard pLSI framework that leverages known similarities between documents to improve inference in topic modeling using a graph formalism. We begin by introducing a set of additional notations and model assumptions, before introducing the algorithm in Section 2.3.
2.1 Assumptions
Let denote an undirected graph induced by a known adjacency matrix on the documents in the corpus. The documents are represented as nodes , and denotes the edge set of size . Throughout this paper, for simplicity, we will assume that is binary, but our approach—as discussed in Section 2.3—can be in principle extended to weighted graphs. We denote the graph’s incidence matrix as where, for any edge between nodes and in the graph, , and for any It is easy to show that the Laplacian of the graph can be expressed in terms of the incidence matrix as (Hütter & Rigollet 2016). Let be the pseudo-inverse of , and denote by its columns, so that . We also define the inverse scaling factor of the incidence matrix (Hütter & Rigollet 2016), a quantity necessary for assessing the performance of GpLSI:
| (3) |
We focus on the estimation of the topic mixture matrix under the assumption that neighboring documents have similar topic mixture proportions: if . This implies that the rows of are assumed to be smooth with respect to the graph . Noting that the difference of mixture proportions between neighboring nodes and () can be written as , this smoothness assumption effectively implies sparsity on the rows of the matrix .
Assumption 1 (Graph-Aligned mixture matrix).
The support (i.e, the number of non-zero rows) of the difference matrix is small:
| (4) |
where
The previous assumption is akin to assuming that the underlying mixture matrix is piecewise-continuous with respect to the graph , or more generally, that it can be well approximated by a piecewise-continuous function.
Our setting is not limited to connected document graphs. Denote the number of connected subgraphs of and the number of nodes in the connected subgraph. Let be the size of the smallest connected component:
| (5) |
The error bound of our estimators will depend on both and . In the rest of this paper, we will assume that all connected components have roughly the same size: .
Assumption 2 (Anchor document).
For each topic there exists at least one document (called an anchor document) such that and for all .
Remark 1.
Assumption 2 is standard in the topic modeling community, as it is a sufficient condition for the identifiability of the topic and mixture matrices and (Donoho & Stodden 2003). Beyond identifiability, we contend that the “anchor document” assumption functions not only as a sufficient condition for identifiability but also as a necessary condition for interpretability: Topics are interpretable only when associated with archetypes—that is, “extreme“ representations (in our case, anchor documents)—that illustrate the topic more expressively.
Assumption 3 (Equal Document Sizes).
In this paper, for ease of presentation, we will also assume that the documents have equal sizes: . More generally, our results also hold if we assume that the document lengths satisfy (), in which case denotes the average document length.
Assumption 4 (Condition number of and ).
There exist two constants such that
Assumption 5 (Assumption on the minimum word frequency).
We assume that the expected word frequencies defined as: are bounded below by:
where is a constant that does not depend on parameters or .
Remark 2.
Assumption 5 is a relatively strong assumption that essentially restricts the scope of this paper’s analysis to small vocabulary sizes (thereafter referred to as the “low-” regime). Indeed, since , under Assumption 5, it immediately follows that:
This assumption might not reflect the large vocabulary sizes found in many practical problems, where we could expect to grow with . A solution to this potential limitation is to assume weak sparsity on the matrix and to threshold away rare terms using the thresholding procedure proposed in Tran et al. (2023), selecting a subset of words with large enough frequency. In this case, the rest of our analysis should follow, replacing simply the data matrix by its subset,
2.2 Estimation procedure: pLSI
Since the smoothness assumption (Assumption 1) pertains to the rows of the document-topic mixture matrix , we build on the pLSI algorithm developed by Klopp et al. (2021). In this subsection, we provide a brief overview of their method.
When we assume we directly observe the true expected frequency matrix defined in Equation (2), Klopp et al. (2021) propose a fast and simple procedure to recover the mixture matrix . Specifically, let and be the left and right singular vectors obtained from the singular value decomposition (SVD) of the true signal , so that . A critical insight from their work is that can be decomposed as:
| (6) |
where is a full-rank, -dimensional matrix. From this decomposition, it follows that the rows of , which can be viewed as -dimensional embeddings of the documents, lie on the -dimensional simplex . The simplex’s vertices, represented by the rows of , correspond to the anchor documents (Assumption 2). Thus, identifying these vertices through any standard vertex-finding algorithm applied to the rows of will enable the estimation of . The procedure of Klopp et al. (2021) can be summarized as follows:
- Step 1:
-
Compute the singular value decomposition (SVD) of the matrix , reduced to rank , to obtain: .
- Step 2: Vertex-Hunting Step:
-
Apply the successive projection algorithm (SPA) (Araújo et al. 2001) (a vertex-hunting algorithm) on the rows of . This algorithm returns the indices of the selected “anchor documents,” with . Define , where each row corresponds to one of the vertices of the simplex .
- Step 3: Recovery of :
-
can simply be recovered from and as
(7) - Step 4: Recovery of :
-
Finally, can subsequently be estimated as
In the noisy setting, the procedure is adapted by plugging the observed frequency instead of in Step 1 and getting estimates of the singular vectors: . Under a similar set of assumptions as ours (Assumptions 2-4), Theorem 1 of (Klopp et al. 2021) states that the error of is such that: , where denotes the set of all permutation matrices. Their analysis provides one of the best error bounds on the estimation of the topic mixture matrix for pLSI.
However, this approach has two key limitations. First, the consistency of their estimator relies on having a sufficiently large number of words per document, . In particular, a necessary condition for the aforementioned results to hold is that . The authors establish minimax error bounds, showing that the rate of any estimator’s error for is bounded below by a term on the order of (Theorem 3, Klopp et al. (2021)). In other words, the accurate estimation of requires that each document contains enough words. In many practical scenarios—such as the tumor microenvironment example mentioned earlier—this condition may not hold. However, we might still have access to additional information indicating that certain documents are more similar to one another.
Second, the method is relatively rigid and does not easily accommodate additional structural information, such as document-level similarities. Indeed, this method does not rely on a convex optimization formulation to which we could simply add a regularization term, and the vertex-hunting algorithm does not readily incorporate metadata of the documents.
2.3 Estimation procedure: GpLSI
Theoretical insights from Klopp et al. (2021) help explain why topic modeling deteriorates in low- regimes. When the number of words per document is too small, the observed frequency matrix can be viewed as a highly noisy approximation of , causing the estimated singular vectors to deviate significantly from the true underlying point cloud . To mitigate this issue, Klopp et al. (2021) suggest a preconditioning step that improves the estimation of the singular vectors in noisy settings.
In this paper, we take a different approach by exploiting the graph structure associated with the documents to reduce the noise in . Rather than preconditioning the empirical frequency matrix, we propose an additional denoising step that leverages the graph structure to produce more accurate estimates of , , and . Specifically, we modify the SVD of in Step 1 and estimation of topic matrix in Step 4 described in Section 2.2.
- Step 1: Iterative Graph-Aligned SVD of :
-
We replace Step 1 of Section 2.2 with a graph-aligned SVD of the empirical word-frequency matrix . More specifically, in the graph-aligned setting, we assume that the underlying frequency matrix belongs to the set:
(8) Throughout the paper, we shall allow and to vary. We will assume the number of topics to be fixed.
- Step 2, 3
-
Same as Step 2,3 in Section 2.2.
- Step 4: Recovery of :
-
can subsequently be estimated by solving a constrained regression problem of on :
(9)
Iterative Graph-Aligned SVD.
We propose a power iteration method for Step 1 that iteratively updates the left and right singular vectors while constraining the left singular vector to be aligned with the graph (Algorithm 1). A similar approach has already been studied under Gaussian noise in Yang et al. (2016) where sparsity constraints were imposed on the left and right singular vectors.
Drawing inspiration from Yang et al. (2016) and adapting this method to the multinomial noise setting, Algorithm 1 iterates between three steps. The first consists of denoising the left singular subspace by leveraging the graph-smoothness assumption (Assumption 1). At iteration , we solve:
| (10) |
Here, is a denoised version of the projection that leverages the graph structure to yield an estimate closer to the true . We then take a rank- SVD of to extract (an estimate of ) with orthogonal columns.
Finally, we update . Since we are not assuming any particular structure on the right singular subspace, we simply apply a rank- SVD on the projection . Denoting the projections onto the columns of the estimates as and , we iterate the procedure until for a fixed threshold .
Denoting the final estimates after iterations as , these estimates can then be plugged into Steps 2-4 to estimate and . The improved estimation of can be shown to translate into a more accurate estimation of the matrices and (Theorems 3 and 4 presented in the next section).
Although our theoretical results depend on choosing an appropriate level of regularization , the theoretical value of depends on unknown graph quantities. In practice, therefore, the optimal must be chosen in each iteration using cross-validation. We devise a novel graph cross-validation method which effectively finds the optimal graph regularization parameter by partitioning nodes into folds using a minimum spanning tree. We defer the detailed procedure to Section A of the Appendix.
Remark 3.
While in the rest of the paper, we typically assume that the graph is binary, our method is in principle generalizable to a weighted graph where represents the weighted edge set. In this case, we denote weighted incidence matrix as where is a diagonal matrix with entry corresponding to the weight of the edge. We note that scaling with does not change the projection onto the row space of , thus preserving our theoretical results. Without loss of generality, we work with an unweighted incidence matrix .
Remark 4.
The penalty is known as the total-variation penalty in the computer vision literature. As noted in Hütter & Rigollet (2016), this type of penalty is usually a good idea whenever the rows of take similar values, or may at least be well approximated by piecewise-constant functions. In the implementation of our algorithm, we employ the solver of developed by Sun et al. (2021), as it is the most efficient algorithm available for this type of problem.
Initialization.
The success of the procedure heavily depends on having access to good initial values for . Since, as highlighted in Remark 2, this manuscript assumes a “low-” regime, we propose to simply take the rank- eigendecomposition of the matrix to obtain an initial estimate :
| (11) |
where is a diagonal matrix where each entry is defined as: and where denotes the matrix of leading eigenvectors of .
Theorem 1.
The proof of the theorem is provided in Section B of the Appendix.
3 Theoretical results
In this section, we provide high-probability bounds on the Frobenius norm of the errors for and . We begin by characterizing the effect of the denoising on the estimates of the singular values of , before showing how the improved estimation of the singular vectors translates into improved error bounds for both and .
3.1 Denoising the singular vectors
The improvement in the estimation of the singular vectors induced by our iterative denoising procedure is characterized in the following theorem.
Theorem 2.
The proof of this result is provided in Section C of the Appendix.
Remark 5.
This result is to be compared against the rates of the estimates obtained without any regularization. In this case, the results of Klopp et al. (2021) show that with probability at least , the error in (13) is of the order of . Both rates thus share a factor . However, the spatial regularization in our setting allows us to introduce an additional factor of the order of . The numerator in this expression can be interpreted as the effective degrees of freedom of the graph, and for disconnected graphs (), the results are identical. However, for other graph topologies (e.g. the 2D grid, for which is bounded by a constant, (see Hütter & Rigollet (2016)) and ), our estimator can considerably improve the estimation of the singular vectors (see Section 3.3).
3.2 Estimation of and
We now show how our denoised singular vectors can be used to improve the estimation of the mixture matrix
Theorem 3.
Let Assumptions 1 to 5 hold. Let , and be given as (3)-(5). Assume and . Let denote the estimator of the mixture matrix (Equation 2) obtained by running the SPA algorithm on the denoised estimates of the singular vectors (Algorithm 1). If satisfies the condition stated in (12), then there exists a constant such that with probability at least ,
| (14) |
where denotes the set of all permutations.
Theorem 3 shows that is highly accurate as long as the document lengths are large enough, as defined by . This requirement is more relaxed than the condition for pLSI provisioned in Theorem 1 and Corollary 1 of Klopp et al. (2021). This indicates that GpLSI can produce accurate estimates even for smaller , by sharing information among neighboring documents. The shrinkage of error due to graph-alignment is characterized by the term , which is equal to one when the graph is empty. In general, the effect of the regularization depends on the graph topology. Hütter & Rigollet (2016) show in fact that the inverse scaling factor verifies: . The quantity , also known as the algebraic connectivity, provides insights into the properties of the graph, such as its connectivity. Intuitively, higher values of reflect more tightly connected graphs (Chung 1997), thereby reducing the effective degrees of freedom induced by the graph-total variation penalty. By contrast, can be coarsely bounded using the maximum degree of the graph: (Anderson Jr & Morley 1985, Zhang 2011). Consequently, we can expect our procedure to work well on well-connected graphs with bounded degree. Examples include for instance grid-graphs, -nearest neighbor graphs, or spatial (or planar) graphs. We provide a more detailed discussion and more explicit bounds for specific graph topologies in Section 3.3.
Furthermore, using the inequality , it immediately follows that:
Corollary 1.
Finally, we characterize the error bound of . The full proofs of Theorems 3 and 4 are deferred to Section D of the Appendix.
Theorem 4.
Remark 6.
The previous error bound of indicates that the accuracy of primarily relies on the accuracy of , which is to be expected, since is estimated by regressing on the estimator . While the error rate may not achieve the minimax-optimal rate derived in Ke & Wang (2017), we found that this procedure is more accurate than the estimator proposed in Klopp et al. (2021), as confirmed by synthetic experiments in Section 3.4.
3.3 Refinements for special graph structures
We now analyze the behavior of the error bound provided in Theorem 3 for different graph structures, further expliciting the dependency of our bounds on graph properties.
Erdös-Rényi random graphs.
We first assume that the graph is an Erdös-Rényi random graph where each pair of nodes is connected with probability for a constant . In this case, Hütter & Rigollet (2016) show that with high probability, the algebraic connectivity is of order . Moreover, the maximal degree is of order and the graph is almost surely connected (Van Der Hofstad 2024). Under this setting, the error associated to our estimator becomes:
| (17) |
Grid graphs.
We also derive error bounds for grid graphs, which are commonly occurrences in the analysis of spatial data and for applications in image processing:
- 2D grid graph:
-
Let be a 2D grid graph on vertices. Hütter & Rigollet (2016) show that, in that case, the inverse scaling factor is such that . The error of our estimator thus becomes:
(18) - -grid graph, :
-
In this case, Hütter & Rigollet (2016) show that the inverse scaling factor is bounded by a constant , that depends on the dimension but is independent of . In this case, the error of our estimator becomes:
(19)
3.4 Synthetic Experiments
We evaluate the performance of our method using synthetic datasets where is aligned with respect to a known graph.
Experimental Protocol
To generate documents, we sample points uniformly on unit square , and cluster them into groups using a simple k-means algorithm. For each group, we generate the topic mixture as where (). Small random noise is added to for each document in the group, and we permute it so that the biggest element of is assigned to the group’s predominant topic. is generated by sampling each entry from a uniform distribution, normalizing each row to ensure that is a stochastic matrix. A detailed description of the data generating process is provided in Section F of the Appendix.

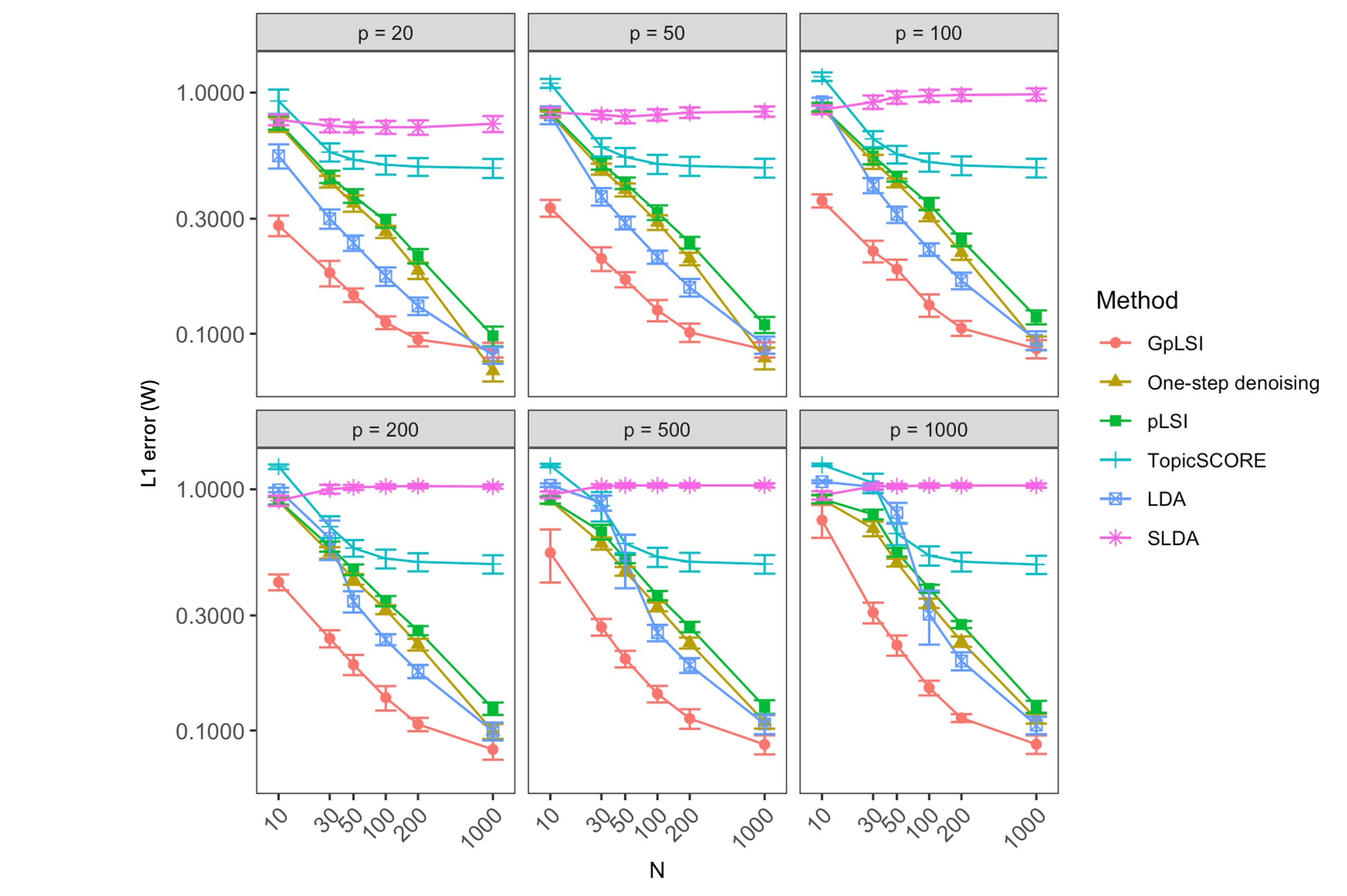
To assess the performance of GpLSI, we compare it against several established methods, including the original pLSI algorithm proposed by Klopp et al. (2021), TopicSCORE (Ke & Wang 2017), LDA (Blei et al. 2001), and the Spatial LDA (SLDA) approach of Chen et al. (2020). In addition, to highlight the efficiency of our iterative algorithm, we present results from a baseline variant that employs only a single denoising step. This one-step method is described in greater detail in Section C of the Appendix. To implement these algorithms, we use the R package TopicScore and the LDA implementation of the Python library sklearn. For SLDA, we use of the Python package spatial-lda with the default settings of the algorithm. We run 50 simulations and record the error, error of and , and the computation time across various parameter settings , reporting medians and interquartile ranges. To evaluate the performance of methods in difficult scenarios where document length is small compared to vocabulary size , we check the errors for different combinations of and .
Results
Figure 1 demonstrates that GpLSI achieves the lowest error for , even in scenarios with very small . This shows that sharing information across similar documents on a graph improves the estimation of topic mixture matrix. Notably, while LDA and pLSI exhibit modest performance, they fail in regimes where and . We also confirm that the one-step denoising variant of our method achieves a lower error estimation error than pLSI and LDA in settings where .

We also examine how the estimation errors scale with the corpus size and the number of topics , as shown in Figure 2. We observe that GpLSI substantially outperforms other methods, particularly for the estimation of . GpLSI achieves the lowest error for , as we show in Section F of the Appendix. Similar patterns hold for errors of and also provided in Section F of the Appendix.
4 Real-World Experiments
To highlight the applicability of our method, we deploy it on three real-life examples. All the code for the experiments is openly accessible at https://github.com/yeojin-jung/GpLSI.
4.1 Tumor Microenvironment discovery: the Stanford Colorectal Cancer dataset
We first consider the analysis of CODEX data, which allows the identification of individual cells in tissue samples, holding valuable insights into cell interaction profiles, particularly in cancer, where these interactions are crucial for immune response. Since cellular interactions are hypothesized to be local, these patterns are often referred to as “tumor microenvironments”. In the context of topic modeling, we can regard a tumor microenvironment as a document, immune cell types as words, and latent characteristics of a microenvironment as a topic. However, due to the small number of words per document, the recovery of the topic mixture matrix and the topics themselves can prove challenging. Chen et al. (2020) propose using the adjacency of documents to assign similar topic proportions to neighboring tumor cells. Similarly, we construct a spatial graph based on proximity of tumor microenvironments to uncover novel tumor-immune cell interaction patterns.
The first CODEX dataset is a collection of 292 tissue samples from 161 colorectal cancer patients collected at Stanford University (Wu et al. 2022). The locations of the cells were retrieved using a Voronoi partitioning of the sample, and the corresponding spatial graphs were constructed encoding the distance between microenvironments. More specifically, we define a tumor microenvironment as the 3-hop neighborhood of each cell, following the definition originally used by Wu et al. (2022). Each microenvironment contains 10 to 30 immune cells of 8 possible types. This aligns with the setting where the document length is small compared to the vocabulary size .

We aggregate frequency matrices and tumor cellular graphs of all samples and fit three methods: our proposed GpLSI, the original pLSI approach of Klopp et al. (2021), and LDA (Blei et al. 2001) to estimate tumor-immune topics. The estimated topic weights of are illustrated in Figure 3(A). After aligning topic weights across methods, we observe similar immune topics (Topic 1, 2, 3) in GpLSI and LDA which are not found in the estimated topics of pLSI.
To determine the optimal number of topics , we use the method proposed by Fukuyama et al. (2023). In this work, the authors construct “topic paths” to track how individual topics evolve, split or merge, as the number of topics , increases. We observe in Figure 3(B) that while the GpLSI path has non-overlapping topics up to , other methods fail to provide consistent and well-separated topics.
To evaluate the quality and stability of the recovered topics, we also measure the coherence of the estimated topic weights of batches of samples, as suggested in Tran et al. (2023). We divide 292 samples into five batches and estimate the topic weights for . For every pair of batches , we align and (we permute with where ) and measure the entry-wise distance and cosine similarity. We repeat this procedure five times and plot the scores in Figure 3(C). We notice that GpLSI provides the most coherent topics across batches for . Combining with the metrics of LDA, we can choose the optimal as 5 or 6.

Next, we conduct survival analysis to identify the immune topics associated with higher risk of cancer recurrence. We consider two logistic models with different covariates to predict cancer recurrence and calculate the area under the curve (AUC) of the receiver-operating characteristic (ROC) curves to evaluate model performance.
In the first model, we use the proportion of each microenvironment topic as covariates for each sample. Since the covariates sum up to one, we apply isometric log-ratio transformation to represent it with orthonormal basis vectors In the second model, we dichotomize each topic proportion to low and high proportion groups. The cutoffs are determined using the maximally selected rank statistics.
The AUC for each number of topics is shown in Figure 4(A). GpLSI achieves the highest area under the curve (AUC) at in both models. We also plot Kaplan Meier curves for each topic using the same dichotomized topic proportions. The result for GpLSI is illustrated in Figure 4(B). We observe that Topic 2, which is characterized by a high prevalence of granulocytes, and Topic 6, a mixture of CD4 T cells and blood vessels, are associated with lower cancer recurrence. Positive effect of granulocytes on cancer prognosis was also reported by Wu et al. (2022), who found out that a microenvironment with clustered granulocyte and tumor cells is associated with better patient outcomes. We observe the same association of granulocyte with lower risk in LDA Figure 16 of the Appendix.
4.2 Understanding Structure in Mouse Spleen Samples

We also apply our method to identify immune topics in mouse spleen. In this setting, each document is anchored to a B cell (Chen et al. 2020). A previous study has processed the original CODEX images from Goltsev et al. (2018) to obtain the frequencies of non-B cells in the 100 pixel neighborhood of each B cell (Chen et al. 2020). The final input for the topic models consists of a 35,271 B cell microenvironments by 24 cell types frequency matrix, along with the positional data of B cells.
In this example, we evaluate GpLSI by examining whether the introduction of our graph-based regularization term in the estimation of topic mixture matrices enhances document clustering. Figure 5(A) presents the estimated topics for all models at . Notably, the topics derived from GpLSI, pLSI, and LDA more clearly demarcate distinct B cell microenvironment domains compared to those estimated by TopicSCORE and LDA. Among these three methods, GpLSI yields the least noisy cellular clustering, as evidenced by the magnified view of a selected subdomain.
We also evaluate the quality of clusters with two metrics, Moran’s I and the percentage of abnormal spots (PAS) (Shang & Zhou 2022). Moran’s I is a classical measure of spatial autocorrelation that assesses the degree to how values are clustered or dispersed across a spatial domain. PAS score measures the percentage of B cells for which more than 60% of its neighboring B cells have different topics. Higher Moran’s I and lower PAS score indicate more spatial smoothness of the estimated topics. From Figure 5(B), we conclude that GpLSI has the highest Moran I, and the lowest PAS scores, demonstrating improved spatial smoothness of the topics.
We observe that the B cell microenvironment topics identified with GpLSI align well with their biological context (Figure 5(C)). By referencing the manual annotations of B cells from the original study by Goltsev et al. (2018), we infer that Topic 1, Topic 2, Topic 3, and Topic 5 correspond to the red pulp, periarteriolar lymphoid sheath (PALS), B-follicles, and the marginal zone. This interpretation is further supported by high expression of CD4+T cells in Topic 2 (PALS) and high expression of marginal zone macrophages in Topic 5 (marginal zone).
4.3 Analysis of the “What’s Cooking” dataset
This dataset contains recipes from 20 different cuisines across Europe, Asia, and South America. Each recipe is a list of ingredients which allow us to convert to a count matrix with 13,597 recipes (documents) and 1,019 unique ingredients (words). Under the assumption that neighboring countries would have similar cuisine styles, we construct a graph of recipes based on the geographical proximity of the countries. Specifically, for each recipe, we select the five closest recipes from neighboring countries (including its own country) based on the distance of the ingredient count vectors and define them as neighboring nodes on the graph. Through this, we aim to identify general cooking styles that are prevalent across various countries worldwide.

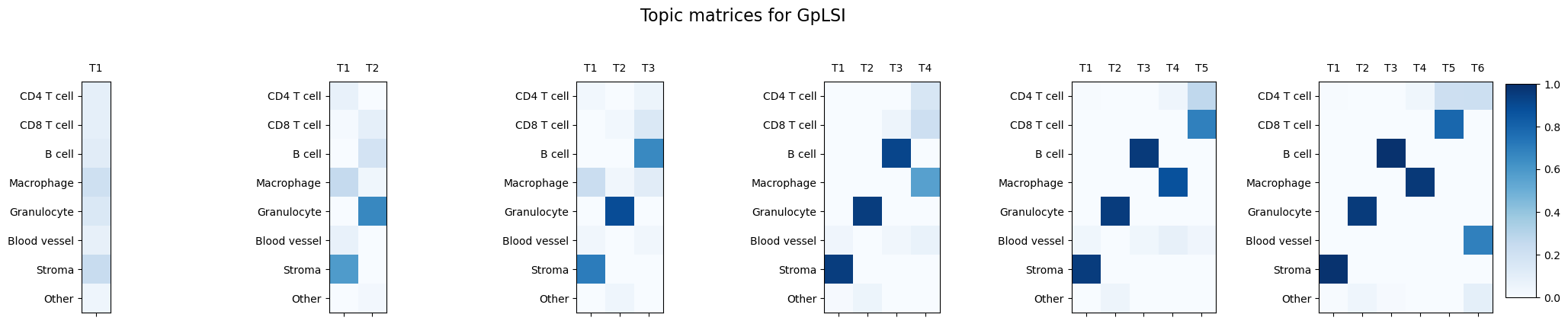
We run GpLSI, pLSI, and LDA with topics. We illustrate the estimated topics of GpLSI for in Figure 6. The results for pLSI and LDA are provided in Section G of the Appendix. With this approach, Topic 1 is clearly a baking topic and Topic 6 is defined by strong spices and sauces common in Mexican or parts of Southeast Asian cuisines. We also observe a general topic for Asian cuisines (Topic 2) and another for Western countries (Topic 7). To evaluate the estimated topics, we compare each topic’s characteristics with the cuisine-by-topic proportion (Figure 6(C)). Indeed, the style of each topic defined by the anchor ingredients aligns with the cuisines that have a high proportion of that topic. For example, the baking topic (Topic 1) is prevalent in British, Irish, French, Russian, and South American cuisines.
In contrast, for pLSI, it is difficult to analyze the characteristics for each topic because Topics 1-4 have one or no identified anchor ingredients. Comparing the cuisine-by-topic proportions of GpLSI and LDA, we observe that GpLSI reveals many cuisines as mixtures of different cooking styles (Figure 6(B)). In contrast, for LDA, many cuisines such as Moroccan, Mexican, Korean, Chinese, Thai have their recipes predominantly classified to a single topic (Figure 18(B) of the Appendix). GpLSI provides estimates of topic mixture and topic weights that are more relevant to our goal of discovering global cooking styles.
5 Conclusion
In this paper, we present Graph-Aligned pLSI (GpLSI), a topic model that leverages document-level metadata to improve estimation of the topic mixture matrix. We incorporate metadata by translating it into document similarity, which is then represented as edges connecting two documents on a graph. GpLSI is a powerful tool that integrates two complementary sources of information: word frequencies that traditional topic models use, and the document graph induced from metadata, which encodes which documents should share similar topic mixture proportions. To the best of our knowledge, this is the first framework to incorporate document-level metadata into topic models with theoretical guarantees.
At the core of GpLSI is an iterative graph-aligned singular value decomposition applied to the observed document-word matrix . This procedure projects word frequencies to low-dimensional topic spaces, while ensuring that neighboring documents on the graph share similar topic mixtures. Our SVD approach can also be applied to other works that require dimension reduction with structural constraints on the samples. Additionally, we propose a novel cross validation technique to optimize the level of graph regularization by using the hierarchy of minimum spanning trees to define folds.
Our theoretical analysis and synthetic experiments confirm that GpLSI outperforms existing methods, particularly in “short-document” cases, where the scarcity of words is mitigated by smoothing mixture proportions along neighboring documents. Overall, GpLSI is a fast, highly effective topic model when there is a known structure in the relationship of documents.
We believe that our work offers valuable insights into structural topic models and opens up several avenues for further exploration. A promising direction is to incorporate structure to the topic matrix while jointly optimizing structural constraints on . While our work focuses on low- regime, real world applications, such as genomics data with large , could benefit from introducing sparsity to the word composition of each topic.
Appendix for “Graph Topic Modeling for Documents with Spatial or Covariate Dependencies”
Yeo Jin Jung and Claire Donnat
Department of Statistics, The University of Chicago
Appendix A Optimizing graph regularization parameter
In this section, we propose a novel graph cross-validation method which effectively finds the optimal graph regularization parameter by partitioning nodes into folds based on a natural hierarchy derived from a minimum spanning tree. The procedure is summarized in the following algorithm.
Conventional cross validation techniques sample either nodes or edges to divide the dataset into folds. However, these approaches can disrupt the graph structure and underestimate the strength of the connectivity of the graph. We instead devise a new rule for dividing documents into folds using a minimum spanning tree. This technique is an extension of the cross-validation procedure proposed by Tibshirani & Taylor (2012) for the line graph. Given a minimum spanning tree of , we randomly choose a source document . For each document , we calculate the shortest path distance . Note that this distance is always an integer. We divide the documents into folds based on the modulus of their distance from the source node: . Through this construction of folds, we can ensure that for every document, at least one of its 1-hop neighbors is in a different fold.
Let be the row of . For each leave-out fold , , we interpolate the corresponding documents , filling the missing document information with the average of corresponding neighbors in . This prevents us from using any information from the leave-out fold in training when calculating the cross-validation error.

Figure 7 demonstrates how GpLSI leverages the graph information. As increases, GpLSI chooses smaller graph regularization parameter , since the need to share information across neighbors diminishes as documents become longer and more informative. Additionally, when is more heterogeneous over the graph—meaning neighboring documents exhibit more heterogeneous topic mixture weights—the error of increases. Here, graph heterogeneity is characterized by our simulation parameter (the number of patches that we create). As increases, the unit square is divided into finer patches, and the generated documents within the same topic become more dispersed. Our result indicates that GpLSI works well in settings where the mixture weights are smoother over the document graph and the performance of GpLSI and pLSI become similar as neighboring documents become more heterogeneous.
Appendix B Analysis of the initialization step
In this section, we show that the initialization step of GpLSI provides reasonable estimators of and .
Proof of Theorem 1
Proof.
Let denote the diagonal matrix where each entry is defined as: Let denote its empirical counterpart, that is, the diagonal matrix defined as: , so that . We have, by definition of the initialization procedure:
where the notation denotes the first left singular vectors of the matrix .
We write , where denotes some multinomial noise. E We have:
| (20) |
as is a centered version of (). Since each row is distributed as a Multinomial:
Thus:
| (21) |
Therefore:
| (22) |
Thus We further note that with so the eigenvectors of the matrix can be considered as estimators of those of the matrix
By the Davis-Kahan theorem (Giraud 2021):
| (23) |
The condition on assumed in Theorem 2 ensures that . ∎
Appendix C Analysis of iterative graph-aligned denoising
Our proof is organized along the following outline:
-
1.
We begin by showing that our graph-total variation penalty yields better estimates of the left and right singular vectors. To this end, we must show that, provided that the initialization is good enough, the estimation error of the singular vectors decreases with the number of iterations.
-
2.
We show that, by a simple readaptation of the proof by Klopp et al. (2021), our estimator—which simply plugs in our singular vector estimates in their procedure —yields a better estimate of the mixture matrix .
-
3.
Finally, we show that our estimator of the topic matrix yields better error.
C.1 Analysis of the graph-regularized SVD procedure
In this section, we derive high-probability error bounds for the estimates and that we obtain in Algorithm 1. For each , we define the error at iteration as:
| (24) |
Our proof operates by recursion. We explicit the dependency of on the error at the previous iteration , and show that forms a geometric series. To this end, we begin by analyzing the error of the denoised matrix , of which we later take an SVD to extract .
At each iteration , the first step of Algorithm 1 is to consider the following optimization problem:
| (25) |
Fix . To simplify notations, we let
| (26) |
Note that with these notations, can be written as:
| (27) |
Lemma 1 (Error bound of Graph-aligned Denoising).
Proof.
By the KKT conditions, the solution of (25) verifies :
This implies:
Therefore:
Using the polarization inequality:
and, choosing
Let . By the triangle inequality, the right-most term in the above inequality can be rewritten as:
since by assumption,
We turn to the control of the error term . Using the decomposition of induced by the projection as , we have:
| (29) |
Bound on (A) in Equation (29)
By Cauchy-Schwarz:
By Lemma 16, with probability at least :
Bound on (B) in Equation (29).
Thus, on the event , we have:
To derive , we first establish the relationship between and ,
Then,
where we used the fact . From Lemma 13, for a choice of , then .
Therefore:
| (30) |
and thus:
The result follows by noting that the Laplacian of the graph is linked to by . ∎
Proof of Theorem 2
Proof.
Recall , the error at each iteration :
| (31) |
Bound on .
We start by deriving a bound for . Let denote the orthogonal complement of so that:
Noting that is the matrix corresponding to the top left singular vectors of the matrix by Theorem 1 of Cai & Zhang (2018) (which we rewrote in Lemma 8 of this manuscript to make it self-contained):
where the second line follows from noting that
Since is a diagonal matrix, we have:
Thus, by Weyl’s inequality:
where By Lemma 1, we know that:
with and Thus:
where the last line follows by assuming that (we will show that this indeed holds). By using a first-order Taylor expansion around for the function for , we obtain:
Therefore, seeing that we have and letting and , we have:
By Assumption 4, we have . Therefore, as soon as:
| (32) |
which is satisfied under the condition (12) of in Theorem 2. Thus, in this setting:
| (33) |
and
Also given that ,
Bound on
By definition of the second step:
We have:
Thus, assuming that :
Furthermore:
where the last inequality follows by noting that and from Lemma 15, which show that with probability at least :
and since :
Therefore, using the same arguments as in the previous paragraph, using and , we have:
Therefore, we have , and letting and ,
when decreases with each iteration. Again, we note that as soon as:
| (34) |
which is satisfied under the condition (12) of in Theorem 2. Then we can show that,
| (35) |
and
Also given that ,
and
Therefore, for all ,
Behavior of
is a decreasing function of for , and by Theorem 1, (We later show in (49)). From the previous sections,
Thus,
| (36) |
where
where In particular, we want to find such that becomes small enough to satisfy . Using (as previously shown) and that ,
Combining with the previous inequality (and since ) and the fact that under Assumption 4, we have , we can choose as,
Thus, it is sufficient to choose as,
| (37) |
∎
C.2 Comparison with One-step Graph-Aligned denoising
We also propose a fast one-step graph-aligned denoising of the matrix that could be an alternative of the iterative graph-aligned SVD in Step 1 of Section 2.3 of the main manuscript. We denoise the frequency matrix by the following optimization problem,
| (39) |
A SVD on the denoised matrix yields estimates of the singular values and . Through extensive experiments with synthetic data, we find that one-step graph-aligned denoising provides more accurate estimates than pLSI but still falls short compared to the iterative graph-aligned denoising (GpLSI). We provide a theoretical upper bound on its error as well as its comparison to the error of pLSI where there is no graph-aligned denoising.
We begin by analyzing the one-step graph-aligned denoising, as proposed in Algorithm 3. We begin by reminding the reader that, in our proposed setting, the observed word frequencies in each document are assumed to follow a “signal + noise” model, where the true probability is assumed to admit the following SVD decomposition:
Theorem 5.
Let the conditions of Theorem 3 hold. Let and be given as estimators obtained from Algorithm 3. Then, there exists a constant , such that with probability at least ,
| (40) |
Proof.
Let be the solution of (39):
Let , and . By the basic inequality, we have:
| (41) |
where and in the penultimate line, we have used the decomposition of on the two orthogonal subspaces: so that:
We proceed by characterizing the behavior of each of the terms (A) and (B) in the final line of (41) separately.
Concentration of (A).
By Cauchy-Schwarz, it is immediate to see that:
By Lemma 14, with probability at least :
Concentration of (B).
Then, on , we have:
| (42) |
Concentration
We thus have:
Then by applying Wedin’s sin theorem (Wedin 1972),
The derivation for is symmetric, which leads us to the final bound,
This concludes our proof. ∎
We observe first that the error bound for one-step graph-aligned denoising has better rate than the one with no regularization, , provided in Klopp et al. (2021). We also note that the rate of one-step denoising and GpLSI is equivalent up to a constant. Although the dependency of the error on parameters and is the same for both methods, our empirical studies in Section 3 reveal that GpLSI still achieves lower errors compared to one-step denoising.
Appendix D Analysis of the Estimation of and
In this section, we adapt the proof of Klopp et al. (2021) that derives a high probability bound for the outcome after successive projections. We evaluate the vertices detected by SPA with the rows of as the input. To accomplish this, we first need to bound the row-wise error of which is closely related to the upper bound of the estimated vertices and ultimately, is linked to .
To apply Theorem 1 of Gillis & Vavasis (2015) on the estimation with SPA, we need to show that the error on each of the row of the estimated left singular vector of is controlled, which requires us bounding the error: .
Lemma 2 (Baseline two-to-infinity norm bound (Theorem 3.7 of Cape et al. (2019)).
For , denote as the observed matrix that adds perturbation to unobserved . For and , their respective singular value decompositions of are given as
where contain the top singular values of , while contain the remaining singular values. Provided and , then,
| (43) |
where is the solution of .
Proof.
The proof is given in Section 6 of Cape et al. (2019). ∎
Adapting Lemma 2 to our setting, we set and . We also use the notation to denote the oracle, We set and denote the s of and :
Note that we are performing a rank decomposition, so in the previous SVD, , by which (2) becomes,
with We thus need to bound the quantity,
The second term (B) is 0 because . For the first term (A), we note that stems from the SVD of , which is itself the solution of:
where . By the KKT conditions, for any ,
where denotes the subgradient of so that and if and if
Therefore:
| (44) |
Using the derivation of the geometric series of errors in (36), recall
and expressing in terms of and ,
D.1 Deterministic Bounds
First, denote as:
| (46) |
which is the upper bound on the maximum row error, by (D). We need the following assumption on .
Assumption 6.
For a constant , we have
We will show in (50) that this assumption holds in fact with high probability. Similar to Klopp et al. (2021), the proof of the consistency of our estimator relies on the following result from Gillis & Vavasis (2015).
Lemma 3 (Robustness of SPA (Theorem 1 of Gillis & Vavasis (2015)).
Let where is non degenerate, and is such that the sum of the entries of each row of is at most one. Let denote a perturbed version of , with , with:
Then, if is such that:
| (47) |
for some small constant , then SPA identifies the rows of up to error , that is, the index set of vertices identified by SPA verifies:
The notation is the condition number of and denotes the set of all permutations of the set .
Lemma 4 (Adapted from Corollary 5 of Klopp et al. (2021)).
Let Assumptions 1 to 6 hold. Assume that is a rank- matrix. Let be the left singular vectors corresponding to the top singular values of and its perturbed matrix , respectively. Let be the set of indices returned by the SPA with input , and . Let be the same matrix as in (13) of the main manuscript. Then, for a small enough , there exists a constant and a permutation such that,
| (48) |
where is defined as (46).
Proof.
The proof here is a direct combination of Lemma 3 and Corollary 5 of Klopp et al. (2021), for SPA (rather than pre-conditioned SPA). The crux of the argument consists of applying Theorem 1 in (Gillis & Vavasis 2015) (rewritten in a format more amenable to our setting in Lemma 3) which bounds the error of SPA in the near-separable nonnegative matrix factorization setting,
where and is the noise matrix. Note that the rows of lie on a simplex with vertices and weights . We apply Lemma 3 with , and .
Under Assumption 4,6 and Lemma 7, the error satisfies:
for a small enough . Thus the condition on the noise (Equation (47)) in Theorem 3 is met. Noting that and , with the permutation matrix corresponding to , we get
∎
We then readapt the proof of Lemma 2 from Klopp et al. (2021) with our new .
Proof of Theorem 3
We are now ready to prove our main result.
Proof.
We first show that the initialization error in Theorem 1 is upper bounded by . Combining Assumption 4 and Lemma 7, we have
Then using the condition on (Equation 12), in Theorem 2,
| (49) |
Next from the condition on in Theorem 3 (Equation (46)), and Assumption 4,
| (50) |
which proves Assumption 6. Thus, we are ready to use Theorem 2 and Lemma 5. We can now plug in , the result of Equation (46) and the error bound of graph-regularized SVD (Equation (13) in Theorem 2) in the upper bound of formulated in Lemma 5.
Here, we used the bounds on condition numbers in Assumption 4.
∎
Proof of Theorem 4
Using the result of Theorem 3, we now proceed to bound the error of .
Proof.
By the simple basic inequality, letting , we get
which leads us to,
Plugging the upper bound on which we prove below,
where in (*) we have used Weyl’s inequality to conclude,
Also, assume that is large enough so that the condition on in Theorem 2 holds. Combining Lemma 7 and Theorem 3, becomes small enough so that . Thus, for .
By definition, represents some centered multinomial noise, with each entry being independent. Similar to proof of Lemma 15, can be represented as a sum of centered variables:
We have:
since and thus:
Moreover, for each ,
Thus, by Bernstein’s inequality (Lemma 9 with and :
| (51) |
Choosing :
| (52) |
Thus, with probability at least ,
Lastly, we use the fact, to get the final bound of ,
.
where the error is controlled by the first term, . ∎
Appendix E Auxiliary Lemmas
Let matrices be defined as (2) in the main manuscript. In this section, we provide inequalities on the singular values of the unobserved quantities , perturbation bounds for singular spaces, as well as concentration bounds on noise terms, which are useful for proving our main results in Section 3.
E.1 Inequalities on Unobserved Quantities
Lemma 6.
For the matrix , the following inequalities hold:
Proof.
We observe that for each , the variational characterization of the smallest eigenvalue of the matrix yields:
since
Similarly:
∎
We also add the following lemma from Klopp et al. (2021) to make this manuscript self-contained.
Lemma 7 (Lemma 6 from the supplemental material of Klopp et al. (2021)).
Let Assumption 2 be satisfied. For the matrices , , defined in (6) and (7) of the main manuscript, we have
| (53) |
and
| (54) |
E.2 Matrix Perturbation Bounds
In this section, we provide rate-optimal bounds for the left and right singular subspaces. While the original Wedin’s perturbation bound (Wedin 1972) treats the singular subspaces symmetrically, work by Cai & Zhang (2018) provides sharper bounds for each subspace individually. This refinement is particularly relevant in our setting where an additional denoising step of the left singular subspace leads to different perturbation behaviors of left and right singular subspaces as iterations progress.
Consider the SVD of an approximately rank- matrix ,
| (55) |
where , , , and .
Let be a perturbed version of with denoting a perturbation matrix. We can write the SVD of as:
| (56) |
where , , , have the same structures as , , , . We can decompose into two parts,
| (57) |
Lemma 8 (Adapted from Theorem 1 of Cai & Zhang (2018)).
Proof.
This result is a simplified version of the original theorem under the setting . ∎
E.3 Concentration Bounds
We first introduce the general Bernstein inequality and its variant which will be used for proving high probability bounds for noise terms in Section E.3.2.
E.3.1 General Inequalities
Lemma 9 (Bernstein inequality (Corollary 2.11, Boucheron et al. (2013))).
Let be independent random variables such that there exists positive numbers and such that and
| (60) |
for all integers . Then for any ,
A special case of the previous lemma occurs when all variables are bounded by a constant , by taking and .
Lemma 10 (Bernstein inequality for bounded variables (Theorem 2.8.4, Vershynin (2018))).
Let be independent random variables with , and for all . Let . Then for any ,
E.3.2 Technical Lemmas
Lemma 11 (Concentration of the cross-terms ).
Let Assumptions 1-5 hold. With probability at least :
| (61) |
| (62) |
where .
Proof.
The proof is a re-adaptation of Lemma C.4 in Tran et al. (2023) for any word .
Similar to the analysis of Ke & Wang (2017), we rewrite each row as a sum over word entries , where denotes the word in document , encoded as a one-hot vector:
| (63) |
where the notation denotes the entry of the vector . Under this formalism, we rewrite each row of as:
In the previous expression, under the pLSI model, the are i.i.d. samples from a multinomial distribution with parameter .
We can also express each entry as:
| (64) |
Denote .
Fix . The are all independent of one another (for all and ) and . By (64), we note that
where we define
| (65) |
| (66) |
We note that the random variable is centered (), and we need an upper bound with high probability on and . We deal with each of these variables separately.
Upper bound on
We remind the reader that we have fixed . Define as the set of permutations on and . Also define
Then by symmetry (note that the inner sum over in the definition of has summands),
Define, for a given ,
so that . For arbitrary , by Markov’s inequality and the convexity of the exponential function,
Also, define for the identity permutation. Observe that
so is a (double) summation of mutually independent variables. We have , and where . The rest of the proof for is similar to the standard proof for the usual Bernstein’s inequality.
Denote , is increasing as a function of . Hence,
Hence,
Since this bound is applicable to all and not just the identity permutation, we have
Now we choose . Then
where we define the function . Note that we have the inequality
for all . Hence,
or by rescaling,
| (67) |
We can choose and note that by Assumption 5. Hence, with probability ,
By a simple union bound, we note that:
| (68) |
where the last line follows by Assumption 5 (which implies that is small), noting that for some large enough constant such that , . Thus, for large enough, for any , with probability :
Upper bound on
As for , we can just apply the usual Bernstein’s inequality. We remind the reader that ; we further note that . Since ,
| (69) |
- Case 1: If :
- Case 2: If
∎
Lemma 12 (Concentration of the covariance matrix ).
Let Assumptions 1-5 hold. With probability , the following statements hold true:
Proof.
Let .
Concentration of
Concentration of .
For a fixed we have
Note that since , and
| (71) |
(and also ). We apply Bernstein’s inequality to conclude for any :
Choosing . Since (Assumption 5), we obtain that with probability at least ,
Taking a union bound over , we obtain that:
since we assume that . Therefore, with probability at least :
and since :
Concentration of .
Lemma 13 (Concentration of ).
Let Assumptions 1-5 hold. With probability at least , for all edges :
| (72) |
| (73) |
where .
Proof.
Fix and define as in (63). Decomposing each as , we note that the product can be written as a sum of independent terms:
with .
-
1.
Each verifies Bernstein’s condition (60): We have:
We note that: .
Therefore, if for , and:
where the last line follows by noting that so .
For odd (, we note that:
-
2.
Each of the variance is also bounded:
Thus:
Therefore, by Assumption 5, then, with probability at least , .
Therefore, by a simple union bound and following the argument in (68):
since we assume that . Writing , we thus have:
| (74) |
where the last line follows by noting that
Finally, to show that this holds for any , it suffices to apply a simple union bound:
| (75) |
with . Therefore, for a choice of sufficiently large. ∎
Lemma 14 (Concentration of ).
Let Assumptions 1-5 hold. With probability at least :
| (76) |
Proof.
We remind the reader that letting denote the connected component of the graph and its cardinality, can be arranged in a block diagonal form where each block represents a connected component, . Since the components are all disjoint, can be further decomposed as:
By Assumption 3, . Following Equation (63), we rewrite each row of as:
In the previous expression, under the pLSI model, the are i.i.d. samples from a multinomial distribution with parameter . Thus, for each word and each connected component :
Fixing and denoting , we note that the are independent of one another (for all and ), and since , Define . Then,
Therefore, by the Bernstein inequality (Lemma 10), for the connected component of the graph and for any word :
Choosing , the previous inequality becomes:
as long as (which follows from Assumption 5 since ). Therefore, by a simple union bound:
As a consequence of Assumption 5, we know that (see Remark 2) and under the graph-aligned setting, . Thus with probability , for all and all :
where the last equality follows from the fact that Therefore:
∎
Lemma 15 (Concentration of ).
Let Assumptions 1-5 hold. Let denote a projection matrix: , with a term that does not grow with or and , and let denote some centered multinomial noise as in . Then with probability at least :
| (77) |
Proof.
Let We have:
| (78) |
We first note that
| (79) | ||||
| (80) | ||||
| (81) |
Thus, is a sum of centered independent variables.
Fix . We have: where , since . Therefore, as :
Moreover, for each , Thus, by Bernstein’s inequality (Lemma 9, with and ):
Choosing :
Therefore, by Assumption 5, , then, with probability at least ,
Therefore, by a simple union bound:
| (82) |
Since we assume that , the result follows. ∎
Lemma 16 (Concentration of ).
Let Assumptions 1-5 hold. Let be a orthogonal matrix: . Let denote the projection matrix unto , such that . With probability at least :
| (83) |
where .
Proof.
We follow the same procedure as the proof of Lemma 14. Letting denote the connected component of the graph and its cardinality, can be decomposed as:
By Assumption 3, . Using the definition of provided in (63), for each , and each connected component :
Fix and denote . We have and
Therefore, by Bernstein’s inequality (Lemma 10), for the connected component of the graph and for any :
Choosing , the previous inequality becomes:
as long as . Therefore, by a simple union bound:
Thus with probability , for all and all :
and
∎
Lemma 17 (Concentration of and ).
Let Assumptions 1-5 hold. Let , with a projection matrix: , with a term that does not grow with or and . Then with probability at least :
| (84) |
Proof.
We first note that
Thus is a sum of centered independent variables.
Choosing :
Therefore, by Assumption 5, , then, with probability at least , By a simple union bound:
since . Also, since we assume that , the result follows.
Similarly, denote ,
Note that: with probability
Thus is a sum of centered independent variables.
Choosing :
Therefore, by Assumption 5, , then, with probability at least , By a simple union bound:
Since we assume that , the result follows. ∎
Appendix F Synthetic Experiments
We propose the following procedure for generating synthetic datasets such that the topic mixture matrix is aligned with respect to a known graph.
-
1.
Generate spatially coherent documents Generate points (documents) over a unit square . Divide the unit square into equally spaced grids and get the center for each grid. Apply k-means algorithm to the points with these as initial centers. This will divide the unit square into 30 different clusters. Next, randomly assign these clusters to different topics. In the end, within the same topic, we will observe some clusters of documents that are not necessarily next to each other (see Figure 8). This is a more challenging setting where the algorithm has to leverage between the spatial information and document-word frequencies to estimate the topic mixture matrix. Based on the coordinates of documents, construct a spatial graph where for each document, edges are set for the closest documents and weights as the inverse of the euclidean distance between two documents.
-
2.
Generate matrices and For each cluster, we generate a topic mixture weight where (). We order so that the biggest element of is assigned to the cluster’s dominant topic. We also add small Gaussian noise to so that in the end, for each document in the cluster, , . We sample rows of as anchor documents and set them as . The elements of are generated from and normalized so that each row of sums up to 1. Similarly to anchor documents, columns of are selected as anchor words and set to .
-
3.
Generate frequency matrix We obtain the ground truth and sample each row of from . Each row of is obtained by .
Figure 8 illustrates the ground truth mixture weights, , for each topic generated with parameters and . Here, each dot in the unit square represents a document, with lighter colors indicating higher mixture weights. We observe patches of documents that share similar topic mixture weights.




Next, we show the errors of estimated and under the same parameter settings as Section 3.4 of the main manuscript. From Figure 9-11, GpLSI achieves the lowest errors of and in all parameter settings, followed by LDA. For the estimation of , as highlighted in Remark 4, our rates and procedure is not optimal compared with existing results (see in particular Ke & Wang (2017), which achieves similar results to ours in Figure 2 in the main manuscript). However, compared to the procedure proposed by Klopp et al. (2021), the estimation error is considerably improved.
Appendix G Real data
In this section, we provide supplementary plots for our analysis on the real datasets discussed in Section 4 of the main manuscript.
G.1 Estimated tumor-immune microenvironment topic weights
We present the estimated tumor-immune microenvironment topics estimated with GpLSI, pLSI, and LDA for to . The topics are aligned among the methods as well as among different number of topics, . Topics dominated by stroma, granulocyte, and B cells, recur in both GpLSI and LDA.


G.2 Kaplan-Meier curves of Stanford Colorectal Cancer dataset
We plot Kaplan-Meier curves for tumor-immune micro-environment topics using the dichotomized topic proportion for each patient. We observe that granulocyte (Topic 2) is associated with lower risk of cancer recurrence across all methods.

G.3 Topics by top common ingredients in What’s Cooking dataset





We illustrate each topic with the top ten ingredients with the highest estimated weights (Figures 19-21) as well as anchor ingredients for pLSI and LDA (Figures 17-18). Compared to anchor ingredients, we observe that there are more overlapping ingredients among topics. While the top ten and anchor ingredients for each topic in GpLSI and LDA reflect similar styles, it is difficult to match anchor ingredients to the top ten ingredients in pLSI because the top ten ingredients are too similar across topics.
References
- (1)
- Anderson Jr & Morley (1985) Anderson Jr, W. N. & Morley, T. D. (1985), ‘Eigenvalues of the laplacian of a graph’, Linear and multilinear algebra 18(2), 141–145.
- Araújo et al. (2001) Araújo, M. C. U., Saldanha, T. C. B., Galvao, R. K. H., Yoneyama, T., Chame, H. C. & Visani, V. (2001), ‘The successive projections algorithm for variable selection in spectroscopic multicomponent analysis’, Chemometrics and intelligent laboratory systems 57(2), 65–73.
- Bing et al. (2020) Bing, X., Bunea, F. & Wegkamp, M. (2020), ‘Optimal estimation of sparse topic models’, Journal of machine learning research 21(177), 1–45.
- Blei & Lafferty (2006a) Blei, D. & Lafferty, J. (2006a), ‘Correlated topic models’, Advances in neural information processing systems 18, 147.
- Blei & Lafferty (2006b) Blei, D. M. & Lafferty, J. D. (2006b), Dynamic topic models, in ‘Proceedings of the 23rd international conference on Machine learning’, pp. 113–120.
- Blei et al. (2001) Blei, D., Ng, A. & Jordan, M. (2001), ‘Latent dirichlet allocation’, Advances in neural information processing systems 14.
- Boucheron et al. (2013) Boucheron, S., Lugosi, G. & Massart, P. (2013), ‘Concentration inequalities: A nonasymptotic theory of independence oxford, uk: Oxford univ’.
- Cai & Zhang (2018) Cai, T. T. & Zhang, A. (2018), ‘Rate-optimal perturbation bounds for singular subspaces with applications to high-dimensional statistics’.
- Cape et al. (2019) Cape, J., Tang, M. & Priebe, C. E. (2019), ‘The two-to-infinity norm and singular subspace geometry with applications to high-dimensional statistics’.
- Chen et al. (2020) Chen, Z., Soifer, I., Hilton, H., Keren, L. & Jojic, V. (2020), ‘Modeling multiplexed images with spatial-lda reveals novel tissue microenvironments’, Journal of Computational Biology 27(8), 1204–1218.
- Chung (1997) Chung, F. R. (1997), Spectral graph theory, Vol. 92, American Mathematical Soc.
- Dey et al. (2017) Dey, K. K., Hsiao, C. J. & Stephens, M. (2017), ‘Visualizing the structure of rna-seq expression data using grade of membership models’, PLoS genetics 13(3), e1006599.
- Donoho & Stodden (2003) Donoho, D. & Stodden, V. (2003), ‘When does non-negative matrix factorization give a correct decomposition into parts?’, Advances in neural information processing systems 16.
- Feng & Lapata (2010) Feng, Y. & Lapata, M. (2010), Topic models for image annotation and text illustration, in ‘Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the ACL’, Association for Computational Linguistics, pp. 831–839.
- Fukuyama et al. (2023) Fukuyama, J., Sankaran, K. & Symul, L. (2023), ‘Multiscale analysis of count data through topic alignment’, Biostatistics 24(4), 1045–1065.
- Gillis & Vavasis (2015) Gillis, N. & Vavasis, S. A. (2015), ‘Semidefinite programming based preconditioning for more robust near-separable nonnegative matrix factorization’, SIAM Journal on Optimization 25(1), 677–698.
- Giraud (2021) Giraud, C. (2021), Introduction to high-dimensional statistics, Chapman and Hall/CRC.
- Goltsev et al. (2018) Goltsev, Y., Samusik, N., Kennedy-Darling, J., Bhate, S., Hale, M., Vazquez, G., Black, S. & Nolan, G. P. (2018), ‘Deep profiling of mouse splenic architecture with codex multiplexed imaging’, Cell 174(4), 968–981.
- Hütter & Rigollet (2016) Hütter, J.-C. & Rigollet, P. (2016), Optimal rates for total variation denoising, in ‘Conference on Learning Theory’, PMLR, pp. 1115–1146.
- Ke & Wang (2017) Ke, Z. T. & Wang, M. (2017), ‘A new svd approach to optimal topic estimation’, arXiv preprint arXiv:1704.07016 2(4), 6.
- Kho et al. (2017) Kho, S. J., Yalamanchili, H. B., Raymer, M. L. & Sheth, A. P. (2017), A novel approach for classifying gene expression data using topic modeling, in ‘Proceedings of the 8th ACM international conference on bioinformatics, computational biology, and health informatics’, pp. 388–393.
- Klopp et al. (2021) Klopp, O., Panov, M., Sigalla, S. & Tsybakov, A. (2021), ‘Assigning topics to documents by successive projections’.
- Liu et al. (2016) Liu, L., Tang, L., Dong, W., Yao, S. & Zhou, W. (2016), ‘An overview of topic modeling and its current applications in bioinformatics’, SpringerPlus 5, 1–22.
- Mcauliffe & Blei (2007) Mcauliffe, J. & Blei, D. (2007), ‘Supervised topic models’, Advances in neural information processing systems 20.
- Reder et al. (2021) Reder, G. K., Young, A., Altosaar, J., Rajniak, J., Elhadad, N., Fischbach, M. & Holmes, S. (2021), ‘Supervised topic modeling for predicting molecular substructure from mass spectrometry’, F1000Research 10, Chem–Inf.
- Roberts et al. (2014) Roberts, M. E., Stewart, B. M., Tingley, D., Lucas, C., Leder-Luis, J., Gadarian, S. K., Albertson, B. & Rand, D. G. (2014), ‘Structural topic models for open-ended survey responses’, American journal of political science 58(4), 1064–1082.
- Sankaran & Holmes (2019) Sankaran, K. & Holmes, S. P. (2019), ‘Latent variable modeling for the microbiome’, Biostatistics 20(4), 599–614.
- Shang & Zhou (2022) Shang, L. & Zhou, X. (2022), ‘Spatially aware dimension reduction for spatial transcriptomics’, Nature communications 13(1), 7203.
- Shao et al. (2009) Shao, Y., Zhou, Y., He, X., Cai, D. & Bao, H. (2009), Semi-supervised topic modeling for image annotation, in ‘Proceedings of the 17th ACM international conference on Multimedia’, pp. 521–524.
- Sun et al. (2021) Sun, D., Toh, K.-C. & Yuan, Y. (2021), ‘Convex clustering: Model, theoretical guarantee and efficient algorithm’, The Journal of Machine Learning Research 22(1), 427–458.
- Symul et al. (2023) Symul, L., Jeganathan, P., Costello, E. K., France, M., Bloom, S. M., Kwon, D. S., Ravel, J., Relman, D. A. & Holmes, S. (2023), ‘Sub-communities of the vaginal microbiota in pregnant and non-pregnant women’, Proceedings of the Royal Society B 290(2011), 20231461.
- Tibshirani & Taylor (2012) Tibshirani, R. J. & Taylor, J. (2012), ‘Degrees of freedom in lasso problems’.
- Tran et al. (2023) Tran, H., Liu, Y. & Donnat, C. (2023), ‘Sparse topic modeling via spectral decomposition and thresholding’, arXiv preprint arXiv:2310.06730 .
- Tu et al. (2016) Tu, N. A., Dinh, D.-L., Rasel, M. K. & Lee, Y.-K. (2016), ‘Topic modeling and improvement of image representation for large-scale image retrieval’, Information Sciences 366, 99–120.
- Van Der Hofstad (2024) Van Der Hofstad, R. (2024), Random graphs and complex networks, Vol. 54, Cambridge university press.
- Vershynin (2018) Vershynin, R. (2018), High-dimensional probability: An introduction with applications in data science, Vol. 47, Cambridge university press.
- Wedin (1972) Wedin, P.-Å. (1972), ‘Perturbation bounds in connection with singular value decomposition’, BIT Numerical Mathematics 12, 99–111.
- Wu et al. (2023) Wu, R., Zhang, L. & Tony Cai, T. (2023), ‘Sparse topic modeling: Computational efficiency, near-optimal algorithms, and statistical inference’, Journal of the American Statistical Association 118(543), 1849–1861.
-
Wu et al. (2022)
Wu, Z., Trevino, A. E., Wu, E., Swanson, K., Kim, H. J., D’Angio, H. B., Preska, R., Charville, G. W., Dalerba, P. D., Egloff, A. M., Uppaluri, R., Duvvuri, U., Mayer, A. T. & Zou, J. (2022), ‘Space-gm: geometric deep learning of disease-associated microenvironments from multiplex spatial protein profiles’, bioRxiv .
https://www.biorxiv.org/content/early/2022/05/13/2022.05.12.491707 - Yang et al. (2016) Yang, D., Ma, Z. & Buja, A. (2016), ‘Rate optimal denoising of simultaneously sparse and low rank matrices’, The Journal of Machine Learning Research 17(1), 3163–3189.
- Yang et al. (2019) Yang, J., Feng, X., Laine, A. F. & Angelini, E. D. (2019), ‘Characterizing alzheimer’s disease with image and genetic biomarkers using supervised topic models’, IEEE journal of biomedical and health informatics 24(4), 1180–1187.
- Zhang (2011) Zhang, X.-D. (2011), ‘The laplacian eigenvalues of graphs: a survey’, arXiv preprint arXiv:1111.2897 .
- Zheng et al. (2015) Zheng, Y., Zhang, Y.-J. & Larochelle, H. (2015), ‘A deep and autoregressive approach for topic modeling of multimodal data’, IEEE transactions on pattern analysis and machine intelligence 38(6), 1056–1069.