Graph Ordering: Towards the Optimal by Learning
Abstract.
Graph representation learning has achieved a remarkable success in many graph-based applications, such as node classification, link prediction, and community detection. These models are usually designed to preserve the vertex information at different granularity and reduce the problems in discrete space to some machine learning tasks in continuous space. However, regardless of the fruitful progress, for some kind of graph applications, such as graph compression and edge partition, it is very hard to reduce them to some graph representation learning tasks. Moreover, these problems are closely related to reformulating a global layout for a specific graph, which is an important NP-hard combinatorial optimization problem: graph ordering. In this paper, we propose to attack the graph ordering problem behind such applications by a novel learning approach. Distinguished from greedy algorithms based on predefined heuristics, we propose a neural network model: Deep Order Network (DON) to capture the hidden locality structure from partial vertex order sets. Supervised by sampled partial order, DON has the ability to infer unseen combinations. Furthermore, to alleviate the combinatorial explosion in the training space of DON and make the efficient partial vertex order sampling , we employ a reinforcement learning model: the Policy Network, to adjust the partial order sampling probabilities during the training phase of DON automatically. To this end, the Policy Network can improve the training efficiency and guide DON to evolve towards a more effective model automatically. The training of two networks is performed interactively and the whole framework is called DON-RL. Comprehensive experiments on both synthetic and real data validate that DON-RL outperforms the current state-of-the-art heuristic algorithm consistently. Two case studies on graph compression and edge partitioning demonstrate the potential power of DON-RL in real applications.
1. Introduction
Graphs have been widely used to model complex relations among data, and have been used to support many large real applications including social networks, biological networks, citation networks and road networks. In the literature, in addition to the graph algorithms and graph processing systems designed and developed, graph representation learning have also been studied recently (DBLP:conf/www/AhmedSNJS13, ; DBLP:conf/nips/BelkinN01, ; fu2012graph, ; DBLP:conf/kdd/PerozziAS14, ; DBLP:conf/kdd/GroverL16, ; DBLP:conf/www/TangQWZYM15, ; DBLP:conf/www/TsitsulinMKM18, ; DBLP:conf/kdd/ZhangCWPY018, ; DBLP:conf/aaai/WangCWP0Y17, ; DBLP:conf/icde/FengCKLLC18, ; DBLP:conf/icde/HuAMH16, ; DBLP:conf/ijcai/ManSLJC16, ). They are designed to preserve vertex information at different granularity from microscopic neighborhood structure to macroscopic community structure, and are effectively used for node classification, link prediction, influence diffusion prediction, anomaly detection, network alignment, and recommendation. The surveys can be found in (cui2018survey, ; DBLP:journals/debu/HamiltonYL17, ).


Matrix Visualization for the Reordered Facebook
In this paper, we concentrate ourselves on a rather different set of graph problems: graph visualization (DBLP:journals/cgf/BehrischBRSF16, ), graph compression (KangF11, ), graph edge partitioning (DBLP:conf/kdd/BourseLV14, ; DBLP:conf/kdd/ZhangWLTL17, ). Here, graph visualization is to provide an effective way to visualize complex data, graph compression is to find a compact edge layout, and graph edge partitioning is to partition edges instead of vertices for better load balancing (graphlab, ; DBLP:conf/osdi/GonzalezXDCFS14, ). Such problems can be addressed if we can arrange all vertices in a good order. The-state-of-art graph ordering (DBLP:conf/sigmod/WeiYLL16, ) reassigns every vertex a unique number in where is the number of vertices in the graph by maximizing a cumulated locality score function for vertices in a sliding window of size , which is an NP-hard combinatorial optimization problem as a general form of the maximum Travel Salesman Problem (TSP) (). The GO algorithm proposed in (DBLP:conf/sigmod/WeiYLL16, ) achieves -approximation, and its real performance is very close to the optimal in their testing, as it is close to the upper bound of the optimal solution.
Given such a high-quality solution for graph ordering, a natural question is if we can do better by learning. The answer is yes. We demonstrate it in Fig. 1(b), which shows the matrix visualization for the Facebook (snapnets, ) reordered by the GO algorithm and our new learning-based approach over graph. The left figures are the overall visualizations and the right are the zoom-in details of the upper-left part of the overall ordering. Comparing with the GO algorithm (DBLP:conf/sigmod/WeiYLL16, ) (Fig. 1(a)), our learning-based approach (Fig. 1(b)) keeps the compact permutation better from the local perspective, and has the advantage of avoiding stucking in forming local dense areas from the global perspective. Moreover, the learned permutation has a large potential to support other real applications. Based on our case studies, the learned permutation reduces the storage costs larger than compared with the order for real-graph compression (KangF11, ). And the edge partitioning deriving from our approach outperforms the widely-used partitioning algorithm (DBLP:conf/kdd/BourseLV14, ) up to 37%.
The main contributions of this paper are summarized below.
-
•
For the graph ordering problem, distinguished from the traditional heuristics-based algorithm, we propose a neural network based model: Deep Order Network (DON) to replace the predefined evaluation function to capture the complex implicit locality in graphs. Hence our proposed model can produce a better graph ordering than the current state-of-the-art heuristics-based algorithm.
-
•
To address the combinatorial explosion in the training space of DON, we exploit the idea of reinforcement learning and construct a policy network to learn the sampling probability of vertices. This policy network enables DON to focus on vertices which have more remarkable contribution in the solution and guides DON to evolve towards a more effective model automatically. The whole learning framework is called DON-RL.
-
•
We conduct extensive experiments on both synthetic and real-world graphs with different properties. Experimental results show that DON-RL consistently outperforms the other algorithms. Furthermore, we conduct two case studies: graph compression and graph edge partitioning to demonstrate the potential value of our algorithm in real applications.
The paper is organized as follows. Section 2 introduces the preliminaries, including the problem definition, the intuitions and challenges. Section 3 gives an overview of our learning framework, which is composed of a central network for ordering and an auxiliary Policy Network. The design principles of these two neural networks are introduced in Section 4 and Section 5, respectively. Section 6 presents the experimental result of our approach in solving the graph ordering problem. We review the related works in Section 7. Finally, we conclude our approach in Section 8.
| Notations | Definitions |
|---|---|
| directed graph with the vertex set , the edge set . | |
| The pair-wise similarity function of vertex and . | |
| The locality score function of a permutation . | |
| The given window size. | |
| Deep Order Network (DON). | |
| Policy Network. | |
| () | The vertices sampling probability (at time ). |
| () | The tuning action of vertices sampling probability (at time ). |
| The training data at time t / The evaluation data. |


2. Preliminaries
In this section, first, the graph ordering problem and its existing solution are introduced. Then, we elaborate on our intuitive improvement and the challenges.
2.1. Graph Ordering
Given a graph where is a set of vertices and is a set of edges of , the graph ordering problem is to find the optimal order for all vertices. In brief, let be a permutation function which assigns a vertex a unique number in where . The problem is to find the optimal graph ordering by maximizing a cumulated locality score (Eq. (1)) over a sliding window of size .
| (1) |
Here, , are two vertices ordered within a window of size in the permutation, and is a pair-wise similarity function to measure the closeness of and . In (DBLP:conf/sigmod/WeiYLL16, ), is defined as , where is the number of times that and are sibling, and is the number of times that and are neighbors.
Example 2.1.
Taking the directed graph shown in Fig. 2(a) as an example, there are 12 nodes numbered from 1 to 12, which is considered as one possible graph ordering. Table 2 lists the pair-wise values, in a matrix form for vertices in Fig. 2(a) due to limited space. Given a window size , consider a partial permutation of length 3, for the vertices in Fig. 2(a), its locality score . Fig. 2(b) shows the optimal graph ordering which maximizes given the window size .
| 1 | 2 | 3 | 4 | 5 | |
| 1 | - | 2 | 0 | 1 | 1 |
| 2 | 2 | - | 0 | 1 | 1 |
| 3 | 0 | 0 | - | 0 | 0 |
| 4 | 1 | 1 | 0 | - | 1 |
| 5 | 1 | 1 | 0 | 1 | - |
In general, maximizing is a variant of maximum TSP (for ) with the sum of weights within a window of size and thus is NP-hard as proven in (DBLP:conf/sigmod/WeiYLL16, ).
Wei et al. in (DBLP:conf/sigmod/WeiYLL16, ) proposed a greedy algorithm (named GO), as sketched in Algorithm 1, which iteratively extends a partial solution by a vertex . The vertex is selected by maximizing a potential function , which measures the quality of the partial solution extended by a vertex , based on the current partial solution .
In details, in -th iteration, it computes the cumulated weight (Eq.2) for each vertex and inserts the one with maximum in the permutation:
| (2) |
where serves as the potential function , are the last inserted vertices. This procedure repeats until all the vertices in are placed. The total time complexity of GO is , where denotes the maximum in-degree of the graph . There are iterations, and in each iteration, it scans the remaining vertices in and computes the score for the scanned vertex in . The algorithm achieves -approximation for maximizing . It can achieve high-quality approximations with small window size and its practical performance is close to the optimal in the experiments.
2.2. Intuitions and Challenges
Intuitions: Given the current greedy-based framework, Algorithm 1 can be regarded as a discrete Markov Decision Process (MDP) (DBLP:books/lib/SuttonB98, ) , where the states are feasible partial permutations, actions are to insert one vertex to the permutations. For traditional greedy algorithm with predefined heuristics, the solution is built by a deterministic trajectory which has locally optimal reward. With regards to the graph ordering problem, (Eq. (3)) is simply approximated by the evaluation function , which is specifically defined in Eq. (2). A natural question arises that can we do better by learning an expressive, parameterized instead.
Inspired by universal approximation theorem (csaji2001approximation, ), deep reinforcement learning (DRL) learns a policy from states to actions that specifies what action to take in each state. We can formulate Algorithm 1 as MDP, which is composed by a tuple : 1) is a set of possible states, 2) is a set of possible actions, 3) is the distribution of reward given state-action pair. 4) is the transition probability given pair. 5) is the reward discount factor. The policy is a function : that specifies what action to perform in each state.
The objective of RL is to find the optimal policy which maximizes the expected cumulative discounted reward. This cumulative discounted reward can be defined by the Bellman Equation as below for all states recursively:
| (3) |
where and are the maximum expected cumulative rewards achievable from the state-action pair and the previous state-action pair , respectively. To avoid exhaustively exploring the MDP, Monte Carlo simulation is used to sample the state-action trajectory to estimate the values of downstreaming state-action pairs. In this vein, DRL is adopted to solve the combinational optimization problem (DBLP:journals/corr/BelloPLNB16, ; DBLP:conf/nips/KhalilDZDS17, ), whose policy is learned by specific deep neural networks.

Challenges: Recently, these RL-based approaches (DBLP:journals/corr/BelloPLNB16, ; DBLP:conf/nips/KhalilDZDS17, ) have surpassed traditional greedy strategies on finding better feasible solutions. However, in practice, the pure RL framework is inefficient as the discrete action space becomes large. This drawbacks obstacles RL-base approaches to solve the graph ordering problem over a single large real-world graph. Concretely, RL algorithms use Thompson Sampling (DBLP:conf/icml/GopalanMM14, ) to explore trajectories and estimate the expected cumulative reward (Eq. (3)). The larger the action space is, the lower probability trajectories with high accumulated reward can be sampled in limited steps. The low-quality samples will extremely degrade the effectiveness of the model as well as the convergence in the training phase. Therefore, (DBLP:journals/corr/BelloPLNB16, ; DBLP:conf/nips/KhalilDZDS17, ) can only support training on graphs with tens to one hundred of vertices, where their optimal solutions are provided by state-of-the-art integer programming solvers (cplex201412, ; applegate2006concorde, ). Recall that AlphaGo (DBLP:journals/nature/SilverHMGSDSAPL16, ) has actions at most, which in fact is an enormously large action space requiring high computation power of a large cluster to explore. Unfortunately, due to the combinatorial explosion in the training space of , any real large graph has a larger searching space than that of AlphaGo.
In a nutshell, the construction of the parametric model and the efficient training in an exponential training space are two main challenges when we try to adopt the model-based framework to solve the graph ordering problem.
3. A New Approach: DON-RL
In order to address the challenges mentioned in Section 2.2, we propose a new framework: Deep Ordering Network with Reinforcement Learning (DON-RL) to capture the complex combinatorial structures of a single large graph in solving the graph ordering problem. To make the better approximation of the evaluation function , we propose a new model: Deep Order Network (DON) which take the partial vertex order set as input and predict the next vertex which can maximize the cumulated locality score. Furthermore, to prune the exponential training space and improve the training of DON efficiency, we employ a policy gradient RL model: the Policy Network to explore the valuable vertex order segments efficiently. Fig. 3 demonstrates the overall learning framework.
Deep Order Network: As a parametric permutation-invariant model of the evaluation function (Algorithm 1), DON takes a partial vertex order solution, i.e., a set of vertices as input, and outputs the probability distribution of the decision of next vertex to be selected. In other words, DON is to learn a parameterized function by exploiting vertex sets over the whole graph , where every set encodes the contribution of vertices in the set for constructing if they coexist in a window of size . DON is trained by supervised learning over partial solutions. Here, a partial solution is a set of vertices for a window of size by first sampling vertices from followed by computing the likelihood of th e last vertex to be in the window. The last vertex to be added for a partial solution is by the ground truth of value, which is easy to be calculated when is small.
Since the function has the property of permutation invariant regarding any permutation of the vertices in , we employ a permutation invariant neural network architecture to model it. We present the design and principle of our Deep Order Network in Section 4 in details.
RL-based Training: In practice, the space of the all possible partial vertex order solution is exponential with respect to the number of vertices of a graph. Theoretically, a neural network can memorize and serve as an oracle for any query solution. However, it is intractable to enumerate all the partial solutions in training DON. Hence, sampling the high-quality partial solutions, i.e., sets of vertices, is vital to train DON model with high generalization ability which can inference unseen vertex combinations rather than memorization.
In other words, DON should have the ability to inference unseen vertex combinations rather than memorization. Hence, sampling the high-quality partial solutions, i.e., sets of vertices, is vital for the training of DON.
Rather than specifying the sampling probability uniformly or by human experience, we employ Policy Network to explore how to make adjustments on the probability, based on the evaluation result of DON dynamically. In this vein, we regard DON as an environment and the Policy Network is an agent which obtains rewards from the environment and predicts an adjusting action. The sampler of vertex sets adopts the adjusted sampling probability (i.e., the state transformed from adjusting action of the Policy Network), to sample the training data for next time slot and feeds these data to DON. After DON is trained for a certain number of iterations, the evaluation result of DON is received by the Policy Network as the rewards for updating its weights, as well as subsequent prediction. The training of the two networks is performed interactively as shown in Fig. 3.
The significance of using an RL framework to control the input pipeline is two folds. First, it improves the training efficiency by a self-adaptive sampling scheme. Second, it guides DON to evolve towards a more effective model automatically.
In contrast to applying RL to solve the problem directly, using RL to make decisions on the sampling probability adjustment is feasible. On one hand, in practice, the action space of this probability adjustment task is smaller than that of directly attacking the whole problem. Since a main property of real-world graph is scale-free, we find that among the vertices there exists skewness regarding the significance to build high-quality solutions so that the pattern of rising up and pushing down vertex sampling probability is not diverse. On the other hand, in DON-RL framework, RL only serves as an auxiliary model to improve the training effectiveness and efficiency of DON, instead of estimating directly. Thus, the effectiveness of DON is less sensitive to low-quality state-action trajectories. Section 5 introduces the RL formulation and our algorithm in details.
4. Deep Order Network
In this section, we propose the model Deep Order Network (DON) as a parameterized evaluation function to replace the evaluation function in Algorithm 1. Concretely, takes a vectorized representation of partial solution of vertices as input, and outputs a vector where represents the likelihood of inserting a vertex to the permutation, given the current partial solution . And being learned will replace seamlessly in Algorithm 1 to generate a solution.
To learn , we learn a vertex representation with the preservation of quality of the partial solutions, i.e., partial permutations which are composed by any subsets of vertices of size . For a given graph, this representation encodes the hidden optimality structure of vertices in within a window. Intuitively, vertices with a higher value tend to cluster in the vector space, whereas vertices with a lower value are kept away. A high-quality feasible solution can be constructed by set expansion towards a high value in the vector space. It is worth mentioning that, for a partial permutation within a window, the locality score function should permutation invariant with respect to . Therefore, the learned evaluation function is permutation invariant with any permutation of the elements in .
Property 1.
(DBLP:conf/nips/ZaheerKRPSS17, ) A function of sets , is permutation invariant, i.e., for any set with any permutation of the elements in , .
DeepSets (DBLP:conf/nips/ZaheerKRPSS17, ) is a neural network architecture to model the permutation invariant function defined on sets. For a set x whose domain is the power set of a countable set, any valid, i.e., permutation invariant function can be represented in the form of Eq. (4), for two suitable functions and .
| (4) |
In Eq. (4), is the -th element in the set , , and . Intuitively, generates the element-wise representation for each , and is a pooling function which performs a generalization of classic aggregation functions, e.g., , and on the set. The added-up representation is processed by in the same manner as any neural network. In our problem, the domain of partial solutions is the combinations of with size , where is the vertex set. The evaluation function for any such can be learned by parameterizing the two functions ( and ) with a specified pooling function .
We measure the output of by a distribution , where is the -th element of , meaning how probable the -th vertex can be added into the current partial solution . With the Bayes rule, this probability is in Eq. (5).
| (5) |
In Eq. (5), is the marginal probability of the extended solution, which can be estimated by computing score of the partial permutation explicitly.
| (6) |
Additionally, we use the normalized values (Eq. (6)) to make training more stable. As shown in Fig. 3, a training instance is constructed by sampling a partial solution with vertices as input feature, then (Eq. (6)) serves as the soft label for training. We use the cross entropy as the training loss, as given in Eq. (7). Here, is the prediction of DON.
| (7) |
To model , batches of partial solutions are fed into DON, where a partial solution is generated by sampling vertices over by a probability distribution without replacement.


5. RL-based Training
In this section, we discuss how we adjust the sampling probability adaptively. As shown in Section 4, the feasible input of is all possible combinations of the vertices with size , which indicates that it is intractable to enumerate all the partial solutions in training DON. To alleviate the combinatorial explosion issue, we can employ the sampling strategy in the training space to reduce the candidate partial solutions.
By intuition, high-degree vertices sharing many common neighbors play a significant role in constructing high-quality feasible solutions. However, since the graph ordering is a discrete optimization problem, the significance of a discrete element that contributes to a solution can be very different from others, and there exists skewness regarding such significance among all elements.
To validate this claim, we report the permutation results of two real graphs: Wiki-vote (snapnets, ) and Air Traffic (konect, ) in Fig. 4. Here, the horizontal axis is the linear graph ordering. In vertical, we show the score, the increment of , and the degree of the vertex from top to bottom in three subfigures, respectively. As shown in Fig. 4 we can observe that the patterns of the two solutions are very different. For Wiki-vote, over vertices in the ordering almost make no contribution to enlarging the score, while it is not the case for Air Traffic, as vertex adding into the permutation, the score increases continuously. Interestingly, it is counterintuitive that the high-degree vertices do not always make a significant contribution to increasing the score.
This result inspires us that what if adjusting the sampling probability dynamically during the training phase. This further motives us to use RL framework to tune sampling probability. Therefore, we model the tuning sampling probability in an MDP as follows:
States: a state is a vector of sampling probability , where is the number of vertices. is the probability of sampling vertex for one training instance and is normalized, i.e., . It is worth mentioning that the initialization of cannot be random. What the Policy Network does is to adjust the experienced-based slightly instead of learning it directly without any bias, which is extremely difficult for on-policy RL in an online fashion.
Actions: an action is a vector of 0-1, . Each element denotes a tuning action imposed on , i.e., increase (0) or decrease (1). There is a tuning rate to control the constant delta changes of each element for a given . The adjustment is specified in Eq. (8). The final step of an adjustment is the normalization of .
| (8) |
Transition: given the state-action pair at time , the transition to next state , is deterministic.
Reward: the reward reflects the benefits of updating a state by an action at time . We use the evaluation results (e.g., root mean square error, cross entropy, etc.) of DON trained on the training data generated by updating as . To avoid the over-fitting of DON, instead of sampling the evaluation set according to directly, we adopt the fixed degree sampler, i.e., the initial to sample the first vertex and generate the optimal partial solution with window size . The evaluation is performed on a selected evaluation set, , after training DON a certain number of steps. The cumulative reward is computed by adding future reward discounted by a discounting factor .
Policy: A policy function specifies a tuning operation to perform on a given state . Here we employ a parametric function with parameter to analog output of the policy. This model can be any any multi-label classification model (DBLP:journals/jdwm/TsoumakasK07, ), e.g., multilayer perceptron (MLP), which takes as input and outputs the probability of an action . We use to denote the output probability at time . To distinguish from DON , we use to denote the Policy Network.
5.1. Train Tuning Policy
To find the optimal policy, there are two kinds of RL algorithms (DBLP:books/lib/SuttonB98, ). One is value-based, e.g., Q-learning, which learns the optimal state-action values in Eq. (3) and the corresponding optimal policy is to take the best action in any state. The other is policy-based, which learns the optimal policy directly from a collection of policies. Since the policy-based RL algorithm is more suitable for high dimensional action space and has better convergence properties, we use a model-free, policy-based RL algorithm to train the Policy Network directly. The objective is to find the optimal policy by maximizing the following expected accumulated and discounted rewards of Eq (9), which is estimated by sampling state-action trajectory of steps.
| (9) |
The gradient of the Eq. (9) is formulated using the algorithm (DBLP:journals/ml/Williams92, ) as given in Eq. (10).
| (10) |
Here, as the raw reward of a trajectory, , is always positive, a baseline function is introduced to reduce the variance of the gradients. The formula indicates whether a reward is better or worse than the expected value we should get from state . For the baseline function , we adopt the widely-used moving average of the historical rewards, i.e., the evaluation result of DON.
The training algorithm of the Policy Network is given in Algorithm 2. It takes a graph , an initial and experience-based sampling probability , the evaluation set , and the learning rate of RL as input, and trains Policy Network by interacting with the training process of Deep Order Network . The intuition is if the reward of an action is positive, it indicates the action is good and the gradients should be applied to make the action even more likely to be chosen in the future. However, if the reward is negative, it indicates the action is bad and the opposite gradients should be applied to make this action less likely in the future.
We briefly explain the algorithm below. First, Policy Network is initialized (line 2). The training of policy gradient starts at line 3. Before that, the training of DON has started several steps to collect enough evaluation results for computing the baseline. In each RL step, the algorithm updates once by one Monte Carlo sampling of a trajectory of length (line 4). For each time , it repeats the following 4 steps one by one. First, draw a random action based on the probability output by Policy Network, i.e., (line 5). Instead of directly choosing the action with the highest probability, the random action manages a balance between exploring new actions and exploiting the actions which are learned to work well. Second, apply the action on the state by imposing an increment/decrement of (line 6), to generate the next state . Third, generate the training data set of DON by sampling with probability , and feed to train (line 7). Fourth, after training in a certain number of steps, we use the evaluation set to evaluate DON, and collect the evaluation result as reward (line 8). When a trajectory is simulated, we compute the cumulative rewards (line 11) and apply gradient ascent to update the Policy Network (line 12).
6. Experimental Studies
In this section, we present our experimental evaluations. First, we give the specific setting of the testing including datasets, settings of the models and training. Then, we compare the proposed model: DON-RL with the state-of-the-art algorithmic heuristic, conduct an A/B testing to validate the effect of Policy Network, and observe the performance of models as varies. Finally, two case studies of compressing graph and deriving a competitive edge partitioning from model-based ordering are presented.
6.1. Experimental Setup
| Graphs | Density | Description | ||
| Wiki-vote (snapnets, ) | 7,115 | 103,689 | vote graph | |
| Facebook (snapnets, ) | 4,039 | 88,234 | social graph | |
| p2p (snapnets, ) | 6,301 | 20,777 | file sharing graph | |
| Arxiv-HEP (snapnets, ) | 9,877 | 25,998 | co-authorship graph | |
| Cora (konect, ) | 23,166 | 91,500 | citation graph | |
| PPI (snapnets, ) | 21,557 | 342,353 | biological graph | |
| PL10K_1.6 | 10,000 | 121,922 | power-law graph | |
| PL10K_1.8 | 10,000 | 58,934 | ||
| PL10K_2.0 | 10,000 | 31,894 | ||
| ER10K_0.02 | 10,000 | 1,000,337 | ER graph | |
| ER10K_0.05 | 10,000 | 2,498,836 | ||
| ER10K_0.1 | 10,000 | 5,004,331 |
Datasets: We use six real graphs collected from Stanford SNAP (snapnets, ) and KONECT (The Koblenz Network Collection) (konect, ): Wiki-vote is the Wikipedia adminship vote network. Facebook is the Facebook friendship network. p2p is a snapshot of the Gnutella peer-to-peer file sharing network. Arxiv-HEP is the Arxiv collaboration network between authors in the field of High Energy Physics. Cora is the cora scientific paper citation network. PPI is a protein-protein interaction network where vertices represent human proteins and edges represents physical interactions between proteins.
In addition, to validate the performance of our models on graphs with different structures explicitly, we generate six synthetic graphs by SNAP random graph generator: power-law and Erdös-Rényi. For power-law, we choose three power-law distributions with shape parameter {1.6, 1.8, 2.0} and adopt Newman’s method (newman2001random, ) to generate three power-law graphs: PL10K_1.6, PL10K_1.8 and PL10K_2.0. For Erdös-Rényi, we utilize the parameter which indicates the probability of edge existence between two vertices to generate three synthetic graphs with different densities, that are, ER10K_0.02,ER10K_0.05 and ER10K_0.1. All synthetic graphs have 10,000 vertices. Table 3 summarizes the information of these real and synthetic graphs.
Reduce the Sampling Classes: Recall that DON takes a vertices set sampled from as input to predict the likelihood of appending each vertex to the permutation. Based on the RL-based sampling probability tuning approach we have explored, we can further reduce the sampling classes by a simple but effective strategy. The reduction is based on the automorphism of vertices on the trig of the graph. We use an example in Fig. 5 to illustrate this reduction. In Fig. 5(a), vertices , and have a common in-neighbor , which is also their only neighbor. For , we have and the value is for all the other vertices. , and are automorphism so that permuting them can be regarded as permuting one vertex three times, where and is 0 for the other vertices. In other words, if three positions for the three vertices are targeted in the permutation, the value will be equivalent for all the assignments of . In this vein, we merge , and to one vertex as shown in Fig. 5(b). Sampling vertex sets and inference to generate permutation can be directly conducted on the merged graph (Fig. 5(b)). Each time the model selects to extend the permutation, we insert a vertex randomly drawn from , , . For real-world graph, due to its power-low degree distribution, our experiments show this preprocessing can reduce about 9% vertices on average.
Model settings: In DON, both the and networks are two-layer MLP. We use the as the pooling layer to add up the representations of and the output is further processed by . The input of is an identity vector representation, , of a partial solution with size and the output is a probability distribution generated by a softmax function. All the hidden units are activated by ReLU function .
The Policy Network is a multi-label classifier of two-layers MLP. The input is the state and the output layer predicts the probability to perform action , i.e., a vector by sigmoid activation. Similar to DON, the hidden units are activated by ReLU function.
| Hyper-parameters | Values | |
|---|---|---|
| DON | learning rate | |
| mini-batch size | 64 512 | |
| # hidden units | 32, 64, 128, 256 | |
| global steps | ||
| Policy Network | learning rate | |
| trajectory length | 1 10 | |
| RL steps | 50 300 | |
| discounting factor | 0.9, 0.95 | |
| tuning rate | ||
| # hidden units | 32, 64, 128, 256 | |
| # evaluation set | 2000, 5000 | |
Implementation and training: The learning framework is built on Tensorflow (DBLP:conf/osdi/AbadiBCCDDDGIIK16, ) 1.8 with Python 2.7. We use Adam (DBLP:journals/corr/KingmaB14, ) and RMSProp optimizer to train DON and the Policy Network, respectively, which are trained interactively as shown in Algorithm 2.
Table 4 shows the hyper-parameters settings in the training. The models are learned with these parameters tuned in the corresponding experienced range. In Table 4, the global steps and RL steps are the numbers of parameter updating of DON and the Policy Network, respectively. For one RL step, a trajectory of length DON training is conducted. To this end, (global steps) / (RL steps ) DON steps are trained in one timestamp. For computing the rewards, we use the Root Mean Square Error (RMSE) as the evaluation metric of the evaluation set. The reward is defined as the opposite number of RMSE. We use the best neighbor heuristic to generate the evaluation set by randomly choose the first vertex with initial , the degree distribution. A bare DON is trained by setting sampling probability as . In this section, we use DON and DON-RL to denote the bare DON model and DON with Policy Network respectively.
| GO | DON | DON-RL | ||
| Wiki-vote | 5,880 | 145,736 | 156,871 | 157,669 |
| 3,974 | 230,031 | 207,511 | 234,151 | |
| p2p | 5,624 | 20,472 | 21,422 | 22,086 |
| Arxiv-HEP | 9,877 | 85,958 | 90,629 | 91,001 |
| Cora | 22,317 | 98,334 | 101,063 | 100,966 |
| PPI | 19,041 | 383,343 | 347,237 | 404,728 |
| PL10K_1.6 | 8,882 | 166,540 | 190,021 | 197,622 |
| PL10K_1.8 | 8,292 | 66,272 | 86,840 | 89,930 |
| PL10K_2.0 | 8,484 | 29,373 | 37,332 | 38,071 |
| ER10K_0.02 | 10,000 | 136,925 | 145,084 | 162,462 |
| ER10K_0.05 | 10,000 | 615,706 | 673,357 | 724,743 |
| ER10K_0.1 | 10,000 | 2,319,250 | 2,554,032 | 2,647,686 |











6.2. Result of Graph Ordering
Table 5 shows the overall results of the score of the permutations generated by DON, compared with the baseline graph ordering algorithm GO (DBLP:conf/sigmod/WeiYLL16, ). As a preprocessing step, vertices on the trig of the graph, i.e., vertex whose degree is 1 are merged to one equivalent vertex as shown in Fig. 5. In Table 5, the column is the compacted vertex number of the graph. We can see that this trick compresses up to 17% vertices for real and power-low graphs but it is invalid for three Erdös-Rényi graphs due to their degree distribution. With regards to maximize , the solutions of DON and DON-RL surpass that of the greedy algorithm significantly. For the real graphs, all the solutions of DON-RL outperform that of GO from 1.8% up to 8.2%. And the solution of DON, on the 3 reals graphs, Wiki-Vote, p2p and Cora, the improvements of are 7.6%, 4.7% and 2.8%, respectively. For the synthetic graphs, both the DON and DON-RL can generate solutions of much higher score than GO. The DON-RL performs best and its solutions surpass that of GO up to 35.0% for powerlaw graph, and 18.6% for ER graph. As the matrix visualization results shown in Fig. 1(b), the model-based approach DON-RL focuses on the overall performance and can optimize the permutation of the sub-significant vertices. The greedy heuristic is powerful for ordering the top significant vertices while for the sub-significant vertices, it fails to capture the global information as ordering them w.r.t. the common neighbor relations. It is easy for GO to stuck in forming local dense areas while incurring sparsity in the global scope. This phenomenon agrees with our intuition, that is, the greedy algorithm could neglect better solutions in the future scope.
6.3. Adaptive Training by RL
In order to validate the effectiveness of the Policy Network, we perform A/B test to observe the effect of RL-based adaptive training, i.e, using the same hyper-parameters to train a DON model and a conjuncted DON-RL model. During the overall training process, we generate a solution after per 10% global training steps of DON ends. We directly observe the changes of objective function as the loss function of the model is not a direct reflection of the objection of this NP-hard problem. Fig. 6 presents the results over the 12 graphs in Table 3.
We observe that the performance of DON and DON-RL are different among different graphs during training. In general, imposing RL on the sampling probability adjustment improves the performance of DON in most cases. As shown in Fig. 6(a), 6(c), 6(e)-6(g) and 6(j)-6(l), DON-RL can achieve better results than DON in graphs with high density since the locality of vertices is significantly skew on the graph. On the other hand, for the graph with low density and flat degree distribution, such as Cora (Fig. 6(d)) and p2p (Fig. 6(b)), using RL does not make significant improvement during the training. We conjecture, in this scenario, the potential action space is relatively large so that it is difficult for RL algorithm to find an action trajectory with high reward, especially when the locality has been well captured by DON. In addition, due to the dynamic adjusting mechanism, DON-RL can make the training process robust and avoid over-fitting. As shown in Fig. 6(b) and 6(i), DON reaches its best effect much earlier than DON-RL then it goes worse as over-fitting. In contrast, DON-RL can rectify the over-fitting autonomously in Fig. 6(c) and 6(h). The performance of DON-RL increases constantly and surpasses DON in the end.

Therefore, the RL-based DON-RL is suitable for the graphs whose structures are highly skew. The results in Fig. 6 also confirms the effectiveness of the Policy Network in DON-RL.




6.4. Varying the Window Size
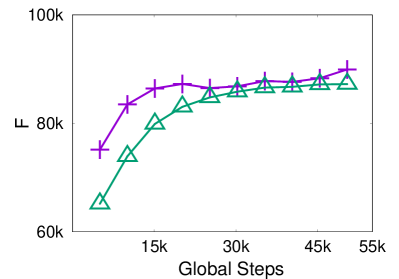
In this section, we investigate the effect of the window size in Eq. (1). Fig. 7 shows for graph PL10K_1.6, the scores of 5 models training with is set to . For these DON models, they perform stably better than GO as grows. In Fig. 7, DON-RL is the 5 models associated with RL training, which generates permutations of highest . Recall that the approximate ratio of GO is , which means theoretically, the larger the , the larger the gap between GO and the optimal solution, i.e., the improvement space of GO. Interestingly, in Fig 7, as grows, the increment of locality score of model-based approaches grow a little faster than that of GO. It implies that the model-based approaches can better take advantage of the gap to optimized the learned solution.
In addition, another interesting observation is that models trained with smaller have better performance than that of larger . It indicates that we can use pre-trained models with small to generate different permutations of larger .
6.5. Case Studies
In this section, we perform two case studies to demonstrate the power of DON-RL in solving real-world problems.
Graph Compression: First, we explore the potential of using DON-RL to deal with graph compression problem. Concretely, given a graph, we want to layout its edges so that its adjacency matrix is easy to be compressed. Formally, this problem is equivalent to find a vertex ordering to minimize the storage cost , where is the block width. Concretely, we divide the matrix into square matrix blocks and count the number of the nonempty block as (KangF11, ). Since is not comparable for different block size . Here we adopt a normalized version :
| (11) |
where is the number of blocks in . A good ordering for the compression should have low for given block size .
Fig. 8 demonstrates the compression cost on the 5 real graphs in Table 3, when the block wide is (Fig. 8(a)), (Fig. 8(b)) and (Fig. 8(c)). We compare the compression performance with two methods: Degree permutes the vertex based on the decreasing degree. SlashBurn (KangF11, ) is the graph ordering algorithm proposed for graph compression. We set for our method: DON-RL for all datasets. As shown in Fig. 8, DON-RL outperforms the other methods on three datasets (Wikivote, Facebook and Cora) and achieves comparable results on two datasets (p2p and PPI). For the number of nonempty blocks, DON-RL reduces the counts by and compared with the second best orderings on Facebook and Cora. Interestingly, Degree is a quite good heuristic ordering for the graph compression. It achieves the best performance on p2p and PPI. The results validate that our learned vertex order is a good potential criteria for graph compression.
Graph Edge Partitioning: The second application we investigate is graph edge partitioning, which can achieve better load balancing than traditional vertex partitioning for skew graph data in the parallel/distribution environment. The problem is, given a partition number , partitioning the edge set disjointly into balanced subsets , to minimize the replication factor (RF) of the vertices in partitions:
| (12) |
The problem is also NP-hardness (DBLP:conf/kdd/ZhangWLTL17, ). Since the graph ordering is based on vertex locality, we use the ordering result of DON-RL to generate an edge partitioning directly. The partition is conducted by assigning edges of adjacent vertices in the permutation to one partition under the balance constraint.
Fig 9 shows the partitioning derives from DON-RL with , and 5 other edge partitioning and graph ordering algorithms over Facebook. Here, Random (DBLP:conf/kdd/BourseLV14, ) assigns each edge independently and uniformly to k partitions. The Greedy (DBLP:conf/kdd/BourseLV14, ) heuristic preferentially assigns an edge to a partition already contains the two or one of its end vertices with trading off the balance. NE and SNE (DBLP:conf/kdd/ZhangWLTL17, ) are the state-of-the-art edge partitioning heuristic based on neighbor expansion. The replication factor of DON-RL is smaller than that of the widely used Greedy up to 37%. Also, as the number of partition increases, the replication factor of DON-RL increases much slower than Greedy and SlashBurn . It is interesting that a good partitioning derives from a high-quality ordering result.
7. Related Works
Graph Representation Learning is to learn an effective graph representation to encode sufficient features for downstream machine learning/deep learning tasks. Recently, graph representation learning have been extensively studied. The surveys can be found in (cui2018survey, ; DBLP:journals/debu/HamiltonYL17, ). The traditional graph representation learning, that uses matrix factorization to find a low-rank space for the adjacency matrix (DBLP:conf/www/AhmedSNJS13, ; DBLP:conf/nips/BelkinN01, ; fu2012graph, ), cannot be used to solve our problem, because they are designed to reconstruct the original graph. Structure preserving representation learning techniques can encode/decode graph structures and properties. DeepWalk (DBLP:conf/kdd/PerozziAS14, ) and Node2Vec (DBLP:conf/kdd/GroverL16, ) encode the neighborhood relationship by exploiting truncated random walks as embedding context. Furthermore, there are the graph representations to preserve vertex information at different granularity from microscopic neighborhood structure to macroscopic community structure. (DBLP:conf/www/TangQWZYM15, ; DBLP:conf/www/TsitsulinMKM18, ; DBLP:conf/kdd/ZhangCWPY018, ) carry high-order proximity and closeness measures, to provide flexible and diverse representations for unsupervised graph learning tasks. M-NMF (DBLP:conf/aaai/WangCWP0Y17, ) incorporates graph macroscopic proximity, the community affiliation of vertex. Such approaches are designed to machine learning tasks (e.g., node classification, link prediction, as well as recommendation). Unfortunately, these representations cannot be directly applied to our problem. First, these representations are learned by unsupervised fashion. Second, they do not contain abundant vertex features, the learned graph proximity is insufficient. Third, our problem aims to find an optimal combinatorial structure instead of performing inference on individual instances which only involves local information.
There are reported studies on representation learning over special graphs, such as representation of heterogeneous graphs (DBLP:conf/kdd/DongCS17, ), dynamic graphs (DBLP:journals/corr/abs-1803-04051, ), attributed graphs (DBLP:journals/corr/KipfW16, ). And there are specified graph machine learning applications that require specialized graph representation, for instance, influence diffusion prediction (DBLP:conf/icde/FengCKLLC18, ), anomaly detection (DBLP:conf/icde/HuAMH16, ), and network alignment (DBLP:conf/ijcai/ManSLJC16, ). These models are too specific to deal with our problem.
Neural Networks for Combinatorial Optimization: Early works that use neural network to construct solutions for NP-hard optimization problems are summarized in (DBLP:journals/informs/Smith99, ). Recently, deep learning has also been adopted to solve combinatorial optimization. A new attention-based sequence-to-sequence neural architecture, Pointer Network (NIPS2015_5866, ), is proposed and is used to solve the planar Travel Salesman Problem (TSP). Pointer Network learns the planar convex hull supervised by a set of problem instances and solutions alone, and then (DBLP:journals/corr/BelloPLNB16, ) uses reinforcement learning, the Actor-Critic algorithm (DBLP:conf/nips/KondaT99, ), to train Pointer Network. Instead of using given training instances, an actor network makes trials of tour and evaluates the trials using a critic network. To further improve the performance, (anonymous2019attention, ) proposes an alternative neural network which encodes input nodes with multi-head attention (DBLP:conf/nips/VaswaniSPUJGKP17, ). These approaches (NIPS2015_5866, ; DBLP:journals/corr/BelloPLNB16, ; anonymous2019attention, ) concentrate on 2D Euclidean space TSP, and it is non-trivial to extend them to deal with graphs. For graph data, Dai et. al. (DBLP:conf/nips/KhalilDZDS17, ) propose a framework to learn a greedy meta-algorithm over graphs. First, a graph is encoded by a graph embedding network. Second, the embedding is fed into some more layers to estimate an evaluation function. The overall network is trained by deep Q-learning (DBLP:journals/ml/Williams92, ) in an end-to-end fashion. The framework is demonstrated to solve Minimum Vertex Cover, Maximum Cut and TSP. These studies aim to generalize the process of problem-solving for a distribution of problem instances offline. A recent study provides a supervised learning approach to deal with NP problems equivalent to maximum independent set (MIS). It adopts graph convolutional network (GCN) (DBLP:journals/corr/KipfW16, ) to predict the likelihood whether each vertex is in the optimal solution (DBLP:conf/nips/LiCK18, ). Since it relies on the state-of-the-art MIS local search heuristics to refine the candidate solutions, the bare utility of the model needs to be further studied.
8. Conclusion
In this paper, we focus on an NP-hard problem, graph ordering, in a novel, machine learning-based perspective. Distinguished from recent research, the NP-hard problem is over an specific larger graph. We design a new model: Deep Order Network (DON) to learn the underlying combinatorial closeness over the vertices of graph, by sampling small vertex sets as locally partial solutions. To further improve the sampling effectiveness, we propose an adaptive training approach based on reinforcement learning, which automatically adjusts the sampling probabilities. Compare with the high-quality greedy algorithm, our overall model, DON-RL improves the quality of solution up to 7.6% and 35% for real graphs and synthetic graphs, respectively. Our study reveals that a simple neural network has the ability to deal with NP optimization problem by encoding hidden features of the combination structures. We will public our code and pre-trained models later.
References
- [1] KONECT (the koblenz network collection). http://konect.uni-koblenz.de.
- [2] M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, M. Kudlur, J. Levenberg, R. Monga, S. Moore, D. G. Murray, B. Steiner, P. A. Tucker, V. Vasudevan, P. Warden, M. Wicke, Y. Yu, and X. Zheng. Tensorflow: A system for large-scale machine learning. In Proc. of OSDI’16, 2016.
- [3] A. Ahmed, N. Shervashidze, S. M. Narayanamurthy, V. Josifovski, and A. J. Smola. Distributed large-scale natural graph factorization. In Proc. of WWW’13, 2013.
- [4] Anonymous. Attention, learn to solve routing problems! In Submitted to International Conference on Learning Representations, 2019.
- [5] D. Applegate, R. Bixby, V. Chvatal, and W. Cook. Concorde tsp solver, 2006.
- [6] M. Behrisch, B. Bach, N. H. Riche, T. Schreck, and J. Fekete. Matrix reordering methods for table and network visualization. Comput. Graph. Forum, 35(3), 2016.
- [7] M. Belkin and P. Niyogi. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Proc. of NIPS’01, 2001.
- [8] I. Bello, H. Pham, Q. V. Le, M. Norouzi, and S. Bengio. Neural combinatorial optimization with reinforcement learning. CoRR, abs/1611.09940, 2016.
- [9] F. Bourse, M. Lelarge, and M. Vojnovic. Balanced graph edge partition. In Proc. of KDD’14, 2014.
- [10] I. I. CPLEX. 12.6. CPLEX User?s Manual, 2014.
- [11] B. C. Csáji. Approximation with artificial neural networks. Faculty of Sciences, Etvs Lornd University, Hungary, 24:48, 2001.
- [12] P. Cui, X. Wang, J. Pei, and W. Zhu. A survey on network embedding. IEEE Trans. on Knowledge and Data Engineering, 2018.
- [13] Y. Dong, N. V. Chawla, and A. Swami. metapath2vec: Scalable representation learning for heterogeneous networks. In Proc. of KDD’17, 2017.
- [14] S. Feng, G. Cong, A. Khan, X. Li, Y. Liu, and Y. M. Chee. Inf2vec: Latent representation model for social influence embedding. In Proc. of ICDE’18, 2018.
- [15] Y. Fu and Y. Ma. Graph embedding for pattern analysis. Springer Science & Business Media, 2012.
- [16] J. E. Gonzalez, Y. Low, H. Gu, D. Bickson, and C. Guestrin. Powergraph: Distributed graph-parallel computation on natural graphs. In Proc. of OSDI’12, 2012.
- [17] J. E. Gonzalez, R. S. Xin, A. Dave, D. Crankshaw, M. J. Franklin, and I. Stoica. Graphx: Graph processing in a distributed dataflow framework. In Proc. of OSDI’14, 2014.
- [18] A. Gopalan, S. Mannor, and Y. Mansour. Thompson sampling for complex online problems. In Proc. of ICML’14, 2014.
- [19] A. Grover and J. Leskovec. node2vec: Scalable feature learning for networks. In Proc. of KDD’16, 2016.
- [20] W. L. Hamilton, R. Ying, and J. Leskovec. Representation learning on graphs: Methods and applications. IEEE Data Eng. Bull., 40(3), 2017.
- [21] R. Hu, C. C. Aggarwal, S. Ma, and J. Huai. An embedding approach to anomaly detection. In Proc. of ICDE’16, 2016.
- [22] U. Kang and C. Faloutsos. Beyond ’caveman communities’: Hubs and spokes for graph compression and mining. In Proc. of ICDM’11, 2011.
- [23] E. B. Khalil, H. Dai, Y. Zhang, B. Dilkina, and L. Song. Learning combinatorial optimization algorithms over graphs. In Proc. of NIPS’17, 2017.
- [24] D. P. Kingma and J. Ba. Adam: A method for stochastic optimization. In Proc. of ICLR’15, 2015.
- [25] T. N. Kipf and M. Welling. Semi-supervised classification with graph convolutional networks. CoRR, abs/1609.02907, 2016.
- [26] V. R. Konda and J. N. Tsitsiklis. Actor-critic algorithms. In Proc. of NIPS’99, 1999.
- [27] J. Leskovec and A. Krevl. SNAP Datasets: Stanford large network dataset collection. http://snap.stanford.edu/data, June 2014.
- [28] Z. Li, Q. Chen, and V. Koltun. Combinatorial optimization with graph convolutional networks and guided tree search. In Proc. of NeurIPS’18, 2018.
- [29] T. Man, H. Shen, S. Liu, X. Jin, and X. Cheng. Predict anchor links across social networks via an embedding approach. In Proc. of IJCAI’16, 2016.
- [30] M. E. Newman, S. H. Strogatz, and D. J. Watts. Random graphs with arbitrary degree distributions and their applications. Physical review E, 64(2):026118, 2001.
- [31] B. Perozzi, R. Al-Rfou, and S. Skiena. Deepwalk: online learning of social representations. In Proc. of KDD’14, 2014.
- [32] D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. van den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N. Kalchbrenner, I. Sutskever, T. P. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel, and D. Hassabis. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587), 2016.
- [33] K. A. Smith. Neural networks for combinatorial optimization: A review of more than a decade of research. INFORMS Journal on Computing, 11(1), 1999.
- [34] R. S. Sutton and A. G. Barto. Reinforcement learning - an introduction. Adaptive computation and machine learning. MIT Press, 1998.
- [35] J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, and Q. Mei. LINE: large-scale information network embedding. In Proc. of WWW’15, 2015.
- [36] R. Trivedi, M. Farajtabar, P. Biswal, and H. Zha. Representation learning over dynamic graphs. CoRR, abs/1803.04051, 2018.
- [37] A. Tsitsulin, D. Mottin, P. Karras, and E. Müller. VERSE: versatile graph embeddings from similarity measures. In Proc. of WWW’18, 2018.
- [38] G. Tsoumakas and I. Katakis. Multi-label classification: An overview. IJDWM, 3(3), 2007.
- [39] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin. Attention is all you need. In Proc. of NIPS’17, 2017.
- [40] O. Vinyals, M. Fortunato, and N. Jaitly. Pointer networks. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett, editors, Advances in Neural Information Processing Systems 28. 2015.
- [41] X. Wang, P. Cui, J. Wang, J. Pei, W. Zhu, and S. Yang. Community preserving network embedding. In Proc. of AAAI’17, 2017.
- [42] H. Wei, J. X. Yu, C. Lu, and X. Lin. Speedup graph processing by graph ordering. In Proc. of SIGMOD’16, 2016.
- [43] R. J. Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 8, 1992.
- [44] M. Zaheer, S. Kottur, S. Ravanbakhsh, B. Póczos, R. R. Salakhutdinov, and A. J. Smola. Deep sets. In Proc. of NIPS’17, 2017.
- [45] C. Zhang, F. Wei, Q. Liu, Z. G. Tang, and Z. Li. Graph edge partitioning via neighborhood heuristic. In Proc. of KDD’17, 2017.
- [46] Z. Zhang, P. Cui, X. Wang, J. Pei, X. Yao, and W. Zhu. Arbitrary-order proximity preserved network embedding. In Proc. of KDD’18, 2018.